A Bandwidth-Enhanced Differential LC-Voltage Controlled Oscillator (LC-VCO) and Superharmonic Coupled Quadrature VCO for K-Band Applications
Abstract
:1. Introduction
2. Design Consideration for Low PN and Wideband VCO
2.1. Technology Overview
2.2. Class-C
3. Circuit Description
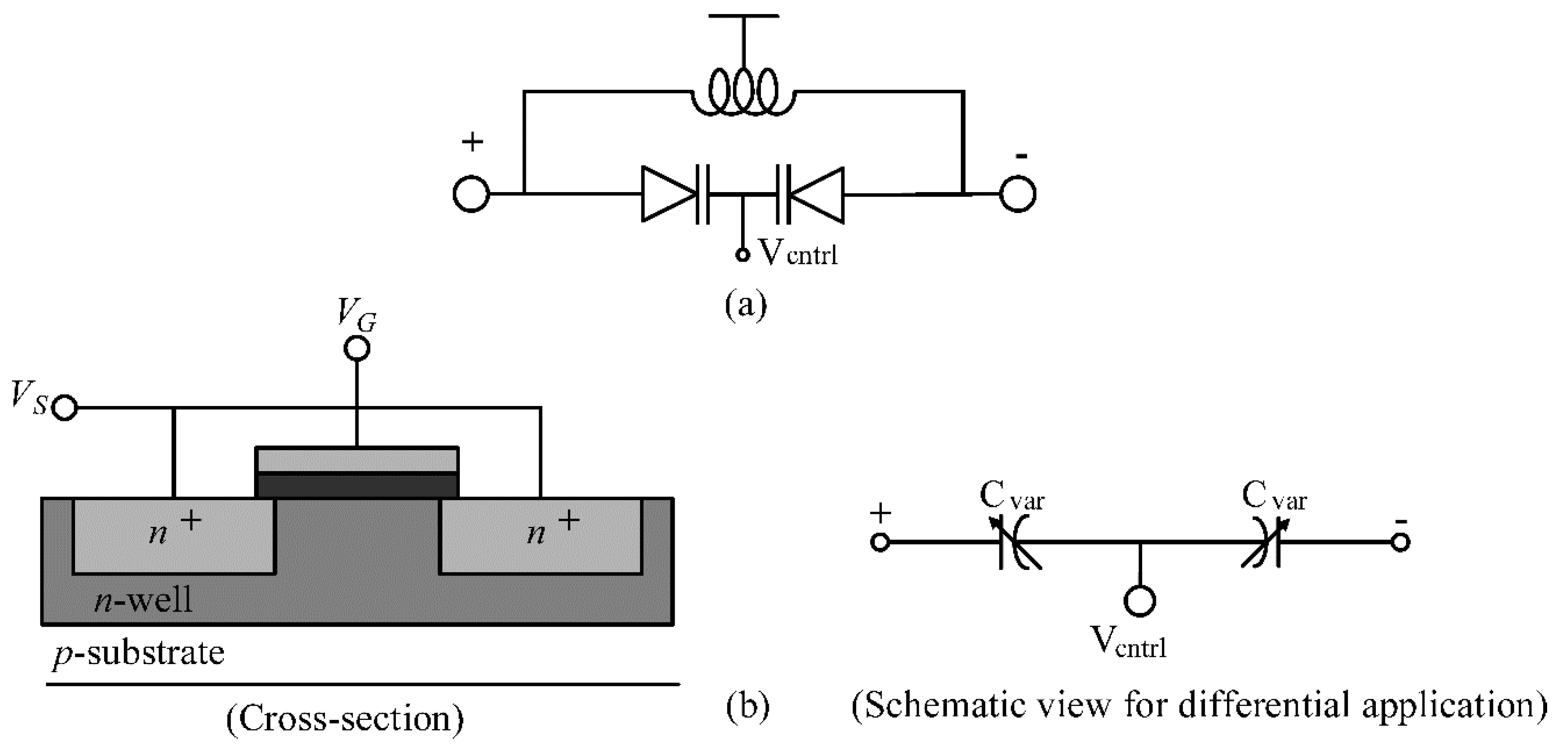
3.1. Varactor
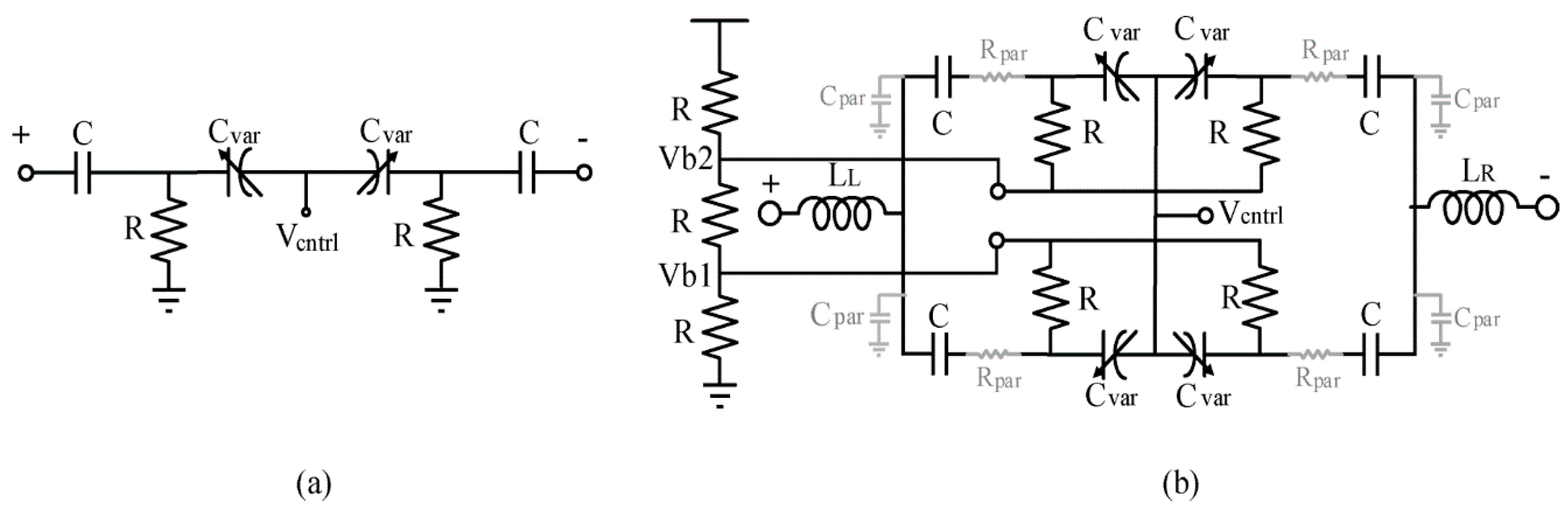
3.2. Proposed Varactor Circuit Implementation
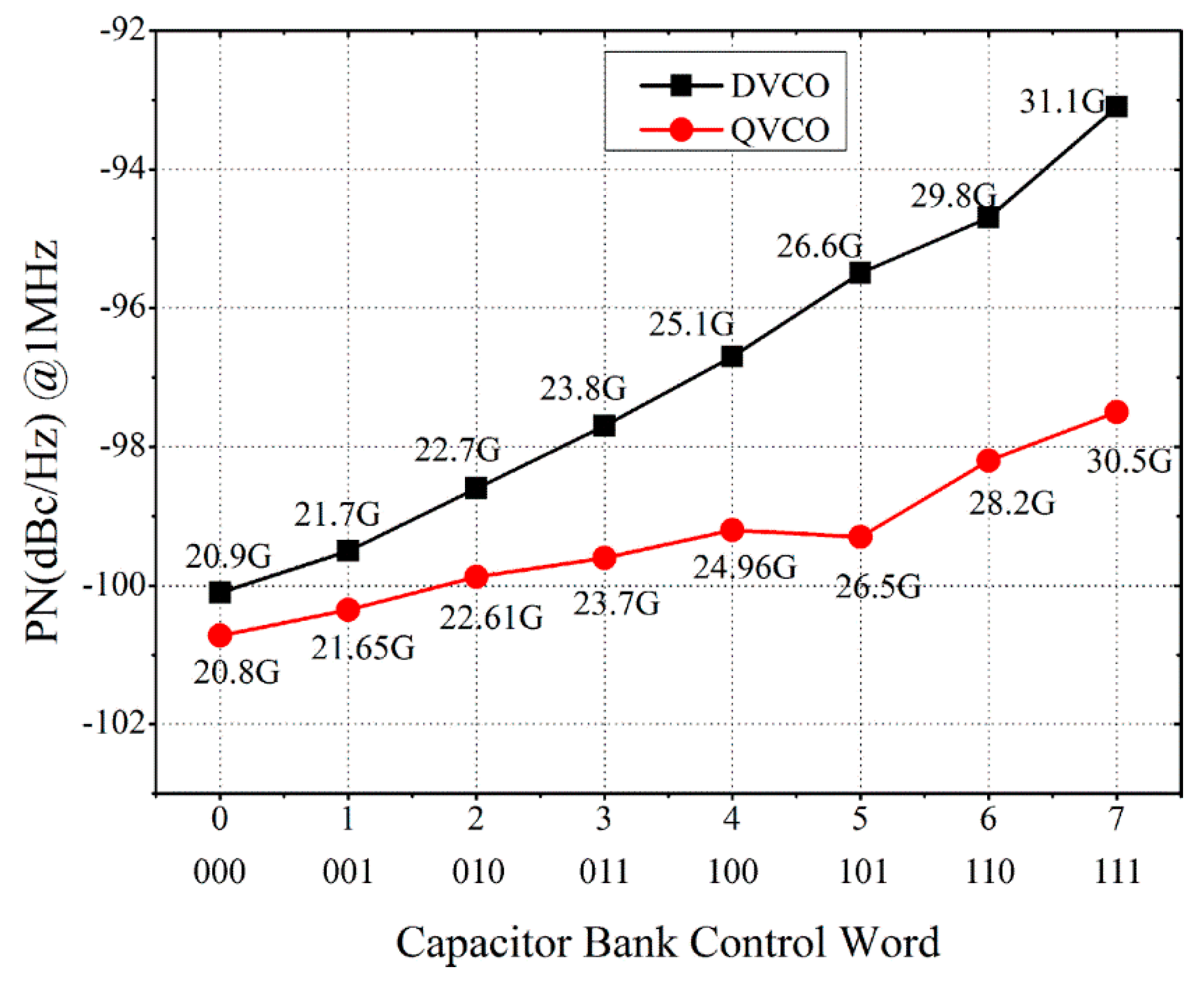
4. Post-Layout Simulation Results and Discussion
4.1. Differential VCO (DVCO)
4.2. Quadrature VCO Using Superharmonic Coupling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Padovan, F.; Tiebout, M.; Mertens, K.L.R.; Bevilacqua, A.; Neviani, A. Design of low-noise K-band SiGe bipolar VCOs: Theory and Implementation. IEEE Trans. Circuits Syst. Regul. Pap. 2015, 62, 607–615. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, M.; Chen, J.X.; Liang, W.F.; Yan, P.P.; Zhai, J.F.; Hong, W. Linear CMOS LC-VCO Based on triple-coupled inductors and its application to 40-GHz phase-locked loop. IEEE Trans. Microw. Theory Tech. 2017, 65, 2977–2989. [Google Scholar] [CrossRef]
- Chang, H.Y.; Chiu, Y.T. K-Band CMOS differential and quadrature voltage-controlled oscillators for low phase-noise and low-power applications. IEEE Trans. Microw. Theory Tech. 2012, 60, 46–59. [Google Scholar] [CrossRef]
- Yang, J.; Kim, C.Y.; Kim, D.W.; Hong, S. Design of a 24-GHz CMOS VCO with an asymmetric-width transformer. IEEE Trans. Circuits Syst. Express Briefs 2010, 57, 173–177. [Google Scholar] [CrossRef]
- Kucharski, M.; Herzel, F.; Ng, H.J.; Kissinger, D. A Ka-band BiCMOS LC-VCO with wide tuning range and low phase noise using switched coupled inductors. In Proceedings of the 2016 11th European IEEE Conference of Microwave Integrated Circuits Conference (EuMIC), London, UK, 3–4 October 2016; pp. 201–204. [Google Scholar]
- Li, C.C.; Wang, T.P.; Kuo, C.C.; Chuang, M.C.; Wang, H. A 21 GHz complementary transformer coupled CMOS VCO. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 278–280. [Google Scholar]
- Hsieh, C.K.; Kao, K.Y.; Tseng, J.R.; Lin, K.Y. A K-Band CMOS low power modified colpitts VCO using transformer feedback. In Proceedings of the 2009 IEEE MTT-S International Microwave Symposium Digest, Boston, MA, USA, 7–12 June 2009; pp. 1293–1296. [Google Scholar]
- Kuo, Y.H.; Jeng-Han, T.; Huang, T.W. In A 1.7-mw, 16.8% frequency tuning, 24-GHz transformer-based lc-vco using 0.18µm CMOS technology. In Proceedings of the 2009 IEEE Conference of Radio Frequency Integrated Circuits Symposium, Boston, MA, USA, 7–9 June 2009; pp. 79–82. [Google Scholar]
- Lee, W.; Lee, S.; Choi, J.; So, J.; Kwon, Y. Ka-band VCO with parasitic capacitance cancelling technique. Electron. Lett. 2016, 53, 38–40. [Google Scholar] [CrossRef]
- Wu, Q.; Quach, T.K.; Mattamana, A.; Elabd, S.; Orlando, P.L.; Dooley, S.R.; McCue, J.J.; Creech, G.L.; Khalil, W. Frequency tuning range extension in LC-VCOs using negative-capacitance circuits. IEEE Trans. Circuits Syst. Express Briefs 2013, 60, 182–186. [Google Scholar] [CrossRef]
- Mazzanti, A.; Uggetti, P.; Svelto, F. Analysis and design of injection-locked LC dividers for quadrature generation. IEEE J. Solid-State Circuits 2004, 39, 1425–1433. [Google Scholar] [CrossRef]
- Crols, J.; Steyaert, M.S.J. A single-chip 900 MHz CMOS receiver front-end with a high performance low-if topology. IEEE J. Solid-State Circuits 1995, 30, 1483–1492. [Google Scholar] [CrossRef]
- Törmänen, M.; Sjoland, H. A 24-ghz LC-QVCO in 130-nm CMOS using 4-bit switched tuning. In Proceedings of the 2008 IEEE Conference of International Conference on Microelectronics (ICM), Sharjah, UAE, 14–17 December 2008; pp. 421–424. [Google Scholar]
- Andreani, P.; Xiaoyan, W. On the phase-noise and phase-error performances of multiphase LC CMOS VCOs. IEEE J. Solid-State Circuits 2004, 39, 1883–1893. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.Y.; Wang, L.H.; Lin, Y.H. A CMOS quadrature VCO with subharmonic and injection-locked techniques. IEEE Trans. Circuits Syst. Express Briefs 2010, 57, 843–847. [Google Scholar] [CrossRef]
- Hancock, T.M.; Rebeiz, G.M. A novel superharmonic coupling topology for quadrature oscillator design at 6 GHz. In Proceedings of the 2004 IEEE Conference of Radio Frequency Integrated Circuits (RFIC) Systems, Forth Worth, TX, USA, 6–8 June 2004; pp. 285–288. [Google Scholar]
- Hye-Ryoung, K.; Choong-Yul, C.; Seung-Min, O.; Moon-Su, Y.; Sang-Gug, L. A very low-power quadrature VCO with back-gate coupling. IEEE J. Solid-State Circuits 2004, 39, 952–955. [Google Scholar] [CrossRef]
- Yi, X.; Liang, Z.; Feng, G.; Boon, C.C.; Meng, F. A 93.4-to-104.8 GHz 57 mW fractional-N cascaded sub-sampling PLL with true in-phase injection-coupled QVCO in 65 nm CMOS. In Proceedings of the 2016 IEEE Conference of Radio Frequency Integrated Circuits Symposium (RFIC), San Francisco, CA, USA, 22–24 May 2016; pp. 122–125. [Google Scholar]
- Yun, S.-J.; Yoon, D.-Y.; Lee, S.-G. A complementary-coupled CMOS LC quadrature oscillator. IEICE Trans. Electron. 2008, 91, 1806–1810. [Google Scholar] [CrossRef]
- Gierkink, S.L.J.; Levantino, S.; Frye, R.C.; Samori, C.; Boccuzzi, V. A low-phase-noise 5-GHz CMOS quadrature VCO using superharmonic coupling. IEEE J. Solid-State Circuits 2003, 38, 1148–1154. [Google Scholar] [CrossRef]
- Xi, T.; Guo, S.; Gui, P.; Zhang, J.; Kenneth, Κ.O.; Fan, Y.; Huang, D.; Gu, R.; Morgan, M. Low-phase-noise 54 GHz quadrature VCO and 76GHz/90GHz VCOs in 65 nm CMOS process. In Proceedings of the 2014 IEEE Conference of Radio Frequency Integrated Circuits Symposium, Tampa, FL, USA, 1–3 June 2014; pp. 257–260. [Google Scholar]
- Choul-Young, K.; Jaemo, Y.; Dong-Wook, K.; Songcheol, H. A K-band quadrature VCO based on asymmetric coupled transmission lines. In Proceedings of the 2008 IEEE Conference of MTT-S International Microwave Symposium Digest, Atlanta, GA, USA, 15–20 June 2008; pp. 363–366. [Google Scholar]
- Mingquan, B.; Yinggang, L.; Jacobsson, H. A 25-GHz ultra-low phase noise lnGap/GaAs HBT VCO. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 751–753. [Google Scholar] [CrossRef]
- Shin, H.; Kim, J. A 17-GHz Push-Push VCO based on output extraction from a capacitive common node in GaInp/GaAs HBT technology. IEEE Trans. Microw. Theory Tech. 2006, 54, 3857–3863. [Google Scholar] [CrossRef]
- Chang, H.Y.; Lin, C.H.; Liu, Y.C.; Yeh, Y.L.; Chen, K.; Wu, S.H. 65-nm CMOS dual-gate device for ka-band broadband low-noise amplifier and high-accuracy quadrature voltage-controlled oscillator. IEEE Trans. Microw. Theory Tech. 2013, 61, 2402–2413. [Google Scholar] [CrossRef]
- Tormanen, M.; Sjoland, H. A 26-GHz LC-QVCO in 0.13-μm CMOS. In Proceedings of the 2007 IEEE Conference of Asia Pasific Microwave Conference (APMC), Bangkok, Thailand, 11–14 December 2007; pp. 1–4. [Google Scholar]
- Mazzanti, A.; Andreani, P. Class-C harmonic CMOS VCOs, with a general result on phase noise. IEEE J. Solid-State Circuits 2008, 43, 2716–2729. [Google Scholar] [CrossRef]
- Fanori, L.; Andreani, P. Highly efficient class-C CMOS VCOs, including a comparison with class-B VCOs. IEEE J. Solid-State Circuits 2013, 48, 1730–1740. [Google Scholar] [CrossRef]
- Fard, A.; Andreani, P. An analysis of 1/f2 phase noise in bipolar colpitts oscillators (with a digression on bipolar differential-Pair oscillators). IEEE J. Solid-State Circuits 2007, 42, 374–384. [Google Scholar] [CrossRef]
- Boscolo, F.; Padovan, F.; Quadrelli, F.; Tiebout, M.; Neviani, A.; Bevilacqua, A. A 21GHz 20.5%-tuning range colpitts VCO with -119 dBc/Hz phase noise at 1MHz offset. In Proceedings of the 2017 43rd IEEE European Solid State Circuits Conference (ESSCIRC), Leuven, Belgium, 11–14 September 2017; pp. 91–94. [Google Scholar]
- Yamashita, F.; Matsuoka, T.; Kihara, T.; Takobe, I.; Park, H.-J.; Taniguchi, K. Analytical design of a 0.5V 5GHz CMOS LC-VCO. IEICE Electron. Express 2009, 6, 1025–1031. [Google Scholar] [CrossRef] [Green Version]
- Razavi, B.; Behzad, R. RF Microelectronics, 2nd ed.; Prentice Hall Press: New York, NY, USA, 2011. [Google Scholar]
- Andreani, P.; Mattisson, S. On the Use of MOS Varactors in RF VCO’s. IEEE J. Solid-State Circuits 2000, 35, 905–910. [Google Scholar] [CrossRef]
- Fox-Turnbull, W.H. Design and Technology Support Education; GlobalFoundries: Santa Clara, CA, USA, 2016. [Google Scholar]
- Kamata, T.; Matsuoka, T.; Taniguchi, K. RF Front-end Design for CMOS Terrestrial Wideband TV Tuner IC. IEEE Trans. Consum. Electron. 2010, 56, 1340–1348. [Google Scholar] [CrossRef]
- Changhua, C.; Kenneth, K.O. Millimeter-wave voltage-controlled oscillators in 0.13 µm CMOS technology. IEEE J. Solid-State Circuits 2006, 41, 1297–1304. [Google Scholar]







| Ref. | (GHz) | @1 MHz (dBc/Hz) | (mW) | (%) | Process | |
|---|---|---|---|---|---|---|
| [1] | 22.7 | −114 | 18 | 17 | −193 | SiGe HBT |
| [2] | 20.85 | −100.7 | 8.1 | 15.8 | −181.8 | 90 nm CMOS |
| [3] | 20.8 | −116.4 | 3 | 4.8 | −191.6 | 90 nm CMOS |
| [4] | 24.27 | −100.33 | 7.8 | 2.2 | −179 | 0.18 µm CMOS |
| [5] | 32.55 | −97 | 19 | 18.1 | −180 | 0.13 um SiGe BiCMOS |
| [6] | 21.5 | −113 | 130 | 4.6 | −171.8 | 0.25 um SiGe |
| [7] | 23 | −100 | 4 | 2 | −181 | 0.13 µm CMOS |
| [8] | 24.5 | −95.5 | 1.7 | 16.8 | −185.4 | 0.18 µm CMOS |
| [10] | 40 | −95 | 12 | 27 | −184.9 | 0.13 µm CMOS |
| [30] | 21 | −119 | 70 | 20 | −194 | SiGe BiCMOS |
| Our Work | 25.5 | −96 | 12 | 43 | −186 | 0.13 um SiGe BiCMOS |
| Ref. | Coupling Method | (GHz) | @1 MHz (dBc/Hz) | (mW) | (%) | I/Q Error | Process | |
|---|---|---|---|---|---|---|---|---|
| [3] | Series | 20.9 | −117.2 | 6.3 | 3.1 | −185.4 | n/a | 90 nm CMOS |
| [13] | Parallel | 24.7 | −111.6 | 24 | 4.3 | −186 | n/a | 0.13 µm CMOS |
| [21] | Transformer Coupled | 20 | −111.67 | 40.32 | 10.4 | −181.5 | 1.5° | 0.18 µm CMOS |
| [22] | Transmission Line | 33 | −99 | 2.64 | - | −183.7 | n/a | 0.12 µm SiGe HBT |
| [25] | Series | 25.3 | −109 | 14.4 | 2.81 | −185.5 | 1.8° | 65 nm CMOS |
| [26] | Parallel | 26.1 | −114 | 24 | 3 | −188.5 | n/a | 0.13 µm CMOS |
| Our Work | Superharmonic Coupling | 25.3 | −99.2 | 25 | 42 | −185.8 | 1.2° | 0.13 µm SiGe BiCMOS |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, F.; Liu, Y.; Li, Z.; Wang, X.; Sarfraz, M.M.; Zhang, H. A Bandwidth-Enhanced Differential LC-Voltage Controlled Oscillator (LC-VCO) and Superharmonic Coupled Quadrature VCO for K-Band Applications. Electronics 2018, 7, 127. https://doi.org/10.3390/electronics7080127
Ullah F, Liu Y, Li Z, Wang X, Sarfraz MM, Zhang H. A Bandwidth-Enhanced Differential LC-Voltage Controlled Oscillator (LC-VCO) and Superharmonic Coupled Quadrature VCO for K-Band Applications. Electronics. 2018; 7(8):127. https://doi.org/10.3390/electronics7080127
Chicago/Turabian StyleUllah, Farman, Yu Liu, Zhiqiang Li, Xiaosong Wang, Muhammad Masood Sarfraz, and Haiying Zhang. 2018. "A Bandwidth-Enhanced Differential LC-Voltage Controlled Oscillator (LC-VCO) and Superharmonic Coupled Quadrature VCO for K-Band Applications" Electronics 7, no. 8: 127. https://doi.org/10.3390/electronics7080127




