FPGA-Based Extended Control Set Model Predictive Current Control with a Simplified Search Strategy for Permanent Magnet Synchronous Motor
Abstract
:1. Introduction
2. Discrete Model and Conventional FCS-MPC
2.1. Discrete Mathematical Model
2.2. Conventional FCS-MPC
3. Proposed ECS-MPC Method
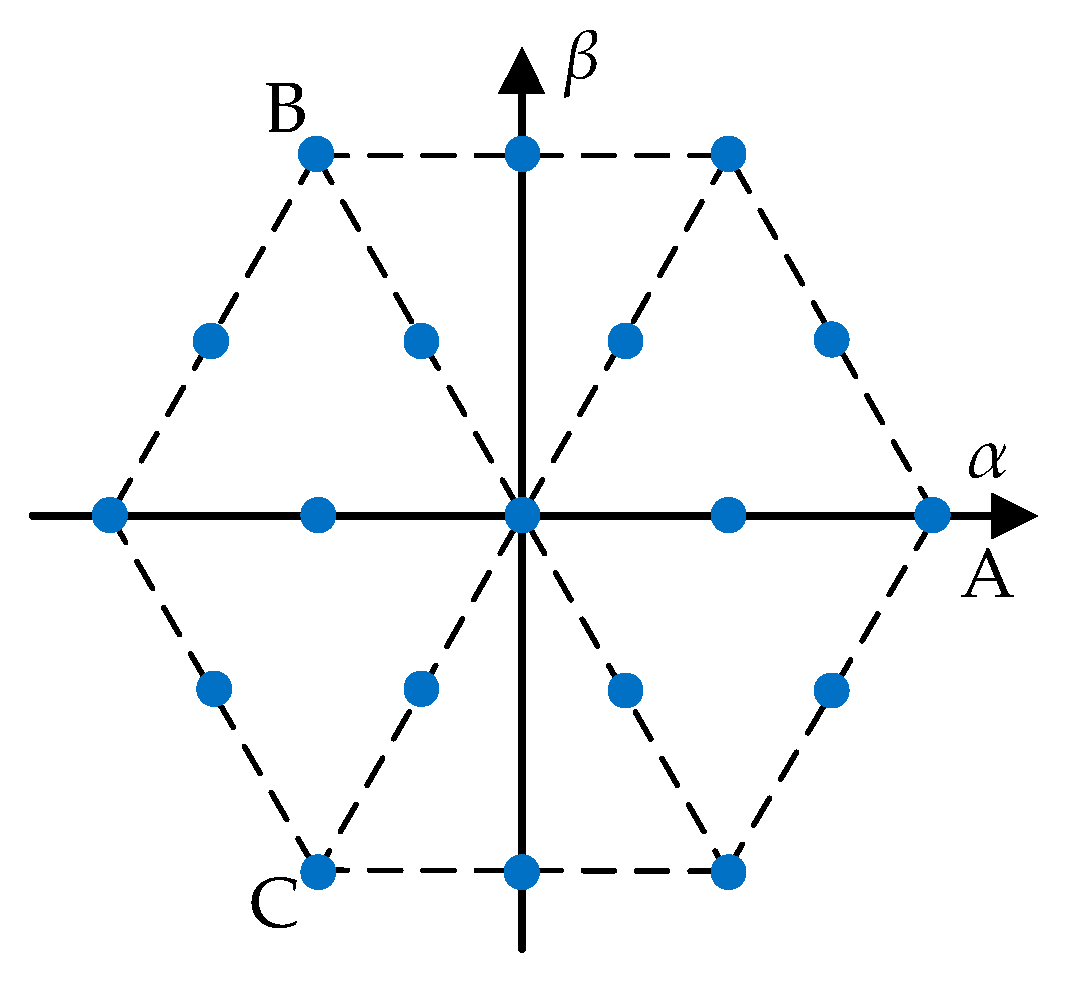
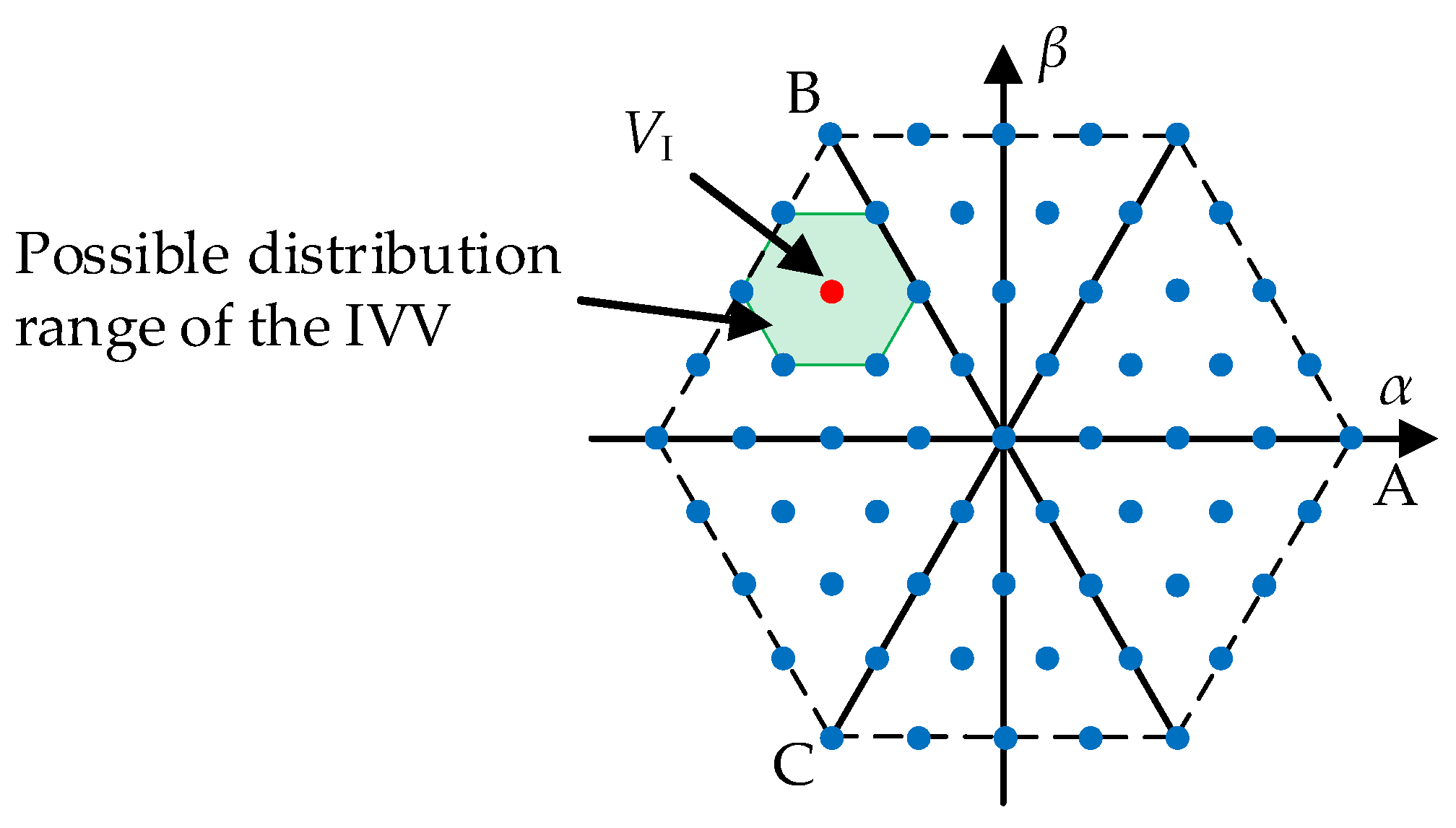
3.1. ECS-MPC
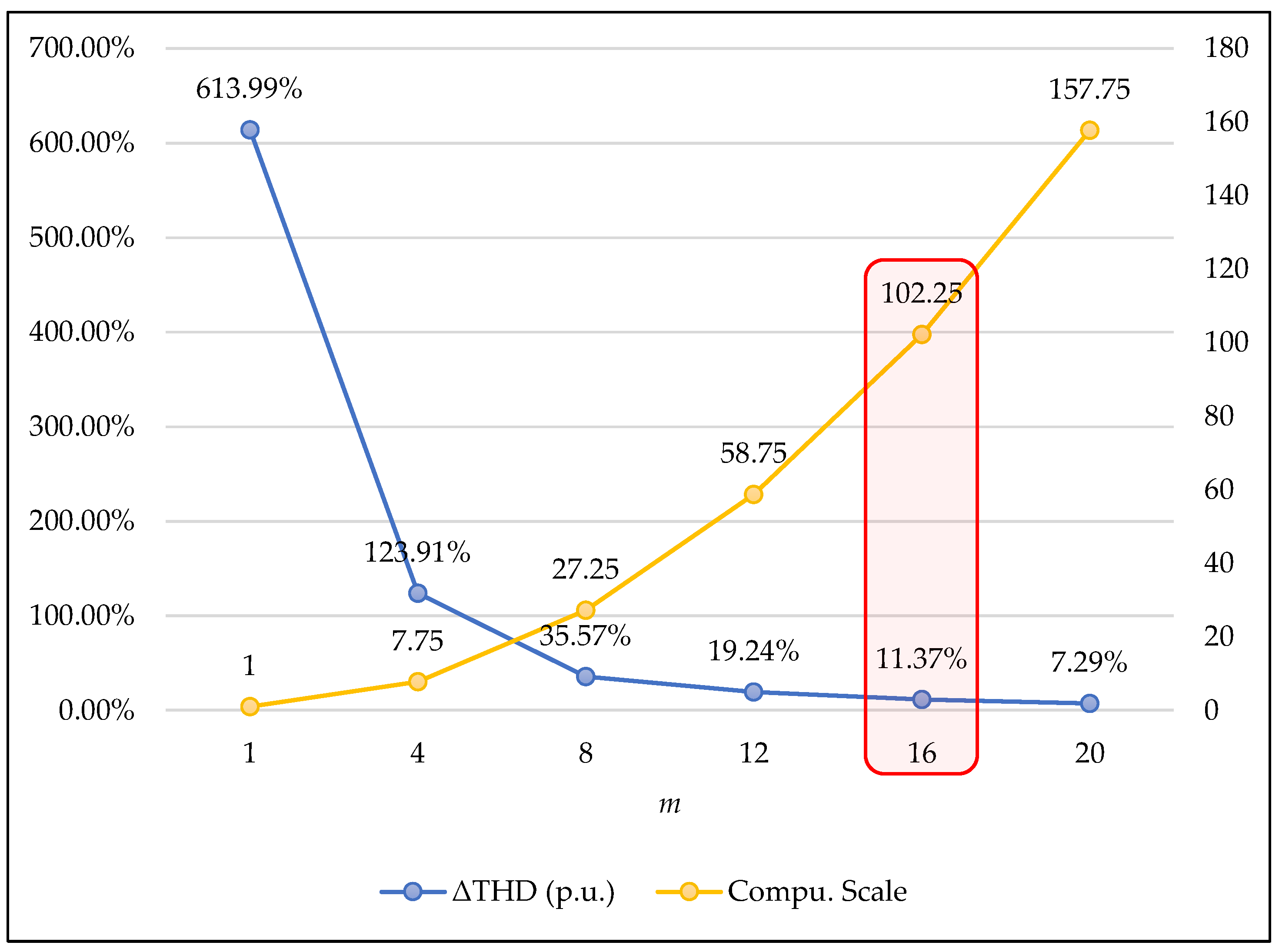
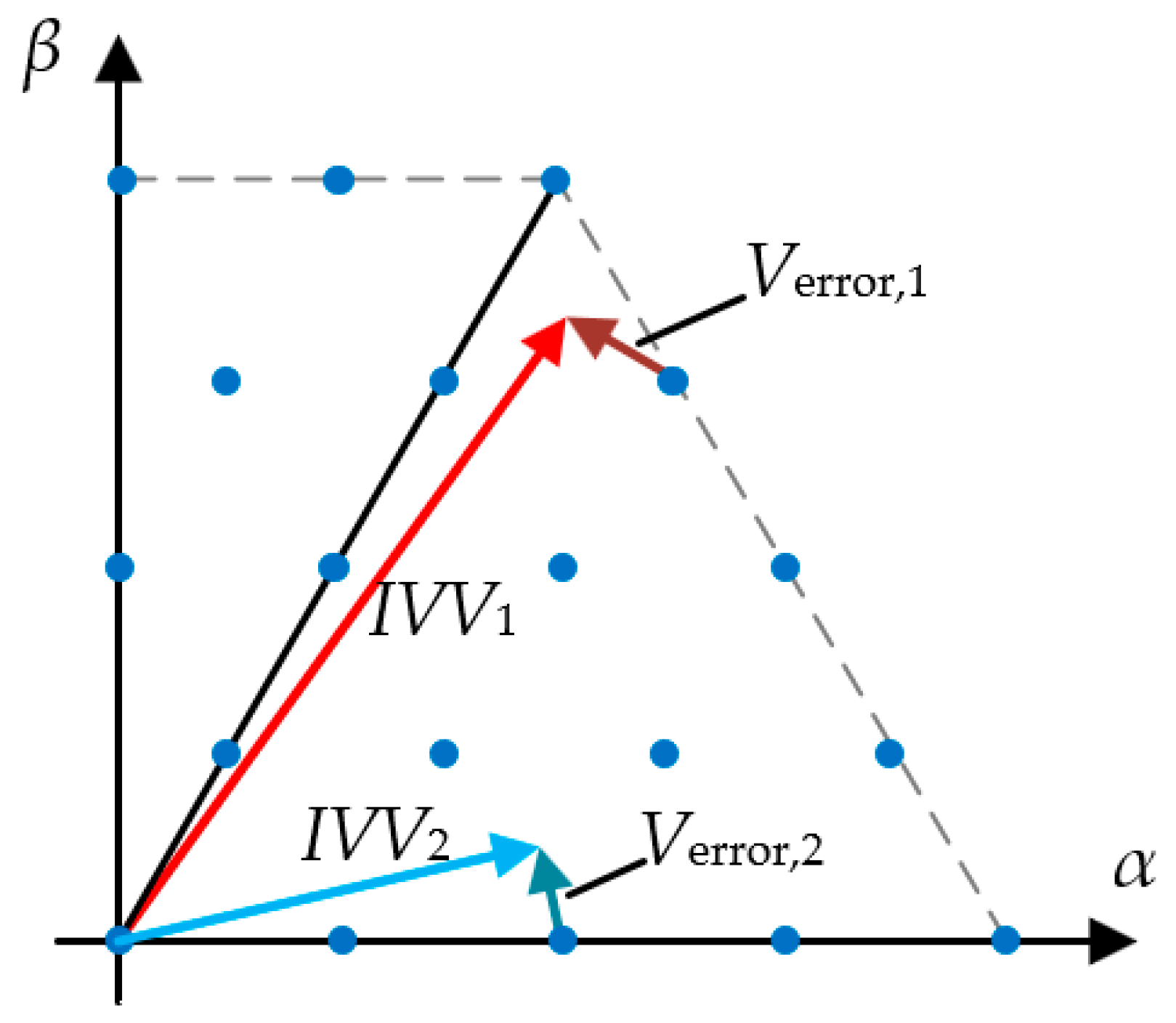
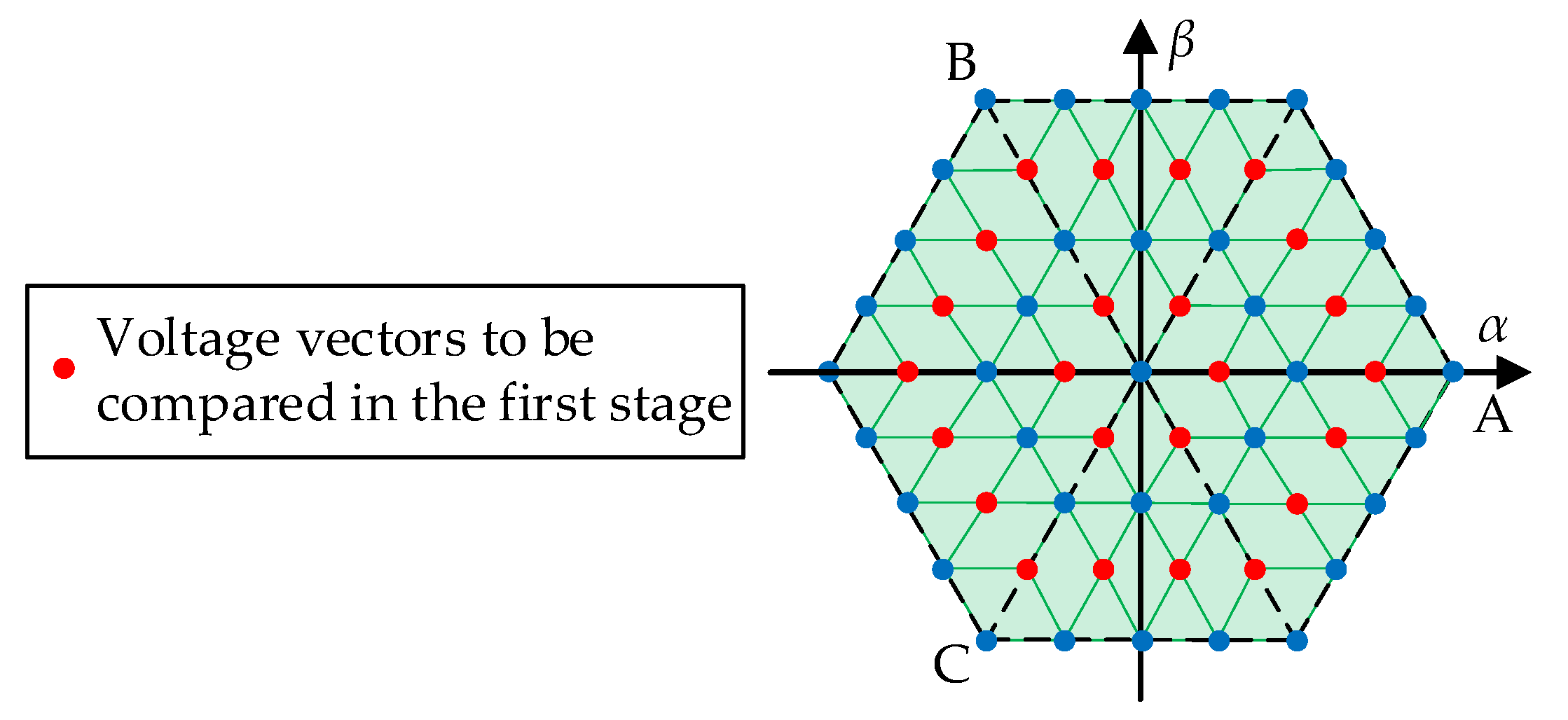
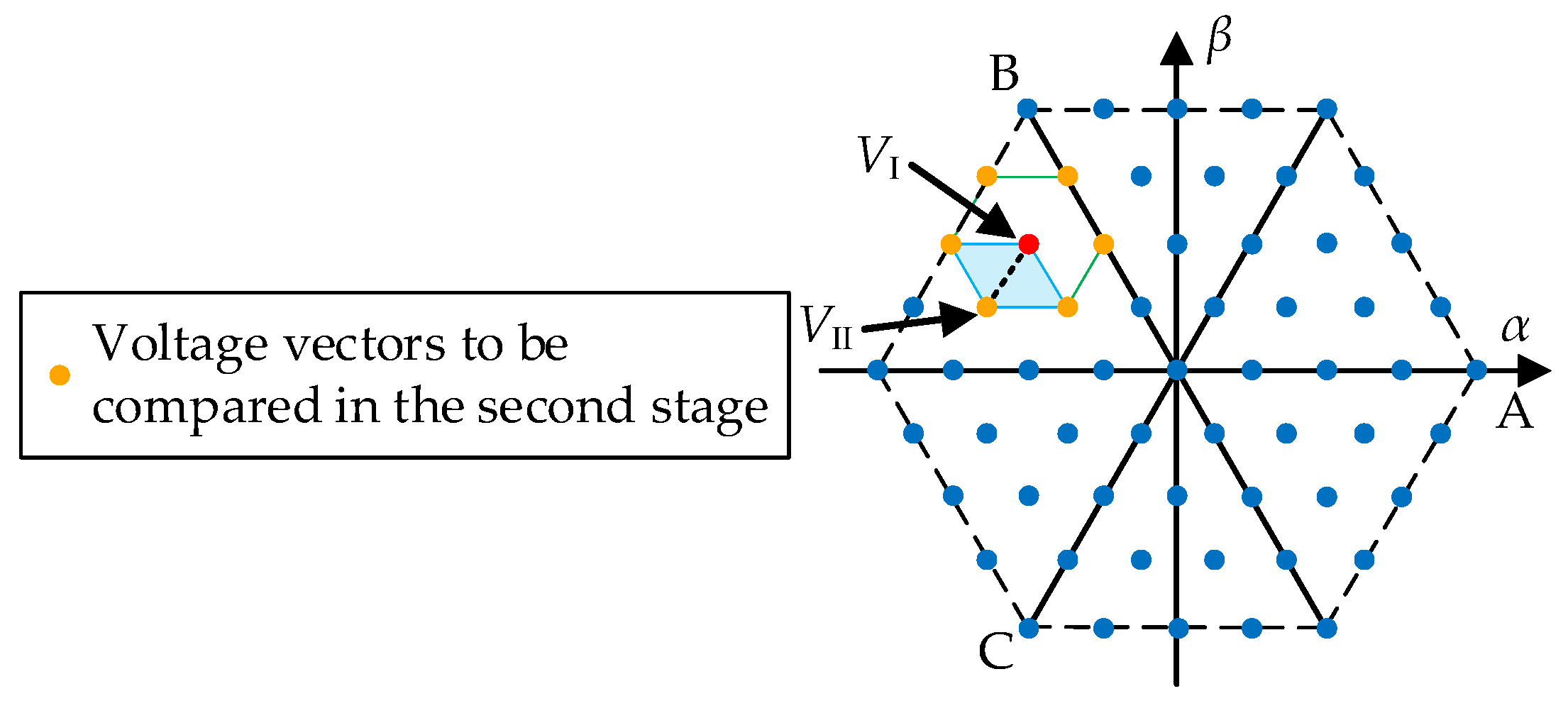
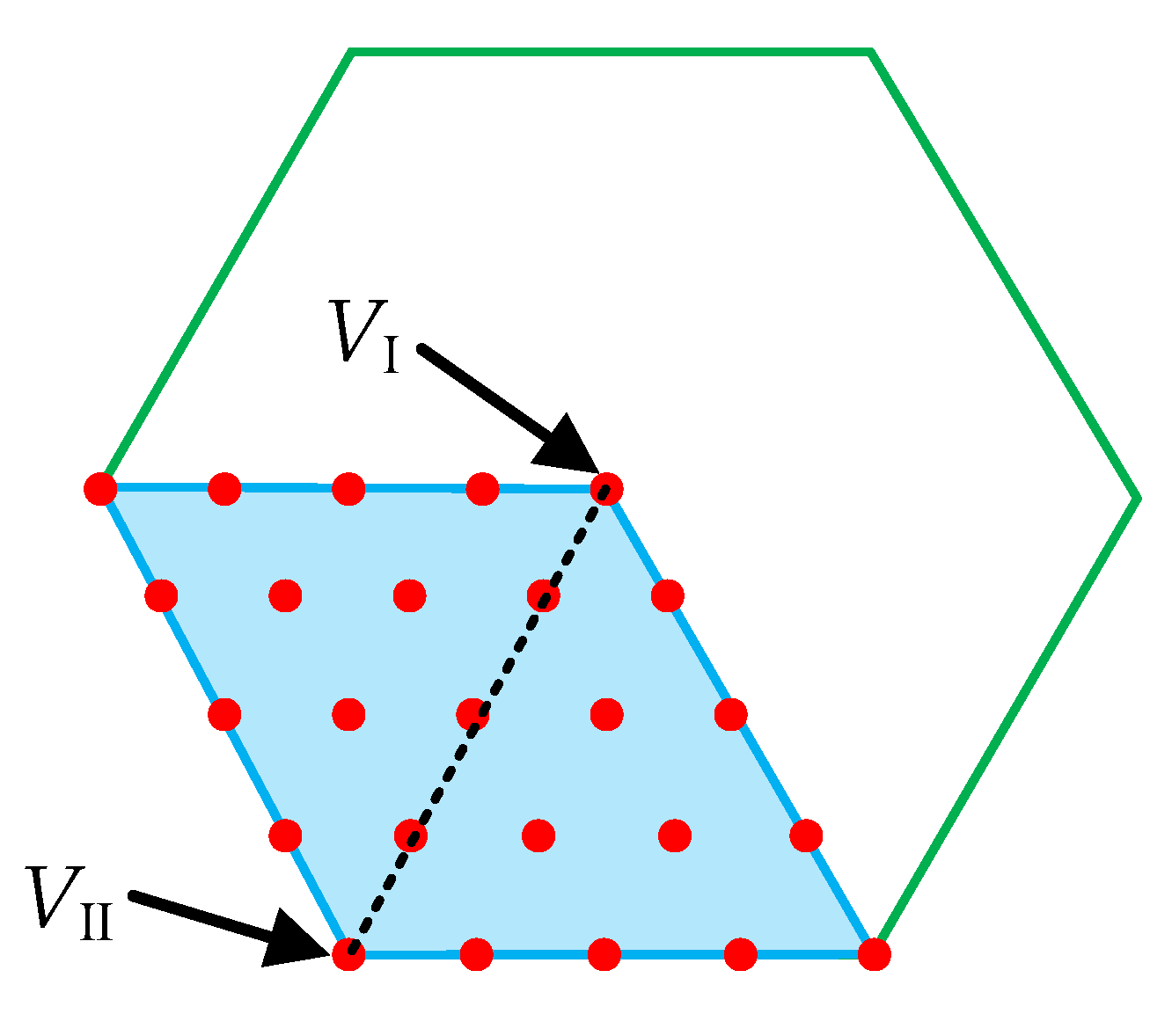
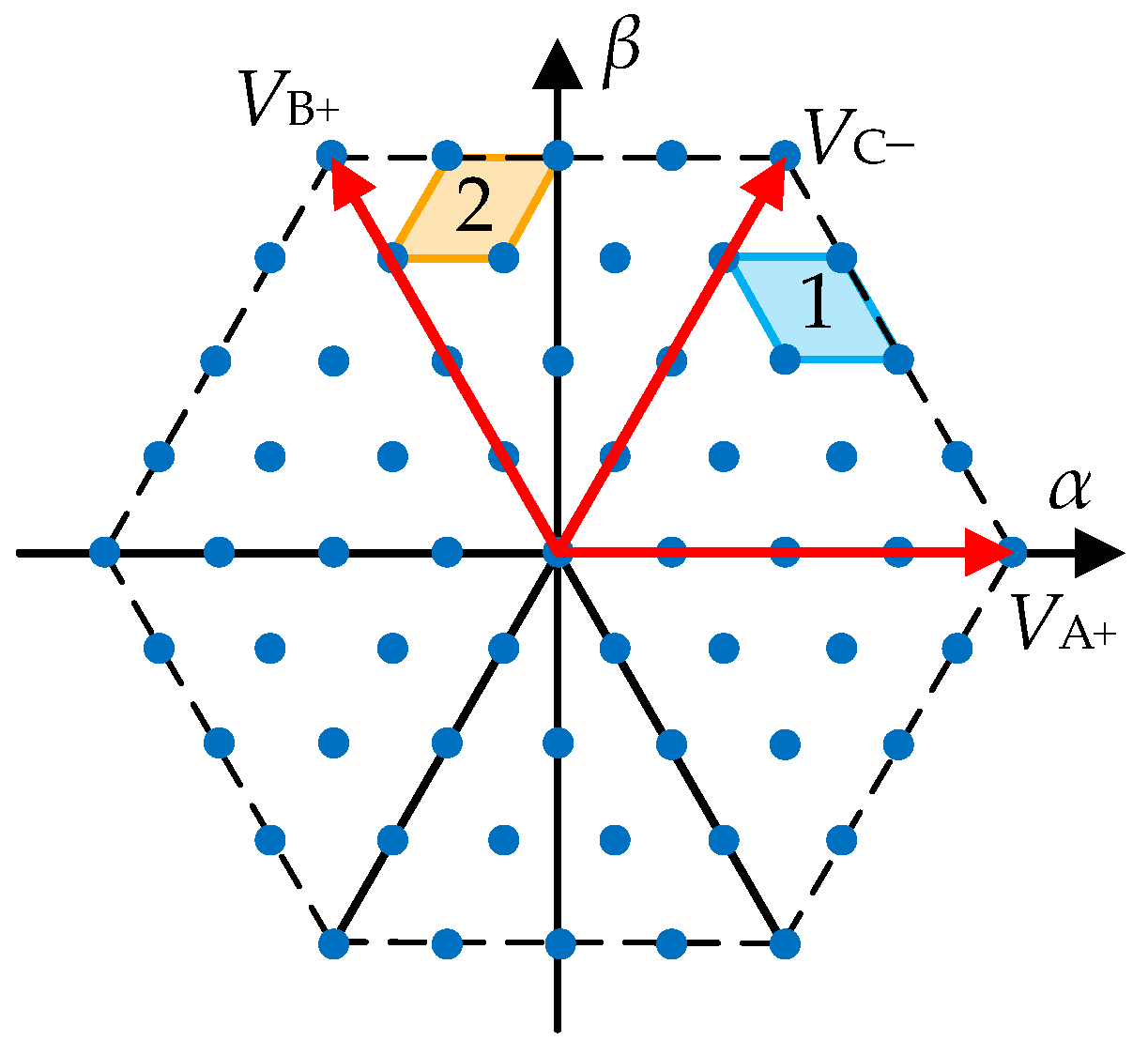
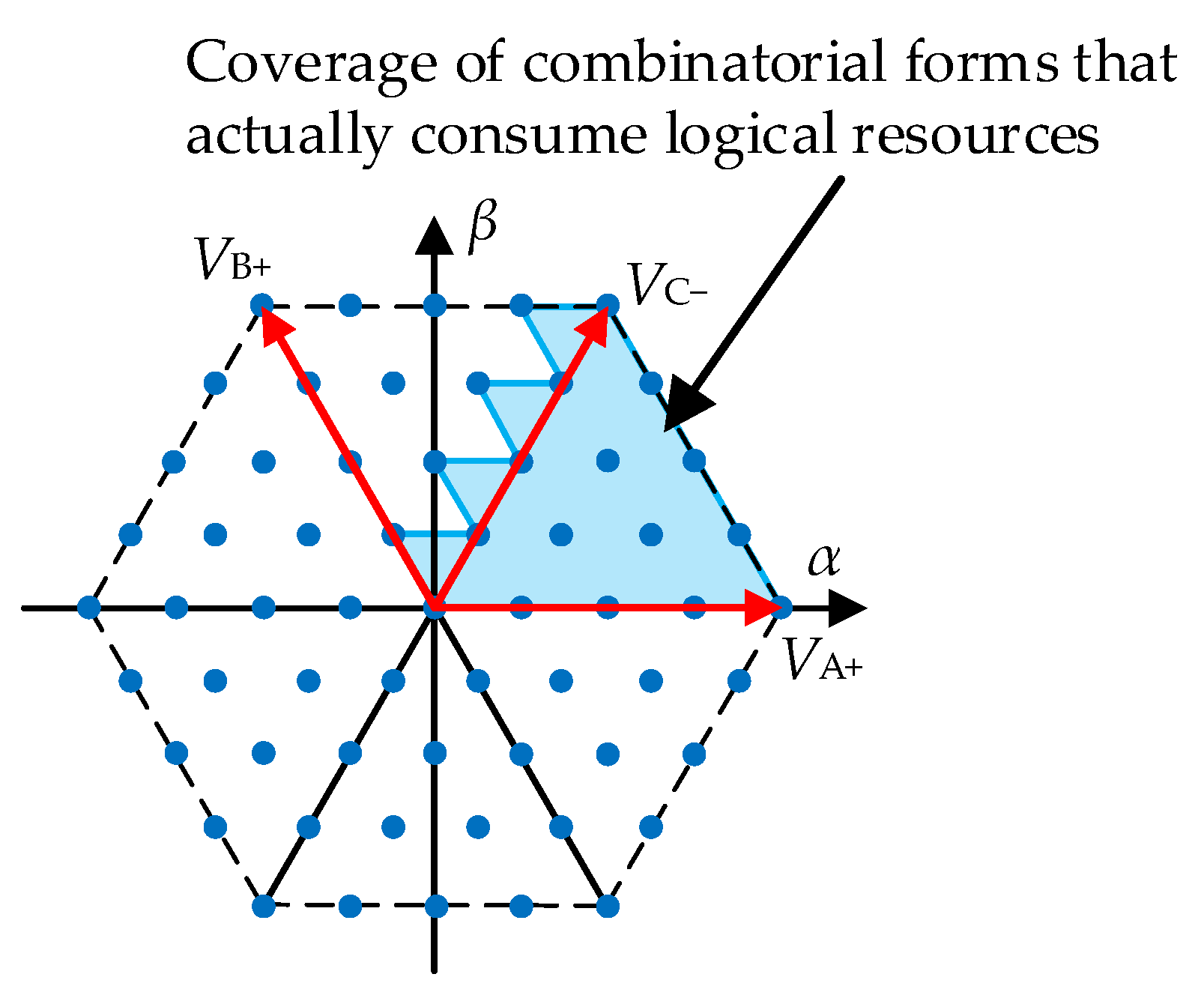
3.2. Simplified Optimal Vector Search Strategy
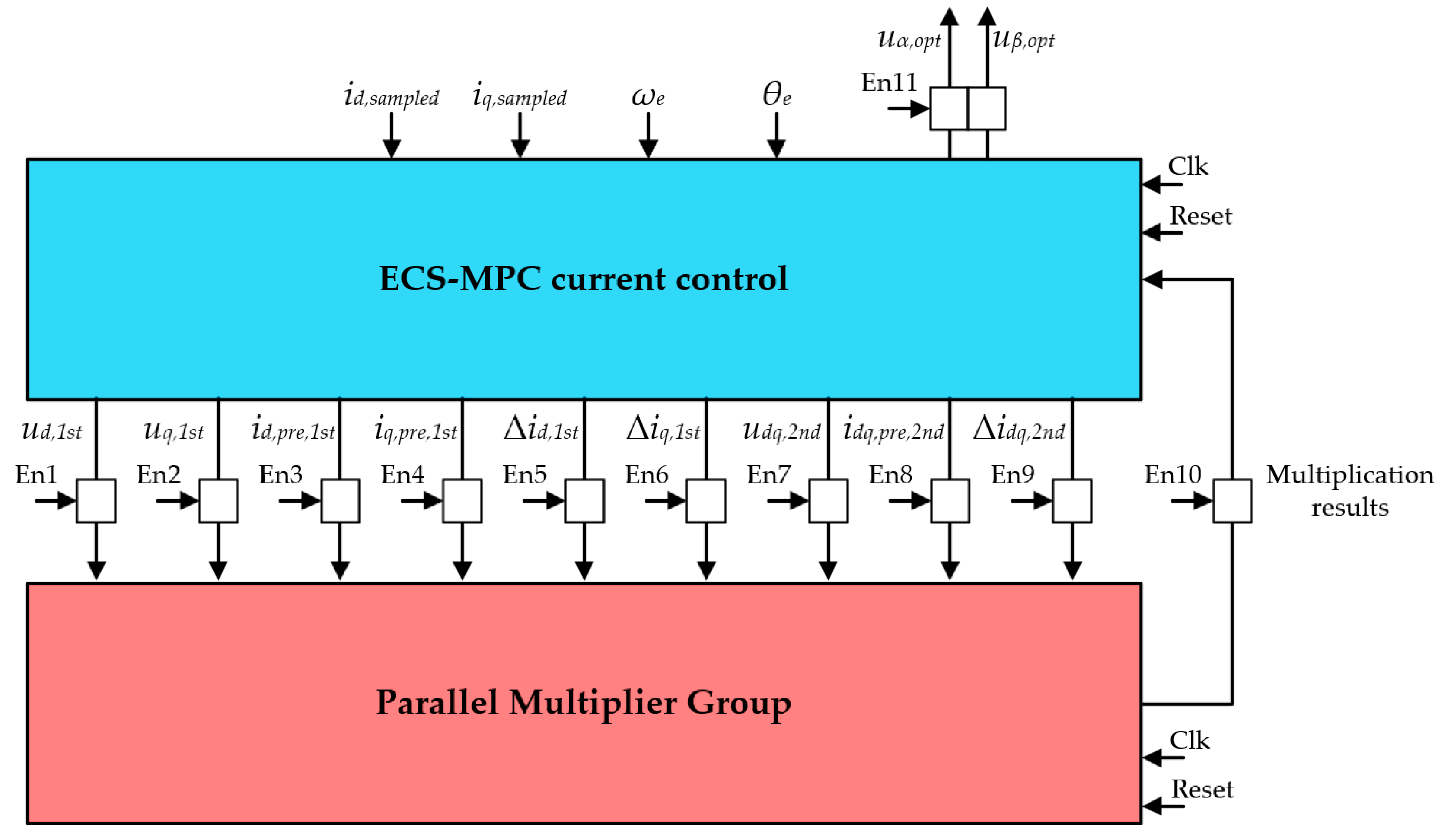
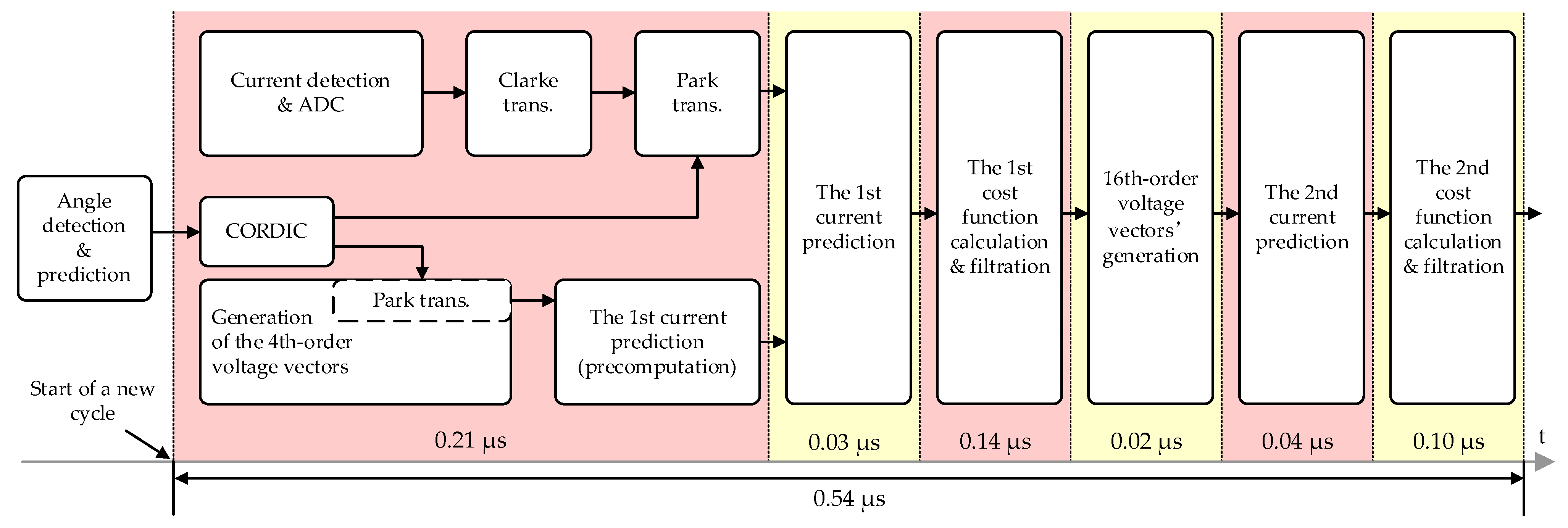
4. FPGA Implementation
4.1. Simplification of the Virtual Voltage Vector Generation Process
4.2. Parallel Multiplier Group
4.3. Minimum Filter with Parallel Acceleration
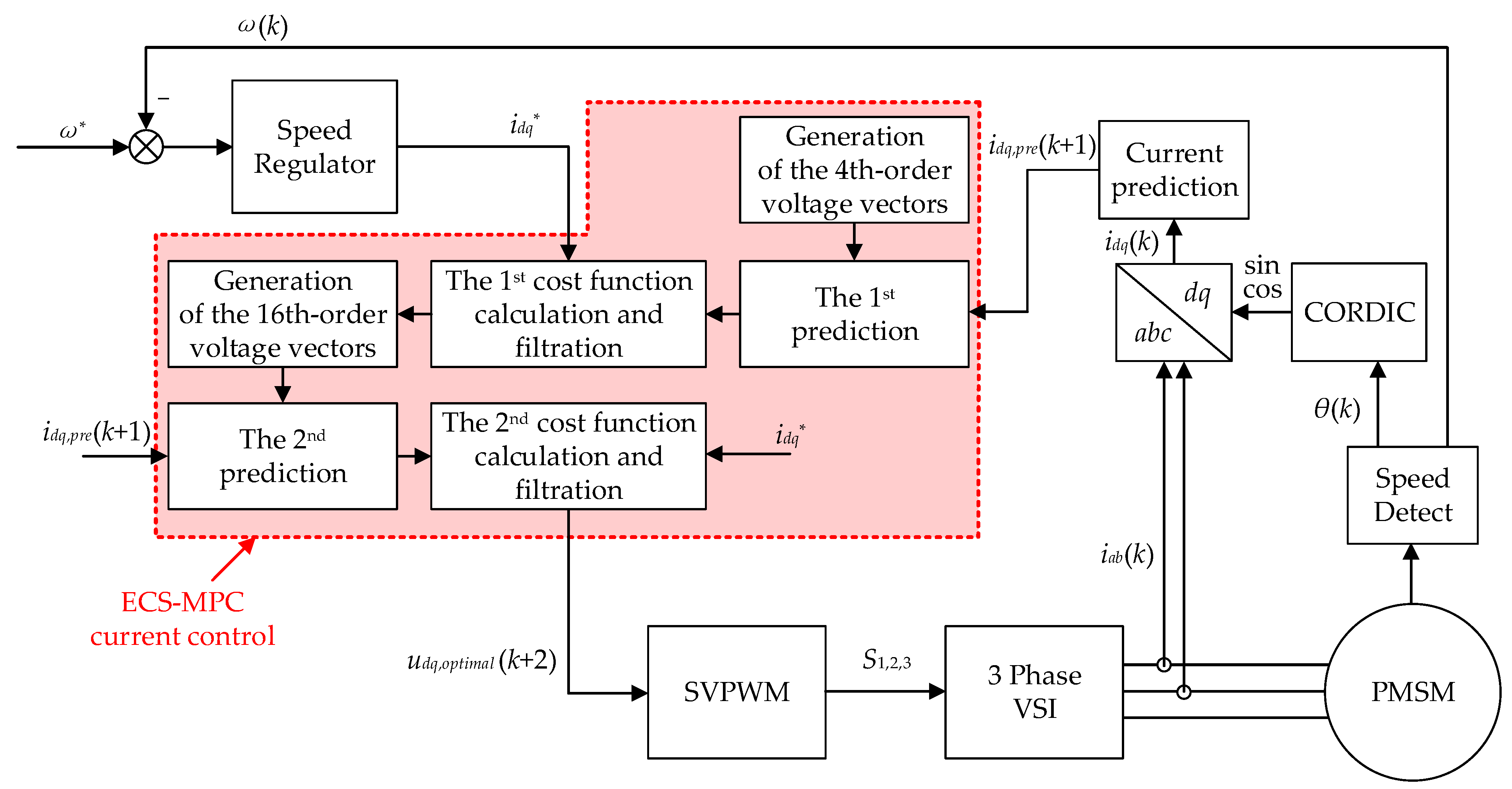
4.4. Overall Structure of the ECS-MPCC
5. Simulation and Experimental Results
5.1. Simulation and Experimental Conditions
5.2. Simulation Results
5.3. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, Q.; Liu, X.; Qi, H.; Sun, C.; Wang, Y. Analysis and evaluation of electromagnetic vibration and noise in permanent magnet synchronous motor with rotor step skewing. Sci. China Technol. Sci. 2019, 62, 839–848. [Google Scholar] [CrossRef]
- Hu, M.; Hua, W.; Wang, Z.; Li, S.; Wang, P.; Wang, Y. Selective Periodic Disturbance Elimination Using Extended Harmonic State Observer for Smooth Speed Control in PMSM Drives. IEEE Trans. Power Electron. 2022, 37, 13288–13298. [Google Scholar] [CrossRef]
- Attaianese, C.; D’Arpino, M.; Monaco, M.D.; Noia, L.P.D. Model-Based Detection and Estimation of DC Offset of Phase Current Sensors for Field Oriented PMSM Drives. IEEE Trans. Ind. Electron. 2023, 70, 6316–6325. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Bakeer, A.; Alhelou, H.H.; Siano, P.; Mossa, M.A. A New Modulated Finite Control Set-Model Predictive Control of Quasi-Z-Source Inverter for PMSM Drives. Electronics 2021, 10, 2814. [Google Scholar] [CrossRef]
- Huang, J.; Jiang, G.; Zhang, P.; Chen, J. A Low Switching Frequency Model Predictive Control Method for an Induction Motor Fed by a 3-Level Inverter. Electronics 2023, 12, 3609. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, Y.; Fan, M.; Ji, A.; Xiao, Y.; Zhang, X.; Zhang, W.; Garcia, C.; Vazquez, S.; Rodriguez, J. An Improved Implicit Model Predictive Current Control with Continuous Control Set for PMSM Drives. IEEE Trans. Transp. Electrif. 2022, 8, 2444–2455. [Google Scholar] [CrossRef]
- Anuchin, A.; Demidova, G.L.; Hao, C.; Zharkov, A.; Bogdanov, A.; Šmídl, V. Continuous Control Set Model Predictive Control of a Switch Reluctance Drive Using Lookup Tables. Energies 2020, 13, 3317. [Google Scholar] [CrossRef]
- Vu, T.M.; Moezzi, R.; Cyrus, J.; Hlava, J. Model Predictive Control for Autonomous Driving Vehicles. Electronics 2021, 10, 2593. [Google Scholar] [CrossRef]
- Comarella, B.V.; Carletti, D.; Yahyaoui, I.; Encarnação, L.F. Theoretical and Experimental Comparative Analysis of Finite Control Set Model Predictive Control Strategies. Electronics 2023, 12, 1482. [Google Scholar] [CrossRef]
- She, Y.; Huo, X.; Tong, X.; Wang, C.; Fu, K. Multi-Sampling Rate Finite Control Set Model Predictive Control and Adaptive Method of Single-Phase Inverter. Electronics 2023, 12, 2848. [Google Scholar] [CrossRef]
- Yang, H.; Long, H.; Zhang, Q.; Sun, X. A Robust CCS Predictive Current Control for Photovoltaic Energy Storage System Based on a Nonlinear Disturbance Observer. Electronics 2023, 12, 1985. [Google Scholar] [CrossRef]
- Lim, C.S.; Lee, S.S.; Levi, E. Continuous-Control-Set Model Predictive Current Control of Asymmetrical Six- Phase Drives Considering System Nonidealities. IEEE Trans. Ind. Electron. 2023, 70, 7615–7626. [Google Scholar] [CrossRef]
- Lin, S.; Fang, X.; Wang, X.; Yang, Z.; Lin, F. Multiobjective Model Predictive Current Control Method of Permanent Magnet Synchronous Traction Motors with Multiple Current Bounds in Railway Application. IEEE Trans. Ind. Electron. 2022, 69, 12348–12357. [Google Scholar] [CrossRef]
- Wróbel, K.; Serkies, P.; Szabat, K. Continuous and Finite Set Model Predictive Control of Induction Motor Drive. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 963–968. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Agoro, S.; Husain, I. Robust Deadbeat Finite-Set Predictive Current Control with Torque Oscillation and Noise Reduction for PMSM Drives. IEEE Trans. Ind. Appl. 2022, 58, 365–374. [Google Scholar] [CrossRef]
- Yang, M.; Lang, X.; Long, J.; Xu, D. Flux Immunity Robust Predictive Current Control with Incremental Model and Extended State Observer for PMSM Drive. IEEE Trans. Power Electron. 2017, 32, 9267–9279. [Google Scholar] [CrossRef]
- Zhu, Y.; Tao, B.; Xiao, M.; Yang, G.; Zhang, X.; Lu, K. Luenberger Position Observer Based on Deadbeat-Current Predictive Control for Sensorless PMSM. Electronics 2020, 9, 1325. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Q. Robust Current Predictive Control-Based Equivalent Input Disturbance Approach for PMSM Drive. Electronics 2019, 8, 1034. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G. Model Predictive Control with Constant Switching Frequency Using a Discrete Space Vector Modulation with Virtual State Vectors. In Proceedings of the IEEE International Conference on Industrial Technology, Churchill, Australia, 19 May 2009; pp. 1389–1394. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xie, W.; Wang, F.; Dou, M.; Kennel, R.M.; Lorenz, R.D.; Gerling, D. Deadbeat Model-Predictive Torque Control with Discrete Space-Vector Modulation for PMSM Drives. IEEE Trans. Ind. Electron. 2017, 64, 3537–3547. [Google Scholar] [CrossRef]
- Yang, H.; Yang, R.; Hu, W.; Huang, Z. FPGA-Based Sensorless Speed Control of PMSM Using Enhanced Performance Controller Based on the Reduced-Order EKF. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 289–301. [Google Scholar] [CrossRef]
- Tu, W.; Luo, G.; Chen, Z.; Liu, C.; Cui, L. FPGA Implementation of Predictive Cascaded Speed and Current Control of PMSM Drives with Two-Time-Scale Optimization. IEEE Trans. Ind. Inform. 2019, 15, 5276–5288. [Google Scholar] [CrossRef]
- Milik, A.; Rudnicki, T. A Mixed Hardware-Software Implementation of a High-Performance PMSM Controller. Electronics 2023, 12, 440. [Google Scholar] [CrossRef]
- Jnayah, S.; Moussa, I.; Khedher, A. IM Fed by Three-Level Inverter under DTC Strategy Combined with Sliding Mode Theory. Electronics 2022, 11, 3656. [Google Scholar] [CrossRef]
- Mishra, I.; Tripathi, R.N.; Singh, V.K.; Hanamoto, T. Step-by-Step Development and Implementation of FS-MPC for a FPGA-Based PMSM Drive System. Electronics 2021, 10, 395. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]







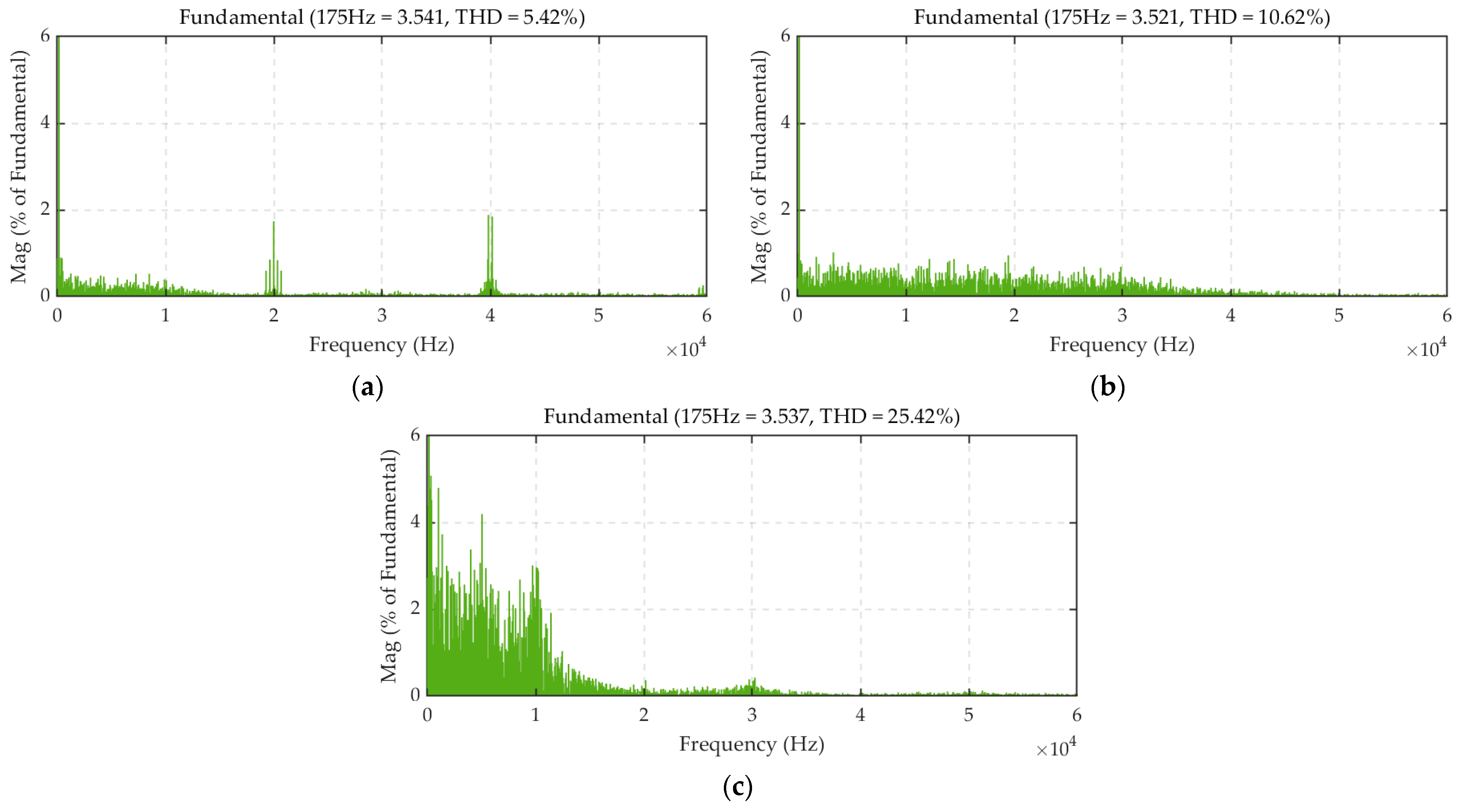


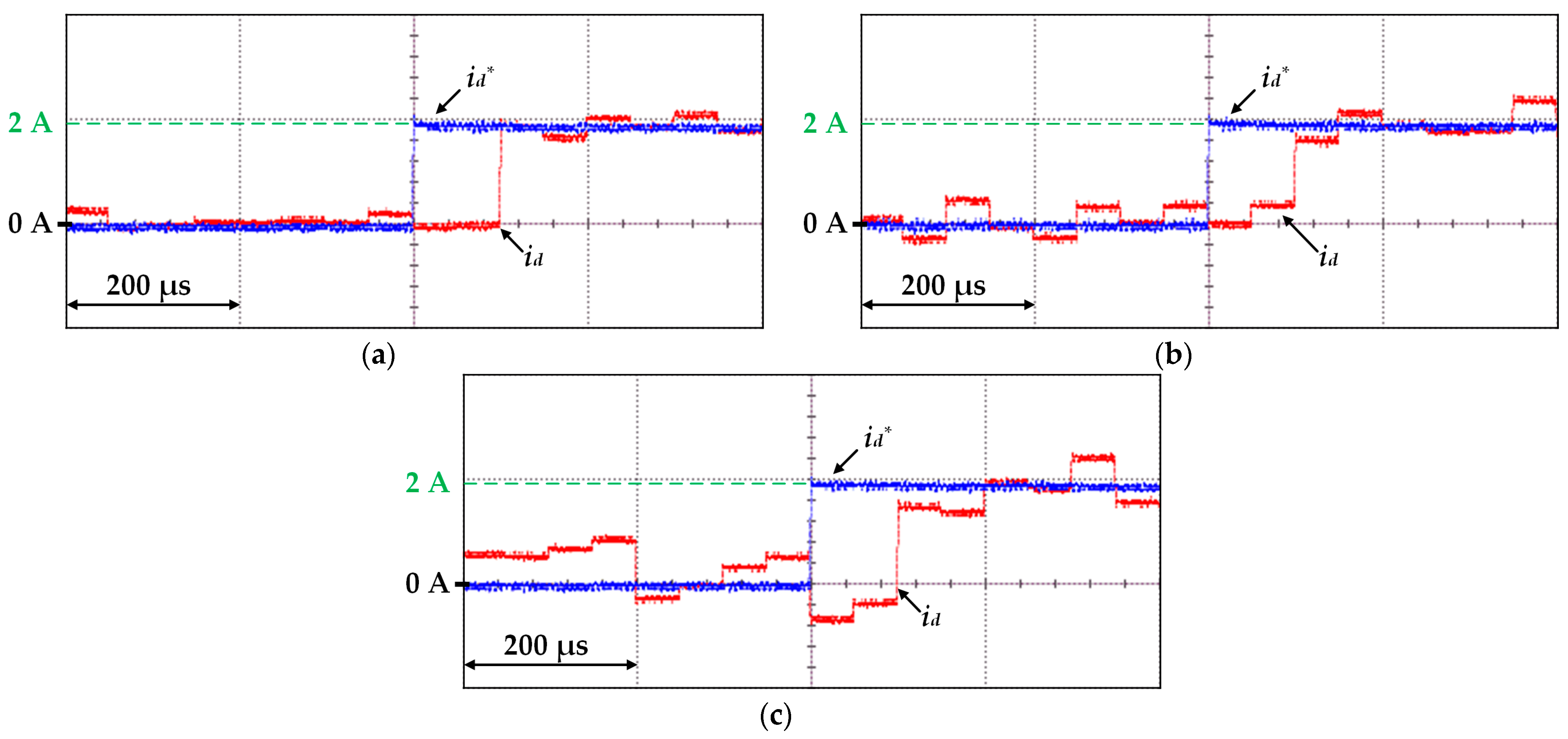
| Item | Value |
|---|---|
| Stator phase resistance Rs (Ω) | 0.297 |
| Stator d-axis inductance Ld (mH) | 0.285 |
| Stator q-axis inductance Lq (mH) | 0.285 |
| Rotor permanent magnet flux ψf (mWb) | 7.170 |
| Number of pole pairs pn | 5 |
| DC bus voltage Udc (V) | 36 |
| Load torque (N⋅m) | 0.2 |
| Sampling frequency fs (kHz) | 20 |
| Load (N·m) | Speed (r/min) | Phase Current THD | ||
|---|---|---|---|---|
| ECS-MPCC | DB-PCC with DSVM | Conventional FCS-MPCC | ||
| 0.2 | 2800 | 3.92% | 7.90% | 23.31% |
| 2100 | 3.82% | 8.78% | 24.49% | |
| 1400 | 3.54% | 9.30% | 30.34% | |
| 0.1 | 2800 | 6.18% | 12.80% | 36.37% |
| 2100 | 6.05% | 14.73% | 43.61% | |
| 1400 | 5.55% | 17.12% | 47.55% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Liu, K.; Hu, M.; Hua, W. FPGA-Based Extended Control Set Model Predictive Current Control with a Simplified Search Strategy for Permanent Magnet Synchronous Motor. Electronics 2023, 12, 4726. https://doi.org/10.3390/electronics12234726
Yang C, Liu K, Hu M, Hua W. FPGA-Based Extended Control Set Model Predictive Current Control with a Simplified Search Strategy for Permanent Magnet Synchronous Motor. Electronics. 2023; 12(23):4726. https://doi.org/10.3390/electronics12234726
Chicago/Turabian StyleYang, Chenyu, Kai Liu, Mingjin Hu, and Wei Hua. 2023. "FPGA-Based Extended Control Set Model Predictive Current Control with a Simplified Search Strategy for Permanent Magnet Synchronous Motor" Electronics 12, no. 23: 4726. https://doi.org/10.3390/electronics12234726
APA StyleYang, C., Liu, K., Hu, M., & Hua, W. (2023). FPGA-Based Extended Control Set Model Predictive Current Control with a Simplified Search Strategy for Permanent Magnet Synchronous Motor. Electronics, 12(23), 4726. https://doi.org/10.3390/electronics12234726








