Design of Sensorless Speed Control System for Permanent Magnet Linear Synchronous Motor Based on Fuzzy Super-Twisted Sliding Mode Observer
Abstract
:1. Introduction
- (1)
- Based on the theoretical basis of SMC and taking PMLSM as the control object, a control system combining CT-SMC and F-ST-SMO is designed.
- (2)
- To solve the problem of the large error of traditional SMO observations, a hyperdistortion algorithm is introduced to maintain the continuity of output to weaken chattering caused by high-frequency switching in sliding mode. Fuzzy rules are introduced to dynamically adjust the sliding mode gain coefficient to reduce chattering near the sliding mode surface.
- (3)
- System verification. The dynamic performance of the designed control system is verified by comparing the CTSMC control system with a traditional SMC and PI control system. The observation performance of F-ST-SMO is compared with that of traditional SMO, and the error analysis is made with the data of the mechanical sensor.
2. Design of Terminal Sliding Mode Speed Controller
2.1. PMLSM Mathematical Model
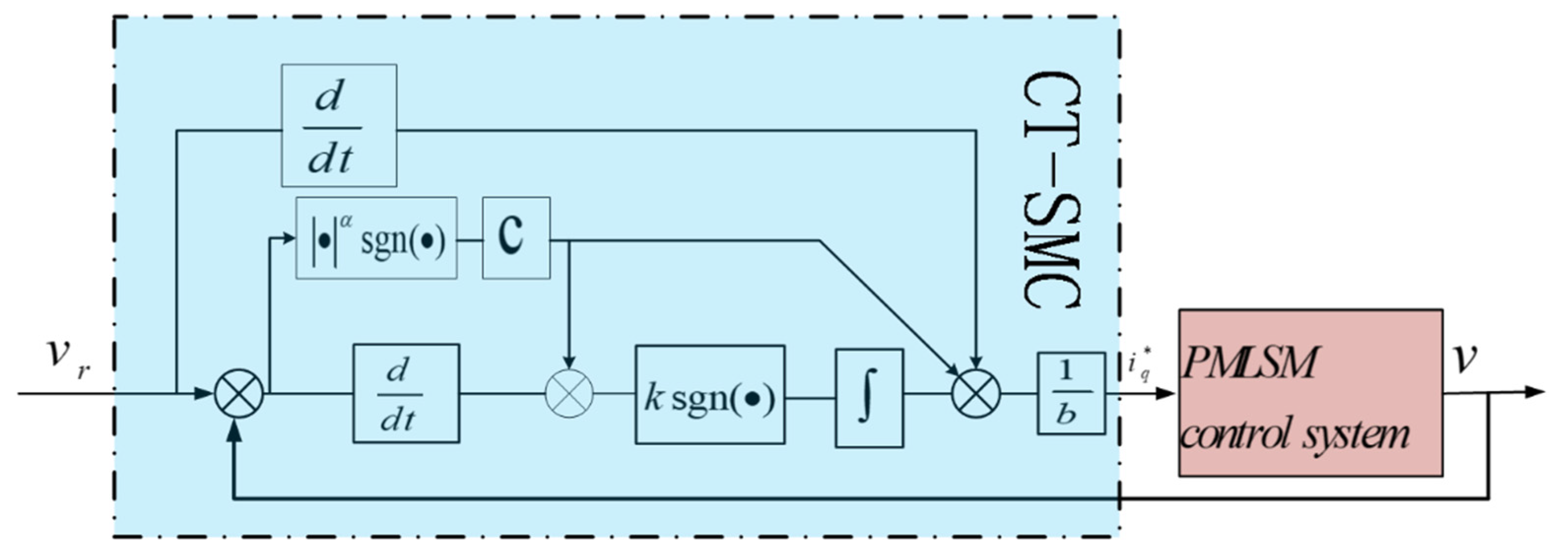
2.2. Design of CT-SMC
2.3. Stability Proof of CT-SMC
3. Design of F-ST-SMO
3.1. Traditional SMO
3.2. Super-Twisted Control Algorithm
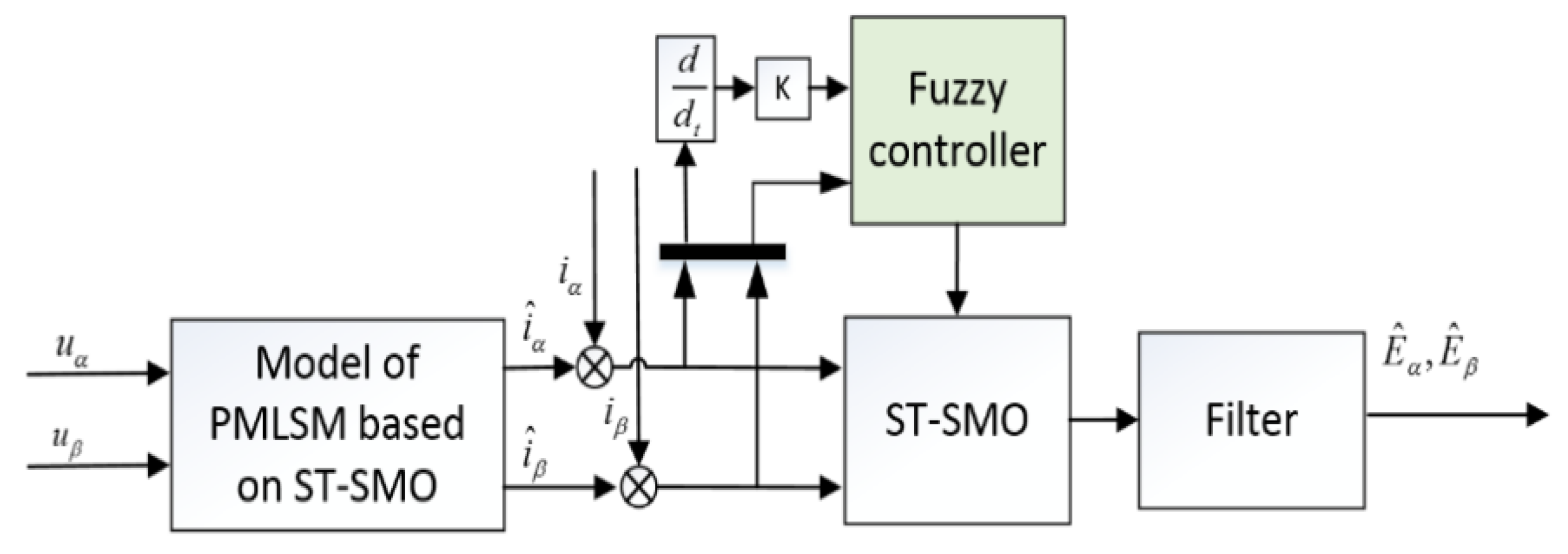
3.3. Design of Fuzzy Controller
3.4. Construction of F-ST-SMO Model
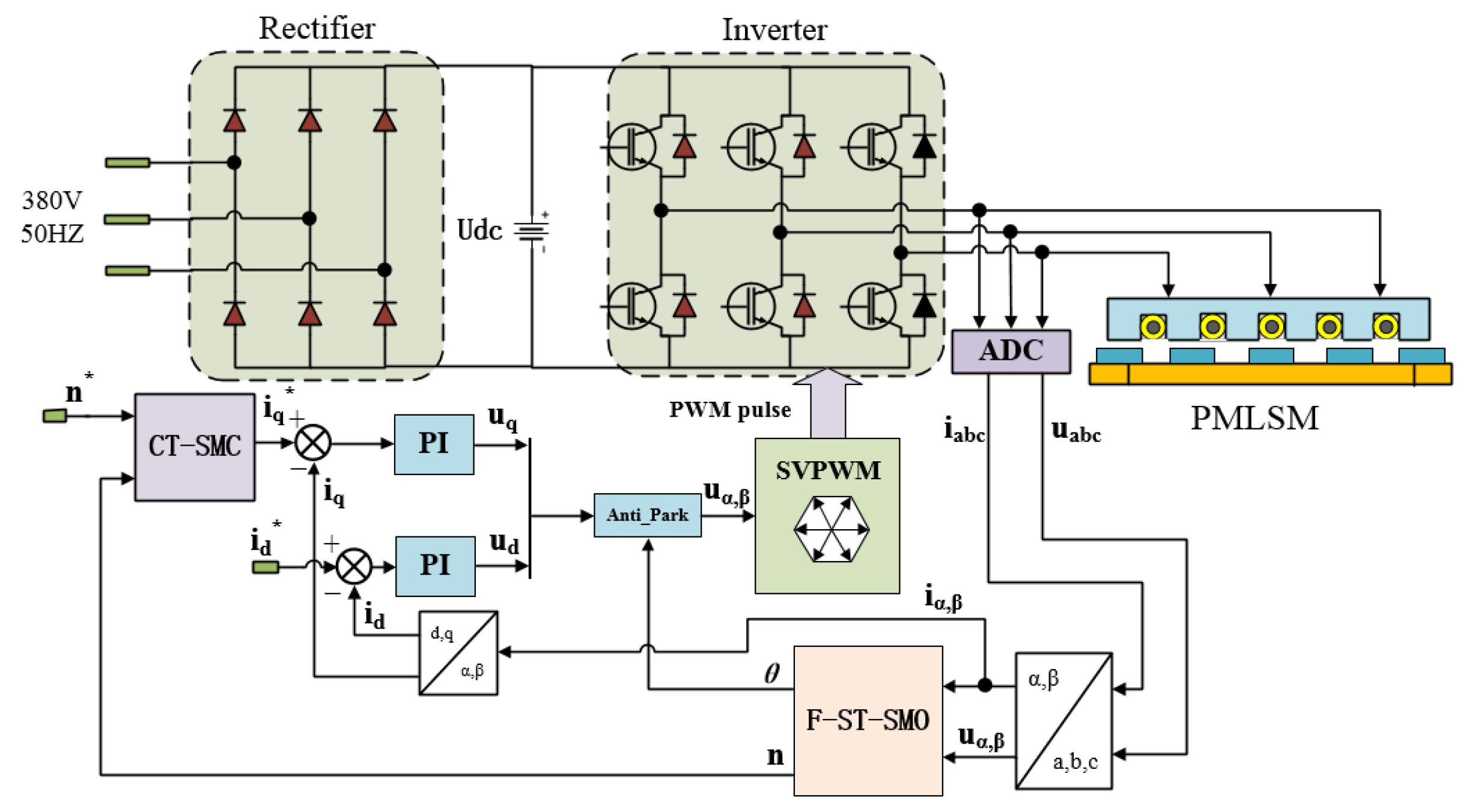
4. Simulation and Experimental Results
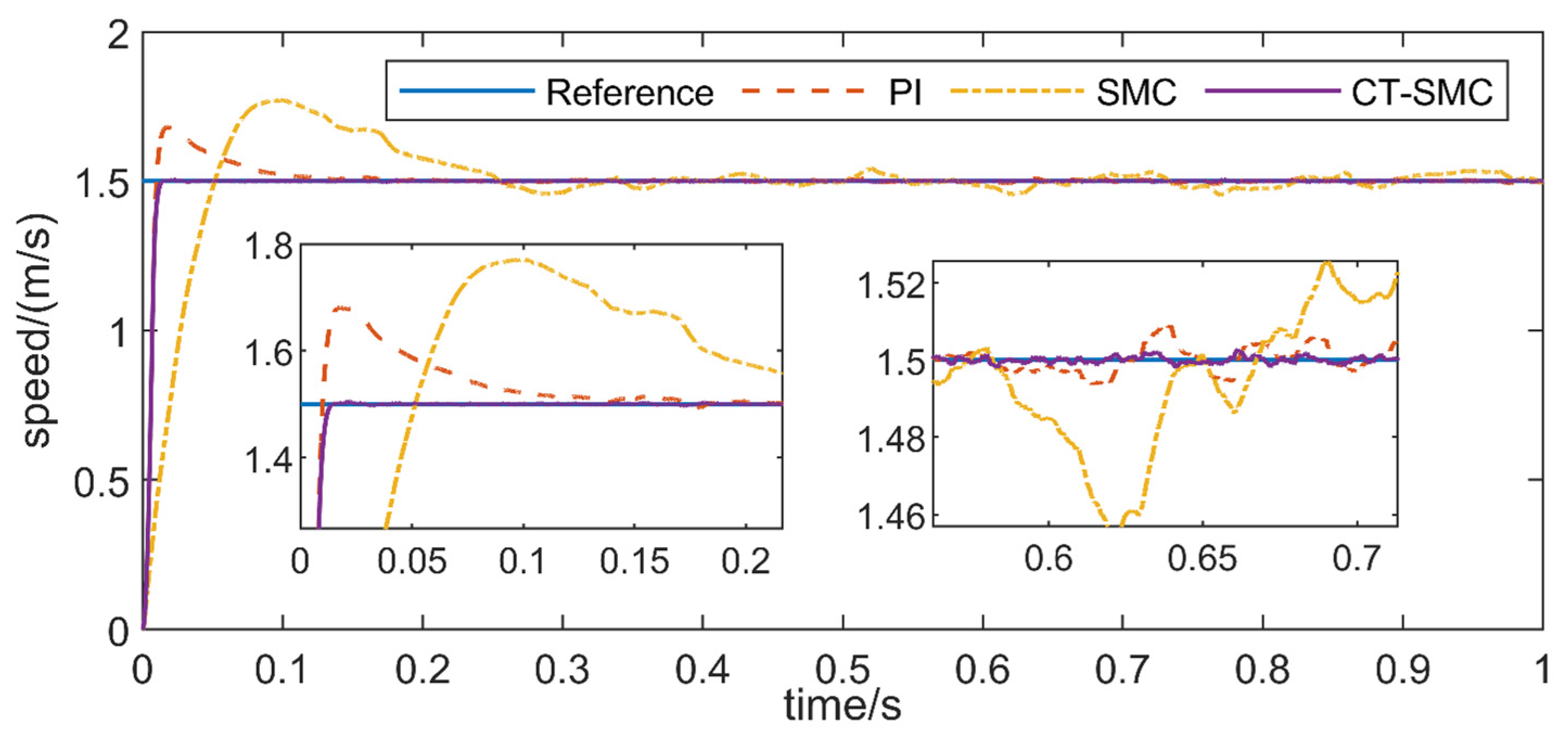
4.1. Comparison of Speed Controllers
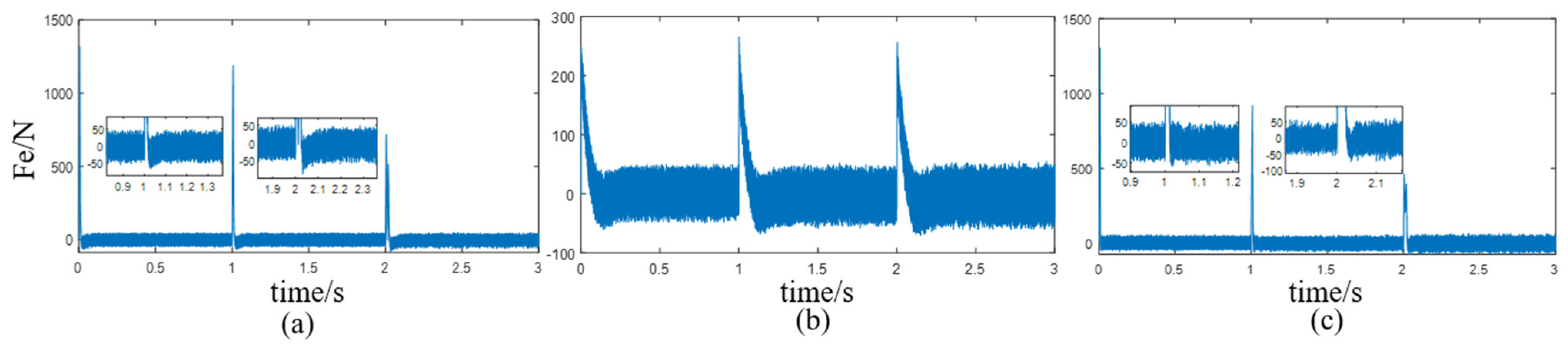
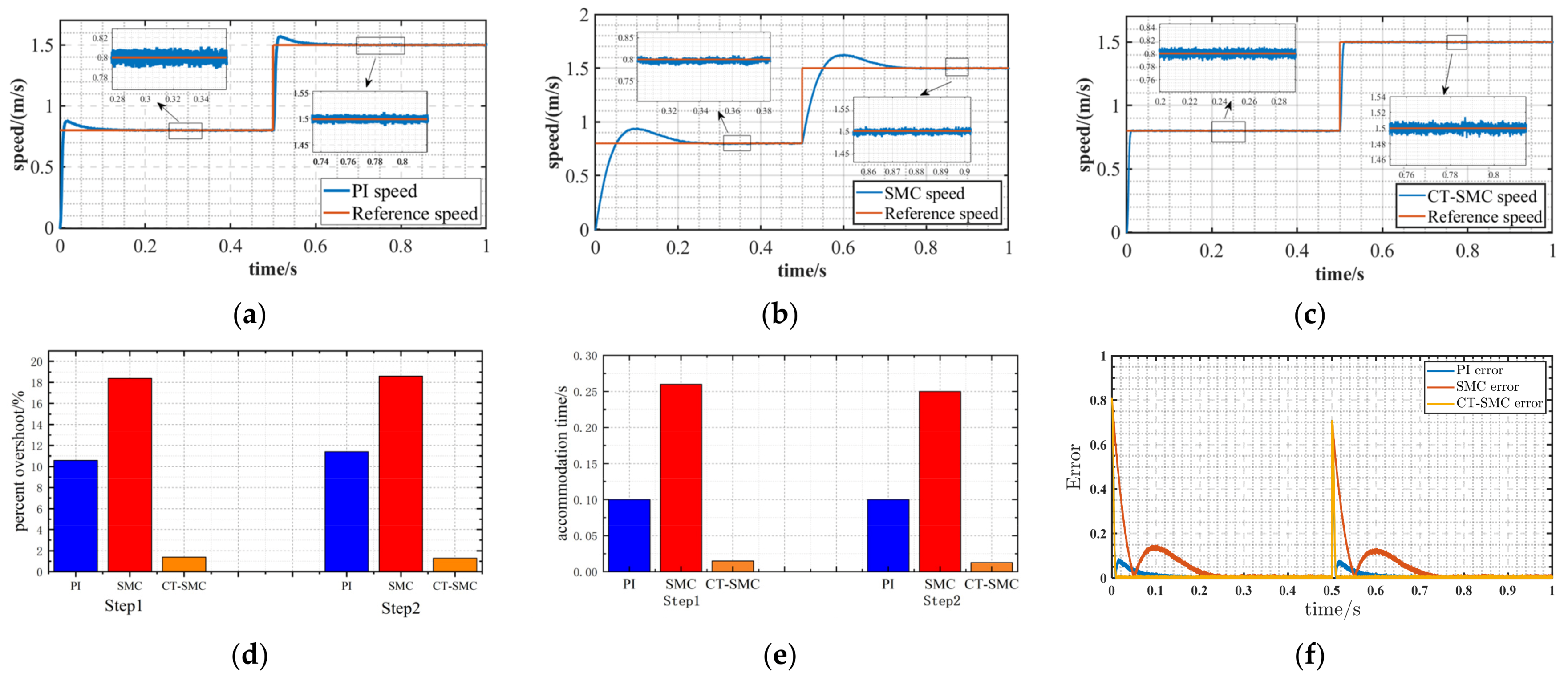
4.1.1. Constant Load, Varying Speed
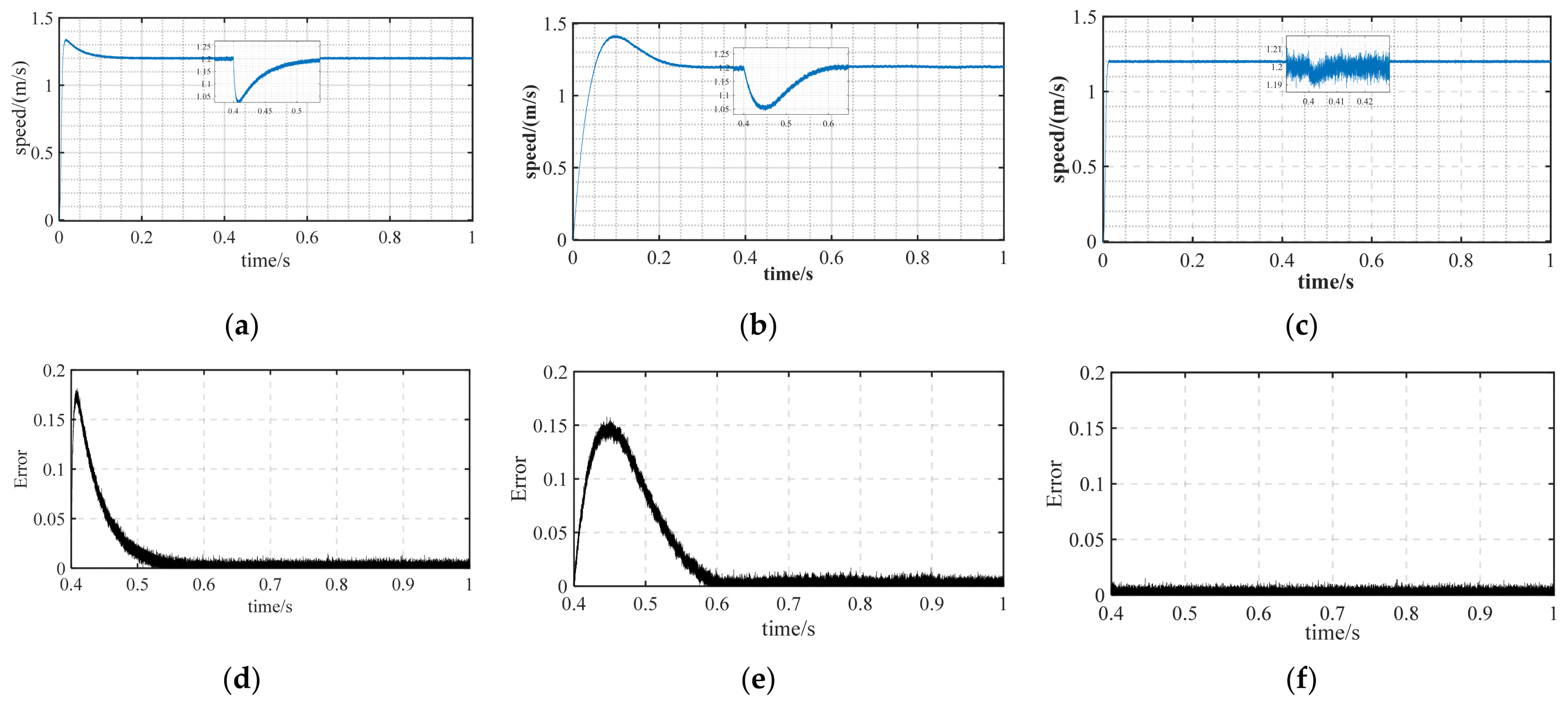
4.1.2. Constant Speed, Varying Load
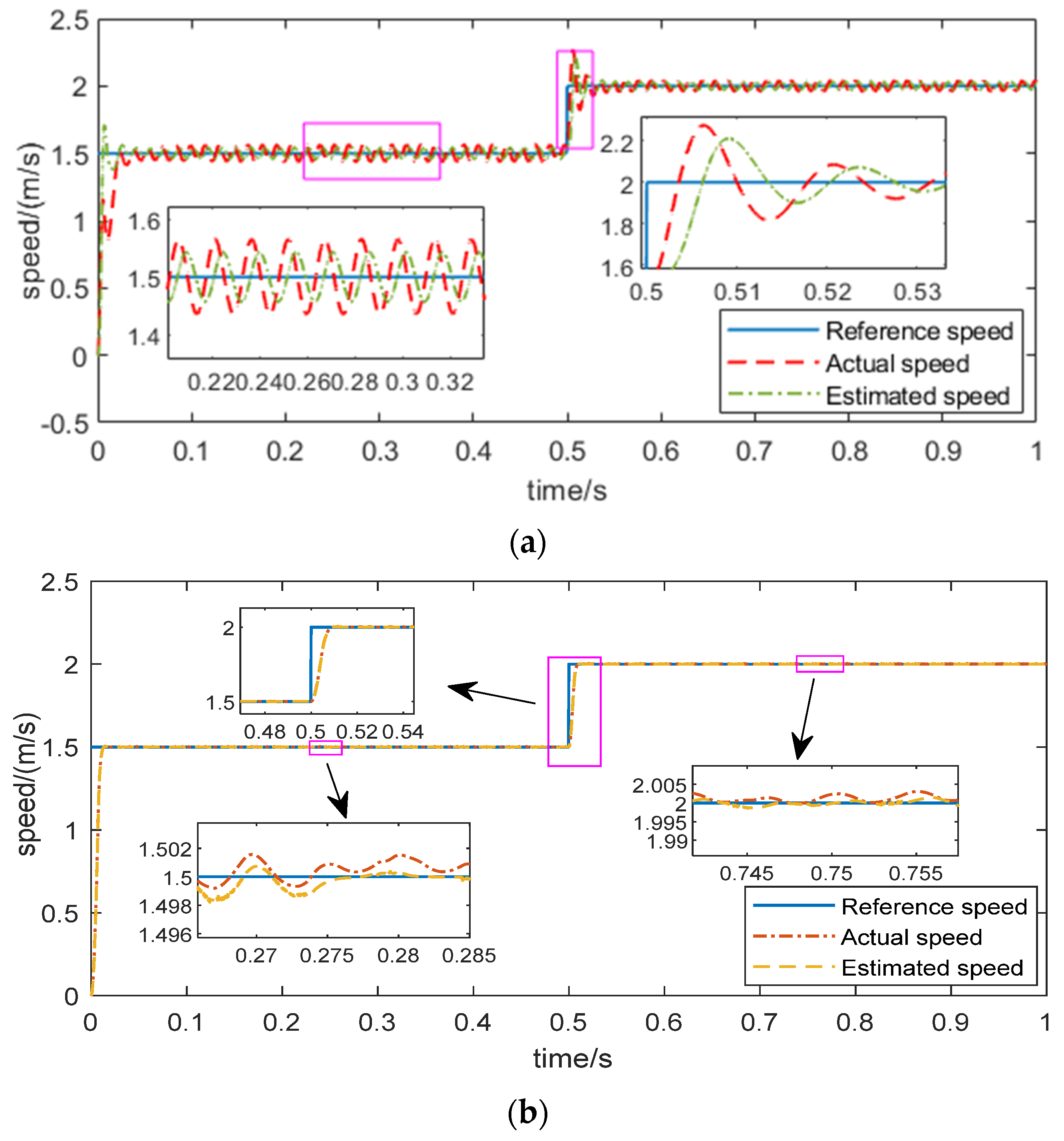
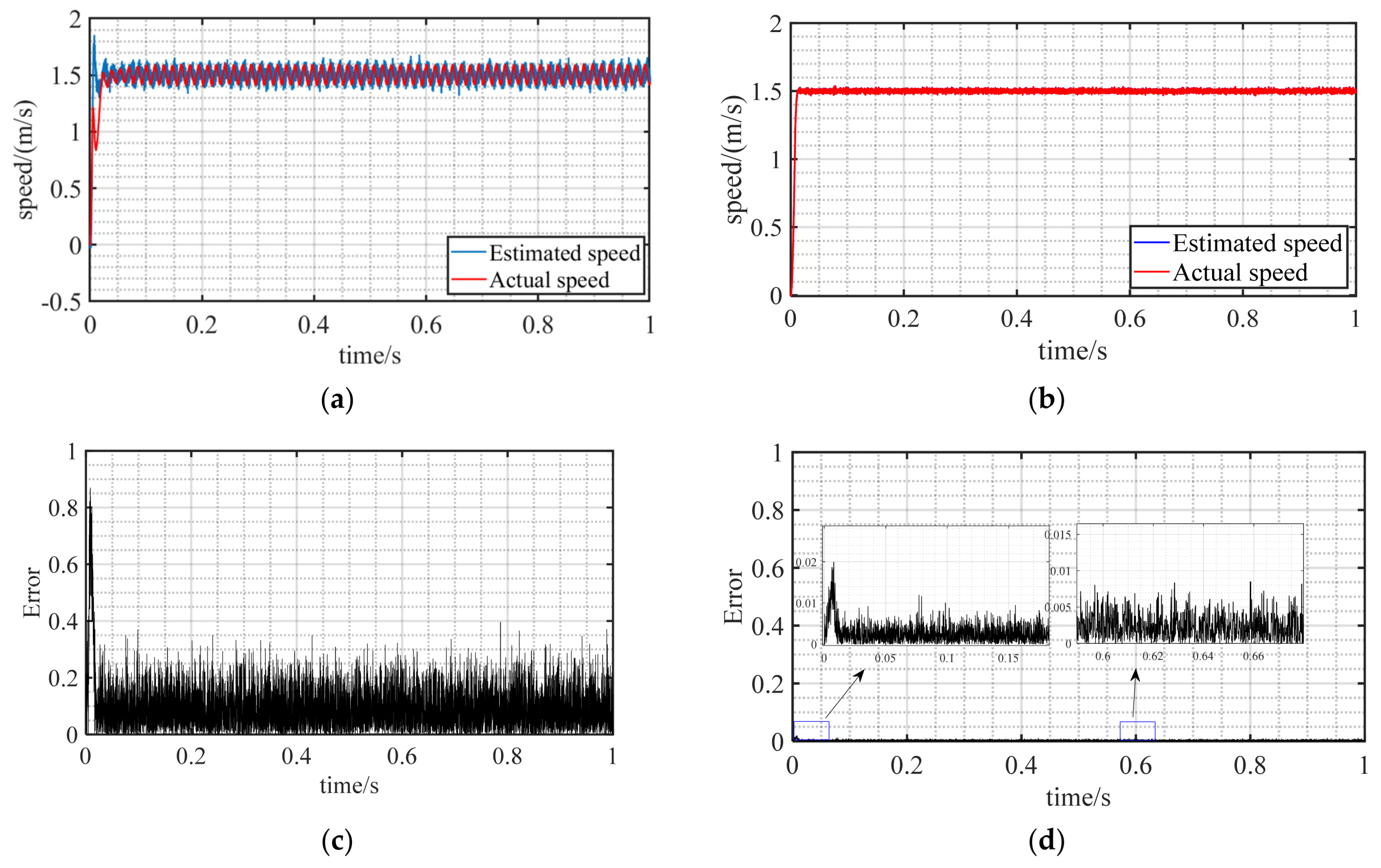
4.1.3. Observer Comparison
4.2. Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, J.-L.; Xiao, F.; Shen, Y.; Mai, Z.-Q.; Li, C.-R. Position-sensorless control technology of permanent-magnet synchronous motor—A review. Trans. China Electrotech. Soc. 2017, 32, 76–88. [Google Scholar]
- Yang, C.; Ma, T.; Che, Z.; Zhou, L. An adaptive-gain sliding mode observer for sensorless control of permanent magnet linear synchronous motors. IEEE Access 2018, 6, 3469–3478. [Google Scholar] [CrossRef]
- Ding, B.; Xu, D.; Jiang, B.; Shi, P.; Yang, W. Disturbance-observer-based terminal sliding mode control for linear traction system with prescribed performance. IEEE Trans. Transp. Electrif. 2021, 7, 649–658. [Google Scholar] [CrossRef]
- Zhao, X.; Fu, D. Adaptive neural network nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor. IEEE Access 2019, 7, 180361–180372. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Fridman, L.M. On adaptive sliding mode control without a priori bounded uncertainty. Automatica 2020, 111, 108650. [Google Scholar] [CrossRef]
- Cheema, M.A.M.; Fletcher, J.E.; Farshadnia, M.; Rahman, M.F. Sliding mode based combined speed and direct thrust force control of linear permanent magnet synchronous motors with first-order plus integral sliding condition. IEEE Trans. Power Electron. 2019, 34, 2526–2538. [Google Scholar] [CrossRef]
- Wang, W.; Lin, H.; Yang, H.; Liu, W.; Lyu, S. Second-order sliding mode-based direct torque control of variable-flux memory machine. IEEE Access 2020, 8, 34981–34992. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A composite sliding mode control for SPMSM drives based on a new hybrid reaching law with disturbance compensation. IEEE Trans. Transp. Electrif. 2021, 7, 1427–1436. [Google Scholar] [CrossRef]
- Jin, H.; Zhao, X. Approach angle-based saturation function of modified complementary sliding mode control for PMLSM. IEEE Access 2019, 7, 126014–126024. [Google Scholar] [CrossRef]
- Cheema, M.A.M.; Fletcher, J.E.; Farshadnia, M.; Xiao, D.; Rahman, M.F. Combined speed and direct thrust force control of linear permanent-magnet synchronous motors with sensorless speed estimation using a sliding-mode control with integral action. IEEE Trans. Ind. Electron. 2017, 64, 3489–3501. [Google Scholar] [CrossRef]
- Yang, R.; Li, L.-Y.; Wang, M.-Y.; Zhang, C.-M.; Zeng-Gu, Y.-M. Force ripple estimation and compensation of PMLSM with incremental extended state modeling-based kalman filter: A practical tuning method. IEEE Access 2019, 7, 108331–108342. [Google Scholar] [CrossRef]
- Wen, T.; Wang, Z.; Xiang, B.; Han, B.; Li, H. Sensorless Control of Segmented PMLSM for Long-Distance Auto-Transportation System Based on Parameter Calibration. IEEE Access 2020, 8, 102467–102476. [Google Scholar] [CrossRef]
- Wang, A.; Jia, X.; Dong, S. A new exponential reaching law of sliding mode control to improve performance of permanent magnet synchronous motor. IEEE Trans. Magn. 2013, 49, 2409–2412. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Ioannou, P.A. An Adaptive Control Framework for Underactuated Switched Euler-Lagrange Systems. IEEE Trans. Autom. Control 2021. [Google Scholar] [CrossRef]
- Xu, Z.; Rahman, M.F. Comparison of a sliding observer and a kalman filter for direct-torque-controlled IPM synchronous motor drives. IEEE Trans. Ind. Electron. 2012, 59, 4179–4188. [Google Scholar] [CrossRef]
- Cao, R.; Jiang, N.; Lu, M. Sensorless control of linear flux-switching permanent magnet motor based on extended kalman filter. IEEE Trans. Ind. Electron. 2020, 67, 5971–5979. [Google Scholar] [CrossRef]
- Zhou, Z.; Xia, C.; Yan, Y.; Wang, Z.; Shi, T. Disturbances attenuation of permanent magnet synchronous motor drives using cascaded predictive-integral-resonant controllers. IEEE Trans. Power Electron. 2018, 33, 1514–1527. [Google Scholar] [CrossRef]
- Wen, T.; Liu, Y.; Wu, Q.H.; Qiu, L. Cascaded sliding-mode observer and its applications in output feedback control part I: Observer design and stability analysis. CSEE J. Power Energy Syst. 2021, 7, 295–306. [Google Scholar]
- Rsetam, K.; Cao, Z.; Man, Z. Cascaded-extended-state-observer-based sliding-mode control for underactuated flexible joint robot. IEEE Trans. Ind. Electron. 2020, 67, 10822–10832. [Google Scholar] [CrossRef]



| NB | NS | ZO | PS | PB | |
|---|---|---|---|---|---|
| NB | PB | PB | B | B | M |
| NS | PB | B | B | M | M |
| ZO | B | M | M | S | S |
| PS | S | M | M | B | B |
| PB | M | B | B | PB | PB |
| Parameter | Value |
|---|---|
| stator resistance Rs/Ω | 4.0 |
| d-q axis inductance Ldq/mH | 8.2 |
| Mover mass m/kg | 1.425 |
| Viscous friction coefficient B/N/m·s | 44 |
| Polar distance τ/m | 0.016 |
| DC Bus Voltage U/V | 48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, J.; Wang, S.; Feng, S.; Zhu, Y.; Sun, H. Design of Sensorless Speed Control System for Permanent Magnet Linear Synchronous Motor Based on Fuzzy Super-Twisted Sliding Mode Observer. Electronics 2022, 11, 1394. https://doi.org/10.3390/electronics11091394
Li Z, Wang J, Wang S, Feng S, Zhu Y, Sun H. Design of Sensorless Speed Control System for Permanent Magnet Linear Synchronous Motor Based on Fuzzy Super-Twisted Sliding Mode Observer. Electronics. 2022; 11(9):1394. https://doi.org/10.3390/electronics11091394
Chicago/Turabian StyleLi, Zheng, Jinsong Wang, Shaohua Wang, Shengdi Feng, Yiding Zhu, and Hexu Sun. 2022. "Design of Sensorless Speed Control System for Permanent Magnet Linear Synchronous Motor Based on Fuzzy Super-Twisted Sliding Mode Observer" Electronics 11, no. 9: 1394. https://doi.org/10.3390/electronics11091394






