AZO Thin Films by Sol-Gel Process for Integrated Optics
Abstract
:1. Introduction
2. Experimental Section
3. Results and Discussion
3.1. Microstructural Characterizations
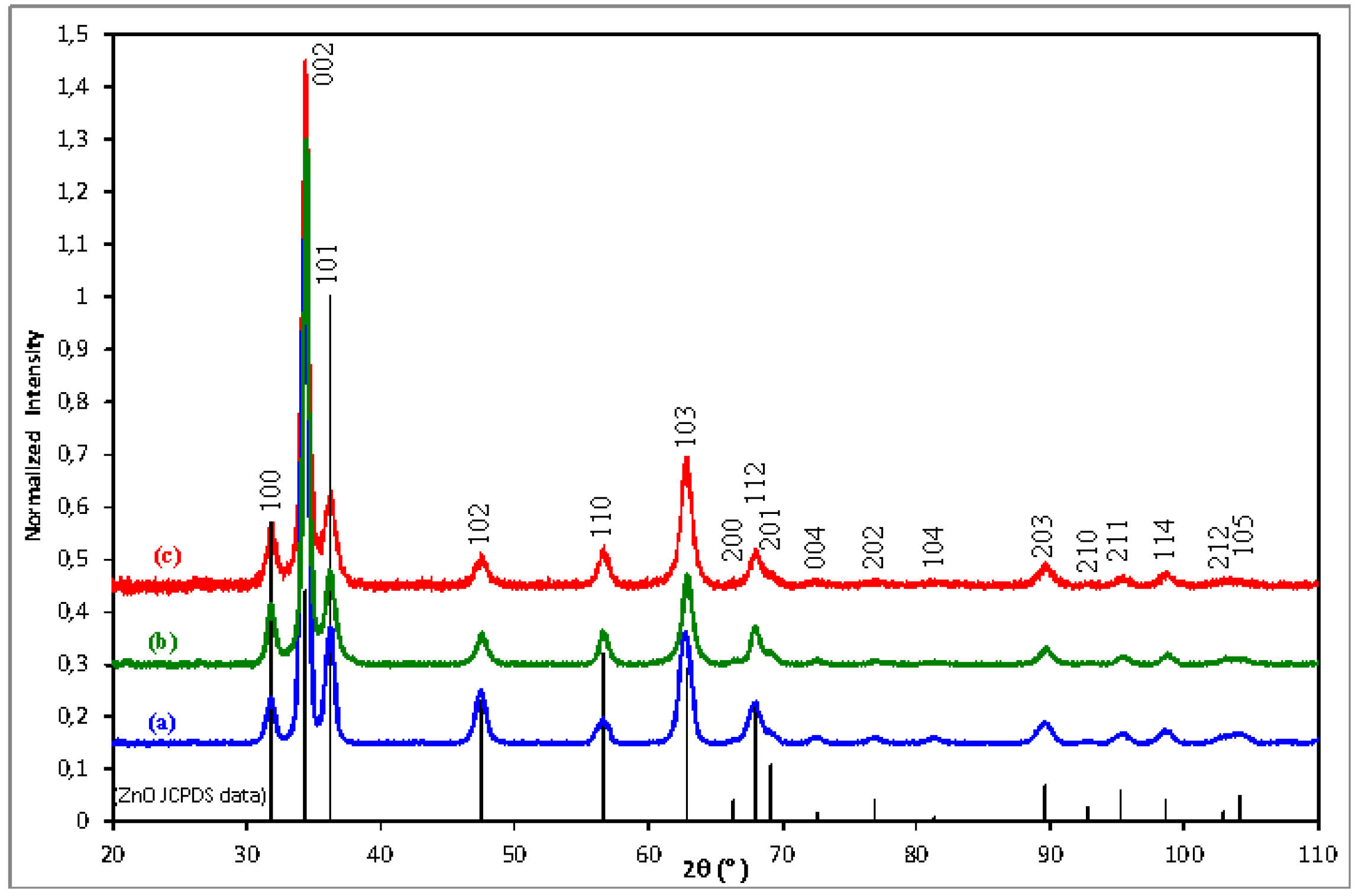
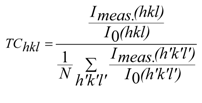
| Sample | Diffraction peaks | ||||||
|---|---|---|---|---|---|---|---|
| (100) | (002) | (101) | (102) | (110) | (103) | (112) | |
| Undoped ZnO | 0.200 | 3.009 | 0.327 | 0.849 | 0.248 | 1.533 | 0.834 |
| 1 at.% Al-doped ZnO | 0.322 | 3.132 | 0.413 | 0.607 | 0.362 | 1.550 | 0.614 |
| 2 at.% Al-doped ZnO | 0.290 | 3.146 | 0.327 | 0.505 | 0.347 | 1.899 | 0.486 |
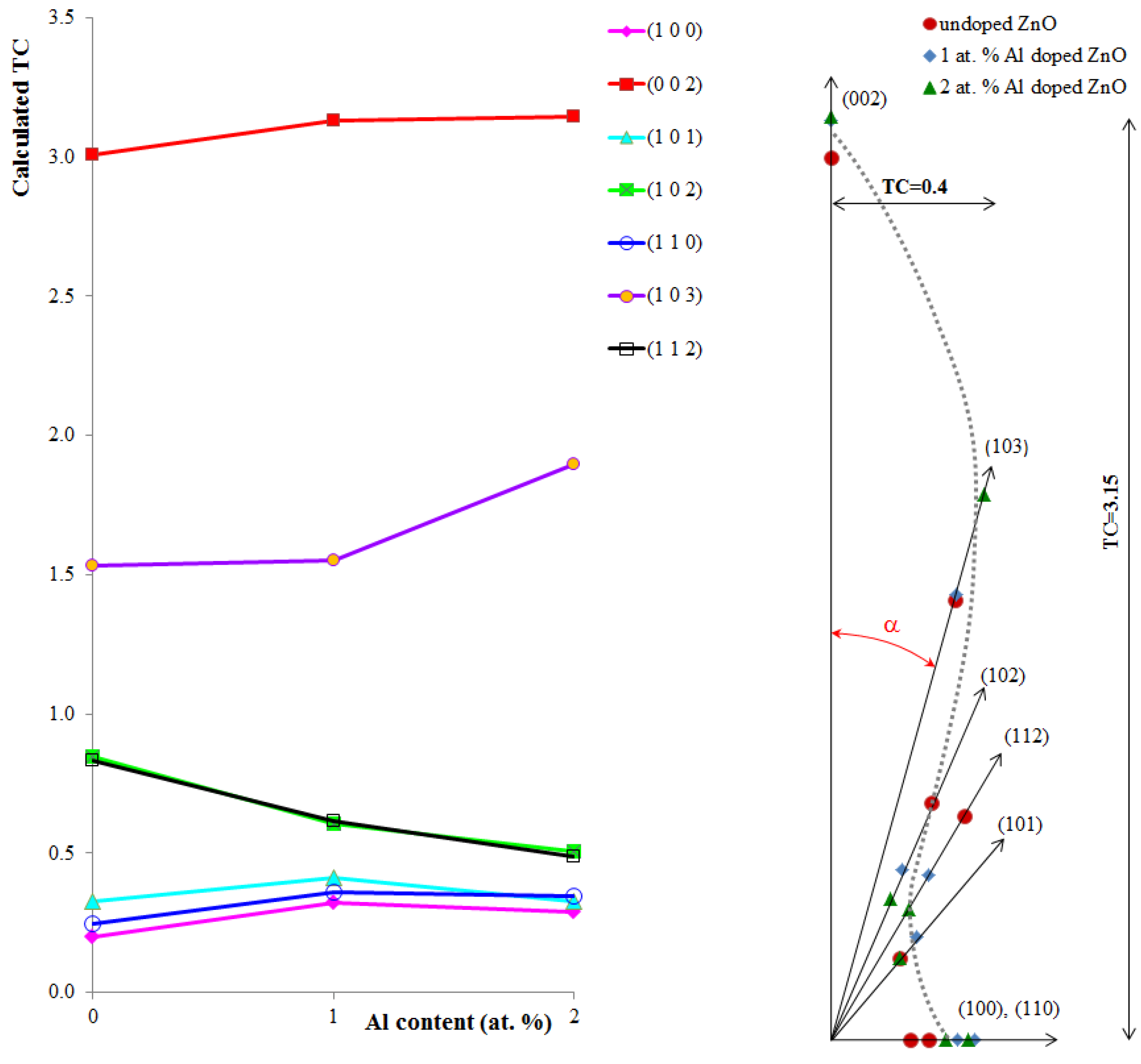


3.2. Optical Characterizations
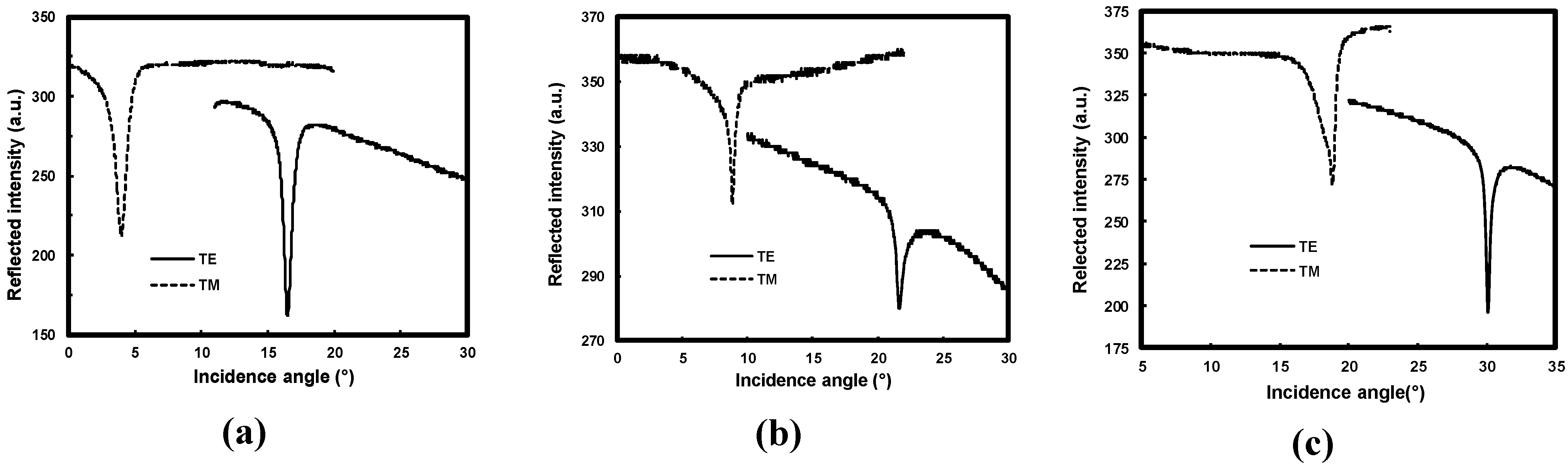
3.2.1. m-Lines Measurements
 and
and  are the phase shift at air/film and film/substrate interfaces, d is the film thickness, λ is the wavelength of the light in vacuum, na and ns are, respectively, the air and substrate refractive indices, m the mode number and Nm the effective index of the mth mode. From Equation 2 we computed the refractive indices and thickness of the film from the measured effective mode indices. At least two modes are generally needed. Because our waveguides are single mode, we use the measured value of the effective indices and that of thickness measured by the SEM. The calculation is based on the least square method widely discussed by Kersten [53] and the results are reported in Table 2.
are the phase shift at air/film and film/substrate interfaces, d is the film thickness, λ is the wavelength of the light in vacuum, na and ns are, respectively, the air and substrate refractive indices, m the mode number and Nm the effective index of the mth mode. From Equation 2 we computed the refractive indices and thickness of the film from the measured effective mode indices. At least two modes are generally needed. Because our waveguides are single mode, we use the measured value of the effective indices and that of thickness measured by the SEM. The calculation is based on the least square method widely discussed by Kersten [53] and the results are reported in Table 2.| Sample | Undoped ZnO | 1 at.% Al-doped ZnO | 2 at.% Al-doped ZnO | |||
|---|---|---|---|---|---|---|
| Thickness (nm), d | 325 | 320 | 240 | |||
| Polarization | TE | TM | TE | TM | TE | TM |
| Effective index, N0 | 1.7540 | 1.7253 | 1.7369 | 1.7066 | 1.6425 | 1.5937 |
| Refractive index, n | 1.8699 | 1.8862 | 1.8545 | 1.8698 | 1.8023 | 1.8137 |
3.2.2. Optical Anisotropy Study
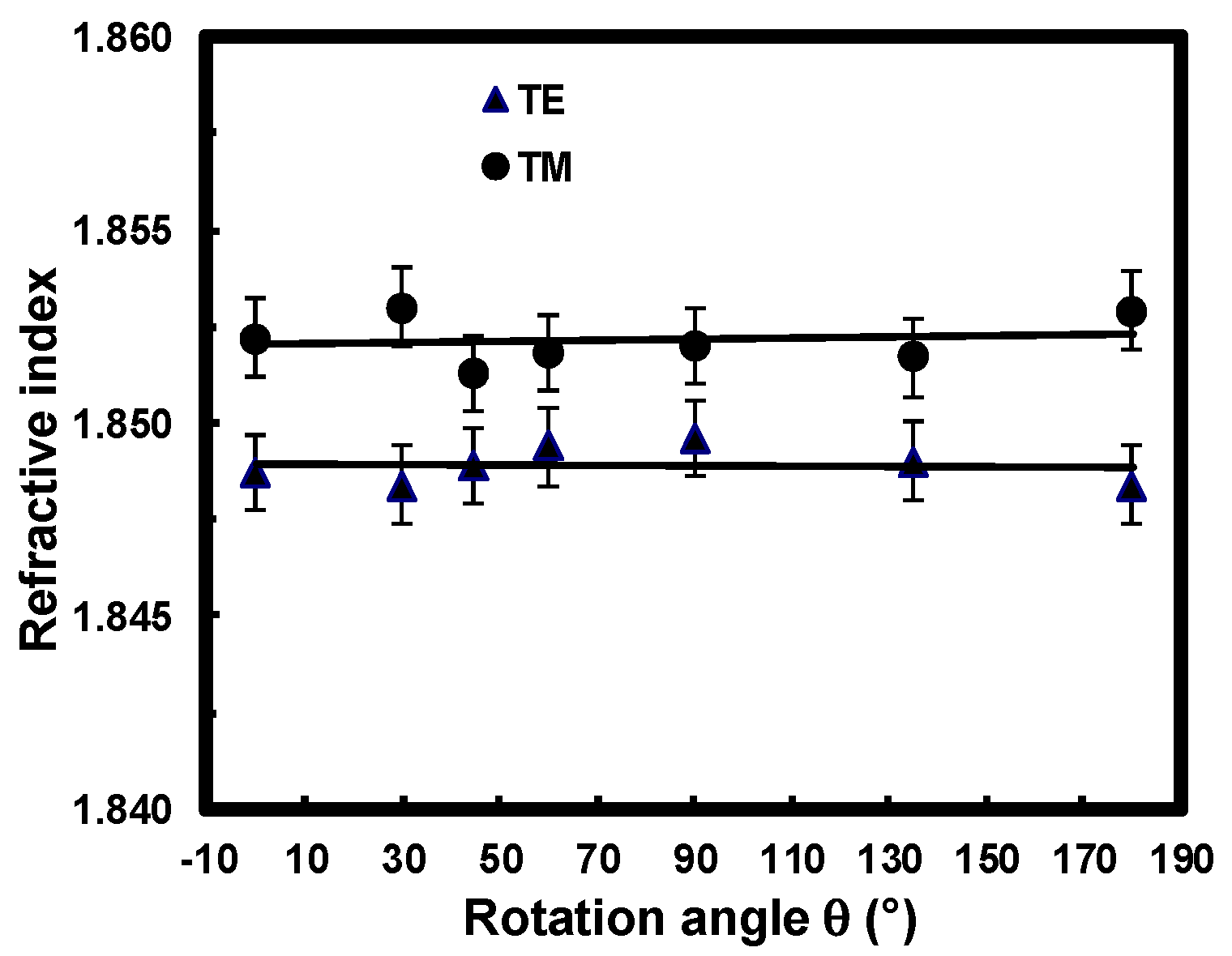
3.2.3. Optical Losses
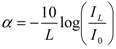
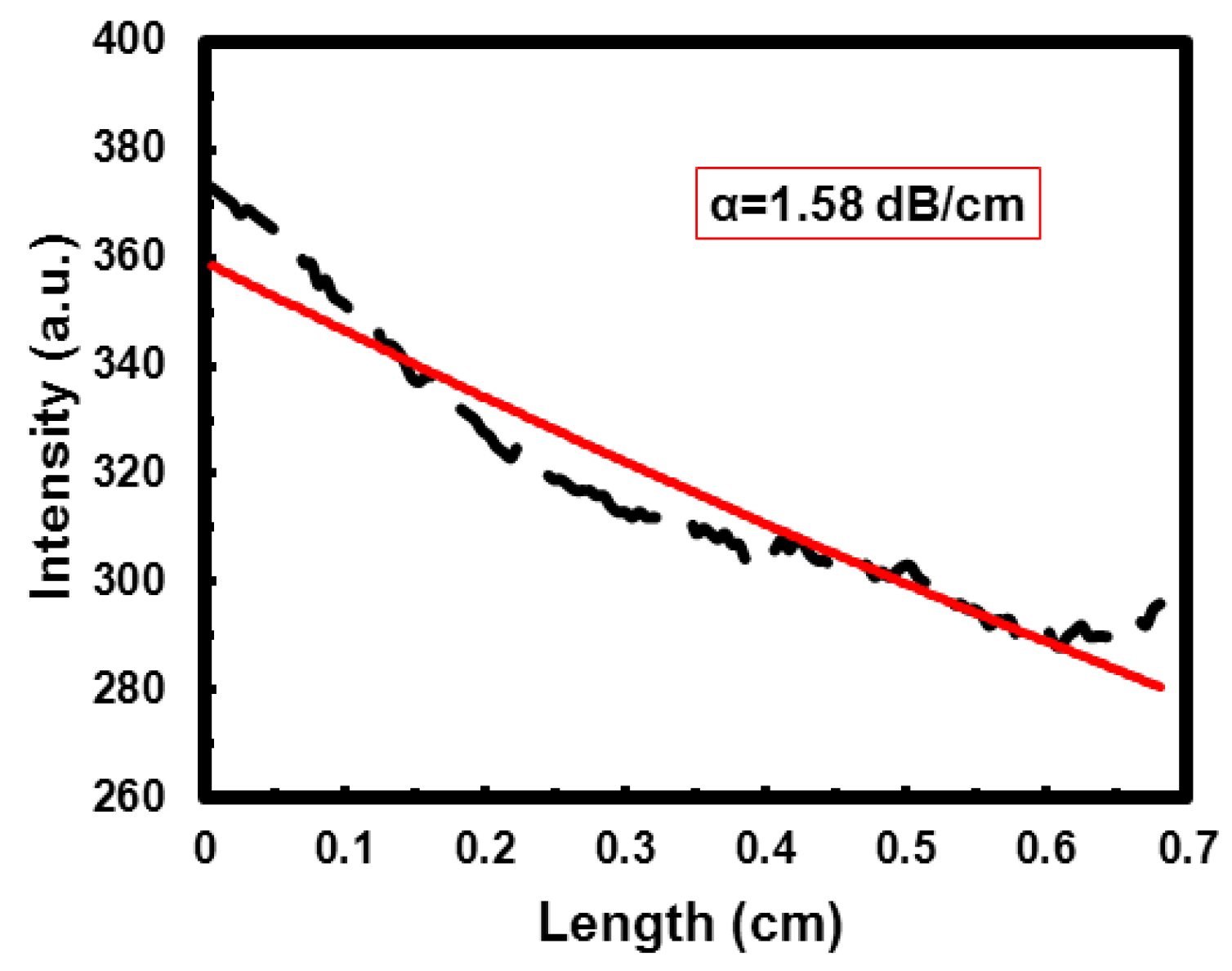
4. Conclusions
Acknowledgments
References
- Ellmer, K.; Klein, A. ZnO and Its Applications. In Transparent Conductive Zinc Oxide—Basics and Applications in Thin Film Solar Cells; Springer Series in Materials Science; Ellmer, K., Klein, A., Rech, B., Eds.; Springer-Verlag: Berlin Heidelberg, Germany, 2008; Volume 104, pp. 1–33. [Google Scholar]
- Bundesmann, C.; Schmidt-Grund, R.; Schubert, M. Optical Properties of ZnO and Related Compounds. In Transparent Conductive Zinc Oxide—Basics and Applications in Thin Film Solar Cells (Springer Series in Materials Science); Ellmer, K., Klein, A., Rech, B., Eds.; Springer-Verlag: Berlin Heidelberg, Germany, 2008; Volume 104, pp. 79–124. [Google Scholar]
- Chen, J.L.; Chen, D.; Chen, Z.H. Optimization of the process for preparing Al-doped ZnO thin films by sol-gel method. Sci. China Ser. E Tech. Sci. 2009, 52, 88–94. [Google Scholar] [CrossRef]
- Tseng, Y.K.; Gao, G.J.; Chien, S.C. Synthesis of c-axis preferred orientation ZnO:Al transparent conductive thin films using a novel solvent method. Thin Solid Films 2010, 518, 6259–6263. [Google Scholar] [CrossRef]
- Lupan, O.; Chow, L.; Shishiyanu, S.; Monaico, E.; Shishiyanu, T.; Şontea, V.; Roldan Cuenya, B.; Naitabdi, A.; Park, S.; Schulte, A. Nanostructured zinc oxide films synthesized by successive chemical solution deposition for gas sensor applications. Mater. Res. Bull. 2009, 44, 63–69. [Google Scholar] [CrossRef]
- Lupan, O.; Shishiyanu, S.; Ursaki, V.; Khallaf, H.; Chow, L.; Shishiyanu, T.; Sontea, V.; Monaico, E.; Railean, S. Synthesis of nanostructured Al-doped zinc oxide films on Si for solar cells applications. Sol. Energy. Mater. Sol. Cells 2009, 93, 1417–1422. [Google Scholar] [CrossRef]
- Von Wenckstern, H.; Schmidt, H.; Brandt, M.; Lajn, A.; Pickenhain, R.; Lorenz, M.; Grundmann, M.; Hofmann, D.M.; Polity, A.; Meyer, B.K.; et al. Anionic and cationic substitution in ZnO. Prog. Solid State Chem. 2009, 37, 153–172. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov Ya, I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doğan, S.; Avrutin, V.; Cho, S.J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301:1–041301:103. [Google Scholar]
- Schmidt-Mende, L.; MacManus-Driscoll, J.L. ZnO-nanostructures, defects, and devices. Mater. Today 2007, 10, 40–48. [Google Scholar] [CrossRef]
- Leprince-Wang, Y.; Bouchaib, S.; Brouri, T.; Capo-chichi, M.; Laurent, K.; Leopoldes, J.; Tusseau-Nenez, S.; Lei, L.; Chen, Y. Fabrication of ZnO micro- and nano-structures by electrodeposition using nanoporous and lithography defined templates. Mater. Sci. Eng. B 2010, 170, 107–112. [Google Scholar] [CrossRef]
- Vayssieres, L. Growth of arrayed nanorods and nanowires of ZnO from aqueous solutions. Adv. Mater. 2003, 15, 464–466. [Google Scholar] [CrossRef]
- Chandramohan, R.; Vijayan, T.A.; Arumugam, S.; Ramalingam, H.B.; Dhanasekaran, V.; Sundaram, K.; Mahalingam, T. Effect of heat treatment on microstructural and optical properties of CBD grown Al-doped ZnO thin films. Mater. Sci. Eng. B 2011, 176, 152–156. [Google Scholar] [CrossRef]
- Barankin, M.D.; Gonzalez, E., II; Ladwig, A.M.; Hicks, R.F. Plasma-enhanced chemical vapor deposition of zinc oxide at atmospheric pressure and low temperature. Sol. Energy. Mater. Sol. Cells 2007, 91, 924–930. [Google Scholar]
- Dai, L.P.; Deng, H.; Zang, J.D.; Mao, F.Y.; Chen, J.J.; Wei, M. The effect of annealing temperature on the properties of ZnO films with preferential nonpolar plane orientation by SSCVD. J. Mater. Sci. 2008, 43, 312–315. [Google Scholar]
- Triboulet, R.; Perrière, J. Epitaxial growth of ZnO films. Prog. Cryst. Growth Charact. Mater. 2003, 47, 65–138. [Google Scholar]
- Szyszka, B. Magnetron Sputtering of ZnO Films. In Transparent Conductive Zinc Oxide—Basics and Applications in Thin Film Solar Cells; Springer Series in Materials Science; Ellmer, K., Klein, A., Rech, B., Eds.; Springer-Verlag: Berlin Heidelberg, Germany, 2008; Volume 104, pp. 187–233. [Google Scholar]
- Hüpkes, J.; Müller, J.; Rech, B. Texture Etched ZnO:Al for Silicon Thin Film Solar Cells. In Transparent Conductive Zinc Oxide—Basics and Applications in Thin Film Solar Cells; Springer Series in Materials Science; Ellmer, K., Klein, A., Rech, B., Eds.; Springer-Verlag: Berlin Heidelberg, Germany, 2008; Volume 104, pp. 359–413. [Google Scholar]
- Sekar, A.; Kim, S.H.; Umar, A.; Hahn, Y.B. Catalyst-free synthesis of ZnO nanowires on Si by oxidation of Zn powders. J. Cryst. Growth 2005, 277, 471–478. [Google Scholar] [CrossRef]
- Ibanga, E.J.; le Luyer, C.; Mugnier, J. Zinc oxide waveguide produced by thermal oxidation of chemical bath deposited zinc sulphide thin films. Mater. Chem. Phys. 2003, 80, 490–495. [Google Scholar] [CrossRef]
- Caglar, M.; Ilican, S.; Caglar, Y.; Yakuphanoglu, F. The effects of Al doping on the optical constants of ZnO thin films prepared by spray pyrolysis method. J. Mater. Sci. Mater. Electron. 2008, 19, 704–708. [Google Scholar] [CrossRef]
- Yen, C.Y.; Jian, S.R.; Chen, G.J.; Lin, C.M.; Lee, H.Y.; Ke, W.C.; Liao, Y.Y.; Yang, P.F.; Wang, C.T.; Lai, Y.S.; et al. Influence of annealing temperature on the structural, optical and mechanical properties of ALD-derived ZnO thin films. Appl. Surf. Sci. 2011, 257, 7900–7905. [Google Scholar] [CrossRef]
- Ghodsi, F.E.; Absalan, H. Comparative study of ZnO thin films prepared by different sol-gel route. Acta. Phys. Pol. A 2010, 118, 659–664. [Google Scholar]
- Znaidi, L. Sol-gel-deposited ZnO thin films: A review. Mater. Sci. Eng. B 2010, 174, 18–30. [Google Scholar] [CrossRef]
- Ohyama, M.; Kozuka, H.; Yoko, T.; Sakka, S. Preparation of ZnO films with preferential orientation by sol-gel method. J. Ceram. Soc. Jpn. 1996, 104, 296–300. [Google Scholar] [CrossRef]
- Ohyama, M.; Kozuka, H.; Yoko, T. Sol-Gel preparation of ZnO films with extremely preferred orientation along (002) plane from zinc acetate solution. Thin Solid Films 1997, 306, 78–85. [Google Scholar] [CrossRef]
- Znaidi, L.; Soler Illia, G.J.A.A.; Ben Yahia, S.; Sanchez, C.; Kanaev, A. Oriented ZnO thin films synthesis by sol-gel process for laser application. Thin Solid Films 2003, 428, 257–262. [Google Scholar] [CrossRef]
- Znaidi, L.; Soler Illia, G.J.A.A.; Le Guennic, R.; Sanchez, C.; Kanaev, A. Elaboration of ZnO thin films with preferential orientation by a soft chemistry route. J. Sol-Gel Sci. 2003, 26, 817–821. [Google Scholar] [CrossRef]
- Ben Yahia, S.; Znaidi, L.; Kanaev, A.; Petitet, J.P. Raman study of oriented ZnO thin films deposited by sol-gel method. Spectrochim. Acta Part. A 2008, 71, 1234–1238. [Google Scholar] [CrossRef]
- Xue, S.W.; Zu, X.T.; Zhou, W.L.; Deng, H.X.; Xiang, X.; Zhang, L.; Deng, H. Effects of post-thermal annealing on the optical constants of ZnO thin film. J. Alloys Compd. 2008, 448, 21–26. [Google Scholar] [CrossRef]
- Serbetçi, Z.; El-Nasser, H.M.; Yakuphanoglu, F. Photoluminescence and refractive index dispersion properties of ZnO nanofibers grown by sol-gel method. Spectrochim. Acta Part. A 2012, 86, 405–409. [Google Scholar] [CrossRef]
- Tang, W.; Cameron, D.C. Aluminum-doped zinc oxide transparent conductors deposited by the sol-gel process. Thin Solid Films 1994, 238, 83–87. [Google Scholar] [CrossRef]
- Ohyama, M. Sol-Gel preparation of transparent and conductive aluminum-doped zinc oxide films with highly preferential crystal orientation. J. Am. Ceram. Soc. 1998, 81, 1622–1632. [Google Scholar] [CrossRef]
- Schuler, T.; Aegerter, M.A. Optical, electrical and structural properties of sol-gel ZnO:Al coatings. Thin Solid Films 1999, 351, 125–131. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Paul, G.K.; Roy, R.; Sen, S.K.; Sen, S. Study of structural and electrical properties of grain-boundary modified ZnO films prepared by sol-gel technique. Mater. Chem. Phys. 2002, 74, 83–91. [Google Scholar] [CrossRef]
- Cheong, K.Y.; Norani Muti, M.; Sutapa, R.R. Physical Investigation on ZnO:Al Thin films derived from non-alkoxide zinc acetate via sol-gel dip coating technique. J. Mater. Sci. Technol. 2003, 11, 78–83. [Google Scholar]
- Lee, J.H.; Park, B.O. Transparent conducting ZnO:Al, In and Sn thin films deposited by the sol-gel method. Thin Solid Films 2003, 426, 94–99. [Google Scholar] [CrossRef]
- Xue, S.W.; Zu, X.T.; Zheng, W.G.; Deng, H.X.; Xiang, X. Effects of Al doping concentration on optical parameters of ZnO:Al thin films by sol-gel technique. Physica B 2006, 381, 209–213. [Google Scholar] [CrossRef]
- Lai, C.M.; Lin, K.M.; Rosmaidah, S. Effect of annealing temperature on the quality of Al-doped ZnO thin films prepared by sol-gel method. J. Sol.-Gel Sci. Technol. 2011. [Google Scholar] [CrossRef]
- Khan, F.; Singh, V.S.N.; Husain, M.; Singh, P.K. Sol-gel derived hydrogen annealed ZnO:Al films for silicon solar cell application. Sol. Energy. Mater. Sol. Cells 2012, 100, 57–60. [Google Scholar] [CrossRef]
- Altamirano-Juárez, D.C.; Torres-Delgado, G.; Jiménez-Sandoval, S.; Jiménez-Sandoval, O.; Castanedo-Pérez, R. Low-resistivity ZnO:F:Al transparent thin films. Sol. Energy. Mater. Sol. Cells 2004, 82, 35–43. [Google Scholar]
- Lv, J.; Huang, K.; Chen, X.; Zhu, J.; Cao, C.; Song, X.; Sun, Z. Optical constants of Na-doped ZnO thin films by sol-gel method. Opt. Commun. 2011, 284, 2905–2908. [Google Scholar]
- Caglar, M.; Yakuphanoglu, F. Structural and optical properties of copper doped ZnO films derived by sol-gel. Appl. Surf. Sci. 2012, 258, 3039–3044. [Google Scholar]
- Tsay, C.Y.; Cheng, H.C.; Tung, Y.T.; Tuan, W.H.; Lin, C.K. Effect of Sn-doped on microstructural and optical properties of ZnO thin films deposited by sol-gel method. Thin Solid Films 2008, 517, 1032–1036. [Google Scholar] [CrossRef]
- Shelke, V.; Sonawane, B.K.; Bhole, M.P.; Patil, D.S. Electrical and optical properties of transparent conducting tin doped ZnO thin films. J. Mater. Sci. 2012, 23, 451–456. [Google Scholar]
- Liu, C.; Yun, F.; Morkoç, H. Ferromagnetism of ZnO and GaN: A review. J. Mater. Sci. Mater. Electron. 2005, 16, 555–597. [Google Scholar]
- Mueller, J.; Mahnke, M.; Schoer, G.; Wiechmann, S. Inorganic Materials Integrated Optics. AIP Conf. Proc. 2004, 709, 268–289. [Google Scholar] [CrossRef]
- Tien, P.K.; Ulrich, R. Theory of prism-film coupler and thin-film light guides. J. Opt. Soc. Am. 1970, 60, 1325–1337. [Google Scholar] [CrossRef]
- Chen, J.; Chen, D.; He, J.; Zhang, S.; Chen, Z. The microstructure, optical, and electrical properties of sol-gel-derived Sc-doped and Al-Sc co-doped ZnO thin films. Appl. Surf. Sci. 2009, 255, 9413–9419. [Google Scholar] [CrossRef]
- Fityk. Available online: http://fityk.nieto.pl/ (accessed on 1 June 2013).
- Barret, C.S.; Massalski, T.B. Structure of Metals: Crystallographic Methods, Principles and Data; Pergamon Press: Oxford, UK, 1980; p. 204. [Google Scholar]
- Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Burton, A.W.; Ong, K.; Rea, T.; Chan, I.Y. On the estimation of average crystallite size of zeolites from the Scherrer equation: A critical evaluation of its application to zeolites with one-dimensional pore systems. Microporous. Mesoporous. Mater. 2009, 117, 75–90. [Google Scholar] [CrossRef]
- Kersten, R.Th. Numerical solution of the mode-equation of planar dielectric waveguides to determine their refractive index and thickness by means of a prism-film coupler. Opt. Commun. 1973, 9, 427–431. [Google Scholar] [CrossRef]
- Strohkendl, F.P.; Fluck, D.; Günter, P.; Irmscher, R.; Buchal, Ch. Nonleaky optical waveguides in KNbO3 by ultralow dose MeV He ion implantation. Appl. Phys. Lett. 1991, 59, 3354–3356. [Google Scholar]
- Weber, H.P.; Dunn, F.A.; Leibolt, W.N. Loss measurements in thin-film optical waveguides. Appl. Opt. 1973, 12, 755–757. [Google Scholar] [CrossRef]
- Boudrioua, A.; Loulergue, J.C. New approach for loss measurements in optical planar waveguides. Opt. Commun. 1997, 137, 37–40. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Znaidi, L.; Touam, T.; Vrel, D.; Souded, N.; Yahia, S.B.; Brinza, O.; Fischer, A.; Boudrioua, A. AZO Thin Films by Sol-Gel Process for Integrated Optics. Coatings 2013, 3, 126-139. https://doi.org/10.3390/coatings3030126
Znaidi L, Touam T, Vrel D, Souded N, Yahia SB, Brinza O, Fischer A, Boudrioua A. AZO Thin Films by Sol-Gel Process for Integrated Optics. Coatings. 2013; 3(3):126-139. https://doi.org/10.3390/coatings3030126
Chicago/Turabian StyleZnaidi, Lamia, Tahar Touam, Dominique Vrel, Nacer Souded, Sana Ben Yahia, Ovidiu Brinza, Alexis Fischer, and Azzedine Boudrioua. 2013. "AZO Thin Films by Sol-Gel Process for Integrated Optics" Coatings 3, no. 3: 126-139. https://doi.org/10.3390/coatings3030126





