Stimuli-Responsive Polymer Brushes for Flow Control through Nanopores
Abstract
:1. Introduction
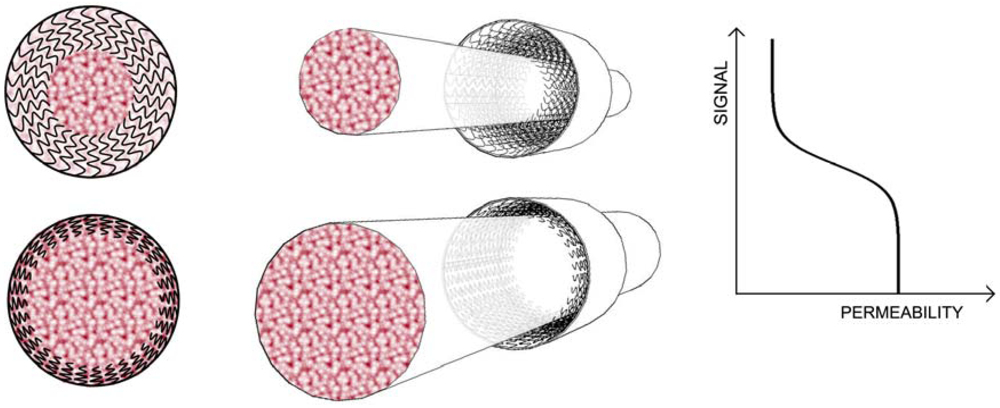
2. Polymer Brushes and Their Responsive Mechanisms
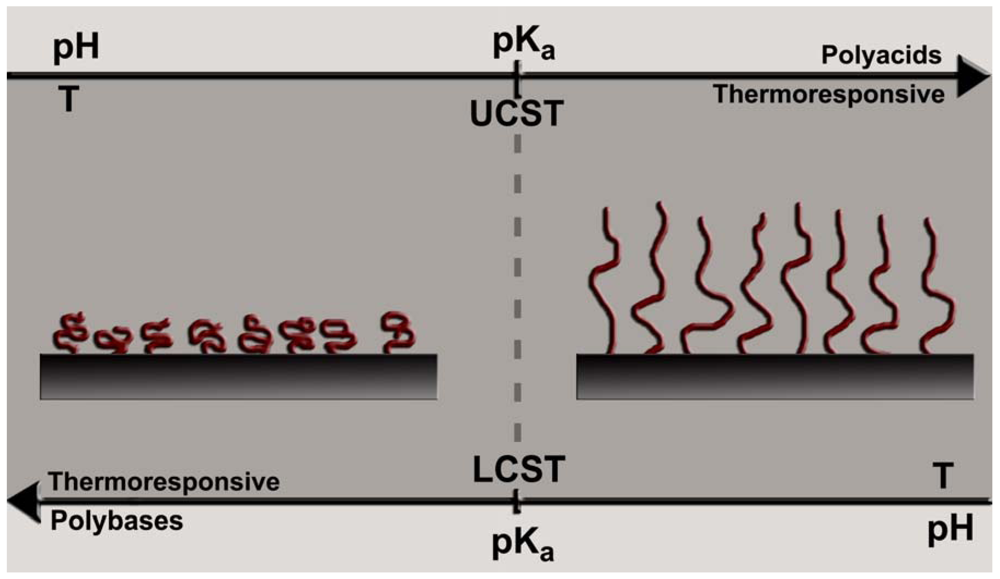
2.1. Thermoresponsive Flow Control
2.2. pH-Responsive Flow Control
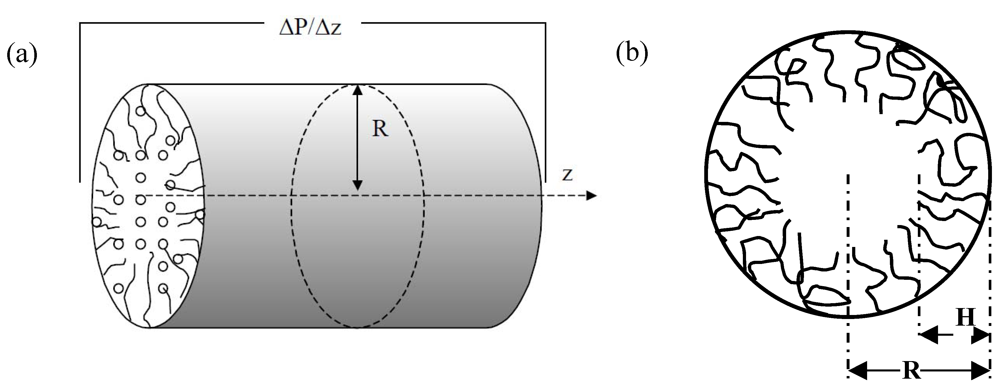
3. Theoretical Analysis
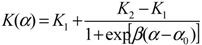
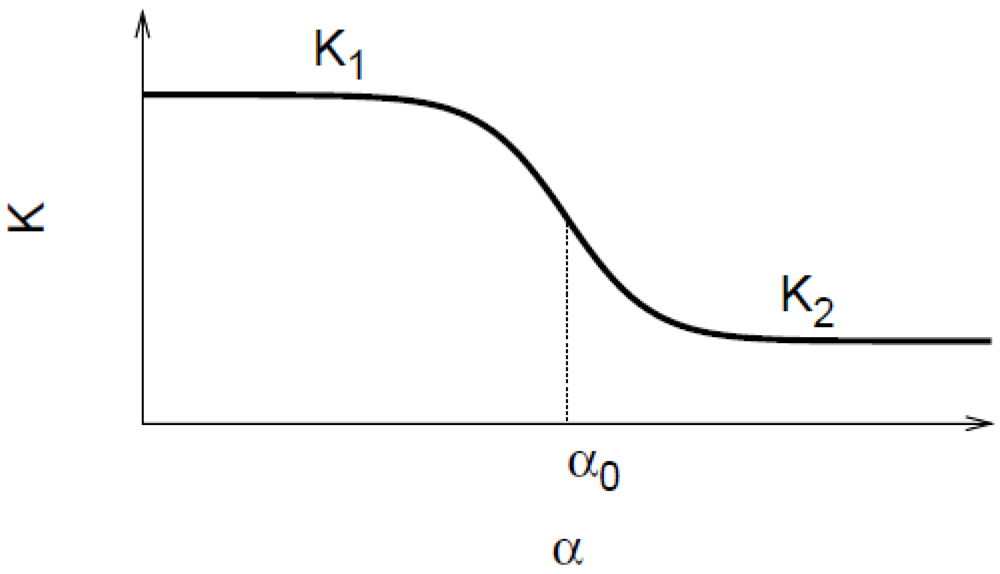


3.1. Modeling Approach
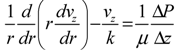
3.2. Calculation of the Monomer Density Profile
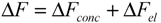
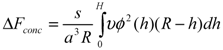
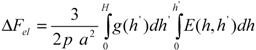
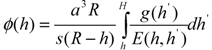
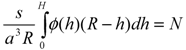
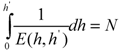
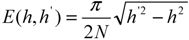
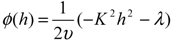
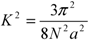
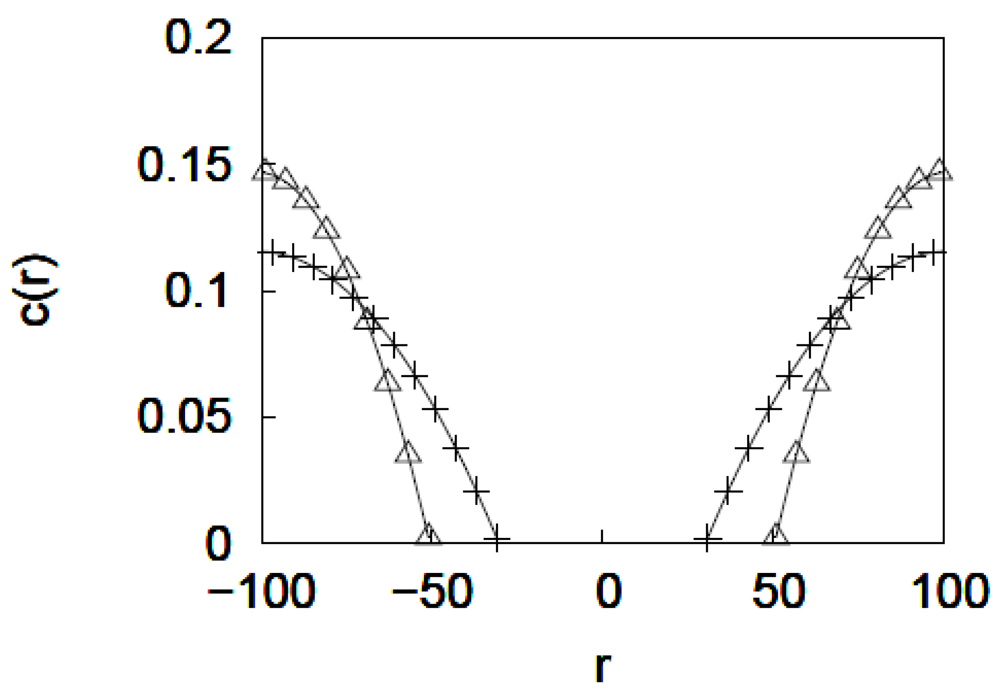
3.3. Calculation of the Velocity Profile
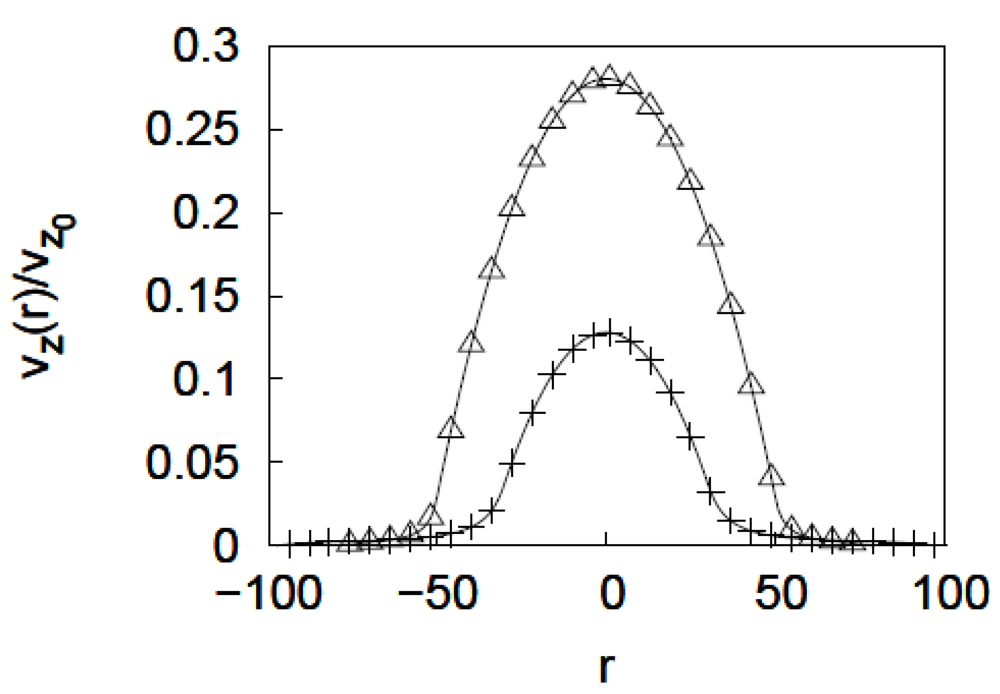

3.4. pH-Responsive Flow Gating via the Helix-Coil Transition of Poly(L-Glutamic Acid) Chains Grafted Inside Nanopores
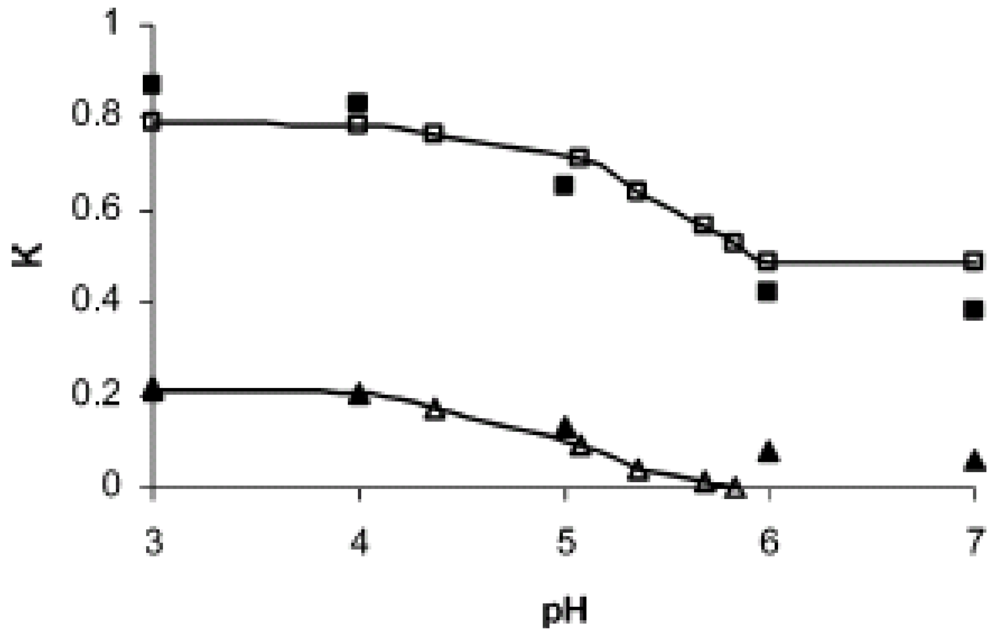
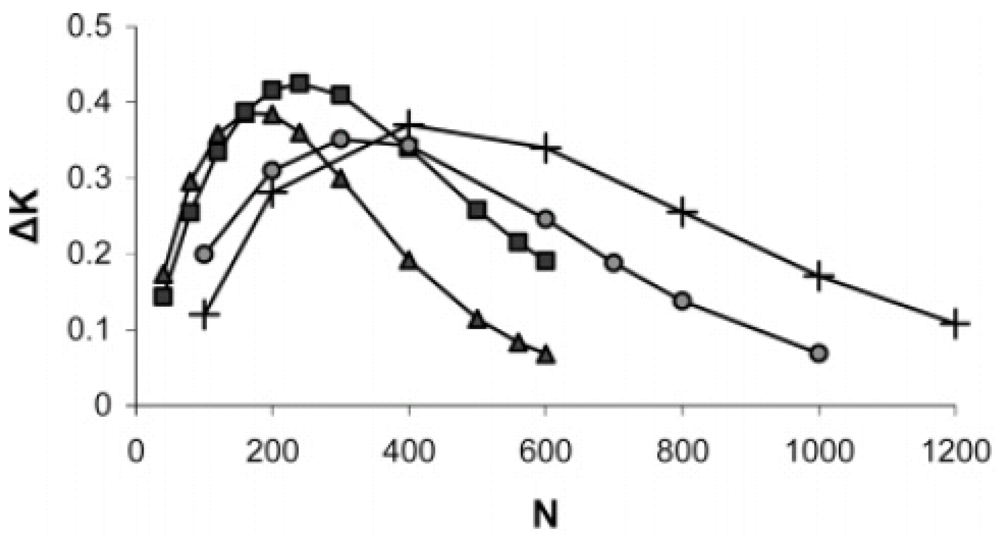
4. Conclusions
Acknowledgments
References
- Miyata, T.; Asami, N.; Uragami, T. A reversibly antigen-responsive hydrogel. Nature 1999, 399, 766–768. [Google Scholar]
- Adiga, S.P.; Curtiss, L.A.; Elam, J.W.; Pellin, M.J.; Shih, C.C.; Shih, C.M.; Lin, S.J.; Su, Y.Y.; Gittard, S.A.; Zhang, J.; Narayan, R.J. Nanoporous materials for biomedical devices. JOM 2008, 60, 26–32. [Google Scholar]
- Tokarev, I.; Minko, S. Multiresponsive, hierarchically structured membranes: New, challenging, biomimetic materials for biosensors, controlled Release, biochemical gates, and nanoreactors. Adv. Mater. 2009, 21, 241–247. [Google Scholar] [CrossRef]
- Bohn, P.W. Nanoscale control and manipulation of molecular transport in chemical analysis. Annu. Rev. Anal. Chem. 2009, 2, 279–296. [Google Scholar] [CrossRef]
- Wandera, D.; Wickramasinghe, S.R.; Husson, S.M. Stimuli-responsive membranes. J. Membr. Sci. 2010, 357, 6–35. [Google Scholar] [CrossRef]
- Kowalczyk, S.W.; Blosser, T.R.; Dekker, C. Biomimetic nanopores: Learning from and about nature. Trends Biotech. 2011, 29, 607–614. [Google Scholar] [CrossRef]
- Yu, C.; Mutlu, S.; Selvaganapathy, P.; Mastrangelo, C.H.; Svec, F.; Frechet, J.M.J. Flow control valves for analytical microfluidic chips without mechanical parts based on thermally responsive monolithic polymers. Anal. Chem. 2003, 75, 1958–1961. [Google Scholar] [CrossRef]
- Spohr, R. Thermal control of drug release by a responsive ion track membrane observed by radio tracer flow dialysis. J. Control. Release 1998, 50, 1–11. [Google Scholar] [CrossRef]
- Akerman, S.; Viinikka, P.; Svarfvarc, B.; Putkonen, K.; Järvinena, K.; Kontturi, K.; Näsman, J.; Urttia, A; Paronen, P. Drug permeation through a temperature-sensitive poly(Nisopropylacrylamide) grafted poly(vinylidene fluoride) membrane. Int. J. Pharm. 1998, 164, 29–36. [Google Scholar]
- Shtanko, N.I.; Kabanov, V.Y.; Apel, P.Y.; Yoshida, M.; Vilenskii, A.I. Preparation of permeability-controlled track membranes on the basis of “smart” polymers. J. Membr. Sci. 2000, 179, 155–161. [Google Scholar] [CrossRef]
- Lokuge, I.; Wang, X.; Bohn, P.W. Temperature-controlled flow switching in nanocapillary array membranes mediated by poly(N-isopropylacrylamide) polymer brushes grafted by atom transfer radical polymerization. Langmuir 2007, 23, 305–311. [Google Scholar] [CrossRef]
- Ito, Y.; Inaba, M.; Chung, D.J.; Imanishi, Y. Control of water permeation by pH and ionic strength through a porous membrane having poly(carboxy1ic acid) surface-grafted. Macromolecules 1992, 25, 7313–7316. [Google Scholar] [CrossRef]
- Iwata, H.; Hirata, I.; Ikada, Y. Atomic force microscopic analysis of a porous membrane with pH-sensitive molecular valves. Macromolecules 1998, 31, 3671–3678. [Google Scholar] [CrossRef]
- Mika, A.M..; Childs, R.F.; Dickson, J.M. Chemical valves based on poly(4-vinylpyridine)-filled microporous membranes. J. Membr. Sci. 1999, 153, 45–56. [Google Scholar]
- Ito, Y.; Park, Y.S.; Imanishi, Y. Nanometer-sized channel gating by a self-assembled polypeptide brush. Langmuir 2000, 16, 5376–5381. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, W. Novel pore-covering membrane as a full open/close valve. J. Membr. Sci. 2005, 258, 133–139. [Google Scholar] [CrossRef]
- Ito, Y.; Park, Y.S. Signal-responsive gating of porous membranes by polymer brushes. Polym. Advan. Technol. 2000, 11, 136–144. [Google Scholar]
- Anzai, J.; Ueno, A.; Sasaki, H.; Shimokawa, K.; Osa, T. Photocontrolled permeation of alkali cations through poly(vinyl chloride)/crown ether membrane. Makromol. Chem. Rapid Commun. 1984, 4, 731–734. [Google Scholar]
- Park, Y.S.; Ito, Y.; Imanishi, Y. Photocontrolled gating by polymer brushes grafted on porous glass filter. Macromolecules 1998, 31, 2606–2610. [Google Scholar] [CrossRef]
- Lokuge, I.; Bohn, P.W. Voltage-tunable volume transitions in nanoscale films of poly(hydroxyethyl methacrylate) surfaces grafted onto gold. Langmuir 2005, 21, 1979–1985. [Google Scholar] [CrossRef]
- Jeon, G.; Yang, S.Y.; Byun, J.; Kim, J.K. Electrically actuatable smart nanoporous membrane for pulsatile drug release. Nano Lett. 2011, 21, 1284–1288. [Google Scholar]
- Alexander, S. Polymer adsorption on small spheres. A scaling approach. J. Phys. 1977, 38, 977–981. [Google Scholar] [CrossRef]
- de Gennes, P.G. Conformations of polymers attached to an interface. Macromolecules 1980, 13, 1069–1075. [Google Scholar] [CrossRef]
- Milner, S.T. Polymer brushes. Science 1991, 251, 905–914. [Google Scholar]
- Barbey, R.; Lavanant, L.; Paripovic, D.; Schuewer, N.; Sugnaux, C.; Tugulu, S.; Klok, H.-A. Polymer brushes via surface-initiated controlled radical polymerization: Synthesis, characterization, properties, and applications. Chem. Rev. 2009, 109, 5437–5527. [Google Scholar] [CrossRef]
- Stuart, M.A.C.; Huck, W.T.S.; Genzer, J.; Muller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.V.; Urban, M.; Winnik, F.; Zauscher, S.; Luzinov, I.; Minko, S. Emerging applications of stimuli-responsive polymer materials. Nature Mater. 2010, 9, 101–113. [Google Scholar]
- Hu, J.; Liu, S. Responsive polymers for detection and sensing applications: Current status and future developments. Macromolecules 2010, 43, 8315–8330. [Google Scholar] [CrossRef]
- Kumar, A.; Srivastava, A.; Galaev, I. Y.; Mattiasson, B. Smart polymers: Physical forms and bioengineering applications. Prog. Polym. Sci. 2007, 32, 1205–1237. [Google Scholar] [CrossRef]
- Lee, H.; Pietrasik, J.; Sheiko, S.S.; Matyjaszewski, K. Stimuli-responsive molecular brushes. Prog. Polym. Sci. 2010, 35, 24–44. [Google Scholar] [CrossRef]
- Schild, H.G. Poly(N-isopropylacrylamide): Experiment, theory and application. Prog. Polym. Sci. 1992, 17, 163–249. [Google Scholar] [CrossRef]
- Schmaljohann, D. Thermo- and pH-responsive polymers in drug delivery. Advan. Drug Delivery Rev. 2006, 58, 1655–1670. [Google Scholar] [CrossRef]
- Xie, R.; Li, Y.; Chu, L.Y. Preparation of thermo-responsive gating membranes with controllable response temperature. J. Membr. Sci. 2007, 289, 76–85. [Google Scholar] [CrossRef]
- Rao, G.V.R.; Balamurugan, S.; Meyer, D.E.; Chilkoti, A.; Lopez, G.P. Hybrid bioinorganic smart membranes that incorporate protein-based molecular switches. Langmuir 2002, 18, 1819–1824. [Google Scholar] [CrossRef]
- Qu, J.B.; Chu, L.Y.; Yang, M.; Xie, R.; Hu, L.; Chen, W.M. A pH-responsive gating membrane system with pumping effects for improved controlled release. Adv. Funct. Mater. 2006, 16, 1865–1872. [Google Scholar] [CrossRef]
- Adiga, S.P.; Brenner, D.W. Virtual molecular design of an environment responsive nanoporous system. Nano Lett. 2002, 2, 567–572. [Google Scholar] [CrossRef]
- Adiga, S.P.; Brenner, D.W. Flow Control through polymer-grafted smart nanofluidic channels: Molecular dynamics simulations. Nano Lett. 2005, 5, 2509–2514. [Google Scholar] [CrossRef]
- Tessier, F.; Slater, G.W. Modulation of electroosmotic flow strength with end-grafted polymer chains. Macromolecules 2006, 39, 1250–1260. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Y.; Laradji, M. Flow control by smart nanofluidic channels: A dissipative particle dynamics simulation. Macromolecules 2006, 39, 5546–5554. [Google Scholar] [CrossRef]
- Adiga, S.P.; Brenner, D.W. Toward designing smart nanovalves: Modeling of flow control through nanopores via the helix-coil transition of grafted polypeptide chains. Macromolecules 2007, 40, 1342–1348. [Google Scholar] [CrossRef]
- Milner, S.T. Hydrodynamic penetration into parabolic brushes. Macromolecules 1991, 24, 3704–3705. [Google Scholar] [CrossRef]
- Brinkman, H.C. Fluid flow in a porous medium. Appl. Sci. Res. A 1947, 27, 143–149. [Google Scholar]
- Zhulina, Y.B.; Pryamitsyn, V.A.; Borisov, O.V. Structure and conformational transitions in grafted polymer chain layers. A new theory. Polym. Sci. USSR 1989, 31, 205–216. [Google Scholar] [CrossRef]
- Field, J.B.; Toprakcioglu, C.; Ball, R. C.; Stanley, H. B.; Dai, L.; Barford, W.; Penfold, J.; Smith, G.; Hamilton, W. Determination of end-adsorbed polymer density profiles by neutron reflectometry. Macromolecules 1992, 25, 434–439. [Google Scholar]
- Fleer, G.J.; Stuart, M.A.C.; Scheutjens, J.M.H.M.; Cosgrove, T.; Vincent, B. Polymers at Interfaces; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Egorov, S.A.; Milchev, A.; Klushin, L.; Binder, K. Structural properties of concave cylindrical brushes interacting with free chains. Soft Matter 2011, 7, 5669–5676. [Google Scholar]
- Tagliazucchi, M.; Azzaroni, O.; Szleifer, I. Responsive polymers end-tethered in solid-statenanochannels: When nanoconfinement really matters. J. Am. Chem. Soc. 2010, 132, 12404–12411. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Adiga, S.P.; Brenner, D.W. Stimuli-Responsive Polymer Brushes for Flow Control through Nanopores. J. Funct. Biomater. 2012, 3, 239-256. https://doi.org/10.3390/jfb3020239
Adiga SP, Brenner DW. Stimuli-Responsive Polymer Brushes for Flow Control through Nanopores. Journal of Functional Biomaterials. 2012; 3(2):239-256. https://doi.org/10.3390/jfb3020239
Chicago/Turabian StyleAdiga, Shashishekar P., and Donald W. Brenner. 2012. "Stimuli-Responsive Polymer Brushes for Flow Control through Nanopores" Journal of Functional Biomaterials 3, no. 2: 239-256. https://doi.org/10.3390/jfb3020239



