An Energy Landscape Treatment of Decoy Selection in Template-Free Protein Structure Prediction
Abstract
:1. Introduction
1.1. Related Work
2. Results
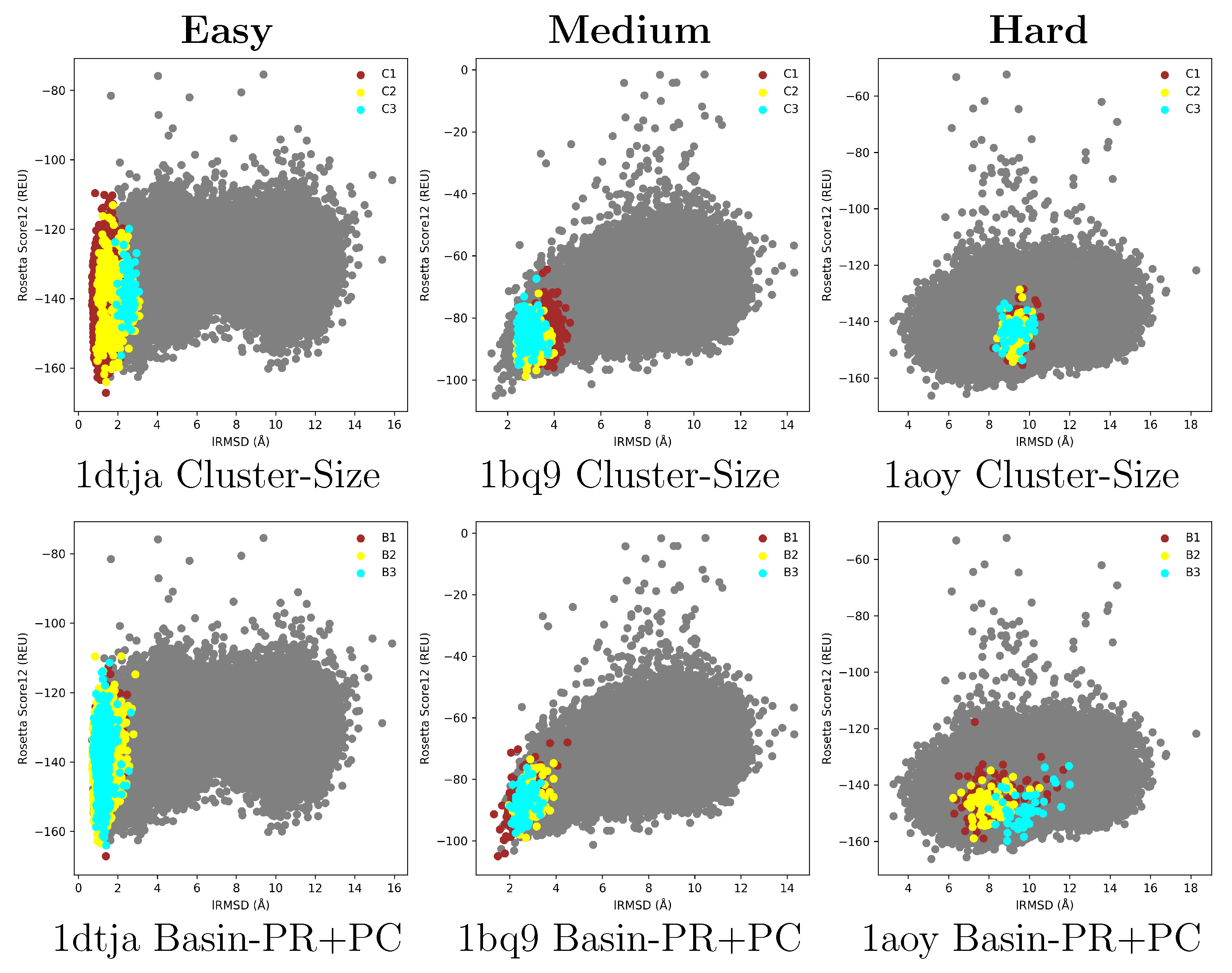
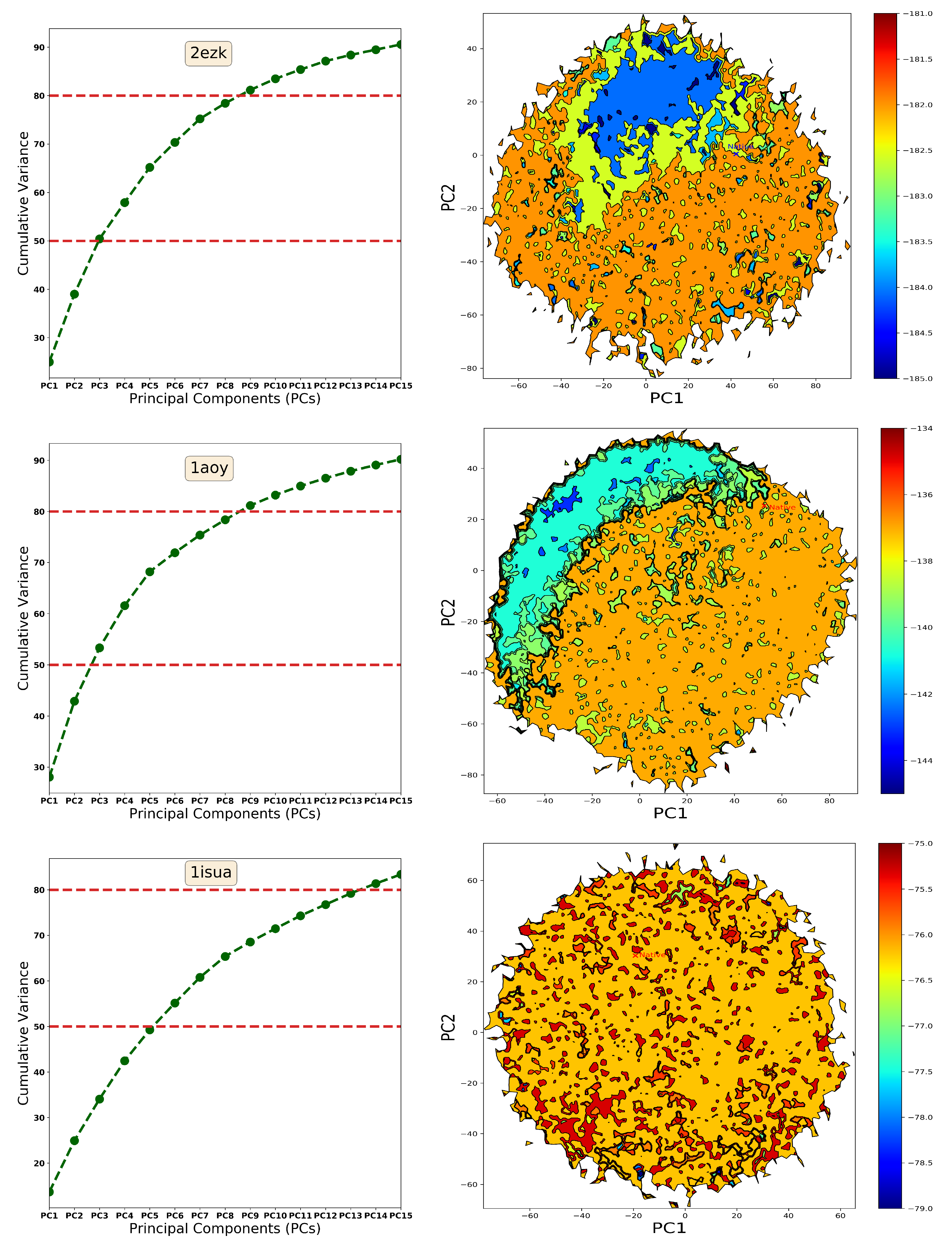
2.1. Summary of Evaluation of Basin Selection for Decoy Selection
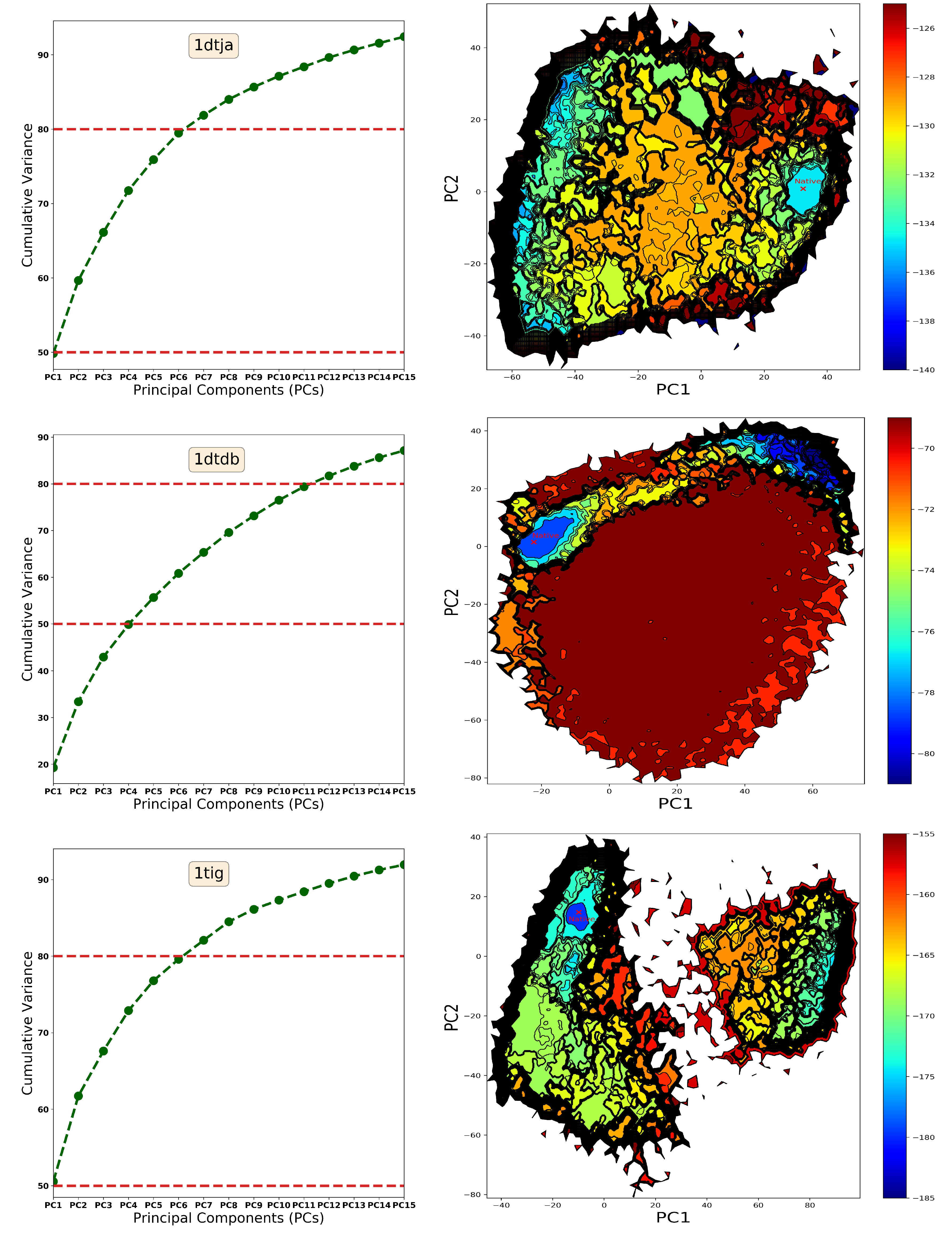
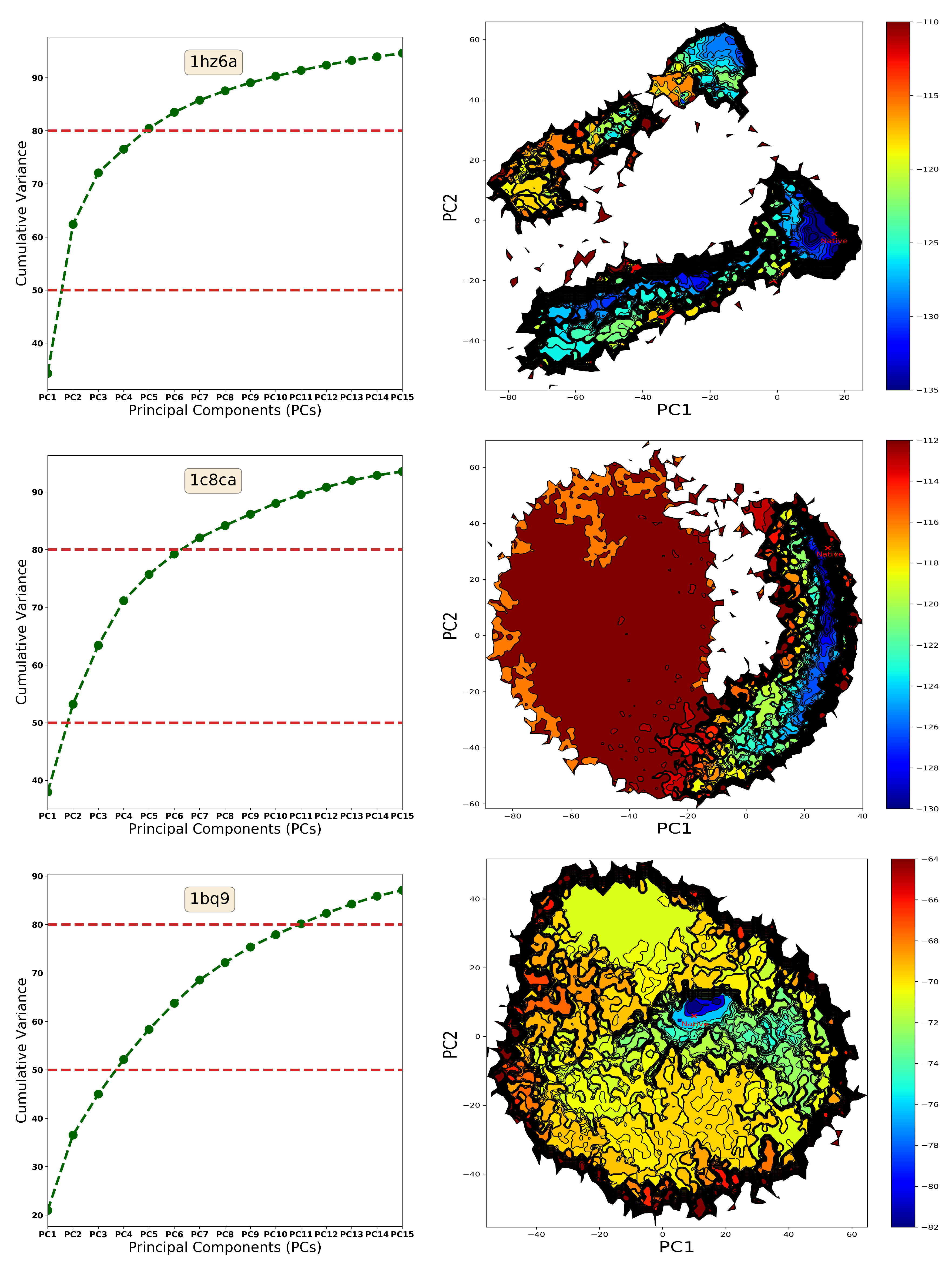
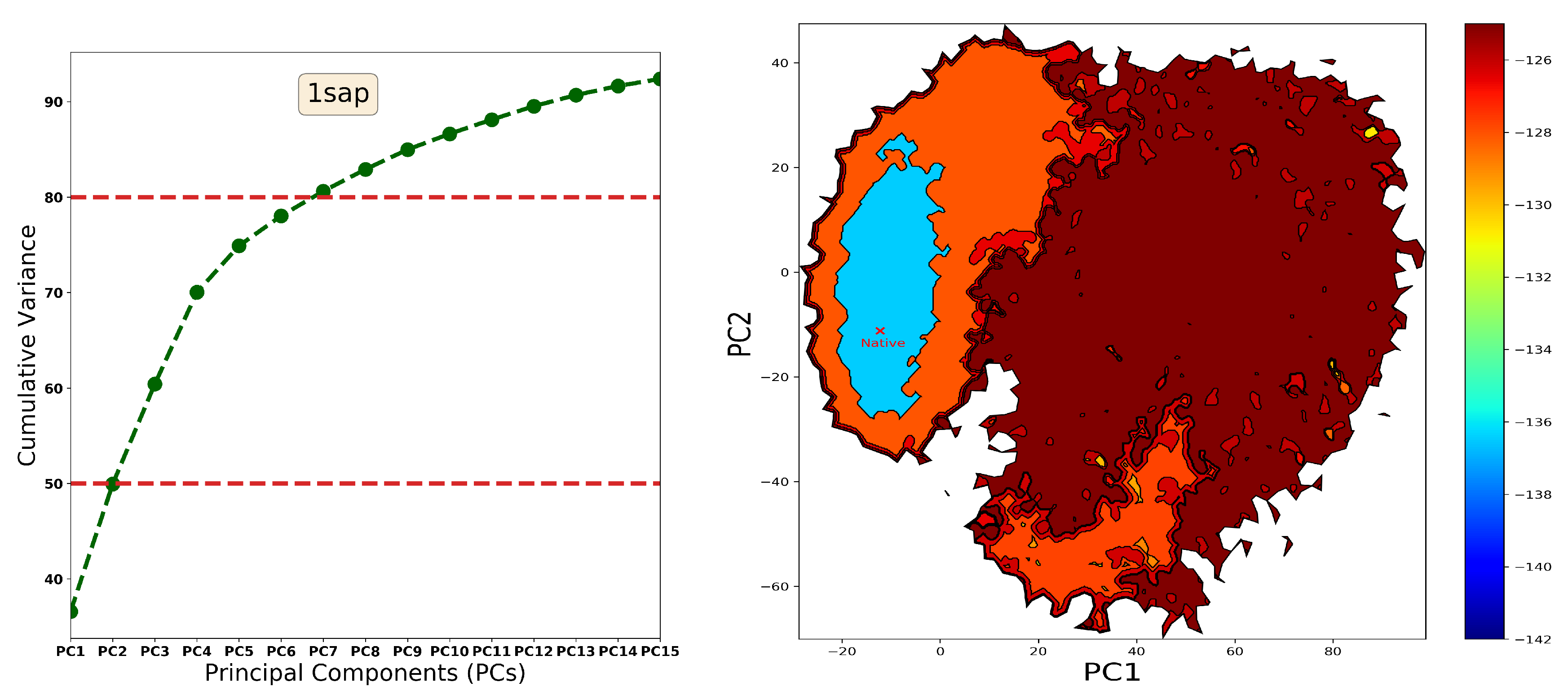
2.2. Summary of Evaluation of Landscape Reconstruction for Decoy Selection
3. Discussion
4. Materials and Methods
4.1. The Energy Landscape
4.1.1. From Decoy Embedding to Basins
4.1.2. From Landscape Reconstruction to Basins
4.2. Implementation Details
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PDB | Protein Data Bank |
| CASP | Critical Assessment of protein Structure Prediction |
| lRMSD | least root-mean-squared-deviation |
| ML | Machine Learning |
| NN | Neural Network |
| Random Forest | RF |
| PC | Pareto Count |
| PR | Pareto Rank |
| SVM | Support Vector Machines |
References
- Blaby-Haas, C.E.; de Crécy-Lagard, V. Mining high-throughput experimental data to link gene and function. Trends Biotechnol. 2013, 29, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Henrick, K.; Nakamura, H. Announcing the worldwide Protein Data Bank. Nat. Struct. Biol. 2003, 10, 980. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A. A Review of Evolutionary Algorithms for Computing Functional Conformations of Protein Molecules. In Computer-Aided Drug Discovery; Zhang, W., Ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Leaver-Fay, A.; Tyka, M.; Lewis, S.M.; Lange, O.F.; Thompson, J.; Jacak, R.; Kaufman, K.W.; Renfrew, P.D.; Smith, C.A.; Sheffler, W.; et al. ROSETTA3: An object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 2011, 487, 545–574. [Google Scholar] [PubMed]
- Xu, D.; Zhang, Y. Ab initio protein structure assembly using continuous structure fragments and optimized knowledge-based force field. Proteins Struct. Funct. Bioinform. 2012, 80, 1715–1735. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A. Probabilistic Search and Optimization for Protein Energy Landscapes. In Handbook of Computational Molecular Biology; Chapman & Hall/CRC Computer & Information Science Series; Aluru, S., Singh, A., Eds.; CRC Press: London, UK, 2013. [Google Scholar]
- Verma, A.; Schug, A.; Lee, K.H.; Wenzel, W. Basin hopping simulations for all-atom protein folding. J. Chem. Phys. 2006, 124, 044515. [Google Scholar] [CrossRef] [PubMed]
- Kryshtafovych, A.; Fidelis, K.; Tramontano, A. Evaluation of model quality predictions in CASP9. Proteins 2011, 79, 91–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kryshtafovych, A.; Barbato, A.; Fidelis, K.; Monastyrskyy, B.; Schwede, T.; Tramontano, A. Assessment of the assessment: Evaluation of the model quality estimates in CASP10. Proteins 2014, 82, 112–126. [Google Scholar] [CrossRef] [PubMed]
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Schwede, T.; Tramontano, A. Critical assessment of methods of protein structure prediction (CASP)—Round X. Proteins Struct. Funct. Bioinform. 2014, 82, 109–115. [Google Scholar] [CrossRef] [PubMed]
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Schwede, T.; Tramontano, A. Critical Assessment of Methods of Protein Structure Prediction (CASP)—Round XII. Proteins 2017. [Google Scholar] [CrossRef] [PubMed]
- Ginalski, K.; Elofsson, A.; Fischer, D.; Rychlewski, L. 3D-Jury: A simple approach to improve protein structure predictions. Bioinformatics 2003, 19, 1015–1018. [Google Scholar] [CrossRef] [PubMed]
- Wallner, B.; Elofsson, A. Identification of correct regions in protein models using structural, alignment, and consensus information. Protein Sci. 2006, 15, 900–913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molloy, K.; Saleh, S.; Shehu, A. Probabilistic Search and Energy Guidance for Biased Decoy Sampling in Ab-initio Protein Structure Prediction. IEEE/ACM Trans. Bioinform. Comp. Biol. 2013, 10, 1162–1175. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A.; Plaku, E. A Survey of omputational Treatments of Biomolecules by Robotics-inspired Methods Modeling Equilibrium Structure and Dynamics. J. Artif. Intell. Res. 2016, 597, 509–572. [Google Scholar]
- Maximova, T.; Moffatt, R.; Ma, B.; Nussinov, R.; Shehu, A. Principles and Overview of Sampling Methods for Modeling Macromolecular Structure and Dynamics. PLoS Comp. Biol. 2016, 12, e1004619. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A.; Clementi, C.; Kavraki, L.E. Sampling Conformation Space to Model Equilibrium Fluctuations in Proteins. Algorithmica 2007, 48, 303–327. [Google Scholar] [CrossRef]
- Okazaki, K.; Koga, N.; Takada, S.; Onuchic, J.N.; Wolynes, P.G. Multiple-basin energy landscapes for large-amplitude conformational motions of proteins: Structure-based molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2006, 103, 11844–11849. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, F.; Xu, J. A position-specific distance-dependent statistical potential for protein structure and functional study. Structure 2012, 20, 1118–1126. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Zhang, J.; Xu, Y.; Shang, Y.; Xu, D. Protein structural model selection based on protein-dependent scoring function. Stat. Interface 2012, 5, 109–115. [Google Scholar] [CrossRef]
- Mirzaei, S.; Sidi, T.; Keasar, C.; Crivelli, S. Purely Structural Protein Scoring Functions Using Support Vector Machine and Ensemble Learning. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins Struct. Funct. Bioinform. 1995, 21, 167–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, B.; Kumar, S.; Tsai, C.; Nussinov, R. Folding funnels and binding mechanisms. Protein Eng. 1999, 12, 713–720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, C.; Kumar, S.; Ma, B.; Nussinov, R. Folding funnels, binding funnels, and protein function. Protein Sci. 1999, 8, 1181–1190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, C.; Ma, B.; Nussinov, R. Folding and binding cascades: Shifts in energy landscapes. Proc. Natl. Acad. Sci. USA 1999, 96, 9970–9972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nussinov, R.; Wolynes, P.G. A second molecular biology revolution? The energy landscapes of biomolecular function. Phys. Chem. Chem. Phys. 2014, 16, 6321–6322. [Google Scholar] [CrossRef] [PubMed]
- Uziela, K.; Wallner, B. ProQ2: Estimation of model accuracy implemented in Rosetta. Bioinformatics 2016, 32, 1411–1413. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Wang, Y.; Eickholt, J.; Wang, Z. Benchmarking deep networks for predicting residue-specific quality of individual protein models in CASP11. Sci. Rep. 2016, 6, 19301. [Google Scholar] [CrossRef] [PubMed]
- Jing, X.; Wang, K.; Lu, R.; Dong, Q. Sorting protein decoys by machine-learning-to-rank. Sci. Rep. 2016, 6, 31571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wallner, B.; Elofsson, A. Can correct protein models be identified? Protein Sci. 2003, 12, 1073–1086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef] [PubMed]
- McConkey, B.J.; Sobolev, V.; Edelman, M. Discrimination of native protein structures using atom–atom contact scoring. Proc. Natl. Acad. Sci. USA 2003, 100, 3215–3220. [Google Scholar] [CrossRef] [PubMed]
- Samudrala, R.; Moult, J. An all-atom distance-dependent conditional probability discriminatory function for protein structure prediction1. J. Mol. Biol. 1998, 275, 895–916. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Skolnick, J. A distance-dependent atomic knowledge-based potential for improved protein structure selection. Proteins Struct. Funct. Bioinform. 2001, 44, 223–232. [Google Scholar] [CrossRef] [PubMed]
- Berrera, M.; Molinari, H.; Fogolari, F. Amino acid empirical contact energy definitions for fold recognition in the space of contact maps. BMC Bioinform. 2003, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Simons, K.T.; Ruczinski, I.; Kooperberg, C.; Fox, B.A.; Bystroff, C.; Baker, D. Improved recognition of native-like protein structures using a combination of sequence-dependent and sequence-independent features of proteins. Proteins Struct. Funct. Bioinform. 1999, 34, 82–95. [Google Scholar] [CrossRef] [Green Version]
- Bahar, I.; Jernigan, R.L. Inter-residue potentials in globular proteins and the dominance of highly specific hydrophilic interactions at close separation. J. Mol. Biol. 1997, 266, 195–214. [Google Scholar] [CrossRef] [PubMed]
- Reva, B.A.; Finkelstein, A.V.; Sanner, M.F.; Olson, A.J. Residue-residue mean-force potentials for protein structure recognition. Protein Eng. 1997, 10, 865–876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyazawa, S.; Jernigan, R.L. An empirical energy potential with a reference state for protein fold and sequence recognition. Proteins Struct. Funct. Bioinform. 1999, 36, 357–369. [Google Scholar] [CrossRef] [Green Version]
- Park, B.; Levitt, M. Energy functions that discriminate X-ray and near-native folds from well-constructed decoys. J. Mol. Biol. 1996, 258, 367–392. [Google Scholar] [CrossRef] [PubMed]
- Felts, A.K.; Gallicchio, E.; Wallqvist, A.; Levy, R.M. Distinguishing native conformations of proteins from decoys with an effective free energy estimator based on the opls all-atom force field and the surface generalized Born solvent model. Proteins Struct. Funct. Bioinform. 2002, 48, 404–422. [Google Scholar] [CrossRef] [PubMed]
- Lazaridis, T.; Karplus, M. Discrimination of the native from misfolded protein models with an energy function including implicit solvation. J. Mol. Biol. 1999, 288, 477–487. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thomas, P.D.; Dill, K.A. Statistical potentials extracted from protein structures: How accurate are they? J. Mol. Biol. 1996, 257, 457–469. [Google Scholar] [CrossRef] [PubMed]
- Ben-Naim, A. Statistical potentials extracted from protein structures: Are these meaningful potentials? J. Chem. Phys. 1997, 107, 3698–3706. [Google Scholar] [CrossRef]
- Moult, J. Comparison of database potentials and molecular mechanics force fields. Curr. Opin. Struct. Biol. 1997, 7, 194–199. [Google Scholar] [CrossRef]
- Bradley, P.; Chivian, D.; Meiler, J.; Misura, K.; Rohl, C.A.; Schief, W.R.; Wedemeyer, W.J.; Schueler-Furman, O.; Murphy, P.; Schonbrun, J.; et al. Rosetta predictions in CASP5: Successes, failures, and prospects for complete automation. Proteins Struct. Funct. Bioinform. 2003, 53, 457–468. [Google Scholar] [CrossRef] [PubMed]
- Lorenzen, S.; Zhang, Y. Identification of near-native structures by clustering protein docking conformations. Proteins Struct. Funct. Bioinform. 2007, 68, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Shortle, D.; Simons, K.T.; Baker, D. Clustering of low-energy conformations near the native structures of small proteins. Proc. Natl. Acad. Sci. USA 1998, 95, 11158–11162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Skolnick, J. SPICKER: A clustering approach to identify near-native protein folds. J. Comput. Chem. 2004, 25, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Estrada, T.; Armen, R.; Taufer, M. Automatic selection of near-native protein-ligand conformations using a hierarchical clustering and volunteer computing. In Proceedings of the First ACM International Conference on Bioinformatics and Computational Biology, Niagara Falls, NY, USA, 2–4 August 2010; pp. 204–213. [Google Scholar]
- Li, S.C.; Ng, Y.K. Calibur: A tool for clustering large numbers of protein decoys. BMC Bioinform. 2010, 11, 25. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xu, D. Fast algorithm for clustering a large number of protein structural decoys. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine, Atlanta, GA, USA, 12–15 November 2011; pp. 30–36. [Google Scholar]
- Li, S.C.; Bu, D.; Li, M. Clustering 100,000 protein structure decoys in minutes. IEEE/ACM Trans. Comput. Biol. Bioinform. (TCBB) 2012, 9, 765–773. [Google Scholar]
- Zhou, J.; Wishart, D.S. An improved method to detect correct protein folds using partial clustering. BMC Bioinform. 2013, 14, 11. [Google Scholar] [CrossRef] [PubMed]
- Berenger, F.; Zhou, Y.; Shrestha, R.; Zhang, K.Y. Entropy-accelerated exact clustering of protein decoys. Bioinformatics 2011, 27, 939–945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, Z.; Alazmi, M.; Zhang, J.; Xu, D. Protein structural model selection by combining consensus and single scoring methods. PLoS ONE 2013, 8, e74006. [Google Scholar] [CrossRef] [PubMed]
- Pawlowski, M.; Kozlowski, L.; Kloczkowski, A. MQAPsingle: A quasi single-model approach for estimation of the quality of individual protein structure models. Proteins Struct. Funct. Bioinform. 2016, 84, 1021–1028. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Sheffler, W.; Baker, D.; Noble, W.S. Ranking predicted protein structures with support vector regression. Proteins Struct. Funct. Bioinform. 2008, 71, 1175–1182. [Google Scholar] [CrossRef] [PubMed]
- Ray, A.; Lindahl, E.; Wallner, B. Improved model quality assessment using ProQ2. BMC Bioinform. 2012, 13, 224. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Skolnick, J. GOAP: A generalized orientation-dependent, all-atom statistical potential for protein structure prediction. Biophys. J. 2011, 101, 2043–2052. [Google Scholar] [CrossRef] [PubMed]
- Cao, R.; Wang, Z.; Wang, Y.; Cheng, J. SMOQ: A tool for predicting the absolute residue-specific quality of a single protein model with support vector machines. BMC Bioinform. 2014, 15, 120. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Ghosh, S.; Vishveshwara, S. Network properties of decoys and CASP predicted models: A comparison with native protein structures. Mol. BioSyst. 2013, 9, 1774–1788. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, S.P.; Shang, Y.; Xu, D. DL-PRO: A novel deep learning method for protein model quality assessment. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2071–2078. [Google Scholar]
- Faraggi, E.; Kloczkowski, A. A global machine learning based scoring function for protein structure prediction. Proteins Struct. Funct. Bioinform. 2014, 82, 752–759. [Google Scholar] [CrossRef] [PubMed]
- Manavalan, B.; Lee, J.; Lee, J. Random forest-based protein model quality assessment (RFMQA) using structural features and potential energy terms. PLoS ONE 2014, 9, e106542. [Google Scholar] [CrossRef] [PubMed]
- Akhter, N.; Shehu, A. From Extraction of Local Structures of Protein Energy Landscapes to Improved Decoy Selection in Template-free Protein Structure Prediction. Molecules 2017, 23, 216. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. On the interpretation of χ2 from contingency tables, and the calculation of P. J. R. Stat. Soc. 1922, 85, 87–94. [Google Scholar] [CrossRef]
- Frauenfelder, H.; Sligar, S.G.; Wolynes, P.G. The energy landscapes and motion on proteins. Science 1991, 254, 1598–1603. [Google Scholar] [CrossRef] [PubMed]
- Samoilenko, S. Fitness Landscapes of Complex Systems: Insights and Implications On Managing a Conflict Environment of Organizations. Complex. Organ. 2008, 10, 38–45. [Google Scholar]
- Shehu, A. Conformational Search for the Protein Native State. In Protein Structure Prediction: Method and Algorithms; Rangwala, H., Karypis, G., Eds.; Wiley Book Series on Bioinformatics: Fairfax, VA, USA, 2010; Chapter 21. [Google Scholar]
- Boehr, D.D.; Nussinov, R.; Wright, P.E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009, 5, 789–796. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cazals, F.; Dreyfus, T. The structural bioinformatics library: Modeling in biomolecular science and beyond. Bioinformatics 2017, 33, 997–1004. [Google Scholar] [CrossRef] [PubMed]
- Luenberger, D.G. Introduction to Linear and Nonlinear Programming; Addison-Wesley: Boston, MA, USA, 1973. [Google Scholar]
- Clausen, R.; Shehu, A. A Data-driven Evolutionary Algorithm for Mapping Multi-basin Protein Energy Landscapes. J. Comput. Biol. 2015, 22, 844–860. [Google Scholar] [CrossRef] [PubMed]
- Pandit, R.; Shehu, A. A Principled Comparative Analysis of Dimensionality Reduction Techniques on Protein Structure Decoy Data. In Proceedings of the International Conference on Bioinformatics and Computational Biology, Las Vegas, NV, USA, 4–6 April 2016; Ioerger, T., Haspel, N., Eds.; ISCA: Winona, MN, USA, 2016; pp. 43–48. [Google Scholar]
- Rodriguez-Casal, H. Set estimation under convexity type assumptions. Ann. l’Inst. Henri Poincare (B) Probab. Stat. 2007, 43, 763–774. [Google Scholar] [CrossRef]
- Pateiro-Lopez, B. Set Estimation under Convexity Type Restrictions. Ph.D. Thesis, Universidad de Santiago de Compostela, Galicia, Spain, 2008. [Google Scholar]
| PDB ID | Fold | Length | min_dist (Å) | |||
|---|---|---|---|---|---|---|
| Easy | 1dtdb | 61 | ||||
| 1tig | 88 | |||||
| 1dtja | 74 | |||||
| Medium | 1hz6a | 64 | ||||
| 1c8ca | * | 64 | ||||
| 1bq9 | 53 | |||||
| 1sap | 66 | |||||
| Hard | 2ezk | 93 | ||||
| 1aoy | 78 | |||||
| 1isua | 62 |
| 1dtdb | 1tig | 1dtja | 1hz6a | 1c8ca | 1bq9 | 1sap | 2ezk | 1aoy | 1isua | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster-Size | C | n:97.6% | n:57.3% | n:95.5% | n:0% | n:10% | n:0.6% | n:0% | n:0% | n:0% | n:0% |
| p:99.9% | p:99.1% | p:99.2% | p:0% | p:32.1% | p:1.5% | p:0% | p:0% | p:0% | p:0% | ||
| s:22.3% | s:8.7% | s:21.6% | s:4.4% | s:3.4% | s:0.64% | s:9.3% | s:0.02% | s:0.03% | s:0.02% | ||
| C | n:97.6% | n:88.4% | n:97.8% | n:26.4% | n:20.5% | n:21% | n:55.9 | n:0% | n:0% | n:0% | |
| p:93.3% | p:98.4% | p:97.2% | p:27.7% | p:36.3% | p:24% | p:7.4 | p:0% | p:0% | p:0% | ||
| s:23.9% | s:13.6% | s:22.6% | s:10.8% | s:6.2% | s:1.4% | s:17.4% | s:0.07% | s:0.06% | s:0.05% | ||
| Basin-PR+PC | B | n:85.3% | n:28.8% | n:19.9% | n:55.5% | n:14% | n:9.3% | n:32.4% | n:1.02% | n:0.18% | n:0% |
| p:99% | p:100% | p:99.6% | p:85.5% | p:96.3% | p:80.4% | p:20.2% | p:45.9% | p:9.8% | p:0% | ||
| s:19.7% | s:4.4% | s:4.5% | s:7.3% | s:1.6% | s:0.18% | s:3.7% | s:0.29% | s:0.2% | s:0.05% | ||
| B | n:95.4% | n:42.8% | n:70.7% | n:55.5% | n:23.5% | n:22.7% | n:51.4% | n:2.0% | n:0.23% | n:0.03% | |
| p:98.8% | p:98.8% | p:99.2% | p:39.3% | p:58.5% | p:74.3% | p:11.5% | p:39.7% | p:5.5% | p:1.2% | ||
| s:22% | s:6.6% | s:16% | s:16% | s:4.4% | s:0.46% | s:10.3% | s:0.66% | s:0.46% | s:0.14% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhter, N.; Qiao, W.; Shehu, A. An Energy Landscape Treatment of Decoy Selection in Template-Free Protein Structure Prediction. Computation 2018, 6, 39. https://doi.org/10.3390/computation6020039
Akhter N, Qiao W, Shehu A. An Energy Landscape Treatment of Decoy Selection in Template-Free Protein Structure Prediction. Computation. 2018; 6(2):39. https://doi.org/10.3390/computation6020039
Chicago/Turabian StyleAkhter, Nasrin, Wanli Qiao, and Amarda Shehu. 2018. "An Energy Landscape Treatment of Decoy Selection in Template-Free Protein Structure Prediction" Computation 6, no. 2: 39. https://doi.org/10.3390/computation6020039





