LES and Wind Tunnel Test of Flow around Two Tall Buildings in Staggered Arrangement
Abstract
:1. Introduction
2. Simulation on Shear Stress/Friction Velocity on Roofs
2.1. Governing Equations
2.2. Computational Domain and Boundary Conditions
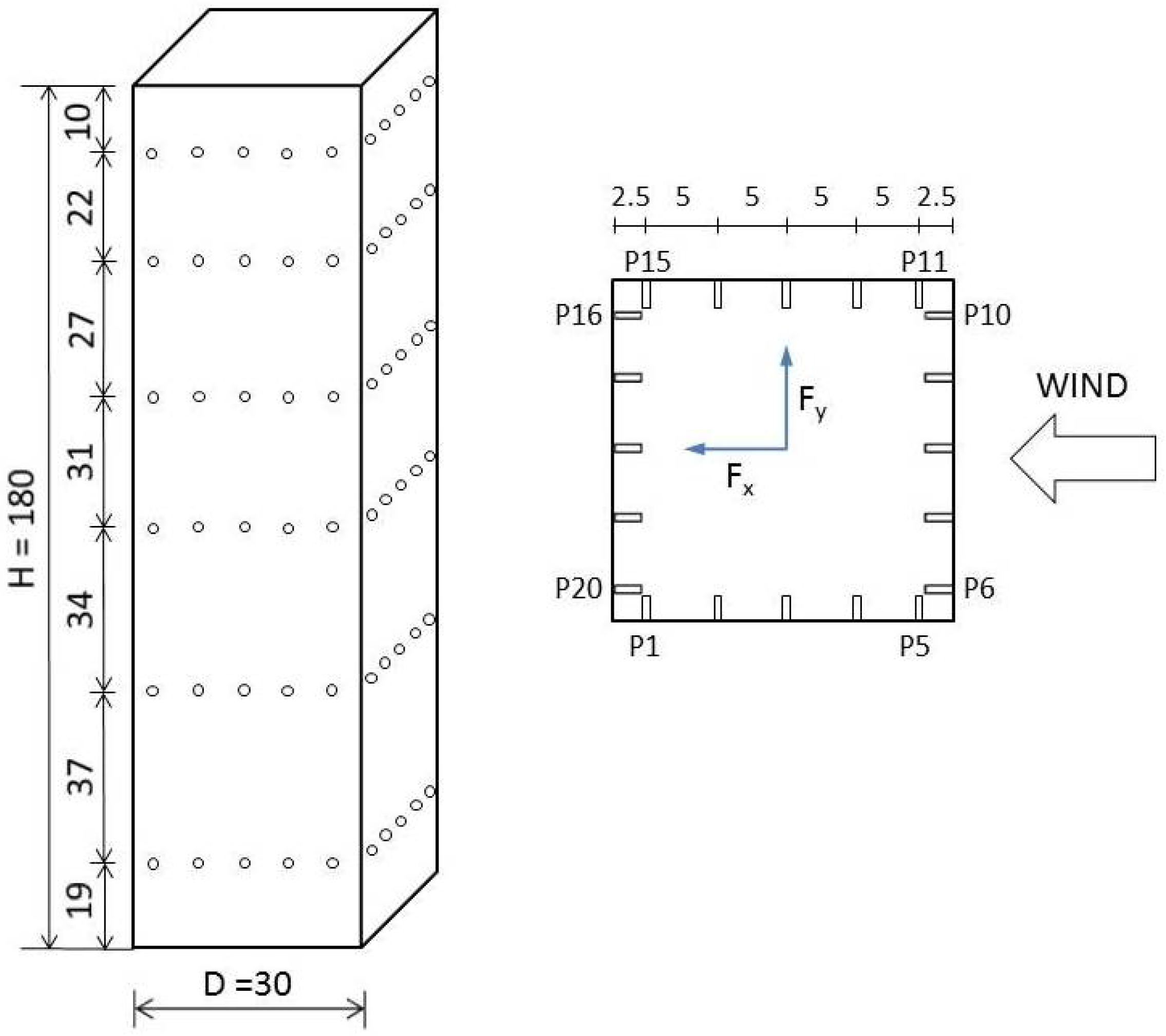
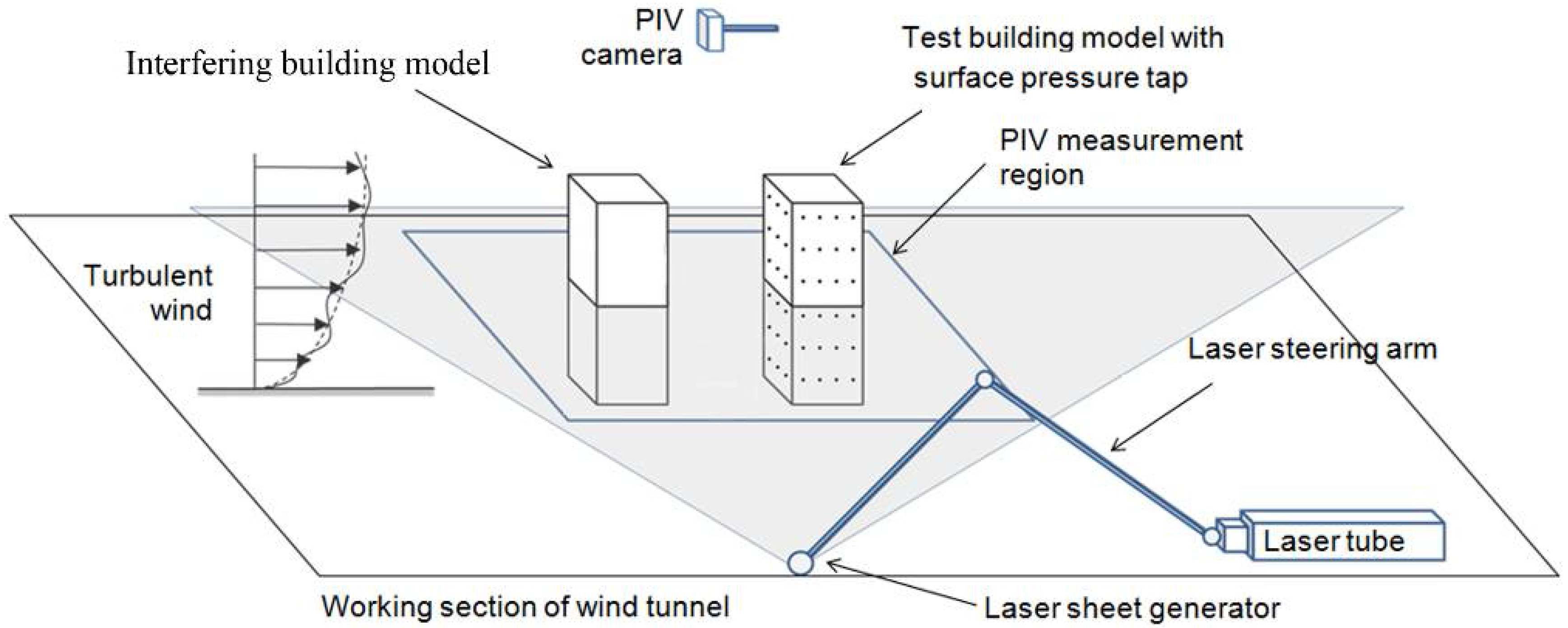
3. Description of Wind Tunnel Test
4. Result Analysis and Discussion
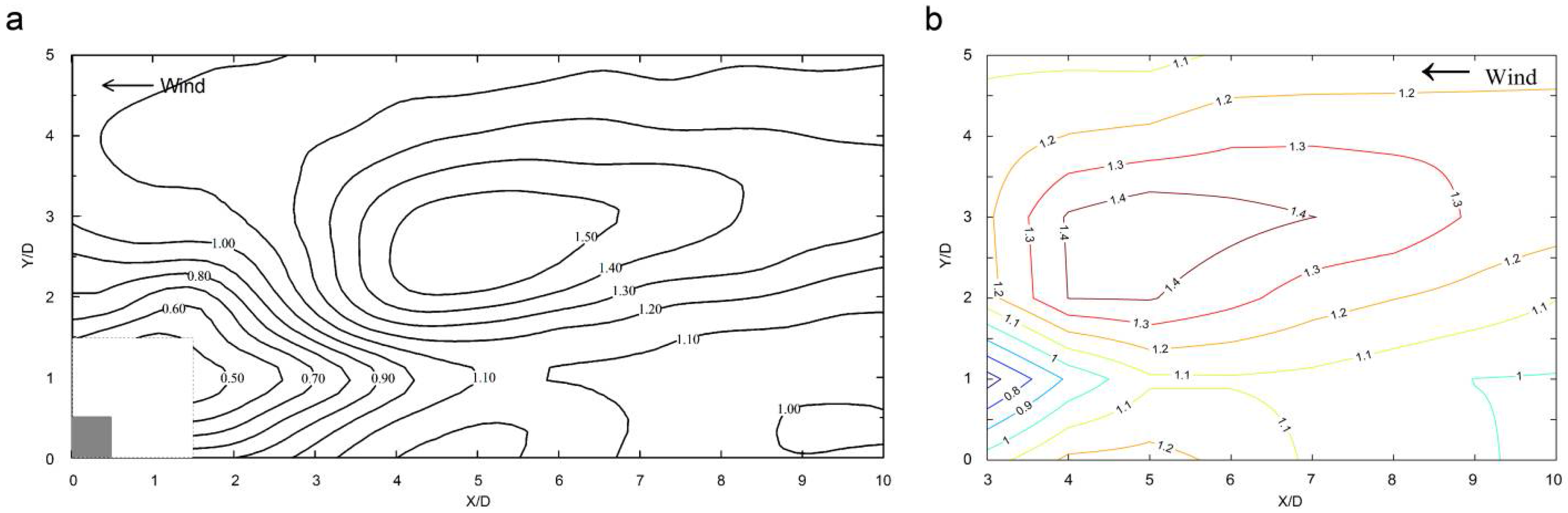
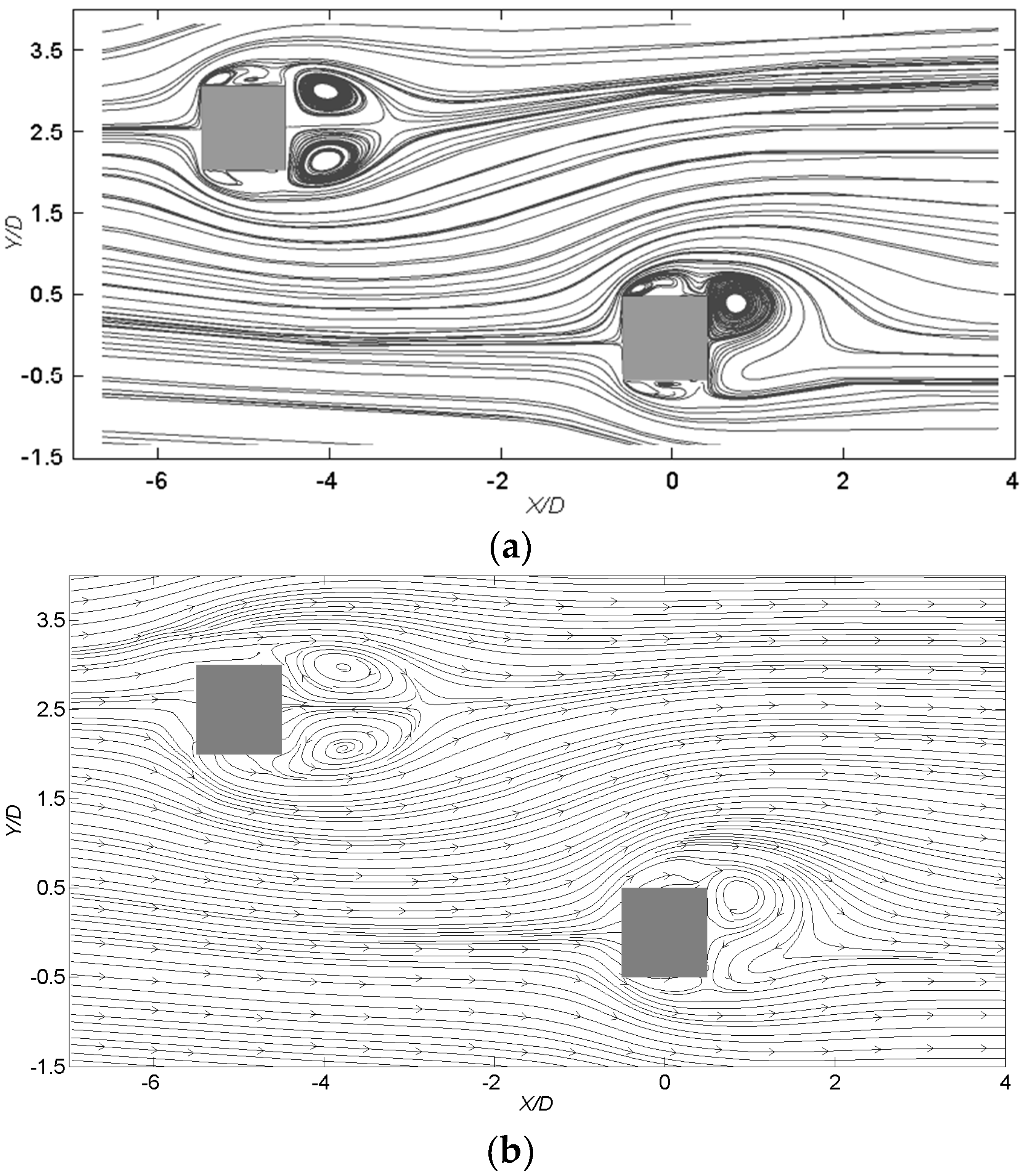
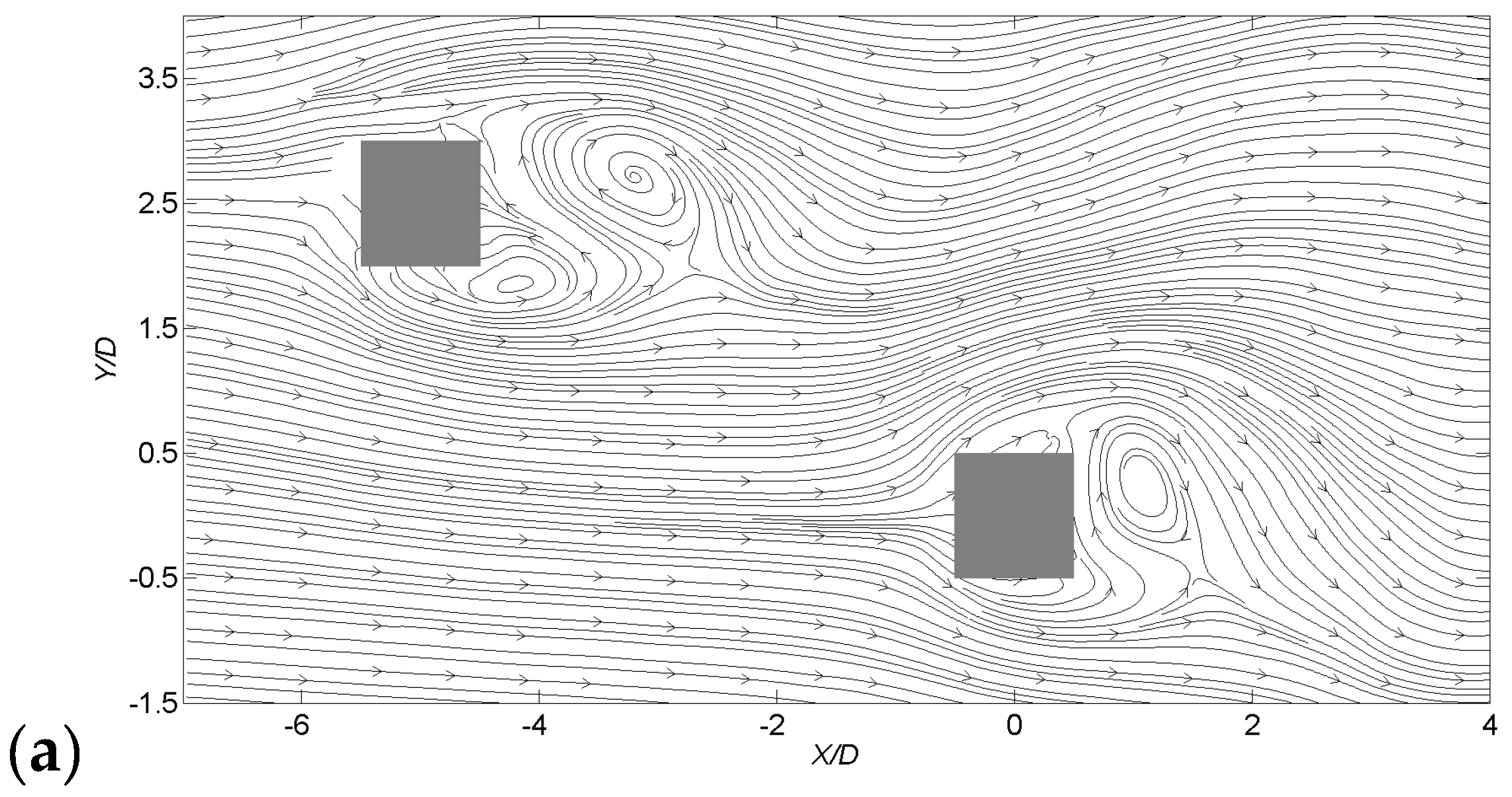
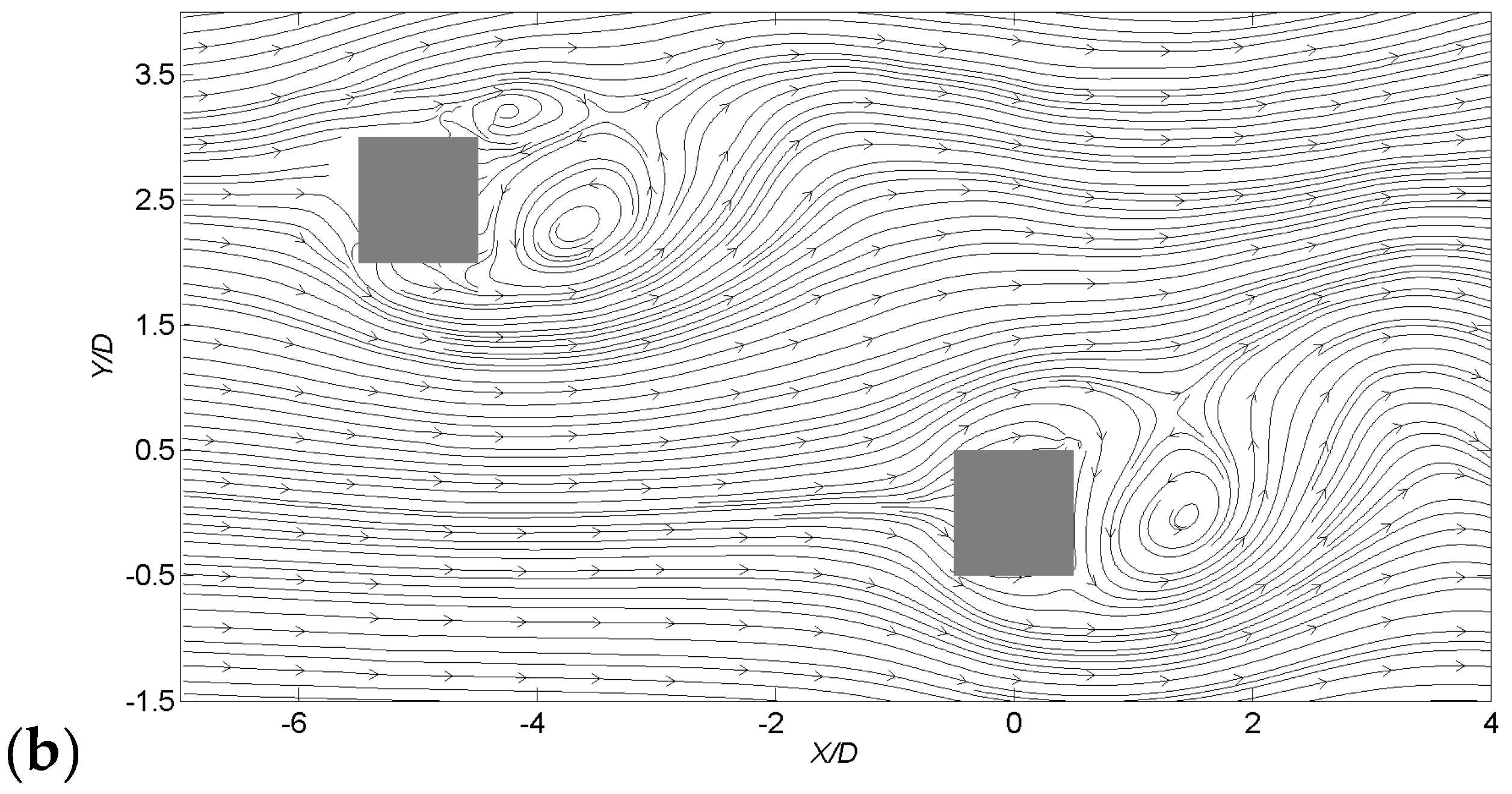
4.1. Time-Averaged Wind Flow Characteristics
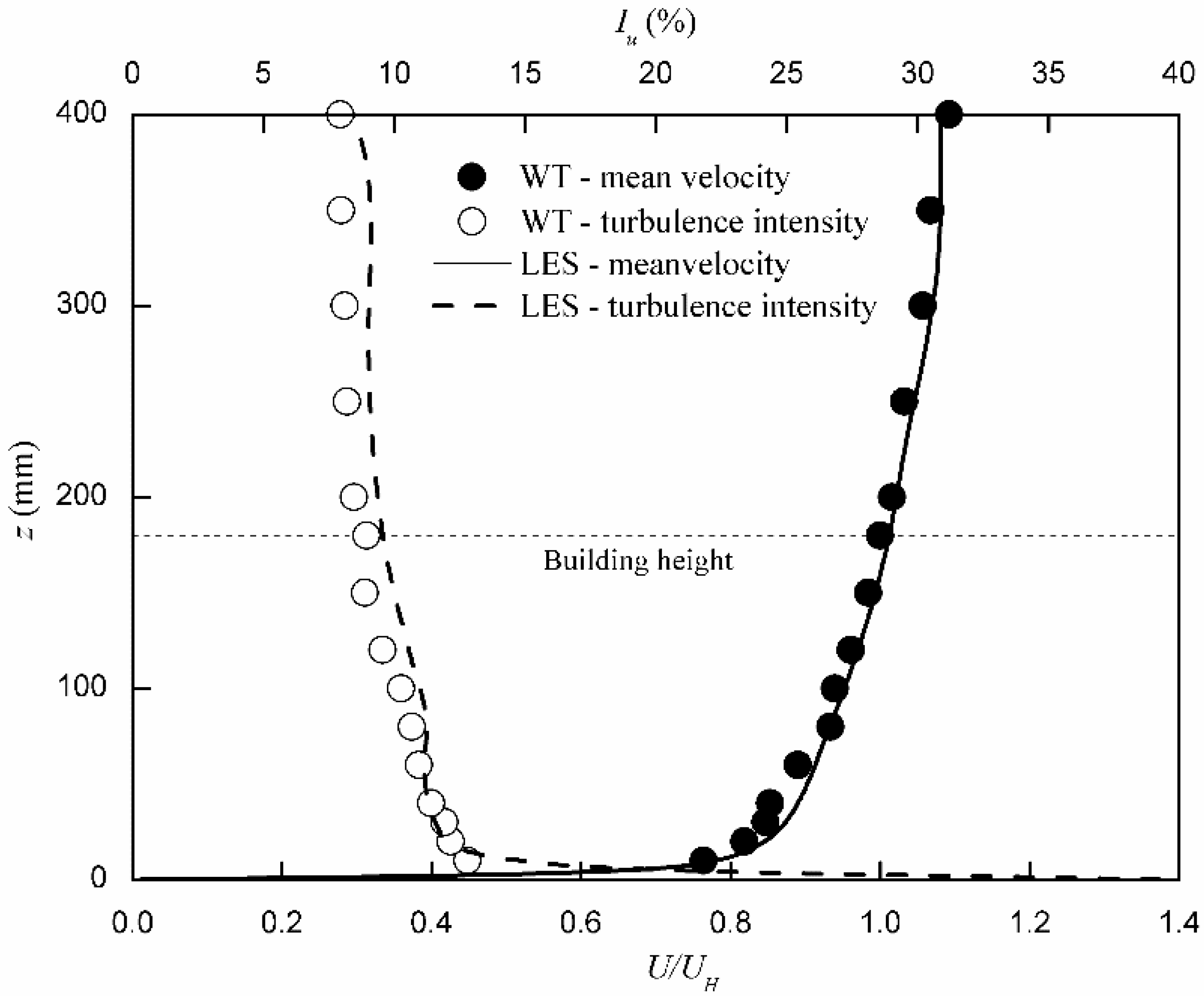
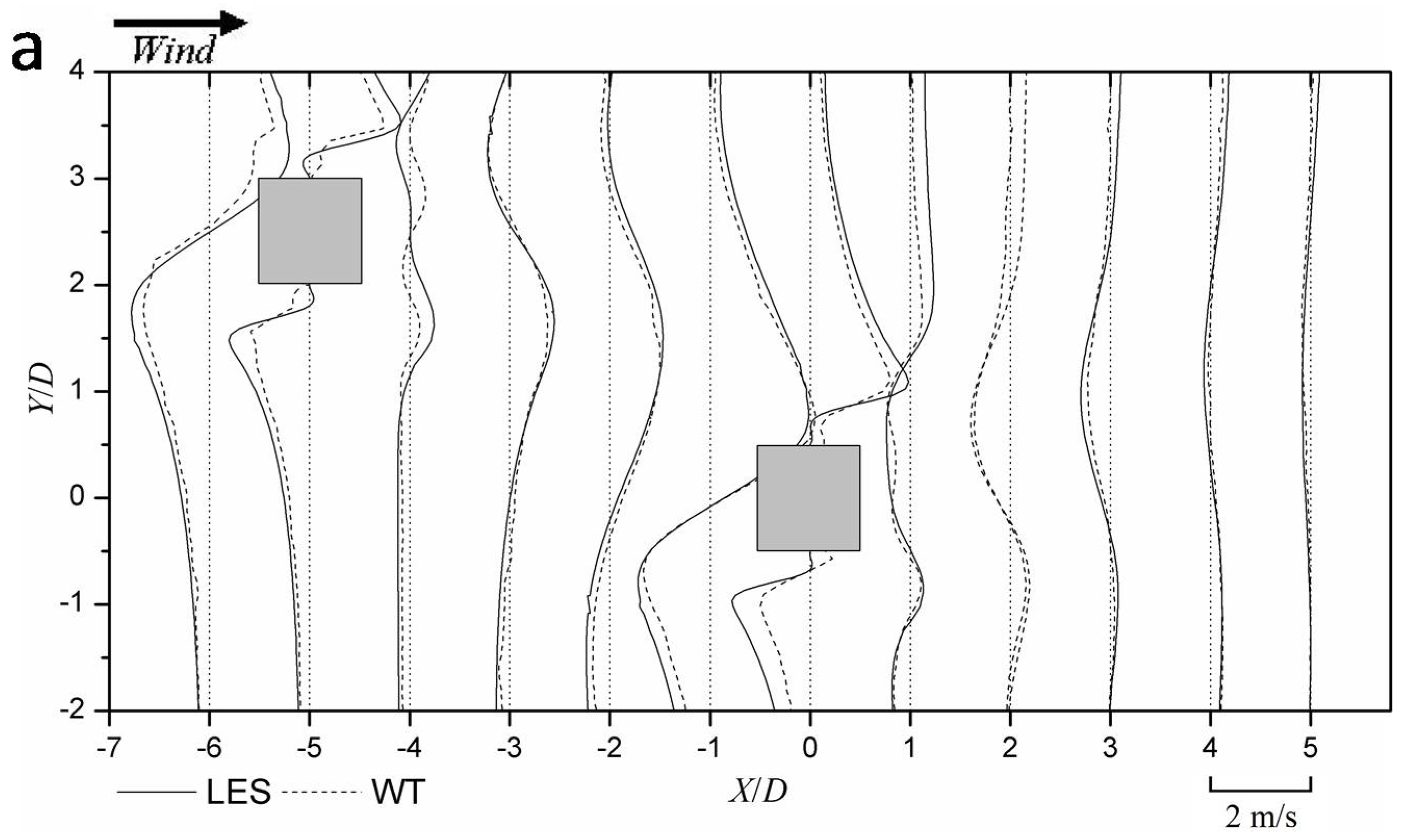
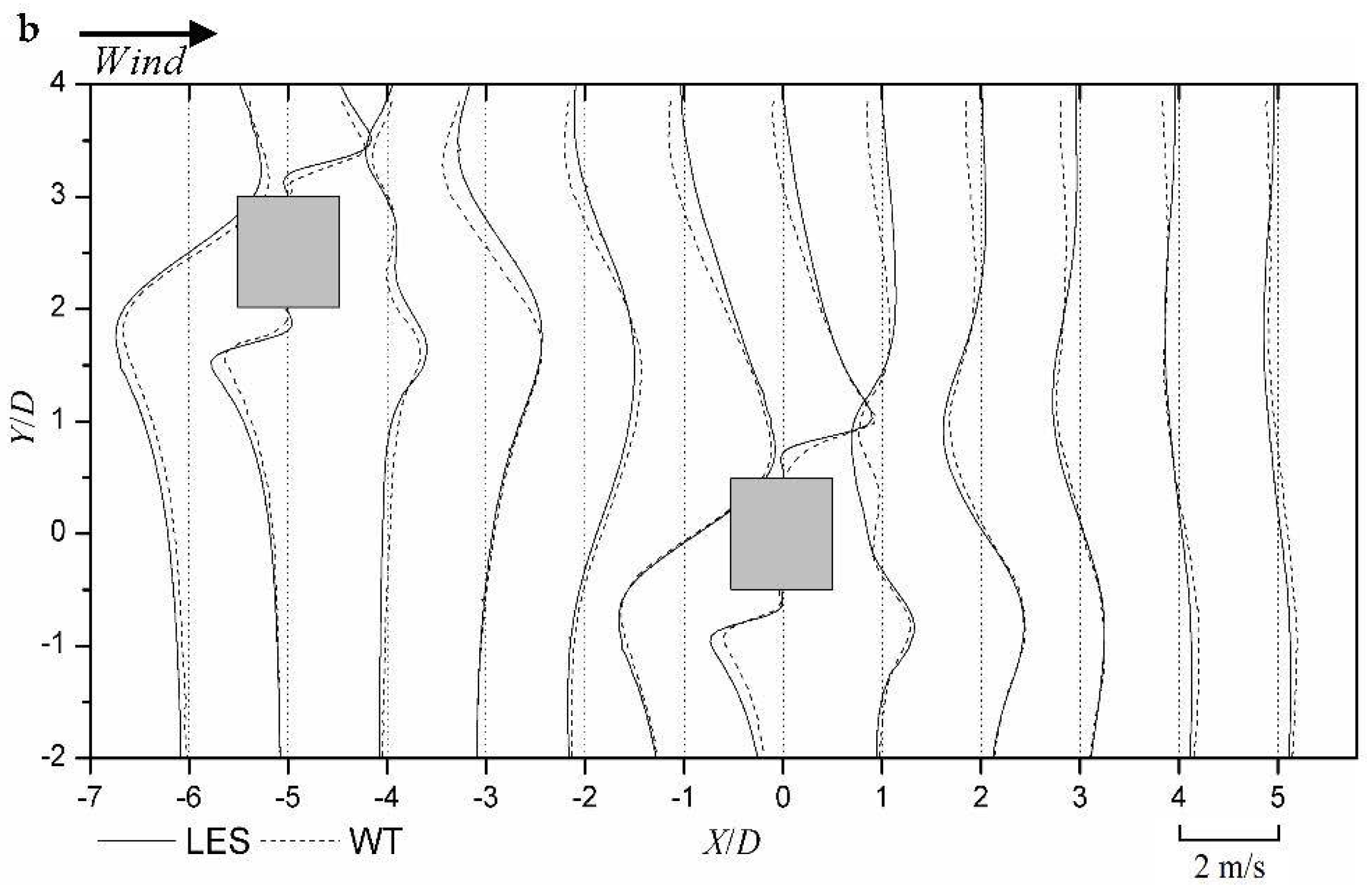
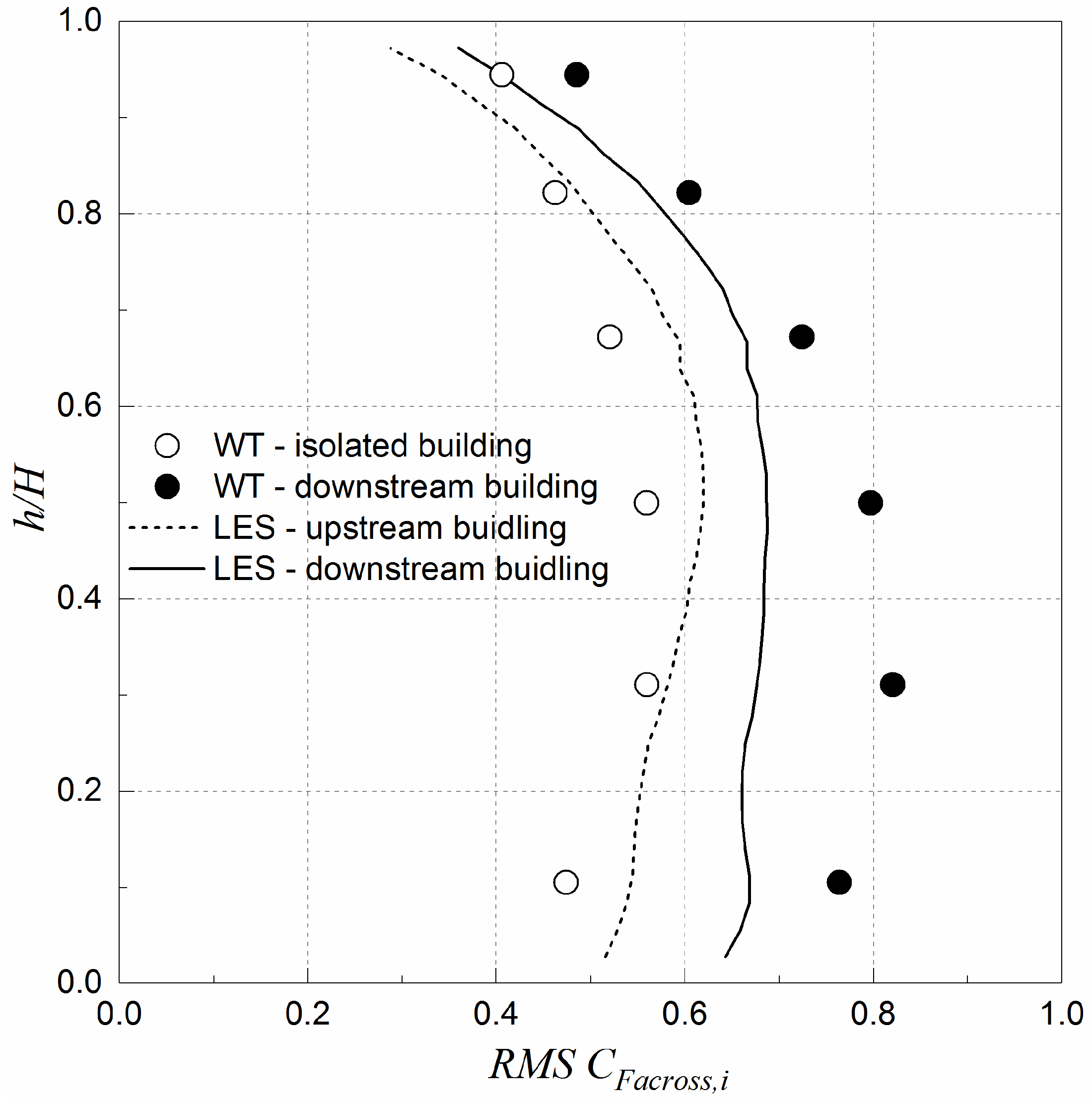
4.2. LES Validation by Wind Tunnel Result
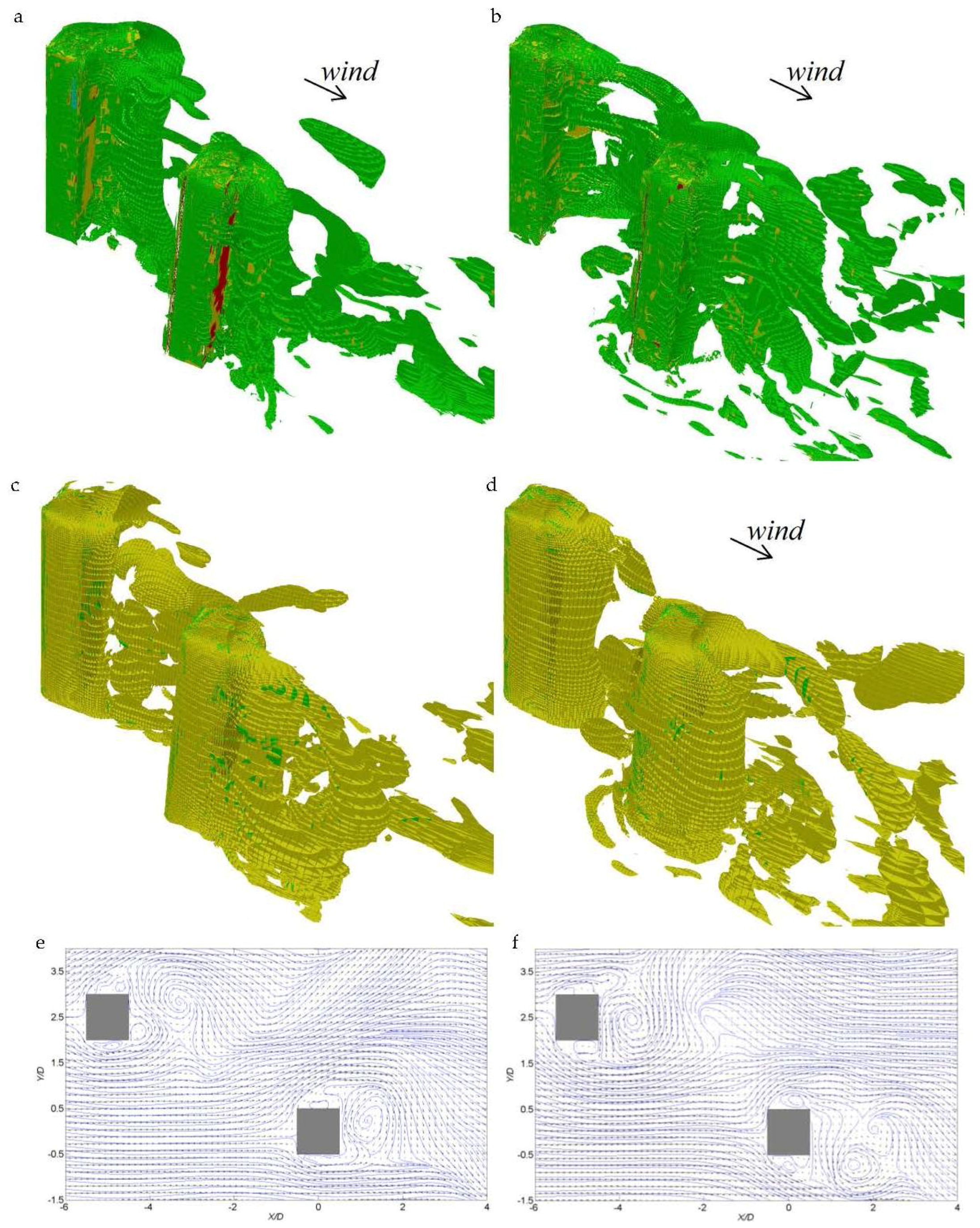
4.3. Vortex Structures of Tall Buildings under Interference
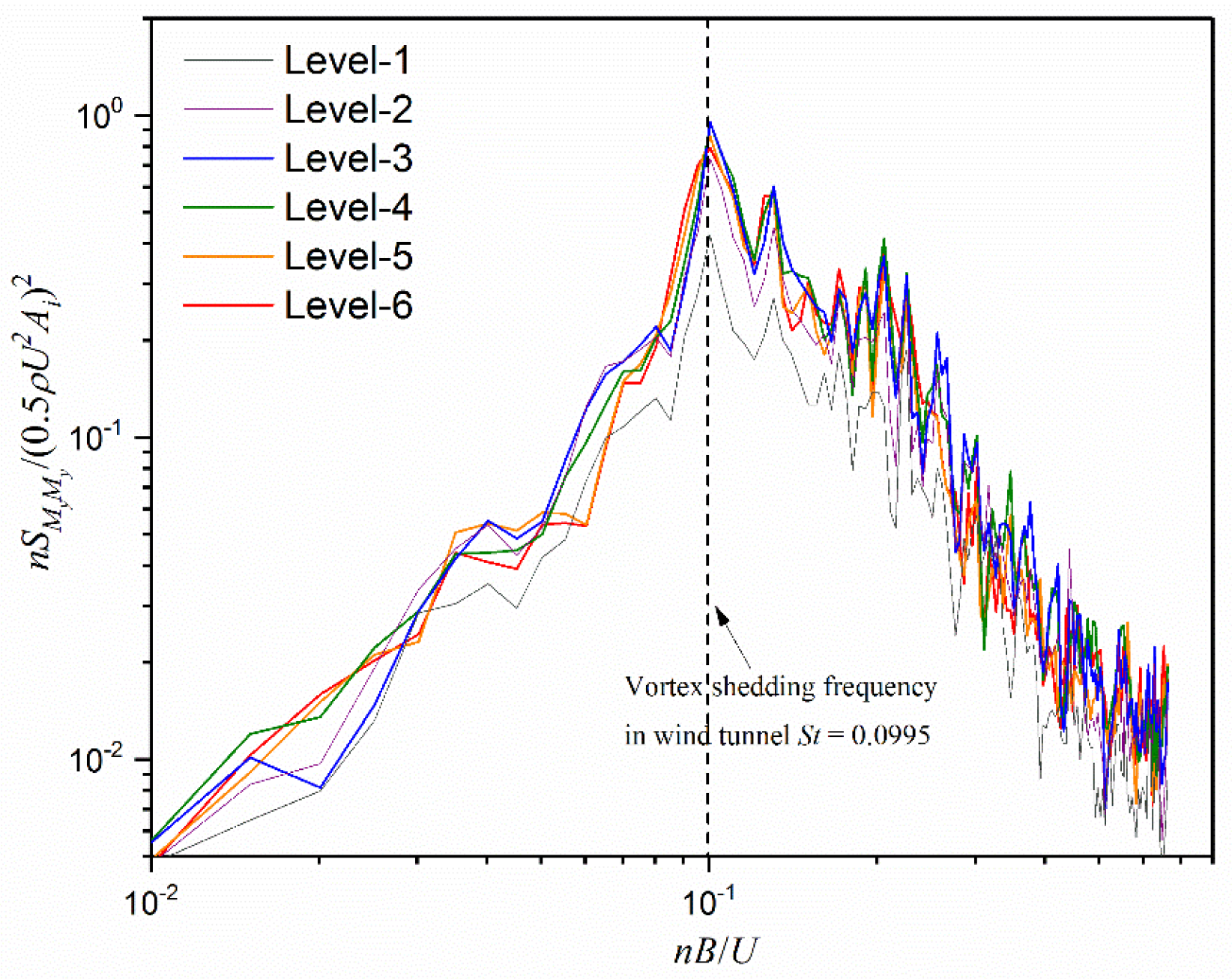
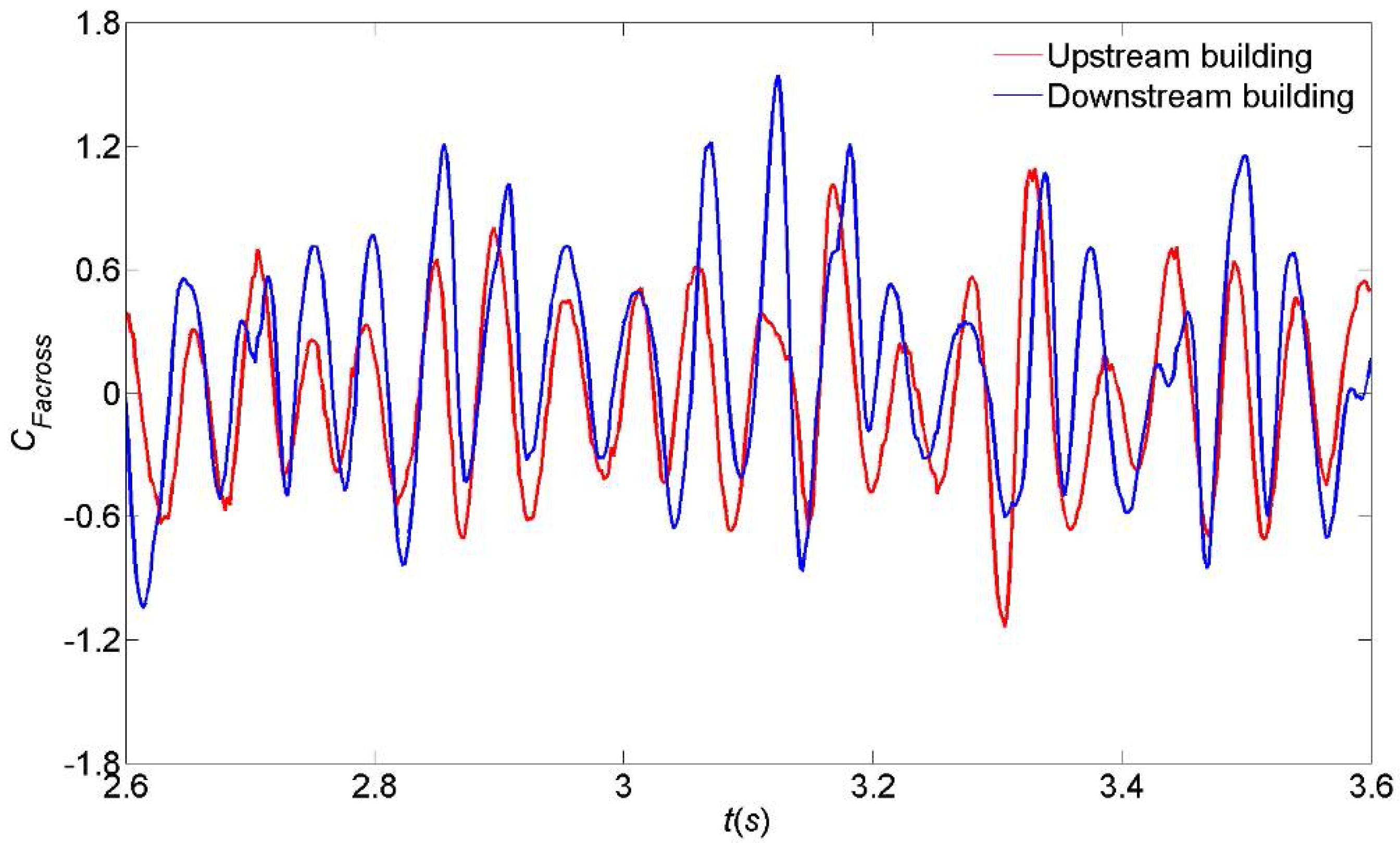
4.4. Excitation of Across-Wind Forces on Buildings
5. Conclusions
- The results of wind flow around two buildings, including time-averaged mean and fluctuating streamwise and transverse velocity distributions obtained by LES agree well with the wind tunnel measurements. A better agreement is found for time-averaged mean flow field than the fluctuating velocity distributions.
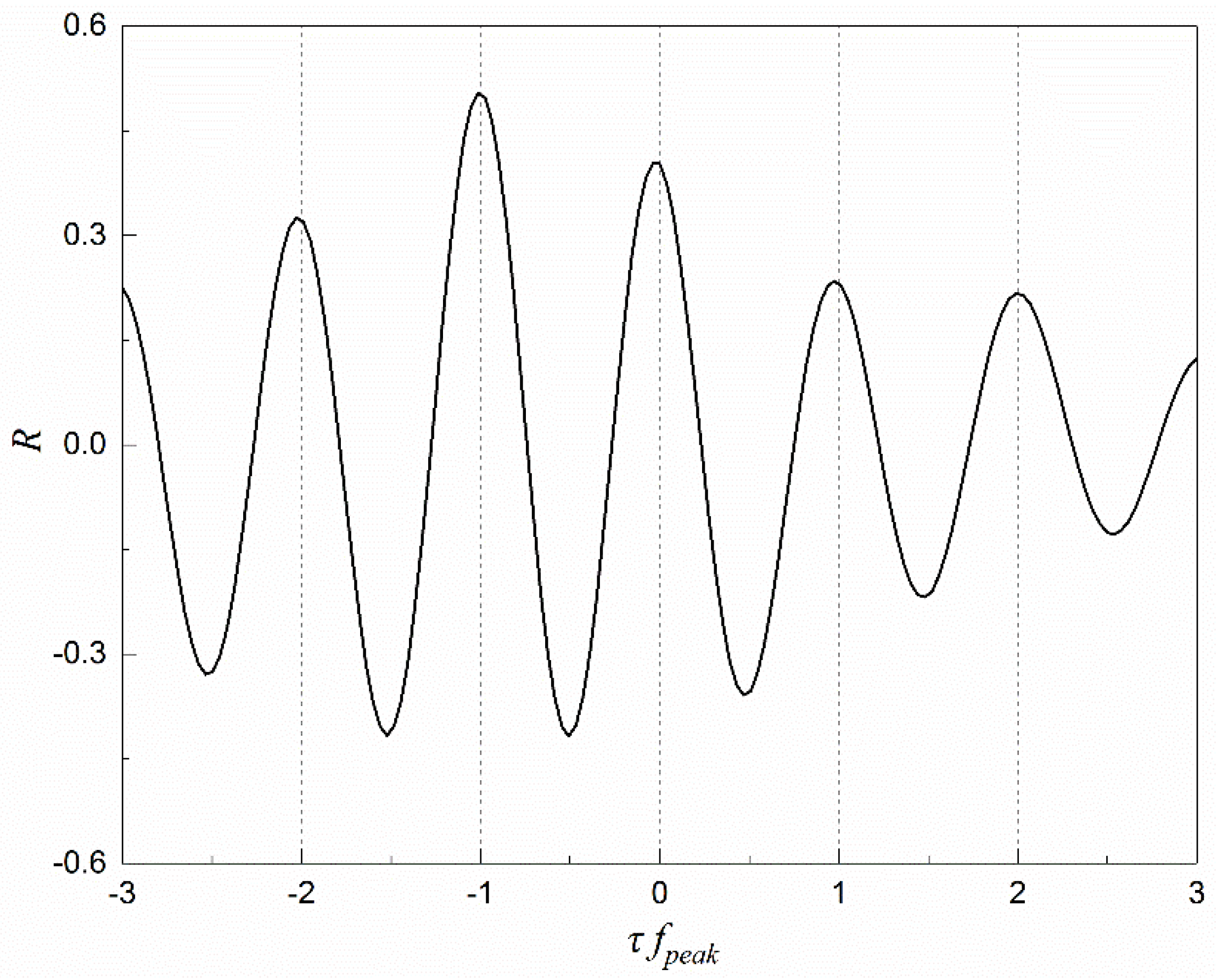
- The large scale coherent patterns are successfully revealed by numerical simulation and wind tunnel test. A distinct relationship between the across-wind peak forces and the phases of alternating vortex shedding is observed. Three-dimensional flow structures are further observed by LES.
- An in-phase synchronization of the vortex shedding from both buildings is observed and confirmed by the wind forces analysis. This would be the cause of largely amplified across-wind excitation of the downstream building.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bailey, P.A.; Kwok, K.C.S. Interference excitation of twin tall buildings. J. Wind Eng. Ind. Aerodyn. 1985, 21, 323–338. [Google Scholar] [CrossRef]
- Taniike, Y.; Inaoka, H. Aeroelastic behavior of tall buildings in wakes. J. Wind Eng. Ind. Aerodyn. 1988, 28, 317–327. [Google Scholar] [CrossRef]
- Xie, Z.N.; Gu, M. Simplified formulas for evaluation of wind-induced interference effects among three tall buildings. J. Wind Eng. Ind. Aerodyn. 2007, 95, 31–52. [Google Scholar] [CrossRef]
- Lam, K.M.; Zhao, J.G.; Leung, M.Y.H. Wind-induced loading and dynamic responses of a row of tall buildings under strong interference. J. Wind Eng. Ind. Aerodyn. 2011, 99, 573–583. [Google Scholar] [CrossRef] [Green Version]
- Khanduri, A.C.; Stathopoulos, T.; Bedard, C. Wind-induced interference effects on buildings—A review of the state-of-the-art. Eng. Struct. 1998, 20, 617–630. [Google Scholar] [CrossRef]
- English, E.C.; Fricke, F.R. The interference index and its prediction using a neural network analysis of wind-tunnel data. J. Wind Eng. Ind. Aerodyn. 1999, 83, 567–575. [Google Scholar] [CrossRef]
- Kim, W.; Tamura, Y.; Yoshida, A. Interference effects on local peak pressures between two buildings. J. Wind Eng. Ind. Aerodyn. 2011, 99, 584–600. [Google Scholar] [CrossRef]
- Yu, X.F.; Xie, Z.N.; Zhu, J.B.; Gu, M. Interference effects on wind pressure distribution between two high-rise buildings. J. Wind Eng. Ind. Aerodyn. 2015, 142, 188–197. [Google Scholar] [CrossRef]
- Taniike, Y. Interference mechanism for enhanced wind forces on neighboring tall buildings. J. Wind Eng. Ind. Aerodyn. 1992, 42, 1073–1083. [Google Scholar] [CrossRef]
- Sakamoto, H.; Haniu, H. Aerodynamic forces acting on two square prisms placed vertically in a turbulent boundary-layer. J. Wind Eng. Ind. Aerodyn. 1988, 31, 41–66. [Google Scholar] [CrossRef]
- Gowda, B.H.L.; Sitheeq, M.M. Interference effects on the wind pressure distribution on prismatic bodies in tandem arrangement. Indian J. Technol. 1993, 31, 485–495. [Google Scholar]
- Hui, Y.; Tamura, Y.; Yoshida, A.; Kikuchi, H. Pressure and flow field investigation of interference effects on external pressures between high-rise buildings. J. Wind Eng. Ind. Aerodyn. 2013, 115, 150–161. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T. CFD simulation of pedestrian-level wind conditions around buildings: Past achievements and prospects. J. Wind Eng. Ind. Aerodyn. 2013, 121, 138–145. [Google Scholar] [CrossRef]
- Sohankar, A. A LES study of the flow interference between tandem square cylinder pairs. Theor. Comp. Fluid Dyn. 2014, 28, 531–548. [Google Scholar] [CrossRef]
- Tamura, T. Towards practical use of LES in wind engineering. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1451–1471. [Google Scholar] [CrossRef]
- Mara, T.G.; Terry, B.K.; Ho, T.C.E.; Isyumov, N. Aerodynamic and peak response interference factors for an upstream square building of identical height. J. Wind Eng. Ind. Aerodyn. 2014, 133, 200–210. [Google Scholar] [CrossRef]
- Zu, G.B.; Lam, K.M. Interference mechanism of two tall buildings in staggered arrangement. In Proceedings of the 9th Asia-Pacific Conference on Wind Engineering, Auckland, New Zealand, 3–8 December 2017. [Google Scholar]
- Ansys Inc. Ansys Fluent 13.0, User’s Guide; Ansys Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure model. Phys. Fluids 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid scale eddy viscosity model. Phys. Fluids 1991, A3, 1760–1765. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; Vanheijst, G.J.F. Quality assessment of large-eddy simulation of wind flow around a high-rise building: Validation and solution verification. Comput. Fluids 2013, 79, 120–133. [Google Scholar] [CrossRef]
- Franke, J. Recommendations of the COST action C14 on the use of CFD in predicting pedestrian wind environment. In Proceedings of the Fourth International Symposium on Computational Wind Engineering, Yokohama, Japan, 16–19 July 2006. [Google Scholar]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. COST 732. Best Practice Guideline for the CFD Simulation of Flows in the Urban Environment; University of Hamburg, Meteorological Inst.: Hamburg, Germany, 2007. [Google Scholar]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Lam, K.M.; Leung, M.Y.H.; Zhao, J.G. Interference effects on wind loading of a row of closely spaced tall buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 562–583. [Google Scholar] [CrossRef]
- Theunissen, R.; Scarano, F.; Riethmuller, M.L. Spatially adaptive PIV interrogation based on data ensemble. Exp. Fluids 2010, 48, 875–887. [Google Scholar] [CrossRef]
- Willert, C.E.; Gharib, M. Digital particle image velocimetry. Exp. Fluids 1991, 10, 181–193. [Google Scholar] [CrossRef]
- Adrian, R.J. Multi-point optical measurements of simultaneous vectors in unsteady flow—A review. Int. J. Heat Fluid Flow 1986, 7, 127–145. [Google Scholar] [CrossRef]
- Adrian, R.J.; Westerweel, J. Particle Image Velocimetry; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Wang, H.F.; Zhou, Y. The finite-length square cylinder near wake. J. Fluid Mech. 2009, 638, 453–490. [Google Scholar] [CrossRef]
- To, A.P.; Lam, K.M.; Xie, Z.N. Effect of a through-building gap on wind-induced loading and dynamic responses of a tall building. Wind Struct. 2012, 15, 531–553. [Google Scholar] [CrossRef]
- Lam, K.M.; Zhao, J.G. Occurrence of peak lifting actions on a large horizontal cantilevered roof. J. Wind Eng. Ind. Aerodyn. 2002, 90, 897–940. [Google Scholar] [CrossRef] [Green Version]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zu, G.; Lam, K.M. LES and Wind Tunnel Test of Flow around Two Tall Buildings in Staggered Arrangement. Computation 2018, 6, 28. https://doi.org/10.3390/computation6020028
Zu G, Lam KM. LES and Wind Tunnel Test of Flow around Two Tall Buildings in Staggered Arrangement. Computation. 2018; 6(2):28. https://doi.org/10.3390/computation6020028
Chicago/Turabian StyleZu, Gongbo, and Kit Ming Lam. 2018. "LES and Wind Tunnel Test of Flow around Two Tall Buildings in Staggered Arrangement" Computation 6, no. 2: 28. https://doi.org/10.3390/computation6020028




