Efficient Listening and Sleeping Scheduling Mechanism Based on Self-Similarity for Duty Cycle Opportunistic Mobile Networks †
Abstract
:1. Introduction
2. Related Work
3. Network Model
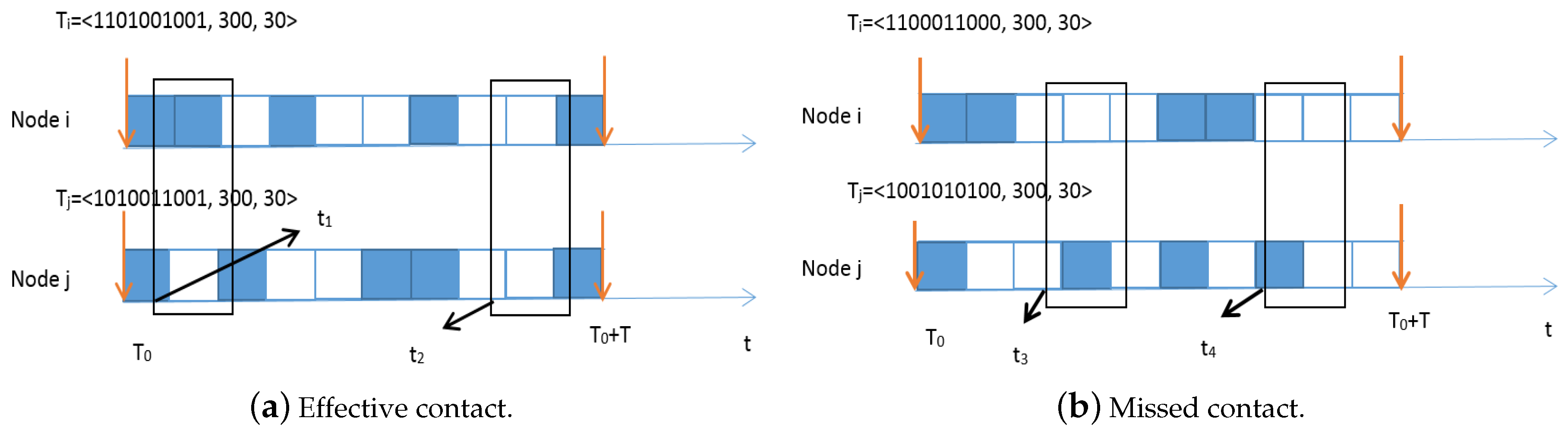
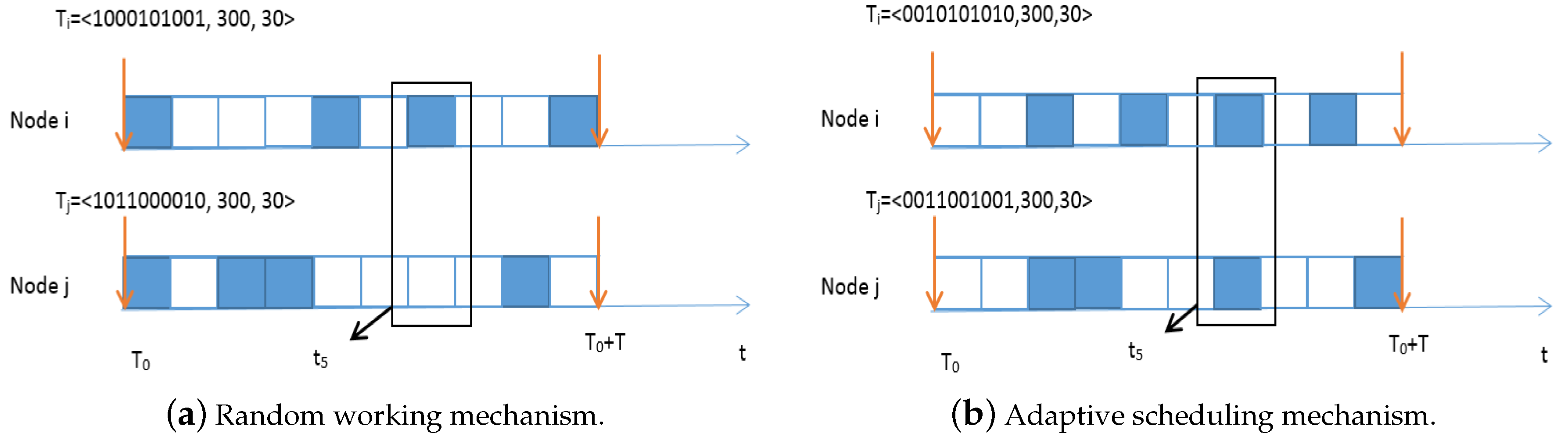
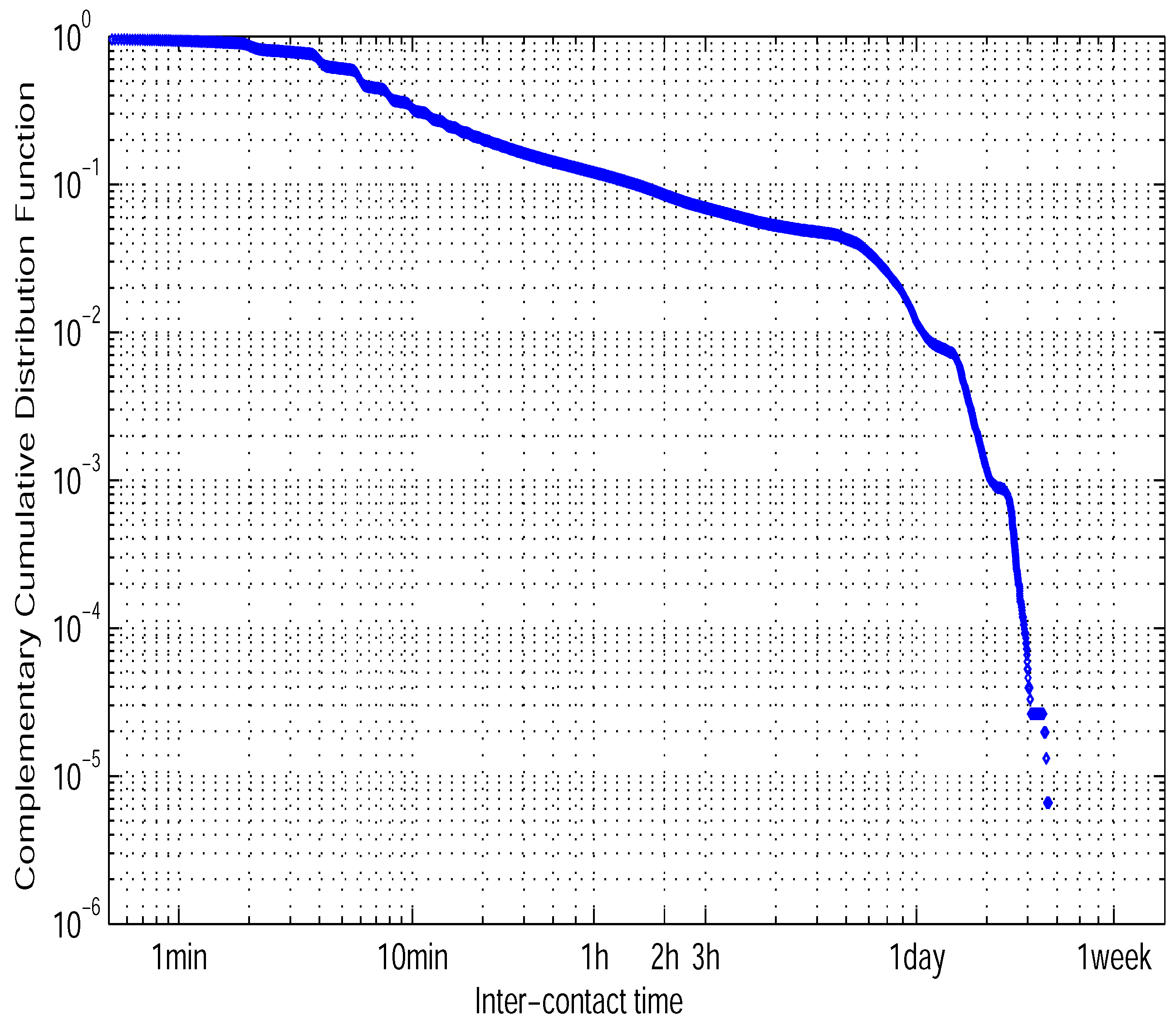
4. Motivations
5. Adaptive Scheduling Mechanism Based on Self-Similarity
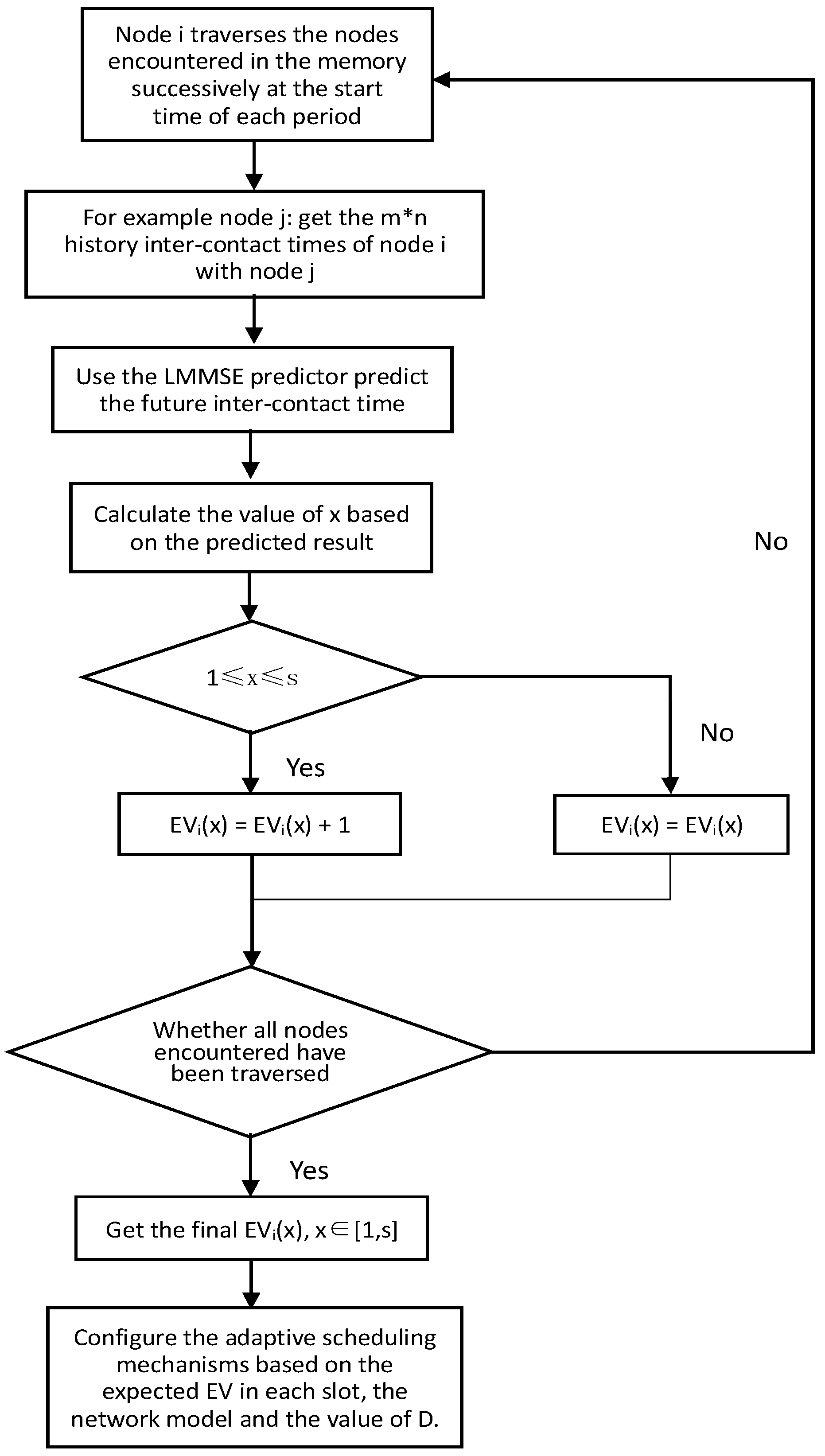
5.1. The LMMSE Predictor
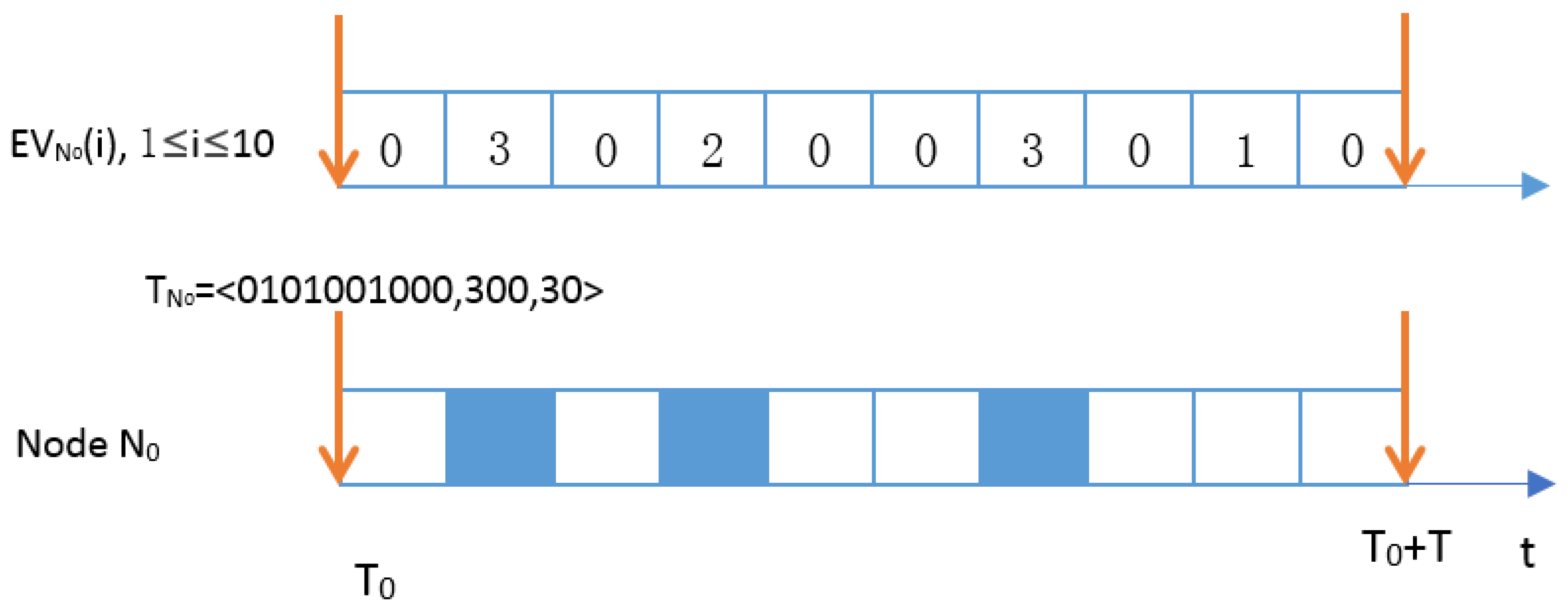
5.2. The Proposed ASMSS
6. Performance Evaluation
6.1. Simulation Setup
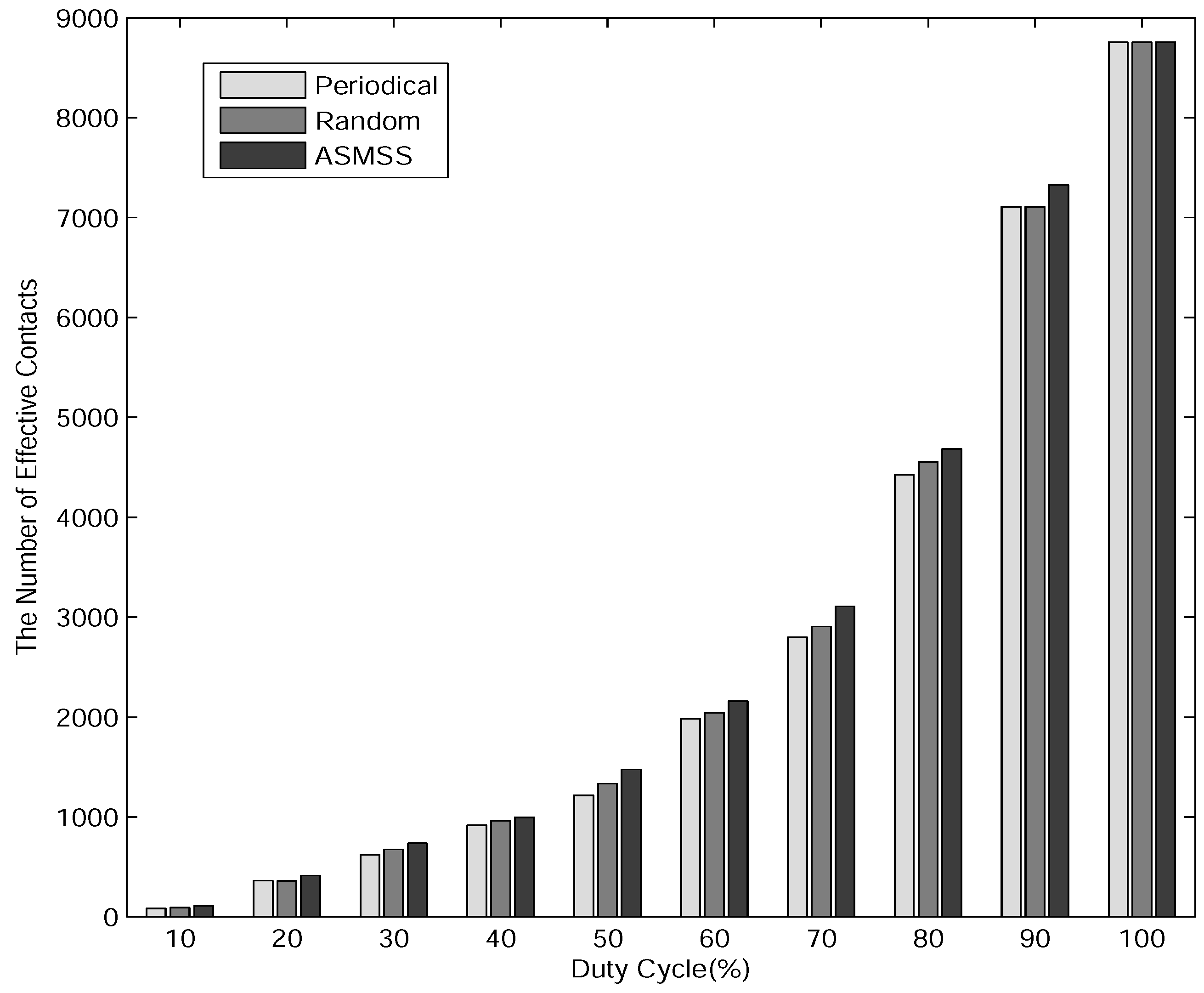
- The Number of Effective Contacts: the number of effective contacts of the nodes in the network within a certain period.
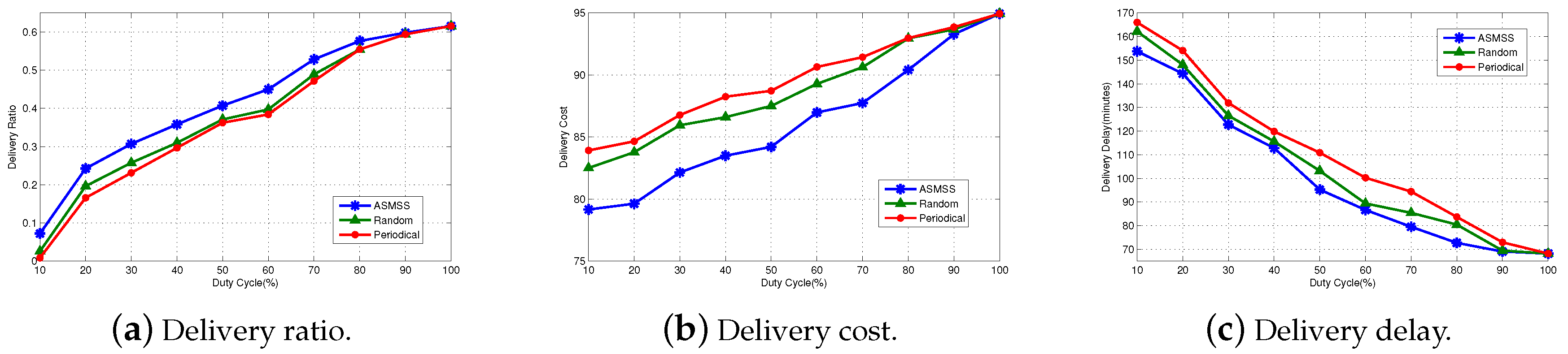
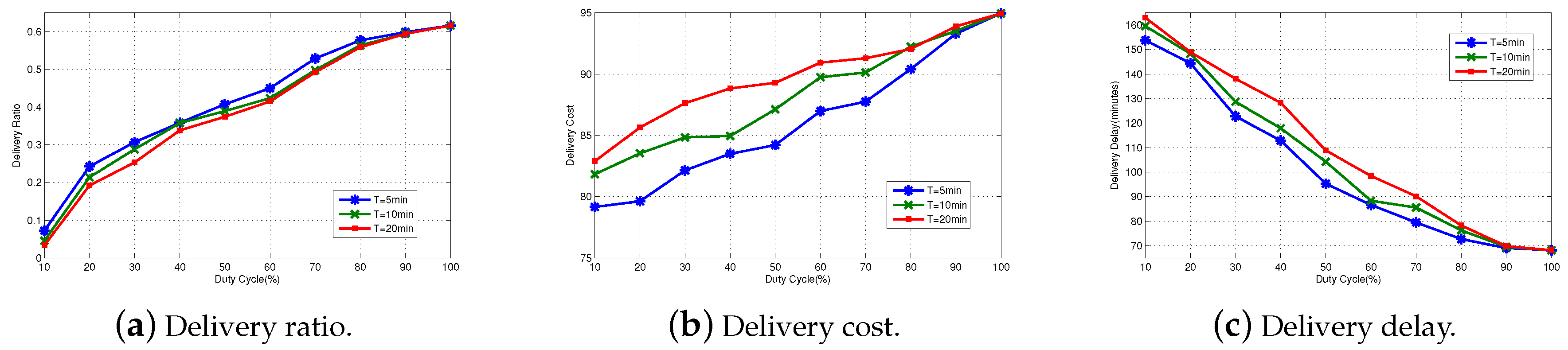
- Delivery Ratio: the ratio of the number of data packets successfully reached the destination node and the amount of data packets sent by the source node within a certain time.
- Delivery Delay: the average time it takes for a packet to reach the destination after it leaves the source.
- Delivery Cost: the average number of data transmitted by nodes in the network.
6.2. Performance Comparison of Three Mechanisms
6.3. Performance Comparision of Different T
6.4. Performance Comparison of Different m and n
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mota, V.F.; Cunha, F.D.; Macedo, D.F.; Nogueira, J.M.; Loureiro, A.A. Protocols, mobility models and tools in opportunistic networks: A survey. Comput. Commun. 2014, 48, 5–19. [Google Scholar] [CrossRef]
- Li, Y.; Bartos, R. A survey of protocols for intermittently connected delay-tolerant wireless sensor networks. J. Netw. Comput. Appl. 2014, 41, 411–423. [Google Scholar] [CrossRef]
- Hossmann, T.; Spyropoulos, T.; Legendre, F. A complex network analysis of human mobility. In Proceedings of the Computer Communications Workshops (INFOCOM WKSHPS), Shanghai, China, 10–15 April 2011; pp. 876–881. [Google Scholar]
- Zhou, H.; Chen, J.; Zheng, H.; Wu, J. Energy efficiency and contact opportunities tradeoff in opportunistic mobile networks. IEEE Trans. Veh. Technol. 2016, 65, 3723–3734. [Google Scholar] [CrossRef]
- Fan, J.; Chen, J.; Du, Y.; Gao, W.; Wu, J.; Sun, Y. Geocommunity-based broadcasting for data dissemination in mobile social networks. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 734–743. [Google Scholar]
- Wu, J.; Xiao, M.; Huang, L. Homing spread: Community home-based multi-copy routing in mobile social networks. In Proceedings of the INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2319–2327. [Google Scholar]
- Xiao, M.; Wu, J.; Liu, C.; Huang, L. Tour: Time-sensitive opportunistic utility-based routing in delay tolerant networks. In Proceedings of the INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2085–2091. [Google Scholar]
- Zhang, F.; Wang, X.; Jiang, L.; Zhang, L. Energy Efficient Forwarding Algorithm in Opportunistic Networks. Chin. J. Electron. 2016, 25, 957–964. [Google Scholar] [CrossRef]
- Karagiannis, T.; Le Boudec, J.Y.; Vojnovic, M. Power law and exponential decay of intercontact times between mobile devices. IEEE Trans. Mob. Comput. 2010, 9, 1377–1390. [Google Scholar] [CrossRef]
- Banerjee, N.; Corner, M.D.; Levine, B.N. Design and field experimentation of an energy-efficient architecture for DTN throwboxes. IEEE/ACM Trans. Netw. (TON) 2010, 18, 554–567. [Google Scholar] [CrossRef]
- Banerjee, N.; Corner, M.; Levine, B.N. An Energy-Efficient Architecture for DTN Throwboxes. In Proceedings of the 26th IEEE International Conference on Computer Communications, Barcelona, Spain, 6–12 May 2007; pp. 776–784. [Google Scholar]
- Li, Z.; Li, M.; Liu, Y. Towards energy-fairness in asynchronous duty-cycling sensor networks. ACM Trans. Sens. Netw. (TOSN) 2014, 10, 38. [Google Scholar] [CrossRef]
- Trullols-Cruces, O.; Morillo-Pozo, J.; Barcelo-Ordinas, J.M.; Garcia-Vidal, J. Power saving trade-offs in delay/disruptive tolerant networks. In Proceedings of the World of Wireless, Mobile and Multimedia Networks (WoWMoM), Lucca, Italy, 20–24 June 2011; pp. 1–9. [Google Scholar]
- Zhou, H.; Chen, J.; Zhao, H.; Gao, W.; Cheng, P. On exploiting contact patterns for data forwarding in duty-cycle opportunistic mobile networks. IEEE Trans. Veh. Technol. 2013, 62, 4629–4642. [Google Scholar] [CrossRef]
- Chaintreau, A.; Hui, P.; Crowcroft, J.; Diot, C; Gass, R.; Scott, J. Impact of human mobility on the design of opportunistic forwarding algorithms. In Proceedings of the IEEE INFOCOM, Barcelona, Spain, 23–29 April 2006. [Google Scholar]
- Hui, P.; Chaintreau, A.; Scott, J.; Gass, R.; Crowcroft, J.; Diot, C. Pocket switched networks and human mobility in conference environments. In Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-Tolerant Networking, Philadelphia, PA, USA, 22–26 August 2005; pp. 244–251. [Google Scholar]
- Chen, L.J.; Chen, Y.C. An Analytical Study of People Mobility in Opportunistic Networks. J. Inf. Sci. Eng. 2010, 26, 197–214. [Google Scholar]
- Gao, Y.; He, G.; Hou, J.C. On exploiting traffic predictability in active queue management. In Proceedings of the Twenty-First Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, 23–27 June 2002; Volume 3, pp. 1630–1639. [Google Scholar]
- Wang, W.; Motani, M.; Srinivasan, V. Opportunistic energy-efficient contact probing in delay-tolerant applications. IEEE/ACM Trans. Netw. (TON) 2009, 17, 1592–1605. [Google Scholar] [CrossRef]
- Qin, S.; Feng, G.; Zhang, Y. How the contact-probing mechanism affects the transmission capacity of delay-tolerant networks. IEEE Trans. Veh. Technol. 2011, 60, 1825–1834. [Google Scholar]
- Drula, C.; Amza, C.; Rousseau, F.; Duda, A. Adaptive energy conserving algorithms for neighbor discovery in opportunistic bluetooth networks. IEEE J. Select. Areas Commun. 2007, 25, 96–107. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Y.; Jin, D.; Su, L.; Zeng, L. Optimal opportunistic forwarding policies for energy-constrained delay tolerant networks. In Proceedings of the 2010 IEEE International Conference on Communications (ICC), Cape Town, South Africa, 23–27 May 2010; pp. 1–5. [Google Scholar]
- Li, Y.; Hui, P.; Jin, D.; Su, L.; Zeng, L. Performance evaluation of routing schemes for energy-constrained delay tolerant networks. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–5. [Google Scholar]
- Li, Y.; Jiang, Y.; Jin, D.; Su, L.; Zeng, L.; Wu, D. Energy-efficient optimal opportunistic forwarding for delay-tolerant networks. IEEE Trans. Veh. Technol. 2010, 59, 4500–4512. [Google Scholar]
- Shih, E.; Bahl, P.; Sinclair, M.J. Wake on wireless: An event driven energy saving strategy for battery operated devices. In Proceedings of the 8th Annual International Conference on Mobile Computing and Networking, Atlanta, GA, USA, 23–28 September 2002; pp. 160–171. [Google Scholar]
- Yang, S.; Yeo, C.K.; Lee, F.B.S. Cooperative Duty Cycling For Energy-Efficient Contact Discovery in Pocket Switched Networks. IEEE Trans. Veh. Technol. 2013, 62, 1815–1826. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, H.; Chen, J.; Liu, C.H.; Fan, J. Adaptive working schedule for duty-cycle opportunistic mobile networks. IEEE Trans. Veh. Technol. 2014, 63, 4694–4703. [Google Scholar] [CrossRef]
- Nelson, S.C.; Bakht, M.; Kravets, R.; Harris, A.F., III. Encounter: Based routing in DTNs. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2009, 13, 56–59. [Google Scholar] [CrossRef]
- Keränen, A.; Ott, J.; Kärkkäinen, T. The ONE Simulator for DTN Protocol Evaluation. In Proceedings of the 2nd International Conference on Simulation Tools and Techniques, Rome, Italy, 2–6 March 2009. [Google Scholar]
- CRAWDAD. Available online: http://www.crawdad.org/uoi/haggle/20160828/ (accessed on 5 July 2017).
| Trace | Infocom6 |
|---|---|
| Device | iMote |
| Network type | Bluetooth |
| Duration (days) | 4 |
| Granularity (seconds) | 120 |
| No. of internal contacts | 170,601 |
| No. of devices | 98 |
| Contact frequency/pair/day | 6.7% |
| Parameter | Value |
|---|---|
| Simulation duration (seconds) | 343,000 |
| Bluetooth interface | Simple Broadcast Interface |
| Bluetooth transmit Speed (bytes per second) | 250 k |
| Bluetooth transmit Range (meters) | 10 |
| Node buffer Size | 5 M |
| TTL of the messages-msg Ttl (minutes) | 300 |
| Message Event Generator interval (seconds) | 1000, 2000 |
| Message size | 1 k |
| m = 1 | m = 2 | m = 4 | m = 6 | m = 8 | m = 10 | |
|---|---|---|---|---|---|---|
| LMMSE | 0.10 | 0.092 | 0.080 | 0.078 | 0.072 | 0.075 |
| n = 2 | n = 4 | n = 6 | n = 8 | |
|---|---|---|---|---|
| Delivery Ratio | 0.3855 | 0.3869 | 0.4105 | 0.3899 |
| Delivery Overhead | 82.9419 | 85.2306 | 84.1749 | 86.2299 |
| Delivery Delay | 97.2503 | 99.0865 | 95.8766 | 97.0855 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, F.; Dou, Y.; Chen, Z.; Liu, H. Efficient Listening and Sleeping Scheduling Mechanism Based on Self-Similarity for Duty Cycle Opportunistic Mobile Networks. Information 2017, 8, 87. https://doi.org/10.3390/info8030087
Zeng F, Dou Y, Chen Z, Liu H. Efficient Listening and Sleeping Scheduling Mechanism Based on Self-Similarity for Duty Cycle Opportunistic Mobile Networks. Information. 2017; 8(3):87. https://doi.org/10.3390/info8030087
Chicago/Turabian StyleZeng, Feng, Yueyue Dou, Zhigang Chen, and Hui Liu. 2017. "Efficient Listening and Sleeping Scheduling Mechanism Based on Self-Similarity for Duty Cycle Opportunistic Mobile Networks" Information 8, no. 3: 87. https://doi.org/10.3390/info8030087





