Comparison of T-Norms and S-Norms for Interval Type-2 Fuzzy Numbers in Weight Adjustment for Neural Networks
Abstract
:1. Introduction
2. Related Work
3. Proposed Methodology
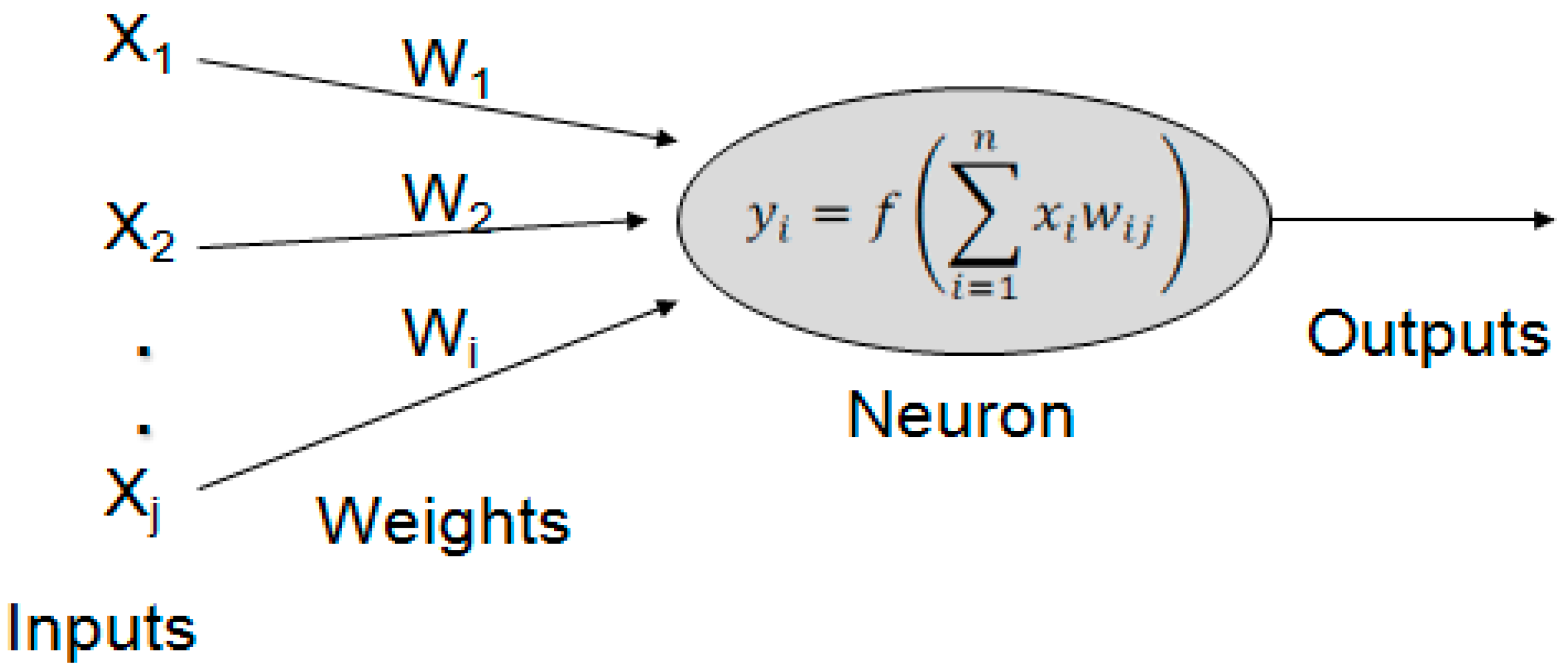
3.1. Architecture of the Traditional Neural Network
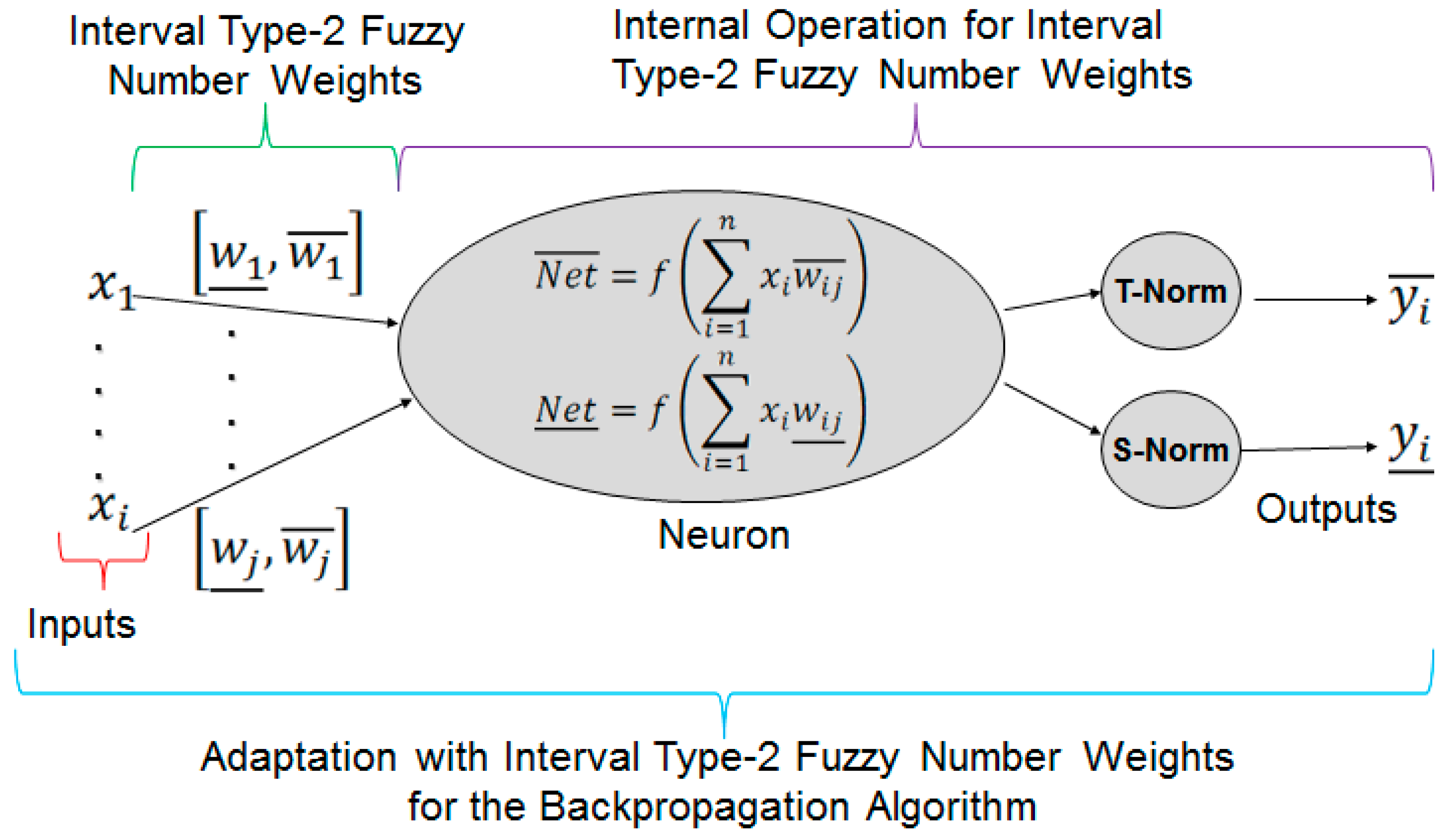
3.2. Architecture of the Fuzzy Neural Network with Interval Type-2 Fuzzy Numbers Weights
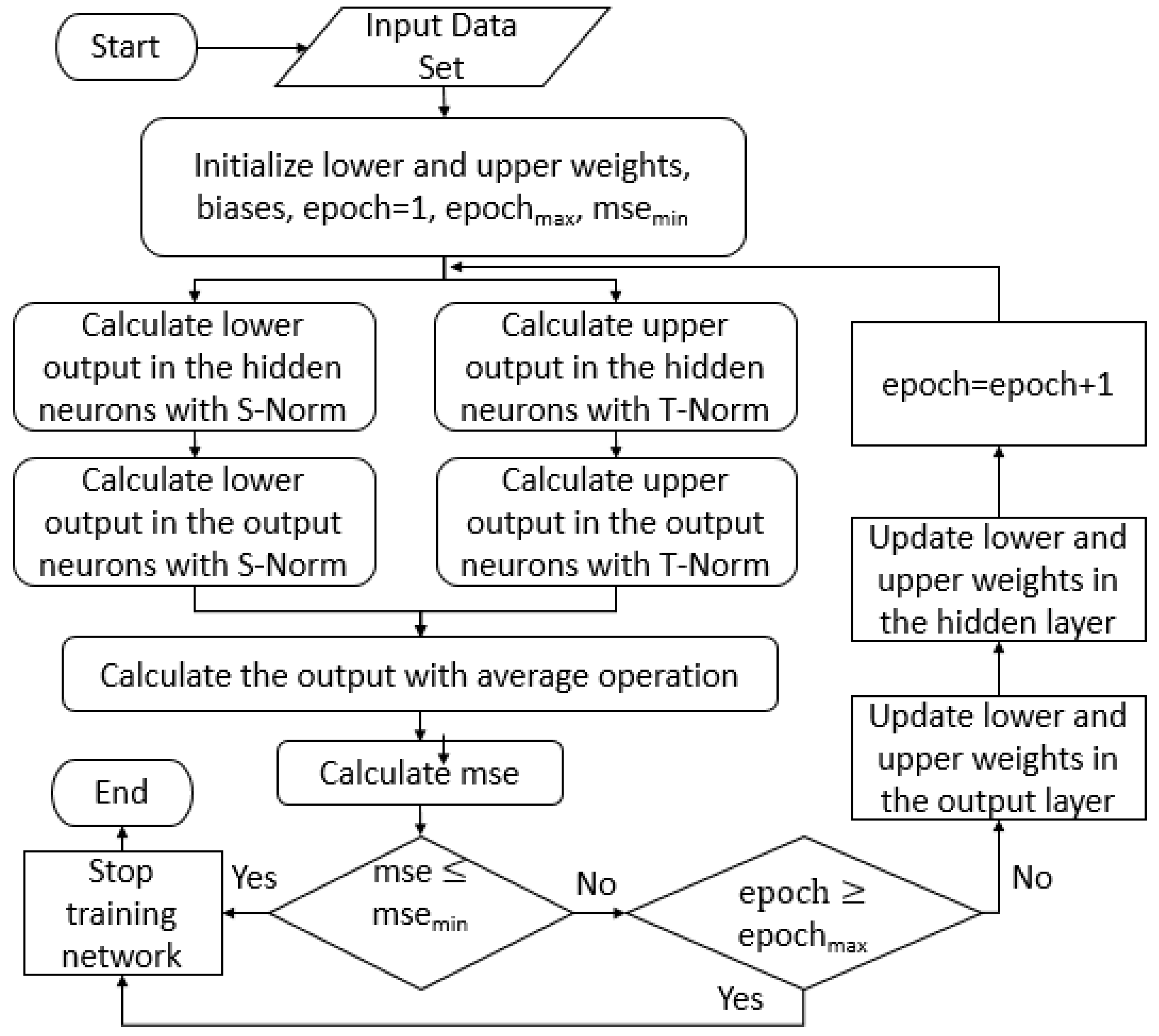
3.3. Proposed Adjustment for Interval Type-2 Fuzzy Numbers with Backpropagation Learning
- Stage 1:
- The Nguyen-Widrow algorithm is utilized to initialize the lower and upper values of the interval type-2 fuzzy numbers weights for the neural network.
- Stage 2:
- The input pattern and the wanted output for the neural network is established.
- Stage 3:
- The output of the neural network is calculated. In the first instance, the inputs for the network are introduced and the output of the network is obtained performing the calculations of the outputs from the input layer until the output layer.
- Stage 4:
- Determine the error terms for the neurons of the layers. In the output layer, the calculation of lower () and upper () delta for each neuron “k” is performed with the follow equations:In the hidden layer, the calculation of lower () and upper () delta for each neuron “j” is perform with the follow equations:
- Stage 5:
- The utilization of a recursive algorithm allows the actualization of the interval type-2 fuzzy number weights, beginning from the output neurons and updating backwards until the neurons in the input layer. The adjustment is described as follows:The calculation of the change of interval type-2 fuzzy number weights is achieved with the equations described as follows:Calculations of the output neurons:Calculations of the hidden neurons:
- Stage 6:
- The method is recurrent until for each of the learned patterns the error terms are small enough.
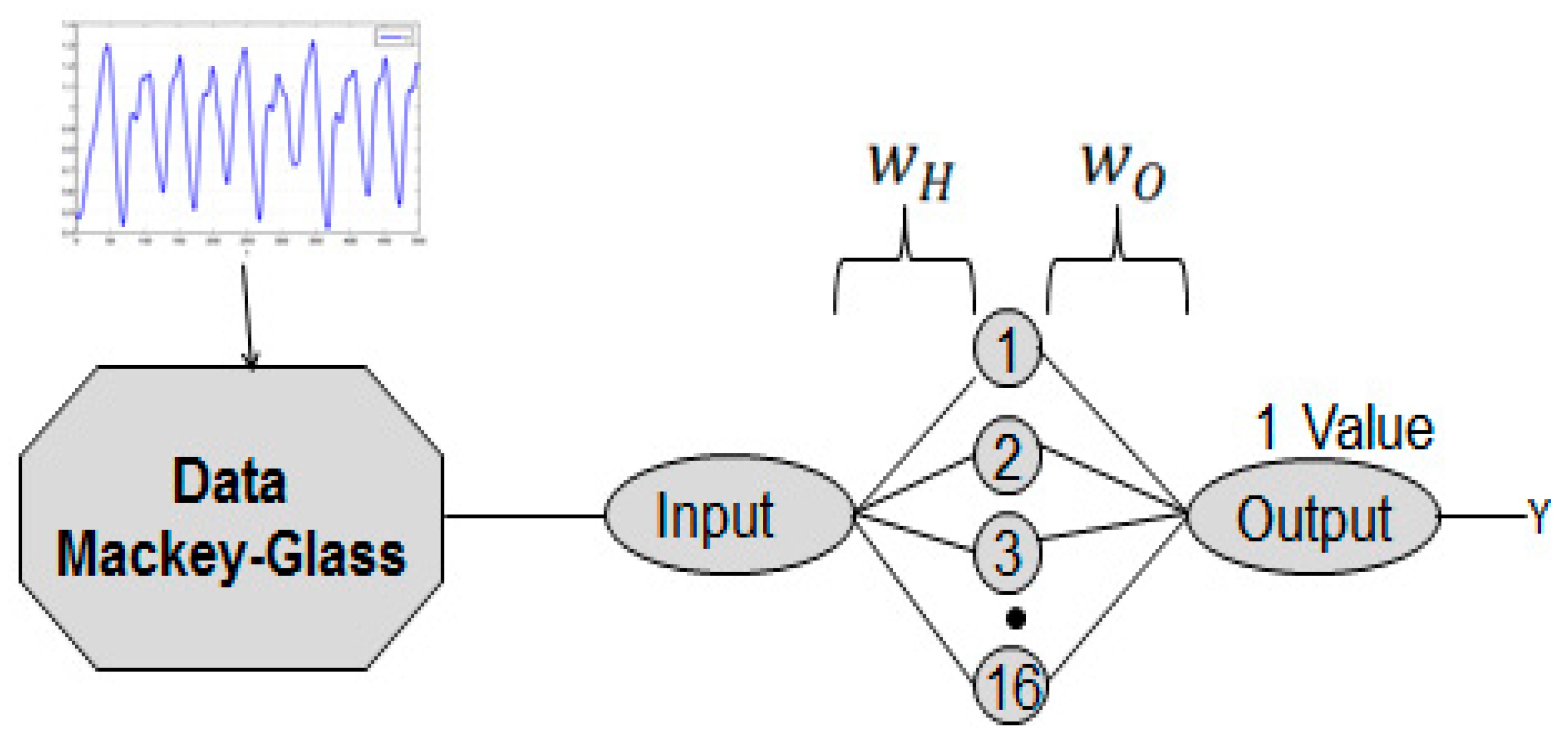
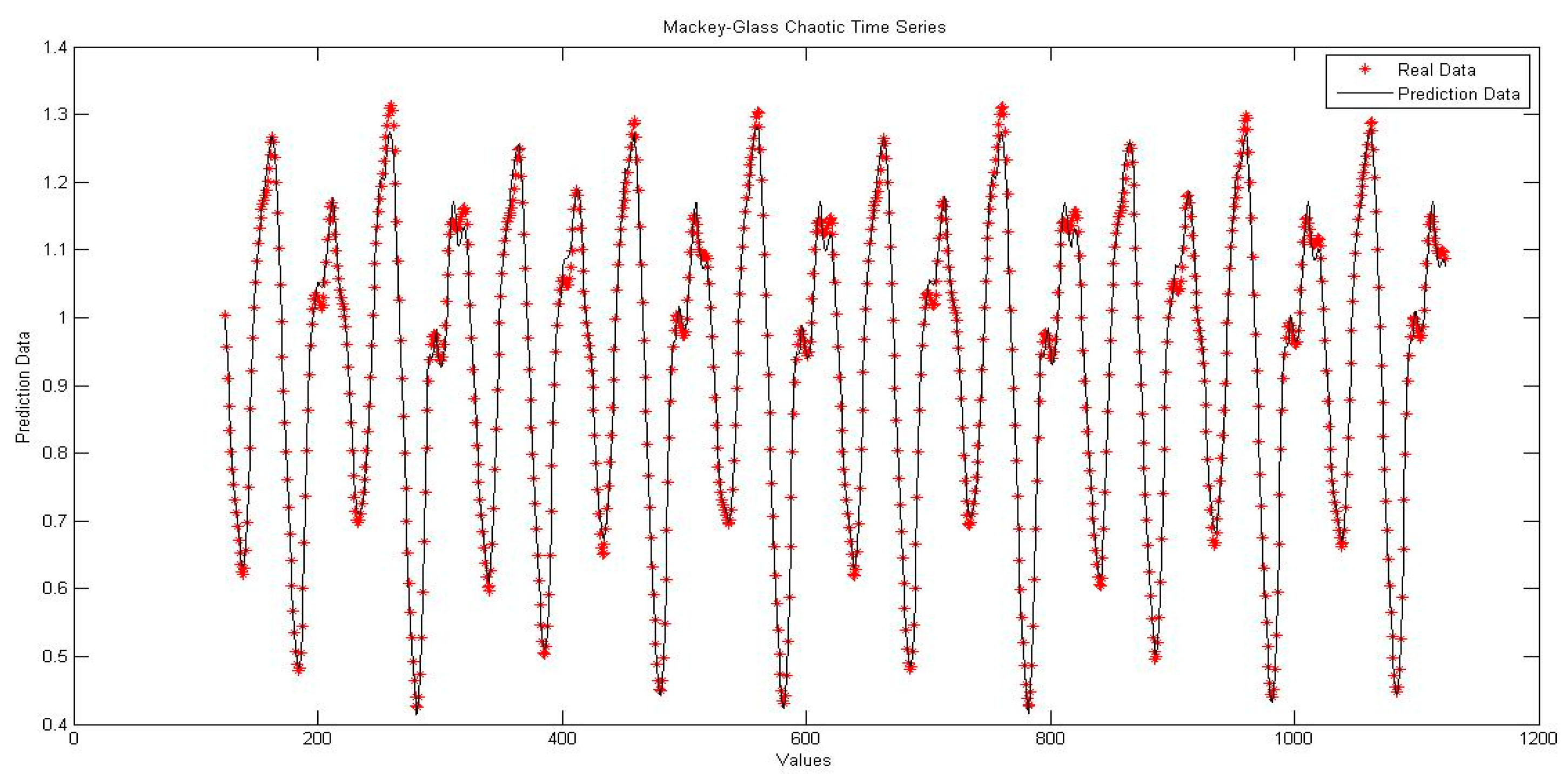
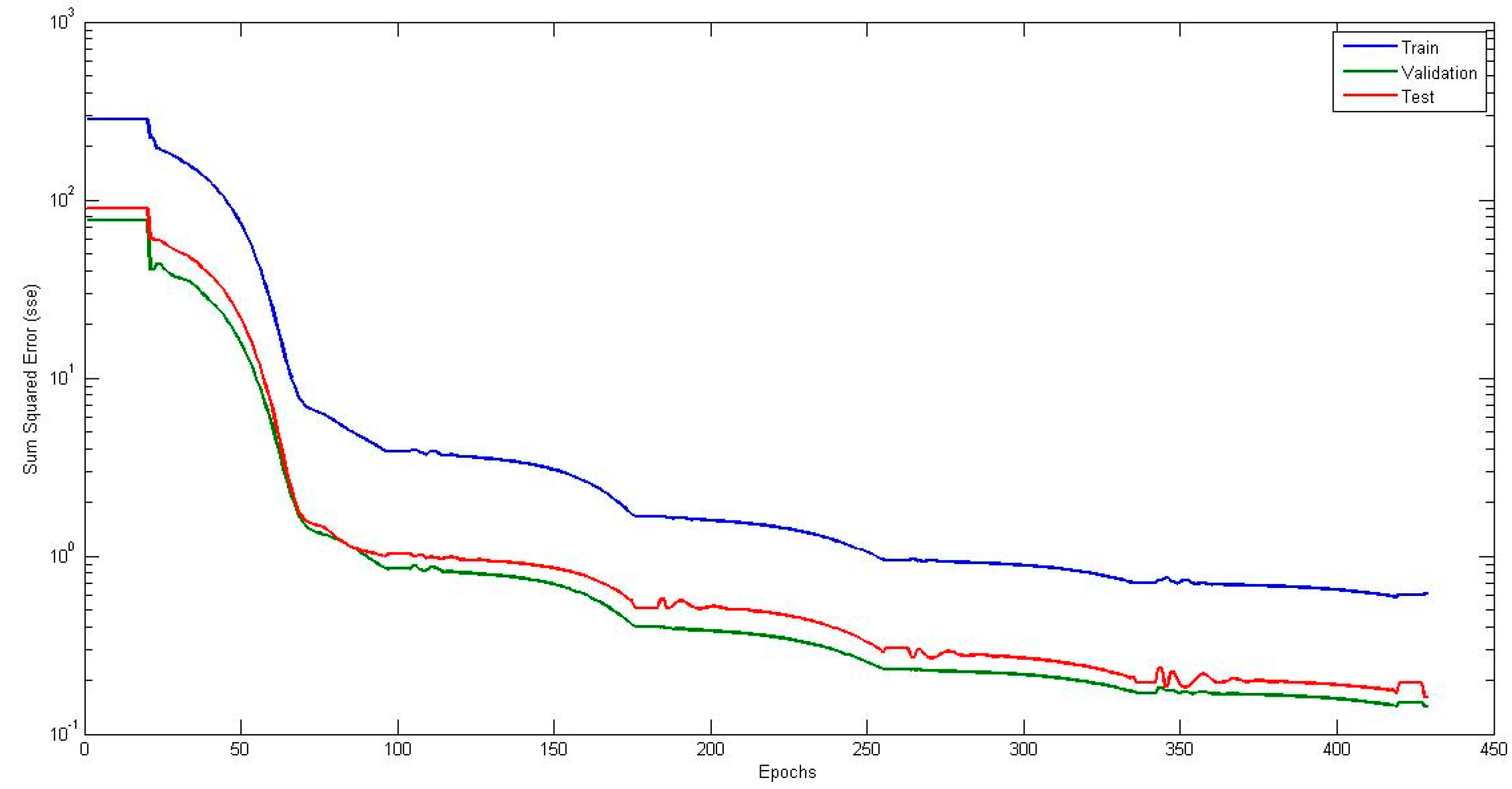
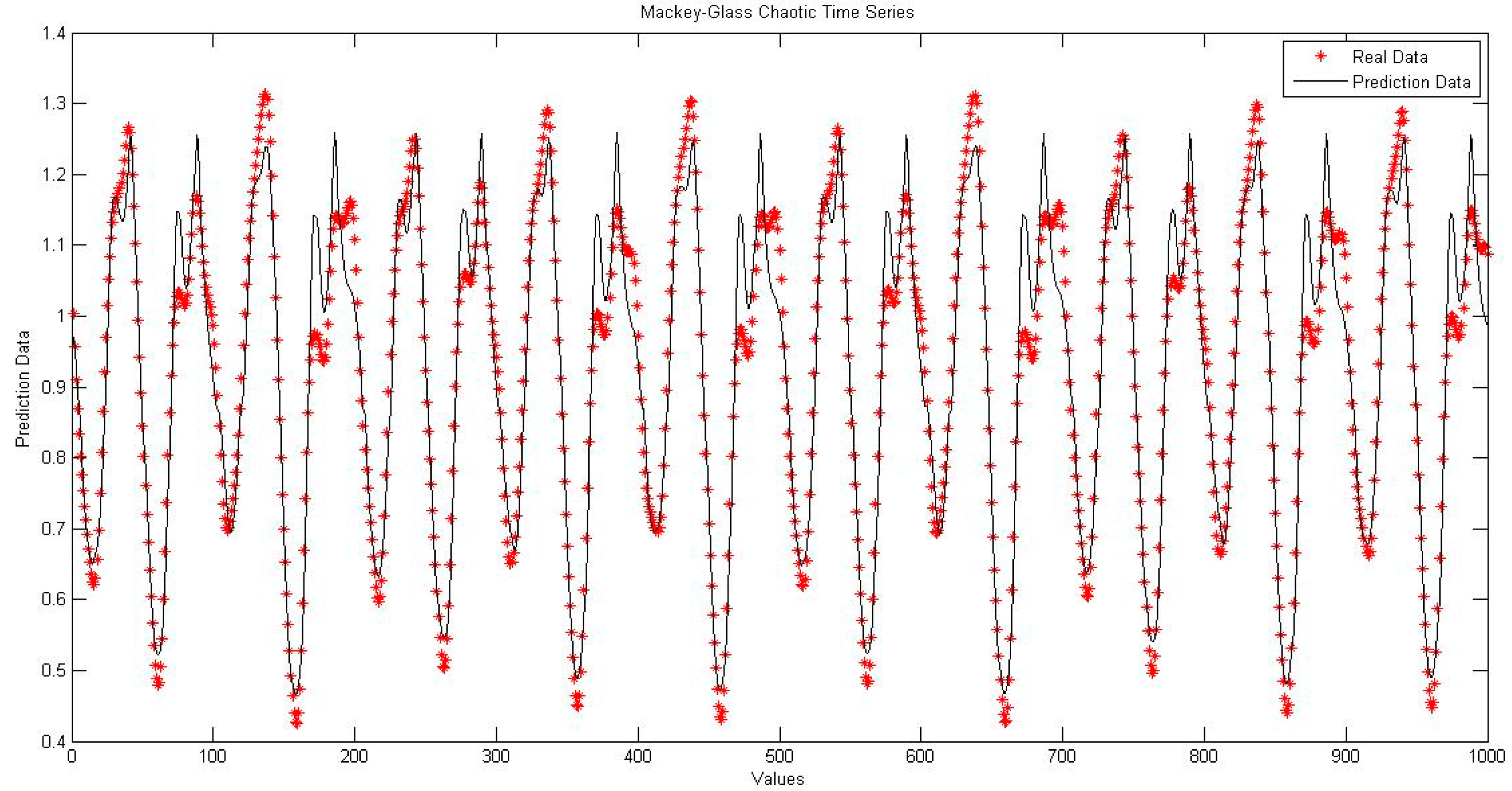
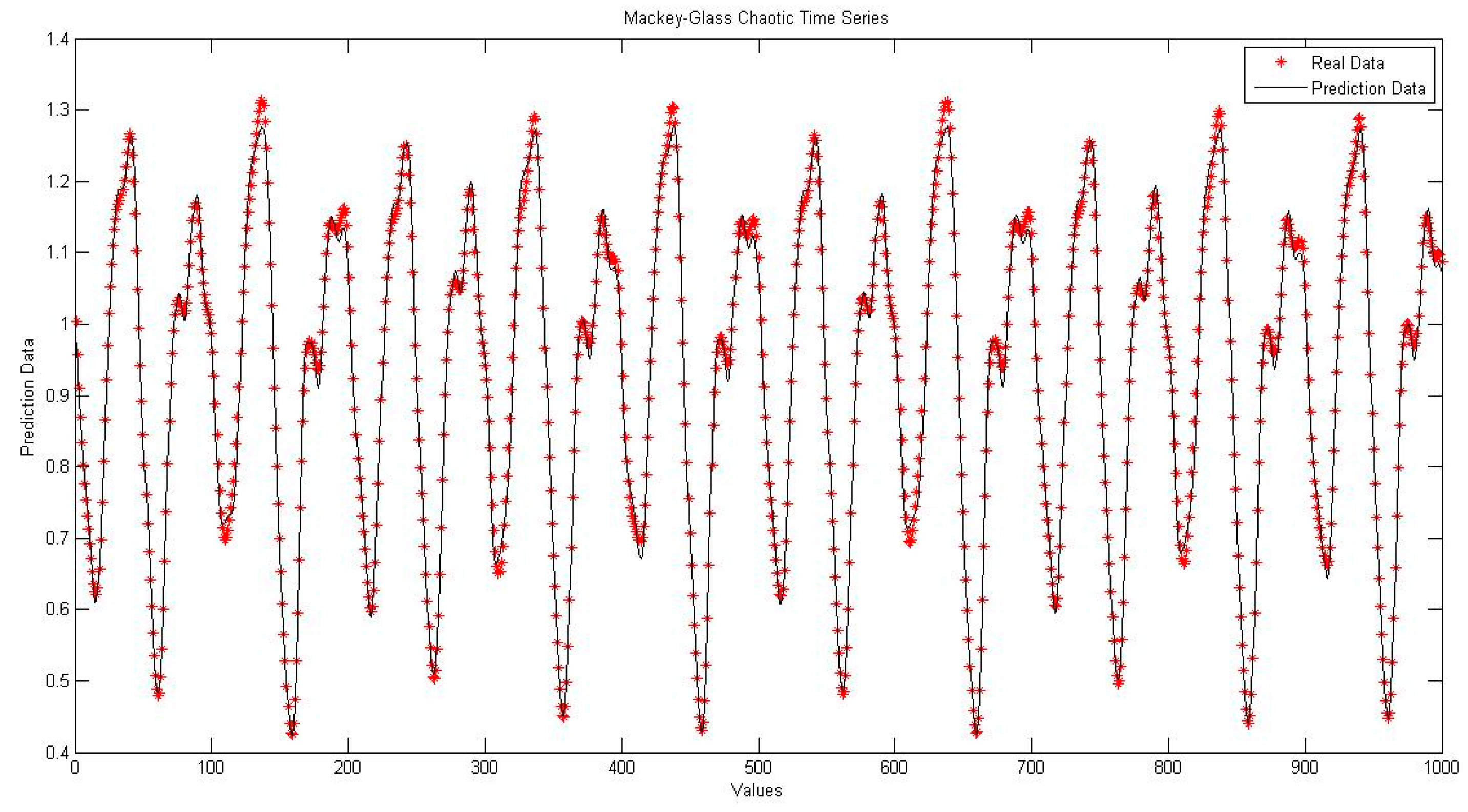
4. Simulation Results
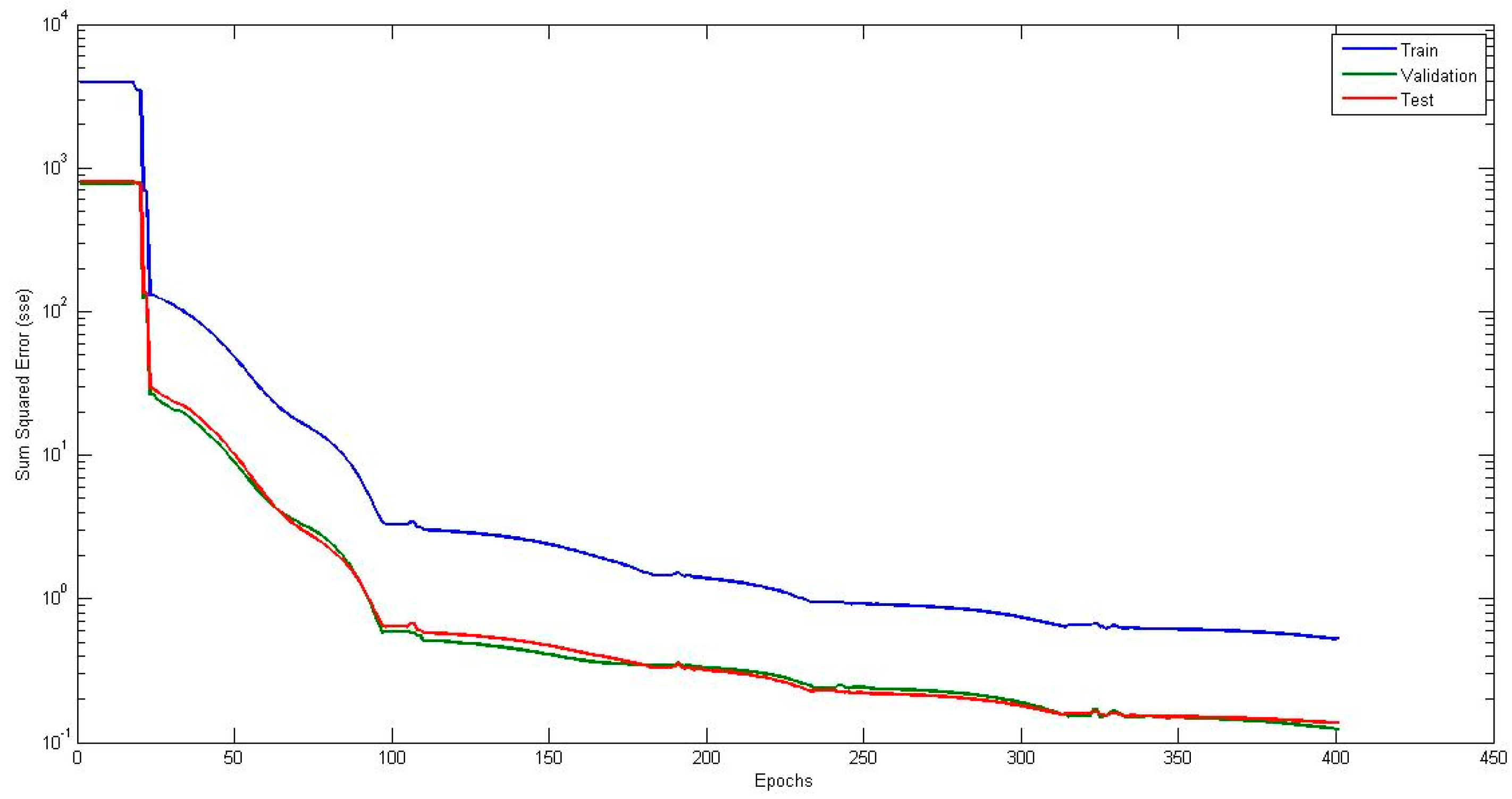
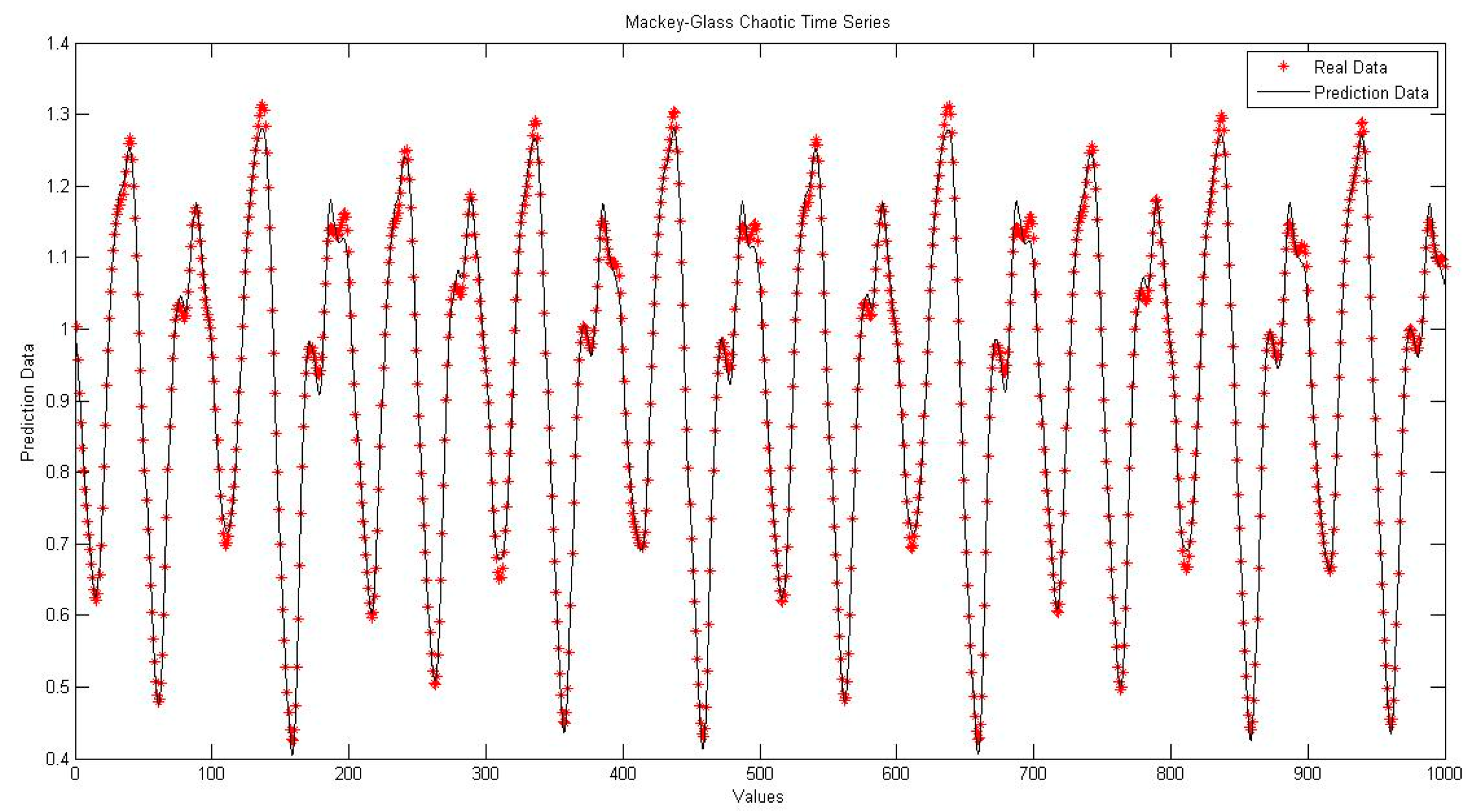
4.1. Neural Network with Interval Type-2 Fuzzy Numbers Weights (NNIT2FNW) for T-Norm and S-Norm of Sum-Product
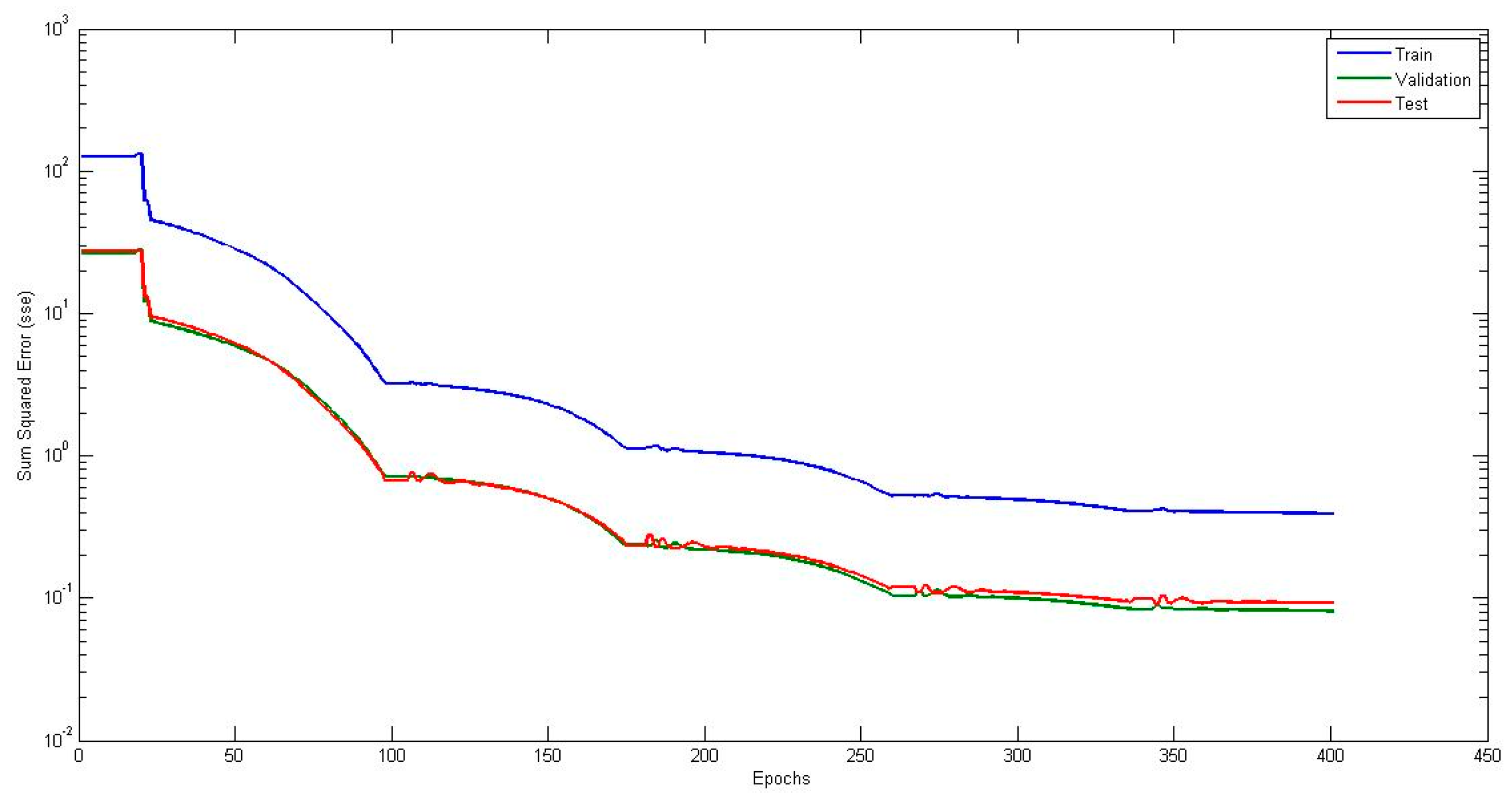
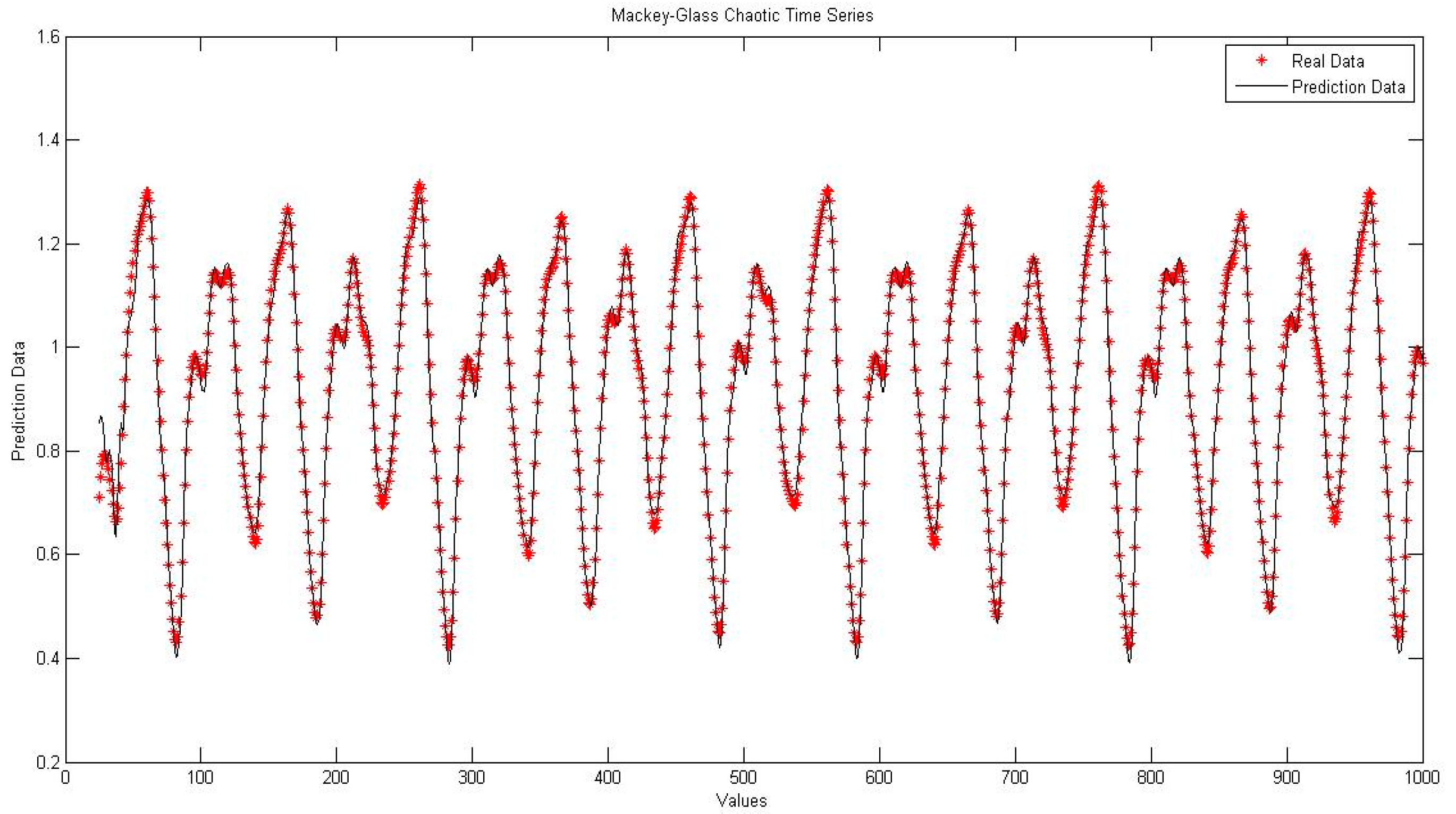
4.2. NNIT2FNW for T-Norm and S-Norm of Dombi
4.3. NNIT2FNW for T-Norm and S-Norm of Hamacher
4.4. NNIT2FNW for T-Norm and S-Norm of Frank
4.5. Comparison of Traditional Neural Network Against NNIT2FNW for T-Norm and S-Norm
4.6. Comparison of the Proposed Methods for Mackey-Glass Data with Noise
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Dunyak, J.; Wunsch, D. Fuzzy Number Neural Networks. Fuzzy Sets Syst. 1999, 108, 49–58. [Google Scholar] [CrossRef]
- Li, Z.; Kecman, V.; Ichikawa, A. Fuzzified Neural Network based on fuzzy number operations. Fuzzy Sets Syst. 2002, 130, 291–304. [Google Scholar] [CrossRef]
- Beale, E.M.L. A Derivation of Conjugate Gradients. In Numerical Methods for Non-Linear Optimization; Lootsma, F.A., Ed.; Academic Press: London, UK, 1972; pp. 39–43. [Google Scholar]
- Fletcher, R.; Reeves, C.M. Function Minimization by Conjugate Gradients. Comput. J. 1964, 7, 149–154. [Google Scholar] [CrossRef]
- Moller, M.F. A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Powell, M.J.D. Restart Procedures for the Conjugate Gradient Method. Math. Program. 1977, 12, 241–254. [Google Scholar] [CrossRef]
- Gaxiola, F.; Melin, P.; Valdez, F.; Castillo, O. Interval Type-2 Fuzzy Weight Adjustment for Backpropagation Neural Networks with Application in Time Series Prediction. Inf. Sci. 2014, 260, 1–14. [Google Scholar] [CrossRef]
- Gaxiola, F.; Melin, P.; Valdez, F.; Castillo, O. Generalized Type-2 Fuzzy Weight Adjustment for Backpropagation Neural Networks in Time Series Prediction. Inf. Sci. 2015, 325, 159–174. [Google Scholar] [CrossRef]
- Casasent, D.; Natarajan, S. A Classifier Neural Net with Complex-Valued Weights and Square-Law Nonlinearities. Neural Netw. 1995, 8, 989–998. [Google Scholar] [CrossRef]
- Draghici, S. On the Capabilities of Neural Networks using Limited Precision Weights. Neural Netw. 2002, 15, 395–414. [Google Scholar] [CrossRef]
- Kamarthi, S.; Pittner, S. Accelerating Neural Network Training using Weight Extrapolations. Neural Netw. 1999, 12, 1285–1299. [Google Scholar] [CrossRef]
- Dombi, J. A general class of fuzzy operators, the De Morgan class of fuzzy operators and fuzziness induced by fuzzy operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Weber, S. A general concept of fuzzy connectives, negations and implications based on t-norms and t-conorms. Fuzzy Sets Syst. 1983, 11, 115–134. [Google Scholar] [CrossRef]
- Hamacher, H. Über logische verknupfungen unscharfer aussagen und deren zugehorige bewertungsfunktionen. In Progress in Cybernetics and Systems Research, III; Trappl, R., Klir, G.J., Ricciardi, L., Eds.; Hemisphere: New York, NY, USA, 1975; pp. 276–288. (In Germany) [Google Scholar]
- Frank, M.J. On the simultaneous associativity of F(x, y) and x + y − F(x, y). Aequ. Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Neville, R.S.; Eldridge, S. Transformations of Sigma–Pi Nets: Obtaining Reflected Functions by Reflecting Weight Matrices. Neural Netw. 2002, 15, 375–393. [Google Scholar] [CrossRef]
- Yam, J.; Chow, T. A Weight Initialization Method for Improving Training Speed in Feedforward Neural Network. Neurocomputing 2000, 30, 219–232. [Google Scholar] [CrossRef]
- Martinez, G.; Melin, P.; Bravo, D.; Gonzalez, F.; Gonzalez, M. Modular Neural Networks and Fuzzy Sugeno Integral for Face and Fingerprint Recognition. Adv. Soft Comput. 2006, 34, 603–618. [Google Scholar]
- De Wilde, O. The Magnitude of the Diagonal Elements in Neural Networks. Neural Netw. 1997, 10, 499–504. [Google Scholar] [CrossRef]
- Salazar, P.A.; Melin, P.; Castillo, O. A New Biometric Recognition Technique Based on Hand Geometry and Voice Using Neural Networks and Fuzzy Logic. Soft Comput. Hybrid Intell. Syst. 2008, 154, 171–186. [Google Scholar]
- Cazorla, M.; Escolano, F. Two Bayesian Methods for Junction Detection. IEEE Trans. Image Process. 2003, 12, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing: Boston, MA, USA, 1996; p. 736. [Google Scholar]
- Phansalkar, V.V.; Sastry, P.S. Analysis of the Back-Propagation Algorithm with Momentum. IEEE Trans. Neural Netw. 1994, 5, 505–506. [Google Scholar] [CrossRef] [PubMed]
- Fard, S.; Zainuddin, Z. Interval Type-2 Fuzzy Neural Networks Version of the Stone–Weierstrass Theorem. Neurocomputing 2011, 74, 2336–2343. [Google Scholar] [CrossRef]
- Asady, B. Trapezoidal Approximation of a Fuzzy Number Preserving the Expected Interval and Including the Core. Am. J. Oper. Res. 2013, 3, 299–306. [Google Scholar] [CrossRef]
- Coroianu, L.; Stefanini, L. General Approximation of Fuzzy Numbers by F-Transform. Fuzzy Sets Syst. 2016, 288, 46–74. [Google Scholar] [CrossRef]
- Yang, D.; Li, Z.; Liu, Y.; Zhang, H.; Wu, W. A Modified Learning Algorithm for Interval Perceptrons with Interval Weights. Neural Process Lett. 2015, 42, 381–396. [Google Scholar] [CrossRef]
- Requena, I.; Blanco, A.; Delgado, M.; Verdegay, J. A Decision Personal Index of Fuzzy Numbers based on Neural Networks. Fuzzy Sets Syst. 1995, 73, 185–199. [Google Scholar] [CrossRef]
- Kuo, R.J.; Chen, J.A. A Decision Support System for Order Selection in Electronic Commerce based on Fuzzy Neural Network Supported by Real-Coded Genetic Algorithm. Expert. Syst. Appl. 2004, 26, 141–154. [Google Scholar] [CrossRef]
- Molinari, F. A New Criterion of Choice between Generalized Triangular Fuzzy Numbers. Fuzzy Sets Syst. 2016, 296, 51–69. [Google Scholar] [CrossRef]
- Chai, Y.; Xhang, D. A Representation of Fuzzy Numbers. Fuzzy Sets Syst. 2016, 295, 1–18. [Google Scholar] [CrossRef]
- Figueroa-García, J.C.; Chalco-Cano, Y.; Roman-Flores, H. Distance Measures for Interval Type-2 Fuzzy Numbers. Discret. Appl. Math. 2015, 197, 93–102. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Nii, M. Numerical Analysis of the Learning of Fuzzified Neural Networks from Fuzzy If–Then Rules. Fuzzy Sets Syst. 1998, 120, 281–307. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J. Operations on type-2 fuzzy sets. Fuzzy Sets Syst. 2001, 122, 327–348. [Google Scholar] [CrossRef]
- Raj, P.A.; Kumar, D.N. Ranking Alternatives with Fuzzy Weights using Maximizing Set and Minimizing Set. Fuzzy Sets Syst. 1999, 105, 365–375. [Google Scholar]
- Chu, T.C.; Tsao, T.C. Ranking Fuzzy Numbers with an Area between the Centroid Point and Original Point. Comput. Math. Appl. 2002, 43, 111–117. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Morioka, K.; Tanaka, H. A Fuzzy Neural Network with Trapezoid Fuzzy Weights. In Proceedings of the Fuzzy Systems, IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 26–29 June 1994; Volume 1, pp. 228–233. [Google Scholar]
- Ishibuchi, H.; Tanaka, H.; Okada, H. Fuzzy Neural Networks with Fuzzy Weights and Fuzzy Biases. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; Volume 3, pp. 1650–1655. [Google Scholar]
- Feuring, T. Learning in Fuzzy Neural Networks. In Proceedings of the IEEE International Conference on Neural Networks, Washington, DC, USA, 3–6 June 1996; Volume 2, pp. 1061–1066. [Google Scholar]
- Castro, J.; Castillo, O.; Melin, P.; Rodríguez-Díaz, A. A Hybrid Learning Algorithm for a Class of Interval Type-2 Fuzzy Neural Networks. Inform. Sci. 2009, 179, 2175–2193. [Google Scholar] [CrossRef]
- Castro, J.; Castillo, O.; Melin, P.; Mendoza, O.; Rodríguez-Díaz, A. An Interval Type-2 Fuzzy Neural Network for Chaotic Time Series Prediction with Cross-Validation and Akaike Test. Soft Comput. Intell. Control Mob. Robot. 2011, 318, 269–285. [Google Scholar]
- Abiyev, R. A Type-2 Fuzzy Wavelet Neural Network for Time Series Prediction. Lect. Notes Comput. Sci. 2010, 6098, 518–527. [Google Scholar]
- Karnik, N.; Mendel, J. Applications of Type-2 Fuzzy Logic Systems to Forecasting of Time-Series. Inform. Sci. 1999, 120, 89–111. [Google Scholar] [CrossRef]
- Pulido, M.; Melin, P.; Castillo, O. Genetic Optimization of Ensemble Neural Networks for Complex Time Series Prediction. In Proceedings of the 2011 International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011; pp. 202–206. [Google Scholar]
- Pedrycz, W. Granular Computing: Analysis and Design of Intelligent Systems; CRC Press/Francis Taylor: Boca Raton, FL, USA, 2013. [Google Scholar]
- Tung, S.W.; Quek, C.; Guan, C. eT2FIS: An Evolving Type-2 Neural Fuzzy Inference System. Inform. Sci. 2013, 220, 124–148. [Google Scholar] [CrossRef]
- Zarandi, M.H.F.; Torshizi, A.D.; Turksen, I.B.; Rezaee, B. A new indirect approach to the type-2 fuzzy systems modeling and design. Inform. Sci. 2013, 232, 346–365. [Google Scholar] [CrossRef]
- Zhai, D.; Mendel, J. Uncertainty Measures for General Type-2 Fuzzy Sets. Inform. Sci. 2011, 181, 503–518. [Google Scholar] [CrossRef]
- Biglarbegian, M.; Melek, W.; Mendel, J. On the robustness of Type-1 and Interval Type-2 fuzzy logic systems in modeling. Inform. Sci. 2011, 181, 1325–1347. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence; Prentice Hall: Englewood Cliffs, NJ, USA, 1997; p. 614. [Google Scholar]
- Chen, S.; Wang, C. Fuzzy decision making systems based on interval type-2 fuzzy sets. Inform. Sci. 2013, 242, 1–21. [Google Scholar] [CrossRef]
- Nguyen, D.; Widrow, B. Improving the Learning Speed of 2-Layer Neural Networks by choosing Initial Values of the Adaptive Weights. In Proceedings of the International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; Volume 3, pp. 21–26. [Google Scholar]
- Montiel, O.; Castillo, O.; Melin, P.; Sepúlveda, R. The evolutionary learning rule for system identification. Appl. Soft Comput. 2003, 3, 343–352. [Google Scholar] [CrossRef]
- Sepúlveda, R.; Castillo, O.; Melin, P.; Montiel, O. An Efficient Computational Method to Implement Type-2 Fuzzy Logic in Control Applications. In Analysis and Design of Intelligent Systems Using Soft Computing Techniques; Springer: Berlin/Heidelberg, Germany, 2007; Volume 41, pp. 45–52. [Google Scholar]
- Castillo, O.; Melin, P. A review on the design and optimization of interval type-2 fuzzy controllers. Appl. Soft Comput. 2012, 12, 1267–1278. [Google Scholar] [CrossRef]
- Hagras, H. Type-2 Fuzzy Logic Controllers: A Way Forward for Fuzzy Systems in Real World Environments. IEEE World Congr. Comput. Intell. 2008, 5050, 181–200. [Google Scholar]
- Melin, P. Modular Neural Networks and Type-2 Fuzzy Systems for Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2012; 204 p. [Google Scholar]


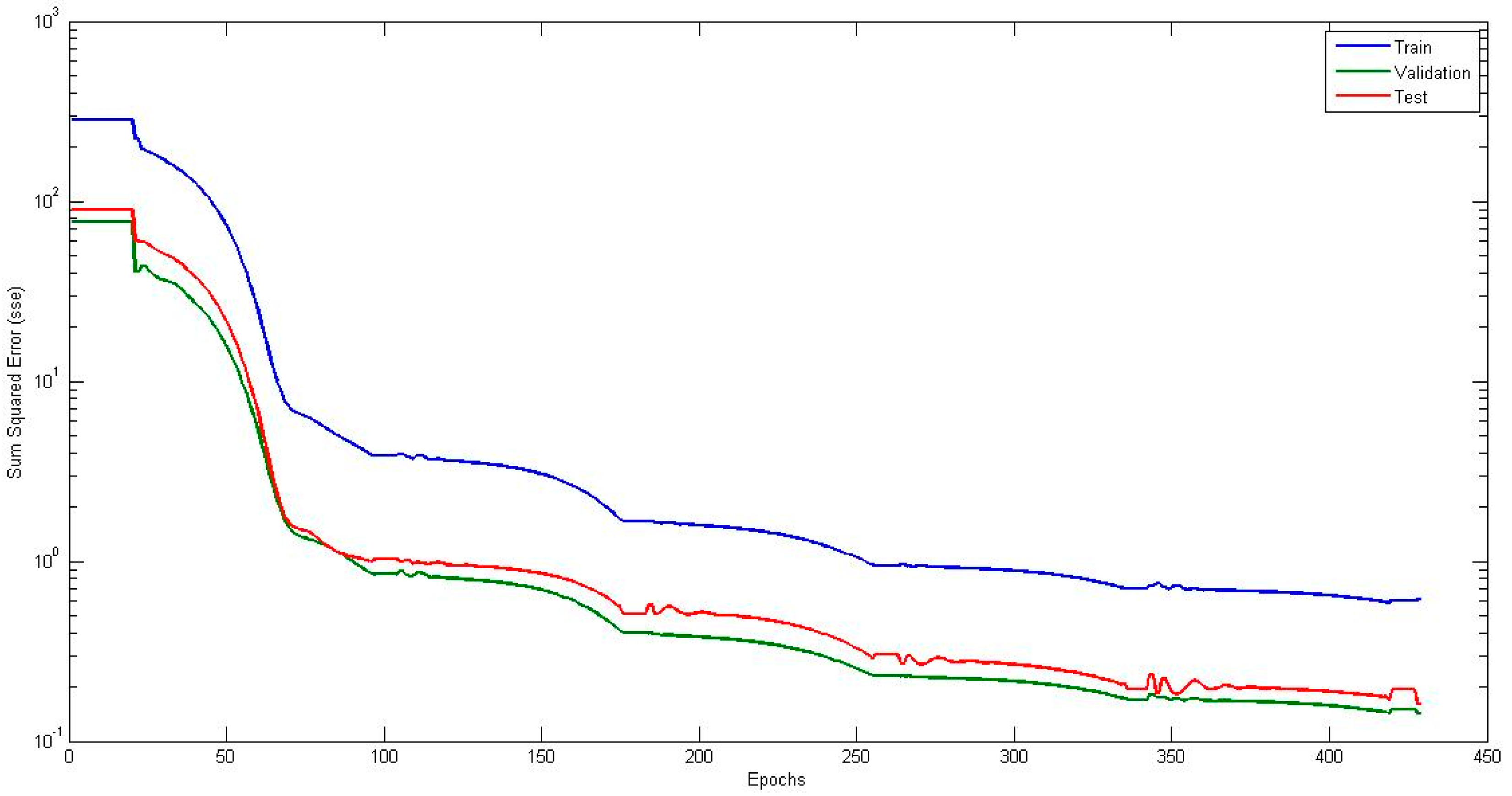
| No. Neurons | Best Prediction Error MAE | Average MAE |
|---|---|---|
| 5 | 0.0187 | 0.0240 |
| 6 | 0.0197 | 0.0245 |
| 7 | 0.0188 | 0.0250 |
| 8 | 0.0172 | 0.0231 |
| 9 | 0.0198 | 0.0259 |
| 10 | 0.0170 | 0.0246 |
| 11 | 0.0190 | 0.0252 |
| 12 | 0.0192 | 0.0248 |
| 13 | 0.0198 | 0.0255 |
| 14 | 0.0191 | 0.0251 |
| 15 | 0.0185 | 0.0227 |
| 16 | 0.0149 | 0.0180 |
| 17 | 0.0180 | 0.0238 |
| 18 | 0.0202 | 0.0242 |
| 19 | 0.0205 | 0.0239 |
| 20 | 0.0164 | 0.0247 |
| 21 | 0.0201 | 0.0243 |
| 22 | 0.0189 | 0.0241 |
| 23 | 0.0178 | 0.0249 |
| 24 | 0.0195 | 0.0250 |
| 25 | 0.0195 | 0.0259 |
| 26 | 0.0189 | 0.0233 |
| 27 | 0.0195 | 0.0246 |
| 28 | 0.0191 | 0.0248 |
| 29 | 0.0175 | 0.0245 |
| 30 | 0.0149 | 0.0233 |
| 31 | 0.0193 | 0.0245 |
| 32 | 0.0182 | 0.0259 |
| 33 | 0.0195 | 0.0252 |
| 34 | 0.0170 | 0.0243 |
| 35 | 0.0195 | 0.0241 |
| 36 | 0.0188 | 0.0251 |
| 37 | 0.0209 | 0.0248 |
| 38 | 0.0187 | 0.0243 |
| 39 | 0.0195 | 0.0254 |
| 40 | 0.0190 | 0.0246 |
| 41 | 0.0188 | 0.0263 |
| 42 | 0.0172 | 0.0233 |
| 43 | 0.0188 | 0.0249 |
| 44 | 0.0192 | 0.0237 |
| 45 | 0.0192 | 0.0247 |
| 46 | 0.0157 | 0.0247 |
| 47 | 0.0188 | 0.0252 |
| 48 | 0.0189 | 0.0246 |
| 49 | 0.0204 | 0.0247 |
| 50 | 0.0151 | 0.0246 |
| 51 | 0.0190 | 0.0250 |
| 52 | 0.0179 | 0.0239 |
| 53 | 0.0191 | 0.0242 |
| 54 | 0.0177 | 0.0240 |
| 55 | 0.0168 | 0.0240 |
| 56 | 0.0202 | 0.0251 |
| 57 | 0.0196 | 0.0255 |
| 58 | 0.0181 | 0.0250 |
| 59 | 0.0192 | 0.0248 |
| 60 | 0.0173 | 0.0239 |
| 61 | 0.0168 | 0.0236 |
| 62 | 0.0188 | 0.0239 |
| 63 | 0.0168 | 0.0240 |
| 64 | 0.0183 | 0.0238 |
| 65 | 0.0169 | 0.0252 |
| 66 | 0.0185 | 0.0250 |
| 67 | 0.0174 | 0.0253 |
| 68 | 0.0171 | 0.0230 |
| 69 | 0.0185 | 0.0244 |
| 70 | 0.0186 | 0.0248 |
| 71 | 0.0210 | 0.0251 |
| 72 | 0.0182 | 0.0249 |
| 73 | 0.0206 | 0.0247 |
| 74 | 0.0169 | 0.0249 |
| 75 | 0.0170 | 0.0240 |
| 76 | 0.0174 | 0.0233 |
| 77 | 0.0206 | 0.0245 |
| 78 | 0.0185 | 0.0244 |
| 79 | 0.0190 | 0.0247 |
| 80 | 0.0178 | 0.0246 |
| 81 | 0.0179 | 0.0247 |
| 82 | 0.0185 | 0.0243 |
| 83 | 0.0192 | 0.0254 |
| 84 | 0.0170 | 0.0237 |
| 85 | 0.0178 | 0.0242 |
| 86 | 0.0186 | 0.0260 |
| 87 | 0.0197 | 0.0233 |
| 88 | 0.0197 | 0.0256 |
| 89 | 0.0178 | 0.0252 |
| 90 | 0.0191 | 0.0257 |
| 91 | 0.0183 | 0.0265 |
| 92 | 0.0193 | 0.0240 |
| 93 | 0.0199 | 0.0240 |
| 94 | 0.0166 | 0.0242 |
| 95 | 0.0206 | 0.0248 |
| 96 | 0.0181 | 0.0236 |
| 97 | 0.0191 | 0.0252 |
| 98 | 0.0199 | 0.0248 |
| 99 | 0.0173 | 0.0249 |
| 100 | 0.0181 | 0.0248 |
| 101 | 0.0168 | 0.0237 |
| 102 | 0.0173 | 0.0250 |
| 103 | 0.0198 | 0.0245 |
| 104 | 0.0191 | 0.0237 |
| 105 | 0.0205 | 0.0245 |
| 106 | 0.0197 | 0.0246 |
| 107 | 0.0179 | 0.0256 |
| 108 | 0.0185 | 0.0244 |
| 109 | 0.0189 | 0.0241 |
| 110 | 0.0164 | 0.0242 |
| 111 | 0.0190 | 0.0254 |
| 112 | 0.0198 | 0.0250 |
| 113 | 0.0173 | 0.0245 |
| 114 | 0.0203 | 0.0244 |
| 115 | 0.0168 | 0.0248 |
| 116 | 0.0170 | 0.0233 |
| 117 | 0.0199 | 0.0254 |
| 118 | 0.0188 | 0.0252 |
| 119 | 0.0196 | 0.0247 |
| 120 | 0.0189 | 0.0250 |
| Experiment | Prediction Error |
|---|---|
| 1 | 0.0457 |
| 2 | 0.0466 |
| 3 | 0.0549 |
| 4 | 0.0581 |
| 5 | 0.0599 |
| 6 | 0.0636 |
| 7 | 0.0656 |
| 8 | 0.0671 |
| 9 | 0.0675 |
| 10 | 0.0694 |
| Average | 0.0622 |
| Experiment | Prediction Error |
|---|---|
| 1 | 0.0130 |
| 2 | 0.0138 |
| 3 | 0.0149 |
| 4 | 0.0154 |
| 5 | 0.0163 |
| 6 | 0.0165 |
| 7 | 0.0170 |
| 8 | 0.0175 |
| 9 | 0.0177 |
| 10 | 0.0183 |
| Average | 0.0164 |
| Experiment | Prediction Error |
|---|---|
| 1 | 0.0117 |
| 2 | 0.0140 |
| 3 | 0.0153 |
| 4 | 0.0156 |
| 5 | 0.0158 |
| 6 | 0.0163 |
| 7 | 0.0170 |
| 8 | 0.0175 |
| 9 | 0.0177 |
| 10 | 0.0179 |
| Average | 0.0167 |
| Best Prediction Error | Average | |
|---|---|---|
| TNN | 0.0169 | 0.0203 |
| FNNIT2FNSp | 0.0149 | 0.0180 |
| FNNIT2FND | 0.0457 | 0.0622 |
| FNNIT2FNH | 0.0130 | 0.0164 |
| FNNIT2FNF | 0.0117 | 0.0167 |
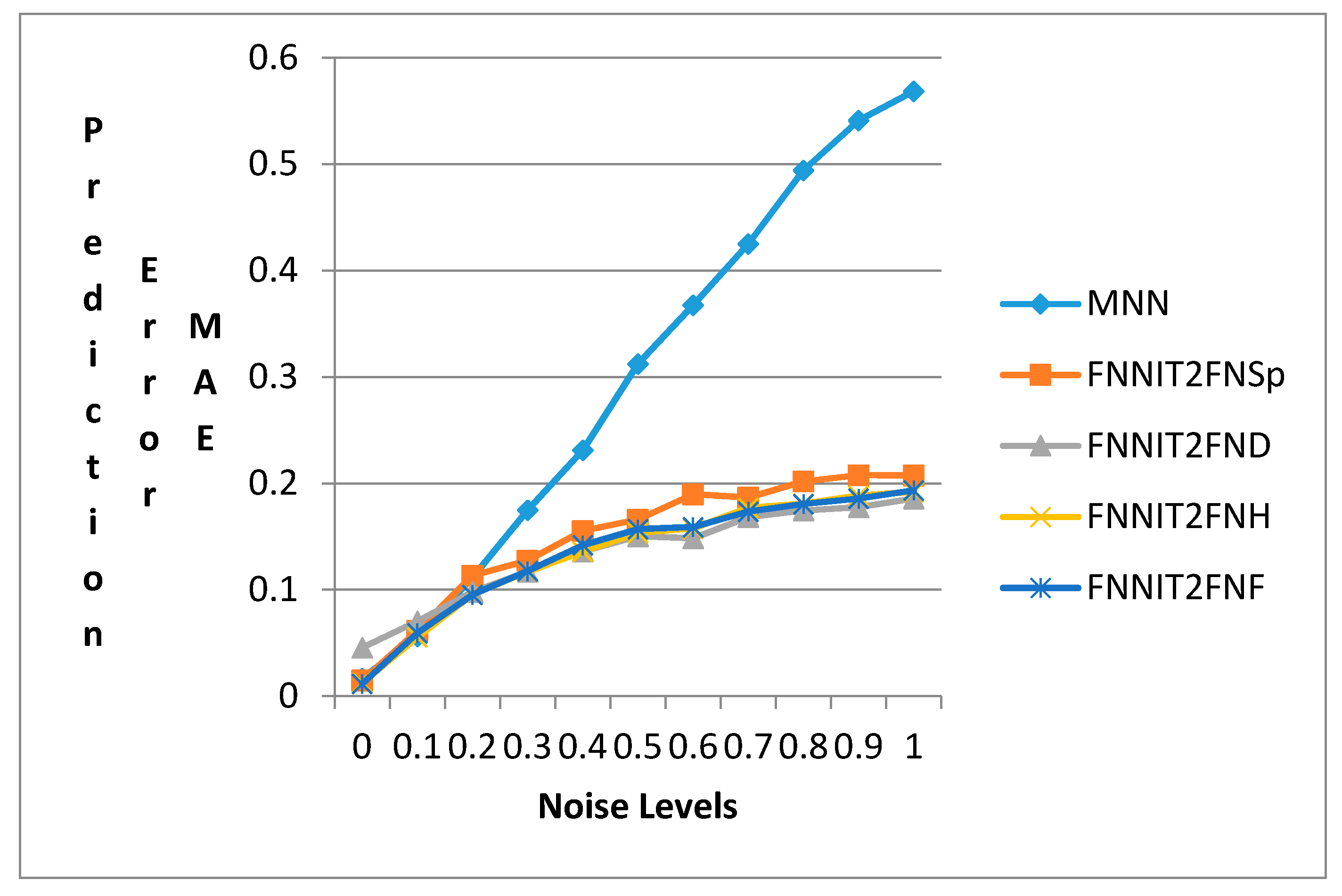
| Noise Level | TNN | FNNIT2FNSp | FNNIT2FND | FNNIT2FNH | FNNIT2FNF |
|---|---|---|---|---|---|
| n = 0 | 0.0169 | 0.0149 | 0.0457 | 0.0130 | 0.0117 |
| n = 0.1 | 0.0564 | 0.0617 | 0.0704 | 0.0556 | 0.0594 |
| n = 0.2 | 0.1115 | 0.1135 | 0.0981 | 0.0960 | 0.0954 |
| n = 0.3 | 0.1749 | 0.1275 | 0.1168 | 0.1171 | 0.1175 |
| n = 0.4 | 0.2311 | 0.1554 | 0.1362 | 0.1360 | 0.1419 |
| n = 0.5 | 0.3124 | 0.1661 | 0.1502 | 0.1536 | 0.1571 |
| n = 0.6 | 0.3676 | 0.1897 | 0.1485 | 0.1576 | 0.1589 |
| n = 0.7 | 0.4250 | 0.1866 | 0.1684 | 0.1770 | 0.1736 |
| n = 0.8 | 0.4941 | 0.2018 | 0.1744 | 0.1811 | 0.1808 |
| n = 0.9 | 0.5411 | 0.2077 | 0.1775 | 0.1887 | 0.1858 |
| n = 1 | 0.5684 | 0.2075 | 0.1858 | 0.1920 | 0.1935 |
| TNN | FNNIT2FNH | FNNIT2FNF | |
|---|---|---|---|
| No. Experiments | 30 | 30 | 30 |
| Mean Data | 0.02028 | 0.01638 | 0.01665 |
| Standard Deviation | 0.00158 | 0.00133 | 0.00123 |
| Standard error of the mean | 0.00029 | 0.00024 | 0.00023 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaxiola, F.; Melin, P.; Valdez, F.; Castillo, O.; Castro, J.R. Comparison of T-Norms and S-Norms for Interval Type-2 Fuzzy Numbers in Weight Adjustment for Neural Networks. Information 2017, 8, 114. https://doi.org/10.3390/info8030114
Gaxiola F, Melin P, Valdez F, Castillo O, Castro JR. Comparison of T-Norms and S-Norms for Interval Type-2 Fuzzy Numbers in Weight Adjustment for Neural Networks. Information. 2017; 8(3):114. https://doi.org/10.3390/info8030114
Chicago/Turabian StyleGaxiola, Fernando, Patricia Melin, Fevrier Valdez, Oscar Castillo, and Juan R. Castro. 2017. "Comparison of T-Norms and S-Norms for Interval Type-2 Fuzzy Numbers in Weight Adjustment for Neural Networks" Information 8, no. 3: 114. https://doi.org/10.3390/info8030114
APA StyleGaxiola, F., Melin, P., Valdez, F., Castillo, O., & Castro, J. R. (2017). Comparison of T-Norms and S-Norms for Interval Type-2 Fuzzy Numbers in Weight Adjustment for Neural Networks. Information, 8(3), 114. https://doi.org/10.3390/info8030114







