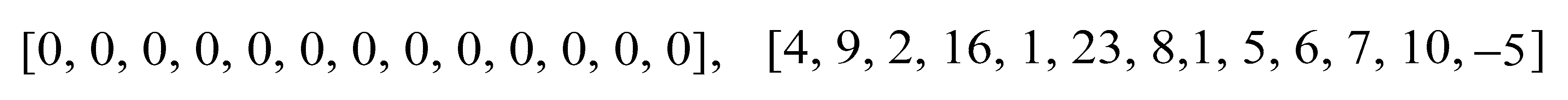1. Introduction
With the increasing size and range of urban networks, the metro, as an important component of public transportation (PT), makes a significant contribution to the daily service in many cities. A considerable factor for retaining existing passengers and attracting new users is improving the reliability of the system by designing a feasibly robust timetable during the planning stage. Thus, guaranteeing a pre-determined timetable for a more robust metro line has become a key task. Owing to its more intelligent control systems and information sharing technology, rail-based metro systems, such as Shanghai’s urban rail transit (URT), Hong Kong’s mass transit railway (MTR), and the Tokyo Metro, are particularly important to a metropolis. The operation of trains is characterized by high-frequency service in several metro systems, where the minimum headway between two successive trains is usually two to five minutes. Especially on the Yizhuang line of the Beijing Metro, it may be as little as 90 s with the development of advanced signaling systems [
1]. In big cities, metro systems transport millions of passengers every day. However, congestion during the morning and evening peak times usually has an adverse effect on the scheduled departure from every station depending on the planning timetable. In other words, there are many real situations that make the original solution virtually unfeasible, such as metro doors or platform screen doors not closing due to crowding passengers. These potential events might exacerbate delays and lead to unreliability of railway systems, which includes train delays, insufficient loading capacity, broken synchronizations, and canceled trains, and may prevent an area from obtaining metro service. Thus, the key issue for enhancing the robustness of a timetable is determining how to estimate the interactions between the trains and passengers from the information collected.
In train timetabling, the word “disturbance” is a common term for these disruptions and is formally defined as the mistakes, malfunctions, or deviating conditions that occur in the railway system or its environment and influence the railway traffic [
2]. Lacking detailed passenger activity information, previous studies on timetable scheduling were conservatively addressed within idealized transit circumstances [
3,
4,
5].
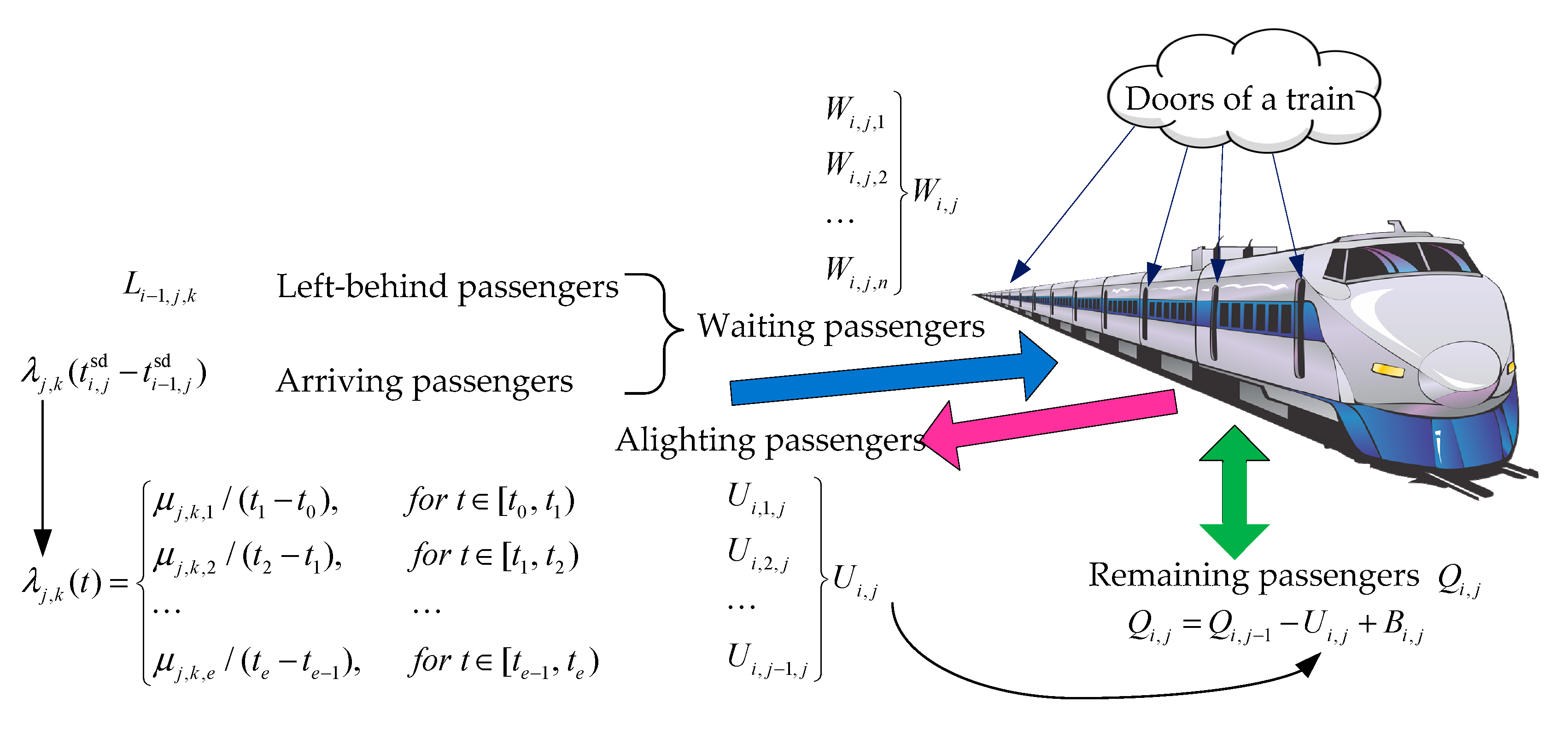
Passenger activity information is defined in this paper as information available to the transit system operator, and concerns the numbers of passengers boarding and disembarking from trains, and waiting on the platform. The most important input data in operation planning studies is the number of passengers boarded and alighted, determined by the aforementioned IC systems. In the planning stage, based on these input data, the scheduling running time and dwell time are computed for different weekdays and holidays by adjusting the buffer time. In practice, many unscheduled events may occur, and the estimated buffer time may change. Therefore, in real-world conditions, a robust timetable is required.
Dwell time refers to the time a train spends at a scheduled stop without moving. Typically, this time is spent on boarding or alighting passengers according to the planned schedule. Dwell time is one common measure of efficiency in PT, with appropriate determination of dwell times being universally desirable.
Delays of trains occur since planned schedule are not able to handle real-time passenger activities, which is usually different from the historical data. However, the planned timetable is a fixed and deterministic plan. In order to cope with unscheduled events, a timetable therefore usually contains time supplements between consecutive train movements on the same part of the infrastructure. By the time supplements, part of the delays can be absorbed without giving rise to delays. The above-described time supplement is defined as buffer time in this study.
The rescheduling process by the means of RTM deals with unexpected events occurring in the original plan. Generally, the quality of the rescheduled timetable is measured by the difference between the two timetables before and after implementation of the proposed approach. That is, the rescheduled timetable is better if it alters the original timetable less. Therefore, from the dispatchers’ perspective, the reliability of a predetermined timetable is a key component in achieving full integration of the operational plan.
One of essential tasks for creating a reliably predetermined timetable is setting the optimal buffer time. Naturally, buffer time needs to be added by considering unscheduled performances which are derived from an imbalance between supply and demand, such as overloaded and almost empty trains, when formulating a timetable. Typically, the correct amount of buffer time finds an optimal balance between extra waiting time, having a superfluous number of trains, and insufficient robustness. The amount of buffer time can greatly diminish the level of service (LOS) by causing an inconvenience to passengers. Conversely, if the buffer time is insufficient, train drivers are not likely able to catch up to the planned timetable when they fall behind, thus decreasing the service reliability. Therefore, determining the optimal buffer time that contributes to the robustness involves a tradeoff between the service quality and the operation reliability.
Various studies have been undertaken to assess the buffer time [
6,
7,
8]. However, the main drawback of the optimizing buffer time approaches is the lack of ability to be applied to metro service combined with passenger activity information, whether for airlines, high-speed railways (HSR), or buses. As proven in [
9], these adjustments in slack or buffer time inserted into the timetable lead to scheduling stability. This also gives drivers the incentive to catch up to the schedule since most transit agencies penalize them for being excessively late.
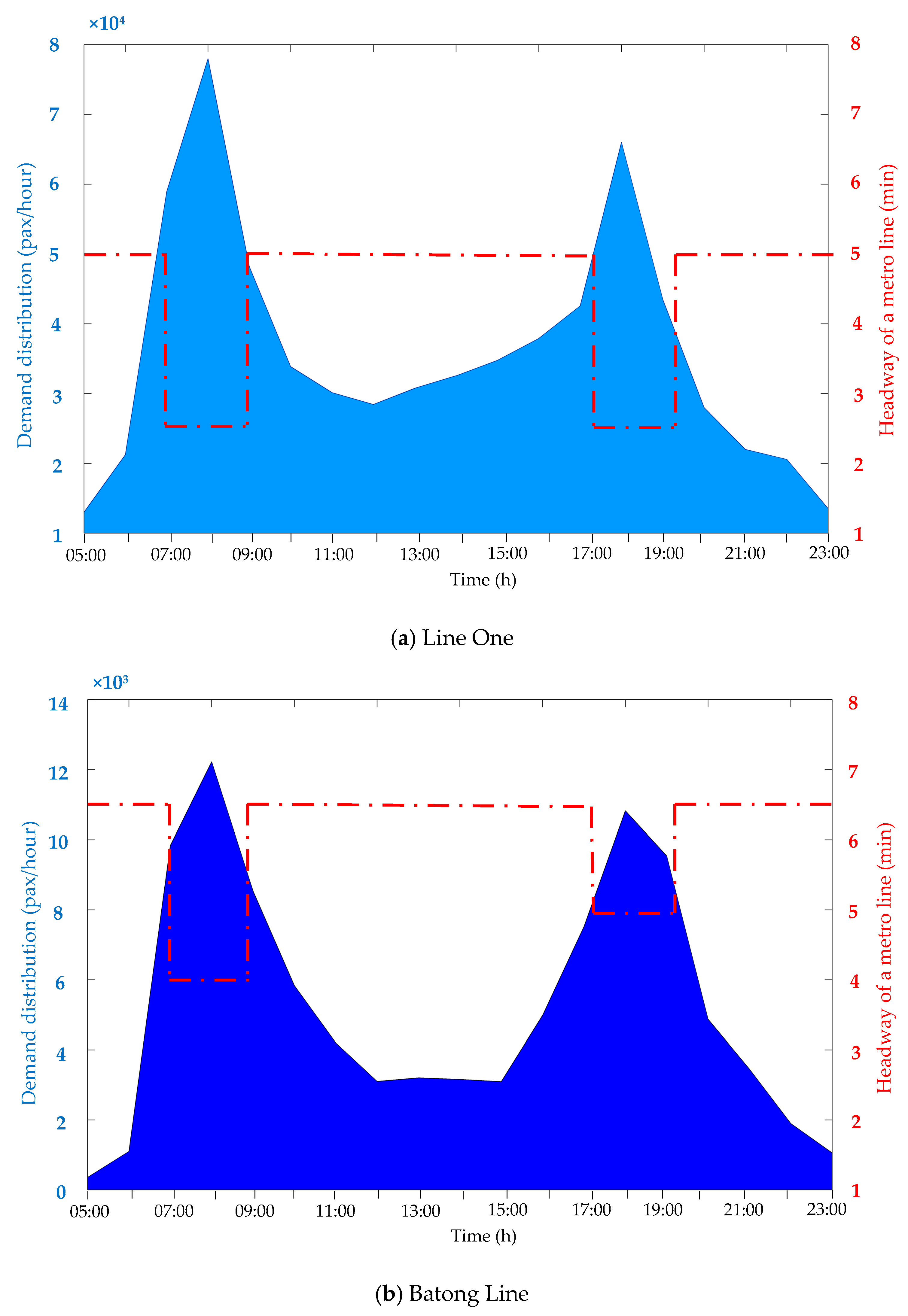
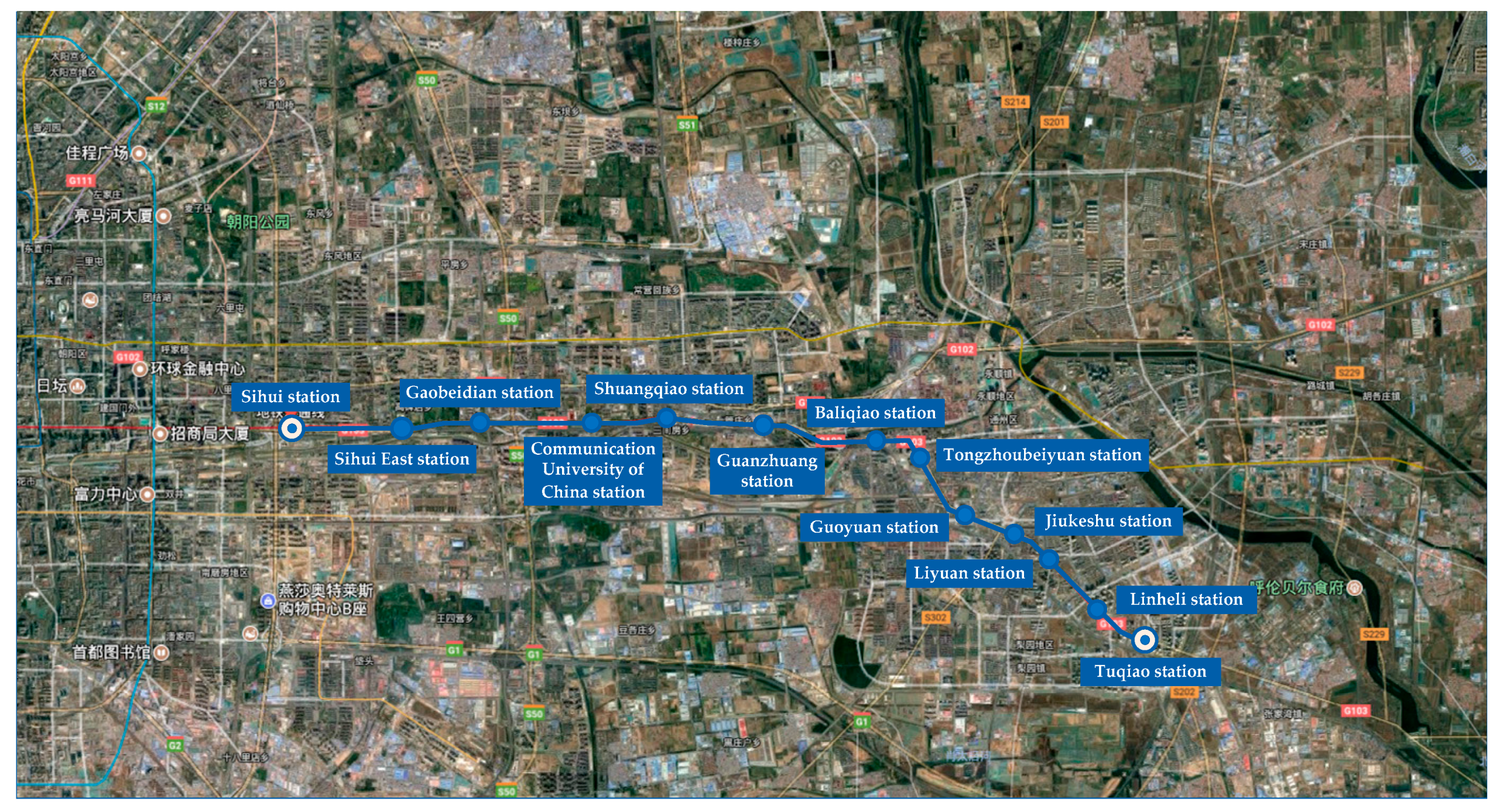
To improve the robustness of a timetable for a metro line, this paper seeks to minimize deviation from the planning timetable by adjusting the buffer time of the train running process so that the timetable is successfully achieved. Within the operating technology constraints of considering train capacity and investigating historical passengers’ information, the actual dwell time was chosen by the interactional relationship between waiting passengers and trains. This approach is applied to a metro line including upstream or downstream directions of the Batong line belonging to the Beijing Metro. This is a line of 13 stations located in a suburb of Beijing. Involving deviations at the planning stage of a metro timetable may yield much better timetabling performance. Furthermore, a well-designed timetable considering punctuality of running time between two major stations can satisfy the needs of critical sections using the time control point strategy.
1.1. Literature Review
Metro operational management is typically classified into three levels: strategic, tactical, and operational [
10]. For the metro service in a PT system, an applicable timetable is at the core of daily operations and solutions to a variety of potential issues. Based on the infrastructure construction in strategic-level decisions, such as rail line design, number and locations of stations [
11], the rail transit command center (TCC) determines the stop patterns from demand estimates obtained from data gathered from IC, which can be considered a tactical-level problem. The tactical decision for selecting a stop pattern is likely to contain numerous conflicts between trains, infeasibilities in train times, headways, dwell times, and other problems. Therefore, after a tactical decision is made, the TCC can adjust and revise the preliminary plan to eliminate all conflicts by analyzing performance of the train type and timetabling [
12,
13].
Fundamentally, there are an enormous number of daily PT passenger trips. There are 11 million daily trips on the Tokyo Subway, nine million on the Shanghai Metro, and five million on the London Underground [
13]. Delays usually occur due to the congestion caused by train doors and platform screen doors not locking when the boarding and alighting passengers are crowded into these areas. The level of congestion and assistant push on the Tokyo Subway during rush hours in the news is shown in
Figure 1.
The problem of creating a robust train timetable has received considerable attention in the literature. For instance, analytical aspects of dispatching policies were investigated for single mode of transportation (bus, train, airline, etc.) routes [
3]. Osuna and Newell formulated the control strategies for an idealized PT system with the objective of minimizing the average wait per passenger [
4]. Ideal buffer times are calculated on the delay distributions of the arriving trains, weighting the different types of waiting times. Moreover, standard linear programming is used at improving the Belgian railway timetable with a 40% cost decrease [
6,
7].
A branch and bound (B&B) algorithm was proven to be technically feasible for solving nonlinear integer programming (NIP) problems characterized by large-scale calculations [
2,
8,
14]. A B&B algorithm was reasonably applied to railway rescheduling problems to speed up the computation to ensure the efficiency of real-time control. A new conflict-free timetable with feasible arrival and departure times was updated, with the objective of minimizing deviations from the original [
8]. The B&B algorithm gained further development during a single-track train timetabling study, in which three approaches were adapted to effectively reduce the solution space. First, a Lagrangian relaxation-based lower bound rule was used to dualize segments and station entering headway capacity constraints. Second, an exact lower bound rule was used to estimate the smallest train delay for resolving the remaining crossing conflicts in a partial schedule. Third, a beam search heuristic method established the tight upper bound [
14]. A B&B algorithm, along with a new heuristic beam search algorithm, is presented to solve robust train timetabling problems. The required buffer times were measured to seek the tradeoffs between the optimality, robustness, and the capacity consumption [
2]. The objective of the model was developed based on the approach of Reference [
15]. Bertsimas and Sim introduced a different robust approach in which the robust counterpart is of the same class and size as the nominal problem. This approach has the advantage of having the ability to control the degree of reliability under uncertainty [
15].
A real time scheduling optimization of a train service in a metro rail terminal was proposed with two objectives performed in two steps. The first step investigated the problem of routing and sequencing trains with a goal of punctuality, which was solved with a fast heuristic. Scheduling train departures with the objective of optimizing the regularity of train service, under the constraint that what was achieved in the first objective does not deteriorate at the second step [
16]. A scenario-based rolling horizon solution approach was proposed to dispatch a single-track train under a dynamic and stochastic environment. The study reduced the expected additional delays under different forecasted scenarios [
17]. In this study, there was a conflict on balancing minimizing train delays and missed connections, in order to provide a set of feasible non-dominated schedules to support this decision process. These objectives involve making decisions about which connections to keep or drop in order to reach a compromise, because whenever train delay reduction requires cancellation of some connected services, it causes longer wait times for transferring passengers [
18].
Disruptions, such as accidents or track damages, were also analyzed given their significant impact on railway operation. Given a disrupted infrastructure situation and a forecast of the characteristics of the disruption, the goal of the model was to design a disposition timetable, specifying which trains needed to still be in operation during the disruption and determining the timetable of these trains [
19]. The definition and distinguishing characteristics between “disruption” and “disturbance” were demonstrated in a recent overview [
20] in detail. These disruptions are less frequent than the unscheduled events caused by congestion in daily operations. In our work, the influence of unscheduled events on daily operations are taken into account rather than the abrupt disruptions in a relatively few cases.
In terms of the service reliability of PT systems, there are five types of vehicle positional situations with reference to a transfer point: Considerably ahead of schedule, ahead of schedule, on schedule, behind schedule, and considerably behind schedule. The developed optimization framework results in selected operational tactics to attain the maximum number of direct transfers, without waiting, and minimizes the total passenger travel time [
21]. With the similar concept of buffer time, a balanced train timetable on a single-line railway with optimized velocity was obtained by using a combination of travel-advance strategy and a genetic algorithm (GA) [
22]. Another effective way to achieve this is to use a stop-skipping pattern after the disruption. The skip-stop pattern means that a service skips some stations [
23,
24,
25] as a robust strategy to insulate against uncertainty.
An inconvenience-minimized rescheduling model was proposed, based on Mixed Integer Programming (MIP) formulation, when train traffic is disrupted. Typically, the dwell times were estimated to match what would be considered a satisfactory connection at a station for extra passengers. As countermeasures against the disruption, changes of train types and rolling stock operation schedules at terminals, as well as changes in the departing order of trains and assignment of trains to a track in a station, are performed [
26]. A rescheduling approach was addressed for a metro line after a disruption, in which the time-dependent congested demand distributions within train capacity, was taken into account. A mixed integer linear programming model (MILP) to investigate this problem was developed and it was solved with a heuristic iterative algorithm. Numerical experiments based on the data from the Beijing Yizhuang metro line were analyzed. Under different conditions, such as increasing and decreasing passenger arrival rates, and short and long disruption periods, the effectiveness and efficiency of our rescheduling method were verified [
27].
4. Solution Algorithm
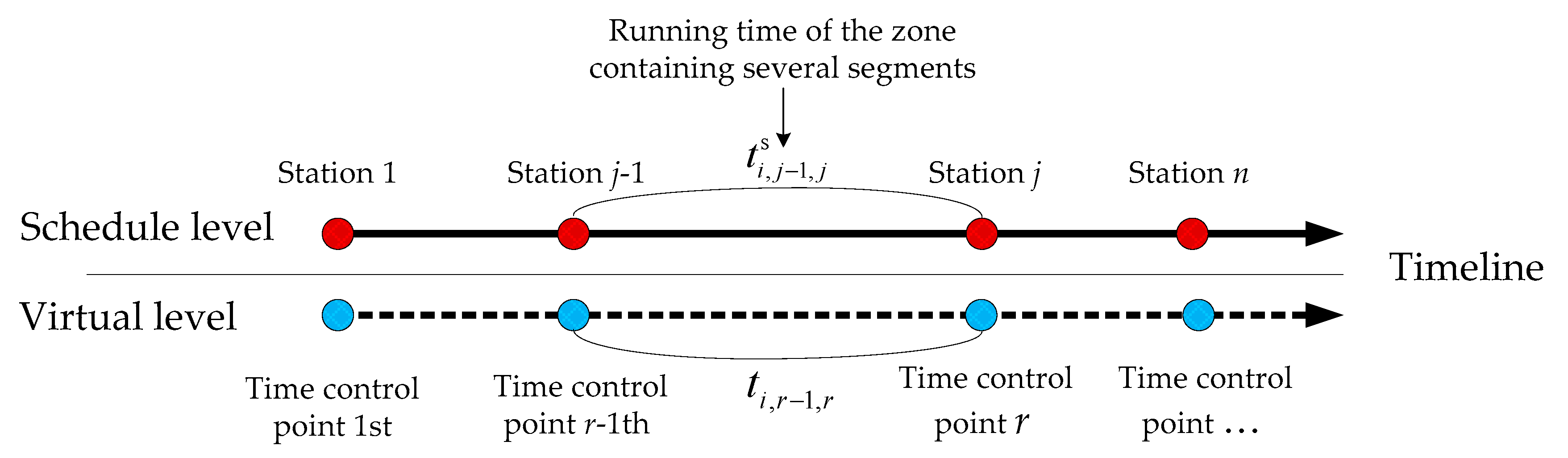
By precisely accounting for the passenger demand records, available resources, and practical regulations, the above section describes a comprehensive model to capture the timetabling constraints, passengers’ activity information, and enhancement of the robust approach on a metro line. The developed model, a mixed integer nonlinear programming (MINLP) model with complicated constraints, cannot be solved by any open-source exact solvers. The objective variable contains two dimensions: i and j. First, for the operating period of train i, we should estimate and handle the passengers’ activity information. Next, at the second step, we need to figure out penalties on delay () and ahead () of scheduled departure time, respectively. Obviously, it is repeated to seek the optimal solution rather than one-time input/output. However, the input set has to be judged on whether delay or ahead of schedule at each segment (). These calculated features (i.e., mixed and nonlinear features) of our model requires the algorithm to be experimental seeking tool and repeated optimization solver. Based on the above characteristics of computation, it is available to apply a heuristic method such as GA. To further provide insights into the train timetabling problem, considering loading capacity, we demonstrate the process of adjusting the buffer times for developing a robust timetabling plan.
- Step 0
(Initialization): Calculate the matrix of actual dwell time based on the demand distribution (origin-destination, OD) and Equations (11)–(20).
- Step 1
(Input): Input the set of actual running and recovery factor . Parameters and are estimated and one arbitrary value is assumed as the upper bound of the objective. Let g = 1 and we set current objective value .
- Step 2
(Encode gens): Encode buffer time of segment e(j − 1,j) for train i as a generation belonging to the solution set (i.e., a chromosome in GA). At the same time, it is also the decision variable. The set of genes is defined as chromosome.
- Step 3
(Crossover and mutation operators): Since the decision variables of the proposed model are
, they are used as genes for any chromosome in the GA. Decision variable
is generated at random by capturing from domain of definition
, and the first chromosome was created randomly. For example, for one metro line of 13 located stations, some sample chromosomes are shown in
Figure 5.
The most common operators used in a genetic algorithm are:
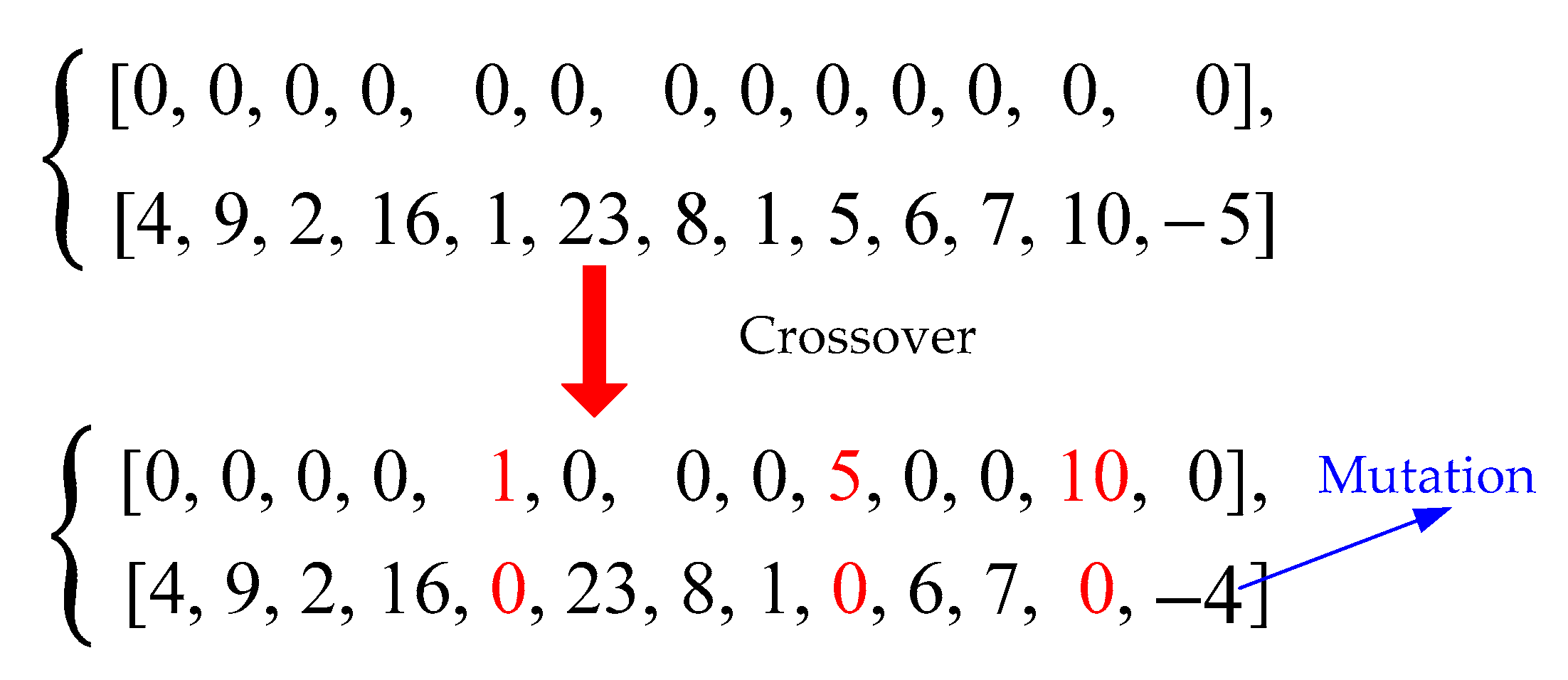
Both operators are used in the algorithm in this research. In linear crossover, a gene value is replaced by the value of the same gene in another chromosome (see
Figure 6). It is clear that linear crossover will result in no conflicts according to the bounds of the variables
, which is the reason behind this decision.
The crossover operation usually results in local optimum solutions. Thus, a mutation operation is used to escape local optimums. In many genetic algorithms, the variables are binary, and mutations indicate the change of a variable from 0 to 1 or vice versa. However, here, we have general integer variables. For a gene
with any possible value, a random number is generated in the range of
. By replacing this number with
, a new value for the variable is created. Next, the objective variables
are calculated with crossover and mutation operators (described in detail in Reference [
13,
25]) based on Equations (21)–(30). If
, then
; otherwise, continue to search.
- Step 4
(Fitness evaluation): Fitness evaluation is used to measure the goodness of individual candidates. The fitness value in the GA is calculated by Equation (32). The genetic search prefers individuals with higher fitness:
- Step 5
(Stopping criterion): We can obtain the optimization solution within the convergence, if no improvement can be made in the specified time and stated number of generations.
The stopping criteria for termination of the genetic algorithm are defined as follows:
The best fitness function does not change after a given number of iterations.
The difference between the best and worst solutions in a chromosome is less than a given value, i.e., 1%.
The algorithm reaches a maximum number of iterations.
We present a solution algorithm for the RTM described in the previous section. The proposed MINLP mathematical model consists of a large number of variables. Therefore, in this section a heuristic algorithm (GA) is proposed to yield satisfactory results.