Spencer-Brown vs. Probability and Statistics: Entropy’s Testimony on Subjective and Objective Randomness
Abstract
: This article analyzes the role of entropy in Bayesian statistics, focusing on its use as a tool for detection, recognition and validation of eigen-solutions. “Objects as eigen-solutions” is a key metaphor of the cognitive constructivism epistemological framework developed by the philosopher Heinz von Foerster. Special attention is given to some objections to the concepts of probability, statistics and randomization posed by George Spencer-Brown, a figure of great influence in the field of radical constructivism.1. Introduction
In several already published articles, I defend the use of Bayesian Statistics in the epistemological framework of cognitive constructivism. In particular, I show how the FBST—The Full Bayesian Significance Test for precise hypotheses—can be used as a tool for detection, recognition and validation of eigen-solutions, see [1–12]. “Objects as eigen-solutions” is a key metaphor of cognitive constructivism as developed by the Austrian-American philosopher Heinz von Foerster, see [13]. For some recent applications in empirical science, see [14–20].
In Statistics, specially in the design of statistical experiments, Randomization plays a role which is in the very core of objective-subjective complementarity, a concept of great significance in the epistemological framework of cognitive constructivism as well as in the theory of Bayesian statistics. The pivotal role of randomization in a well designed statistical experiment is that of a decoupling operation used to sever illegitimate functional links, thus avoiding spurious associations, breaking false influences, separating confounding variables, etc., see [10] and [21].
The use of randomization in Statistics is an original idea of Charles Saunders Peirce and Joseph Jastrow, see [22,23]. Randomization is now a standard requirement for many scientific studies. In [8] and [10] I consider the position of C.S.Peirce as a forerunner of cognitive constructivism, based on the importance, relevance and coherence of his philosophical and scientific work. Among his several contributions, the introduction of randomization in statistical design stands indubitably out. In future articles, I hope to further expand the analysis of the role of Bayesian statistics in cognitive constructivism and provide other interesting applications.
I shall herein analyze some objections to the concepts of probability, statistics and randomization posed by George Spencer-Brown, a figure of great influence in the field of radical constructivism. Abstinence from statistical analysis and related quantitative methods may, at first glance, look like an idyllic fantasy island where many beautiful dreams come true. However, in my personal opinion, this position threatens to exile the cognitive constructivism epistemological framework to a limbo of powerless theories. In this article, entropy is presented as a cornerstone concept for the precise analysis and a key idea for the correct understanding of several important topics in probability and statistics. This understanding should help to clear the way for establishing Bayesian statistics as a preferred tool for scientific inference in mainstream cognitive constructivism.
In what follows, Section 2 corresponds to the first part of this article's title and elaborates upon “the case of Spencer-Brown vs. probability and statistics”. Corresponding to the second part of the title, Section 3 provides “the testimony of entropy on subjective randomness”. Section 4 gives “the testimony of entropy on objective randomness”, presenting several mathematical definitions, theorems and algorithms. In this article, entropy based informational analysis is the key used to “solve” all the probability paradoxes and objections to statistical science posed by Spencer Brown. Section 4 is completely self-contained. Hence, a reader preferring to be exposed first to intuitions and motivations, can read the sections of this article in the order they are presented; meanwhile, a reader seeking a more axiomatic approach can start with Section 4. Section 5 presents our final conclusions.
2. Spencer-Brown, Probability and Statistics
In [24–26], Spencer-Brown analyzed some apparent paradoxes involving the concept of randomness, and concluded that the language of probability and statistics was inappropriate for the practice of scientific inference. In subsequent work, [27], he reformulates classical logic using only a generalized nor operator (marked not-or, unmarked or), that he represents à la mode of Charles Saunders Peirce or John Venn, by a graphical boundary or distinction mark, see [28–34].
Making (or arbitrating) distinctions is, according to Spencer-Brown, the basic (if not the only) operation of human knowledge, an idea that has either influenced or been directly explored by several authors in the radical constructivist movement. The following quotations, from [26] p. 23, p. 66 and p. 105, are typical arguments used by Spencer-Brown in his rejection of probability and statistics:
Retroactive reclassification of observations in one of the scientist's most important tools, and we shall meet it again when we consider statistical arguments. (p. 23)
We have found so far that the concept of probability used in statistical science is meaningless in its own terms; but we have found also that, however meaningful it might have been, its meaningfulness would nevertheless have remained fruitless because of the impossibility of gaining information from experimental results, however significant. This final paradox, in some ways the most beautiful, I shall call the Experimental Paradox (p. 66).
The essence of randomness has been taken to be absence of pattern. But what has not hitherto been faced is that the absence of one pattern logically demands the presence of another. It is a mathematical contradiction to say that a series has no pattern; the most we can say is that it has no pattern that anyone is likely to look for. The concept of randomness bears meaning only in relation to the observer: If two observers habitually look for different kinds of pattern they are bound to disagree upon the series which they call random (p. 105).
Several authors concur, at least in part, with my opinion about Spencer-Brown's technical analysis of probability and statistics, see [35–39]. In Section 3, I carefully explain why I disagree with it. In some of my arguments, which are are based on information theory and the notion of entropy, I dissent from Spencer-Brown's interpretation of measures of order-disorder in sequential signals. In [40–44], some of the basic concepts in this area are reviewed with a minimum of mathematics. For more advanced developments see [45–47].
I also disapprove some of Spencer Brown's proposed methodologies to detect “relevant” event sequences, that is, his criteria to “mark distinct patterns” in empirical observations. My objections have a lot in common with the standard caveats against ex post facto “fishing expeditions” for interesting outcomes, or simple post hoc “sub-group analysis” in experimental data banks. This kind of retroactive or retrospective data analyses is considered a questionable statistical practice, and pointed as the culprit of many misconceived studies, misleading arguments and mistaken conclusions. The literature on statistical methodology for clinical trials has been particularly keen in warning against this kind of practice. See [48,49] for two interesting papers addressing this specific issue and published in high impact medicine journals less than a year before I wrote this text. When consulting for pharmaceutical companies or advising in the design of statistical experiments, I often find it useful to quote Conan Doyle's Sherlock Holmes, in The Adventure of Wisteria Lodge:
Still, it is an error to argue in front of your data. You find yourself insensibly twisting them around to fit your theories.
Finally, I am also suspicious or skeptical about the intention behind some applications of Spencer-Brown's research program, including the use of extrasensory empathic perception for coded message communication, exercises on object manipulation using paranormal powers, etc. Unable to reconcile his psychic research program with statistical science, Spencer-Brown had no regrets in disqualifying the later, as he clearly stated in the prestigious scientific journal Nature, see pp. 594–595 of [25]:
[On telepathy:] Taking the psychical research data (that is, the residuum when fraud and incompetence are excluded), I tried to show that these now threw more doubt upon existing pre-suppositions in the theory of probability than in the theory of communication.
[On psychokinesis:] If such an ‘agency’ could thus ‘upset’ a process of randomizing, then all our conclusions drawn through the statistical tests of significance would be equally affected, including the conclusions about the ‘psychokinesis’ experiments themselves. (How are the target numbers for the die throws to be randomly chosen? By more die throws?) To speak of an ‘agency’ which can ‘upset’ any process of randomization in an uncontrollable manner is logically equivalent to speaking of an inadequacy in the theoretical model for empirical randomness, like the luminiferous ether of an earlier controversy, becomes, with the obsolescence of the calculus in which it occurs, a superfluous term.
Spencer-Brown's conclusions in [24–26], including his analysis of probability, were considered to be controversial (if not unreasonable or extravagant) even by his own colleagues at the Society of Psychical Research, see [50,51]. It seems that current research in this area, even not being free (or afraid) of criticism, has abandoned the path of naïve confrontation with statistical science, see [52,53]. For additional comments, see [54–57].
Curiously, Charles Saunders Peirce and his student Joseph Jastrow, who introduced the idea of randomization in statistical trials, also struggled with some of the very same dilemmas faced by Spencer-Brown, namely, the eventual detection of distinct patterns or seemingly ordered (sub)strings in a long random sequence. Peirce and Jastrow did not have at their disposal the heavy mathematical artillery I have quoted in the previous paragraphs. Nevertheless, as experienced explorers that are not easily lured, when traveling in desert sands, by the mirage of a misplaced oasis, these intrepid pioneers were able to avoid the conceptual pitfalls that lead Spencer-Brown so far astray. For more details see [10], [22,23] and [58–60].
As stated in the introduction, the cognitive constructivist framework can be supported by the FBST, a non-decision theoretic formalism drawn from Bayesian statistics, see [1] and [3–5]. The FBST was conceived as a tool for validating objective knowledge of eigen-solutions and, as such, can be easily integrated to the epistemological framework of cognitive constructivism in scientific research practice. Contrasting our distinct views of cognitive constructivism, it is not at all surprising that I have come to conclusions concerning the use of probability and statistics, and also to the relation between probability and logic, that are fundamentally different from those of Spencer-Brown.
3. Pseudo, Quasi and Subjective Randomness
The focus of the present section are the properties of “natural” and “artificial” random sequences. The implementation of probabilistic algorithms require good random number generators, (RNGs). These algorithms include: Numerical integration methods such as Monte Carlo or Markov Chain Monte Carlo (MCMC); evolutionary computing and stochastic optimization methods such as genetic programming and simulated annealing; and also, of course, the efficient implementation of randomization methods.
The most basic random number generator replicates i.i.d. (independent and identically distributed) random variables uniformly distributed in the unit interval, [0, 1]. From this basic uniform generator one gets a uniform generator in the d-dimensional unit box, [0, 1]d, and, from the later, non-linear generators for many other multivariate distributions, see [61,62].
Historically, the technology of random number generators was developed in the context of Monte Carlo methods. The nature of Monte Carlo algorithms makes them very sensitive to correlations, auto-correlations and other statistical properties of the random number generator used in its implementation. Hence, in this context, the statistical properties of “natural” and “artificial” random sequences came to close scrutiny. For the aforementioned historical and technological reasons, Monte Carlo methods are frequently used as a benchmark for testing the properties of these generators. Hence, although Monte Carlo methods proper lie outside the scope of this article, we shall keep them as a standard application benchmark in our discussions.
The clever ideas and also the caveats of engineering good random number generators are in the core of many paradoxes found by Spencer-Brown. The objective of this section is to explain the basic ideas behind these generators and, in so doing, avoid the conceptual traps and pitfalls that took Spencer-Brown analyses so much off course.
3.1. Random and Pseudo-Random Number Generators
The concept of randomness is usually applied to a variable or a process (to be generated or observed) involving some uncertainty. The following definition is presented at p. 10 of [61]:
A random event is an event which has a chance of happening, and probability is a numerical measure of that chance.
Monte Carlo, and several other probabilistic algorithms, require a random number generator. With the last definition in mind, engineering devices based on sophisticated physical processes have been built in the hope of offering a source of “true” random numbers. However, these special devices were cumbersome, expensive, not portable nor easily available, and often unreliable. Moreover, practitioners soon realized that simple deterministic sequences could successfully be used to emulate a random generator, as stated in the following quotes (our emphasis) at p. 26 of [61] and p. 15 of [62]:
For electronic digital computers it is most convenient to calculate a sequence of numbers one at a time as required, by a completely specified rule which is, however, so devised that no reasonable statistical test will detect any significant departure from randomness. Such a sequence is called pseudorandom. The great advantage of a specified rule is that the sequence can be exactly reproduced for purposes of computational checking.
A sequence of pseudorandom numbers (Ui) is a deterministic sequence of numbers in [0, 1] having the same relevant statistical properties as a sequence of random numbers.
Many deterministic random emulators used today are Linear Congruential Pseudo-Random Generators (LCPRG), as in the following example:
However, LCPRG's are not an universal solution. For example, it is trivial to devise some statistics whose behaviour will be far from random, see [63]. There the importance of the words reasonable and relevant in the last quotations becomes clear: For most practical applications these statistics are irrelevant. LCPRG's can also exhibit very long range auto-correlations and, unfortunately, these are more likely to affect long simulated time series required in some special applications. The composition of several LCPRG's by periodic seed refresh may mitigate some of these difficulties, see [62]. LCPRG's are also not appropriate to some special applications in cryptography, see [64]. Current state of the art generators are given in [65,66].
3.2. Chance is Lumpy—Quasi-Random Generators
“Chance is Lumpy” is Robert Abelson's First Law of Statistics, stated in p. XV of [67]. The probabilistic expectation is a linear operator, that is, E(Ax + b) = AE(x) + b, where x in random vector and A and b are a determined matrix and vector. The Covariance operator is defined as Cov(x) = E((x − E(x)) ⊗ (x − E(x))). Hence, Cov(Ax + b) = ACov(x)A′. Therefore, given n i.i.d. scalar variables, xi | Var(xi) = σ2, the variance of their mean, m = (1/n)1′x (notice the simplified vector notation 1 = [1, 1 …, 1]), is given by
Hence, mean values of iid random variables converge to their expected values at a rate of
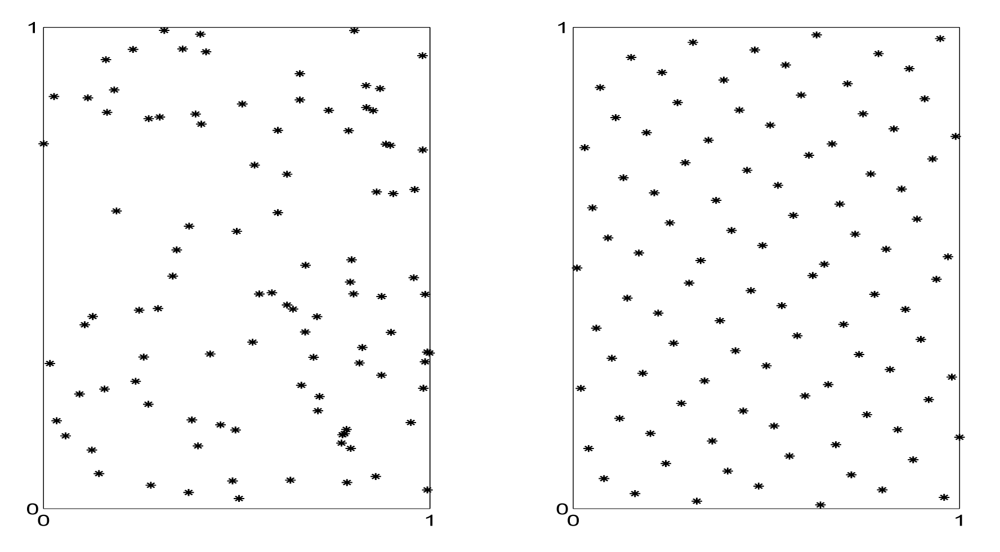
Quasi-random sequences are deterministic sequences built not to emulate random sequences, as pseudo-random sequences do, but to achieve faster convergence rates. For d-dimensional quasi-random sequences, an appropriate measure of fluctuation, called discrepancy, only grows at a rate of log(n)d, hence growing much slower than . Therefore, the convergence rate corresponding to quasi-random sequences, log(n)d/n, is much faster than the one corresponding to (pseudo) random sequences, . Figure 1 allows the visual comparison of typical (pseudo) random (left) and quasi-random (right) sequences in [0, 1]2. By visual inspection we see that the points of the quasi-random sequence are more “homogeneously scattered”, that is, they do not “clump together”, as the point of the (pseudo) random sequence often do.
Let us consider an axis-parallel rectangles in the unit box,
The discrepancy of the sequence s1:n in box R, and the overall discrepancy of the sequence are defined as
It is possible to prove that the discrepancy of the Halton-Hammersley sequence, defined next, is of order O(log(n)d−1), see chapter 2 of [68].
Halton-Hammersley sets: Given d − 1 distinct prime numbers, p(1), p(2), … p(d − 1), the i-th point, xi, in the Halton-Hammersley set, {x1, x2, … xn}, is
That is, the (k + 1)-th coordinate of xi, , is obtained by the bit (or digit) reversal of i written in p(k)-adic or base p(k) notation.
The Halton-Hammersley set is a generalization of van der Corput set, built in the bidimensional unit square, d = 2, using the first prime number, p = 2. The following example, from p. 33 of [61] and p. 117 of [69], builds the 8-point van der Corput set, expressed in binary and decimal notation.
function x= corput(n,b)
% size n base b v.d.corput set
m=floor (log(n)/log(b));
u=1 : n; D=[ ];
for i=0:m
d= rem(u,b);
u= (u–d)/b;
D= [D; d];
end
x=((1./b′).ˆ(1 : (m\ma1)))*D;
| Decimal | Binary | ||
|---|---|---|---|
|
| |||
| i | r2(i) | i | r2(i) |
| 1 | 0.5 | 1 | 0.1 |
| 2 | 0.21 | 10 | 0.01 |
| 3 | 0.75 | 11 | 0.11 |
| 4 | 0.125 | 100 | 0.001 |
| 5 | 0.625 | 101 | 0.101 |
| 6 | 0.375 | 110 | 0.011 |
| 7 | 0.875 | 111 | 0.111 |
| 8 | 0.0625 | 1000 | 0.0001 |
Quasi-random sequences, also known as low-discrepancy sequences, can substitute pseudo-random sequences in some applications of Monte Carlo methods, achieving higher accuracy with less computational effort, see [70–72]. Nevertheless, since by design the points of a quasi-random sequence tend to avoid each other, strong (negative) correlations are expected to appear. In this way, the very reason that can make quasi-random sequences so helpful, can ultimately impose some limits to their applicability. Some of these problems are commented in p. 766 of [73]:
First, quasi-Monte Carlo methods are valid for integration problems, but may not be directly applicable to simulations, due to the correlations between the points of a quasi-random sequence. … A second limitation: the improved accuracy of quasi-Monte Carlo methods is generally lost for problems of high dimension or problems in which the integrand is not smooth.
3.3. Subjective Randomness and Its Paradoxes
When asked to look at patterns like those in Figure 1, many subjects perceive the quasi-random set as “more random” than the (pseudo) random set. How can this paradox be explained? This was the topic of many psychological studies in the field of subjective randomness. The quotation in the next paragraph is from one of these studies, p. 306 in [36], emphasis are ours:
One major source of confusion is the fact that randomness involves two distinct ideas: process and pattern, [74]. It is natural to think of randomness as a process that generates unpredictable outcomes (stochastic process according to [75]). Randomness of a process refers to the unpredictability of the individual event in the series [76,77]. This is what Spencer Brown [26] calls primary randomness. However, one usually determines the randomness of the process by means of its output, which is supposed to be patternless. This kind of randomness refers, by definition, to a sequence. It is labeled secondary randomness by Spencer Brown. It requires that all symbol types, as well as all ordered pairs (diagrams), ordered triplets (trigrams)… n-grams in the sequence be equiprobable. This definition could be valid for any n only in infinite sequences, and it may be approximated in finite sequences only up to ns much smaller than the sequence's length. The entropy measure of randomness is based on this definition, see chapter 1 and 2 of [41].
These two aspects of randomness are closely related. We ordinarily expect outcomes generated by a random process to be patternless. Most of them are. Conversely, a sequence whose order is random supports the hypothesis that it was generated by a random mechanism, whereas sequences whose order is not random cast doubt on the random nature of the generating process.
Spencer-Brown was intrigued by the apparent incompatibility of the notions of primary and secondary randomness. The apparent collision of these two notions generates several interesting paradoxes, taking Spencer-Brown to question the applicability of the concept of randomness in particular and probability and statistical analysis in general, see [24–26], and also [35], [38,39], [54–57] and [78], In fact, several subsequent psychological studies were able to confirm that, for many subjects, the intuitive or common-sense perception of primary and secondary randomness are quite discrepant. However, a careful mathematical analysis makes it possible to reconcile the two notions of randomness. These are the topics discussed in this section.
The relation between the joint and conditional entropy for a pair of random variables, see Section 4,
motivates the definition of first, second and higher order entropies, defined over the distribution of words of size m in a string of letters from an alphabet of size a.
It is possible to use these entropy measures to assess the disorder or lack of pattern in a given finite sequence, using the empirical probability distributions of single letters, pairs, triplets, etc. However, in order to have a significant empirical distribution of m-plets, any possible m-plet must be well represented in the sequence, that is, the word size, m, is required to be very short relative to the sequence log-size, that is, m ≪ loga(n).
In the article [36], Figure 2 displays the typical perceived or apparent randomness of Boolean (0-1) bit sequences, represented as black-and-white pixel in linear arrays, versus the second order entropy of the same strings, see also [41]. Clearly, there is a remarkable bias of the apparent randomness relative to the entropic measure.
This effect is known as the gambler's fallacy when betting on cool spots. It consists of expecting the random sequence to “compensate” finite average fluctuations from expected values. This effect is also described in p. 303 of [36]:
When people invent superfluous explanations because they perceive patterns in random phenomena, they commit what is known in statistical parlance as Type I error. The other way of going awry, known as Type II error, occurs when one dismisses stimuli showing some regularity as random. The numerous randomization studies in which participants generated too many alternations and viewed this output as random, as well as the judgments of over alternating sets as maximally random in the perception studies, were all instances of type II error in research results.
It is known that other gamblers exhibit the opposite behavior, preferring to bet on hot spots, expecting the same fluctuations to occur repeatedly. These effects are the consequence of a perceived coupling, by a negative or positive correlation or other measure of association, between non overlapping segments that are in fact supposed to be decoupled, uncorrelated or have no association, that is, to be independent. For a statistical analysis, see [58,59]. A possible psychological explanation of the gambler's fallacy is given by the constructivist theory of Jean Piaget, see [79], as quoted in p. 316 of [36], in which any “lump” in the sequence is (miss) perceived as non-random order:
In analogy to Piaget's operations, which are conceived as internalized actions, perceived randomness might emerge from hypothetical action, that is, from a thought experiment in which one describes, predicts, or abbreviates the sequence. The harder the task in such a thought experiment, the more random the sequence is judged to be.
The same hierarchical decomposition scheme used for higher order conditional entropy measures can be adapted to measure the disorder or patternless of a sequence, relative to a given subject's model of “computer” or generation mechanism. In the case of a discrete string, this generation model could be, for example, a deterministic or probabilistic Turing machine, a fixed or variable length Markov chain, etc. It is assumed that the model is regulated by a code, program or vector parameter, θ, and outputs a data vector or observed string, x. The hierarchical complexity measure of such a model emulates the Bayesian prior and conditional likelihood decomposition, H(p(θ, x)) = H(p(θ)) + H(p(x | θ)), that is, the total complexity is given by the complexity of the program plus the complexity of the output given the program. This is the starting point for several complexity models, like Andrey Kolmogorov, Ray Solomonoff and Gregory Chaitin's computational complexity models, Jorma Rissanen's Minimum Description Length (MDL), and Chris Wallace and David Boulton's Minimum Message Length (MML). All these alternative complexity models can also be used to successfully reconcile the notions of primary and secondary randomness, showing that they are asymptotically equivalent, see [80–85].
4. Entropy and Its Use in Mathematical Statistics
Entropy is the cornerstone concept of the preceding section, used as a central idea in the understanding of order and disorder in stochastic processes. Entropy is the key that allowed us to unlock the mysteries and solve the paradoxes of subjective randomness, making it possible to reconcile the notions of unpredictability of stochastic process and patternless of randomly generated sequences. Similar entropy based arguments reappear, in more abstract, subtle or intricate forms, in the analysis of technical aspects of Bayesian statistics like, for example, the use of prior and posterior distributions and the interpretation of their informational content. This section gives a short review covering the definition of entropy, its main properties, and some of its most important uses in mathematical statistics.
The origins of the entropy concept lay in the fields of Thermodynamics and Statistical Physics, but its applications have extended far and wide to many other phenomena, physical or not. The entropy of a probability distribution, H(p(x)), is a measure of uncertainty (or impurity, confusion) in a system whose states, x ∈ χ, have p(x) as probability distribution. We follow closely the presentation in the following references. For the basic concepts, see [42] and [86–89]. For maximum entropy (MaxEnt) characterizations, see [45] and [90]. For numerical optimization methods for MaxEnt problems, see [91–95]. For posterior asymptotic convergence, see [96]. For a detailed analysis of the connection between MaxEnt optimization and Bayesian statistics' formalisms, that is, for a deeper view of the relation between MaxEnt and Bayes' rule updates, see [97].
4.1. Convexity
This section introduces the notion of convexity, a concept at the heart of the definition of entropy and generalized directed divergences. Convexity arguments are also needed to prove, in the following sections, important properties of entropy and its generalizations. In this section we use the following notations: 0 and 1 are the origin and unit vector of appropriate dimension. Subscripts are used as an element index in a vector or as a row index in a matrix, and superscripts are used as an index for distinct vectors or as a column index in a matrix.
Definition
A region S ∈ Rn is Convex iff, for any two points, x1, x2 ∈ S, and weights 0 ≤ l1, l2 ≤ 1 | l1 + l2 = 1, the convex combination of these two points remains in S, i.e. l1x1 + l2x2 ∈ S.
Theorem
Finite Convex Combination: A region S ∈ Rn is Convex iff any (finite) convex combination of its points remains in the region, i.e., ∀ 0 ≤ l ≤ 1 | 1′l = 1, X = [x1, x2, … xm], xj ∈ S,
Proof
By induction in the number of points, m.
Definition
The Epigraph of the function φ : Rn → R is the region of X “above the graph” of φ, i.e.,
Definition
A function φ is convex iff its epigraph is convex. A function φ is concave iff −φ is convex.
Theorem
A differentiable function, φ : R → R, with non negative second derivative is convex.
Proof
Consider x0 = l1x1 + l2x2, and the Taylor expansion around x0,
Theorem
Jensen Inequality: If φ is a convex function,
For discrete distributions the Jensen inequality is a special case of the finite convex combination theorem. Arguments of Analysis allow us to extend the result to continuous distributions.
4.2. Boltzmann-Gibbs-Shannon Entropy
If H(p(x)) is to be a measure of uncertainty, it is reasonable that it should satisfy the following list of requirements. For the sake of simplicity, we present several aspects of the theory in finite spaces.
If the system has n possible states, x1, … xn, the entropy of the system with a given distribution, pi≡ p(xi), is a function
H is a continuous function.
H is a function symmetric in its arguments.
The entropy is unchanged if an impossible state is added to the system, i.e.,
The system's entropy is minimal and null when the system is fully determined, i.e.,
The system's entropy is maximal when all states are equally probable, i.e.,
A system maximal entropy increases with the number of states, i.e.,
Entropy is an extensive quantity, i.e., given two independent systems, with distributions p and q, the entropy of the composite system is additive, i.e.,
The Boltzmann-Gibbs-Shannon measure of entropy,
For the Boltzmann-Gibbs-Shannon entropy we can extend requirement 8, and compute the composite Negentopy even without independence:
If we add this last identity as item number 9 in the list of requirements, we have a characterization of Boltzmann-Gibbs-Shannon entropy, see [87–89].
Like many important concepts, this measure of entropy was discovered and re-discovered several times in different contexts, and sometimes the uniqueness and identity of the concept was not immediately recognized. A well known anecdote refers the answer given by von Neumann, after Shannon asked him how to call a “newly” discovered concept in Information Theory. As reported by Shannon in p. 180 of [98]:
“My greatest concern was what to call it. I thought of calling it information, but the word was overly used, so I decided to call it uncertainty. When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have the advantage.”
4.3. Csiszar's Divergence
In order to check that requirement (6) is satisfied, we can use (with q ∝ 1) the following lemma:
Lemma
Shannon Inequality.
If p and q are two distributions over a system with n possible states, and qi≠ 0, then the Information of p Relative to q, In(p, q), is positive, except if p = q, when it is null,
Proof
By Jensen inequality, if φ is a convex function,
Taking
Shannon's inequality motivates the use of the Relative Information as a measure of (non symmetric) “distance” between distributions. In Statistics this measure is known as the Kullback-Leibler distance. The denominations Directed Divergence or Cross Information are used in Engineering. The proof of Shannon inequality motivates the following generalization of divergence:
Definition
Csiszar's φ-divergence.
Given a convex function φ,
For example, we can define the quadratic and the absolute divergence as
4.4. Maximum Entropy under Constraints
This section analyzes solution techniques for some problems formulated as entropy maximization. The results obtained in this section are needed to obtain some fundamental principles of Bayesian statistics, presented in the following sections. This section also presents the Bregman algorithm for solving constrained maxent problems on finite distributions. The analysis of small problems (far from asymptotic conditions) poses many interesting questions in the study of subjective randomness, an area so far neglected in the literature.
Given a prior distribution, q, we would like to find a vector p that minimizes the Relative Information In(p,q), where p is under the constraint of being a probability distribution, and maybe also under additional constraints over the expectation of functions taking values on the system's states, that is, we want
p* is the Minimum Information or Maximum Entropy (MaxEnt) distribution, relative to q, given the constraints {A, b}. We can write the probability normalization constraint as a generic linear constraint, including 1 and 1 as the m-th (or 0-th) rows of matrix A and vector b. So doing, we do not need to keep any distinction between the normalization and the other constraints. In this article, the operators ⊙ and ⊘ indicate the point (element) wise product and division between matrices of same dimension.
The Lagrangian function of this optimization problem, and its derivatives are:
Equating the n + m derivatives to zero, we have a system with n + m unknowns and equations, giving viability and optimality conditions (VOCs) for the problem:
We can further replace the unknown probabilities, pi, writing the VOCs only on w, the dual variables (Lagrange multipliers),
The last form of the VOCs motivates the use of iterative algorithms of Gauss-Seidel type, solving the problem by cyclic iteration. In this type of algorithm, one cyclically “fits” one equation of the system, for the current value of the other variables. For a detailed analysis of this type of algorithm, see [91–95] and [99].
Bregman Algorithm
Initialization: Take t = 0, wt ∈ Rm, and
Iteration step: for t = 1, 2, …, Take
From our discussion of Entropy optimization under linear constraints, it should be clear that the maximum relative entropy distribution for a system under constraints on the expectation of functions taking values on the system's states,
(including the normalization constraint, a0 = 1, b0 = 1) has the form
Notice that we took θ0 = −(w0 − 1),θk = −wk, and we have also indexed the state i by variable x, so to write the last equation in the standard form used in the statistical literature.
Several distributions commonly used in Statistics can be interpreted as MaxEnt densities (relative to the uniform distribution, if not otherwise stated) given some constraints over the expected value of state functions. For example:
The Normal distribution:
The Wishart distribution:
The Dirichlet distribution
Jeffrey's Rule
Richard Jeffrey considered the problem of updating an old probability distribution, q, to a new distribution, p, given new constraints on the probabilities of a partition, that is,
His solution to this problem, known as the Jeffrey's rule, coincides with the minimum information divergence distribution, relative to q, given the new constraints. This solution can be expressed analytically as
4.5. Fisher's Metric and Jeffreys' Prior
In this section the Fisher Information Matrix is defined and used to obtain the geometrically invariant Jeffreys' prior distributions. These distributions also have interesting asymptotic properties concerning the representation of vague or no information. The properties of Fisher's metric discussed in this section are also needed to establish further asymptotic results in the next section.
The Fisher Information Matrix, J(θ), is defined as minus the expected Hessian of the log-likelihood. Under appropriate regularity conditions, the information geometry is defined by the metric in the parameter space given by the Fisher information matrix, that is, the geometric length of a curve is computed integrating the form dl2 = dθ′ J(θ)dθ.
Lemma
The Fisher information matrix can also be written as the covariance matrix of the gradient of the same likelihood, i.e.,
Proof
Harold Jeffreys used the Fisher metric to define a class of prior distributions, proportional to the determinant of the information matrix,
Lemma: Jeffreys' priors are geometric objects in the sense of being invariant by a continuous and differentiable change of coordinates in the parameter space, η = f(θ). The proof follows pp. 41–54 of [100]:
Proof
Example: For the multinomial distribution,
In general Jeffrey's priors are not minimally informative in any sense. However, in pp. 41–54 of [100], Zellner gives the following argument (attributed to Lindley) to present Jeffreys' priors as “knowing little” in the sense of being asymptotically minimally informative. The following equations give several definitions related to the concept of information gain, that is expressed as the prior average information associated with an observation minus the prior information measure: I(θ)—the information measure of p(x | θ), A—the prior average information associated with an observation, G—the information gain, and Ga—the asymptotic information gain
Although Jeffreys' priors in general do not maximize the information gain, G, the asymptotic convergence results presented in the next section imply that Jeffrey's priors maximize the asymptotic information gain, Ga. For further details and generalizations, see [101–110].
Comparing the several versions of noninformative priors in the multinomial example, one can say that Jeffreys' prior “discounts” half an observation of each kind, while the maxent prior discounts one full observation, and the flat prior discounts none. Similarly, slightly different versions of uninformative priors for the multivariate normal distribution are shown in [106]. This situation leads to the possible criticism stated by Berger in p. 89 of [104]:
Perhaps the most embarrassing feature of noninformative priors, however, is simply that there are often so many of them.
One response to this criticism, to which Berger explicitly subscribes in p. 90 of [104], is that
It is rare for the choice of a noninformative prior to markedly affect the answer… so that any reasonable noninformative prior can be used. Indeed, if the choice of noninformative prior does have a pronounced effect on the answer, then one is probably in a situation where it is crucial to involve subjective prior information.
The robustness of the inference procedures to variations on the form of the uninformative prior can be tested using sensitivity analysis, as discussed in Section 4.7 of [104]. For alternative approaches on robustness and sensitivity analysis based on paraconsistent logic, see [4,5].
4.6. Posterior Asymptotic Convergence
Posterior convergence constitutes the principal mechanism enabling information acquisition or learning in Bayesian statistics. Arguments based on relative information, I(p, q), can be used to prove fundamental results concerning posterior distribution asymptotic convergence. This section presents two of these fundamental results, following Appendix B of [96].
Theorem
Posterior Consistency for Discrete Parameters:
Consider a model where f(θ) is the prior in a discrete parameter space, Θ = {θ1, θ2, …}, X = [x1, … xn] is a series of observations, and the posterior is given by
Further, assume that this model has a unique vector parameter, θ0, giving the best approximation for the “true” predictive distribution g(x), in the sense that it minimizes the relative information
Then,
Heuristic Argument
Consider the logarithmic coefficient
The first term is a constant, and the second term is a sum which terms have all negative expected (relative to x, for k ≠ 0) value since, by our hypotheses, θ0 is the unique argument that minimizes I(g(x), p(x|θk)). Hence, (for k ≠ 0), the right hand side goes to minus infinite as n increases. Therefore, at the left hand side, f(θk | X) must go to zero. Since the total probability adds to one, f(θ0 | X) must go to one, QED.
We can extend this result to continuous parameter spaces, assuming several regularity conditions, like continuity, differentiability, and having the argument θ0 as an interior point of Θ with the appropriate topology. In such a context, we can state that, given a pre-established small neighborhood around θ0, like C(θ0, ε) the cube of side size ε centered at θ0, this neighborhood concentrates almost all mass of f(θ | X), as the number of observations grows to infinite. Under the same regularity conditions, we also have that Maximum a Posteriori (MAP) estimator is a consistent estimator, i.e., θ̂ → θ0.
The next results show the convergence in distribution of the posterior to a Normal distribution. For that, we need the Fisher information matrix identity from the last section.
Theorem
Posterior Normal Approximation:
The posterior distribution converges to a Normal distribution with mean θ0 and precision nJ(θ0).
Proof (heuristic)
We only have to write the second order log-posterior Taylor expansion centered at θ̂,
The term of order zero is a constant. The linear term is null, for θ̂ is the MAP estimator at an interior point of Θ. The Hessian in the quadratic term is
The Hessian is negative definite, by the regularity conditions, and because θ̂ is the MAP estimator. The first term is constant, and the second is the sum of n i.i.d. random variables. At the other hand we have already shown that the MAP estimator, and also that all the posterior mass concentrates around θ0. We also see that the Hessian grows (in average) linearly with n, and that the higher order terms can not grow super-linearly. Also for a given n and θ → θ̂, the quadratic term dominates all higher order terms. Hence, the quadratic approximation of the log-posterior in increasingly more precise, Q.E.D.
5. Final Remarks
The objections raised by Spencer-Brown against probability and statistics, analyzed in Sections 1 and 2, are somewhat simplistic and stereotypical, possibly explaining why they had little influence outside a close circle of admirers, most of them related to the radical constructivism movement. However, arguments very similar to those used to demystify Spencer-Brown's misconceptions and elucidate its misunderstandings, reappear in more subtle or abstract forms in the analysis of far more technical matters like, for example, the use and interpretation of prior and posterior distributions in Bayesian statistics.
In this article, entropy is presented as a cornerstone concept for the precise analysis and a key idea for the correct understanding of several important topics in probability and statistics. This understanding should help to clear the way for establishing Bayesian statistics as a preferred tool for scientific inference in mainstream cognitive constructivism.
Acknowledgments
The author is grateful for the support of the Department of Applied Mathematics of the Institute of Mathematics and Statistics of the University of São Paulo, FAPESP—Fundação de Amparo à Pesquisa do Estado de São Paulo, and CNPq—Conselho Nacional de Desenvolvimento Científico e Tecnológico (grant PQ-306318-2008-3). The author is also grateful for the helpful discussions with several of his professional colleagues, including Carlos Alberto de Braganca Pereira, Fernando Bonassi, Luis Esteves, Marcelo de Souza Lauretto, Rafael Bassi Stern, Sergio Wechsler and Wagner Borges.
References
- Borges, W.; Stern, J.M. The rules of logic composition for the bayesian epistemic e-values. Log. J. IGPL 2007, 15, 401–420. [Google Scholar]
- Pereira, C.A.B.; Stern, J.M. Evidence and credibility: Full bayesian significance test for precise hypotheses. Entropy 1999, 1, 69–80. [Google Scholar]
- Pereira, C.A.B.; Wechsler, S.; Stern, J.M. Can a significance test be genuinely bayesian? Bayesian Anal. 2008, 3, 79–100. [Google Scholar]
- Stern, J.M. Significance Tests, Belief Calculi, and Burden of Proof in Legal and Scientific Discourse. In Laptec-2003, Frontiers in Artificial Intelligence and Its Applications; ISO Press: Amsterdam, The Netherlands, 2003; Volume 101, pp. 139–147. [Google Scholar]
- Stern, J.M. Paraconsistent Sensitivity Analysis for Bayesian Significance. Tests SBIA'04; In Lecture Notes Artificial Intelligence; Goebel, R., Siekmann, J., Wahlster, W., Eds.; Springer: Heidelberg , Germany, 2004; Volume 3171, pp. 134–143. [Google Scholar]
- Stern, J.M. Language, Metaphor and Metaphysics: The Subjective Side of Science; Technical Report MAC-IME-USP-06-09; Department of Statistical Science, University College: London, UK, 2006. [Google Scholar]
- Stern, J.M. Cognitive constructivism, eigen-solutions, and sharp statistical hypotheses. Cybern. Hum. Knowing 2007, 14, 9–36. [Google Scholar]
- Stern, J.M. Language and the self-reference paradox. Cybern. Hum. Knowing 2007, 14, 71–92. [Google Scholar]
- Stern, J.M. Complex Structures, Modularity and Stochastic Evolution; Technical Report IME-USP-MAP-07-01; University of Sao Paulo: Sao Paulo, Brazil, 2007. [Google Scholar]
- Stern, J.M. Decoupling, sparsity, randomization, and objective bayesian inference. Cybern. Hum. Knowing 2008, 15, 49–68. [Google Scholar]
- Stern, J.M. Cognitive Constructivism the Epistemic Significance of Sharp Statistical Hypotheses. Presented at MaxEnt 2008, The 28th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Boraceia, Sao Paulo, Brazil; 2008. [Google Scholar]
- Stern, J.M. The Living Intelligent Universe. Proceeding of MBR09-The Internaternational Conference on Model-Based Reasoning in Science and Technology, Unicamp, Brazil; 2009. [Google Scholar]
- von Foerster, H. Understanding Understanding: Essays on Cybernetics and Cognition; Springer Verlag: New York, NY, USA, 2003. [Google Scholar]
- Bernardo, G.G.; Lauretto, M.S.; Stern, J.M. The Full Bayesian Significance Test form Symmetry in Contingency Tables. Proceeding of 30th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Chamonix, France, July 4–9, 2010.
- Chakrabarty, D. CHASSIS-Inverse Modelling of Relaxed Dynamical Systems. Proceedings of the 18th World IMACS MODSIM Congress, Cairns, Australia, 13–17 July 2009.
- Johnson, R.; Chakrabarty, D.; O'Sullivan, E.; Raychaudhury, S. Comparing X-ray and dynamical mass profiles in the early-type galaxy NGC 4636. Astrophys. J. 2009, 706, 980–994. [Google Scholar]
- Loschi, R.H.; Monteiro, J.V.D.; Rocha, G.H.M.A.; Mayrink, V.D. Testing and estimating the non-disjunction fraction in meiosis I using reference priors. Biom. J. 2007, 49, 824–839. [Google Scholar]
- Madruga, M.R.; Esteves, L.G.; Wechsler, S. On the bayesianity of pereira-stern tests. Test 2001, 10, 291–299. [Google Scholar]
- Rifo, L.L.; Torres, S. Full bayesian analysis for a class of jump-diffusion models. Comm. Stat. Theor. Meth. 2009, 38, 1262–1271. [Google Scholar]
- Rodrigues, J. Full bayesian significance test for zero-inflated distributions. Comm. Stat. Theor. Meth. 2006, 35, 299–307. [Google Scholar]
- Colla, E.; Stern, J.M. Sparse factorization methods for inference in bayesian networks. AIP Conf. Proc. 2008, 1073, 136–143. [Google Scholar]
- Hacking, I. Telepathy: Origins of Randomization in Experimental Design. Isis 1988, 79, 427–451. [Google Scholar]
- Peirce, C.S.; Jastrow, J. On small differences of sensation. In Memoirs of the National Academy of Sciences; National Academies Press: Washingtion, DC, USA, 1884; Volume 3, pp. 75–83. [Google Scholar]
- Spencer-Brown, G. Statistical significance in psychical research. Nature 1953, 172, 154–156. [Google Scholar]
- Spencer-Brown, G. Answer to soal et al. Nature 1953, 172, 594–595. [Google Scholar]
- Spencer-Brown, G. Probability and Scientific Inference; Longmans Green: London, UK, 1957. [Google Scholar]
- Spencer-Brown, G. Laws of Form; Allen and Unwin: London, UK, 1969. [Google Scholar]
- Carnielli, W. Formal Polynomials and the Laws of Form. In Dimensions of Logical Concepts; Béziau, J.Y., Costa-Leite, A., Eds.; UNICAMP: Campinas, Brazil, 2009. [Google Scholar]
- Edwards, A.W.F. Cogwheels of the Mind: The Story of Venn Diagrams; The Johns Hopkins University Press: Baltimore, MD, USA, 2004. [Google Scholar]
- Kauffman, L.H. The mathematics of charles sanders peirce. Cybern. Hum. Knowing 2001, 8, 79–110. [Google Scholar]
- Kauffman, L.H. Laws of Form: An Exploration in Mathematics and Foundations, 2006. Available at: http://www.math.uic.edu/kauffman/Laws.pdf(accessed on 1 April 2011).
- Meguire, P. Discovering boundary algebra: A simple notation for boolean algebra and the truth functions. Int. J. Gen. Sys. 2003, 32, 25–87. [Google Scholar]
- Peirce, C.S. A Boolean Algebra with One Constant. In Collected Papers of Charles Sanders Peirce; Hartshorne, C., Weiss, P., Burks, A., Eds.; InteLex: Charlottesville, VA, USA, 1992. [Google Scholar]
- Sheffer, H.M. A Set of five independent postulates for boolean algebras, with application to logical constants. Trans. Amer. Math. Soc. 1913, 14, 481–488. [Google Scholar]
- Flew, A. Probability and statistical inference by G.Spencer-Brown (review). Phil. Q. 1959, 9, 380–381. [Google Scholar]
- Falk, R.; Konold, C. Making sense of randomness: Implicit encoding as a basis for judgment. Psychol. Rev. 1997, 104, 301–318. [Google Scholar]
- Falk, R.; Konold, C. Subjective randomness. In Encyclopedia of Statistical Sciences, 2nd ed.; Wiley: New York, NY, USA, 2005; Volume 13, pp. 8397–8403. [Google Scholar]
- Good, I.J. Probability and statistical inference by G.Spencer-Brown (review). Br. J. Philos. Sci. 1958, 9, 251–255. [Google Scholar]
- Mundle, C.W.K. Probability and statistical inference by G.Spencer-Brown (review). Philosophy 1959, 34, 150–154. [Google Scholar]
- Atkins, P.W. The Second Law; The Scientific American Books: New York, NY, USA, 1984. [Google Scholar]
- Attneave, E. Applications of Information Theory to Psychology: A Summary of Basic Concepts, Methods, and Results; Holt, Rinehart and Winston: New York, NY, USA, 1959. [Google Scholar]
- Dugdale, J.S. Entropy and Its Physical Meaning; Taylor and Francis: London, UK, 1996. [Google Scholar]
- Krippendorff, K. Information Theory: Structural Models for Qualitative Data (Quantitative Applications in the Social Sciences V.62.); Sage: Beverly Hills, CA, USA, 1986. [Google Scholar]
- Tarasov, L. The World Is Built on Probability; MIR: Moscow, Russia, 1988. [Google Scholar]
- Kapur, J.N. Maximum Entropy Models in Science and Engineering; John Wiley: New Delhi, India, 1989. [Google Scholar]
- Rissanen, J. Stochastic Complexity in Statistical Inquiry; World Scientific: New York, NY, USA, 1989. [Google Scholar]
- Wallace, C.S. Statistical and Inductive Inference by Minimum Message Length; Springer: NewYork, NY, USA, 2005. [Google Scholar]
- Tribble, C.G. Industry-sponsored negative trials and the potential pitfalls of post hoc analysis. Arch. Surg. 2008, 143, 933–934. [Google Scholar]
- Wang, R.; Lagakos, S.W.; Ware, J.H.; Hunter, D.J.; Drazen, J.M. Statistics in medicine-reporting of subgroup analyses in clinical trials. New Engl. J. Med. 2007, 357, 2189–2194. [Google Scholar]
- Scott, C.G. Spencer-brown and probability: A critique. J. Soc. Psych. Res. 1958, 39, 217–234. [Google Scholar]
- Soal, S.G.; Stratton, F.J.; Thouless, R.H. Statistical significance in psychical research. Nature 1958, 172, 594. [Google Scholar]
- Atmanspacher, H. Non-physicalist physical approaches. guest editorial. Mind Matter 2005, 3, 3–6. [Google Scholar]
- Ehm, W. Meta-analysis of mind-matter experiments: A statistical modeling perspective. Mind Matter 2005, 3, 85–132. [Google Scholar]
- Henning, C. Falsification of Propensity Models by Statistical Tests and the Goodness-of-Fit Paradox; Technical Report no. 304; Department of Statistical Science, University College: London, 2006. [Google Scholar]
- Kaptchuk, T.J.; Kerr, C.E. Commentary: Unbiased divination, unbiased evidence, and the patulin clinical trial. Int. J. Epidemiol. 2004, 33, 247–251. [Google Scholar]
- Utts, J. Replication and meta-analysis in parapsychology. Stat. Sci. 1991, 6, 363–403. [Google Scholar]
- Wassermann, G.D. Some comments on the methods and statements in parapsychology and other sciences. Br. J. Philos. Sci. 1955, 6, 122–140. [Google Scholar]
- Bonassi, F.V.; Stern, R.B.; Wechsler, S. The gambler's fallacy: a bayesian approach. AIP Conf. Proc. 2008, 1073, 8–15. [Google Scholar]
- Bonassi, F.V.; Nishimura, R.; Stern, R.B. In defense of randomization: A subjectivist bayesian approach. AIP Conf. Proc. 2009, 1193, 32–39. [Google Scholar]
- Dehue, T. Deception, efficiency, and random groups: Psychology and the gradual origination of the random group design. Isis 1997, 88, 653–673. [Google Scholar]
- Hammersley, J.M.; Handscomb, D.C. Monte Carlo Methods; Chapman and Hall: London, UK, 1964. [Google Scholar]
- Ripley, B.D. Stochastic Simulation; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Marsaglia, G. Random numbers fall mainly in the planes. Proc. Natl. Acad. Sci. 1968, 61, 25–28. [Google Scholar]
- Boyar, J. Inferring sequences produced by pseudo-random number generators. J. ACM 1989, 36, 129–141. [Google Scholar]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudorandom number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar]
- Matsumoto, M.; Kurita, Y. Twisted GFSR generators. ACM Trans. Model. Comput. Simul. 1992, 2, 179–194. [Google Scholar]
- Abelson, R.P. Statistics as Principled Argument; LEA: Hillsdale, NJ, USA, 1995. [Google Scholar]
- Matous̆ek, J. Geometric Discrepancy; Springer: Berlin, Germany, 1991. [Google Scholar]
- Günther, M.; Jüngel, A. Finanzderivate mit MATLAB. Mathematische Modellierung und Numerische Simulation; Vieweg Verlag: Wiesbaden, Germany, 2003; p. 117. [Google Scholar]
- Merkel, R. Analysis and Enhancements of Adaptive Random Testing. Ph.D. Thesis, Swinburne University of Technology in Melbourne, Melbourne, Australia, 2005. [Google Scholar]
- Ökten, G. Contributions to the Theory of Monte Carlo and Quasi monte Carlo Methods. Ph.D. Thesis, Clearmont University, Clearmont, CA, USA, 1999. [Google Scholar]
- Sen, S.K.; Samanta, T.; Reese, A. Quasi versus pseudo random generators: Discrepancy, complexity and integration-error based comparisson. Int. J. Innov. Comput. Inform. Control 2006, 2, 621–651. [Google Scholar]
- Morokoff, W.J. Generating quasi-random paths for stochastic processes. SIAM Rev. 1998, 40, 765–788. [Google Scholar]
- Zabell, S.L. The Quest for Randomness and its Statistical Applications. In Statistics for the Twenty-First Century; Gordon, E., Gordon, S., Eds.; Mathematical Association of America: Washington, DC, USA, 1992. [Google Scholar]
- Gell'Mann, M. The Quark and the Jaguar: Adventures in the Simple and the Complex; W. H. Freeman: New York, NY, USA, 1994. [Google Scholar]
- Lopes, L.L. Doing the Impossible: a note on induction and the experience of randomness. J. Exp. Psychol. Learn. Mem. Cognit. 1982, 8, 626–636. [Google Scholar]
- Lopes, L.L.; Oden, G.C. Distinguishing between random and nonrandom events. J. Exp. Psychol. Learn. Mem. Cognit. 1987, 13, 392–400. [Google Scholar]
- Tversky, Y; Kahneman, D. Belief in the law of small numbers. Psychol. Bull. 1971, 76, 105–110. [Google Scholar]
- Piaget, J.; Inhelder, B. The Origin of the Idea of Chance in Children; Leake, L., Burrell, E., Fishbein, H.D., Eds.; Norton: New York, NY, USA, 1975. [Google Scholar]
- Chaitin, G.J. Randomness and mathematical proof. Sci. Amer. 1975, 232, 47–52. [Google Scholar]
- Chaitin, G.J. Randomness in arithmetic. Sci. Amer. 1988, 259, 80–85. [Google Scholar]
- Kac, M. What is random? Amer. Sci. 1983, 71, 405–406. [Google Scholar]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inform. Transm. 1965, 1, 1–7. [Google Scholar]
- Martin-Löf, E. The definition of random sequences. Inform. Contr. 1966, 9, 602–619. [Google Scholar]
- Martin-Löf, P. Algorithms and randomness. Int. Statist. Inst. 1969, 37, 265–272. [Google Scholar]
- Csiszar, I. Information Measures. Proceedings of the 7th Prage Conferences of Information Theory, Prague, Czech Republic; 1974; 2, pp. 73–86. [Google Scholar]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover: New York, NY, USA, 1953. [Google Scholar]
- Renyi, A. On Measures of Entropy and Information. Proceedings of the 4th Berkeley Symposium on Mathematical and Statistical Problems, Statistical Laboratory of the University of California, Berkeley, June 20–July 30, 1960; University of California Press: Berkeley, CA, USA, 1961; VI, pp. 547–561. [Google Scholar]
- Renyi, A. Probability Theory; North-Holland: Amsterdam, the Netherlands, 1970. [Google Scholar]
- Gokhale, D.V. Maximum Entropy Characterization of Some Distributions. In Statistical Distributions in Scientific Work; Patil, G.P., Kotz, G.P., Ord, J.K., Eds.; Springer: Berlin, Germany, 1975; Volume 3, pp. 299–304. [Google Scholar]
- Censor, Y.; Zenios, S. Introduction to Methods of Parallel Optimization; IMPA: Rio de Janeiro, Brazil, 1994. [Google Scholar]
- Censor, Y.; Zenios, S.A. Parallel Optimization: Theory, Algorithms, and Applications; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Elfving, T. On some methods for entropy maximization and matrix scaling. Linear Algebra Appl. 1980, 34, 321–339. [Google Scholar]
- Fang, S.C.; Rajasekera, J.R.; Tsao, H.S.J. Entropy Optimization and Mathematical Programming; Kluwer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Iusem, A.N.; Pierro, A.R. De Convergence results for an accelerated nonlinear cimmino algorithm. Numer. Math. 1986, 46, 367–378. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, 2nd ed; Chapman and Hall/CRC: New York, NY, USA, 2003. [Google Scholar]
- Caticha, A. Lectures on Probability, Entropy and Statistical Physics. Presented at MaxEnt 2008, The 28th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Boracéia, São Paulo, Brazil; 2008. [Google Scholar]
- Tribus, M.; McIrvine, E.C. Energy and information. Sci. Amer. 1971, 224, 178–184. [Google Scholar]
- Garcia, M.V.P.; Humes, C.; Stern, J.M. Generalized line criterion for gauss seidel method. J. Comput. Appl. Math. 2002, 22, 91–97. [Google Scholar]
- Zellner, A. Introduction to Bayesian Inference in Econometrics; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Amari, S.I.; Barndorff-Nielsen, O.E.; Kass, R.E.; Lauritzen, S.L.; Rao, C.R. Differential Geometry in Statistical Inference. In IMS Lecture Notes Monograph; Institute of Mathematical Statistics: Hayward, CA, USA, 1987; Volume 10. [Google Scholar]
- Amari, S.I. Methods of Information Geometry; American Mathematical Society: Providence, RI, USA, 2007. [Google Scholar]
- Berger, J.O.; Bernardo, J.M. On the Development of Reference Priors. In Bayesian Statistics 4; Bernardo, J.M., Berger, J.O., Lindley, D.V., Smith, A.F.M., Eds.; Oxford University Press: Oxford, UK, 1992; pp. 35–60. [Google Scholar]
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis, 2nd ed; Springer: New York, NY, USA, 1993. [Google Scholar]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; Wiley: New York, NY, USA, 2000. [Google Scholar]
- DeGroot, M.H. Optimal Statistical Decisions; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Hartigan, J.A. Bayes Theory; Springer: New York, NY, USA, 1983. [Google Scholar]
- Jeffreys, H. Theory of Probability, 3rd ed.; Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Scholl, H. Shannon optimal priors on independent identically distributed statistical experiments converge weakly to Jeffreys' prior. Test 1998, 7, 75–94. [Google Scholar]
- Zhu, H. Information Geometry, Bayesian Inference, Ideal Estimates and Error Decomposition; Santa Fe Institute: Santa Fe, NM, USA, 1998. [Google Scholar]
© 2011 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Stern, J.M. Spencer-Brown vs. Probability and Statistics: Entropy’s Testimony on Subjective and Objective Randomness. Information 2011, 2, 277-301. https://doi.org/10.3390/info2020277
Stern JM. Spencer-Brown vs. Probability and Statistics: Entropy’s Testimony on Subjective and Objective Randomness. Information. 2011; 2(2):277-301. https://doi.org/10.3390/info2020277
Chicago/Turabian StyleStern, Julio Michael. 2011. "Spencer-Brown vs. Probability and Statistics: Entropy’s Testimony on Subjective and Objective Randomness" Information 2, no. 2: 277-301. https://doi.org/10.3390/info2020277
APA StyleStern, J. M. (2011). Spencer-Brown vs. Probability and Statistics: Entropy’s Testimony on Subjective and Objective Randomness. Information, 2(2), 277-301. https://doi.org/10.3390/info2020277




