Sample Size Requirements for Assessing Statistical Moments of Simulated Crop Yield Distributions
Abstract
:1. Introduction
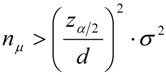
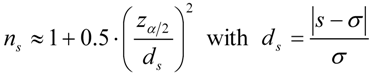
2. Methods
- (1)
- 5000 samples of crop yields were drawn without replacement from the population for sample sizes i = 5,10,15,….,1500.
- (2)
- For each sample size i and realization j, mean (
), standard deviation (
) and skewness (
) were estimated based on the drawn sample.
- (3)
- Relative deviations of the individual estimates from their reference values were computed for all moments as:with analogous equations for the standard deviation and the skewness. Here,
is the relative difference of the mean yield
in the sample j = 1,2,3,…,5000 of size i = 5,10,15,…,1500 from the population’s mean yield μref.
- (4)
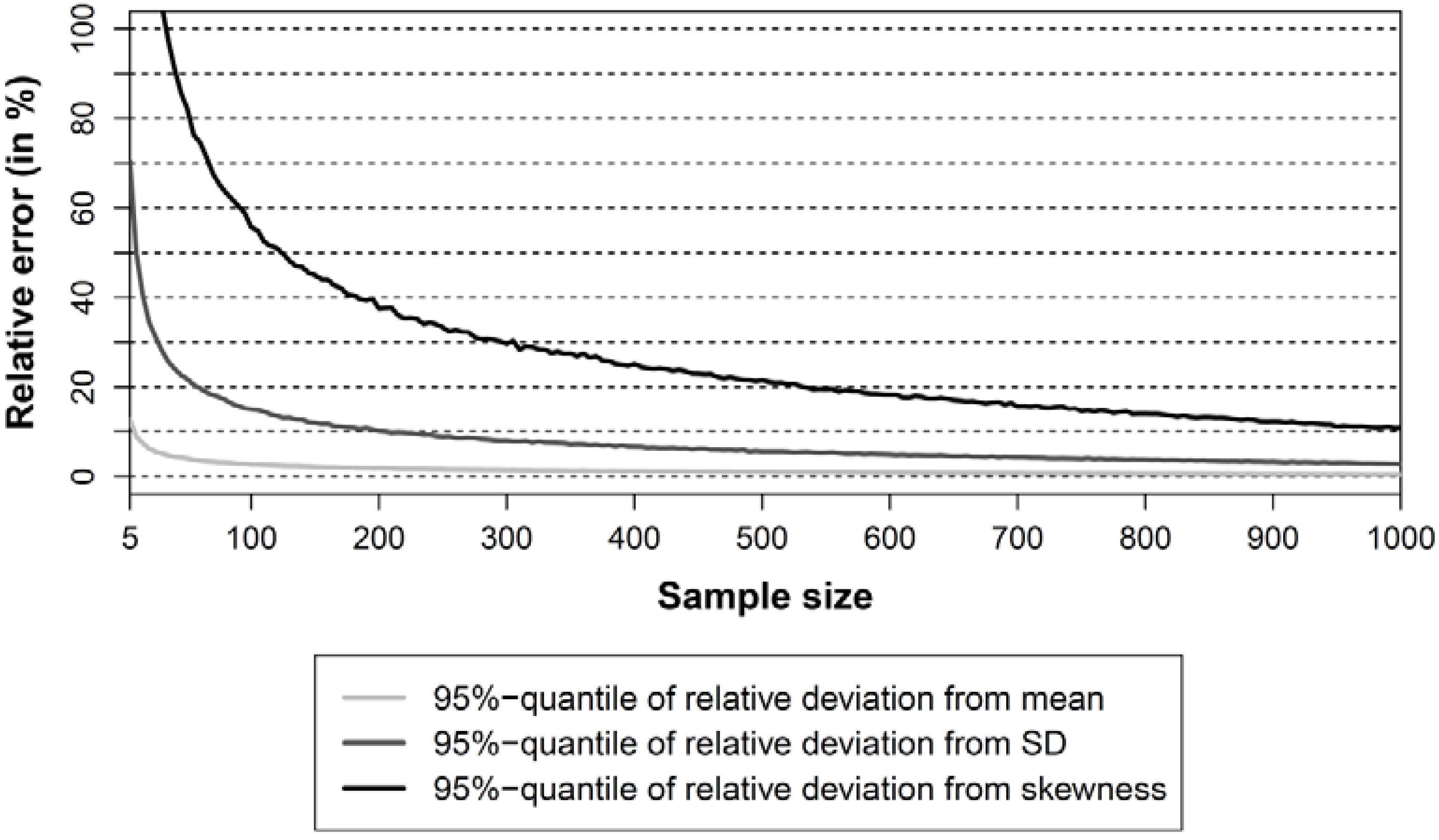
- Finally, upper 95%-quantiles for the distributions of
,
and
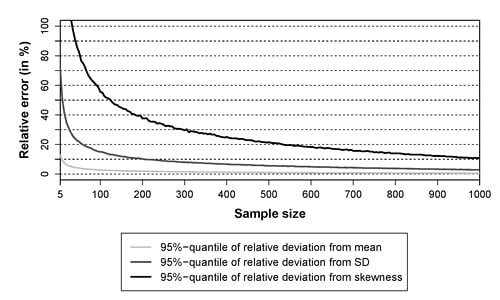
were computed for each sample size i. This measure can be used to determine the minimum sample size leading for 95% of all 5000 samples to a relative error smaller than a pre-defined level ∆ = 5%, 10%, 15% and 25%. The 95%-quantile has been chosen because it represents a robust measure and can directly be compared with the 95%-confidence interval usually applied in conjunction with Equations (1) and (2).
3. Results
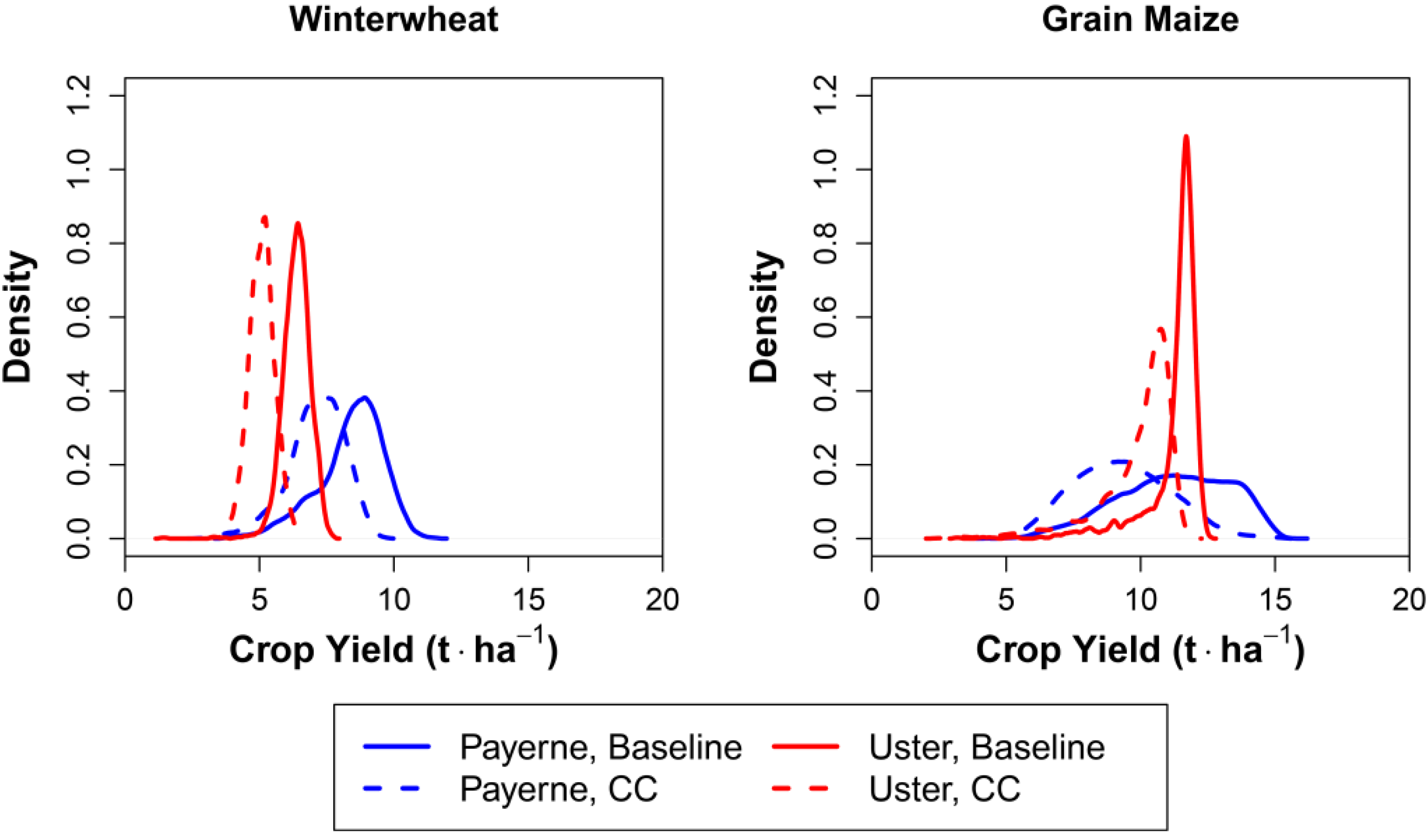
| Payerne | ||||
|---|---|---|---|---|
| Winterwheat Baseline | Winterwheat CC | Maize Baseline | Maize CC | |
| Mean yield μref (t∙ha−1) | 8.393 | 7.109 | 11.221 | 9.318 |
| Standard deviation σref (t∙ha−1) | 1.212 | 1.050 | 2.027 | 1.761 |
| Coefficient of variation | 14.4% | 14.8% | 18.1% | 18.9% |
| Skewness γref | −0.755 | −0.655 | −0.345 | 0.270 |
| Uster | ||||
| Winterwheat Baseline | Winterwheat CC | Maize Baseline | Maize CC | |
| Mean yield μref (t∙ha−1) | 6.375 | 5.086 | 11.261 | 9.881 |
| Standard deviation σref (t∙ha−1) | 0.515 | 0.469 | 1.066 | 1.386 |
| Coefficient of variation | 8.1% | 9.2% | 9.5% | 14.0% |
| Skewness γref | −1.220 | −0.050 | −2.892 | −1.890 |
| Winterwheat Baseline | Winterwheat CC | Maize Baseline | Maize CC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Relative Error a,b | μ | σ | γ | μ | σ | γ | μ | σ | γ | μ | σ | γ |
| <25% | 5 | 40 | 390 | 5 | 40 | 535 | 5 | 25 | 710 | 5 | 30 | 1020 |
| <15% | 5 | 100 | 750 | 5 | 105 | 900 | 10 | 60 | 1060 | 10 | 75 | 1280 |
| <10% | 10 | 205 | 1040 | 10 | 210 | 1155 | 15 | 120 | 1275 | 15 | 145 | 1400 |
| <5% | 35 | 580 | 1355 | 35 | 585 | 1405 | 50 | 400 | 1440 | 55 | 450 | 1475 |
| Winterwheat Baseline | Winterwheat CC | Maize Baseline | Maize CC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Relative Error a,b | μ | σ | γ | μ | σ | γ | μ | σ | γ | μ | σ | γ |
| <25% | 5 | 135 | 1430 | 5 | 35 | 1485 | 5 | 165 | 315 | 5 | 90 | 190 |
| <15% | 5 | 310 | 1430 | 5 | 85 | 1495 | 5 | 395 | 665 | 5 | 225 | 440 |
| <10% | 5 | 525 | 1430 | 5 | 170 | 1500 | 5 | 670 | 965 | 10 | 425 | 715 |
| <5% | 15 | 1040 | 1475 | 15 | 505 | 1500 | 15 | 1145 | 1330 | 30 | 915 | 1180 |
4. Discussion and Conclusions
- A sample size of 15 yield observations is sufficient to obtain estimates of mean yields with a relative error of less than 10% at 95% confidence.
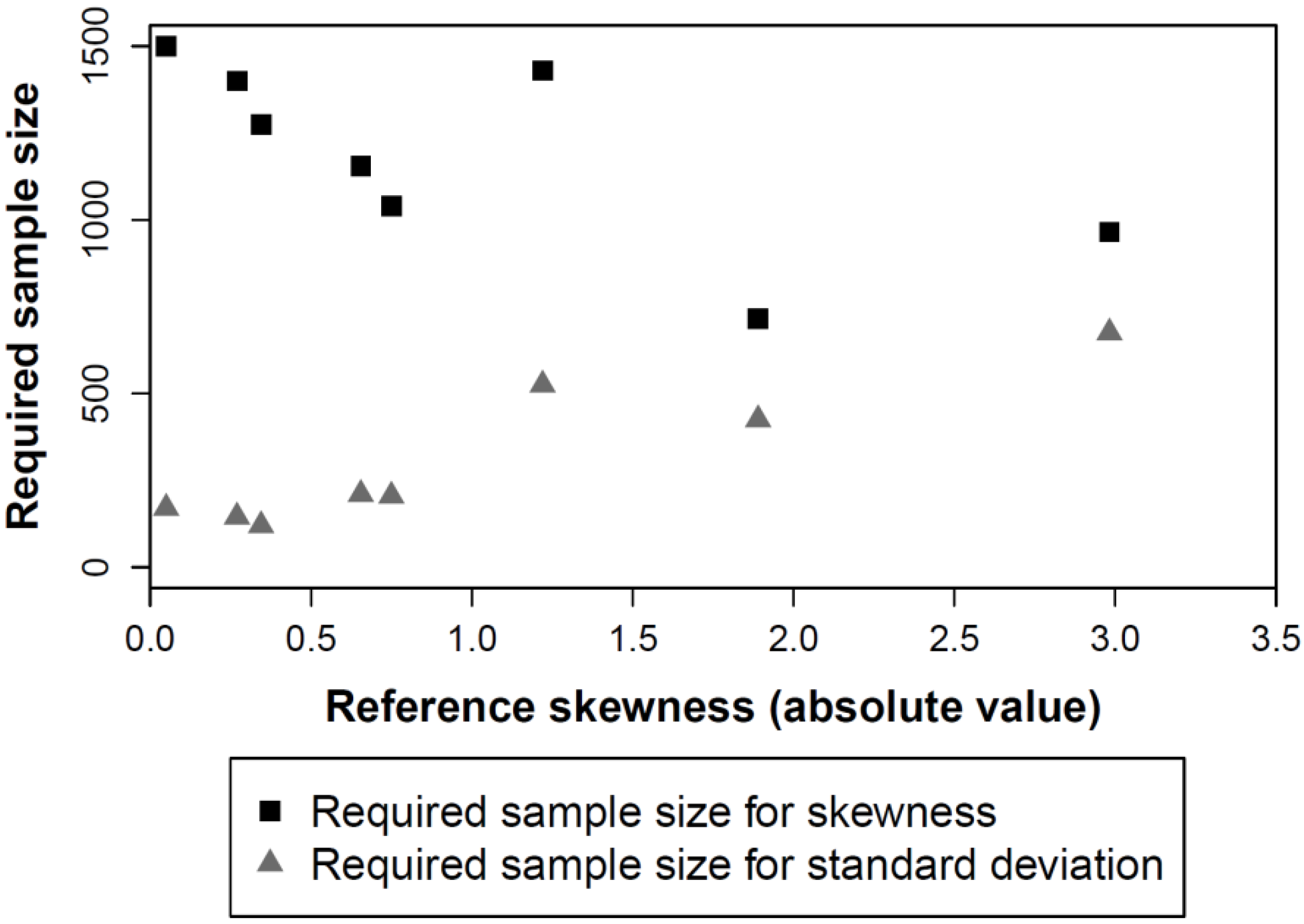
- 200 realizations are in general sufficient to obtain estimates of the standard deviation of crop yields with a relative accuracy of better than 10%. The sample size should be increased to roughly 500 when it can be assumed that the crop yield distribution is strongly skewed (absolute skewness value > 1).
- At least 1000 realizations are needed in most cases to reliably characterize the skewness of the distribution. When a high degree of symmetry is suggested by the available information, much larger samples are needed. This implies that in the absence of prior information, risk analyses should always be based on very large sample sizes.
- In practice, simulating 1000 or more years of crop yields may not always be feasible. In these cases compromises between the computation time and the accuracy of the estimated statistical moments have to be made. For instance, the required sample size is reduced by a factor of about 5 with respect to the estimation of the standard deviation, if the allowable relative estimation error is increased from 10% to 25%. This can be meaningful in studies aiming e.g., at optimizing crop management (e.g., [11,16]) or in studies simulating crop yields in a spatially explicit manner (e.g., [15]).
Acknowledgments
References
- Jalota, S.K.; Sood, A.; Vitale, J.D.; Srinivasan, R. Simulated crop yields response to irrigation water and economic analysis. Agron. J. 2007, 99, 1073–1084. [Google Scholar]
- Hoogenboom, G. Contribution of agrometeorology to the simulation of crop production and its applications. Agric. For. Meteorol. 2000, 103, 137–157. [Google Scholar] [CrossRef]
- Sinclair, T.R.; Hammer, G.L.; van Oosterom, E.J. Potential yield and water-use effficiency benefits in sorghum from limited maximum transpiration rate. Funct. Plant Biol. 2005, 32, 945–952. [Google Scholar] [CrossRef]
- Sinclair, T.R.; Messina, C.D.; Beatty, A.; Samples, M. Assessment across the United States of the benefits of altered soybean drought traits. Agron. J. 2010, 102, 475–482. [Google Scholar] [CrossRef]
- Tubiello, F.N.; Donatelli, M.; Rosenzweig, C.; Stockle, C.O. Effects of climate change and elevated CO2 on cropping systems: Model predictions at two Italian locations. Eur. J. Agron. 2000, 13, 179–189. [Google Scholar] [CrossRef]
- Donatelli, M.; Tubiello, F.; Peruch, U.; Rosenzweig, C. Impacts of climate change and elevated CO2 on sugar beet production in northern and central italy. Ital. J. Agron. 2002, 6, 133–142. [Google Scholar]
- Challinor, A.J.; Wheeler, T.R.; Craufurd, P.Q.; Slingo, J.M.; Grimes, D.I.F. Design and optimisation of a large-area process-based model for annual crops. Agric. For. Meteorol. 2004, 124, 99–120. [Google Scholar] [CrossRef]
- Torriani, D.S.; Calanca, P.; Schmid, S.; Beniston, M.; Fuhrer, J. Potential effects of changes in mean climate and climate variability on the yield of winter and spring crops in Switzerland. Climate Res. 2007, 34, 59–69. [Google Scholar] [CrossRef]
- Finger, R.; Hediger, W.; Schmid, S. Irrigation as adaptation strategy to climate change—A biophysical and economic appraisal for Swiss maize production. Clim. Change 2011, 105, 509–528. [Google Scholar] [CrossRef]
- Finger, R.; Lazzarotto, P.; Calanca, P. Bio-economic assessment of climate change impacts on managed grassland production. Agric. Syst. 2010, 103, 666–674. [Google Scholar] [CrossRef]
- Lehmann, N.; Finger, R.; Klein, T.; Calanca, P.; Walter, A. Adapting crop management practices to climate change: Modeling optimal solutions at the field scale. Agric. Syst. 2013, 117, 55–65. [Google Scholar] [CrossRef]
- Ventrella, D.; Charfeddine, M.; Moriondo, M.; Rinaldi, M.; Bindi, M. Agronomic adaptation strategies under climate change for winter durum wheat and tomato in southern Italy: Irrigation and nitrogen fertilization. Reg. Environ. Change 2012, 12, 407–419. [Google Scholar] [CrossRef]
- Jame, Y.W.; Cutforth, H.W. Crop growth models for decision support systems. Can. J. Plant Sci. 1996, 76, 9–19. [Google Scholar] [CrossRef]
- Apipattanavis, S.; Bert, F.; Podesta, G.; Rajagopalan, B. Linking weather generators and crop models for assessment of climate forecast outcomes. Agric. For. Meteorol. 2010, 150, 166–174. [Google Scholar] [CrossRef]
- Liu, J.G.; Williams, J.R.; Zehnder, A.J.B.; Yang, H. GEPIC—Modelling wheat yield and crop water productivity with high resolution on a global scale. Agric. Syst. 2007, 94, 478–493. [Google Scholar] [CrossRef]
- Royce, R.S.; Jones, J.W.; Hansen, J.W. Model-based optimization of crop management for climate forecast application. Trans. ASAE 2001, 44, 1319–1327. [Google Scholar]
- Cochran, W.G. Sampling Techniques; John Wiley and Sons: New York, NY, USA, 1977. [Google Scholar]
- Noether, G.E. Sample size determination for some common nonparametric tests. J. Am. Stat. Assoc. 1987, 82, 645–647. [Google Scholar] [CrossRef]
- Adcock, C.J. Sample size determination: A review. J. R. Stat. Soc. 1997, 46, 261–283. [Google Scholar]
- Marco, M.; Bindi, M.; Lugeri, N. Modelling yield distribution as affect by extreme events. IOP Conf. Ser. Earth Environ. Sci. 2009, 6, 022011. [Google Scholar] [CrossRef]
- Tingem, M.; Rivington, M.; Bellocchi, G.; Colls, J. Crop yield model validation for Cameroon. Theor. Appl. Climatol. 2009, 96, 275–280. [Google Scholar] [CrossRef]
- Thornton, P.K.; Jones, P.G.; Alagarswamy, G.; Andresen, J. Spatial variation of crop yield response to climate change in East Africa. Glob. Environ. Change Hum. Policy Dimens. 2009, 19, 54–65. [Google Scholar] [CrossRef]
- Finger, R.; Calanca, P. Risk management strategies to cope with climate change in grassland production: An illustrative case study for the Swiss plateau. Reg. Environ. Change 2011, 11, 935–949. [Google Scholar] [CrossRef]
- Kapphan, I.; Calanca, P.; Holzkaemper, A. Climate change, weather insurance design and hedging effectiveness. Geneva Pap. Risk Insur. Issues Pract. 2012, 37, 286–317. [Google Scholar] [CrossRef]
- Thompson, W.A.; Endriss, J. The required sample size when estimating variances. Am. Stat. 1961, 15, 22–23. [Google Scholar]
- Harri, A.; Erdem, C.; Coble, K.H.; Knight, T.O. Crop yield distributions: A reconciliation of previous research and statistical tests for normality. Rev. Agric. Econ. 2009, 31, 163–182. [Google Scholar] [CrossRef]
- Groom, B.; Koundouri, P.; Nauges, C.; Thomas, A. The story of the moment: Risk averse cypriot farmers respond to drought management. Appl. Econ. 2008, 40, 315–326. [Google Scholar] [CrossRef]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Eur. J. Agron. 2003, 18, 289–307. [Google Scholar] [CrossRef]
- Richards, R.A. Defining selection criteria to improve yield under drought. Plant Growth Regul. 1996, 20, 157–166. [Google Scholar] [CrossRef]
- Delcourt, G.; van Kooten, G.C. How resilient is grain production to climatic change? J. Sustain. Agric. 1995, 5, 37–57. [Google Scholar] [CrossRef]
- Klein, T.; Calanca, P.; Holzkamper, A.; Lehmann, N.; Roesch, A.; Fuhrer, J. Using farm accountancy data to calibrate a crop model for climate impact studies. Agric. Syst. 2012, 111, 23–33. [Google Scholar] [CrossRef]
- Amaudruz, M.; Morier, R.; Zimmermann, A.; Weyermann, I.; Hauser, S.; Schüpbach, H.; Uebersax, A.; Santschi, M.; Kessler, V.; Nyffenegger, L. Wegleitung Suisse-Bilanz; Federal Office for Agriculture (BLW) and AGRIDEA: Eschikon, Switzerland, 2011. [Google Scholar]
- Körner, C.; Morgan, J.; Norby, R. CO2 Fertilization: When, Where, How Much? In Terrestrial Ecosystems in a Changing World; Canadell, J., Pataki, D., Pitelka, L., Eds.; Springer: Berlin Heidelberg, Germany, 2007; pp. 9–21. [Google Scholar]
- Semenov, M.A.; Brooks, R.J.; Barrow, E.M.; Richardson, C.W. Comparison of the WGEN and LARS-WG stochastic weather generators for diverse climates. Climate Res. 1998, 10, 95–107. [Google Scholar] [CrossRef]
- Semenov, M.A.; Barrow, E.M. Use of a stochastic weather generator in the development of climate change scenarios. Clim. Change 1997, 35, 397–414. [Google Scholar] [CrossRef]
- Jaeger, E.B.; Anders, I.; Luthi, D.; Rockel, B.; Schar, C.; Seneviratne, S.I. Analysis of ERA40-driven CLM simulations for Europe. Meteorologische Zeitschrift 2008, 17, 349–367. [Google Scholar] [CrossRef]
- Van der Linden, P. ENSEMBLES: Climate Change and Its Impacts at Seasonal, Decadal and Centennial Timescales; Summary of Research and Results from the ENSEMBLES Project; Met Office Hadley Centre: Exter, UK, 2009. [Google Scholar]
- Nakićenović, N.; Swart, R. Emission Scenarios. Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Stein, C. A two-sample test for a linear hypothesis whose power is independent of the variance. Ann. Math. Stat. 1945, 16, 243–258. [Google Scholar] [CrossRef]
- Desu, M.M.; Raghavarao, D. Sample Size Methodology; Academic Press: Boston, MA, USA, 1990. [Google Scholar]
- Tran, T.; Coble, K.H.; Harri, A.; Barnett, B.J.; Riley, J.M. Proposed Farm Bill Impact on the Optimal Hedge Ratios for Crops. In Proceedings of Southern Agricultural Economics Association (SAEA) Annual Meeting, Orlando, FL, USA, 3–5 February 2013.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lehmann, N.; Finger, R.; Klein, T.; Calanca, P. Sample Size Requirements for Assessing Statistical Moments of Simulated Crop Yield Distributions. Agriculture 2013, 3, 210-220. https://doi.org/10.3390/agriculture3020210
Lehmann N, Finger R, Klein T, Calanca P. Sample Size Requirements for Assessing Statistical Moments of Simulated Crop Yield Distributions. Agriculture. 2013; 3(2):210-220. https://doi.org/10.3390/agriculture3020210
Chicago/Turabian StyleLehmann, Niklaus, Robert Finger, Tommy Klein, and Pierluigi Calanca. 2013. "Sample Size Requirements for Assessing Statistical Moments of Simulated Crop Yield Distributions" Agriculture 3, no. 2: 210-220. https://doi.org/10.3390/agriculture3020210
APA StyleLehmann, N., Finger, R., Klein, T., & Calanca, P. (2013). Sample Size Requirements for Assessing Statistical Moments of Simulated Crop Yield Distributions. Agriculture, 3(2), 210-220. https://doi.org/10.3390/agriculture3020210