Pure and Modified Co-Poly(amide-12-b-ethylene oxide) Membranes for Gas Separation Studied by Molecular Investigations
Abstract
:1. Introduction

2. Theoretical Section
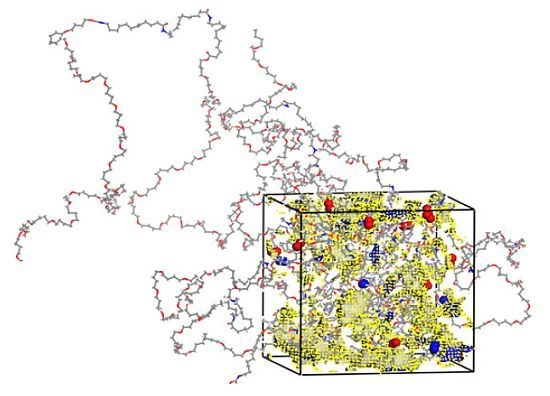
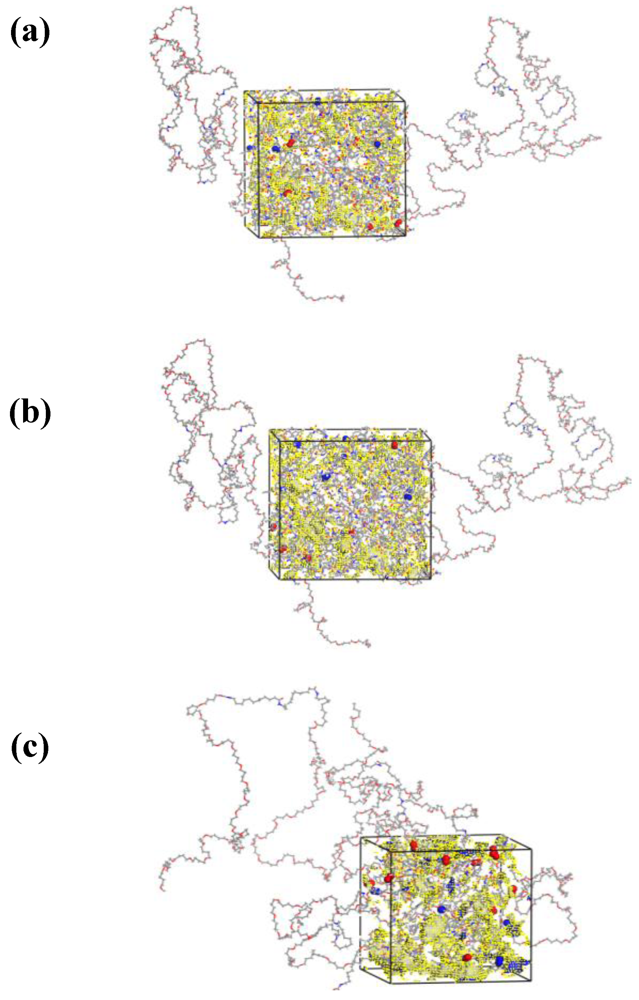
2.1. Preparation of Polymer Models
| Model | DP (–) | N Atoms (–) | N KET | Density, ρsimul.(g/mol) | Cell length (Ǻ) | |
|---|---|---|---|---|---|---|
| PEBAX/KET 70/30 + 10 CH4 + 10 CO2 | I BOX | 8 | 5102 | 46 | 0.8680 | 39.00 |
| II BOX | 8 | 5102 | 46 | 0.8888 | 38.69 | |
| III BOX | 8 | 5102 | 46 | 0.8883 | 38.70 | |
| PEBAX/KET 70/30 + 10 H2 + 10 O2 + 10 N2 | I BOX | 8 | 5082 | 46 | 0.8929 | 38.64 |
| II BOX | 8 | 5082 | 46 | 0.8925 | 38.66 | |
| III BOX | 8 | 5082 | 46 | 0.8921 | 38.65 | |
| PEBAX/KET 50/50 + 10 CH4 + 10 CO2 | I BOX | 8 | 6662 | 106 | 0.9412 | 42.32 |
| II BOX | 8 | 6662 | 106 | 0.9419 | 42.31 | |
| III BOX | 8 | 6662 | 106 | 0.9432 | 42.29 | |
| PEBAX/KET 50/50 + 10 H2 + 10 O2 + 10 N2 | I BOX | 8 | 6642 | 106 | 0.9469 | 42.24 |
| II BOX | 8 | 6642 | 106 | 0.9460 | 42.26 | |
| III BOX | 8 | 6642 | 106 | 0.9472 | 42.24 | |
| PEBAX/KET 30/70 + 10 CH4 + 10 CO2 | I BOX | 8 | 10354 | 248 | 1.0473 | 48.34 |
| II BOX | 8 | 10354 | 248 | 1.0465 | 48.36 | |
| III BOX | 8 | 10354 | 248 | 1.0469 | 48.35 | |
| PEBAX/KET 30/70 + 10 H2 + 10 O2 + 10 N2 | I BOX | 8 | 10334 | 248 | 1.0483 | 48.33 |
| II BOX | 8 | 10334 | 248 | 1.0490 | 48.32 | |
| III BOX | 8 | 10334 | 248 | 1.0494 | 48.32 | |
2.2. Calculation of Diffusion Coefficients

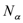 is the number of diffusing molecules of type α,
is the number of diffusing molecules of type α,  and
and  are the initial and final positions of molecules (mass centres of particle i) over the time interval t, and
are the initial and final positions of molecules (mass centres of particle i) over the time interval t, and  is the mean square displacement (MSD) averaged over the possible ensemble. The Einstein relationship assumes a random-walk motion for the diffusing particles [33].
is the mean square displacement (MSD) averaged over the possible ensemble. The Einstein relationship assumes a random-walk motion for the diffusing particles [33].2.3. TST Method
| Gas | Critical Temperature (K)a | Lennard-Jones Diameters dLJ (Ǻ) | ε (KJ·mol−1) |
|---|---|---|---|
| H2 | 33.2 | 2.93 | 0.307 |
| O2 | 154.6 | 3.46 | 0.980 |
| N2 | 126.2 | 3.698 | 0.790 |
| CO2 | 304.2 | 4.00 | 1.881 |
| CH4 | 190.6 | 3.817 | 1.231 |
| H2O | 647.1 | 3.166 | 0.650 |
2.4. Calculation of Solubility Coefficients


2.5. Pair Correlation Functions: (RDF) Analysis
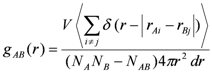
 is the distance between those two particles. The term
is the distance between those two particles. The term  in Equation 4 is set to unity when
in Equation 4 is set to unity when  ≤ dr (i.e., the difference between the desired and the actual distance among the two particles is smaller than a tolerance factor dr) and to zero otherwise.
≤ dr (i.e., the difference between the desired and the actual distance among the two particles is smaller than a tolerance factor dr) and to zero otherwise.2.6. Atom Volumes & Surfaces
3. Results and Discussion
3.1. Morphological Investigations: Chain Mobility
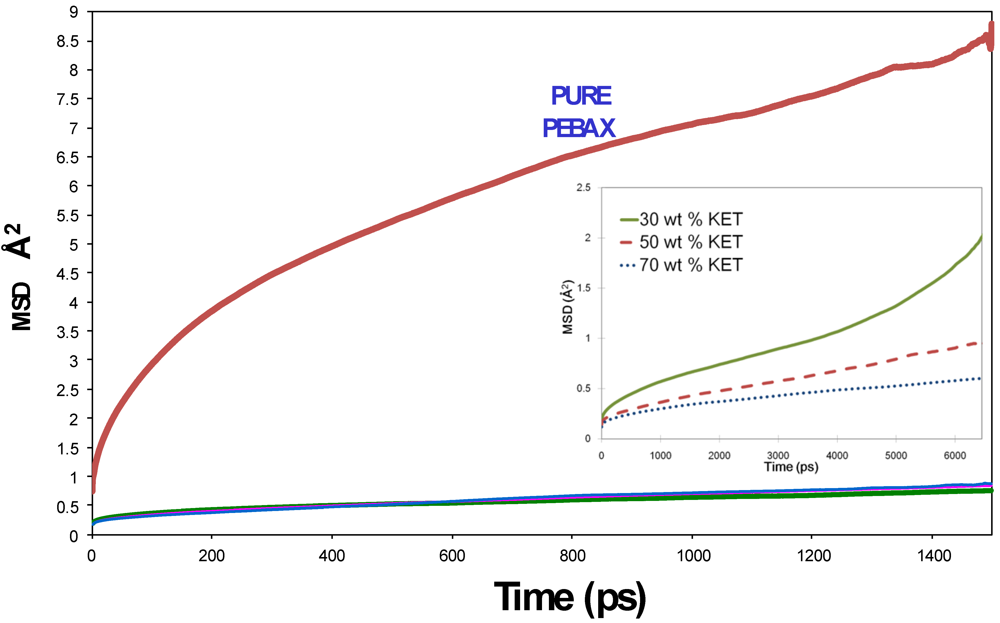
3.2. Gas and Vapor Permeability
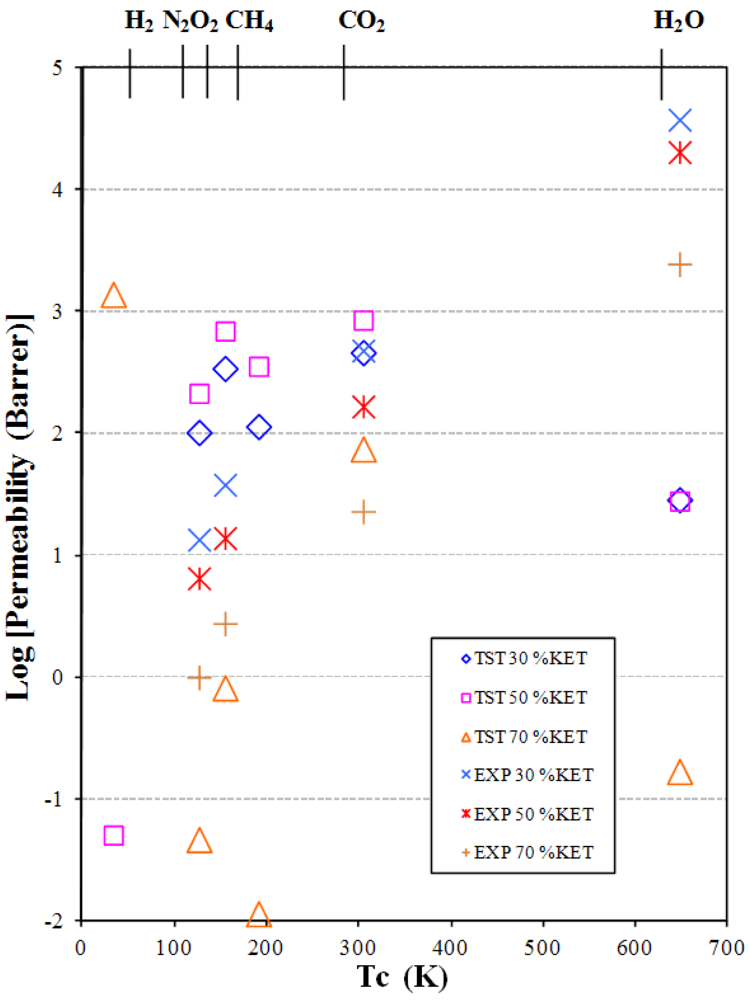
| Gas | TST Permeability coefficient, P barrer a | EXP Permeability coefficient, P barrer a | TST Solubility coefficient, S (cm3STP/cm3·cm Hg) | GCMC Solubility coefficient, S (cm3STP/cm3·cm Hg) | EXP Solubility coefficient, at 25 °C, S (cm3STP/cm3·cm Hg) | TST Diffusion coefficient, D (cm2/s) × 10−6 | MD Diffusion coefficient, D (cm2/s) × 10−6 | EXP Diffusion coefficient, D (cm2/s) × 10−6 | |
|---|---|---|---|---|---|---|---|---|---|
| PEBAX/30KET | H2 | 2.35 × 10−3 | – | 4.27 × 10−3 | 1.5 × 10−3 | – | 5.5 × 10−5 | 444.40 | – |
| CO2 | 461.71 | 480.00 | 0.43 | 0.2933 | 0.047 | 0.11 | 3.33 × 10−4 | 1.021 | |
| O2 | 342.11 | 38.09 | 0.038 | 2.6 × 10−3 | – | 0.88 | 0.64 | – | |
| N2 | 102.16 | 13.52 | 0.026 | 4.8 × 10−3 | – | 0.38 | 0.41 | – | |
| CH4 | 114.33 | – | 0.097 | 0.128 | – | 0.12 | 0.017 | – | |
| H2O | 28.70 | 3.75 × 104 | 0.57 | 0.222 | 7.93 | 5.09 | 0.007 | 0.473 | |
| PEBAX/50KET | H2 | 0.052 | – | 0.00343 | 3.42 × 10−3 | – | 1.5 × 10−4 | 364.3 | |
| CO2 | 852.37 | 167.00 | 0.5182 | 0.6115 | 0.056 | 0.16 | 1.16 × 10−4 | 0.298 | |
| O2 | 694.08 | 13.92 | 0.0428 | 2.6 × 10−3 | – | 1.62 | 2.038 | – | |
| N2 | 214.21 | 6.52 | 0.0300 | 6.8 × 10−3 | – | 0.713 | 1.652 | – | |
| CH4 | 356.58 | – | 0.1146 | 0.1793 | – | 0.31 | 3.33 × 10−3 | – | |
| H2O | 28.00 | 2.033 × 104 | 0.63 | 0.238 | 8.90 | 4.46 | 0.012 | 0.228 | |
| PEBAX/70KET | H2 | 1388.16 | – | 0.00276 | 0.0021 | – | 10.55 | 174.30 | – |
| CO2 | 74.93 | 23.00 | 0.2978 | 0.1878 | 0.039 | 0.025 | 3.3 × 10−5 | 0.059 | |
| O2 | 0.824 | 2.77 | 0.0306 | 0.0034 | – | 2.7 × 10−3 | 0.095 | – | |
| N2 | 0.047 | 1.004 | 0.0198 | 0.0074 | – | 2.3 × 10−4 | 4.5 × 10−3 | – | |
| CH4 | 0.012 | – | 0.0830 | 0.7368 | – | 1.4 × 10−5 | 1.67 × 10−4 | – | |
| H2O | 0.17 | 2455 | 0.57 | 0.294 | 2.29 | 2.97 | 5.00 × 10−4 | 0.107 |
- (1)
- The permeability increases as the additive concentration decreases.
- (2)
- The permeability increases from small non-polar gases to larger and polar ones.
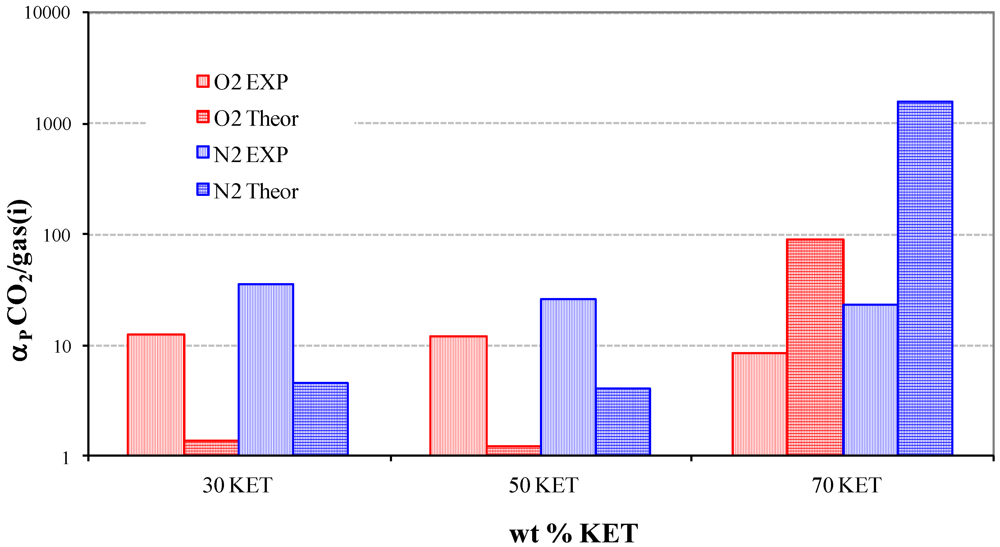
3.3. Solubility coefficients

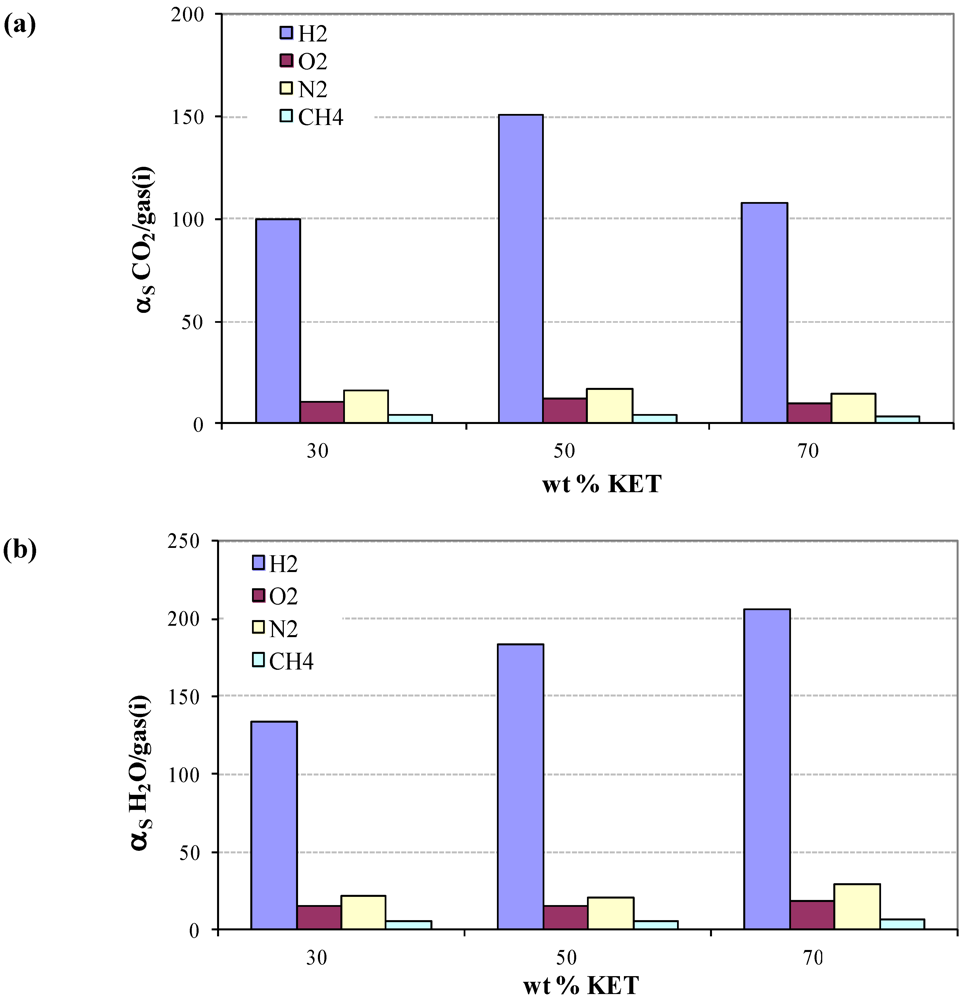
3.4. Diffusivity of Gases and Free Volume in PEBAX/KET Membranes
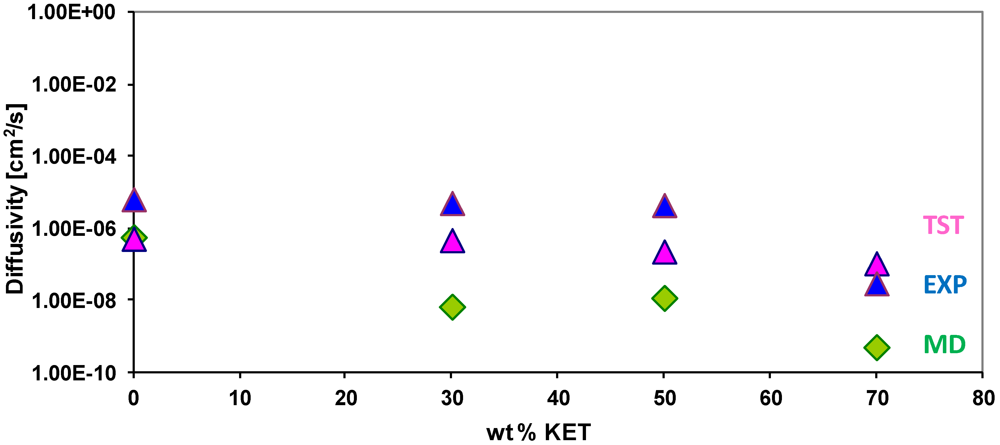
| wt % KET | OV (Ǻ3) | SA (Ǻ2) | FV (Ǻ3) | FFV |
|---|---|---|---|---|
| 30 | 50445 | 11472 | 8873 | 0,149 |
| 50 | 64826 | 14003 | 10972 | 0,144 |
| 70 | 102115 | 17220 | 10875 | 0,096 |
3.5. Structural Analysis: Radial Distribution Functions

4. Conclusions
Acknowledgments
References
- Koros, W.J.; Mahajan, R. Pushing the limits on possibilities for large scale gas separation: Which strategies. J. Membr. Sci. 2000, 175, 181–196. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Stern, S.A. Polymers for gas separations: The next decade. J. Membr. Sci. 1994, 94, 1–65. [Google Scholar] [CrossRef]
- Maier, G. Gas separation with polymer membrane. Angew. Chem. Int.Ed. 1998, 37, 2960–2974. [Google Scholar] [CrossRef]
- Jonquières, A.; Clément, R.; Lochon, P. Permeability of block copolymers to vapors and liquids. Prog. Polym. Sci. 2002, 27, 1803–1877. [Google Scholar] [CrossRef]
- Potreck, J.; Nijmeijer, K.; Kosinski, T.; Wessling, M. Mixed water vapour/gas transport through the rubbery polymer PEBAX-1074. J. Membr. Sci. 2009, 338, 11–16. [Google Scholar] [CrossRef]
- Liu, L.; Chakma, A.; Feng, X. Propylene separation from nitrogen by poly(ether block amide) composite membranes. J. Membr. Sci. 2006, 279, 645–654. [Google Scholar] [CrossRef]
- Cong, H.; Zhang, J.; Radosz, M.; Shen, Y. Carbon nanotube composite membranes of brominated poly(2,6-diphenyl-1,4-phenylene oxide) for gas separation. J. Membr. Sci. 2007, 294, 178–185. [Google Scholar] [CrossRef]
- Gugliuzza, A.; Clarizia, G.; Golemme, G.; Drioli, E. New breathable and waterproof coatings for textiles: Effect of an aliphatic polyurethane on the formation of PEEK-WC porous membranes. Eur. Polym. J. 2002, 8, 235–242. [Google Scholar]
- Gugliuzza, A.; Drioli, E. New performance of a modified poly(amide-12-b-ethyleneoxide). Polymer 2003, 44, 2149–2157. [Google Scholar] [CrossRef]
- Gugliuzza, A.; Drioli, E. Role of modifiers in the water vapor transport through block co-poly(amide/ether) membranes: effects on surface and bulk polymer properties. Eur. Polym. J. 2004, 40, 2381–2389. [Google Scholar] [CrossRef]
- Gugliuzza, A.; Drioli, E. Evaluation of the CO2 permeation through functional assembled monolayers: relationships between structure and transport. Polymer 2005, 46, 9994–10003. [Google Scholar] [CrossRef]
- Gugliuzza, A.; Fabiano, R.; Garavaglia, M.G.; Spisso, A.; Drioli, E. Study of the surface character as responsible for controlling interfacial forces at membrane-feed interface. J. Colloid Interface Sci. 2006, 303, 388–403. [Google Scholar] [CrossRef]
- Gugliuzza, A.; de Luca, G.; Tocci, E.; de Lorenzo, L.; Drioli, E. Intermolecular interactions as controlling factor for water sorption into polymer membranes. J. Phys. Chem. B 2007, 111, 8868–8878. [Google Scholar]
- Tocci, E.; Gugliuzza, A.; de Lorenzo, L.; Macchione, M.; de Luca, G.; Drioli, E. Transport properties of a co-poly(amide-12-b-ethylene oxide) membrane: A comparative study between experimental and molecular modelling results. J. Membr. Sci. 2008, 323, 316–327. [Google Scholar] [CrossRef]
- De Luca, G.; Gugliuzza, A.; Drioli, E. Competitive hydrogen-bonding interactions in modified polymer membranes: A density functional theory investigation. J. Phys. Chem. B 2009, 113, 5473–5477. [Google Scholar]
- De Lorenzo, L.; Tocci, E.; Gugliuzza, A.; Drioli, E. Assembly of nanocomposite PEBAX membranes: A complementary study of affinity and clusterization phenomena. J. Membr. Sci. 2012. submitted for publication. [Google Scholar]
- Hofmann, D.; Entrialgo, M.; Reiche, J.; Kratz, K.; Lendlein, A. Molecular modeling and experimental investigation of hydrolytically degradable polymeric biomaterials. Adv. Sci. Technol. 2010, 76, 16–24. [Google Scholar] [CrossRef]
- Eslami, H.; Müller-Plathe, F. Molecular dynamics simulation of sorption of gases in polystyrene. Macromol. 2007, 40, 6413–6421. [Google Scholar] [CrossRef]
- Heuchel, M.; Hofmann, D.; Pullumbi, P. Molecular modeling of small-molecule permeation in polyimides and its correlation to free-volume. Macromol. 2004, 37, 201–214. [Google Scholar] [CrossRef]
- Pavel, D.; Shanks, R. Molecular dynamics simulation of diffusion of O2 and CO2 in amorphous poly(ethylene terephthalate) and related aromatic polyesters. Polymer 2003, 44, 6713–6724. [Google Scholar] [CrossRef]
- Kucukpinar, E.; Doruker, P. Molecular simulations of gas transport in nitrile rubber and styrene butadiene rubber. Polymer 2006, 47, 7835–7845. [Google Scholar] [CrossRef]
- Meunier, M. Diffusion coefficients of small gas molecules in amorphous cis-1,4-polybutadiene estimated by molecular dynamics simulations. J. Chem. Phys. 2005, 123, 134906:1–13496:7. [Google Scholar]
- Theodorou, D.N.; Suter, U.W. Atomistic modeling of mechanical properties of polymeric glasses. Macromol. 1986, 19, 139–154. [Google Scholar] [CrossRef]
- Theodorou, D.N.; Suter, U.W. Detailed molecular structure of a vinyl polymer glass. Macromol. 1985, 18, 1467–1478. [Google Scholar] [CrossRef]
- Material Studio, version 5.0, Accelrys Inc.: San Diego, CA, USA, 2001.
- Sun, H.; Rigby, D. Polysiloxanes: Ab initio force field and structural, conformational and thermophysical properties. Spectrochim. Acta 1997, 53, 1301–1323. [Google Scholar] [CrossRef]
- Rigby, D.; Sun, H.; Eichinger, B.E. Computer simulations of poly(ethylene oxide): Force field, PVT diagram and cyclization behaviour. Polym. Int. 1997, 44, 311–330. [Google Scholar] [CrossRef]
- Technical Data Pebax® 33 Series; Atofina Chemicals, Inc.: Colombes cedex, France, 2003. Available online: http://www.arkema-inc.com/literature_techpoly.cfm?pag=105 (accessed on 25 June 2012).
- Rezac, M.E.; John, T.; Pfromm, P.H. Effect of copolymer composition on the solubility and diffusivity of water and methanol in a series of polyether amides. J. Appl. Polym. Sci. 1997, 65, 1983–1993. [Google Scholar] [CrossRef]
- Gee, R.H.; Fried, L.E.; Cook, R.C. Structure of chlorotrifluoroethylene/Vinylidene fluoride random copolymers and homopolymers by molecular dynamics simulations. Macromol. 2001, 34, 3050–3059. [Google Scholar] [CrossRef]
- Hofmann, D.; Heuchel, M.; Yampolskii, Yu.; Khotimskii, V.; Shantarovich, V. Free volume distributions in ultrahigh and lower free volume polymers: Comparison between molecular modeling and positron lifetime studies. Macromol. 2002, 35, 2129–2140. [Google Scholar]
- Haile, J.M. Molecular Dynamics Simulation; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Gusev, A.A.; Arizzi, S.; Suter, U.W. Dynamics of light gases in rigid matrices of dense polymers. J. Chem. Phys. 1993, 99, 2221–2227. [Google Scholar] [CrossRef]
- Gusev, A.A.; Arizzi, S.; Suter, U.W. Dynamics of small molecules in dense polymers subject to thermal motion. J. Chem. Phys. 1993, 99, 2228–2234. [Google Scholar] [CrossRef]
- Gsnet & Gsdif Macros, Accelrys Inc.: San Diego, CA, USA, 1999.
- Yampolskii, Y.; Freeman, B.D.; Pinnau, I.; Matteucci, S. Transport of Gases and Vapors in Glassy and Rubbery Polymers. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B.D., Eds.; John Wiley & Sons: New York, NY, USA, 2006; pp. 1–445. [Google Scholar]
- Gusev, A.A.; Müller-Plathe, F.; Van Gunstern, W.F.; Suter, U.W. Dynamics of small molecules in bulk polymers. Adv. Polym. Sci. 1994, 116, 207–247. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Connolly, M.L. Solvent-accessible surfaces of proteins and nucleic acids. Science 1983, 221, 709–713. [Google Scholar]
- Crank, J.; Park, G.S. Diffusion in Polymers; Academic Press: London, UK, 1986. [Google Scholar]
- Rutherford, S.W.; Limmer, D.T.; Smith, M.G.; Honnell, K.G. Gas transport in ethylene-propylene-diene (EPDM) elastomer: Molecular simulation and experimental study. Polymer 2007, 48, 6719–6727. [Google Scholar] [CrossRef]
- Lim, S.Y.; Tsotsis, T.T.; Sahimi, M. Molecular simulation of diffusion and sorption of gases in an amorphous polymer. J. Chem. Phys. 2003, 119, 496–504. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
De Lorenzo, L.; Tocci, E.; Gugliuzza, A.; Drioli, E. Pure and Modified Co-Poly(amide-12-b-ethylene oxide) Membranes for Gas Separation Studied by Molecular Investigations. Membranes 2012, 2, 346-366. https://doi.org/10.3390/membranes2030346
De Lorenzo L, Tocci E, Gugliuzza A, Drioli E. Pure and Modified Co-Poly(amide-12-b-ethylene oxide) Membranes for Gas Separation Studied by Molecular Investigations. Membranes. 2012; 2(3):346-366. https://doi.org/10.3390/membranes2030346
Chicago/Turabian StyleDe Lorenzo, Luana, Elena Tocci, Annarosa Gugliuzza, and Enrico Drioli. 2012. "Pure and Modified Co-Poly(amide-12-b-ethylene oxide) Membranes for Gas Separation Studied by Molecular Investigations" Membranes 2, no. 3: 346-366. https://doi.org/10.3390/membranes2030346
APA StyleDe Lorenzo, L., Tocci, E., Gugliuzza, A., & Drioli, E. (2012). Pure and Modified Co-Poly(amide-12-b-ethylene oxide) Membranes for Gas Separation Studied by Molecular Investigations. Membranes, 2(3), 346-366. https://doi.org/10.3390/membranes2030346