A Program for Solving the Brain Ischemia Problem
Abstract
:“In the medical profession there are three kinds of practitioner:
1. Introduction
Overview of the Present Paper
- To theoretically apply the nonlinear dynamical cell injury model to brain ischemia,
- To serve as a tutorial on the application of pertinent dynamical concepts and methods,
- To do something that, to our knowledge, is unique in the field: to simulate the expected results of experiments beforehand, illustrating the predictive property of a deductive mathematical framework,
- To illustrate application of the equation solutions to neuroprotection.
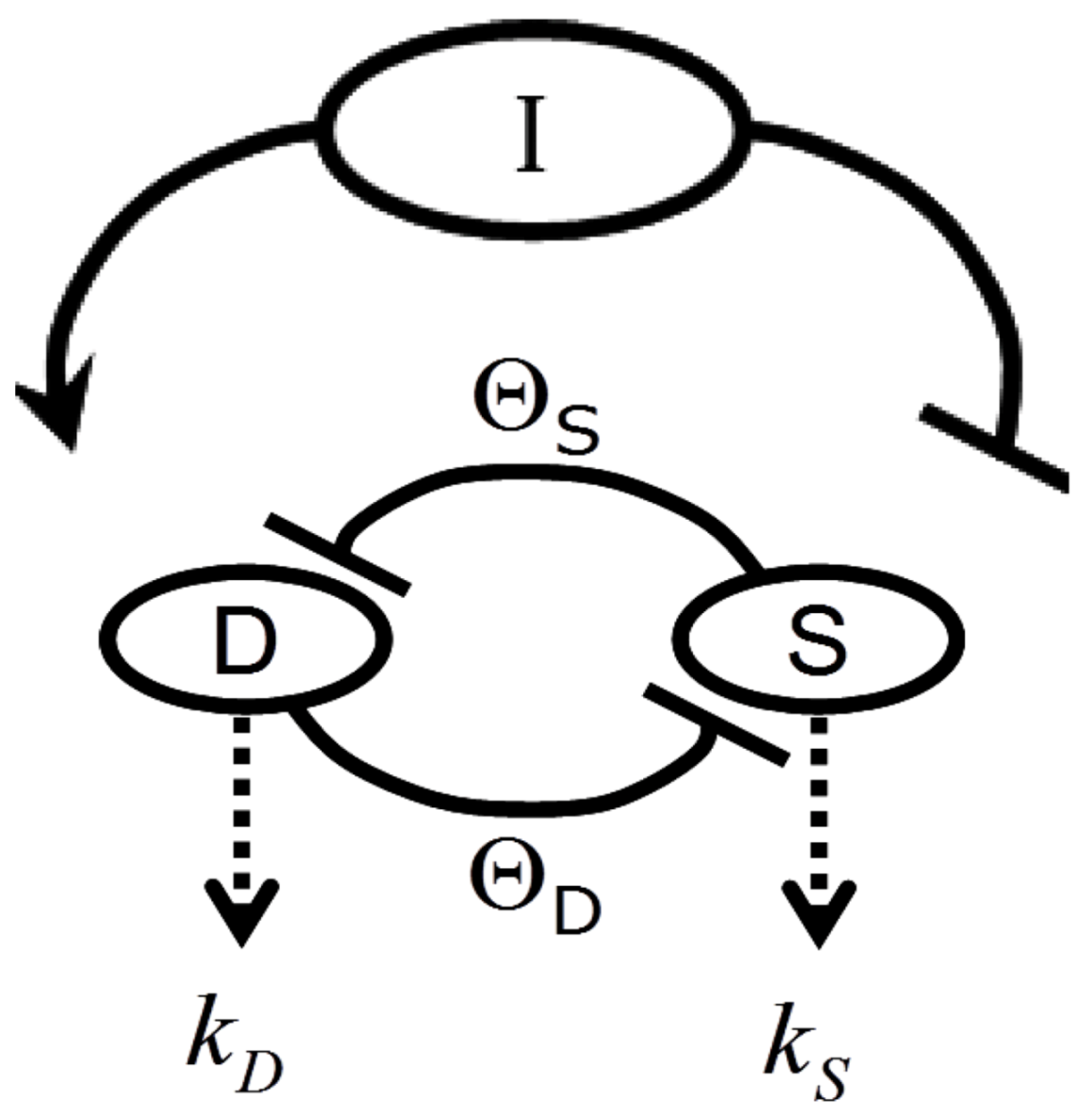
2. The Nonlinear Dynamical Model of Cell Injury Applied to Brain Ischemia
2.1. The Nonlinear Dynamical Model of Cell Injury
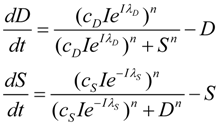
- D is the total amount of damage,
- S is the total induced stress response,
- cD is the toxicity of the damage agent,
- λD is the change in toxicity with injury magnitude,
- I is the injury magnitude,
- cS is the strength of the intrinsic stress response of the given cell type,
- λS is the change in total induced stress responses with injury magnitude,
- n is the Hill coefficient (for convenience we arbitrarily set the n for S and D equal).
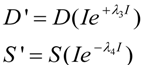
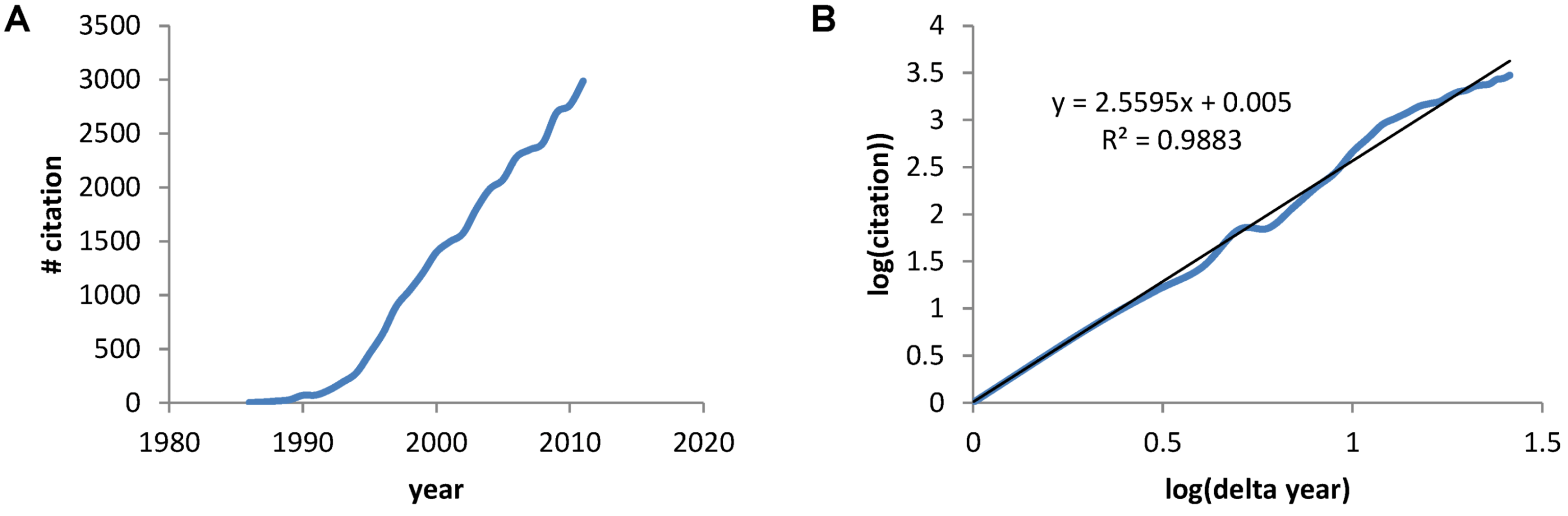
2.2. Exponential Changes and Injury
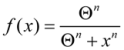
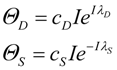
2.3. Threshold Curves
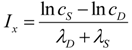
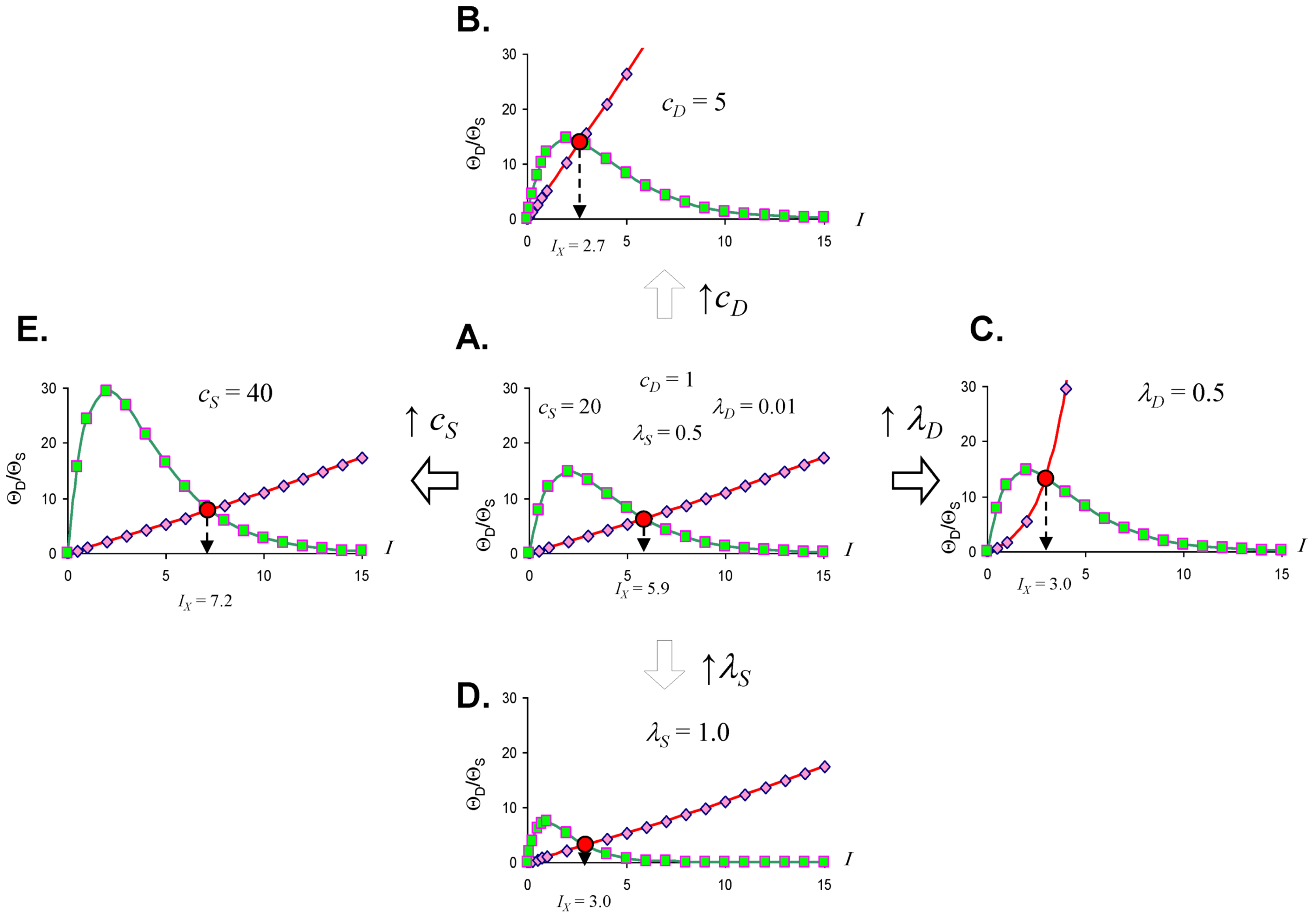
2.4. Quantifying the Toxicity of Ischemia with cD and λD
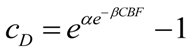
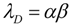
| CBF (%) | cD | D |
|---|---|---|
| 100 | 0 | 0.075 |
| 90 | 0 | 0.075 |
| 80 | 0 | 0.075 |
| 70 | 0 | 0.075 |
| 60 | 0 | 0.075 |
| 50 | 0 | 0.075 |
| 40 | 2.0 × 10−14 | 0.075 |
| 30 | 1.7 × 10−11 | 0.075 |
| 20 | 3.1 × 10−8 | 0.075 |
| 10 | 5.5 × 10−5 | 0.075 |
| 0 | 0.11 | 0.075 |
2.5. The Amount of Ischemia as Injury Magnitude, I
2.6. The Injured Cell as cS and λS

3. Operationalizing the Nonlinear Dynamical Model of Cell Injury
3.1. Preliminary Comments
3.2. Measuring the Model Parameters for Global Ischemia
3.3. Initial Conditions of D and S Time Courses
3.4. How Equation (1) Parameters Relate to the Protocol for D and S Time Course Sampling
- I = the duration of ischemia (e.g., the duration of a specific CBF decrement),
- (cD, λD) = the toxicity of a specific CBF decrement,
- (cS, λS) = the stress response quantifiers of a single cell type,
- n = the Hill coefficient.
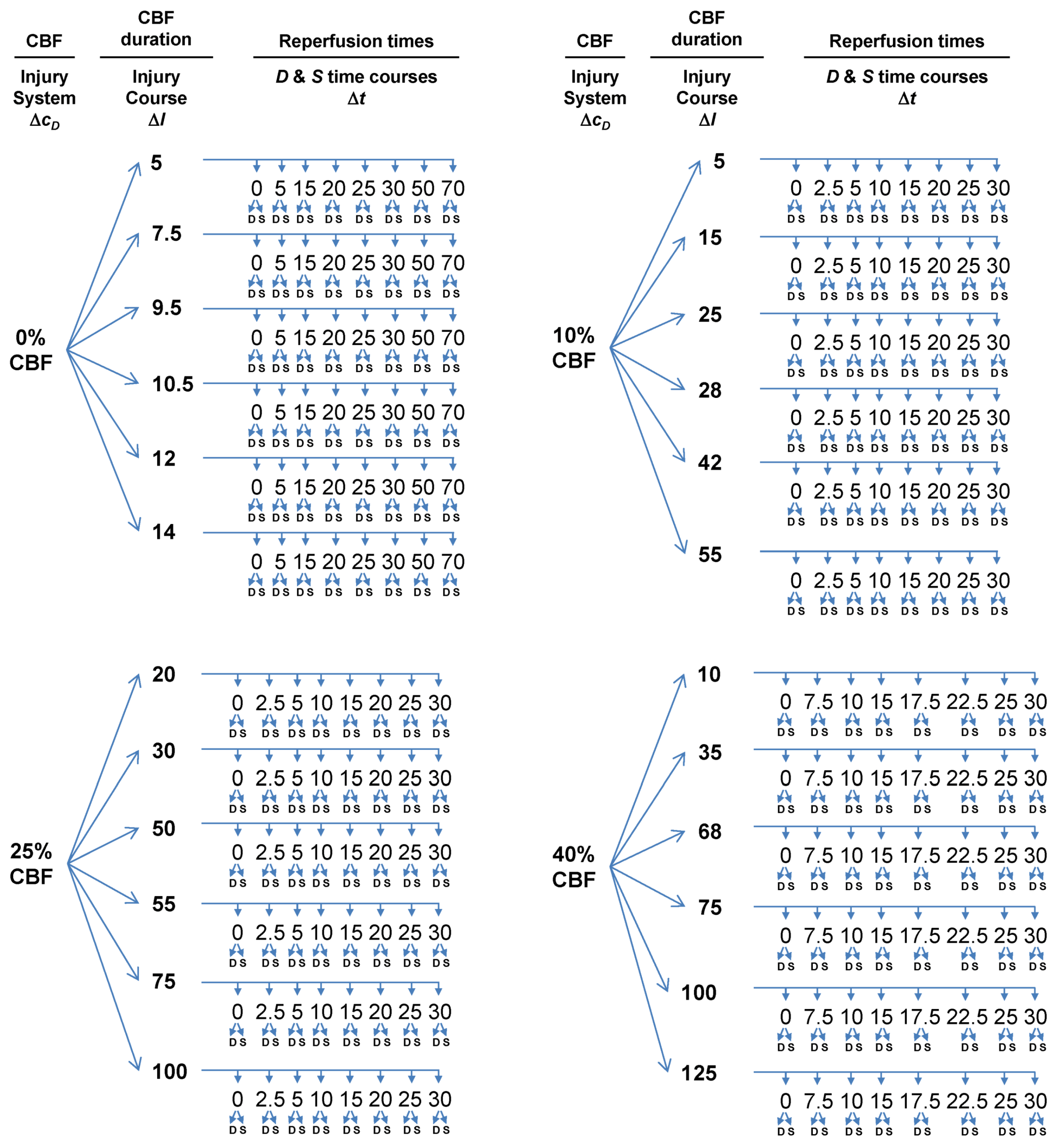
- Choose multiple lethal CBF decrements.
- At each CBF decrement, choose multiple ischemia durations.
- At each ischemia duration choose multiple time points to sample the reperfusion time course.
- At each sampled time point, measure D and S.
3.4.1. Multiple CBF Levels = Injury Systems
3.4.2. Multiple Ischemia Durations = Injury Courses
3.4.3. Reperfusion Time Courses
3.5. The Simulation
| CBF (%) | cD | λD | cS | λS | Ix |
|---|---|---|---|---|---|
| 0 | 0.1052 | 0.075 | 10 | 0.38 | 10.0 |
| 10 | 5.5 × 10−5 | 0.075 | 10 | 0.38 | 26.6 |
| 25 | 7.2 × 10−10 | 0.075 | 10 | 0.38 | 51.3 |
| 40 | 2.2 × 10−14 | 0.075 | 10 | 0.38 | 76.6 |
4. The Simulated Experimental Dataset and Its Analysis
4.1. The Time Series Dataset

4.2. Fixed Point Diagrams
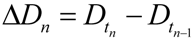

4.3. Parameter Estimation from the Dataset
5. Solving Global Brain Ischemia
| CBF (%) | bistable start | bistable end | bistable I range |
|---|---|---|---|
| 0 | n/a | n/a | 0 |
| 10 | 18.4 | 53.8 | 35.4 |
| 25 | 18.4 | 187.2 | 168.8 |
| 40 | 18.4 | 318.6 | 300.2 |

Master Bifurcation Diagrams

6. Measuring D and S
6.1. General Considerations
6.2. Measuring D
6.3. Measuring S
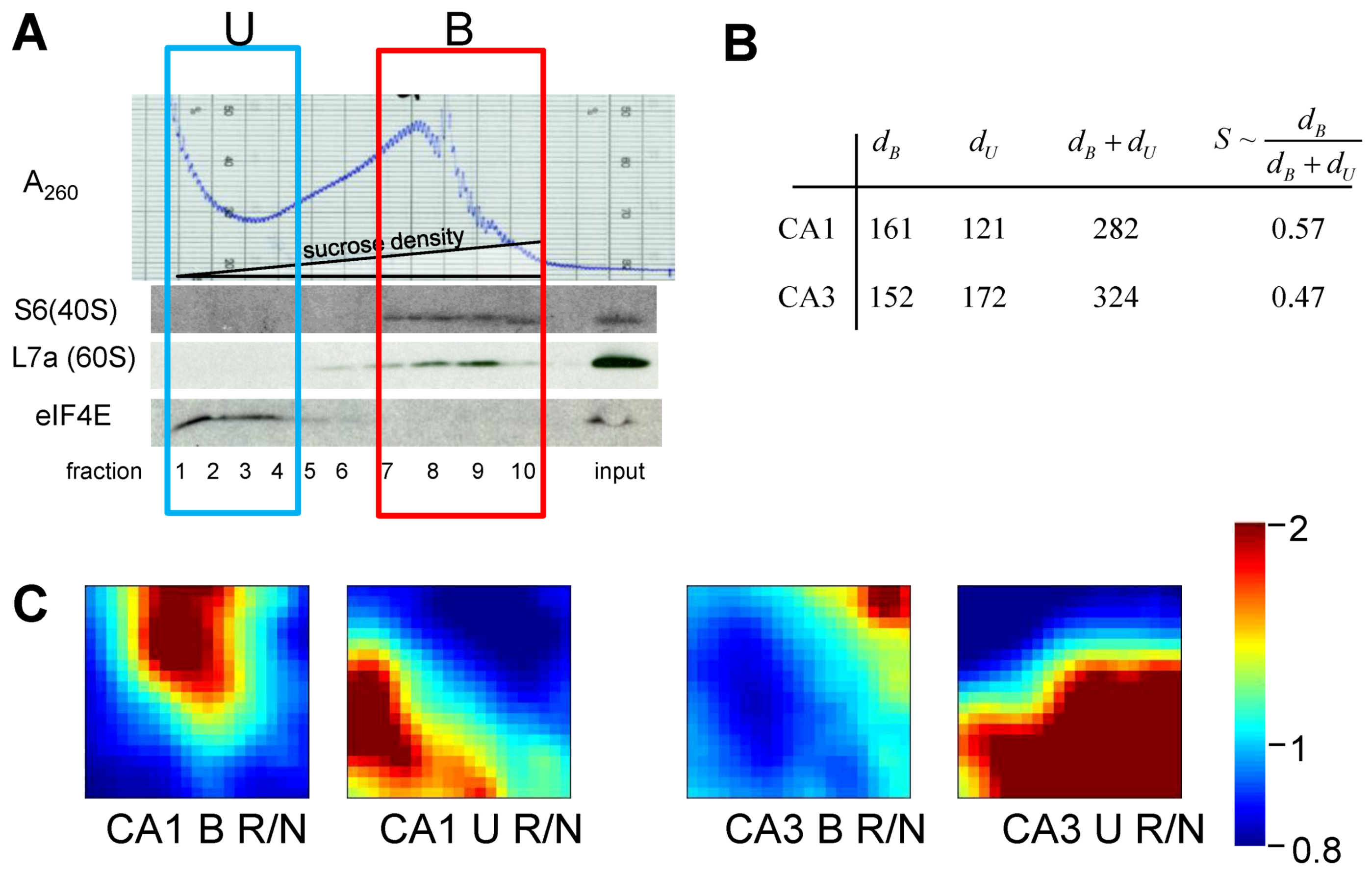
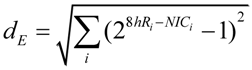
7. The Focal Ischemia Problem
7.1. Other Cell Types in the Brain
7.2. Parameter Values between Global and Focal Ischemia
7.3. Applying Global Ischemia Master Bifurcation Diagrams to Focal Ischemia

7.4. Spatial Considerations for Focal Ischemia
8. Neuroprotection from a Nonlinear Perspective
8.1. Preliminary Thoughts: Neuroprotection Is Technology Not Science
8.2. A Precursor of the Nonlinear Dynamical Model
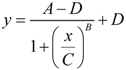
- y = infarct volume,
- x = duration of ischemia,
- A = response at time zero (effectively, a background measurement),
- B = “steepness factor” (effectively, the Hill coefficient),
- C = ischemia duration giving a 50% infarct volume (i.e., a 50% threshold, analogous to that in Equation 6),
- D = maximum infarct volume.

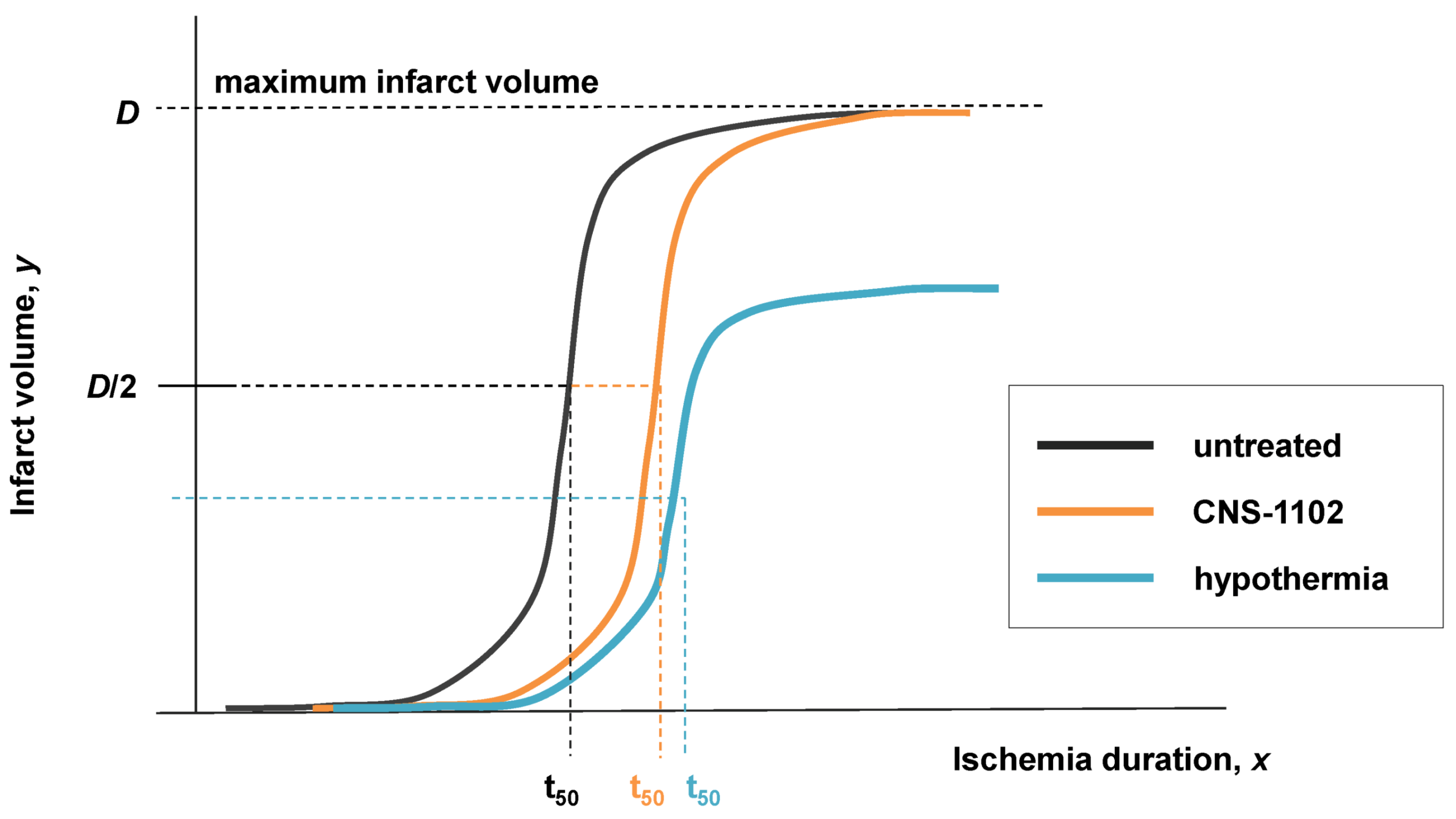
8.3. Neuroprotection and Nonlinear Cell Injury Dynamics
8.4. How to Measure a Presumed Neuroprotectant
8.5. Neuroprotection across an Injury Applies to Global Brain Ischemia
| CBF (%) | Ix | Ib,max | TR |
|---|---|---|---|
| 0 | 10.0 | 10.0 | 0 |
| 10 | 26.6 | 53.8 | 27.2 |
| 25 | 51.3 | 187.2 | 135.9 |
| 40 | 74.2 | 318.6 | 244.4 |
8.5.1. Injury Dynamics
8.5.2. Outcome

8.6. Neuroprotection across Multiple Injury Courses
| 0% CBF | 2.5% CBF | 5% CBF | 10% CBF | 25% CBF | 40% CBF | |
|---|---|---|---|---|---|---|
| IxA − Ix | 0 | 0.8 | 5.5 | 16.5 | 54.6 | 127.5 |
| TR | 0 | 0.8 | 5.5 | 21.4 | 130.7 | 253.4 |
| (IxA − Ix)x/TR % | 0.0% | 100% | 100% | 77% | 43% | 50% |
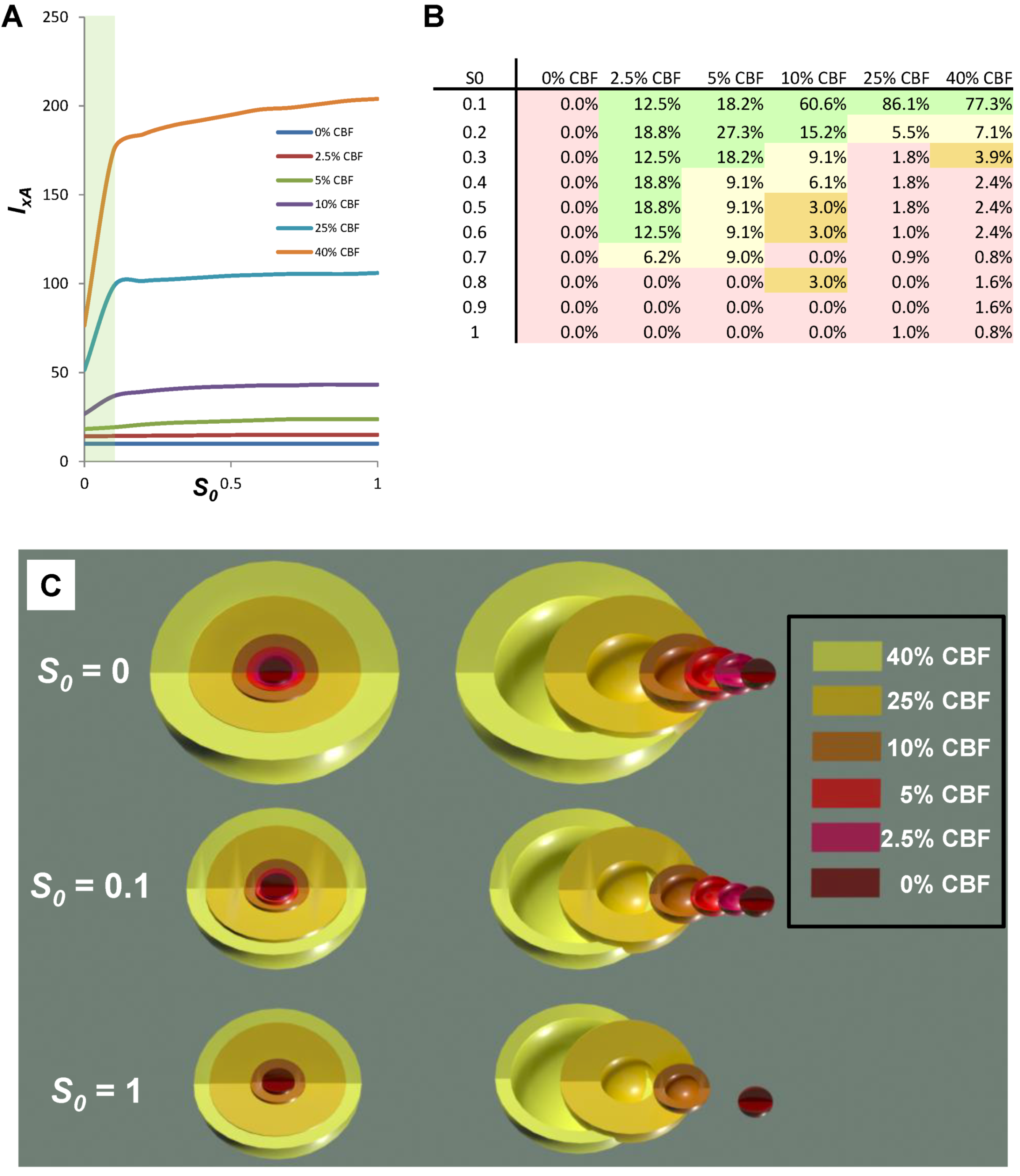
9. Conclusion
9.1. What If Equation (1) Is Wrong?
9.2. Post-Treatments
Acknowledgements
Conflict of Interest
References
- Leibniz, G.W. Note H to Bayle’s article ‘Rorarius’ (1697). In Philosophical Texts; Woolhouse, R., Francks, R., Eds.; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Silverstein, F.S.; Buchanan, K.; Hudson, C.; Johnston, M.V. Flunarizine limits hypoxia-ischemia induced morphologic injury in immature rat brain. Stroke 1986, 17, 477–482. [Google Scholar] [CrossRef]
- Seidl, S.E.; Potashkin, J.A. The promise of neuroprotective agents in Parkinson’s disease. Front. Neurol. 2011, 2, 68. [Google Scholar]
- O’Collins, V.E.; Macleod, M.R.; Donnan, G.A.; Horky, L.L.; van der Worp, B.H.; Howells, D.W. 1,026 experimental treatments in acute stroke. Ann. Neurol. 2006, 59, 467–477. [Google Scholar] [CrossRef]
- Zivin, J.A. Acute stroke therapy with tissue plasminogen activator (tPA) since it was approved by the U.S. Food and Drug Administration (FDA). Ann. Neurol. 2009, 66, 6–10. [Google Scholar] [CrossRef]
- Macleod, M.R.; Petersson, J.; Norrving, B.; Hacke, W.; Dirnagl, U.; Wagner, M.; Schwab, S. European Hypothermia Stroke Research Workshop. Hypothermia for Stroke: Call to action 2010. Int. J. Stroke 2010, 5, 489–492. [Google Scholar] [CrossRef]
- Cheng, Y.D.; Al-Khoury, L.; Zivin, J.A. Neuroprotection for ischemic stroke: Two decades of success and failure. NeuroRx 2004, 1, 36–45. [Google Scholar] [CrossRef]
- Van der Worp, H.B.; de Haan, P.; Morrema, E.; Kalkman, C.J. Methodological quality of animal studies on neuroprotection in focal cerebral ischaemia. J. Neurol. 2005, 252, 1108–1114. [Google Scholar] [CrossRef]
- Savitz, S.I.; Fisher, M. Future of neuroprotection for acute stroke: In the aftermath of the SAINT trials. Ann. Neurol. 2007, 61, 396–402. [Google Scholar]
- O’Collins, V.E.; Macleod, M.R.; Cox, S.F.; van Raay, L.; Aleksoska, E.; Donnan, G.A.; Howells, D.W. Preclinical drug evaluation for combination therapy in acute stroke using systematic review, meta-analysis, and subsequent experimental testing. J. Cereb. Blood Flow Metab. 2011, 31, 962–975. [Google Scholar] [CrossRef]
- Macrae, I.M. Preclinical stroke research—advantages and disadvantages of the most common rodent models of focal ischaemia. Br. J. Pharmacol. 2011, 164, 1062–1078. [Google Scholar] [CrossRef]
- DeGracia, D.J.; Huang, Z.F.; Huang, S. A nonlinear dynamical theory of cell injury. J. Cereb. Blood Flow Metab. 2012, 32, 1000–1013. [Google Scholar] [CrossRef]
- DeGracia, D.J. Towards a dynamical network view of brain ischemia and reperfusion. Part I: Background and preliminaries. J. Exp. Stroke Transl. Med. 2010, 3, 59–71. [Google Scholar] [CrossRef]
- DeGracia, D.J. Towards a dynamical network view of brain ischemia and reperfusion. Part II: A post-ischemic neuronal state space. J. Exp. Stroke Transl. Med. 2010, 3, 72–89. [Google Scholar] [CrossRef]
- DeGracia, D.J. Towards a dynamical network view of brain ischemia and reperfusion. Part III: Therapeutic implications. J. Exp. Stroke Transl. Med. 2010, 3, 90–103. [Google Scholar] [CrossRef]
- DeGracia, D.J. Towards a dynamical network view of brain ischemia and reperfusion. Part IV: Additional considerations. J. Exp. Stroke Transl. Med. 2010, 3, 104–114. [Google Scholar] [CrossRef]
- Hossmann, K.A. Pathophysiological basis of translational stroke research. Folia Neuropathol. 2009, 47, 213–227. [Google Scholar]
- Hossmann, K.A. Viability thresholds and the penumbra of focal ischemia. Ann. Neurol. 1994, 36, 557–565. [Google Scholar]
- Symon, L.; Lassen, N.A.; Astrup, J.; Branston, N.M. Thresholds of ischaemia in brain cortex. Adv. Exp. Med. Biol. 1977, 94, 775–782. [Google Scholar]
- Kaplan, B.; Brint, S.; Tanabe, J.; Jacewicz, M.; Wang, X.J.; Pulsinelli, W. Temporal thresholds for neocortical infarction in rats subjected to reversible focal cerebral ischemia. Stroke 1991, 22, 1032–1039. [Google Scholar] [CrossRef]
- Heiss, W.D. Experimental evidence of ischemic thresholds and functional recovery. Stroke 1992, 23, 1668–1672. [Google Scholar] [CrossRef]
- Heiss, W.D. Flow thresholds of functional and morphological damage of brain tissue. Stroke 1983, 14, 329–331. [Google Scholar]
- Rossolini, G.; Piantanelli, L. Mathematical modeling of the aging processes and the mechanisms of mortality: Paramount role of heterogeneity. Exp. Gerontol. 2001, 36, 1277–1288. [Google Scholar] [CrossRef]
- Kirino, T. Delayed neuronal death. Neuropathology 2000, 20, S95–S97. [Google Scholar] [CrossRef]
- Bodine-Fowler, S. Skeletal muscle regeneration after injury: An overview. J. Voice 1994, 8, 53–62. [Google Scholar]
- Hertz, L.; Dienel, G.A. Energy metabolism in the brain. Int. Rev. Neurobiol. 2002, 51, 1–102. [Google Scholar]
- Mainzer, K. Thinking in Complexity: The Computational Dynamics of Matter, Mind, and Mankind, 5th ed; Springer: Berlin, Germany, 2007. [Google Scholar]
- Glass, L.; Kaplan, D. Time series analysis of complex dynamics in physiology and medicine. Med. Prog. Technol. 1993, 19, 115–128. [Google Scholar]
- Gourévitch, B.; Bouquin-Jeannès, R.L.; Faucon, G. Linear and nonlinear causality between signals: Methods, examples and neurophysiological applications. Biol. Cybern. 2006, 95, 349–369. [Google Scholar]
- Kaplan, D.; Glass, L. Understanding Nonlinear Dynamics; Springer: New York, NY, USA, 1995. [Google Scholar]
- Pereda, E.; Quiroga, R.Q.; Bhattacharya, J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 2005, 77, 1–37. [Google Scholar] [CrossRef]
- Chou, I.C.; Voit, E.O. Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 2009, 219, 57–83. [Google Scholar]
- Smith, M.L.; Bendek, G.; Dahlgren, N.; Rosen, I.; Wieloch, T.; Siesjo, B.K. Models for studying long-term recovery following forebrain ischemia in the rat. 2. A 2-vessel occlusion model. Acta Neurol. Scand. 1984, 69, 385–401. [Google Scholar]
- Levenberg, K. A Method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Hu, B. Personal communication. University of Maryland: Baltimore, MD, USA, 2012. [Google Scholar]
- Dienel, G. Personal communication. University of Arkansas: Little Rock, AR, USA, 2012. [Google Scholar]
- VanGilder, R.L.; Huber, J.D.; Rosen, C.L.; Barr, T.L. The transcriptome of cerebral ischemia. Brain Res. Bull. 2012, 88, 313–319. [Google Scholar] [CrossRef]
- Mehra, A.; Lee, K.H.; Hatzimanikatis, V. Insights into the relation between mRNA and protein expression patterns: I. Theoretical considerations. Biotechnol. Bioeng. 2003, 84, 822–833. [Google Scholar] [CrossRef]
- Sonenberg, N.; Hershey, J.W.B.; Mathews, M.B. Translational Control of Gene Expression; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2000. [Google Scholar]
- Eichler, G.S.; Huang, S.; Ingber, D.E. Gene Expression Dynamics Inspector (GEDI): For integrative analysis of expression profiles. Bioinformatics 2003, 19, 2321–2322. [Google Scholar] [CrossRef]
- DeGracia, D.J.; Jamison, J.T.; Szymanski, J.J.; Lewis, M.K. Translation arrest and ribonomics in post-ischemic brain: Layers and layers of players. J. Neurochem. 2008, 106, 2288–2301. [Google Scholar] [CrossRef]
- Huang, S.; Guo, Y.P.; May, G.; Enver, T. Bifurcation dynamics in lineage-commitment in bipotent progenitor cells. Dev. Biol. 2007, 305, 695–713. [Google Scholar] [CrossRef]
- Nedergaard, M.; Dirnagl, U. Role of glial cells in cerebral ischemia. Glia 2005, 50, 281–286. [Google Scholar]
- Del Zoppo, G.J. Virchow’s triad: The vascular basis of cerebral injury. Rev. Neurol. Dis. 2008, 5 (Suppl. 1), S12–S21. [Google Scholar]
- Lipton, S.A. Similarity of neuronal cell injury and death in AIDS dementia and focal cerebral ischemia: Potential treatment with NMDA open-channel blockers and nitric oxide-related species. Brain Pathol. 1996, 6, 507–517. [Google Scholar]
- Baron, J.C. How healthy is the acutely reperfused ischemic penumbra? Cerebrovasc. Dis. 2005, 20 (Suppl. 2), 25–31. [Google Scholar] [CrossRef]
- Hossmann, K.A. Cerebral ischemia: Models, methods and outcomes. Neuropharmacology 2008, 55, 257–270. [Google Scholar] [CrossRef]
- Sommer, C. Neuronal plasticity after ischemic preconditioning and TIA-like preconditioning ischemic periods. Acta Neuropathol. 2009, 117, 511–523. [Google Scholar]
- Hadjiev, D.I.; Mineva, P.P. Transient ischemic attack may present a target for normobaric hyperoxia treatment. Med. Hypotheses 2010, 75, 128–130. [Google Scholar] [CrossRef]
- Powers, W.J.; Zazulia, A.R. The use of positron emission tomography in cerebrovascular disease. Neuroimaging Clin. N. Am. 2003, 13, 741–758. [Google Scholar]
- Carey, L.M.; Seitz, R.J. Functional neuroimaging in stroke recovery and neurorehabilitation: Conceptual issues and perspectives. Int. J. Stroke 2007, 2, 245–264. [Google Scholar] [CrossRef]
- Kitagawa, K. Ischemic tolerance in the brain: Endogenous adaptive machinery against ischemic stress. J. Neurosci. Res. 2012, 90, 1043–1054. [Google Scholar] [CrossRef]
- Aronowski, J.; Ostrow, P.; Samways, E.; Strong, R.; Zivin, J.A.; Grotta, J.C. Graded bioassay for demonstration of brain rescue from experimental acute ischemia in rats. Stroke 1994, 25, 2235–2240. [Google Scholar] [CrossRef]
- Motulsky, H.J.; Ransnas, L.A. Fitting curves to data using nonlinear regression: A practical and nonmathematical review. FASEB J. 1987, 1, 365–374. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
DeGracia, D.J. A Program for Solving the Brain Ischemia Problem. Brain Sci. 2013, 3, 460-503. https://doi.org/10.3390/brainsci3020460
DeGracia DJ. A Program for Solving the Brain Ischemia Problem. Brain Sciences. 2013; 3(2):460-503. https://doi.org/10.3390/brainsci3020460
Chicago/Turabian StyleDeGracia, Donald J. 2013. "A Program for Solving the Brain Ischemia Problem" Brain Sciences 3, no. 2: 460-503. https://doi.org/10.3390/brainsci3020460




