An Experimental Study of the Leakage Mechanism in Static Seals
Abstract
:1. Introduction
2. Review the Leak Rate Prediction Model
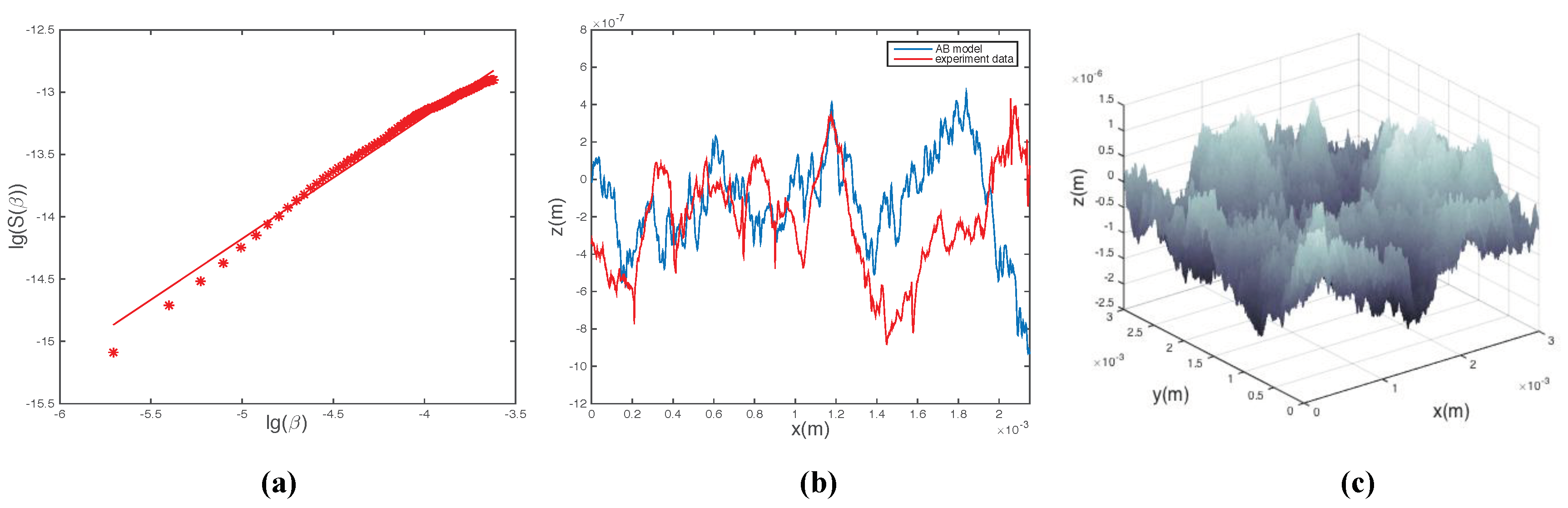
2.1. Fractal Surface
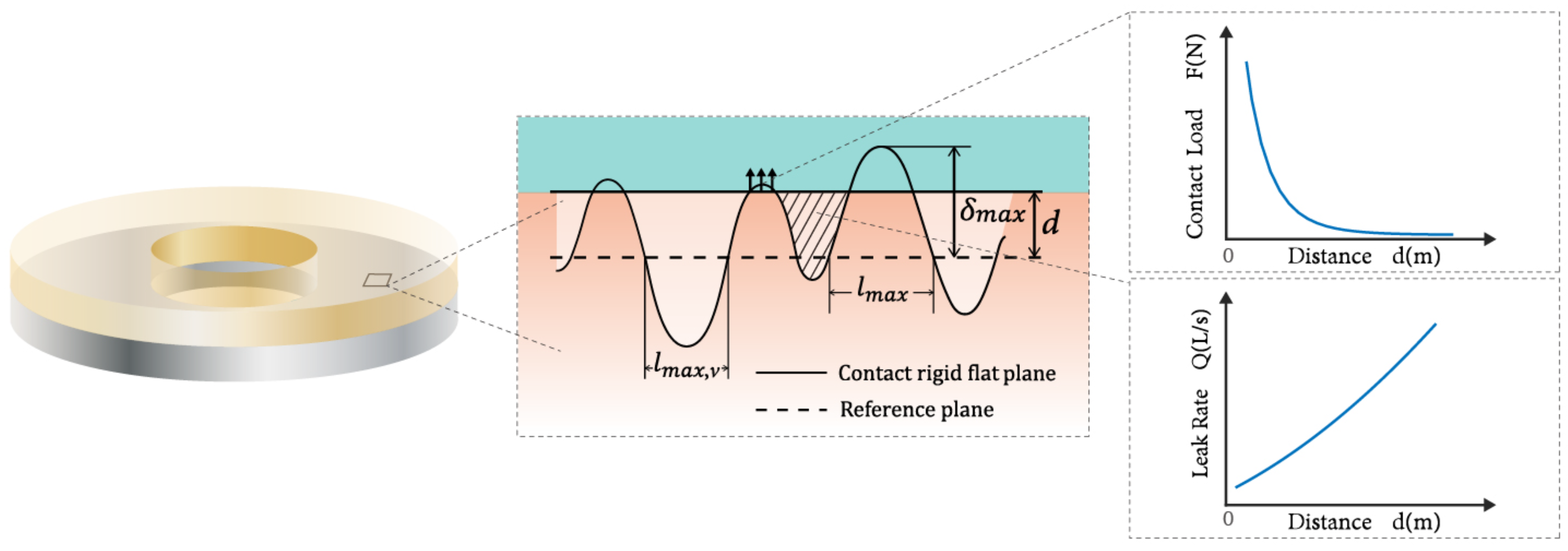
2.2. Contact Process
2.3. Leakage Process
3. Experimental Design for Sealing Surface Leak-Rate Measurement
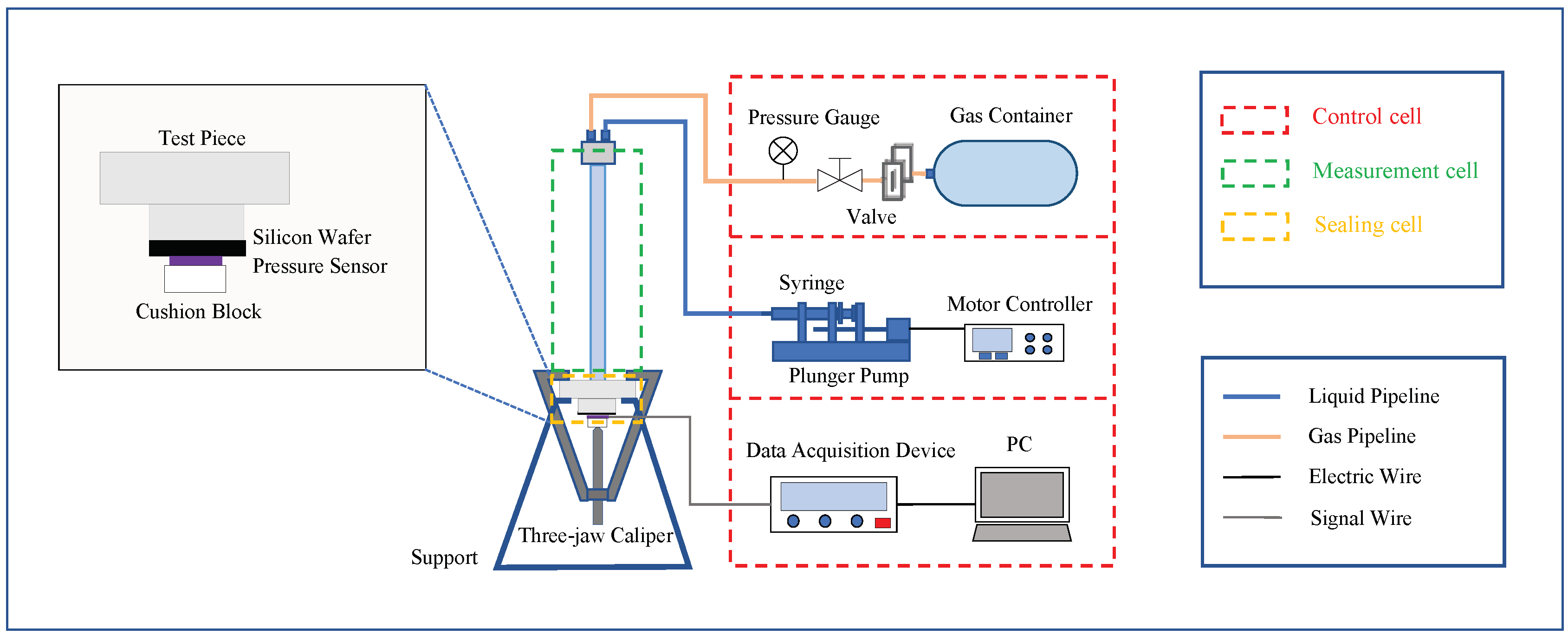
3.1. Experimental Devices
3.2. Experimental Samples
3.3. Experimental Implementation
3.3.1. Effect of Sealing Surface Characteristics on Leak Rate
3.3.2. Effect of Sealing Device Working Conditions on Leak Rate
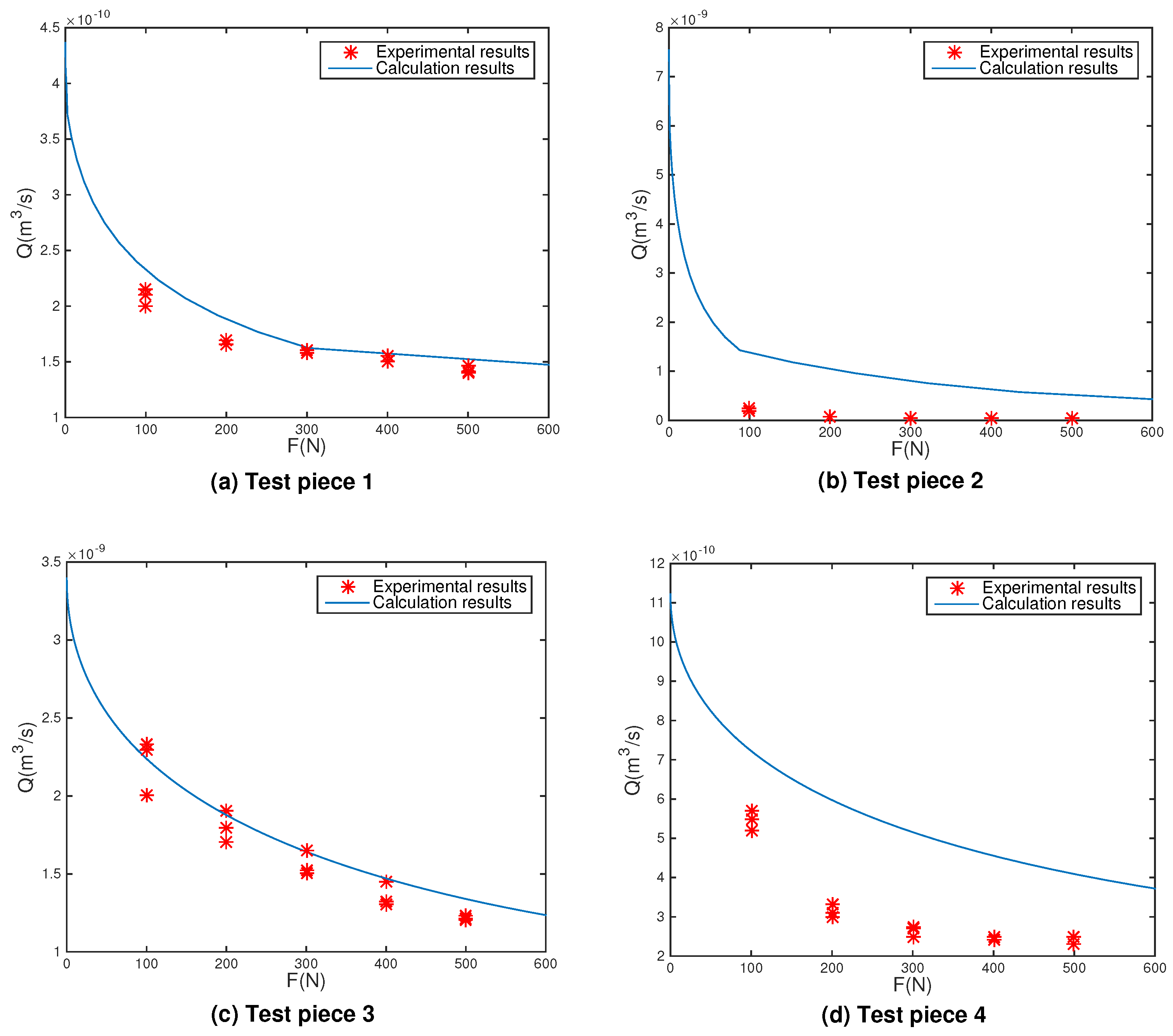
4. Results and Analysis
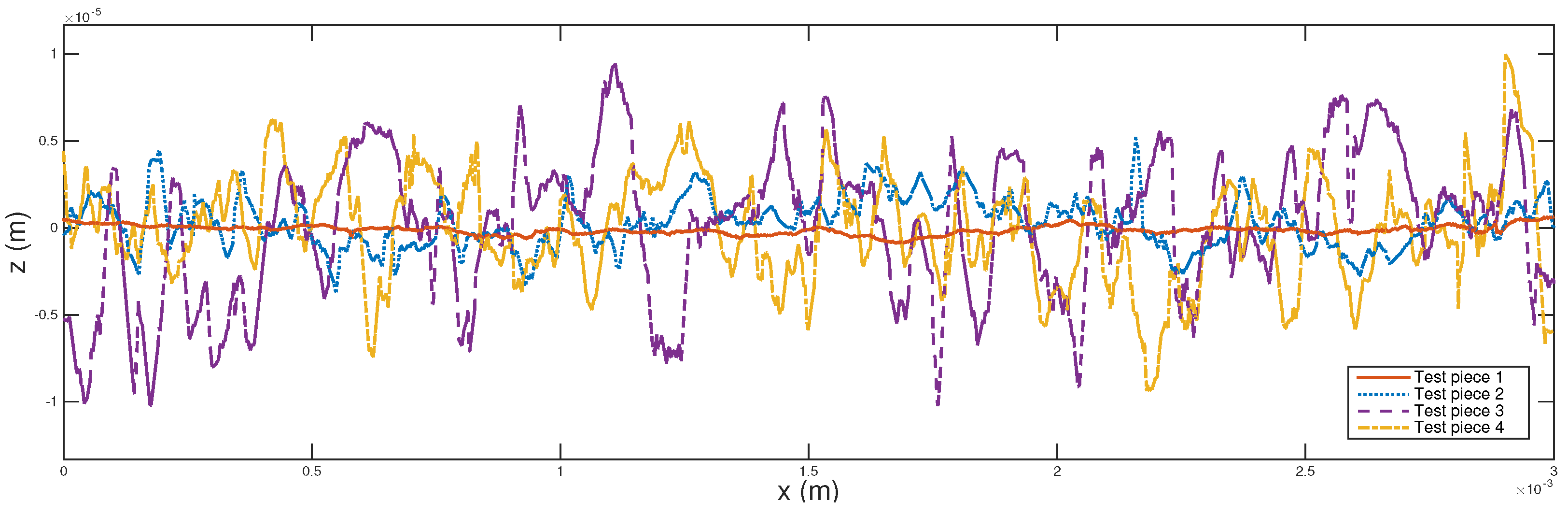
4.1. Effect of Surface Characteristics on Leak Rate
4.2. Effect of Sealing Device Parameters on Leak Rate
4.2.1. Effect of Sealing Surface Contact Load on Leak Rate
4.2.2. Effect of Fluid Pressure on Leak Rate
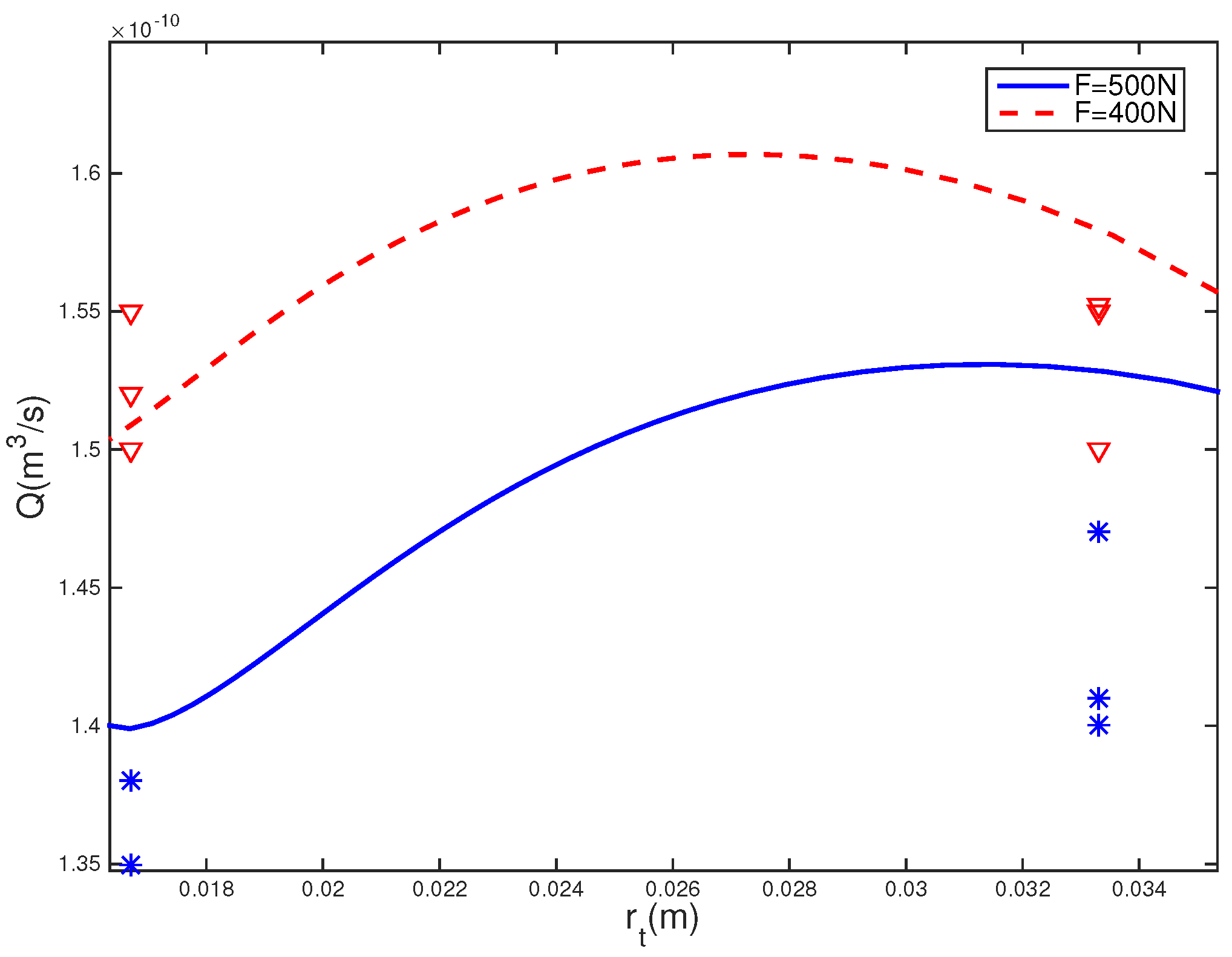
4.2.3. Effect of Size on Leak Rate
5. Conclusions
- Surface topography plays a decisive role in the order of magnitude of leak rate, which means that the roughness and the leak rate are positively correlated, i.e., the rougher the surface (the larger the fractal dimension), the larger the leak rate.
- The contact load and the leak rate are negatively correlated. In the case of a high contact load (depending on the surface characteristics), its impact on the leak rate is negligible.
- The smaller the leak rate, the smaller the effect of fluid pressure on sealing performance.
- When the requirements for the processing technology and structure are satisfied, in the case of the contact load is constant, the smaller the apparent contact area of the sealing device, the better the sealing performance.
Author Contributions
Funding
Conflicts of Interest
References
- Goryacheva, I. Contact Mechanics in Tribology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Rodriguez, P.; Markovitch, R. Space Station Freedom Seal Leakage Rate Analysis and Testing Summary: Air Leaks in Ambient Versus Vacuum Exit Conditions; NASA Marshall Space Flight Center: Huntsville, AL, USA, 1992. Available online: https://ntrs.nasa.gov/search.jsp?R=19930002961 (accessed on 18 July 2018).
- Liu, Y.; Wang, J.; Wang, W. Strain Behaviors of Seal Cone in Connection Pipeline for the Ultrahigh Pressure easurement. Equip. Manuf. Technol. 2015, 5, 4–6. [Google Scholar]
- Greenwood, J.; Williamson, J. Contact of nominally flat surfaces. Proc. R. Soc. A 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Greenwood, J.; Tripp, J. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Greenwood, J. A simplified elliptic model of rough surface contact. Wear 2006, 261, 191–200. [Google Scholar] [CrossRef]
- Berry, M.; Lewis, Z. On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. A 1980, 370, 459–484. [Google Scholar] [CrossRef]
- Jana, T.; Mitra, A.; Sahoo, P. Dynamic contact interactions of fractal surfaces. Appl. Surf. Sci. 2016, 392, 872–882. [Google Scholar] [CrossRef]
- Heinze, E. Besonderer BerÜcksichti- dung ihrer Verwendung im Kältema schinenbau. Kältetechnik 1949, 1, 26–32. [Google Scholar]
- Mayer, E. Mechanical Seals; Newnes Butterworth: London, UK, 1997. [Google Scholar]
- Lebeck, A.O. Hydrodynamic lubrication in wavy contacting face seals—A two dimensional model. J. Lubr. Technol. 1981, 103, 578–586. [Google Scholar] [CrossRef]
- Lebeck, A.O. Contacting mechanical seal design using a simple hydrostatic mode. Tribol. Int. 1988, 21, 2–14. [Google Scholar] [CrossRef]
- Persson, B.; Albohr, O.; Creton, C. Contact area between a viscoelastic solid and a hard, randomly rough, substrate. J. Chem. Phys. 2004, 120, 8779–9793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Persson, B.N.; Yang, C. Theory of the leak-rate of seals. J. Phys. Condens. Matter 2008, 20, 315011. [Google Scholar] [CrossRef]
- Campañá, C.; Persson, B.; Müser, M. Transverse and normal interfacial stiffness of solids with randomly rough surfaces. J. Phys. Condens. Matter 2011, 23, 085001. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, B.; Persson, B.N. Leak rate of seals: Comparison of theory with experiment. Europhys. Lett. 2009, 86, 44006. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A.; Bushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, X.; Huang, Y.; Chen, Y. Fractal modeling of fluidic leakage through metal sealing surfaces. AIP Adv. 2018, 8, 045310. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Sanada, M.; Komiya, M.; Tanoue, H.; Hirabayashi, H. Fundamental Study of the Sealing Performance of a C-Shaped Metal Seal. In Proceedings of the 2nd Inter-national Symposium on Fluid Sealing, Nashville, TN, USA, 17–21 June 1990; pp. 18–20. [Google Scholar]
- Yanagisawa, T.; Sanada, M.; Koga, T.; Hirabayashi, H. The Influence of Designing Factors on the Sealing Performance of C-Seal. SAE Trans. 1991, 27, 178–182. [Google Scholar]
- Matsuzaki, Y.; Kazamaki, T. Effect of Surface Roughness on Com-pressive Stress of Static Seals. JSME Int. J. 1988, 3, 99–106. [Google Scholar]
- Matsuzaki, Y.; Hosokawa, K.; Funabashi, K. Effect of Surface Roughness on Contact Pressure of Static Seals. JSME Int. J. 1992, 3, 470–476. [Google Scholar]
- Marie, C.; Lasseux, D. Experimental Leak-Rate Measurement Through a Static Metal Seal. J. Fluid. Eng. 2007, 5, 799–805. [Google Scholar] [CrossRef]
- Ausloos, M.; Berman, D. A Multivariate Weierstrass-Mandelbrot Function. Proc. Roy. Soc. 1985, 400, 331–350. [Google Scholar] [CrossRef]
- Yan, W.; Komvopoulos, K. Contact analysis of elastic-plastic fractal surfaces. J. Appl. Phys. 1998, 84, 3617–3624. [Google Scholar] [CrossRef]
- Li, J.; Tang, Y.; Li, Z.; Ding, X.; Li, Z. Study on the optical performance of thin-film light-emitting diodes using fractal micro-roughness surface model. Appl. Surf. Sci. 2017, 410, 60–69. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. Some Fractal Characters of Porous Media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A Fractal Permeability Model for Bi-Dispersed Porous Media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, J.; Yang, B.; Yu, B. A fractal model for gaseous leak rates through contact surfaces under non-isothermal condition. Appl. Therm. Eng. 2013, 52, 54–61. [Google Scholar] [CrossRef]
- Yu, B. Fractal Porous Media Transport Physics; Science Press: Beijing, China, 2014. [Google Scholar]



| Material | No. 2 | Material Parameters | Measurement Parameters of Surface Topography | |||||
|---|---|---|---|---|---|---|---|---|
| Elastic Modulus | Poisson’s Ratio | Hardness | Process | D | G | Ra | ||
| Mold steel skd11 | 1 | 210 GPa | 0.3 | 850 MPa | Forging | 1.51 | 6.59 × 10 | 0.3 |
| PTFE | 2 | 1.42 GPa | 0.4 | 4.54 MPa | Turning | 1.46 | 8.28 × 10 | 1.3 |
| Stainless steel | 3 | 195 GPa | 0.3 | 187 MPa | EDM | 1.35 | 1.87 × 10 | 3.7 |
| Stainless steel | 4 | 195 GPa | 0.3 | 187 MPa | Fine | X: 1.42 Y: 1.47 | X: 2.98 × 10 Y: 3.81 × 10 | 2.5 |
| Test Piece | Contact Load (N) | Gas Pressure (MPa) | Silicon Wafer Diameter (mm) |
|---|---|---|---|
| Test piece No. 1 | 100, 200, 300, 400, 500 | 0.1, 0.2, 0.3 | 33.3, 66.7 |
| Test piece No. 2 | 0.1 | 66.7 | |
| Test piece No. 3 | 0 | ||
| Test piece No. 4 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Chen, X.; Huang, Y.; Zhang, X. An Experimental Study of the Leakage Mechanism in Static Seals. Appl. Sci. 2018, 8, 1404. https://doi.org/10.3390/app8081404
Zhang Q, Chen X, Huang Y, Zhang X. An Experimental Study of the Leakage Mechanism in Static Seals. Applied Sciences. 2018; 8(8):1404. https://doi.org/10.3390/app8081404
Chicago/Turabian StyleZhang, Qiang, Xiaoqian Chen, Yiyong Huang, and Xiang Zhang. 2018. "An Experimental Study of the Leakage Mechanism in Static Seals" Applied Sciences 8, no. 8: 1404. https://doi.org/10.3390/app8081404




