A Study on Stability Control of Grid Connected DC Distribution System Based on Second Order Generalized Integrator-Frequency Locked Loop (SOGI-FLL)
Abstract
:1. Introduction
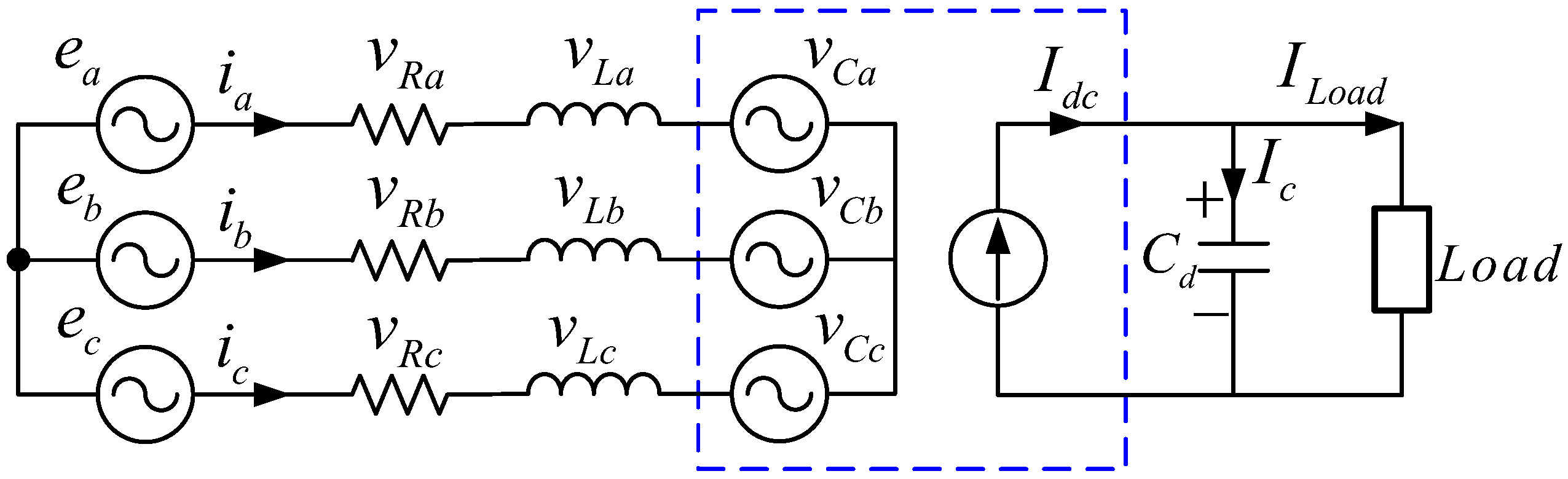
2. 3-Phase AC/DC PWM Converter Used in DC Distribution System
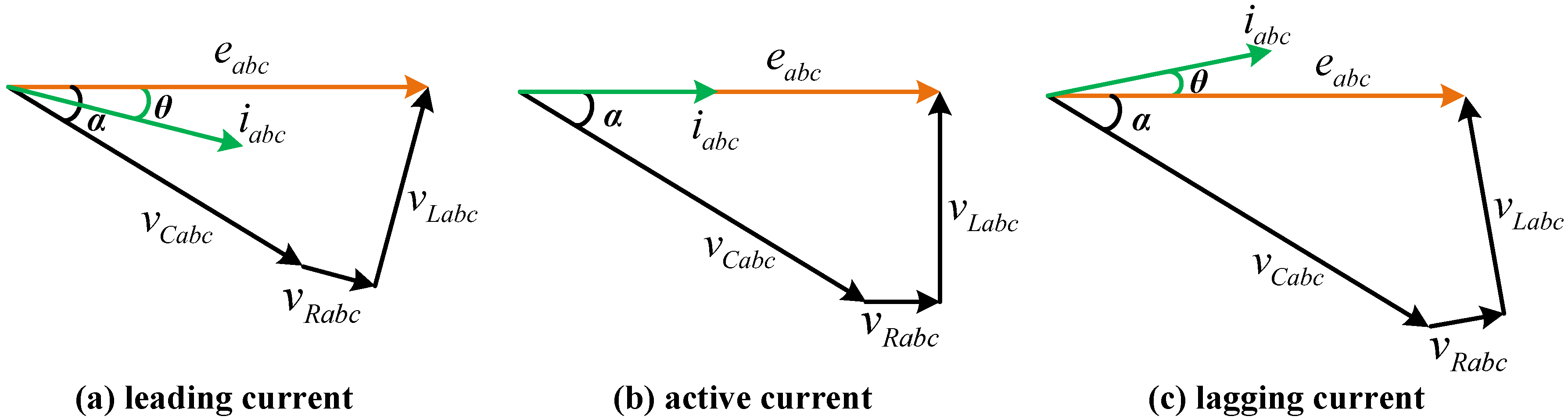
2.1. 3-Phase AC/DC PWM Converter [12,13,14]
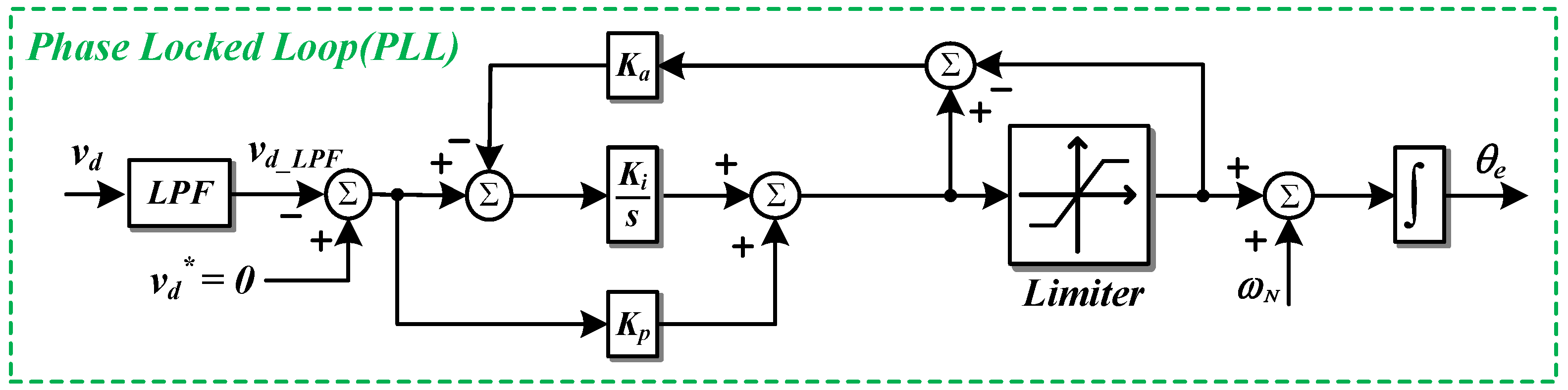
2.2. Positive Sequence Voltage and Phase Detector [15,16]
3. Proposed Control Scheme of 3-Phase AC/DC PWM Converter Using SOGI-FLL
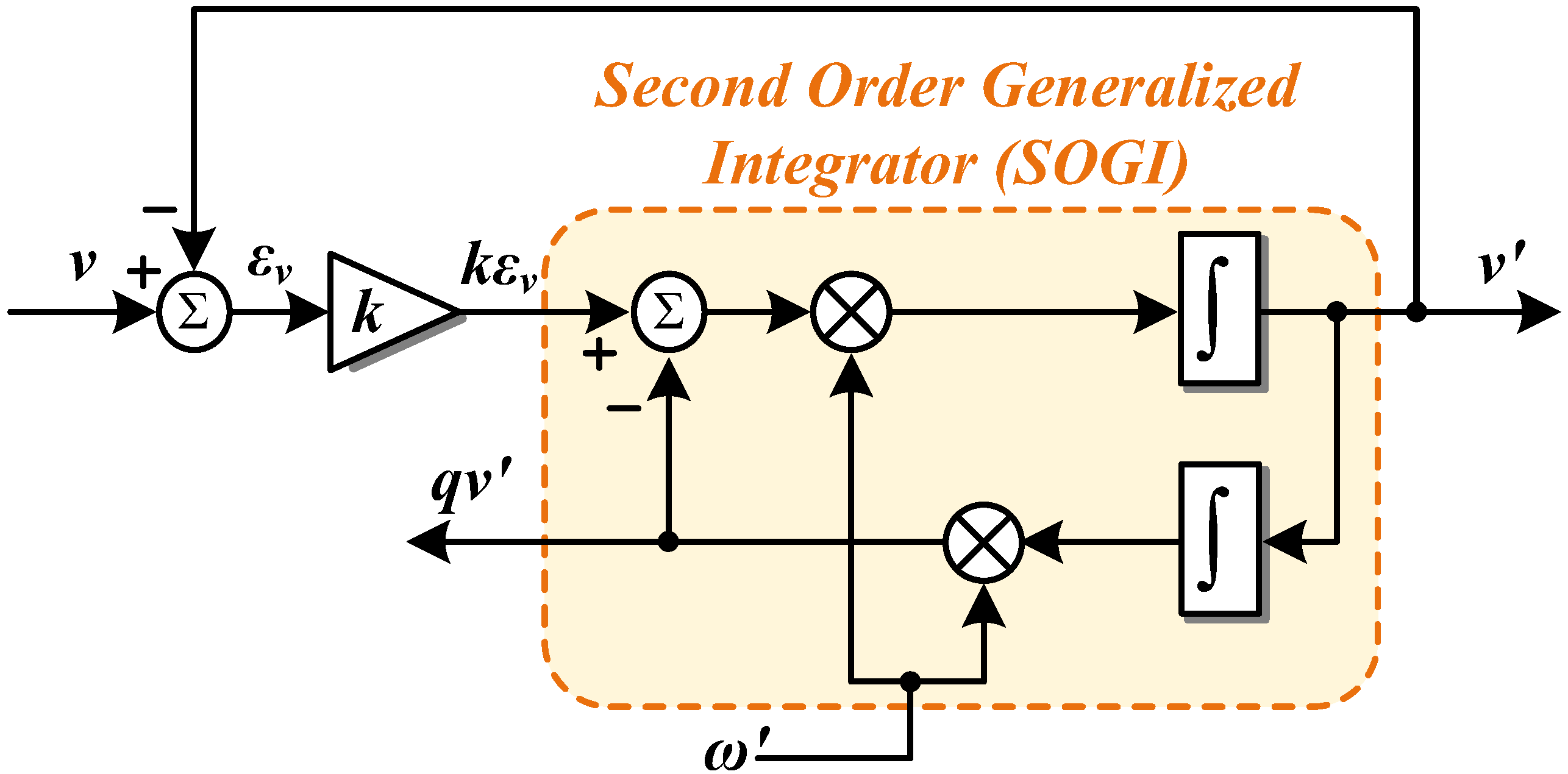
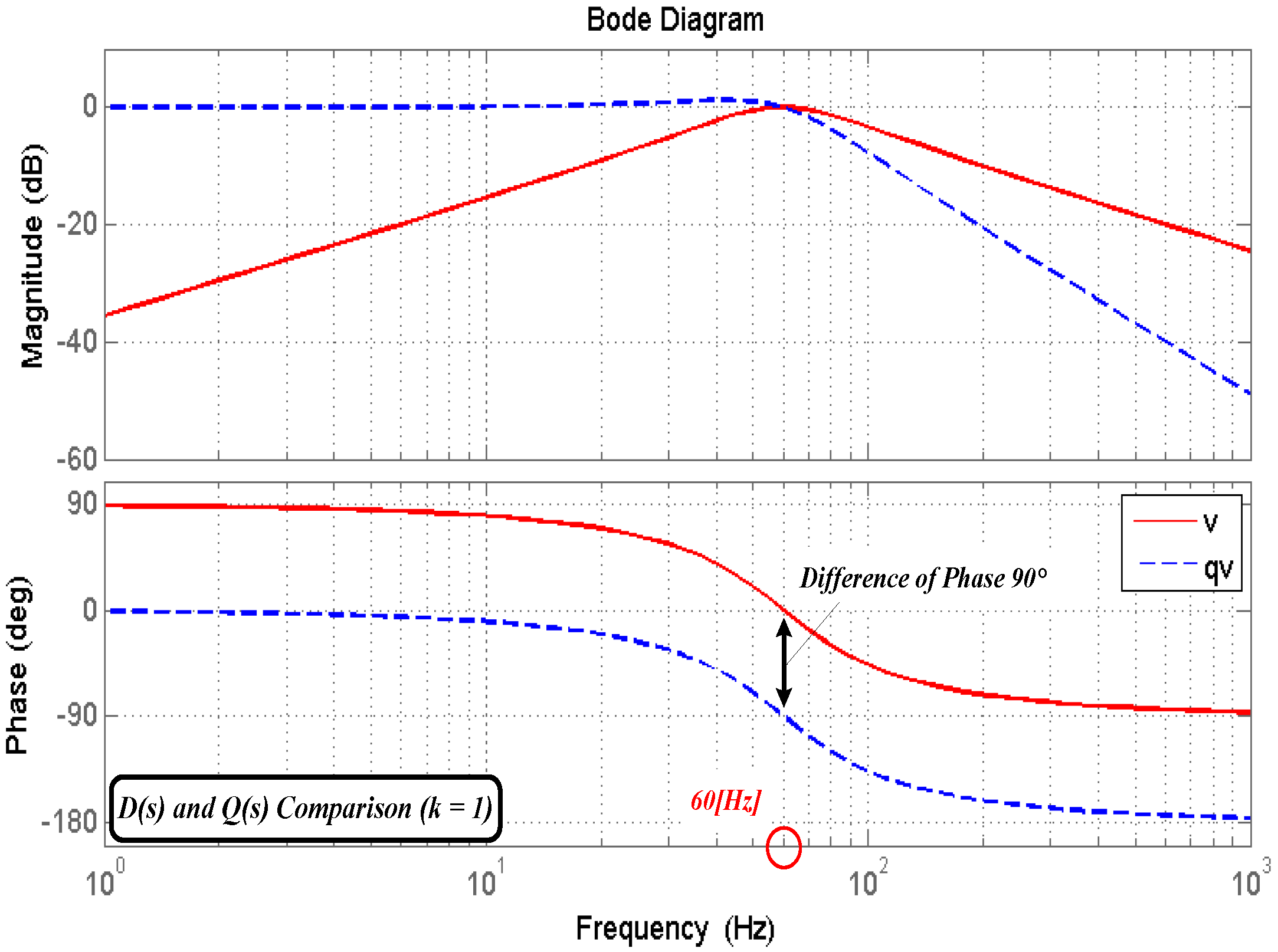
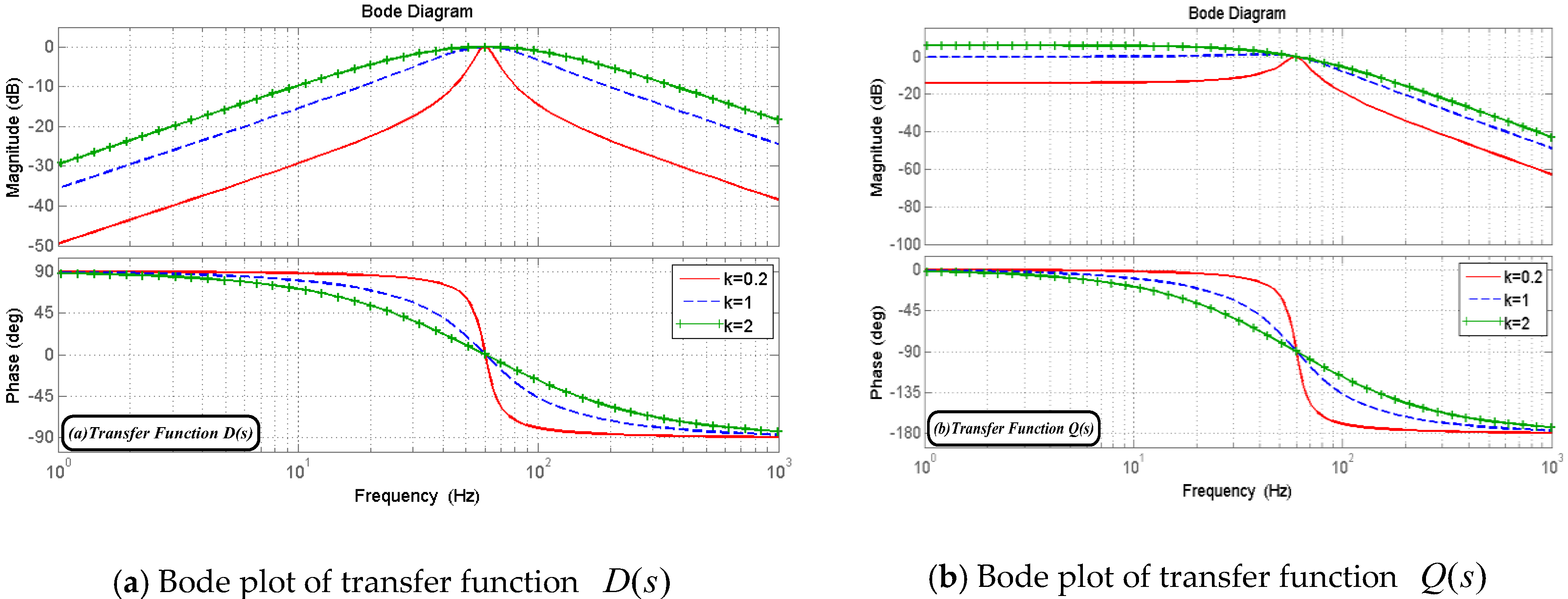
3.1. Second Order Generalized Integrator
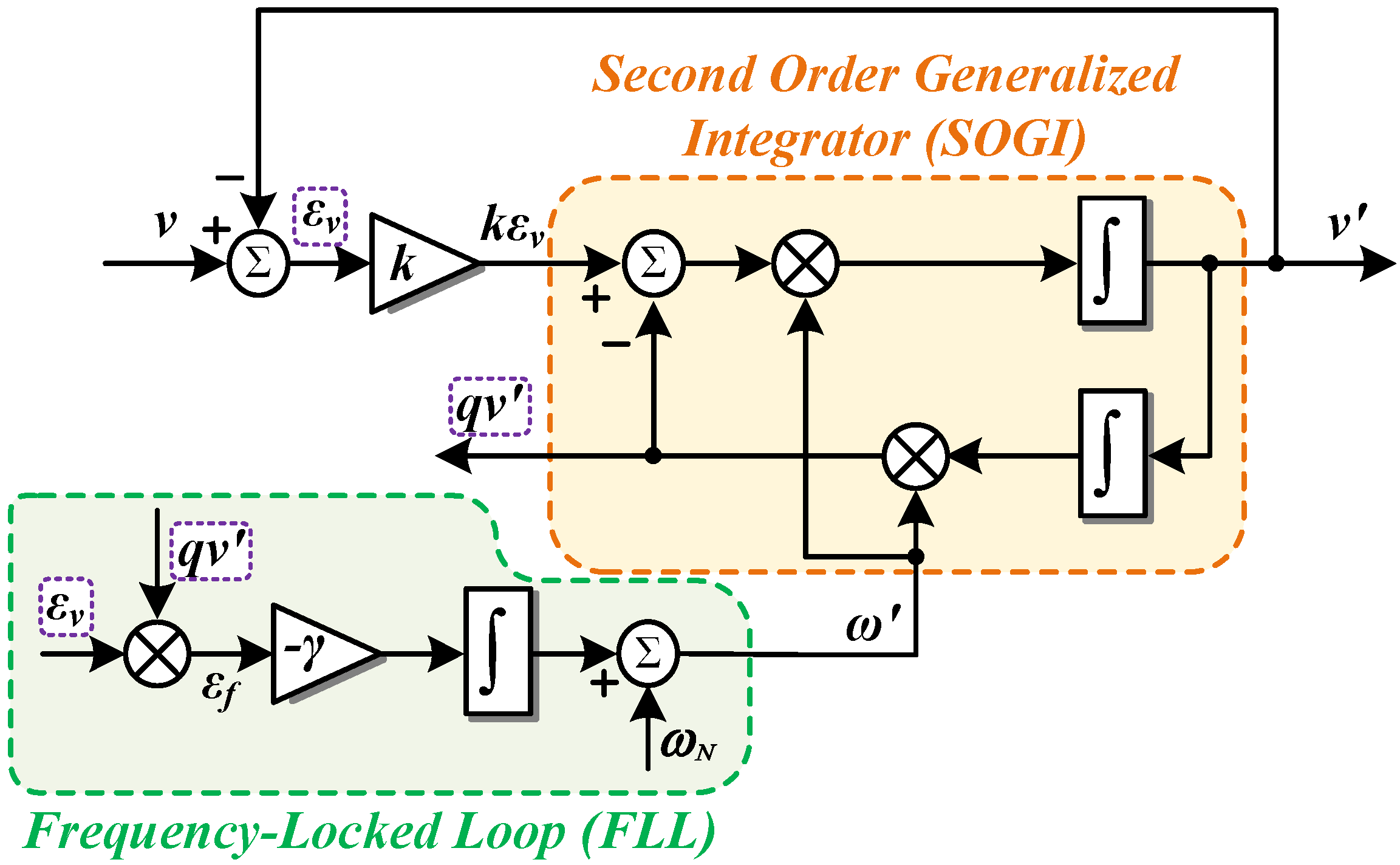
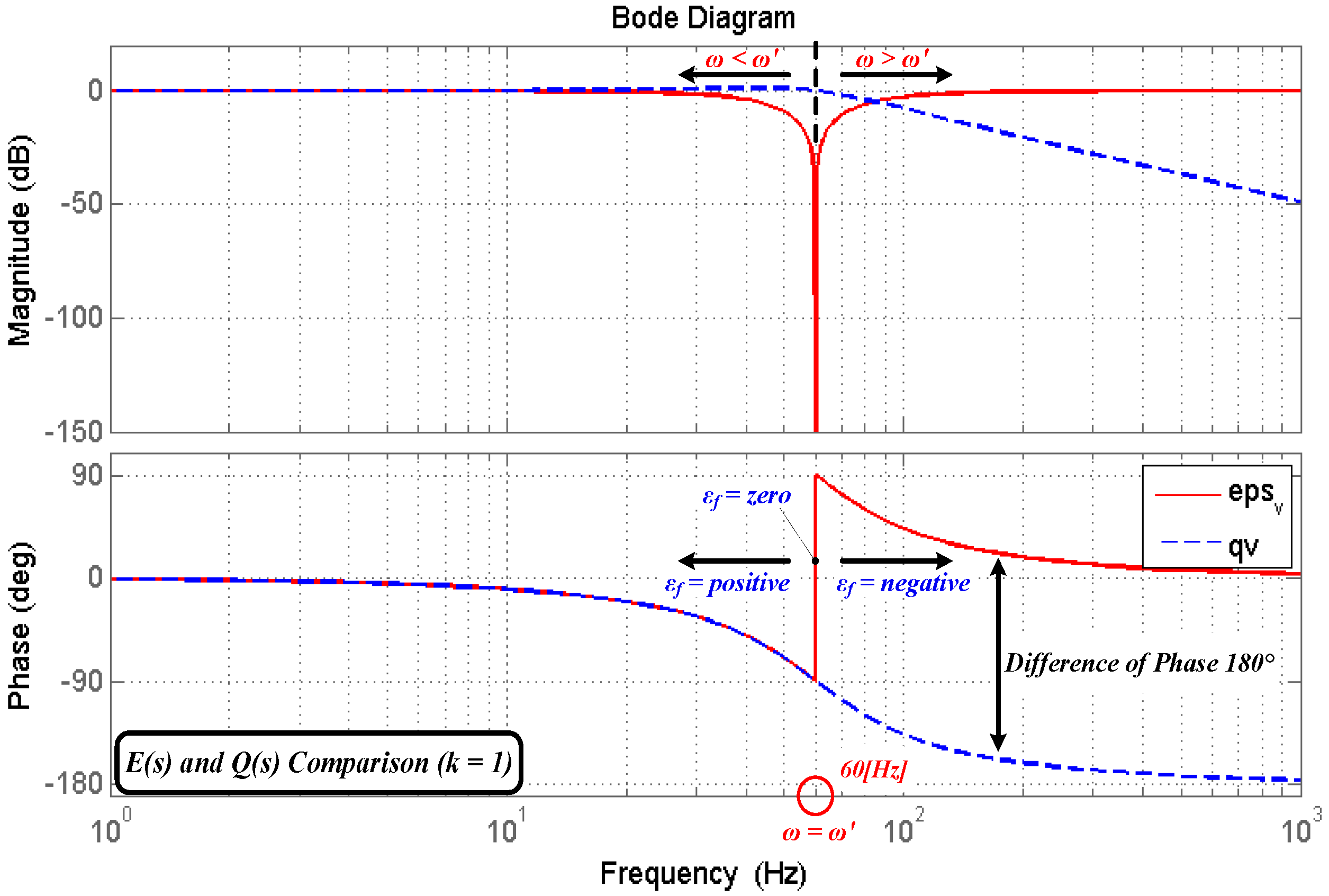
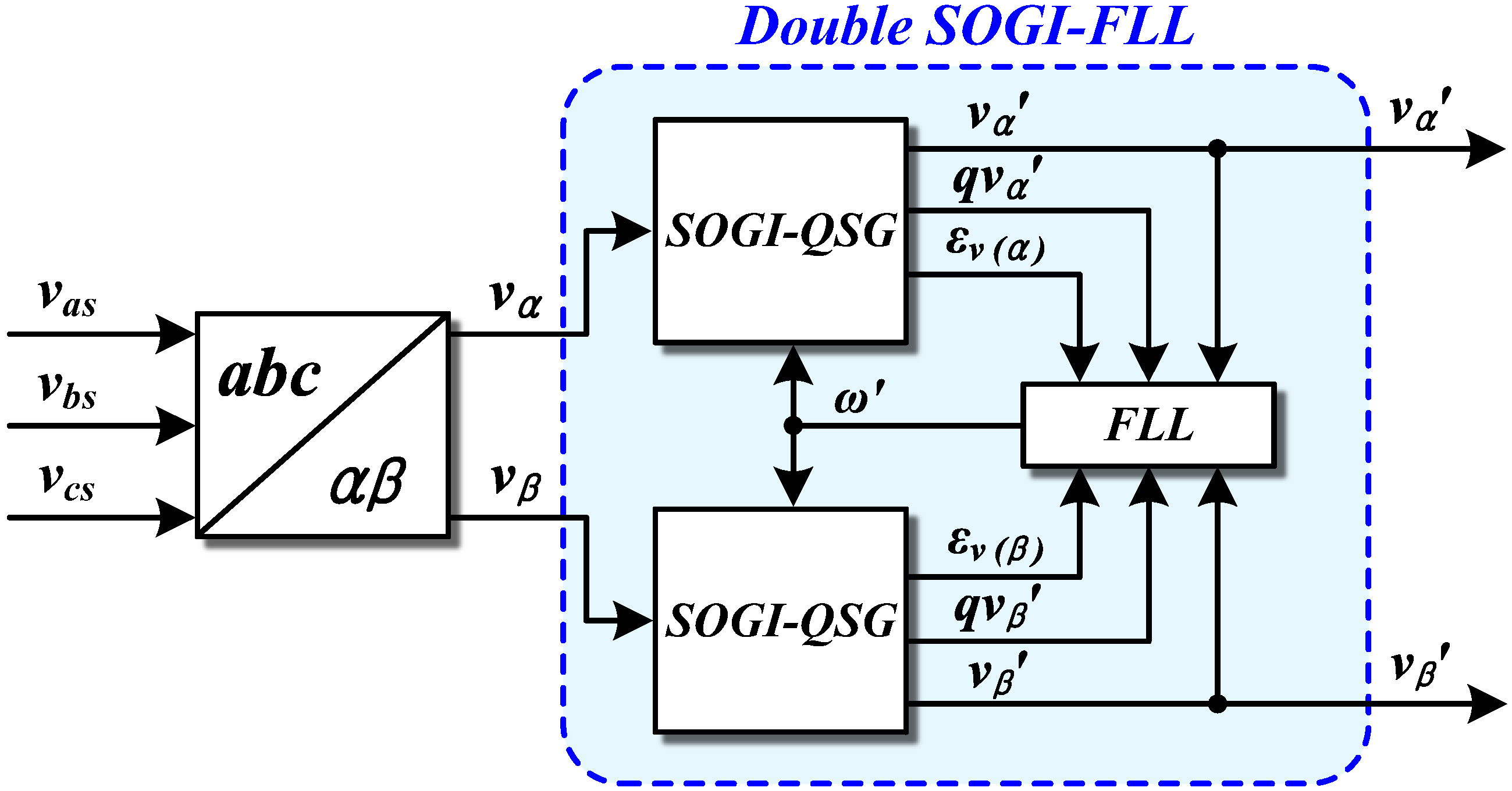
3.2. SOGI-FLL
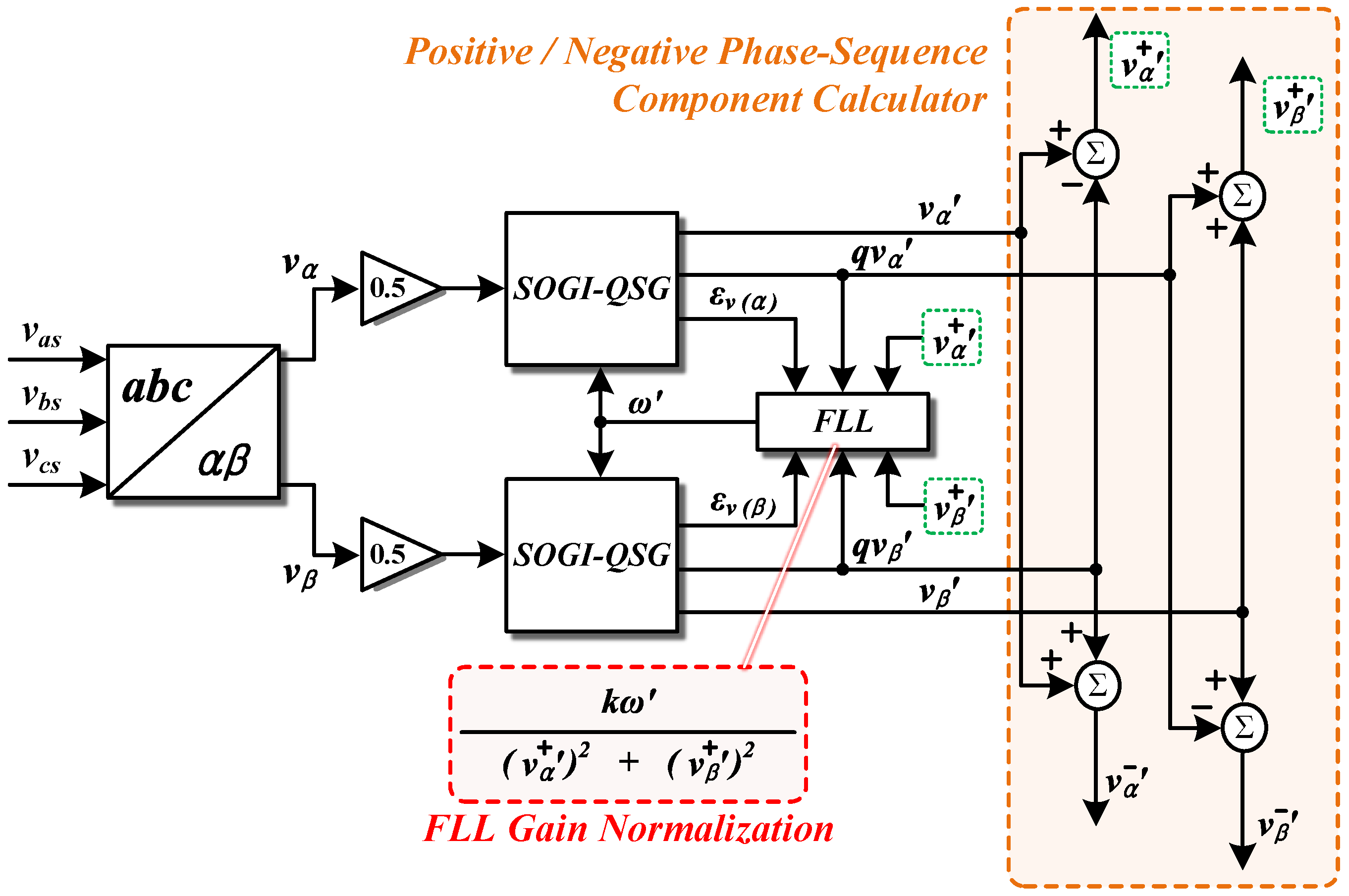
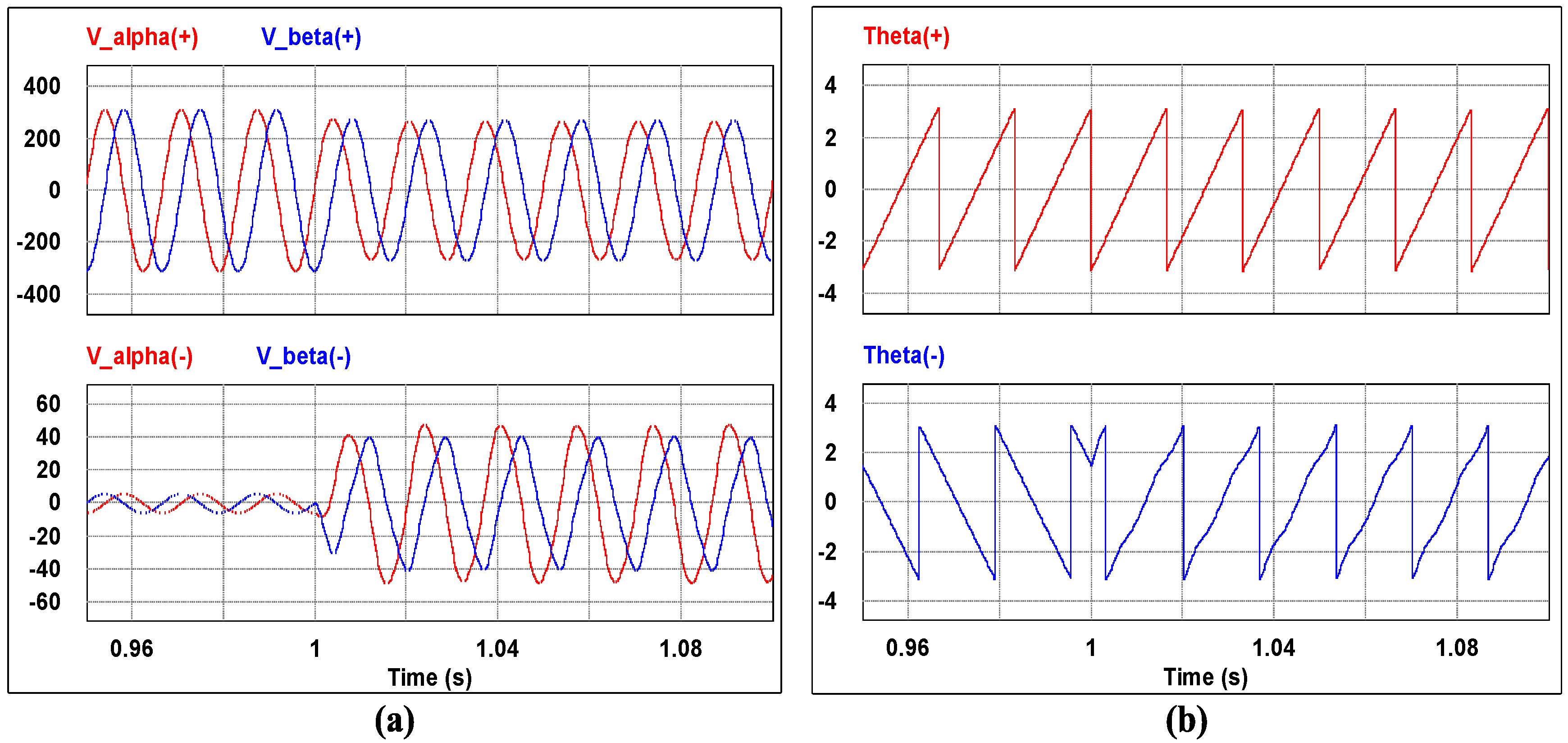
3.3. Positive Sequence Voltage Extraction and Phase Detection Using 3-Phase SOGI-FLL
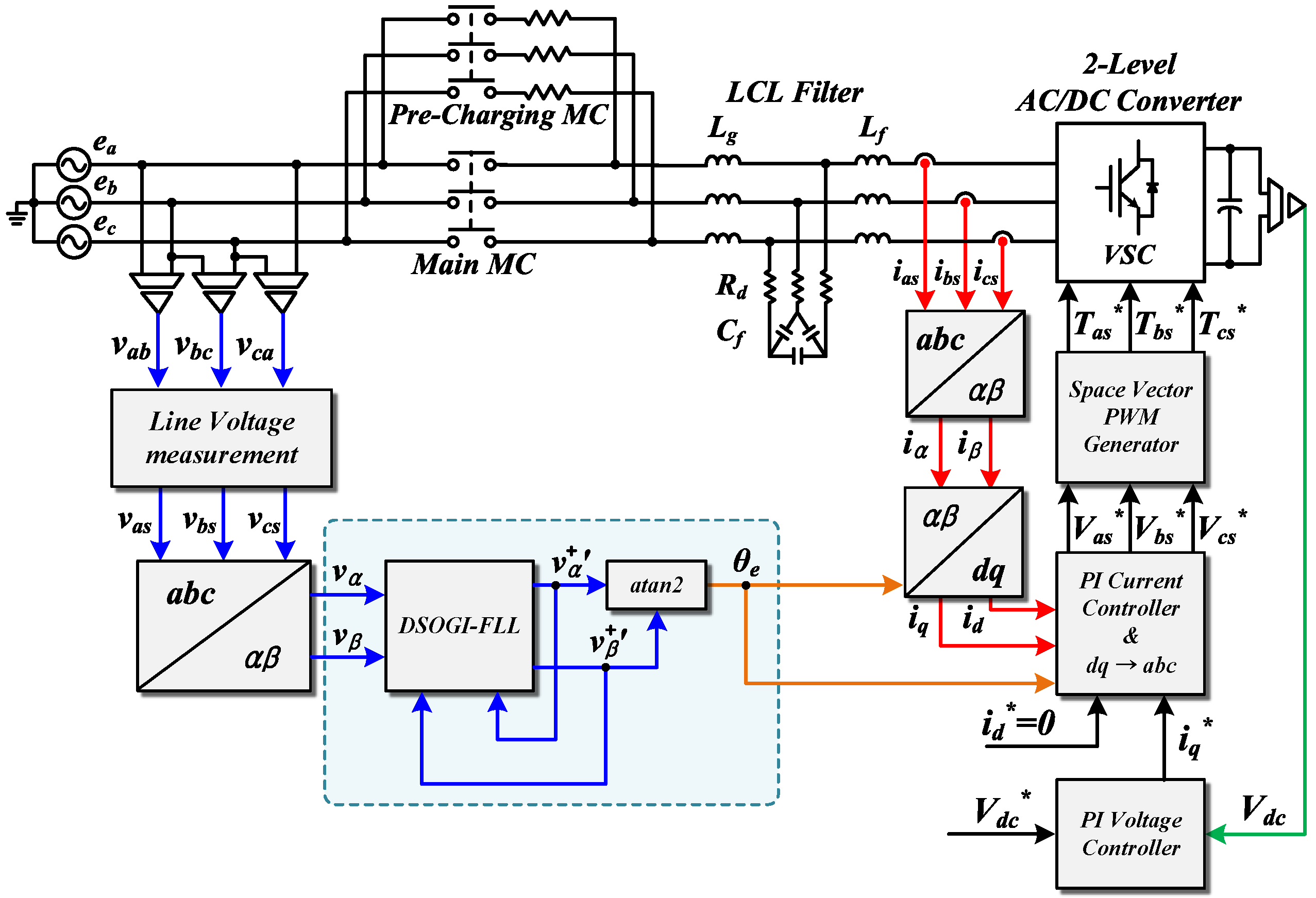
3.4. Control Block Diagram of Overall System with SOGI-FLL
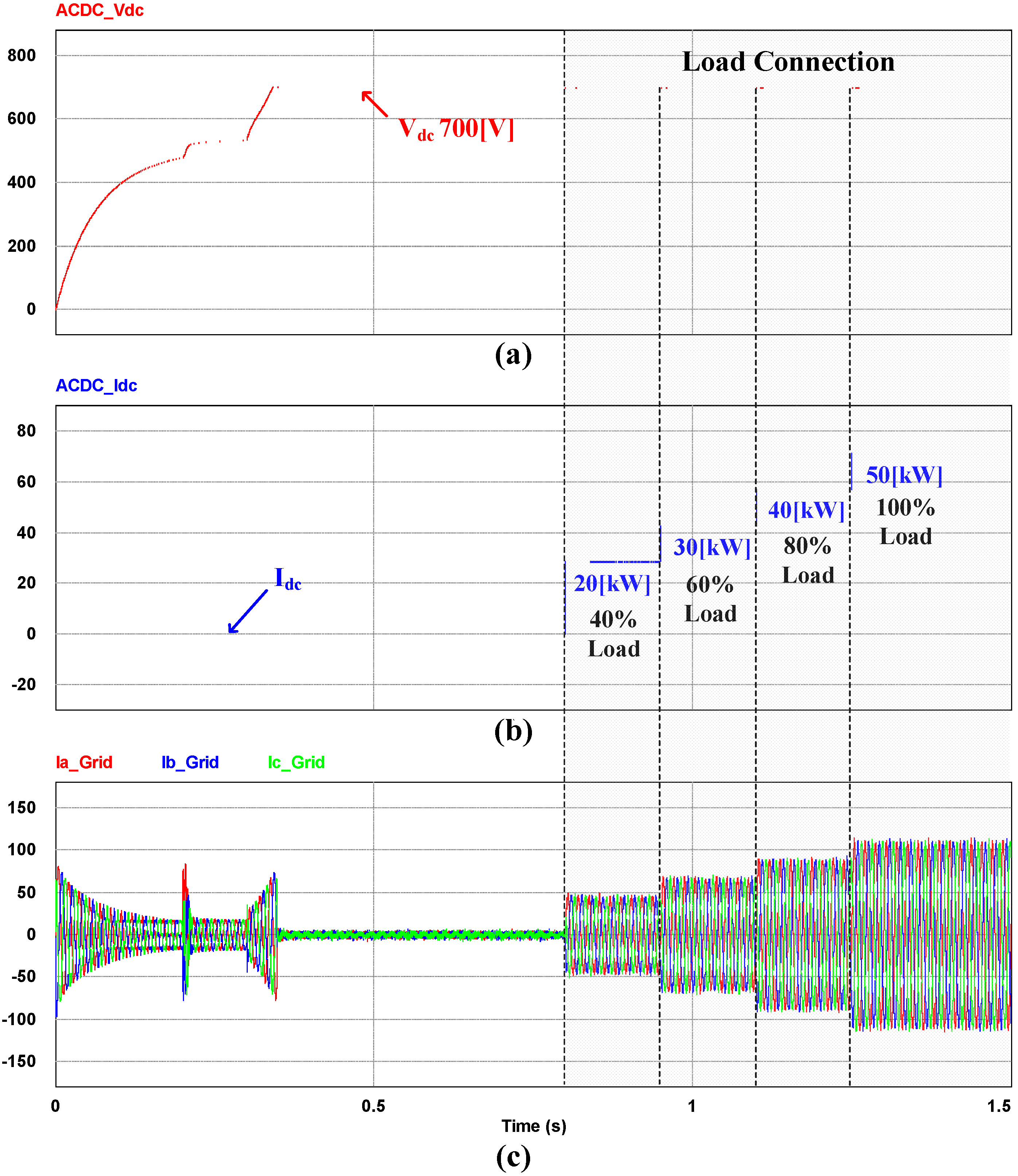
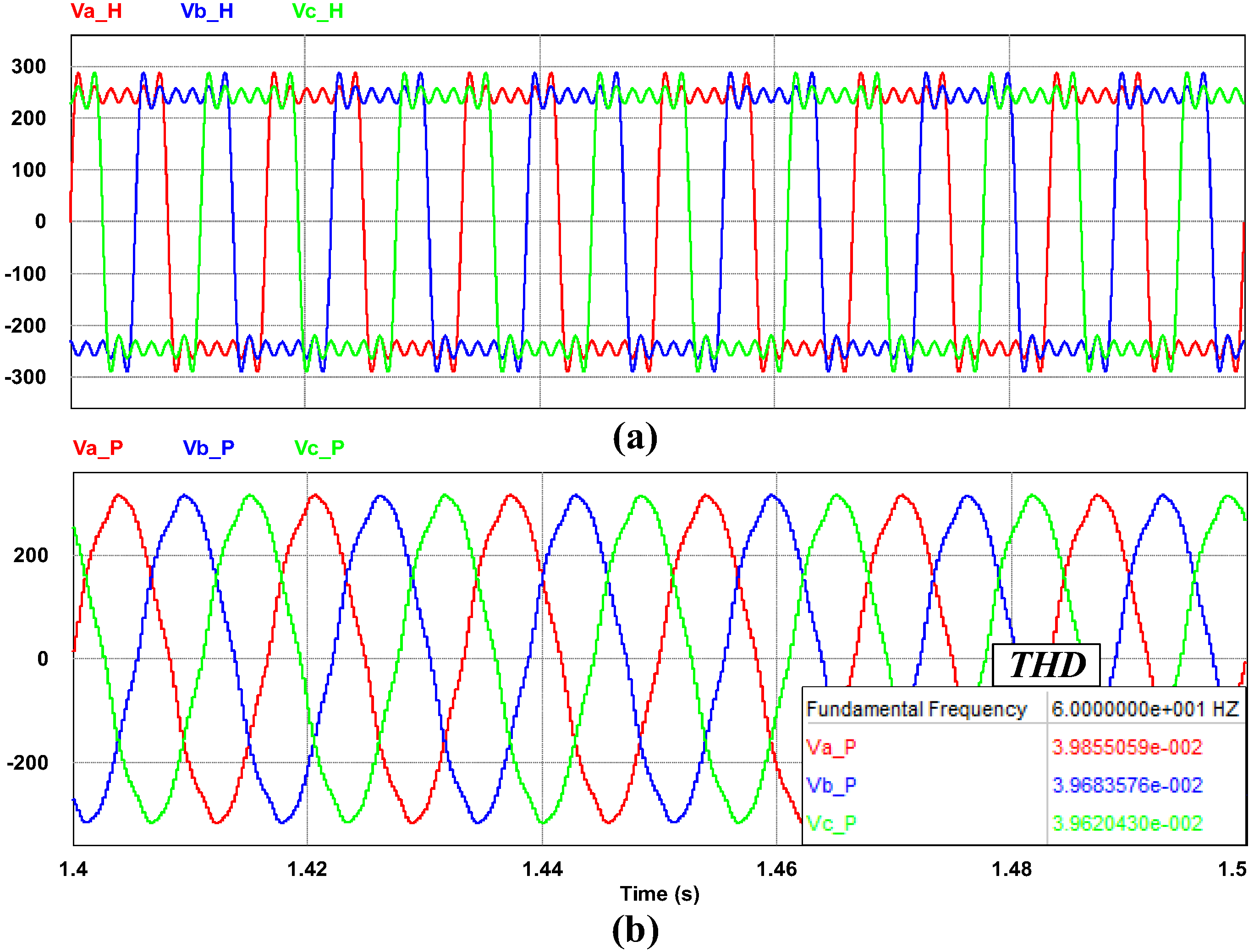
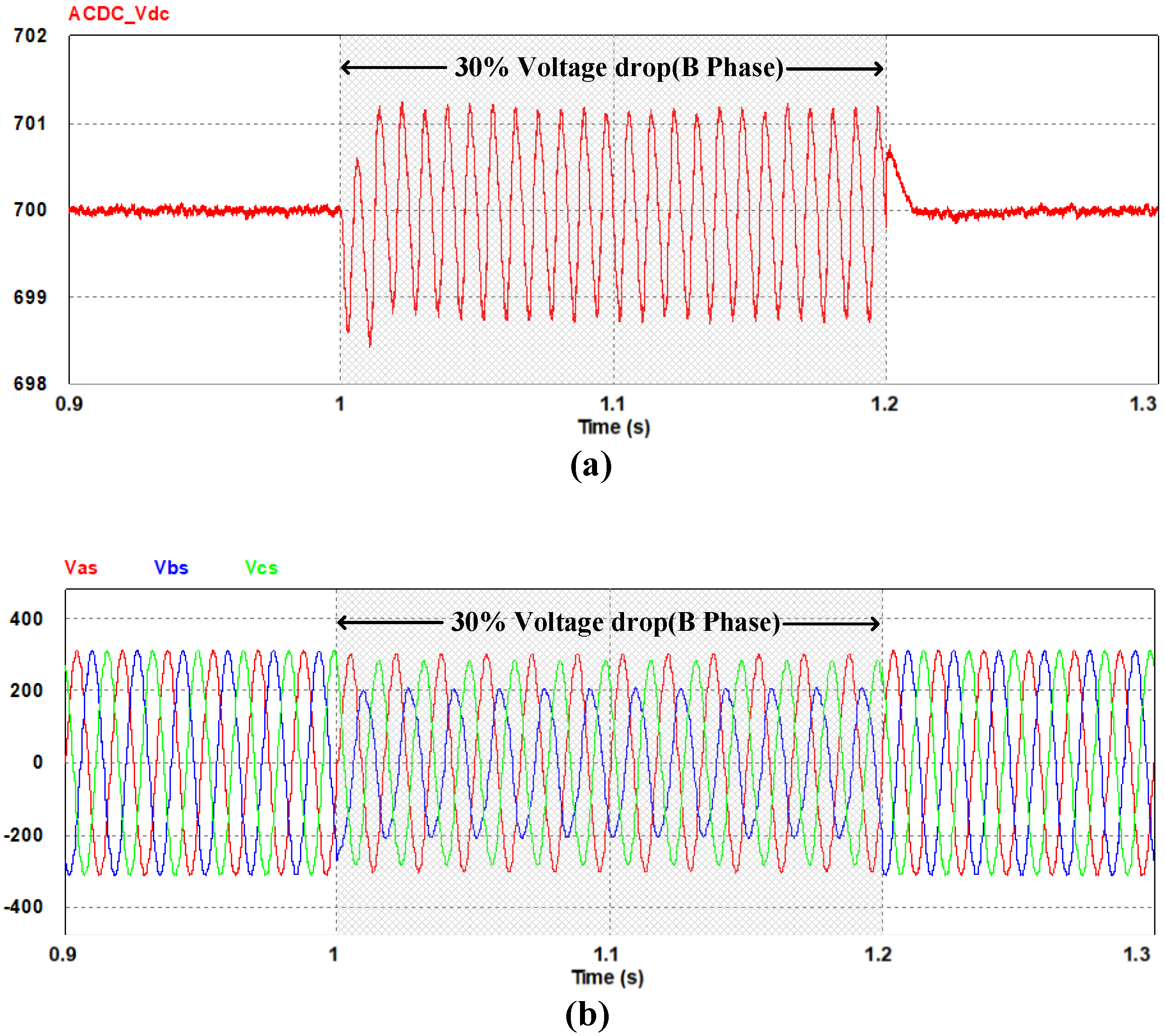
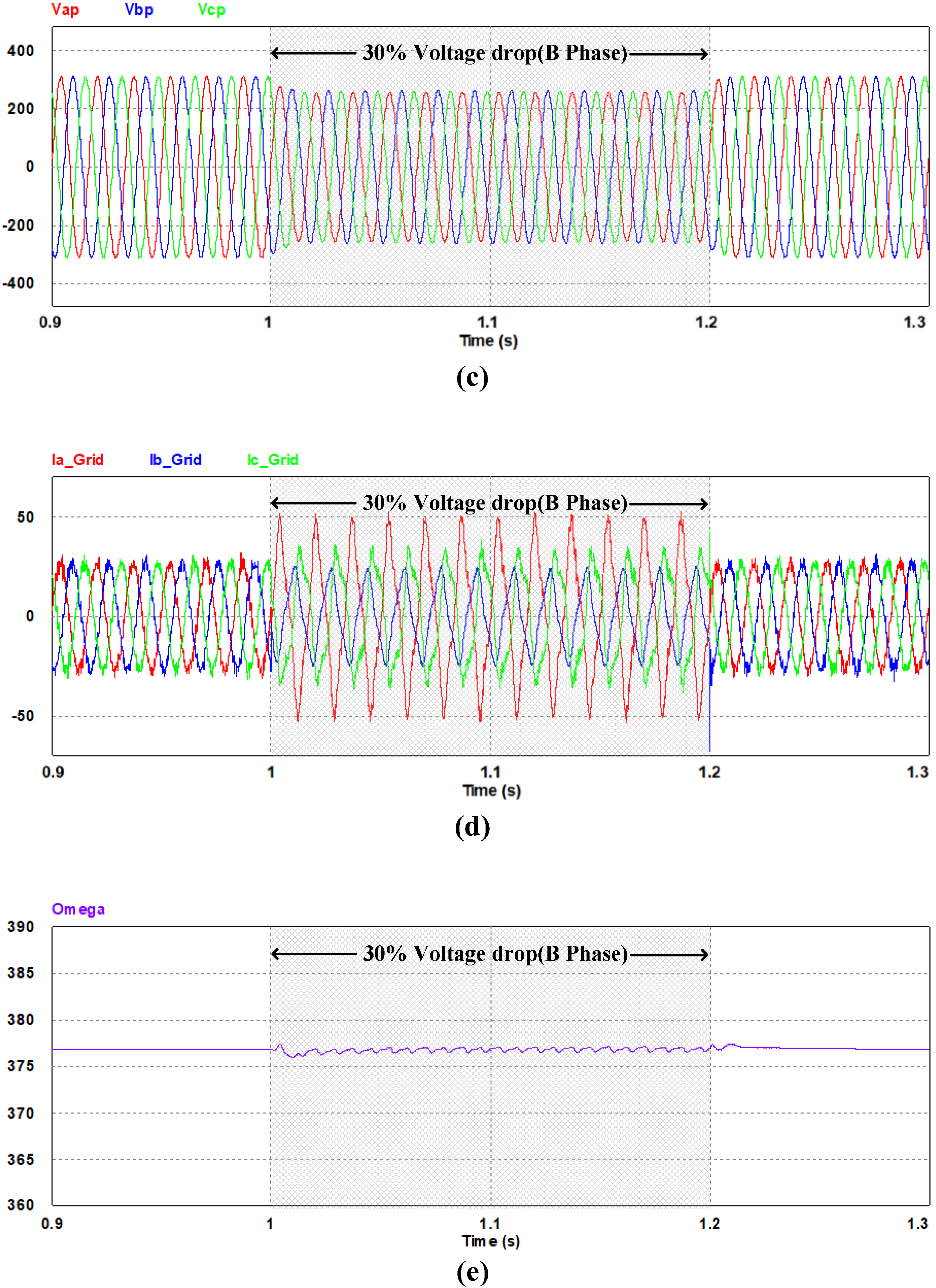
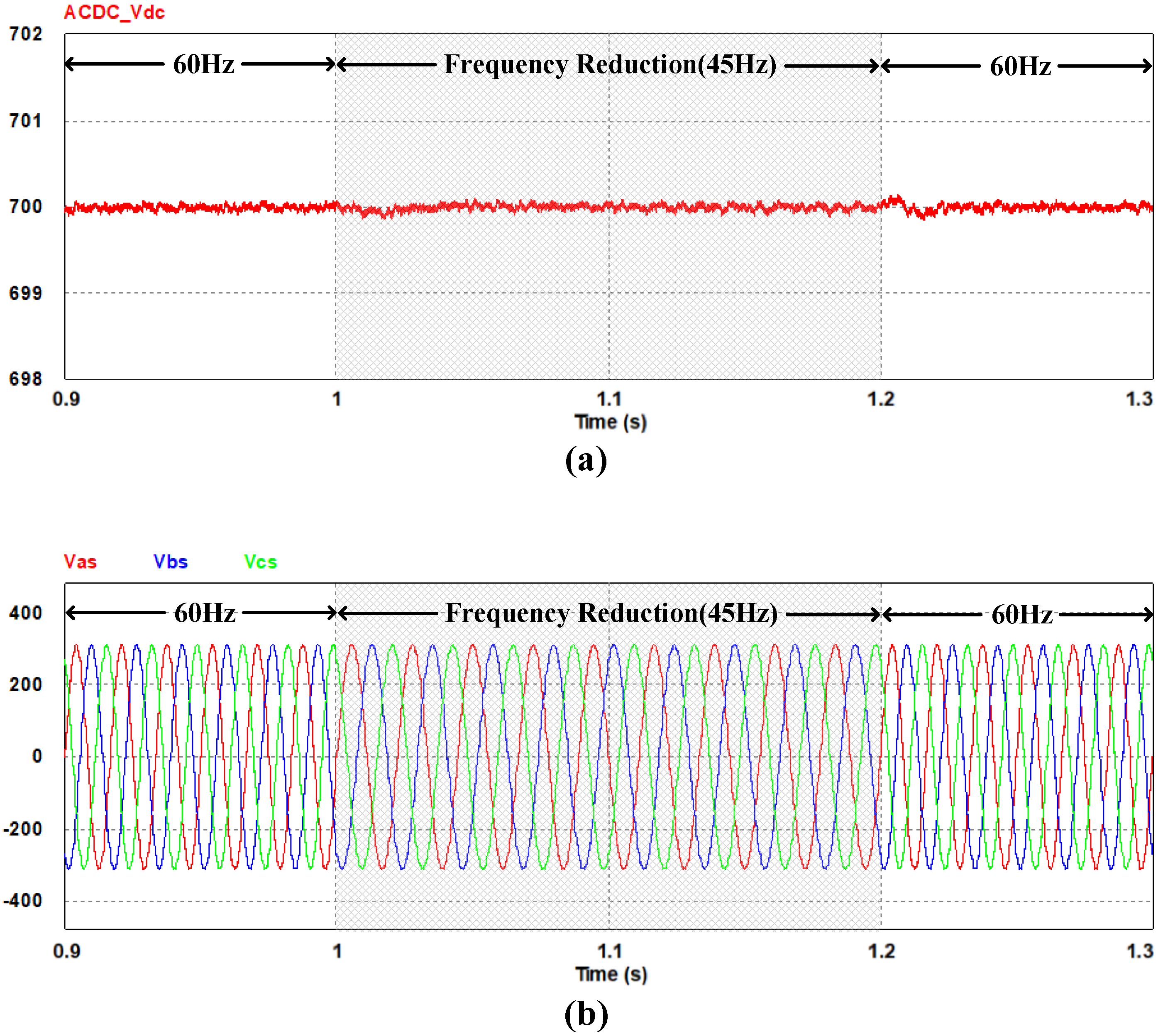
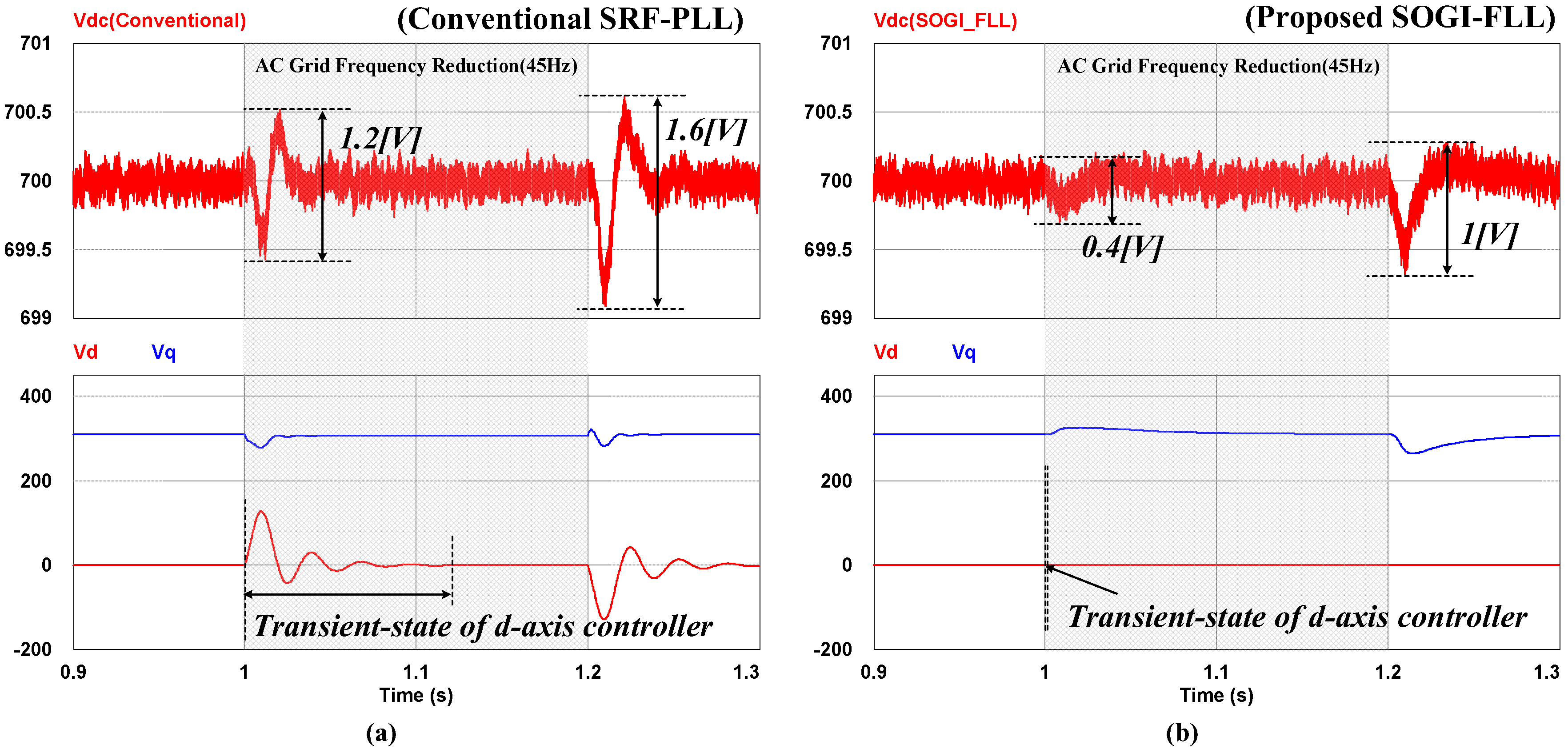
4. Simulation Results
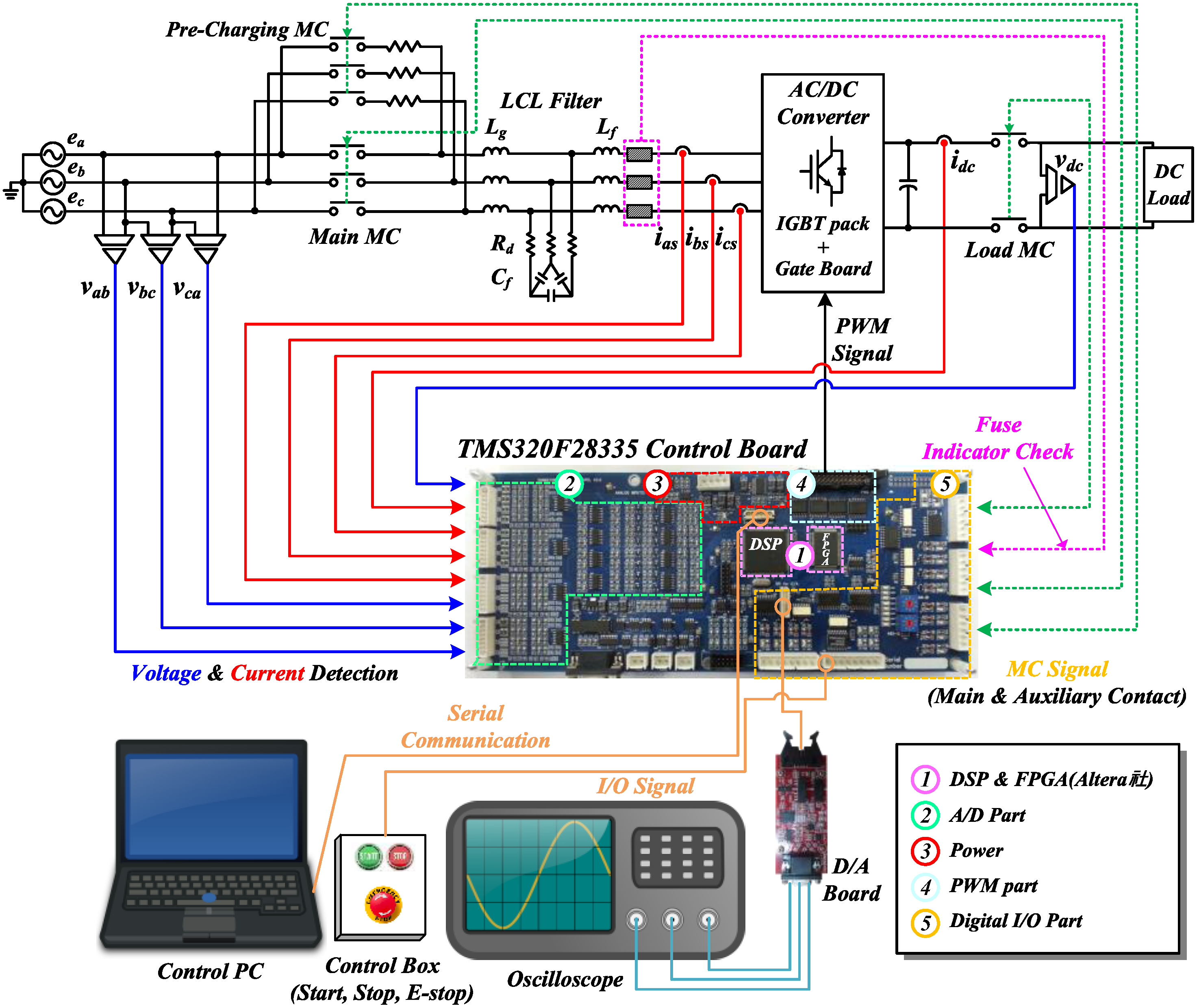
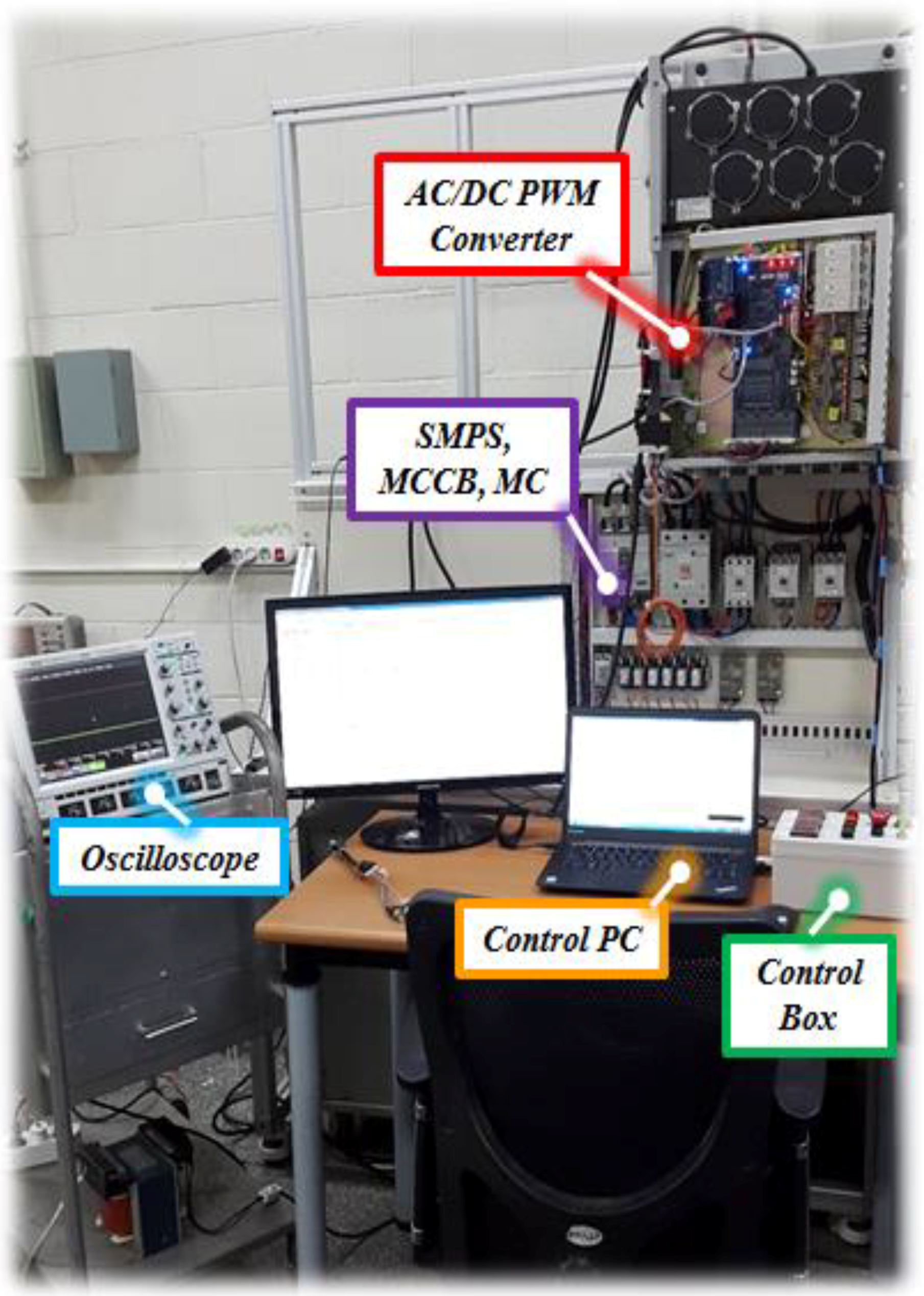
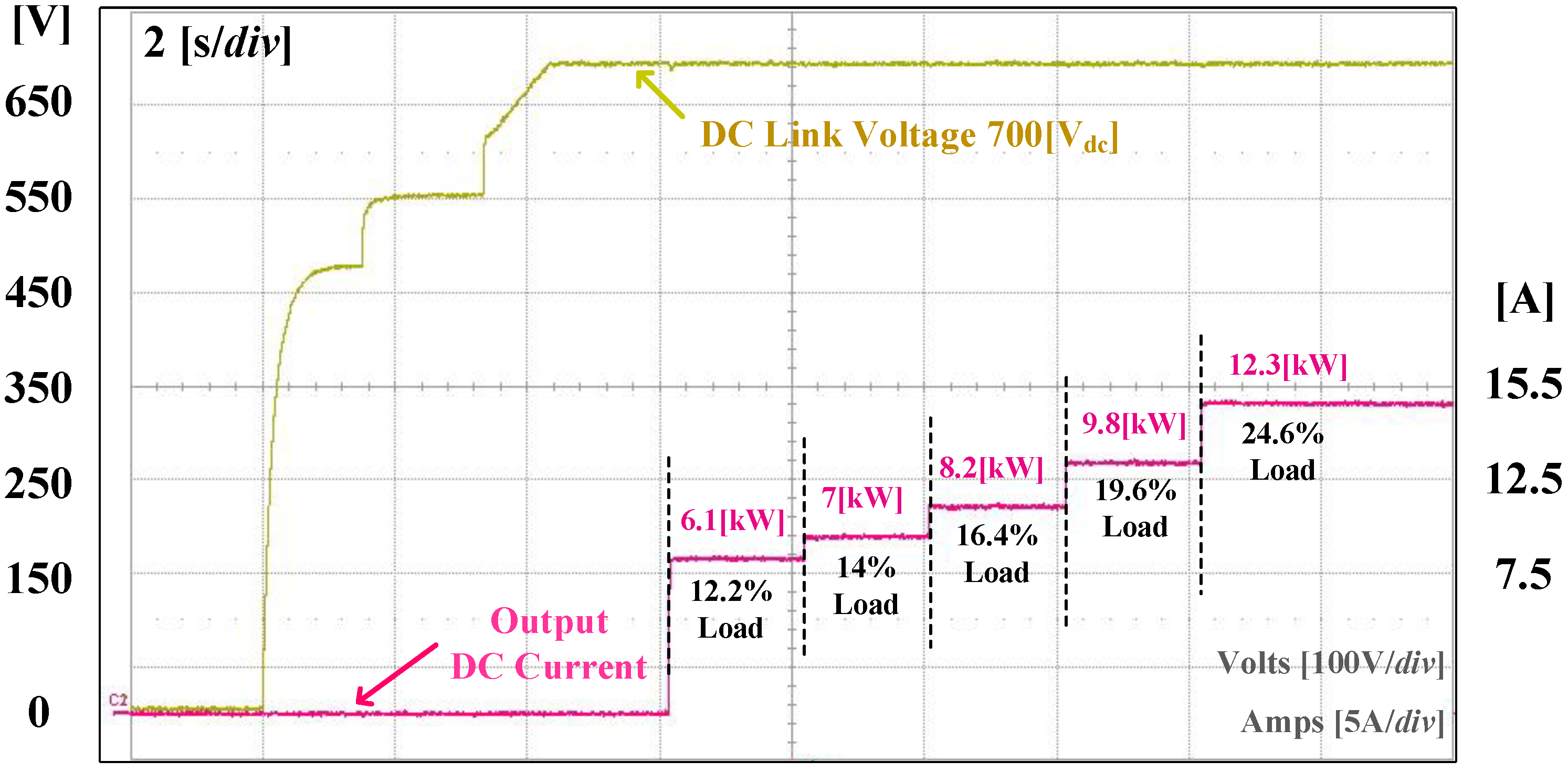
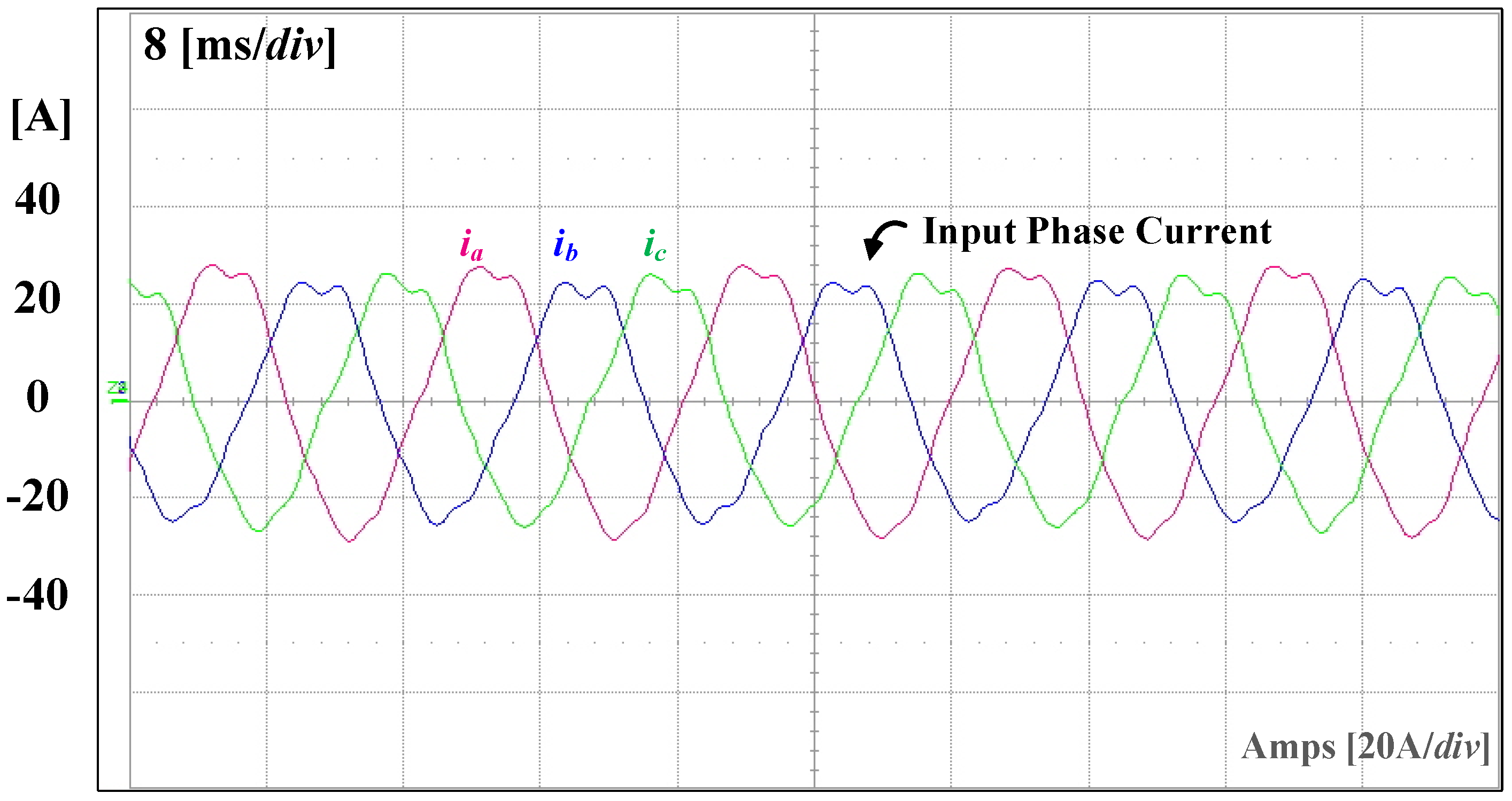
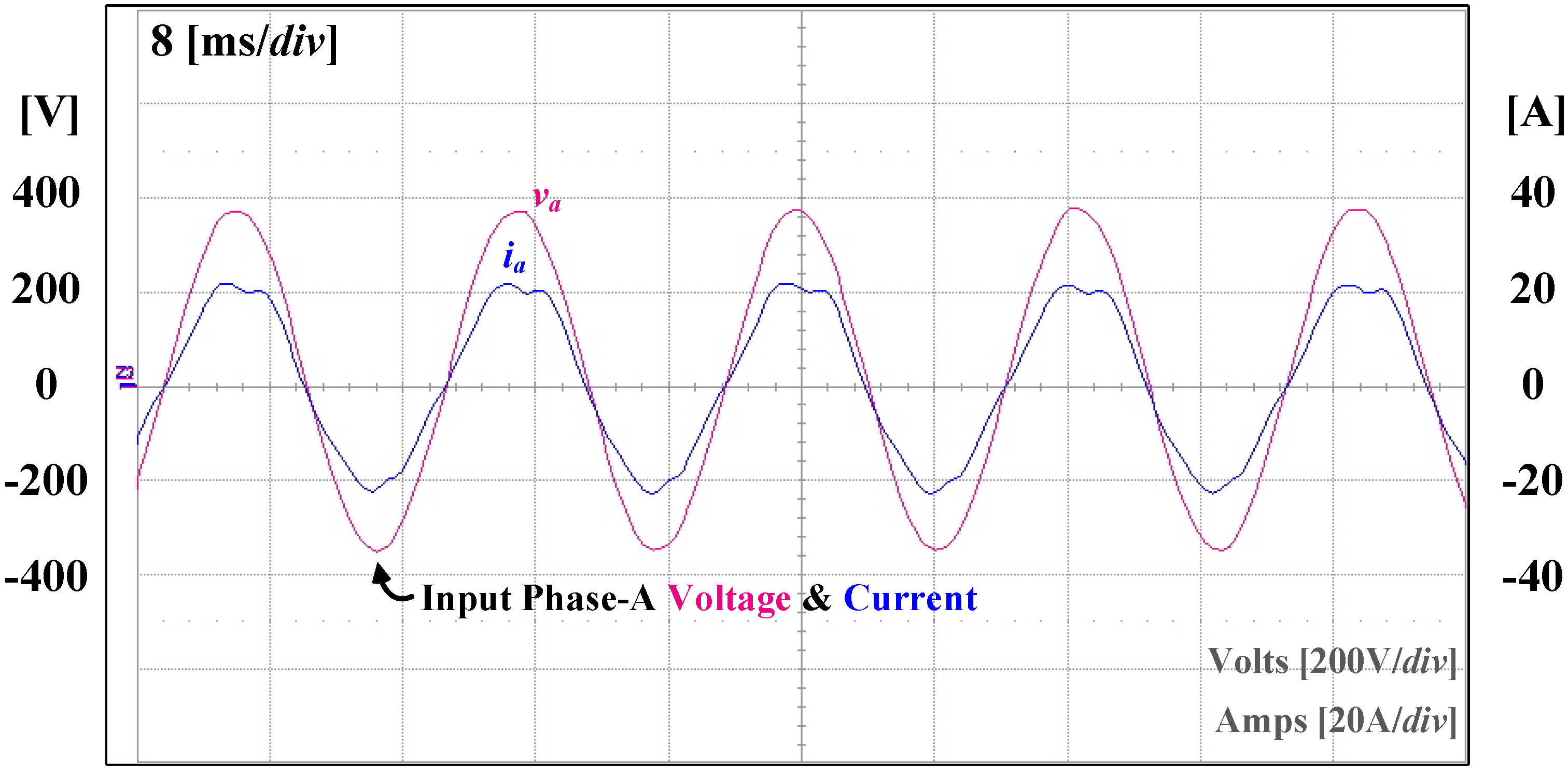
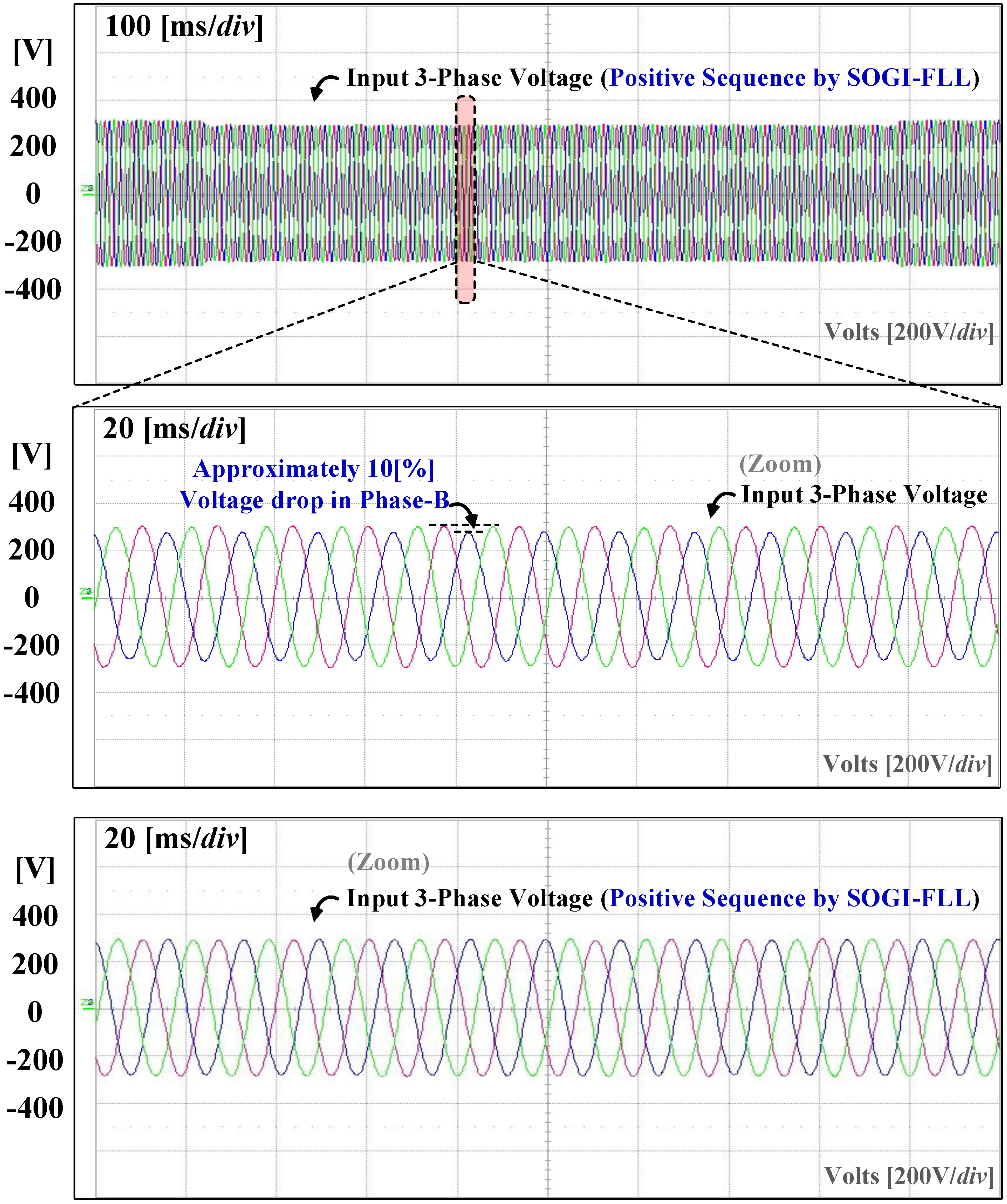
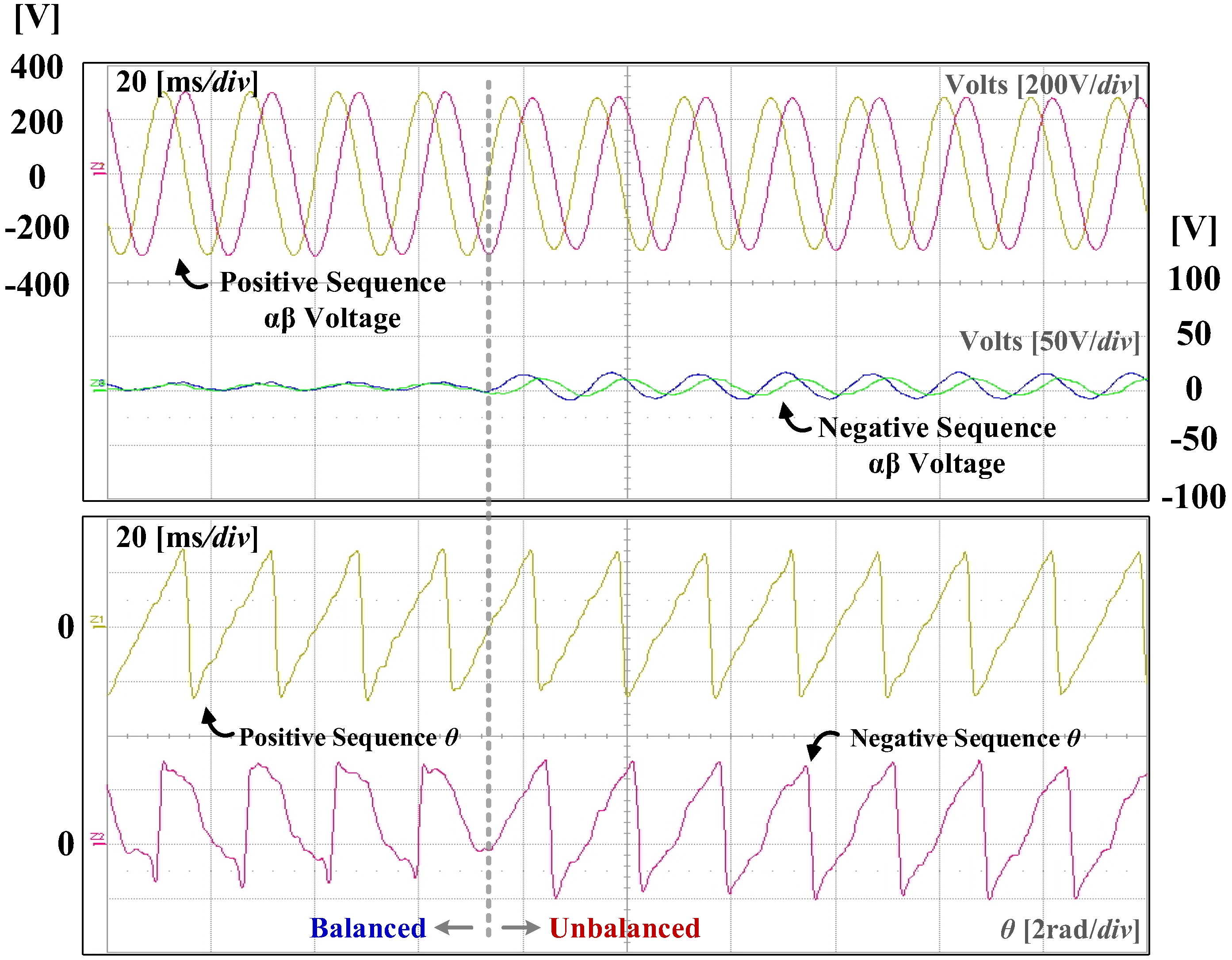
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, H.S.; Ryu, M.H.; Baek, J.W.; Jung, J.H. High-Efficiency Isolated Bidirectional AC–DC Converter for a DC Distribution System. IEEE Trans. Power Electron. 2013, 28, 1642–1654. [Google Scholar] [CrossRef]
- Bosich, D.; Mastromauro, R.A.; Sulligoi, G. AC-DC interface converters for MW-scale MVDC distribution systems: A survey. In Proceedings of the 2017 IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, USA, 15–17 August 2017; pp. 44–49. [Google Scholar]
- Rodríguez, P.; Teodorescu, R.; Candela, I.; Timbus, A.V.; Liserre, M.; Blaabjerg, F. New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–7. [Google Scholar]
- Bacon, V.D.; Oliveira da Silva, S.A. Performance improvement of a three-phase phase-locked-loop algorithm under utility voltage disturbances using non-autonomous adaptive filters. IET Power Electron. 2015, 8, 2237–2250. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M.R. A method for synchronization of power electronic converters in polluted and variable-frequency environments. IEEE Trans. Power Syst. 2004, 19, 1263–1270. [Google Scholar] [CrossRef]
- Jung, J.; Kim, H.; Ryu, M.; Kim, J.; Baek, J. Single-phase bidirectional AC-DC boost rectifier for DC distribution system. In Proceedings of the IEEE ECCE Asia Downunder, Melbourne, Australia, 3–6 June 2013; pp. 544–549. [Google Scholar]
- Jung, T.; Gwon, G.; Kim, C.; Han, J.; Oh, Y.; Noh, C. Voltage Regulation Method for Voltage Drop Compensation and Unbalance Reduction in Bipolar Low-Voltage DC Distribution System. IEEE Trans. Power Deliv. 2018, 33, 141–149. [Google Scholar] [CrossRef]
- Kim, H.; Ryu, M.; Baek, J.; Jung, J. High-Efficiency Isolated Bidirectional AC–DC Converter for a DC Distribution System. IEEE Trans. Power Electron. 2013, 28, 1642–1654. [Google Scholar] [CrossRef]
- Rodríguez, P.; Luna, A.; Muñoz-Aguilar, R.S.; Etxeberria-Otadui, I.; Teodorescu, R.; Blaabjerg, F. A Stationary Reference Frame Grid Synchronization System for Three-Phase Grid-Connected Power Converters under Adverse Grid Conditions. IEEE Trans. Power Electron. 2012, 27, 99–112. [Google Scholar] [CrossRef]
- Kang, J.; Hyun, S.; Hong, S.; Won, C. Advanced control method of 3-phase AC/DC PWM converter for DC distribution using the SOGI-FLL. In Proceedings of the IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 2120–2124. [Google Scholar]
- Kang, J.W.; Lee, H.; Hyun, S.W.; Kim, J.; Won, C.Y. An Enhanced Control Scheme Based on New Adaptive Filters for Cascaded NPC/H-Bridge System. Energies 2018, 11, 1034. [Google Scholar] [CrossRef]
- Jung, C.H. Control Method for Reducing Circulating Current in Parallel Operation of DC Distribution System for Building Applications. Master’s Thesis, Sungkyunkwan University, Suwon, Korea, February 2013. [Google Scholar]
- Han, D.W. Integrated Parallel Operation of Power Conversion Module for DC Distribution System. Master’s Thesis, Sungkyunkwan University, Suwon, Korea, February 2014. [Google Scholar]
- Park, Y.W. Parallel Control Using Current Droop Control of Cubic Equation for DC-grid Distribution Systems. Master’s Thesis, Sungkyunkwan University, Suwon, Korea, August 2014. [Google Scholar]
- Hadjidemetriou, L.; Kyriakides, E.; Blaabjerg, F. A New Hybrid PLL for Interconnecting Renewable Energy Systems to the Grid. IEEE Trans. Ind. Appl. 2013, 49, 2709–2719. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Advanced Grid Synchronization System for Power Converters under Unbalanced and Distorted Operating Conditions. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 5173–5178. [Google Scholar]
- Mnider, A.M.; Atkinson, D.J.; Dahidah, M.; Zbede, Y.B.; Armstrong, M. A programmable cascaded LPF based PLL scheme for single-phase grid-connected inverters. In Proceedings of the 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22–24 March 2016; pp. 1–6. [Google Scholar]
- Yuan, X.M.; Merk, W.; Stemmler, H.; Allmeling, J. Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions. IEEE Trans. Ind. Appl. 2002, 38, 523–532. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, P.; Luna, A.; Candela, I.; Teodorescu, R.; Blaabjerg, F. Grid synchronization of power converters using multiple second order generalized integrators. In Proceedings of the 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 755–760. [Google Scholar]
- Rodriguez, P.; Luna, A.; Etxeberria, I.; Hermoso, J.R.; Teodorescu, R. Multiple. Second order generalized integrators for harmonic synchronization of power converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 2239–2246. [Google Scholar]
- Xin, Z.; Qin, Z.; Lu, M.; Loh, P.C.; Blaabjerg, F. A new second-order generalized integrator based quadrature signal generator with enhanced performance. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Ciobotaru, M.; Teodorescu, R.; Blaabjergc, F. A new single-phase PLL structure based on second order generalized integrator. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–6. [Google Scholar]
- Rocha, C.X.; Camacho, J.R.; Viajante, G.P. Fault detection in a three-phase system grid connected using SOGI structure to calculate vector components. In Proceedings of the International Conference on Renewable Energies and Power Quality (2015 ICREPQ), La Coruña, Spain, 25–27 March 2015; pp. 25–27. [Google Scholar]
- Nam, K.Y.; Choi, S.B.; Ryoo, H.S.; Jeong, S.H.; Lee, J.D.; Jung, D.H.; Kim, D.K. Establishment of Test Field for Application of IEC 60364-4-44 in Korea. In Proceedings of the IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1944–1949. [Google Scholar]
- Golestan, S.; Guerrero, J.M. Conventional Synchronous Reference Frame Phase-Locked Loop is an Adaptive Complex Filter. IEEE Trans. Ind. Electron. 2015, 62, 1679–1682. [Google Scholar] [CrossRef] [Green Version]






| Parameter | Value | Unit |
|---|---|---|
| Rated power of system | 50 | [kW] |
| 3 phase line-to-line grid voltage | 380 | [Vrms] |
| Grid frequency | 60 | [Hz] |
| Switching frequency | 5 | [kHz] |
| Output DC-link voltage | 700 | [Vdc] |
| DC-link capacitance | 10200 | [] |
| LCL filter inductance at grid side | 120 | [] |
| LCL filter capacitance | 50 | [] |
| LCL filter inductance at converter side | 500 | [] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.-W.; Shin, K.-W.; Lee, H.; Kang, K.-M.; Kim, J.; Won, C.-Y. A Study on Stability Control of Grid Connected DC Distribution System Based on Second Order Generalized Integrator-Frequency Locked Loop (SOGI-FLL). Appl. Sci. 2018, 8, 1387. https://doi.org/10.3390/app8081387
Kang J-W, Shin K-W, Lee H, Kang K-M, Kim J, Won C-Y. A Study on Stability Control of Grid Connected DC Distribution System Based on Second Order Generalized Integrator-Frequency Locked Loop (SOGI-FLL). Applied Sciences. 2018; 8(8):1387. https://doi.org/10.3390/app8081387
Chicago/Turabian StyleKang, Jin-Wook, Ki-Woong Shin, Hoon Lee, Kyung-Min Kang, Jintae Kim, and Chung-Yuen Won. 2018. "A Study on Stability Control of Grid Connected DC Distribution System Based on Second Order Generalized Integrator-Frequency Locked Loop (SOGI-FLL)" Applied Sciences 8, no. 8: 1387. https://doi.org/10.3390/app8081387





