A Robust Cover Song Identification System with Two-Level Similarity Fusion and Post-Processing
Abstract
:1. Introduction
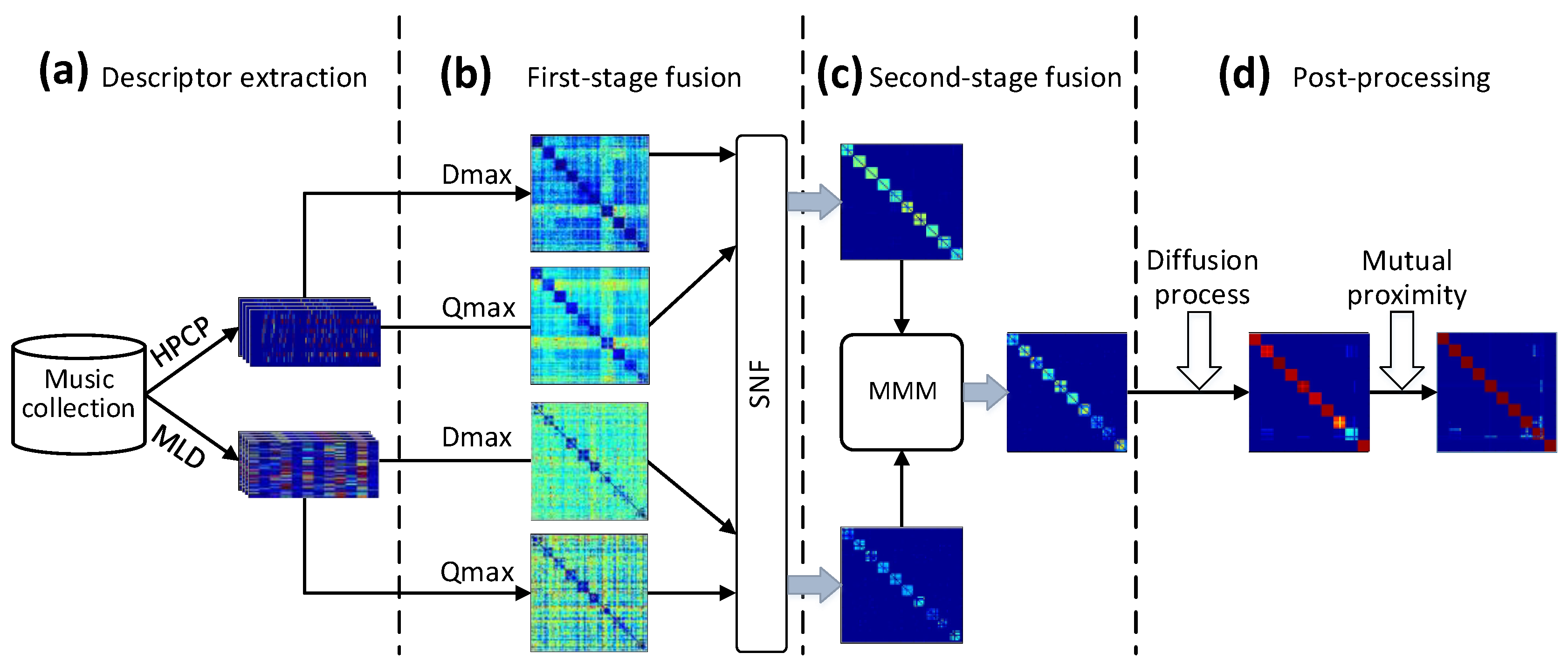
2. Proposed Model
- Function list : where extracts the i-th kind of descriptor from the track .
- Function list : where computes the j-th similarity score between the i-th descriptors of the input tracks and .
2.1. Descriptor Extraction
2.2. First-Level Fusion
2.3. Second-Level Fusion
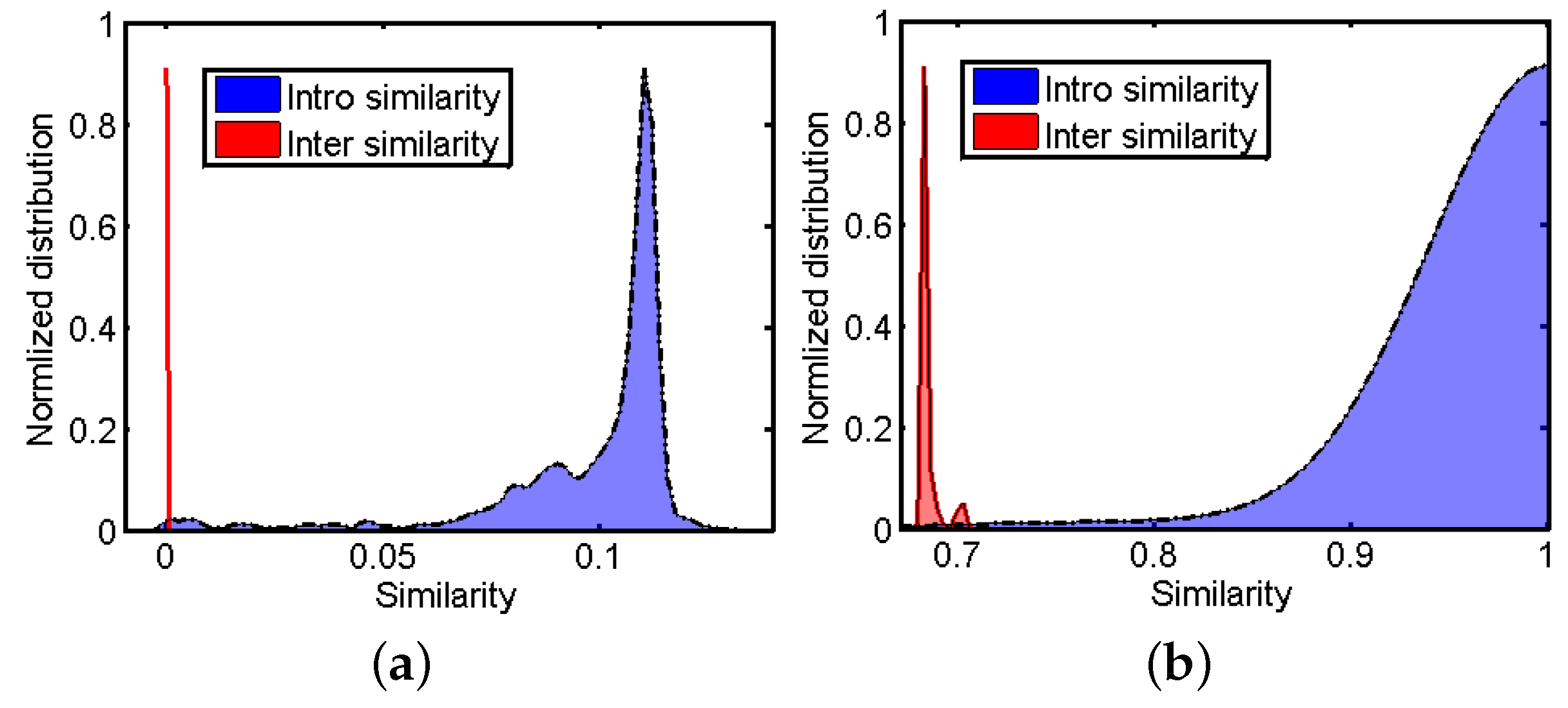
2.4. Post-Processing
2.4.1. Diffusion Processing
2.4.2. Hubness Reduction
3. Experiments
3.1. Datasets
3.2. Experiment Settings
3.3. Experimental Results
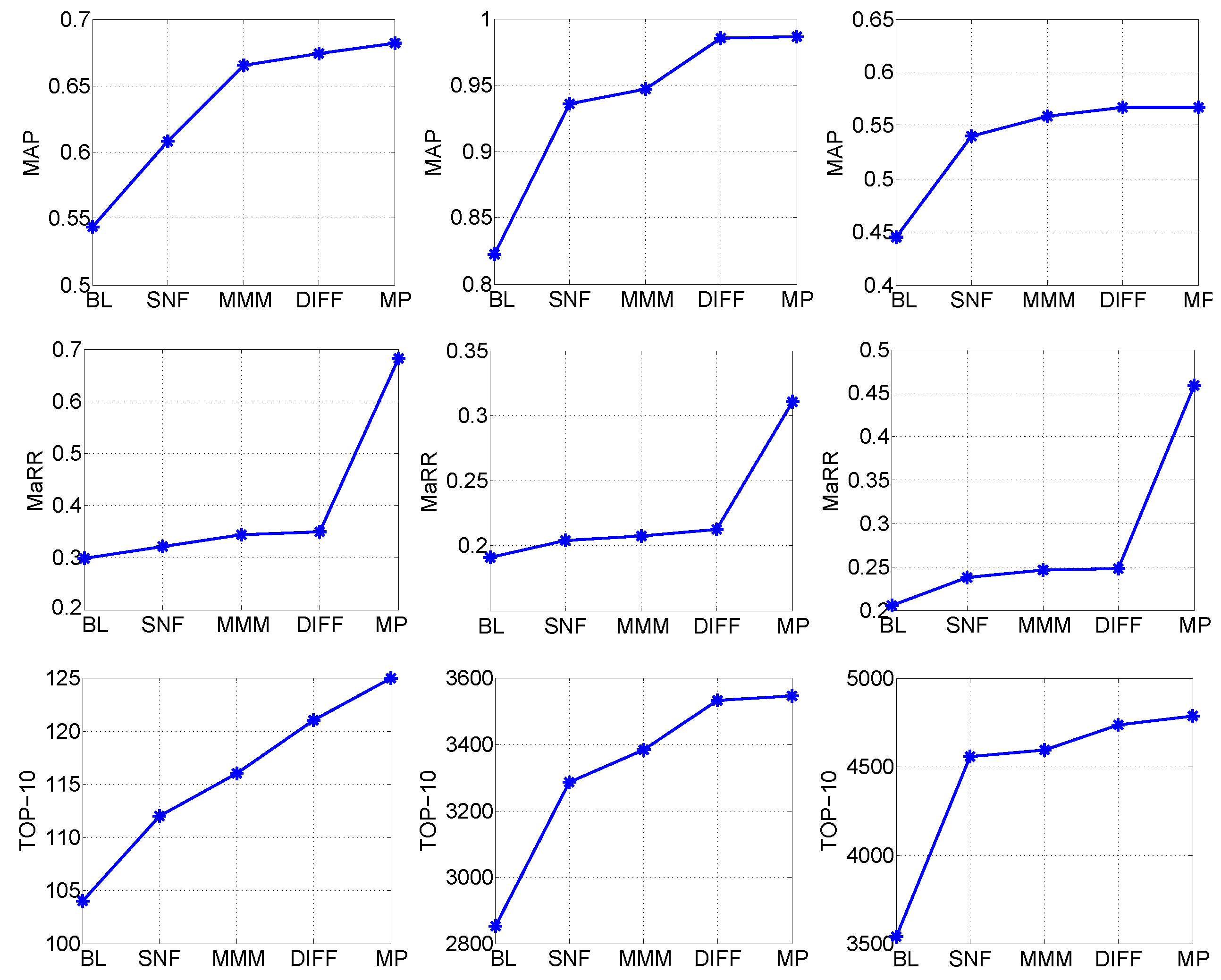
3.3.1. Necessity and Importance of Each Step Included in the Proposed Model
3.3.2. Comparison with State-Of-The-Art CSI Schemes
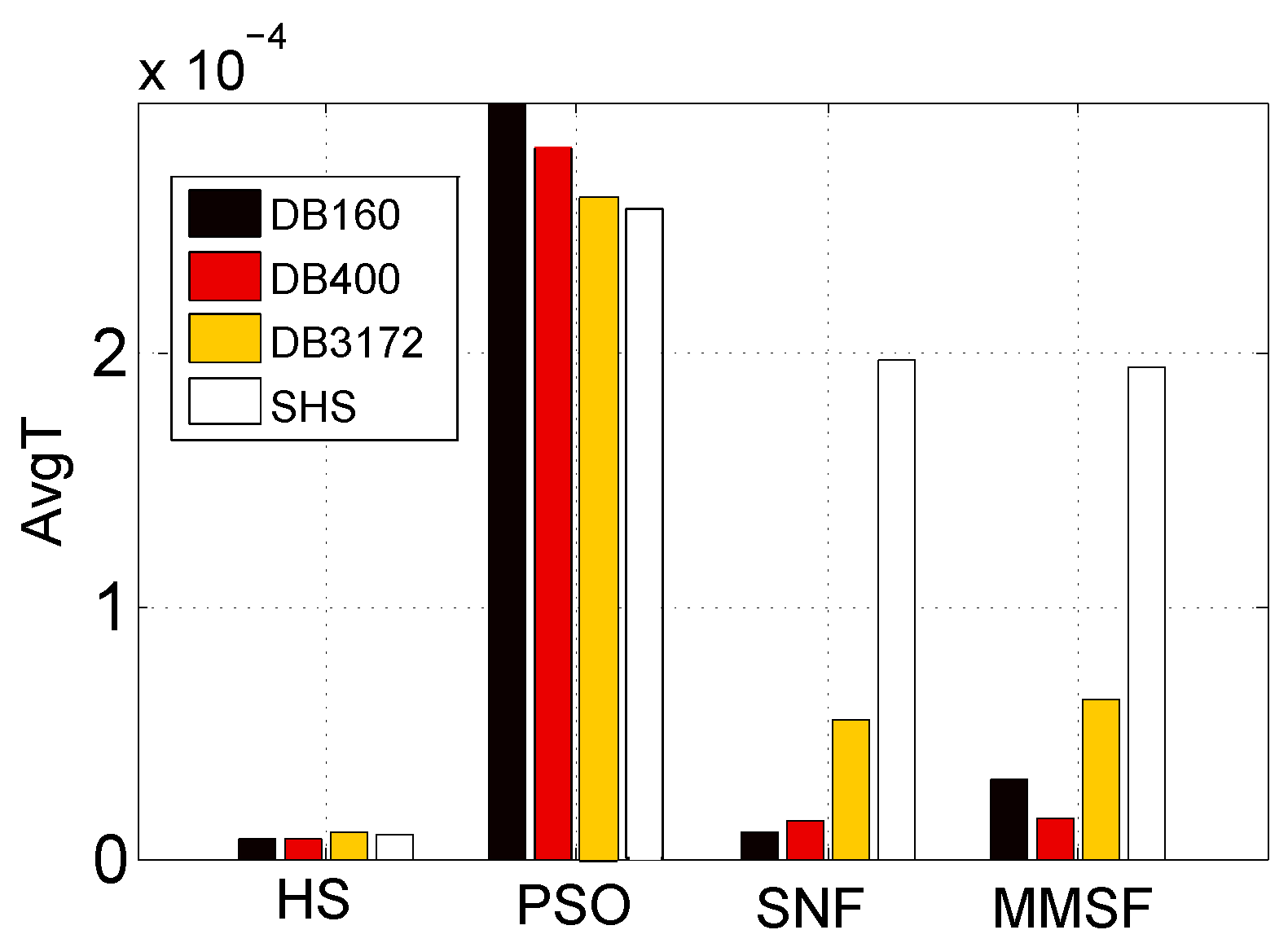
3.3.3. Computational Complexity Comparison
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BL | BaseLine |
| CSI | Cover Song Identification |
| HPCP | Harmonic Pitch Class Profile |
| HS | High Space |
| K-NN | K Nearest Neighbor |
| LCDP | Locally Constrained Diffusion Process |
| MAP | Mean of Average Precision |
| MaRR | Mean Averaged Reciprocal Rank |
| MMM | Mixture Markov Model |
| MLD | Melody |
| MIR | Music Information Retrieval |
| MIREX | Music Information Retrieval Evaluation eXchange |
| MP | Mutual Proximity |
| PSO | Particle Swarm Optimization |
| SHS | Second Hand Songs |
| SNF | Similarity Network Fusion |
| TLSFP | Two-Level Similarity Fusion and Post-Processing |
| TOP-10 | Total Number of Covers Identified in TOP 10 |
References
- Berenzweig, A.; Logan, B.; Ellis, D.P.; Whitman, B. A large-scale evaluation of acoustic and subjective music-similarity measures. Comput. Music J. 2004, 28, 63–76. [Google Scholar] [CrossRef]
- Dannenberg, R.B.; Goto, M. Music structure analysis from acoustic signals. In Handbook of Signal Processing in Acoustics; Springer: New York, NY, USA, 2008; pp. 305–331. [Google Scholar]
- Ellis, D.P. Identifying ‘cover songs’ with beat-synchronous chroma features. MIREX 2006, 1–4. [Google Scholar] [CrossRef]
- Serra, J.; Serra, X.; Andrzejak, R.G. Cross recurrence quantification for cover song identification. New J. Phys. 2009, 11, 093017. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Chen, N. Cover Song Identification Based on Cross Recurrence Plot and Local Alignment. J. East China Univ. Sci. Technol. 2016, 42, 247–253. [Google Scholar]
- Salamon, J.; Serrà, J.; Gómez, E. Melody, bass line, and harmony representations for music version identification. In Proceedings of the 21st International Conference Companion on World Wide Web, Lyon, France, 16–20 April 2012; pp. 887–894. [Google Scholar]
- Chen, N.; Li, M.; Xiao, H. Two-layer similarity fusion model for cover song identification. EURASIP J. Audio Speech Music Process. 2017, 2017, 12. [Google Scholar] [CrossRef]
- Chen, N.; Li, W.; Xiao, H. Fusing similarity functions for cover song identification. Multimed. Tools Appl. 2018, 77, 2629–2652. [Google Scholar] [CrossRef]
- Foucard, R.; Durrieu, J.L.; Lagrange, M.; Richard, G. Multimodal similarity between musical streams for cover version detection. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 5514–5517. [Google Scholar]
- Ravuri, S.; Ellis, D.P. Cover song detection: From high scores to general classification. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 65–68. [Google Scholar]
- Degani, A.; Dalai, M.; Leonardi, R.; Migliorati, P. A heuristic for distance fusion in cover song identification. In Proceedings of the 14th International Workshop on Image Analysis for Multimedia Interactive Services (WIAMIS), Paris, France, 3–5 July 2013; pp. 1–4. [Google Scholar]
- Chen, N.; Xiao, H.D. Similarity fusion scheme for cover song identification. Electron. Lett. 2016, 52, 1173–1175. [Google Scholar] [CrossRef]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Tralie, C.J. Early MFCC And HPCP Fusion for Robust Cover Song Identification. arXiv, 2017; arXiv:1707.04680. [Google Scholar]
- Schnitzer, D.; Flexer, A.; Schedl, M.; Widmer, G. Local and global scaling reduce hubs in space. J. Mach. Learn. Res. 2012, 13, 2871–2902. [Google Scholar]
- Yang, X.; Koknar-Tezel, S.; Latecki, L.J. Locally constrained diffusion process on locally densified distance spaces with applications to shape retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 357–364. [Google Scholar]
- Zhou, D.; Burges, C.J. Spectral clustering and transductive learning with multiple views. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 1159–1166. [Google Scholar]
- Gómez, E. Tonal Description of Music Audio Signals. Ph.D. Thesis, Universitat Pompeu Fabra, Barcelona, Spain, 2006. [Google Scholar]
- Tsai, W.H.; Yu, H.M.; Wang, H.M. Using the Similarity of Main Melodies to Identify Cover Versions of Popular Songs for Music Document Retrieval. J. Inf. Sci. Eng. 2008, 24, 1669–1687. [Google Scholar]
- Salamon, J. Melody Extraction from Polyphonic Music Signals. Ph.D. Thesis, Universitat Pompeu Fabra, Barcelona, Spain, 2013. [Google Scholar]
- Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on evolutionary computation, Seoul, Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar]
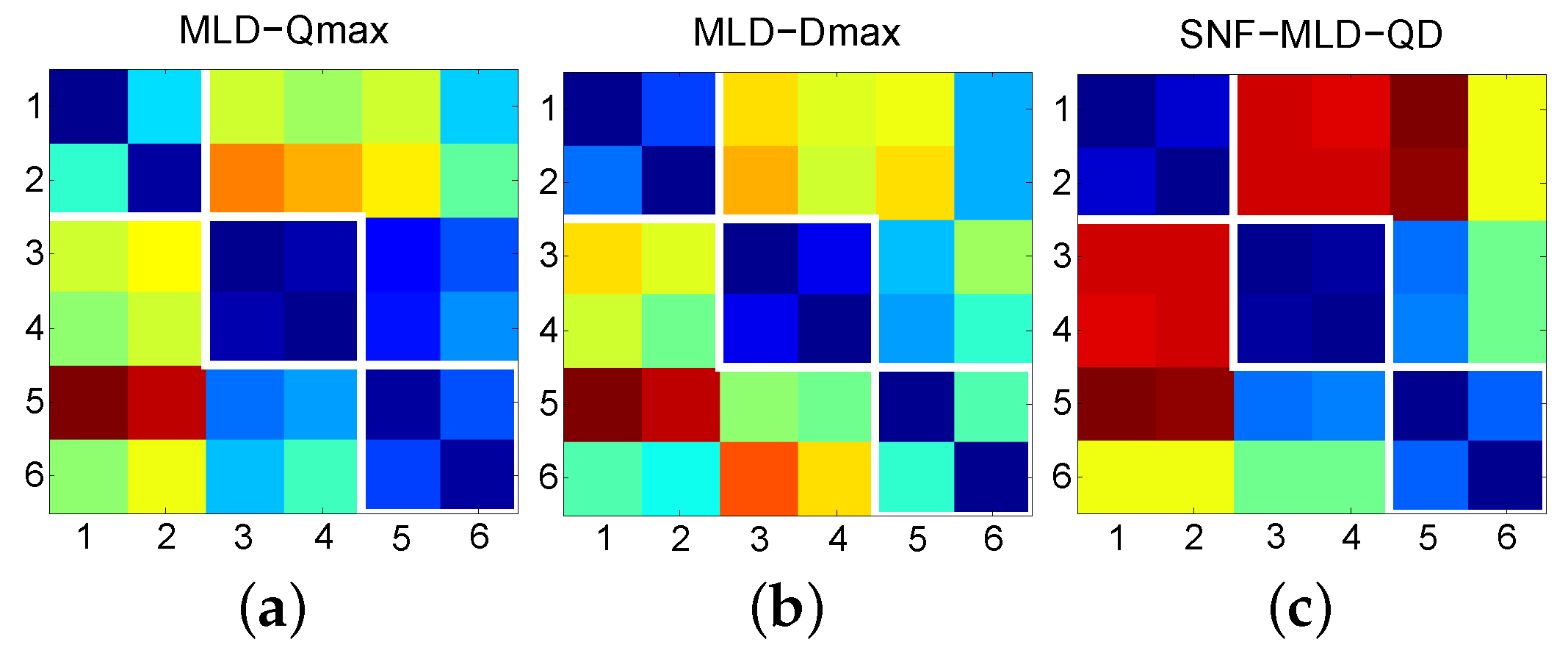

| Cover Sets | Title of the Tracks | Artists | Track ID |
|---|---|---|---|
| No. 1 | Wish You Were Here | Wyclef Jean | 1 |
| Pink Floyd | 2 | ||
| No. 2 | White Room | Sheryl Crow | 3 |
| Cream | 4 | ||
| No. 3 | Yesterday | En Vogue | 5 |
| Beatles | 6 |
| Dataset Name | Num. of Tracks | Num. of Cover Sets | Ave. Num. of Tracks in Each Cover Set |
|---|---|---|---|
| DB160 | 160 | 80 | 2 |
| DB400 | 400 | 40 | 10 |
| DB3172 | 3172 | 1119 | 2.83 |
| DB3183 | 3183 | 985 | 3.23 |
| DB3187 | 3187 | 1030 | 3.09 |
| DB3188 | 3188 | 1101 | 2.90 |
| Datasets | Algorithm | MAP | MaRR | TOP-10 |
|---|---|---|---|---|
| DB160 | HPCP-Qmax [4] | 0.5435 | 0.2831 | 98 |
| HPCP-Dmax [5] | 0.5709 | 0.2979 | 104 | |
| PSO (HPCP-Qmax) [21] | 0.5758 | 0.2993 | 101 | |
| HS [11] | 0.5868 | 0.3086 | 107 | |
| SNF-2 [8] | 0.6247 | 0.3269 | 114 | |
| SNF-3 [12] | 0.6413 | 0.3346 | 113 | |
| SNF-4 | 0.6479 | 0.3369 | 114 | |
| Two-layer-fusion [7] | 0.6680 | 0.6680 | 119 | |
| TLSFP | 0.6817 | 0.6817 | 125 | |
| DB400 | HPCP-Qmax [4] | 0.8227 | 0.1907 | 2852 |
| HPCP-Dmax [5] | 0.7945 | 0.1907 | 2717 | |
| PSO [21] | 0.7933 | 0.2445 | 2571 | |
| HS [11] | 0.7564 | 0.1883 | 2651 | |
| SNF-2 [8] | 0.9359 | 0.2040 | 3286 | |
| SNF-3 [12] | 0.9611 | 0.2080 | 3408 | |
| SNF-4 | 0.9848 | 0.2118 | 3529 | |
| Two-layer-fusion [7] | 0.9754 | 0.3094 | 3482 | |
| TLSFP | 0.9866 | 0.3107 | 3545 | |
| DB3172 | HPCP-Qmax [4] | 0.4448 | 0.2831 | 3538 |
| HPCP-Dmax [5] | 0.4412 | 0.2059 | 3501 | |
| PSO [21] | 0.4593 | 0.2101 | 3634 | |
| HS [11] | 0.3536 | 0.1691 | 2832 | |
| SNF-2 [8] | 0.5399 | 0.2379 | 4556 | |
| SNF-3 [12] | 0.5004 | 0.2238 | 3962 | |
| SNF-4 | 0.5602 | 0.2468 | 4602 | |
| Two-layer-fusion [7] | 0.5622 | 0.4579 | 4734 | |
| TLSFP | 0.5673 | 0.4590 | 4787 | |
| DB3183 | HPCP-Qmax [4] | 0.4296 | 0.1877 | 4647 |
| HPCP-Dmax [5] | 0.4321 | 0.1921 | 4567 | |
| PSO [21] | 0.4442 | 0.1938 | 4768 | |
| HS [11] | 0.2947 | 0.1366 | 3103 | |
| SNF-2 [8] | 0.5512 | 0.2285 | 6015 | |
| SNF-3 [12] | 0.4893 | 0.2064 | 5177 | |
| SNF-4 | 0.5508 | 0.2285 | 6015 | |
| Two-layer-fusion [7] | 0.5546 | 0.4147 | 6309 | |
| TLSFP | 0.5693 | 0.4221 | 6461 | |
| DB3187 | HPCP-Qmax [4] | 0.4270 | 0.1909 | 4025 |
| HPCP-Dmax [5] | 0.4189 | 0.1918 | 3862 | |
| PSO [21] | 0.4398 | 0.1967 | 4128 | |
| HS [11] | 0.3127 | 0.1472 | 2981 | |
| SNF-2 [8] | 0.5325 | 0.2270 | 5198 | |
| SNF-3 [12] | 0.4865 | 0.2119 | 4487 | |
| SNF-4 | 0.5513 | 0.2339 | 5410 | |
| Two-layer-fusion [7] | 0.5358 | 0.4168 | 5421 | |
| TLSFP | 0.5444 | 0.4207 | 5502 | |
| DB3188 | HPCP-Qmax [4] | 0.4485 | 0.2031 | 3835 |
| HPCP-Dmax [5] | 0.4502 | 0.2084 | 3815 | |
| PSO [21] | 0.4609 | 0.2098 | 3938 | |
| HS [11] | 0.3630 | 0.1711 | 3173 | |
| SNF-2 [8] | 0.5391 | 0.2361 | 4792 | |
| SNF-3 [12] | 0.4951 | 0.2199 | 4193 | |
| SNF-4 | 0.5429 | 0.2383 | 4755 | |
| Two-layer-fusion [7] | 0.5484 | 0.4456 | 4946 | |
| TLSFP | 0.5571 | 0.4504 | 5029 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Chen, N. A Robust Cover Song Identification System with Two-Level Similarity Fusion and Post-Processing. Appl. Sci. 2018, 8, 1383. https://doi.org/10.3390/app8081383
Li M, Chen N. A Robust Cover Song Identification System with Two-Level Similarity Fusion and Post-Processing. Applied Sciences. 2018; 8(8):1383. https://doi.org/10.3390/app8081383
Chicago/Turabian StyleLi, Mingyu, and Ning Chen. 2018. "A Robust Cover Song Identification System with Two-Level Similarity Fusion and Post-Processing" Applied Sciences 8, no. 8: 1383. https://doi.org/10.3390/app8081383





