MHD Steady/Unsteady Porous Boundary Layer of Cu–Water Nanofluid with Micropolar Effect over a Permeable Surface
Abstract
:1. Introduction
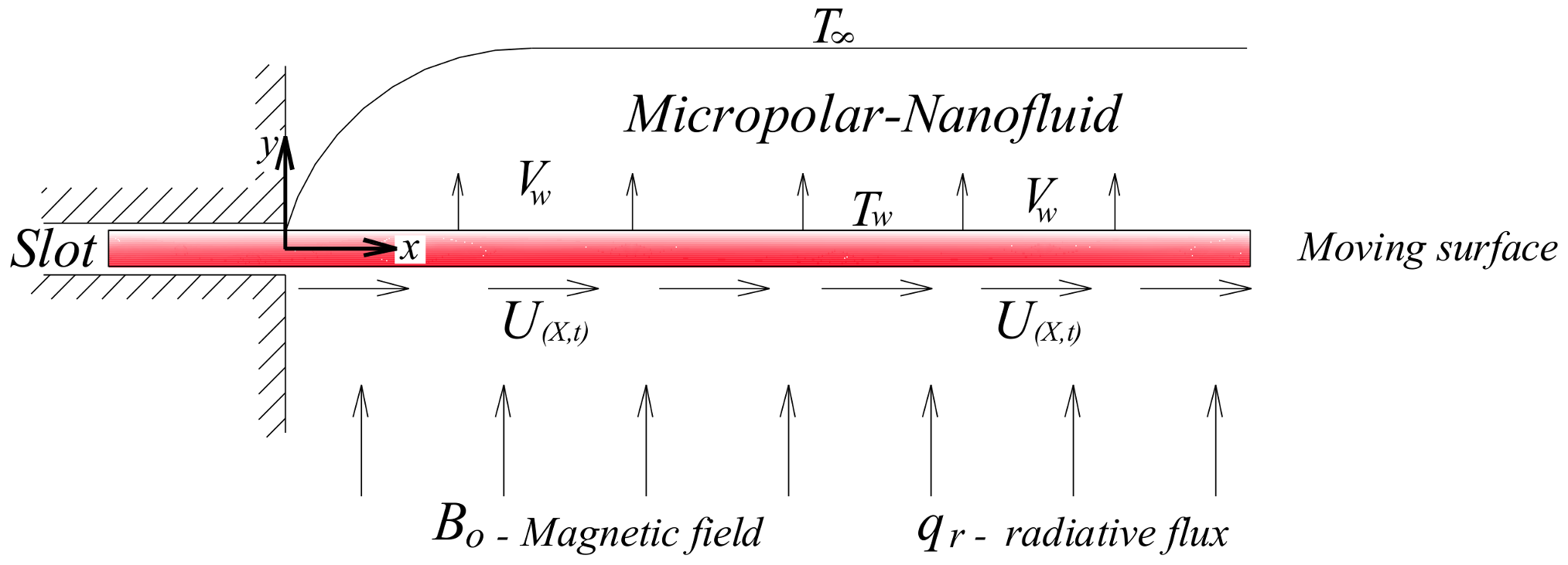
2. Formulation of the Problem
3. Solutions and Results
3.1. Steady Weak Concentration Boundary Layer
3.1.1. Exact Solution of the Momentum Boundary Layer Problem
3.1.2. Exact Solution of the Momentum Boundary Layer Problem
3.2. Unsteady Weak Concentration Boundary Layer
4. Physical Aspect of the Problem
4.1. Surface Shear Stress
4.2. Surface Couple Stress
4.3. Surface Heat Flux
5. Discussion
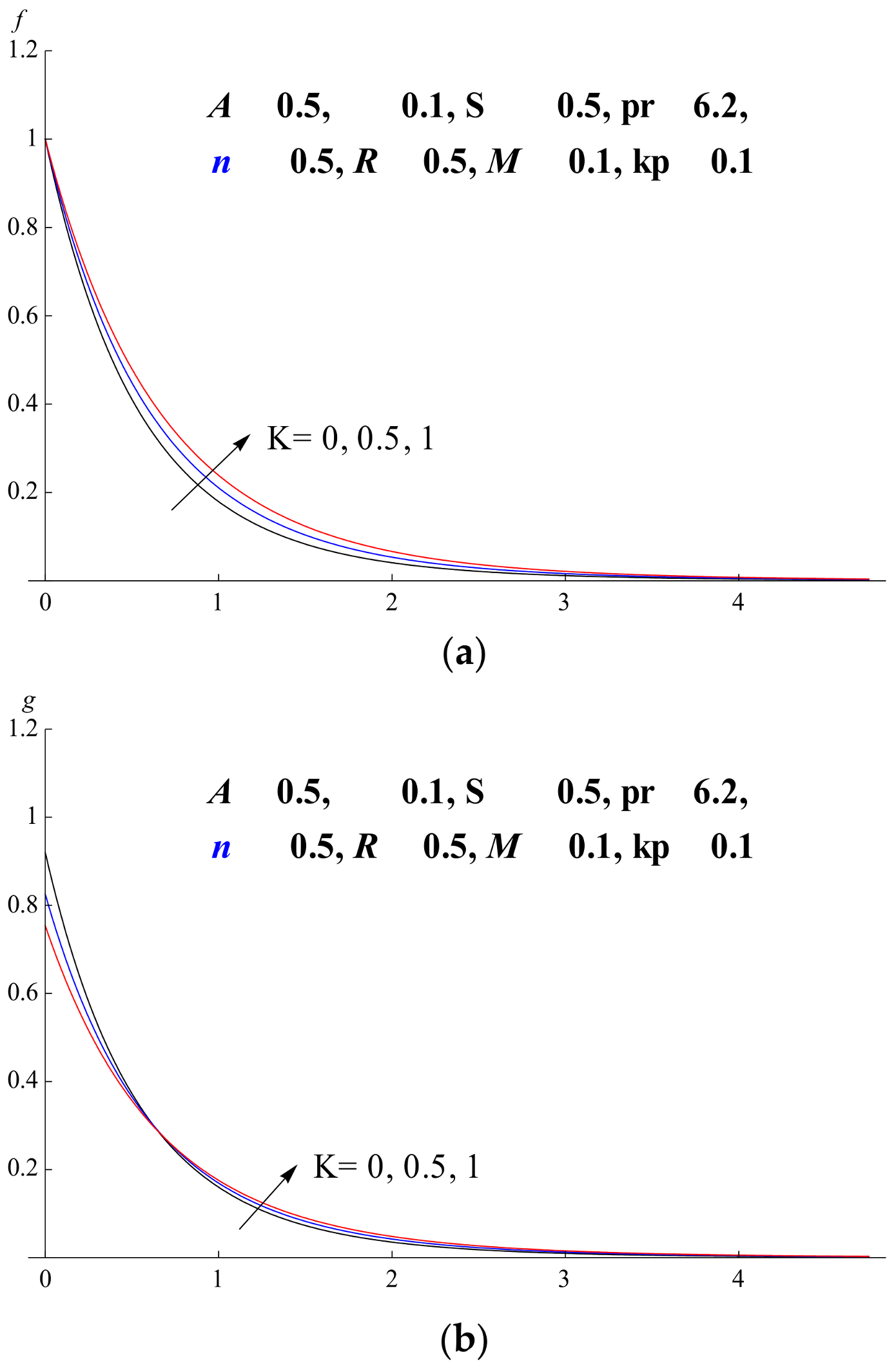
5.1. Material Parameter
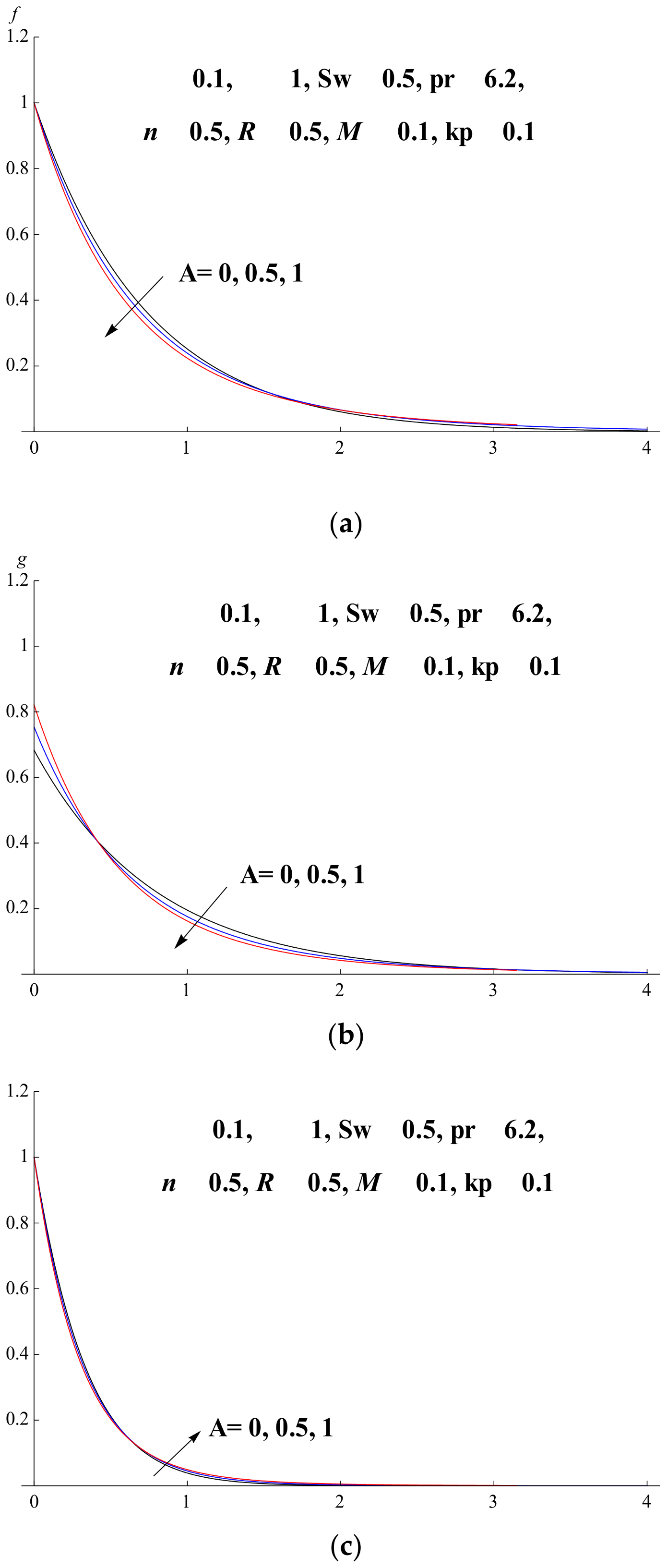
5.2. Steady/Unsteady Boundary Layer
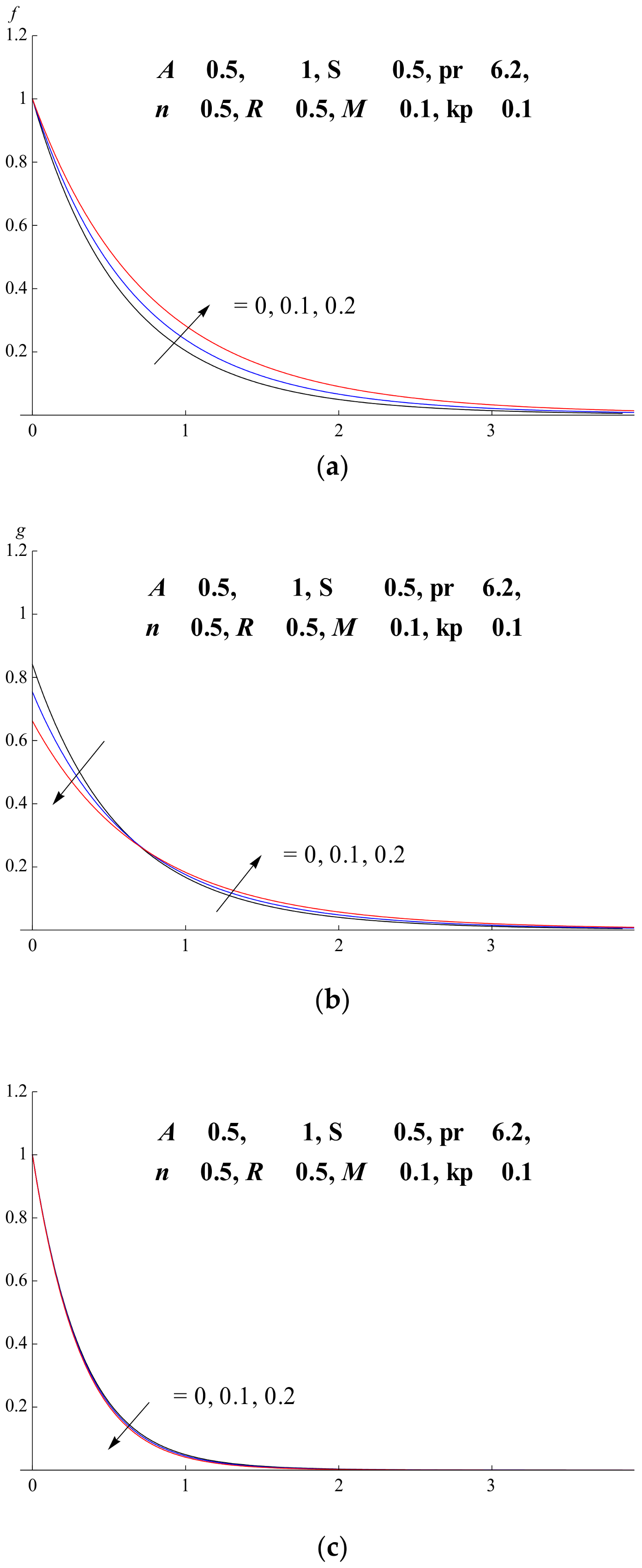
5.3. Nanoparticle Concentration
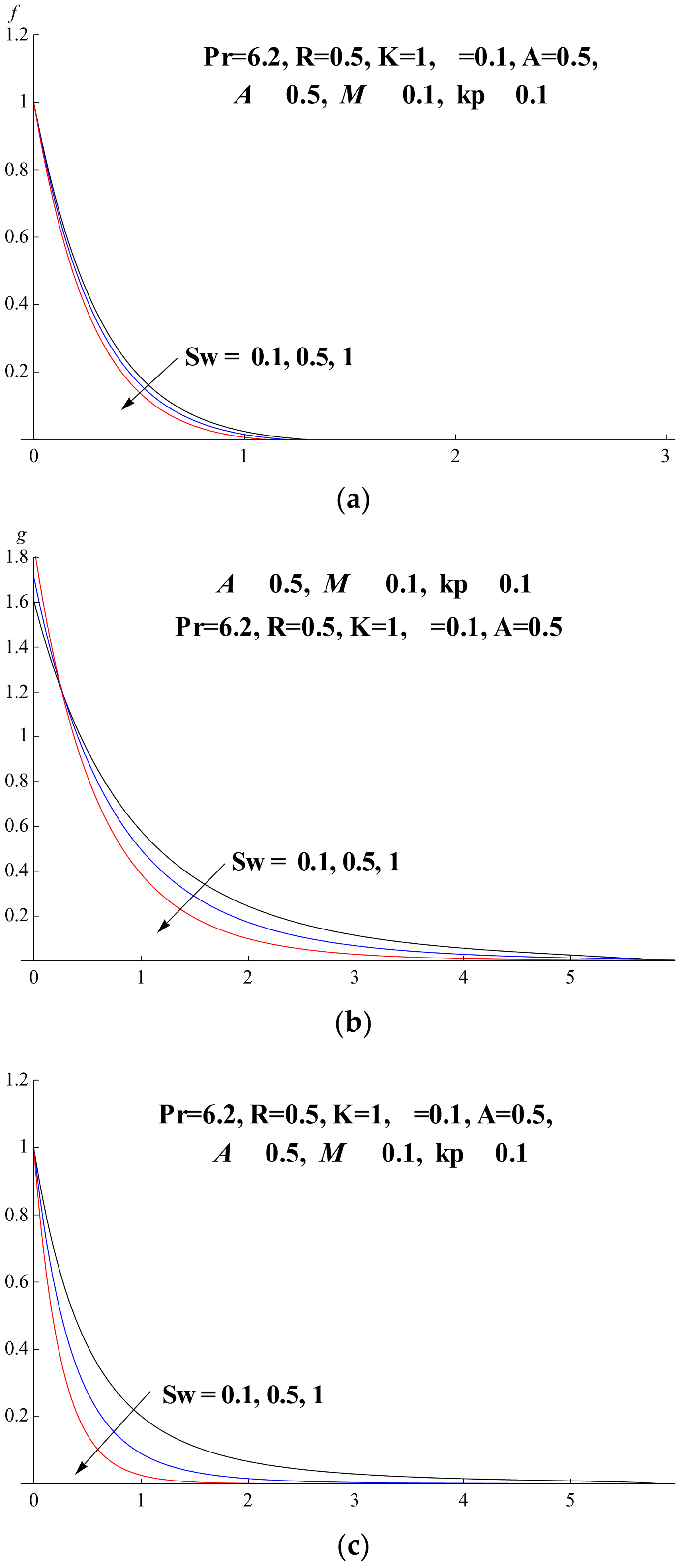
5.4. Suction Parameter Effect
5.5. Permeability Effect
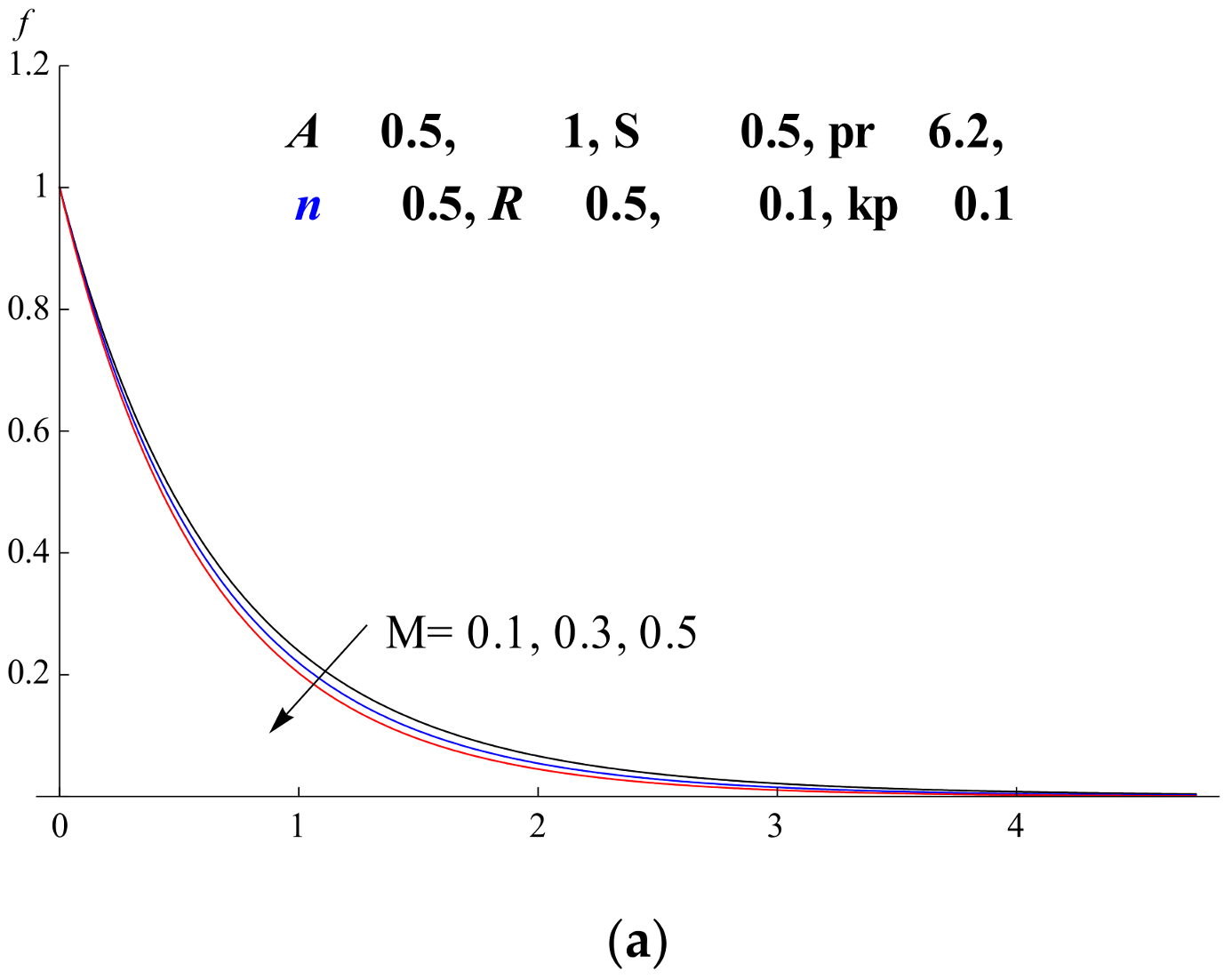
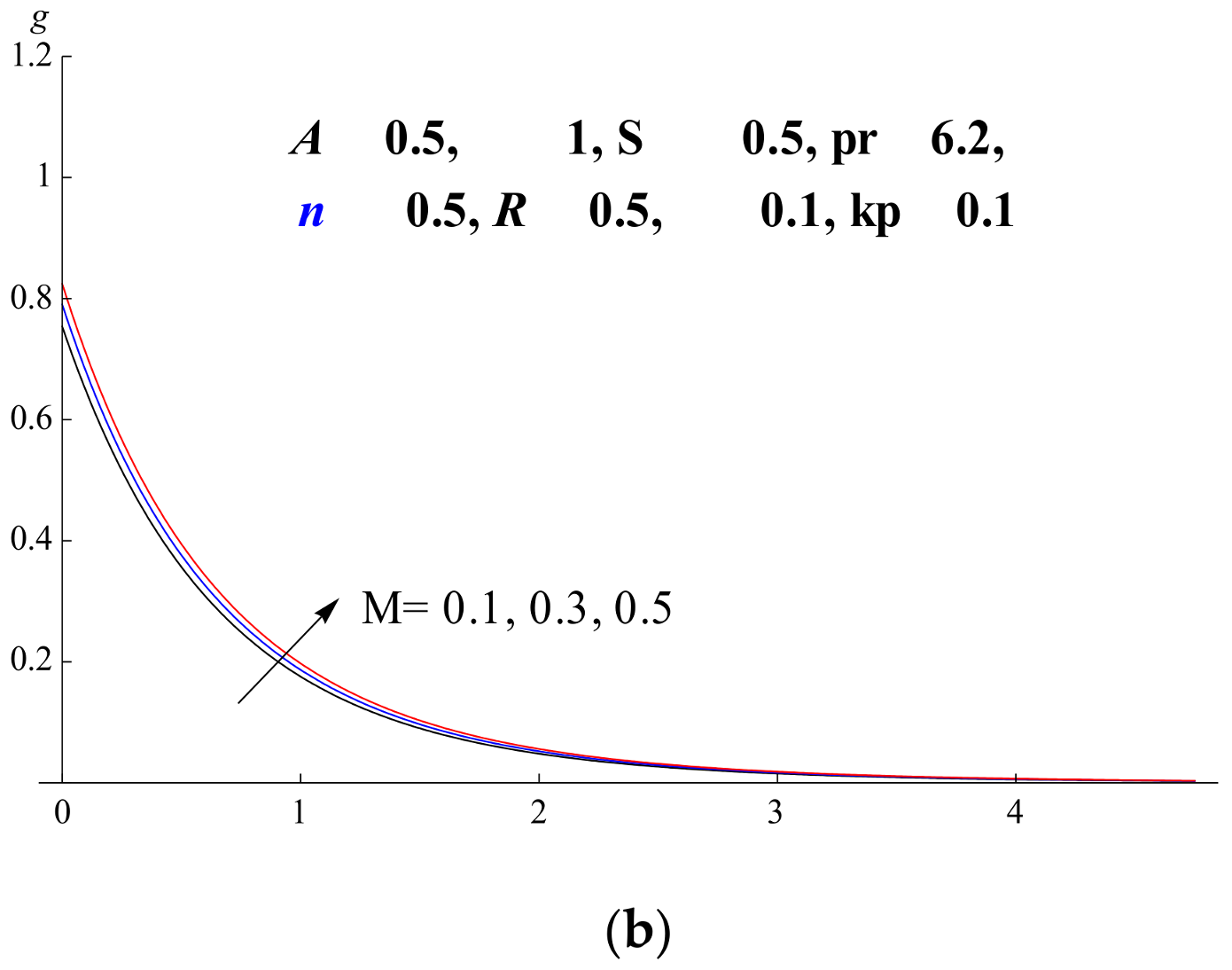
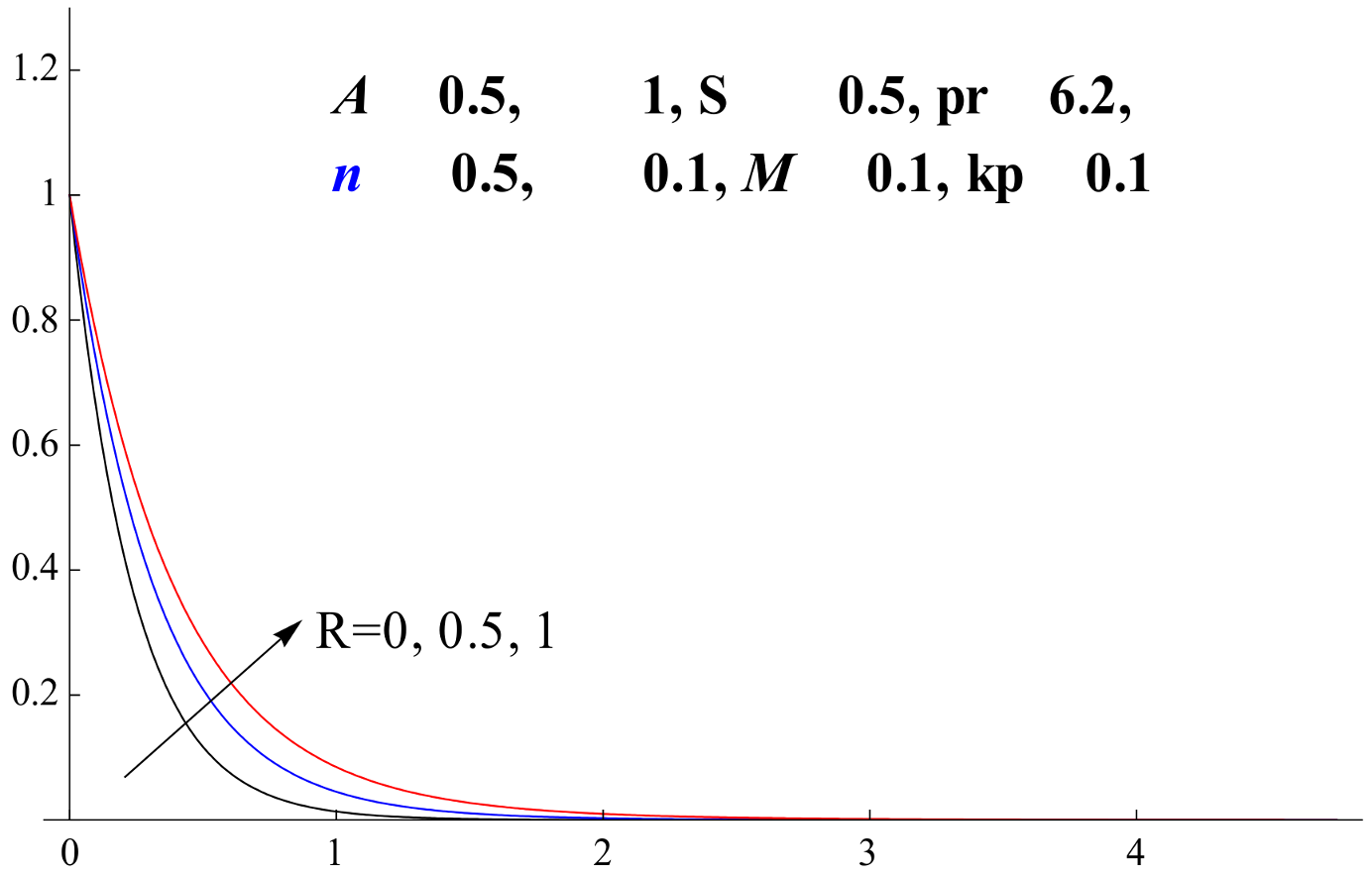
5.6. Magnetic–Radiation Effect
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Cartesian coordinate system | |
| Constants | |
| Velocity components along the x-, y-directions | |
| Angular velocity | |
| Time | |
| The stream function | |
| Velocity of the stretching sheet along x- and y-directions | |
| Fluid temperature | |
| boundary parameter | |
| vortex viscosity | |
| Porous medium parameter | |
| Suction parameter | |
| Material parameter | |
| Magnetic field | |
| Unsteadiness parameter | |
| Radiative heat flux | |
| Mean absorption coefficient | |
| Micro-inertia per unit mass | |
| Prandtl number | |
| Radiation parameter | |
| f, g | Dimensionless components of velocities |
| Shear stress | |
| Skin friction | |
| Dimensionless couple stress | |
| Nusselt number | |
| Density of the fluid | |
| Spin gradient viscosity | |
| Stefen–Boltzmann constant | |
| thermal diffusivity of the nanofluid | |
| Thermal conductivity | |
| Dynamic viscosity | |
| kinematic viscosity | |
| Similarity variable | |
| Nanoparticles concentration | |
| Dimensionless temperature. | |
| Subscripts | |
| Fluid phase | |
| Nanofluid | |
| Solid particles | |
| Condition of the wall | |
| Ambient condition |
References
- Elbashbeshy, E.M.A.; Emam, T.G.; Abdel-Wahed, M.S. Effect of heat treatment process with a new cooling medium (nanofluid) on the mechanical properties of an unsteady continuous moving cylinder. J. Mech. Sci. Technol. 2013, 27, 3843–3850. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, T. Nanofluids: Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 978-0-470-07473-2. [Google Scholar]
- Choi, S.U.S.; Eastman, J.A. Enhancing conductivity of fluids with nanoparticles. ASME Fluid Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Sheikholeslami, M.; Hayat, T.; Alsaedi, A. MHD free convection of Al2O3–water nanofluid considering thermal radiation: A numerical study. Int. J. Heat Mass Transf. 2016, 96, 513–524. [Google Scholar] [CrossRef]
- Azizah, M.; Syakila, A.; Pop, I. Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids. Int. J. Heat Mass Transf. 2011, 55, 1888–1897. [Google Scholar]
- Hamad, M. Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int. Commun. Heat Mass Transf. 2011, 38, 487–492. [Google Scholar] [CrossRef]
- Nazar, R.; Tham, L.; Pop, I. Mixed convection boundary layer flow from a horizontal circular cylinder embedded in a porous medium filled with a nanofluid. Transp. Porous Med. 2011, 86, 517–536. [Google Scholar] [CrossRef]
- Yacob, N.A.; Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow past a stretching/shrinking surface beneath an external uniform shear flow with a convective surface boundary condition in a nanofluid. Nanoscale Res. Lett. 2011, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Elbashbeshy, E.M.A.; Emam, T.G.; Abdel-Wahed, M.S. Effect of magnetic field on flow and heat transfer of a nanofluid over an unsteady continuous moving surface in the presence of suction/injection. Int. J. Appl. Math. 2012, 14, 436–442. [Google Scholar]
- Qasim, M.; Khan, Z.; Lopez, R.; Khan, W. Heat and mass transfer in nanofluid thin film over an unsteady stretching sheet using Buongiorno’s model. Eur. Phys. J. Plus 2016, 131, 16. [Google Scholar] [CrossRef]
- Anbuchezhian, N.; Srinivasan, K.; Chandrasekaran, K.; Kandasamy, R. Thermophoresis and Brownian motion effects on boundary layer flow of nanofluid in presence of thermal stratification due to solar energy. Appl. Math. Mech. 2012, 33, 765–780. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Emam, T.G.; Abdel-Wahed, M.S. Flow and heat transfer over a moving surface with non-linear velocity and variable thickness in a nanofluid in the presence of thermal radiation. Can. J. Phys. 2013, 91, 699–708. [Google Scholar]
- Elbashbeshy, E.M.A.; Emam, T.G.; Abdel-Wahed, M.S. An exact solution of boundary layer flow over a moving surface embedded into a nanofluid in the presence of magnetic field and suction/injection. Heat Mass Transf. 2014, 50, 57–64. [Google Scholar] [CrossRef]
- EElbashbeshy, M.A.; Emam, T.G.; Abdel-Wahed, M.S. The effect of thermal radiation and heat generation on the mechanical properties of unsteady continuous moving cylinder in a nanofluid in the presence of suction or injection. Therm. Sci. 2015, 19, 1591–1601. [Google Scholar] [CrossRef]
- Abdel-wahed, M.S.; Elbashbeshy, E.M.A.; Emam, T.G. Flow and heat transfer over a moving surface with non-linear velocity and variable thickness in a nanofluid in the presence of Brownian motion. Appl. Math. Comput. 2015, 254, 1591–1601. [Google Scholar] [CrossRef]
- Yain, Y.; Amin, N.; Pop, I. Unsteady boundary layer flow of a micropolar fluid near rear stagnation point of a plane surface. Int. J. Therm. Sci. 2003, 42, 995–1001. [Google Scholar]
- Sandeep, N.; Sulochana, C. Dual solution for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink. Eng. Sci. Technol. 2015, 18, 738–745. [Google Scholar] [CrossRef]
- Abo-Eldahab, E.M.; El Aziz, M.A. Flow and heat transfer in a micropolar fluid past a stretching surface embedded in a non-Darcian porous medium with uniform free stream. Appl. Math. Comput. 2005, 162, 881–899. [Google Scholar] [CrossRef]
- Rahman, M.; Sultana, T. Radiative Heat transfer flow of micropolar fluid with variable heat flux in a porous medium. Nonlinear Anal. Model. Control 2008, 13, 17–87. [Google Scholar]
- Ishak, A.; Nazar, R.; Pop, I. Heat transfer over a stretching surface with variable heat flux in micropolar fluids. Phys. Lett. A 2007, 372, 559–561. [Google Scholar] [CrossRef]
- Khedr, M.E.M.; Chamkha, A.J.; Bayomi, M. MHD flow of a micropolar fluid past a stretched permeable surface with heat generation or absorption. Nonlinear Anal. Model. Control 2009, 14, 27–40. [Google Scholar]
- Rahman, M.; El-tayeb, A.; Rahman, S.M.M. Thermo-micropolar fluid flow along a vertical permeable plate with uniform surface heat flux in the presence of heat generation. Therm. Sci. 2009, 13, 23–36. [Google Scholar] [CrossRef]
- Saad, A.A.; Abdel-Wahed, M.S. Heat transfer over unsteady moving surface with heat generation and thermal radiation in micropolar fluid in the presence of suction/injection. Int. J. Energy Technol. 2011, 3, 1–7. [Google Scholar]
- L-Arabawy, H.A.M.E. Effects of suction/injection on the flow of micropolar fluid past a continuously moving plate in the presence of radiation. Int. J. Heat Mass Transf. 2003, 46, 1471–1477. [Google Scholar] [CrossRef]
- Hussain, S.T.; Nadeem, S.; Haq, R.U. Model-based analysis of micropolar nanofluid flow over a stretching surface. Eur. Phys. J. Plus 2014, 129, 161. [Google Scholar] [CrossRef]
- Ezzah, L.A.; Syakila, A.; Pop, I. Flow over a permeable stretching sheet in micropolar nanofluids with suction. AIP Conf. Proc. 2014, 1605, 428–433. [Google Scholar]
- Turkyilmazoglu, M. Flow of a micropolar fluid due to a porous stretching sheet and heat transfer. Int. J. Non-Linear Mech. 2016, 83, 59–64. [Google Scholar] [CrossRef]
- Mabood, F.; Ibrahim, S.M.; Rashidi, M.M.; Shadloo, M.S. Giulio Lorenzini, Nonuniform heat source/sink and Soret effects on MHD non-Darcian convective flow past a stretching sheet in a micropolar fluid with radiation. Int. J. Heat Mass Transf. 2016, 93, 674–682. [Google Scholar] [CrossRef]
- Ramzan, M.; Farooq, M.; Hayat, T.; Chung, J.D. Radiative and Joule heating effects in the MHD flow of a micropolar fluid with partial slip and convective boundary condition. J. Mol. Liq. 2016, 221, 394–400. [Google Scholar] [CrossRef]
- Hsiao, K. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Mahmood, A.; Chen, B.; Ghaffari, A. Hydromagnetic Hiemenz flow of micropolar fluid over a nonlinearly stretching/shrinking sheet: Dual solutions by using Chebyshev Spectral Newton Iterative Scheme. J. Magn. Magn. Mater. 2016, 416, 329–334. [Google Scholar] [CrossRef]
- Borrelli, A.; Giantesio, G.; Patria, M.C. MHD orthogonal stagnation-point flow of a micropolar fluid with the magnetic field parallel to the velocity at infinity. Appl. Math. Comput. 2015, 264, 44–60. [Google Scholar] [CrossRef]
- Abdel-Wahed, M.S. Lorentz force effect on mixed convection micropolar flow in a vertical conduit. Eur. Phys. J. Plus 2017, 132, 195. [Google Scholar] [CrossRef]
- Abdel-wahed, M.S. Flow and heat transfer of a weak concentration micropolar nanofluid over steady/unsteady-moving surface. Appl. Phys. A 2017, 123, 195. [Google Scholar] [CrossRef]
- Vo, T.Q.; Kim, B.H. Molecular Dynamics Study of Thermodynamic Properties of Nanoclusters for Additive Manufacturing. Int. J. Precis. Eng. Manuf. Green Technol. 2017, 4, 301–306. [Google Scholar] [CrossRef]
- Vo, T.Q.; Park, B.; Park, C.; Kim, B. Nano-scale liquid film sheared between strong wetting surfaces: Effects of interface region on the flow. J. Mech. Sci. Technol. 2015, 29, 1681–1688. [Google Scholar] [CrossRef]
- Priezjev, N.V. Molecular dynamics simulations of oscillatory Couette flows with slip boundary conditions. Microfluid Nanofluid 2013, 14, 225–233. [Google Scholar] [CrossRef]
- Kim, B.H.; Beskok, A.; Cagin, T. Viscous heating in nanoscale shear driven liquid flows. Microfluid Nanofluid 2010, 9, 31–40. [Google Scholar] [CrossRef]
- Rodrıguez-Lopez, J.L.; Montejano-Carrizales, J.M.; Jose-Yacaman, M. Molecular dynamics study of bimetallic nanoparticles: The case of AuxCuy alloy clusters. Appl. Surf. Sci. 2003, 219, 56–63. [Google Scholar] [CrossRef]
- Kim, B. Thermal resistance at a liquid–solid interface dependent on the ratio of thermal oscillation frequencies. Chem. Phys. Lett. 2012, 554, 77–81. [Google Scholar] [CrossRef]
- Murad, S.; Puri, I.K. Molecular simulation of thermal transport across hydrophilic interfaces. Chem. Phys. Lett. 2008, 467, 110–113. [Google Scholar] [CrossRef]

| Properties | Fluid (Water) | Cu |
|---|---|---|
| 4179 | 385 | |
| 997.1 | 8933 | |
| 0.613 | 400 |
| Parameter | Present Results | Ezzah [26] | ||||
|---|---|---|---|---|---|---|
| Exact Solution | Numerical Solution | |||||
| 2 | 3.9182 | 1.9190 | 3.9182 | 1.9190 | 3.9183 | 1.9191 |
| 3 | 5.27412 | 3.4770 | 5.27412 | 3.4770 | 5.2741 | 3.4770 |
| K | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | −0.5 | 0.1 | 4.038346 | 0.979447 | 0.531071 | −8.076692 | 0.531071 | −1.958894 |
| 0.1 | 3.584031 | 0.712813 | 0.518383 | −7.189817 | 0.690297 | −1.699500 | ||
| 0.2 | 3.130794 | 0.576239 | 0.564942 | −4.220449 | 0.986223 | −1.152478 | ||
| 0 | 0.0 | 4.464803 | 1.728692 | 0.924024 | −13.39440 | 0.924024 | −4.321730 | |
| 0.1 | 3.913861 | 1.421675 | 1.020822 | −5.672146 | 1.359363 | −2.843350 | ||
| 0.2 | 3.378040 | 0.990240 | 1.344222 | −5.857106 | 2.346619 | −2.263903 | ||
| 0.5 | 0.0 | 4.936295 | 3.625016 | 1.828576 | −9.872590 | 1.828576 | −7.250032 | |
| 0.1 | 4.274045 | 2.593231 | 1.895725 | −8.574034 | 2.524416 | −6.182824 | ||
| 0.2 | 3.644810 | 1.769211 | 2.522203 | −4.913365 | 4.403029 | −3.538422 | ||
| 0.5 | −0.5 | 0.0 | 3.405583 | 0.803944 | 0.522100 | −10.21674 | 0.522100 | −2.009860 |
| 0.1 | 3.124187 | 0.686680 | 0.551381 | −4.527714 | 0.734239 | −1.373360 | ||
| 0.2 | 2.814292 | 0.574242 | 0.594486 | −4.879636 | 1.037798 | −1.312841 | ||
| 0 | 0.0 | 3.743495 | 1.450575 | 0.992598 | −7.486990 | 0.992598 | −2.901150 | |
| 0.1 | 3.400468 | 1.189547 | 1.054966 | −6.821577 | 1.404831 | −2.836137 | ||
| 0.2 | 3.030169 | 0.926740 | 1.126033 | −4.084802 | 1.965724 | −1.853480 | ||
| 0.5 | 0.0 | 4.141100 | 2.661302 | 1.888458 | −12.42330 | 1.888458 | −6.653255 | |
| 0.1 | 3.715203 | 2.044583 | 1.944352 | −5.384242 | 2.589170 | −4.089166 |
| K | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | −0.5 | 0.0 | 4.190553 | 3.102011 | 1.339903 | −8.381106 | 1.339903 | −6.204022 |
| 0.1 | 3.717099 | 2.476667 | 1.365301 | −7.456761 | 1.818084 | −5.904910 | ||
| 0.2 | 3.245327 | 1.915456 | 1.393946 | −4.374844 | 2.433422 | −3.830912 | ||
| 0 | 0.0 | 4.613003 | 4.263178 | 1.777243 | −13.83900 | 1.777243 | −10.65794 | |
| 0.1 | 4.043774 | 3.276003 | 1.810996 | −5.860422 | 2.411588 | −6.552006 | ||
| 0.2 | 3.490167 | 2.440392 | 2.177493 | −6.051520 | 3.801266 | −5.579264 | ||
| 0.5 | 0.0 | 5.079028 | 5.919060 | 2.410378 | −10.15805 | 2.410378 | −11.83812 | |
| 0.1 | 4.399817 | 4.367775 | 2.450397 | −8.826341 | 3.263038 | −10.41372 | ||
| 0.2 | 3.753898 | 3.128262 | 3.065966 | −5.060420 | 5.352281 | −6.256524 | ||
| 0.5 | −0.5 | 0.0 | 3.6246638 | 2.481260 | 1.366782 | −10.87399 | 1.366782 | −6.203150 |
| 0.1 | 3.308656 | 2.072541 | 1.386910 | −4.795055 | 1.846860 | −4.145082 | ||
| 0.2 | 2.965490 | 1.670736 | 1.410602 | −5.141795 | 2.462499 | −3.819664 | ||
| 0 | 0.0 | 3.958321 | 3.301533 | 1.810306 | −7.916642 | 1.810306 | −6.603066 | |
| 0.1 | 3.5798703 | 2.679505 | 1.837633 | −7.181471 | 2.447059 | −6.388520 | ||
| 0.2 | 3.177986 | 2.096067 | 1.869445 | −4.284066 | 3.263504 | −4.192134 | ||
| 0.5 | 0.0 | 4.330744 | 4.434499 | 2.446977 | −12.99223 | 2.446977 | −11.08624 | |
| 0.1 | 3.878216 | 3.489879 | 2.479820 | −5.620487 | 3.302219 | −6.979758 | ||
| 0.2 | 3.408446 | 2.6443808 | 2.517496 | −5.909826 | 4.394812 | −6.045627 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raslan, K.; Mohamadain, S.; Abdel-wahed, M.; Abedel-aal, E.M. MHD Steady/Unsteady Porous Boundary Layer of Cu–Water Nanofluid with Micropolar Effect over a Permeable Surface. Appl. Sci. 2018, 8, 736. https://doi.org/10.3390/app8050736
Raslan K, Mohamadain S, Abdel-wahed M, Abedel-aal EM. MHD Steady/Unsteady Porous Boundary Layer of Cu–Water Nanofluid with Micropolar Effect over a Permeable Surface. Applied Sciences. 2018; 8(5):736. https://doi.org/10.3390/app8050736
Chicago/Turabian StyleRaslan, Kamal, Selim Mohamadain, Mohamed Abdel-wahed, and Elsayed M. Abedel-aal. 2018. "MHD Steady/Unsteady Porous Boundary Layer of Cu–Water Nanofluid with Micropolar Effect over a Permeable Surface" Applied Sciences 8, no. 5: 736. https://doi.org/10.3390/app8050736





