Immediate Settlement of Ring Footings Resting on Inhomogeneous Finite Stratum

Abstract

This paper describes the immediate settlement of uniformly loaded rough ring footings with any stiffness on an inhomogeneous finite layer overlying a rough rigid base, which is not yet covered in the literature. Numerical solutions for a wide range of geometric and material combinations are obtained by finite element method. The effects of dimensionless parameters related to footing internal opening, compressibility, footing stiffness, finite layer thickness and soil inhomogeneity are examined. Based on the results, design charts are presented in the form of settlement influence factors that can be used to calculate the immediate settlements at the inner and outer points of ring footings.

1. Introduction

Ring footings are continuous footings that have been wrapped into a circle. In engineering practice, they are commonly used to support columns or walls of axisymmetric structures such as silos, smokestacks, television antennas, communication towers, and bridge piers [1]. Ring footings with internal openings can reduce the material volume required for their construction, providing a more cost-effective design. Additionally, the ring footing has an increase in overturning stability when compared to a solid circular footing with the same area [2]. However, the contents of special structures (e.g., liquid storage tanks) are spread evenly across the total base area, and this weight is probably greater than that of the tank itself. Therefore, the response of tanks is considered to be a solid circular footing with diameters equal to the diameter of the tank [3]. The behavioral characteristics of ring footings interacting with supporting medium are dependent on the soil and loading conditions, as well as the geometry of these opening. For the realistic design of ring footings, it is essential to understand their settlement and bearing capacity.

The immediate and consolidation settlement checks are an important part of footing design. Immediate settlement is caused either by the undrained distortion of clay beneath the footings, or the drained settlement of footings on sand [4]. In general, the immediate settlement of footings on clay is small when compared with consolidation settlement. However, it may be significant, especially for highly plastic clays or organic soils. Immediate settlement is also termed elastic settlement, because it is usually calculated from the theory of elasticity using the linearly elastic soil models [5].

Several studies have been conducted to predict the immediate settlement of footings with various shapes (e.g., strip, rectangular, square and circular footings). This has been done by using the integral transform technique, semi-analytical procedures, the finite element method and the boundary element approach [4,6,7,8]. In contrast, the available investigations on immediate settlement of ring footings are few. For example, Fisher [9] presented a theoretical formulation for the elastic settlements under uniformly loaded flexible footings resting on a homogeneous isotropic elastic half-space by superposition of two circular loads of diameters corresponding to the outer and inner diameters of the annular footing. Ismael [10] performed plate loading tests to examine the load-settlement behavior of ring footings situated on cemented sands and compared the measured settlements with the predicted settlements from the elastic theory. Chandrashekhara and Antony [11] proposed a combined finite element-analytical approach to analyze the elastic settlement of rigid footings on an isotropic elastic half-space. Antony and Chandrashekhara [12] investigated the effect of soil anisotropy in the elastic settlement of rigid footings on an isotropic elastic half-space. Choobbasti et al. [13] analyzed the immediate settlement of ring footings using the finite element method by considering soil nonlinearity. Eskandari-Ghadi et al. [14] studied the vertical deflection of multiple concentric annular footings on a transversely isotropic elastic half-space. Recently, Naseri and Hosseininia [15] determined the settlement of ring footings in infinite elastic medium based on the finite difference method. Although most studies have dealt with ring footings, consideration is given to a soil layer extending to an infinite depth. The footings, however, can be placed on layered soil systems in practice. The simplest case is that of a compressible soil underlain by a rigid incompressible base, for which the estimation of immediate settlement is needed.

This paper presents results of a systematic numerical investigation of the settlements under rough ring footings of arbitrary stiffness on inhomogeneous soil of limited thickness (i.e., finite elastic stratum whose modulus increases linearly with depth) overlying a rigid frictional base. Finite element solutions for elastic settlement are obtained at both the inner and outer points of the ring footings, which allow understanding differential settlement of uniformly loaded ring footings. Settlement influence factors corresponding to the relevant range of inner-to-outer radius ratios, Poisson’s ratio, footing stiffness, finite layer thickness ratio, and modulus inhomogeneity are provided.

2. Background

The general form of the immediate settlement s at the base of a distributed load q with a characteristic dimension B is expressed as

$$s=\frac{qB}{E_s}I$$

(1)

where E_s is the elastic modulus of the soil, I is the settlement influence factor accounting for the point where the settlement is desired. The settlement influence factors depend on parameters associated to the geometry and properties of ground and footing, including soil homogeneity, Poisson’s ratio, soil layering, layer thickness, footing shape, footing stiffness, and base roughness. For the simple case of a uniformly loaded smooth circular footing on the surface of a homogeneous isotropic elastic half-space, the immediate settlement is given by

$$s=\frac{qD}{E_s}\left(1-{\nu }_s^2\right)I$$

(2)

where D is the footing diameter and ν_s is the Poisson’s ratio of the soil. For a flexible circular footing, I is equal to 1 and 2/π for the center and edge points, respectively, and 0.85 for the average settlement [10]. For a rigid circular footing, I is equal to π/4 [16].

3. Numerical Analysis

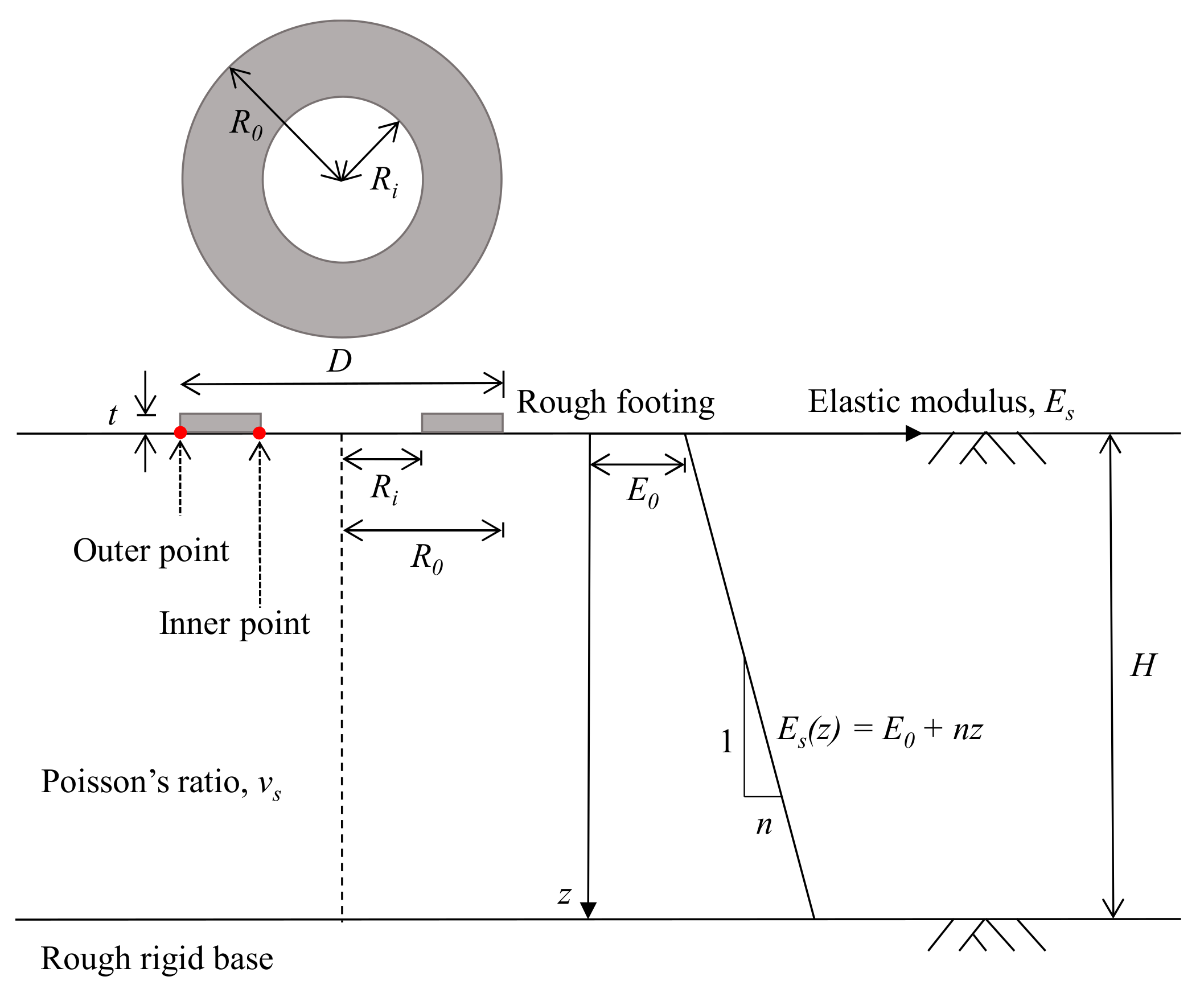
3.1. Geometry and Parameters

This study has considered ring footings placed on a layered system in which an elastic layer of finite thickness overlying a rigid rough base, as illustrated schematically in Figure 1. The ring footing is specified with inner and outer radii R_i and R₀, respectively. In this study, five inner-to-outer radius ratios (R_i/R₀ = 0, 0.2, 0.4, 0.6, and 0.8) are investigated, which covers most problems of practical interest [17]. The footing roughness is assumed to be perfectly rough, which does not permit any relative movement at all along the soil-footing interface. A similar assumption was used in the literature [18] for elastic settlement of shallow footings. The soil is modeled as an isotropic inhomogeneous continuum which obeys Hooke’s law. The soil deformation is represented by two parameters, i.e., elastic modulus E_s and Poisson’s ratio ν_s. The E_s was idealized as varying linearly with depth:

$$E_s=E_0+nz$$

(3)

where E₀ is the elastic modulus at the surface, n is the rate of increase of modulus with depth z. For a footing of diameter D (=2R₀), the degree of soil nonhomogeneity beneath the footing can be characterized by the dimensionless ratio nD/E₀, indicating that this is particularly important for large footings. As studied by Rowe and Booker [19], examinations are made for the nD/E₀ values of 0.01 to 100. As nD/E₀ ≈ 0, the modeling approaches the pure homogeneous cases. The Poisson’s ratio is assumed to be constant with depth, and the values of ν_s ranging from 0 to 0.495 are prescribed to simulate the compressible and incompressible soils. The relative stiffness K between the soil and footing for a ring footing is quantified by [20]:

$$K=\frac{E_f}{E_0}\left(1-{\nu }_s^2\right){\left(\frac{t}{R_{av}}\right)}^3$$

(4)

where E_f and t are the elastic modulus and thickness of the footing, respectively. R_av is the average radius of the footing:

$$R_{av}=\frac{R_0+R_i}{2}$$

(5)

From Equations (4) and (5), it is obvious that the decrease in the value of R_i/R₀ increases the footing stiffness, at constant values of other parameters. The footing stiffness typically lies in the range of 0.01 < K < 100 [4], and the following categories can be defined: perfectly flexible (K < 0.01), intermediate stiffness (0.01 ≤ K ≤ 10), and perfectly rigid (K > 10) [4]. To obtain solutions to layered media, the relative thickness of finite layer defined as the ratio of the upper layer thickness to the footing diameter H/D is introduced, encompassing values of H/D varying from 0.1 to 100 [21].

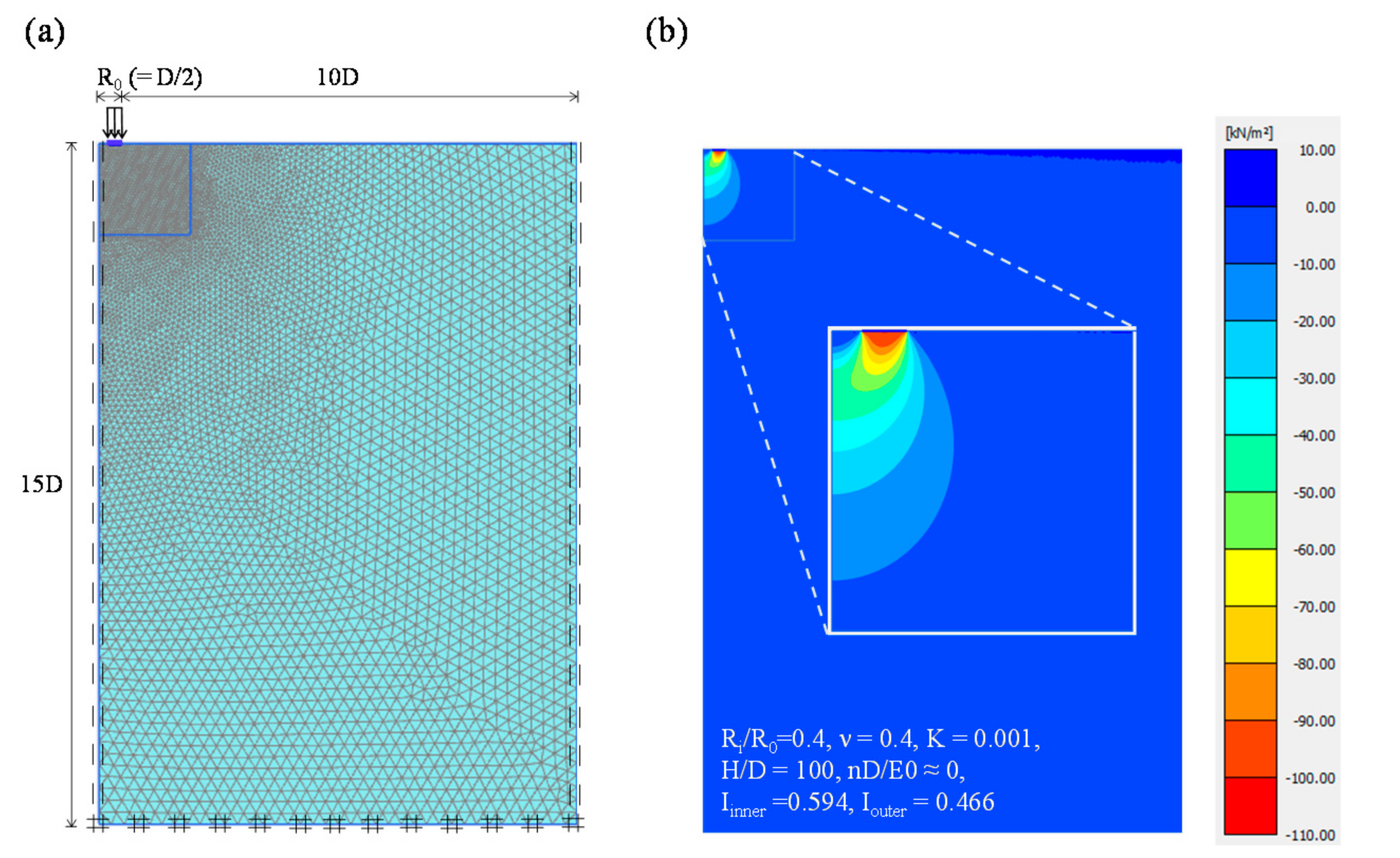
3.2. Analysis Details

Small-displacement finite element analyses were conducted using the commercial software PLAXIS 2D version 2012 [22]. The finite element model consisted of two parts: the footing and the soil. The footing was modeled with six-node triangular plate elements, and the soil was modeled with fifteen-node triangular elements. Owing to an axisymmetric distribution of the stress about a vertical line passing through the center of the footing, only one half of the total domain is employed (Figure 2a). A full fixity was set at the base of the soil domain and roller conditions at the sides. The soil domain was chosen as 10D in diameter and 15D in depth. A fine mesh was created in the region adjacent to the footing to obtain precise calculations; the distribution and concentration of the elements depend on the geometrical parameters considered. The footing was simulated as a non-porous linear elastic material with 1 m thickness and elastic modulus for concrete E_c = 30 GPa. The outer radius of the ring footing was kept constant at 5 m and other parameters were varied for the systematic exploration. The interface of the footing was rough and fully attached to the soil. A uniform stress was applied to weightless footings with different configurations and stiffnesses to determine the corresponding settlements. The elastic settlement of ring footings is obtained from a series of numerical analyses, and the settlement influence factor is calculated using Equation (1). It is noted that, for brevity, only settlement results were taken into account, although the contact pressure distribution, stress distribution in soil medium and bending moment variation in footing are readily available from this analysis (Figure 2b).

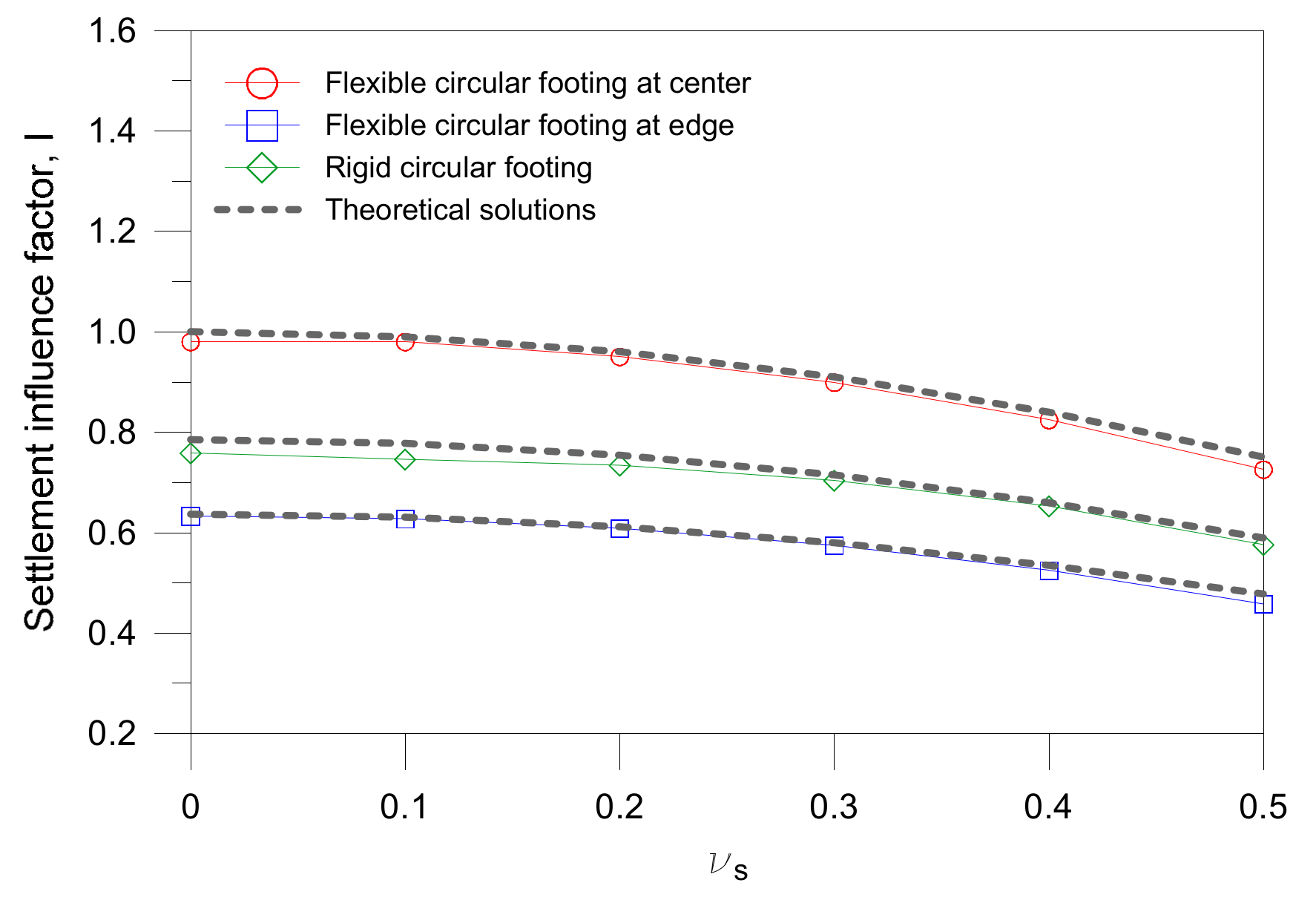
3.3. Validation

For validation, results of the numerical analyses presented in this study were compared with the theoretical values presented by Milovic [23] for perfectly flexible footings at the center and edge, and by Timoshenko and Goodier [16] for rigid footings. Figure 3 shows such comparison for circular footings resting on infinite homogeneous elastic half-space. It can be seen that the obtained results are in good agreement with the elastic settlement data, supporting the reliability of the numerical analysis used in this study for predicting the immediate settlement of ring footings.

4. Results and Discussion

Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show the numerical solutions for uniformly loaded ring footings, as related to inner-to-outer radius ratio R_i/R₀, Poisson’s ratio ν_s, footing stiffness K, finite layer thickness ratio H/D, and modulus inhomogeneity nD/E₀. The results are presented in the familiar form of the settlement influence factors at the points investigated: in the perfectly flexible footing case (K = 0.001), the influence charts for the inner and outer settlement of a footing are given; in the perfectly rigid footing case (K = 100), the influence charts for inner settlement (representing any settlement beneath the footing) are provided. This is because a flexible footing imposes non-uniform settlement but a rigid footing induces uniform settlement.

Figure 4 shows the variation of the settlement influence factor I_P of perfectly flexible and rigid ring footings on a homogeneous elastic half-space for different combinations of ν_s and R_i/R₀. It can be seen that an increase in Poisson’s ratio leads to a decrease in I_P, regardless of footing stiffness. However, the effect of the Poisson’s ratio on the results is independent of R_i/R₀. Figure 4 also provides a comparison of the I_P values obtained in this study with the theoretical solutions of Fischer [9] for flexible ring footings on incompressible elastic medium. It can be observed that the present solutions compare reasonably well with the results of Fischer [9]. Meanwhile, it should be noted that the contribution of Poisson’s ratio to the settlement of ring footings can be reflected by the product of a correction factor (1 − ν_s²) and a value of I_K for ν_s = 0.

Figure 5 highlights the effects of K and R_i/R₀ on the settlement influence factor I_K of ring footings on a homogeneous elastic half-space. It can be seen that at the inner point of the footing (Figure 5a), the I_K values decrease with increasing the values of K, implying that the higher footing stiffness reduces the inner settlement of the footing. At the outer point of the footing (Figure 5b), the I_K values increase with increasing values of K; that is, higher footing stiffness causes a larger outer settlement of the footing. It can be also noticed that for smaller values of R_i/R₀, the change in I_K with respect to the footing stiffness is significant, irrespective of the point studied. Meanwhile, the values of I_K for the circular footing were compared with those obtained by Brown [20] using integral transform technique. As shown in Figure 5a, the present I_K values are found to be invariably lower than the solutions of Brown [20]. This result is unsurprising, given the different footing roughnesses (i.e., rough and smooth roughnesses) for which current and Brown’s analyses were adopted, so they are not directly comparable.

Figure 6 shows the variation of the settlement influence factor I_H of perfectly flexible and rigid ring footings on homogeneous elastic layer of finite thickness for different combinations of H/D and R_i/R₀. It is clear that the I_H value has a general tendency to increase with increasing values of H/D. However, the rate of such increase diminishes for footings with high values of H/D and R_i/R₀. Increasing the finite layer thickness ratio to values greater than a critical one does not affect the footing settlement, because a small portion of applied load reaches the underlying rigid base. The critical finite layer thickness ratio is insensitive to the values of R_i/R₀. For the circular footing, the values of I_H obtained from the present analysis were compared with the results from Harr [24] and Rowe and Booker [19]. As shown, the computed solutions show good agreement with those by Rowe and Booker [19], although the results of Harr [24] normally underpredict, resulting in lower values of H/D.

Figure 7 shows the variation of the settlement influence factor I_N of perfectly flexible and rigid ring footings on inhomogeneous elastic half-space for different combinations of nD/E₀ and R_i/R₀. It can be seen that the values of I_N decrease continuously with an increase in nD/E₀. At smaller values of R_i/R₀, the effect of nD/E₀ on the results is found to be more predominant. Figure 7 also compares the obtained values of I_N for the flexible and rigid circular footings with the analyses of Mayne and Poulos [4] using approximate integration technique. It is noted that the present I_N values match well with the solutions of Mayne and Poulos [4].

From Figure 4, Figure 5, Figure 6 and Figure 7, it is observed that the ring footing always has lower settlement influence factors than the circular footing, and the settlement influence factor of ring footings decreases with increasing the values of R_i/R₀. This implies that using narrower ring footings becomes more applicable to reducing the settlement of footings under a given working load. It is also noted that the settlement influence factors of the rigid ring footing fall within the range of the inner and outer settlement influence factors of the flexible footing.

The relationships between inner and outer settlements of ring footings are presented in Figure 8, in terms of the footing stiffness K, finite layer thickness ratio H/D, and modulus inhomogeneity nD/E₀. Figure 8a indicates that at a given value of R_i/R₀, the values of s_outer/s_inner gradually decrease from 1 at the rigid footing to a certain value at the flexible footing, indicating that a flexible footing imposes non-uniform settlement and a rigid footing induces uniform settlement. It is also observed that the rate of decrease with K is more extensive for greater values of R_i/R₀. Also shown in Figure 8a is the s_outer/s_inner values suggested by Mayne and Poulos [4] for circular footings. When compared to the present calculations, the results of Mayne and Poulos [4] appear to be overpredictive, particulary for lower values of K. Figure 8b demonstrates that as the value of H/D increases, the value of s_outer/s_inner initially decreases to a minimum value at a certain finite layer thickness ratio, and thereafter it increases up to a limiting value. This is attributable to the fact that the contribution by the underlying rigid base to the footing settlement increases as the finite layer grows increasingly thin. Figure 8c explains more significant change in s_outer/s_inner as the value of nD/E₀ increases, suggesting that the variation of modulus with depth has a marked effect on the footing settlement.

The general form of the elastic settlement equation for a surface ring footing with R_i/R₀ that is a function of the Poisson’s ratio, footing stiffness, finite layer thickness ratio with an underlying rigid base, and modulus variation with depth is estimated by

$$s=\frac{qD}{E_0}{I}_P{R}_K{R}_H{R}_N$$

(6)

where q is the uniform load, D is the outer diameter of the footing, E₀ is the elastic modulus at the surface, ν_s is the Poisson’s ratio, I_P is obtained by Figure 4 for a given R_i/R₀. R_K is the ratio of I_K value for a target K to I_H value for K ≈ 0 in Figure 5. R_H is the ratio of I_H value for a target H/D to I_H value for H/D ≈ ∞ in Figure 6; R_N is the ratio of I_N value for a target nD/E₀ to I_H value for nD/E₀ ≈ 0 in Figure 7. Consequently, the use of Equation (6) in combination with graphical solutions of Figure 4, Figure 5, Figure 6 and Figure 7 enables hand calculations for predicting the settlement under perfectly flexible and rigid ring footings on a finite layer of a heterogeneous isotropic medium underlain by a rigid rough base.

5. Conclusions

The purpose of this study is to analyze the settlement of a rough ring footing of any stiffness in an isotropic elastic finite layer with the modulus of elasticity linearly varying with the depth, overlying a rough rigid base. The consideration of an inhomogeneous finite stratum has not been covered in the literature for evaluation of the elastic settlement of ring footings. By means of finite element analysis, numerical solutions for a wide range of geometrical and material parameters were determined. The effects of inner-to-outer radius ratios, Poisson’s ratio, footing stiffness, finite layer thickness ratio, and modulus inhomogeneity have been investigated. The results are presented in the familiar form of the settlement influence factors, forming non-dimensional design charts, and also compared with other available solutions. Based on the numerical results, the following conclusions can be drawn:

(1)

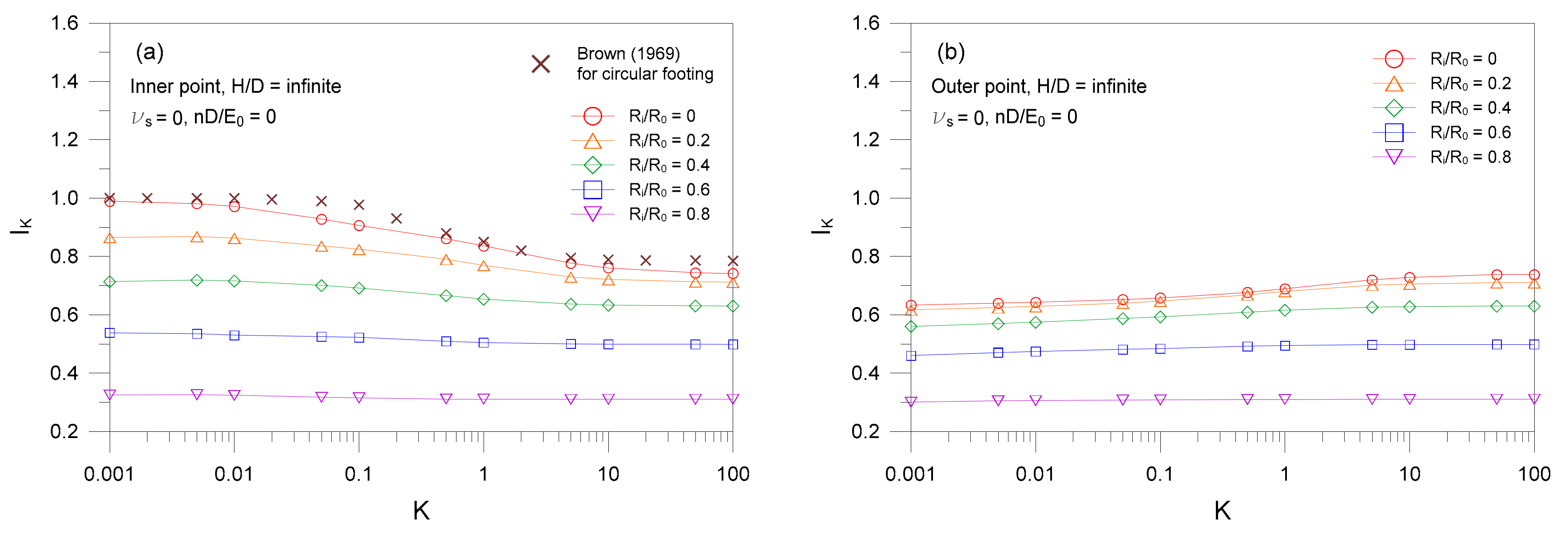
For circular footings, settlement influence factors obtained from the FE analyses are comparable with those reported in the literature.

(2)

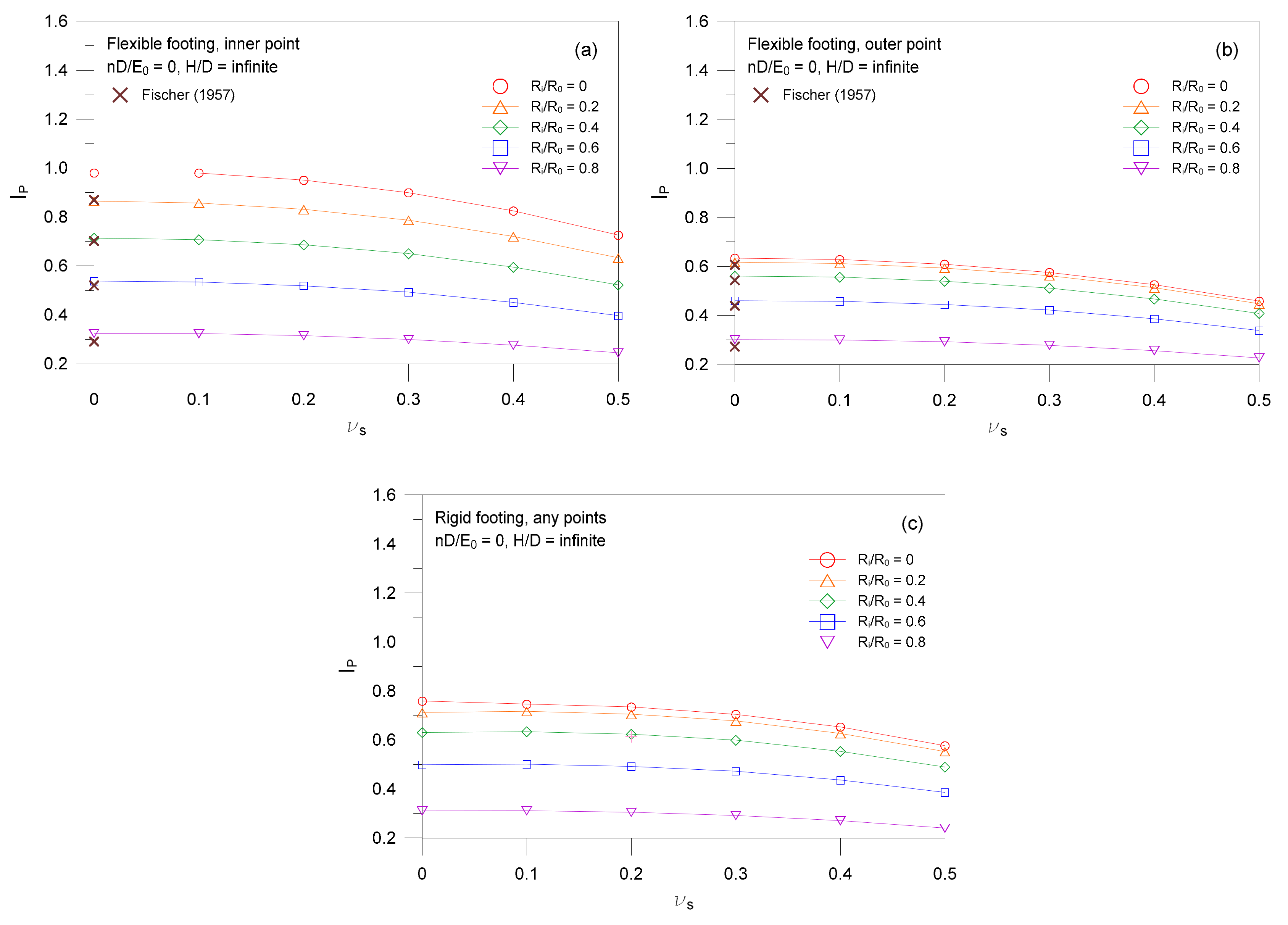
An increase in Poisson’s ratio ν_s causes a decrease in settlement influence factor I of ring footings, and the rate of decrease of I with ν_s is insensitive to footing’s inner-to-outer radius ration R_i/R₀.

(3)

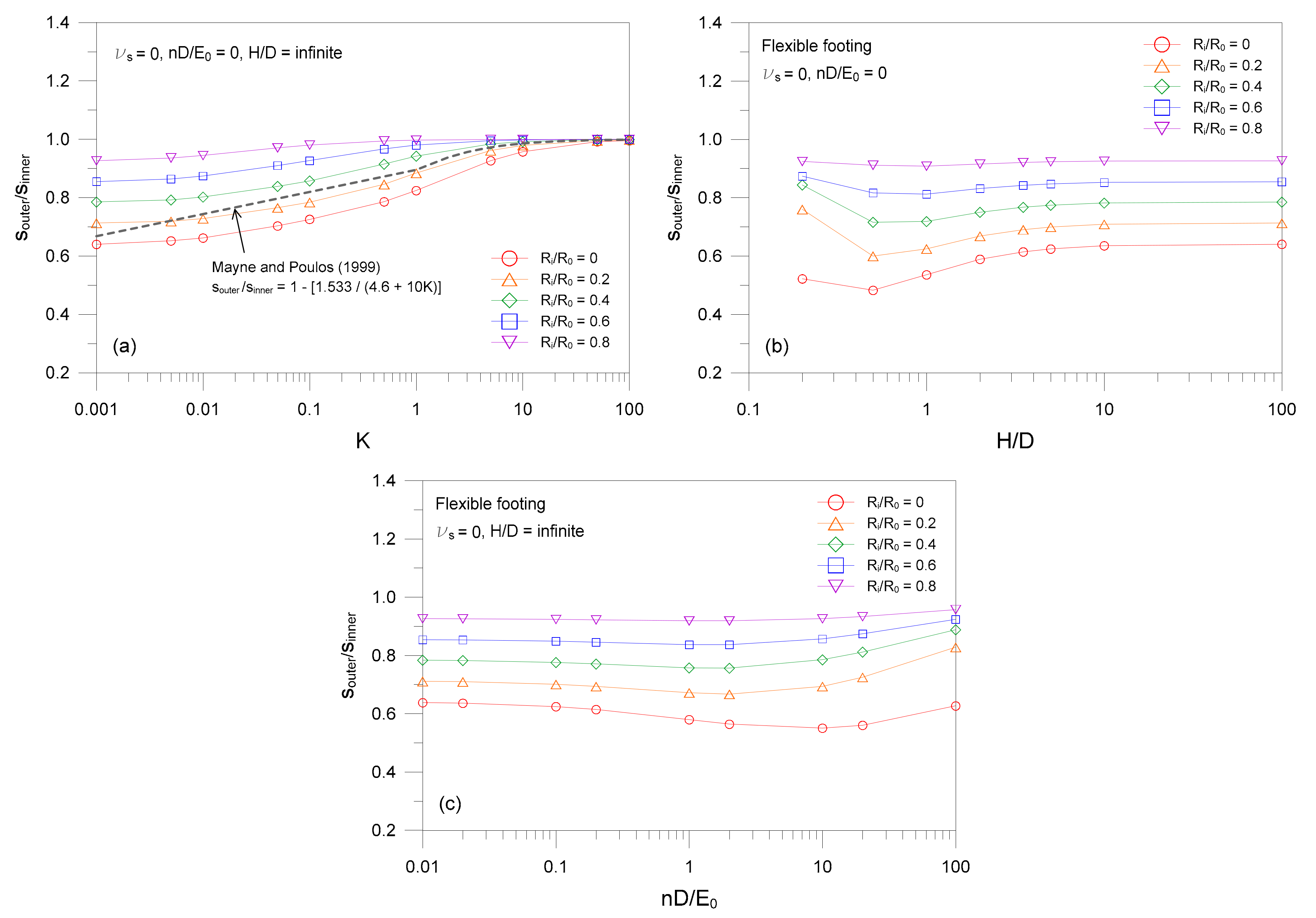
For the inner point of the ring footing, the settlement influence factor I_K decreases with increasing the values of footing stiffness K. For the outer point of the ring footing, in contrast, the I_K values increase with increasing values of K. The variation of I_K with K is more prominent for smaller values of R_i/R₀.

(4)

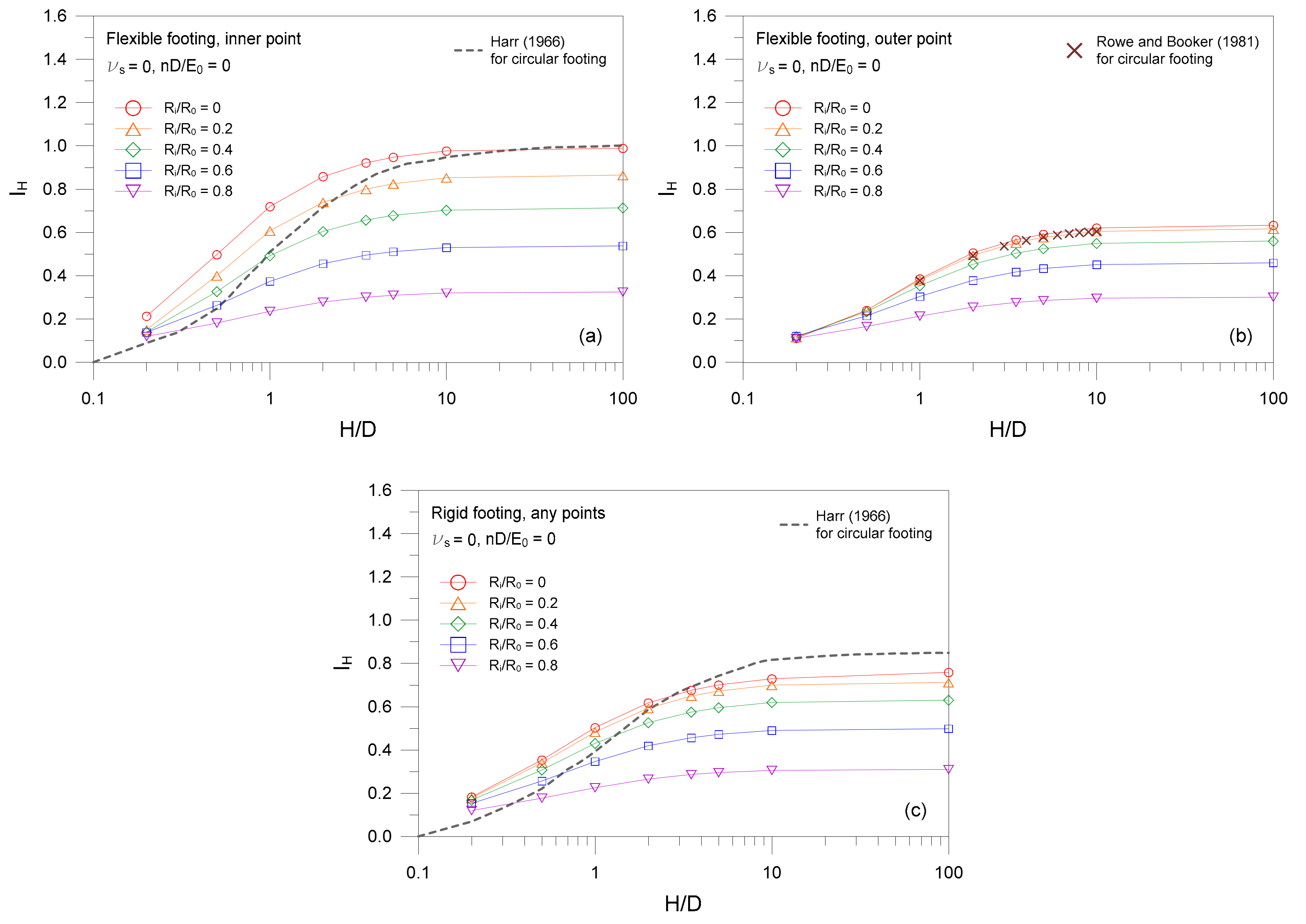
Increasing the finite layer thickness ratio H/D to values greater than a critical one does not impact the settlement of ring footings. This is attributed to the fact that the contribution by the underlying rigid base becomes less as the finite layer grows thicker. The critical value of H/D is independent of R_i/R₀.

(5)

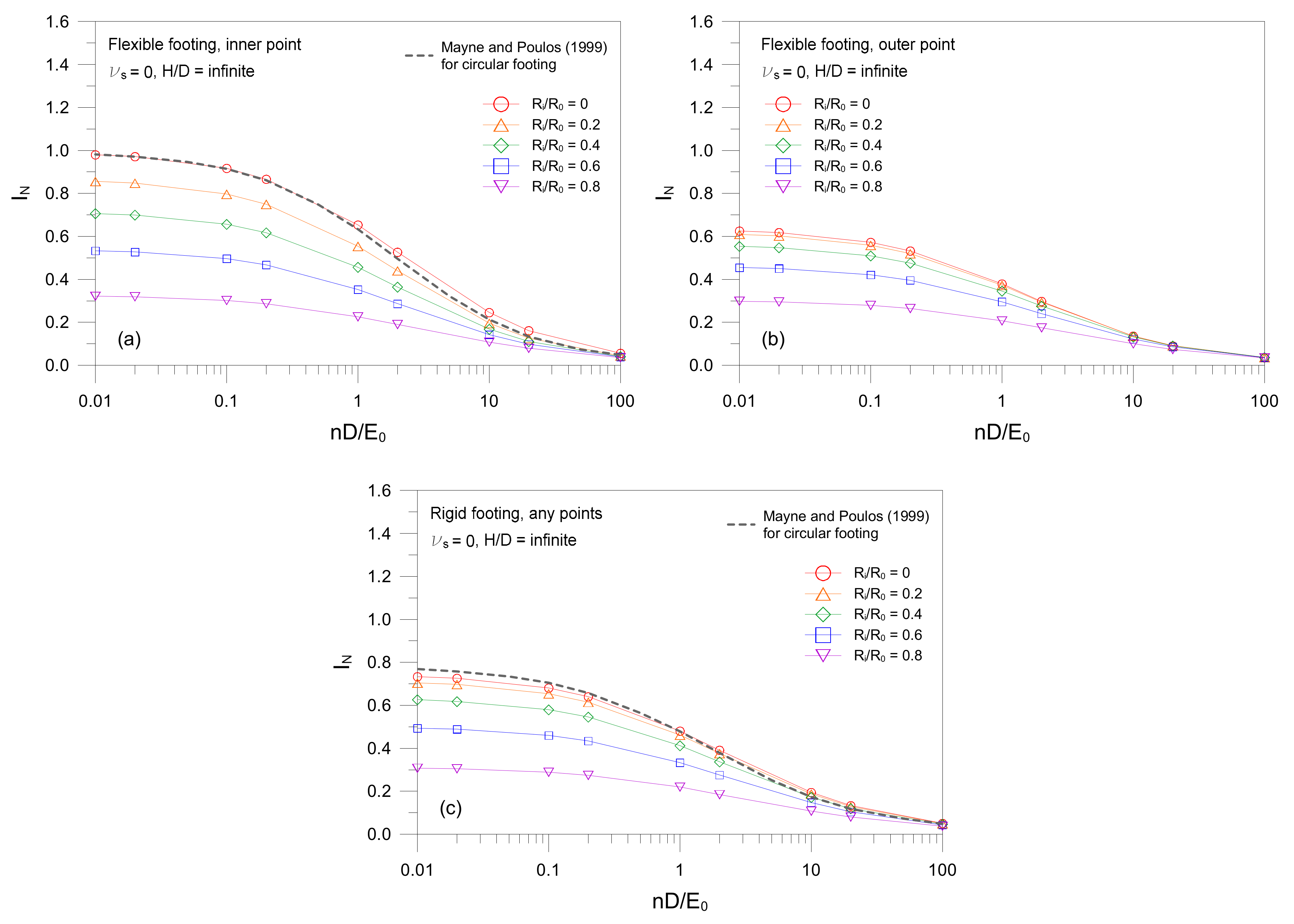
Settlement influence factor decreases with an increase in soil nonhomogeneity nD/E₀, and the decreasing tendency is more significant for smaller values of R_i/R₀.

(6)

A systematic procedure is proposed for estimating the footing settlement for a wide range of practical cases and to help in choosing the optimum internal opening and stiffness of ring footings that limit footing settlement to tolerable levels.