A Two-Stage Approach to Note-Level Transcription of a Specific Piano
Abstract
:1. Introduction
- (1)
- The note recognition stage yields a note-level transcription by estimating the pitch at each onset. Compared to existing deep-learning-based methods which use a single network, two consecutive CNNs yield better performance.
- (2)
- An extra stage of note verification is conducted for the specific piano, in which the spectrogram factorization improves the precision of transcription. Compared with the traditional NMF, the proposed note verification stage could save computing time and storage space to a great extent.
- (3)
- The proposed method achieves better performance in specific piano transcription compared to the state-of-the-art approach.
2. Proposed Framework
2.1. Note Recognition
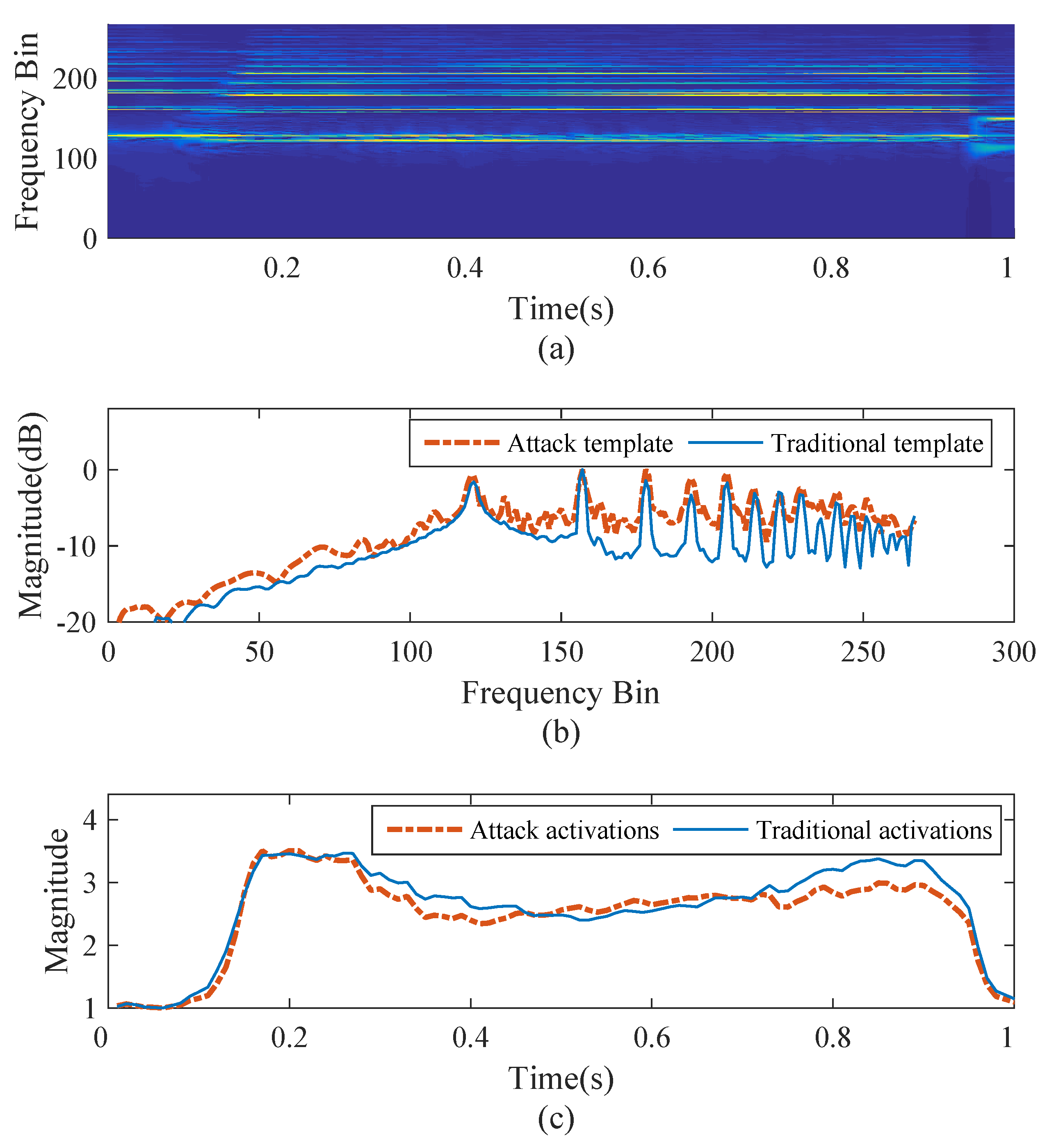
2.2. Note Verification
3. Experiments
3.1. Dataset
3.2. Experimental Settings
3.3. Results
3.3.1. Onset Detection
3.3.2. Multi-Pitch Estimation
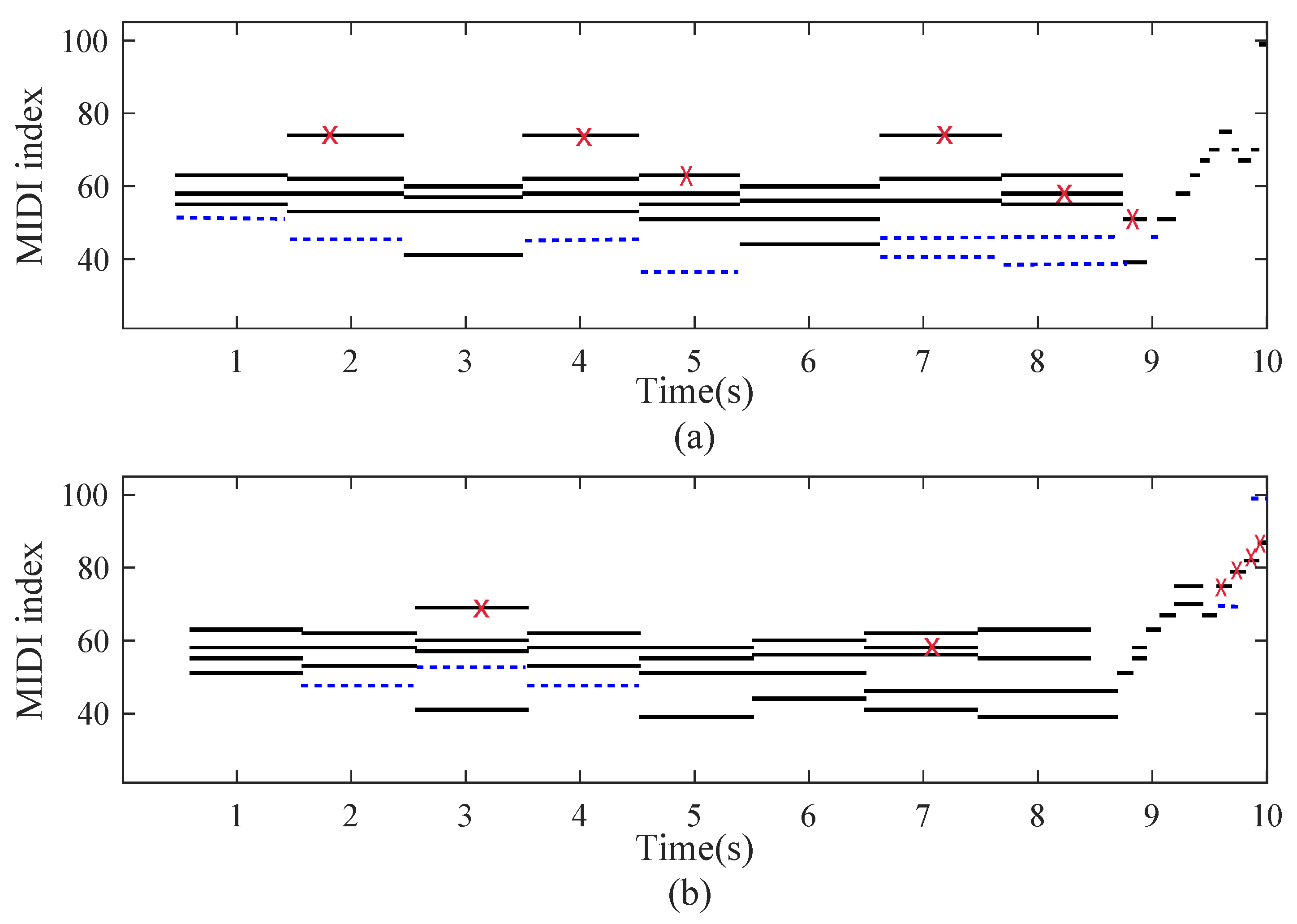
3.3.3. Note Recognition
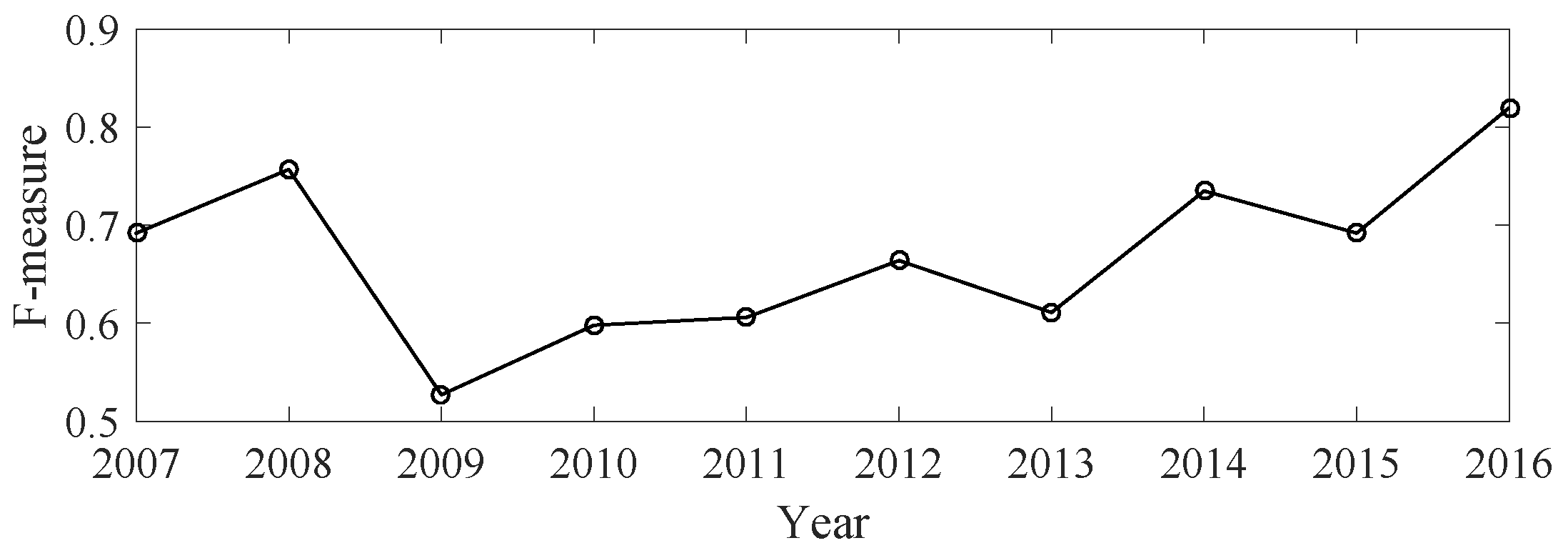
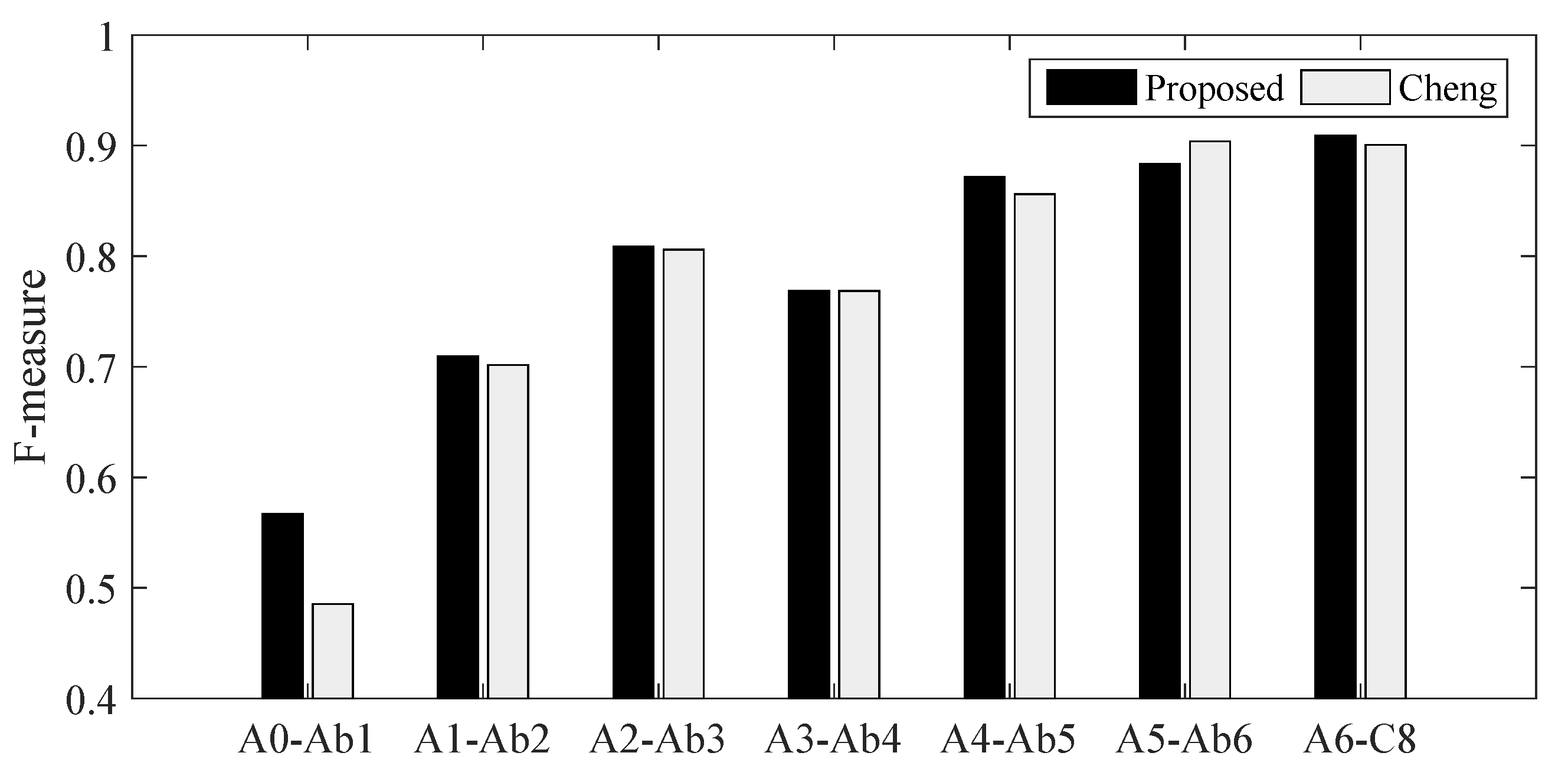
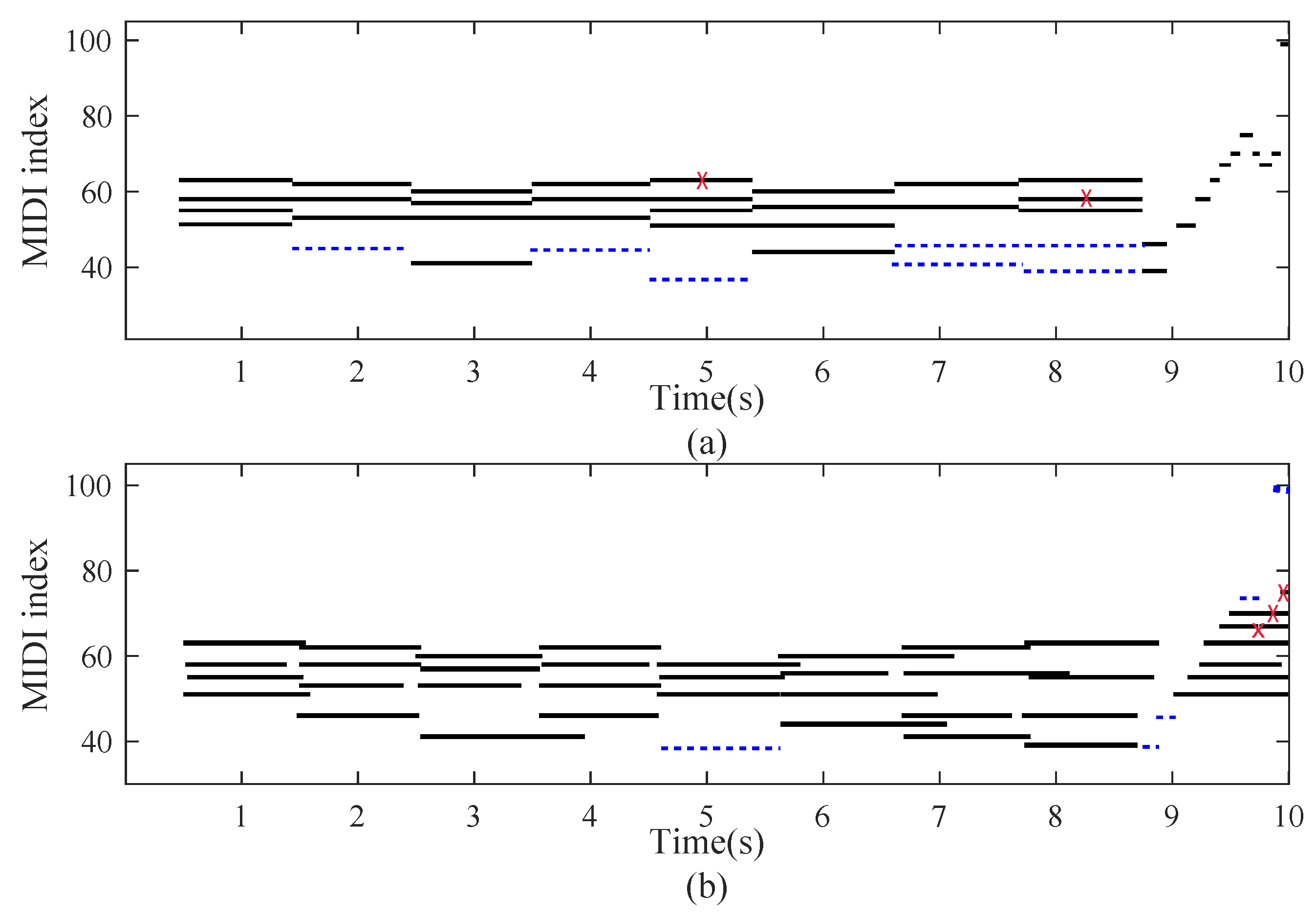
3.3.4. Transcription for Specific Piano
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Moorer, J.A. On the transcription of musical sound by computer. Comput. Music J. 1977, 1, 32–38. [Google Scholar]
- Piszczalski, M.; Galler, B.A. Automatic music transcription. Comput. Music J. 1977, 1, 24–31. [Google Scholar]
- Klapuri, A. Introduction to music transcription. In Signal Processing Methods for Music Transcription; Springer: Boston, MA, USA, 2006; pp. 3–20. [Google Scholar]
- Cogliati, A.; Duan, Z.; Wohlberg, B. Piano transcription with convolutional sparse lateral inhibition. IEEE Signal Process. Lett. 2017, 24, 392–396. [Google Scholar] [CrossRef]
- Benetos, E.; Dixon, S.; Giannoulis, D.; Kirchhoff, H.; Klapuri, A. Automatic music transcription: Challenges and future directions. J. Intell. Inf. Syst. 2013, 41, 407–434. [Google Scholar] [CrossRef]
- Klapuri, A.P. Multiple fundamental frequency estimation based on harmonicity and spectral smoothness. IEEE Trans. Speech Audio Process. 2003, 11, 804–816. [Google Scholar] [CrossRef]
- Pertusa, A.; Inesta, J.M. Multiple fundamental frequency estimation using Gaussian smoothness. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 31 March–4 April 2008; pp. 105–108. [Google Scholar]
- Brown, J.C. Calculation of a constant Q spectral transform. J. Acoust. Soc. Am. 1991, 89, 425–434. [Google Scholar] [CrossRef]
- Zhou, R.; Reiss, J.D. A real-time polyphonic music transcription system. In Proceedings of the 4th Music Information Retrieval Evaluation eXchange (MIREX), Philadelphia, PA, USA, 14–18 September 2008. [Google Scholar]
- Dressler, K. Multiple fundamental frequency extraction for MIREX 2012. In Proceedings of the 8th Music Information Retrieval Evaluation eXchange (MIREX), Porto, Portugal, 8–12 October 2012. [Google Scholar]
- Smaragdis, P.; Brown, J.C. Non-negative matrix factorization for polyphonic music transcription. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 19–22 October 2003; pp. 177–180. [Google Scholar]
- Smaragdis, P.; Raj, B.; Shashanka, M. A probabilistic latent variable model for acoustic modeling. Adv. Models Acoust. Process. 2006, 148, 1–8. [Google Scholar]
- Benetos, E.; Dixon, S. A shift-invariant latent variable model for automatic music transcription. Comput. Music J. 2012, 36, 81–94. [Google Scholar] [CrossRef]
- Nam, J.; Ngiam, J.; Lee, H.; Slaney, M. A classification-based polyphonic piano transcription approach using learned feature representations. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Miami, FL, USA, 24–28 October 2011; pp. 175–180. [Google Scholar]
- Sigtia, S.; Benetos, E.; Boulanger-Lewandowski, N.; Weyde, T.; Garcez, A.S.D.; Dixon, S. A hybrid recurrent neural network for music transcription. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19–24 April 2015; pp. 2061–2065. [Google Scholar]
- Kelz, R.; Widmer, G. An experimental analysis of the entanglement problem in neural-network-based music transcription systems. In Proceedings of the AES Conference on Semantic Audio, Erlangen, Germany, 22–24 June 2017. [Google Scholar]
- Berg-Kirkpatrick, T.; Andreas, J.; Klein, D. Unsupervised transcription of piano music. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 Demcember 2014; pp. 1538–1546. [Google Scholar]
- Ewert, S.; Plumbley, M.D.; Sandler, M. A dynamic programming variant of non-negative matrix deconvolution for the transcription of struck string instruments. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19–24 April 2015; pp. 569–573. [Google Scholar]
- Kameoka, H.; Nishimoto, T.; Sagayama, S. A multipitch analyzer based on harmonic temporal structured clustering. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 982–994. [Google Scholar] [CrossRef]
- Böck, S.; Schedl, M. Polyphonic piano note transcription with recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 121–124. [Google Scholar]
- Sigtia, S.; Benetos, E.; Dixon, S. An end-to-end neural network for polyphonic piano music transcription. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 927–939. [Google Scholar] [CrossRef]
- Marolt, M. A connectionist approach to automatic transcription of polyphonic piano music. IEEE Trans. Multimed. 2004, 6, 439–449. [Google Scholar] [CrossRef]
- Costantini, G.; Perfetti, R.; Todisco, M. Event based transcription system for polyphonic piano music. Signal Process. 2009, 89, 1798–1811. [Google Scholar] [CrossRef]
- Barbancho, I.; de la Bandera, C.; Barbancho, A.M.; Tardon, L.J. Transcription and expressiveness detection system for violin music. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Taipei, Taiwan, 19–24 April 2009; pp. 189–192. [Google Scholar]
- Marolt, M. Automatic transcription of bell chiming recordings. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 844–853. [Google Scholar] [CrossRef]
- Barbancho, A.M.; Klapuri, A.; Tardón, L.J.; Barbancho, I. Automatic transcription of guitar chords and fingering from audio. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 915–921. [Google Scholar] [CrossRef]
- Wan, Y.; Wang, X.; Zhou, R.; Yan, Y. Automatic Piano Music Transcription Using Audio-Visual Features. Chin. J. Electron. 2015, 24, 596–603. [Google Scholar] [CrossRef]
- 2016: Multiple Fundamental Frequency Estimation Tracking Results—MIREX Dataset. Available online: http://www.music-ir.org/mirex/wiki/2016:Multiple_Fundamental_Frequency_Estimation_%26_ Tracking_Results_-_MIREX_Dataset (accessed on 15 October 2016).
- Cogliati, A.; Duan, Z. Piano music transcription modeling note temporal evolution. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19–24 April 2015; pp. 429–433. [Google Scholar]
- Cogliati, A.; Duan, Z.; Wohlberg, B. Context-dependent piano music transcription with convolutional sparse coding. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 2218–2230. [Google Scholar] [CrossRef]
- Ewert, S.; Sandler, M. Piano transcription in the studio using an extensible alternating directions framework. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 1983–1997. [Google Scholar] [CrossRef]
- Cheng, T.; Mauch, M.; Benetos, E.; Dixon, S. An attack/decay model for piano transcription. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), New York, NY, USA, 7–11 August 2016. [Google Scholar]
- Gao, L.; Su, L.; Yang, Y.H.; Lee, T. Polyphonic piano note transcription with non-negative matrix factorization of differential spectrogram. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 291–295. [Google Scholar]
- Li, T.L.; Chan, A.B.; Chun, A. Automatic musical pattern feature extraction using convolutional neural network. In Proceedings of the International Multi Conference of Engineers and Computer Scientists, Hongkong, China, 17–19 March 2010. [Google Scholar]
- Dieleman, S.; Brakel, P.; Schrauwen, B. Audio-based music classification with a pretrained convolutional network. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Miami, FL, USA, 24–28 October 2011; pp. 669–674. [Google Scholar]
- Humphrey, E.J.; Bello, J.P. Rethinking automatic chord recognition with convolutional neural networks. In Proceedings of the International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 12–15 December 2012; Volume 2, pp. 357–362. [Google Scholar]
- Schluter, J.; Bock, S. Improved musical onset detection with convolutional neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6979–6983. [Google Scholar]
- Emiya, V.; Badeau, R.; David, B. Multipitch estimation of piano sounds using a new probabilistic spectral smoothness principle. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1643–1654. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Bay, M.; Ehmann, A.F.; Downie, J.S. Evaluation of Multiple-F0 Estimation and Tracking Systems. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Kobe, Japan, 26–30 October 2009; pp. 315–320. [Google Scholar]
- Eyben, F.; Böck, S.; Schuller, B.W.; Graves, A. Universal Onset Detection with Bidirectional Long Short-Term Memory Neural Networks. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Utrecht, The Netherlands, 9–13 August 2010; pp. 589–594. [Google Scholar]
- Benetos, E.; Weyde, T. An efficient temporally-constrained probabilistic model for multiple-instrument music transcription. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Malaga, Spain, 20–26 October 2015. [Google Scholar]
- Troxel, D. Automatic Music Transcription Software. Available online: https://www.lunaverus.com/ (accessed on 9 December 2016).





| Method | Recall | Precision | F-Measure |
|---|---|---|---|
| CNN | 0.9731 | 0.9590 | 0.9660 |
| DNN | 0.9319 | 0.8683 | 0.8990 |
| RNN | 0.9530 | 0.9259 | 0.9393 |
| Method | Recall | Precision | F-Measure |
|---|---|---|---|
| CNN | 0.7810 | 0.8319 | 0.8056 |
| DNN | 0.6223 | 0.6727 | 0.6465 |
| RNN | 0.6020 | 0.8221 | 0.6950 |
| Method | Recall | Precision | F-Measure |
|---|---|---|---|
| CNNs | 0.7524 | 0.8593 | 0.8023 |
| Sigtia | 0.6786 | 0.8023 | 0.7353 |
| Benetos | 0.5857 | 0.6305 | 0.6073 |
| Troxel | 0.7477 | 0.8687 | 0.8037 |
| Method | Recall | Precision | F-Measure |
|---|---|---|---|
| Proposed | 0.7503 | 0.9039 | 0.8200 |
| Cheng | 0.7381 | 0.9070 | 0.8139 |
| Adapted CNNs | 0.7458 | 0.8792 | 0.8070 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhou, R.; Yan, Y. A Two-Stage Approach to Note-Level Transcription of a Specific Piano. Appl. Sci. 2017, 7, 901. https://doi.org/10.3390/app7090901
Wang Q, Zhou R, Yan Y. A Two-Stage Approach to Note-Level Transcription of a Specific Piano. Applied Sciences. 2017; 7(9):901. https://doi.org/10.3390/app7090901
Chicago/Turabian StyleWang, Qi, Ruohua Zhou, and Yonghong Yan. 2017. "A Two-Stage Approach to Note-Level Transcription of a Specific Piano" Applied Sciences 7, no. 9: 901. https://doi.org/10.3390/app7090901
APA StyleWang, Q., Zhou, R., & Yan, Y. (2017). A Two-Stage Approach to Note-Level Transcription of a Specific Piano. Applied Sciences, 7(9), 901. https://doi.org/10.3390/app7090901





