Spectral Correction of CPV Modules Equipped with GaInP/GaInAs/Ge Solar Cells and Fresnel Lenses

Featured Application

This study presents a straightforward method based on analytical equations for applying a spectral correction on multijunction concentrating photovoltaics taking into account the optics.

Abstract

Photovoltaic (PV) devices are spectrally selective, and their performance is influenced by unavoidable spectral variations. In addition, multijunction-based concentrating photovoltaic (CPV) devices show a strong spectral dependence due to the series connection of various junctions with different absorption bands, and also due to the use of concentrator optics. In this work, the accuracy of a new set of analytical equations that quantify the spectral impact caused by the changes in air mass (AM), aerosol optical depth (AOD) and precipitable water (PW) is discussed. Four different CPV devices based on lattice-matched and metamorphic triple-junction solar cells and a poly(methyl methacrylate) (PMMA) and silicon-on-glass (SoG) Fresnel lenses are considered. A long-term outdoor experimental campaign was carried out at the Centre for Advanced Studies on Energy and Environment (CEAEMA) of the University of Jaén, Spain. Results show a high accuracy in the estimations of the spectral factor (SF), with an average mean absolute percentage error (MAPE) within 0.91% and a mean relative error (MRE) within −0.32%.

1. Introduction

Concentrating photovoltaic (CPV) systems employ optical components that focus the direct sunlight by reflection or refraction onto a smaller area usually made of high efficiency III-V multijunction (MJ) solar cells. Such solar cells overcome the thermodynamic Shockley–Queisser limit of single junction solar cells [1]; and even though their market share is small and relatively young, there is still a great interest in the technology due to the higher efficiencies especially at sites with high annual direct normal irradiation [2]. In addition to these, CPVs can achieve greater energy density, and thus less semiconductor material is required [3]. This technology, however, must overcome the technical and economic challenges to achieve success in the energy market [3,4]. The state-of-the-art triple-junction (3J) solar cell on the market is the lattice-matched (LM) 3J solar cell made of GaInP/GaInAs/Ge subcells [5], while the record efficiency of 46% was achieved by a four-junction (4J) solar cell [6].

It is well-known that the performance of photovoltaic (PV) devices is influenced by the unavoidable spectral variations that are mainly caused by changes in air mass (AM, i.e., the path length of the sun through the atmosphere relative to the zenith), aerosol optical depth (AOD, i.e., the amount of aerosols in the atmosphere) and precipitable water (PW, i.e., the total amount of water in a column in the zenith direction). The influence varies depending on the PV technology and, specifically, its corresponding spectral absorption band. In particular, MJ solar cells exhibit a higher spectral sensitivity compared to single-junction ones due to the series connection of different band-gap solar cells [7]. Moreover, the assembly of concentrator optics modifies the input spectra and introduce a strong angular dependence in the system. Therefore, a spectral correction has to be introduced in order to correct the incident irradiance and, thereby, improve the MJ-based CPV performance evaluation and modelling [8,9].

A new procedure that uses a simple set of analytical equations and takes into account the AM, AOD and PW has been recently proposed and evaluated by the authors for the case of a typical lattice-matched solar cell [10,11]. The main advantages of the proposed analytical equations are:

• Bulk spectral simulations are not required and therefore the procedure is easy to handle;
• The equations can be applied worldwide using ground-based (e.g., the aerosol robotic network, AERONET) or satellite (e.g., the moderate resolution imaging spectroradiometer, MODIS) observations;
• Therefore, relatively expensive measuring equipment that evaluates the solar spectrum is not required, given that a meteorological database is available at the specific site

In our previous study [10], the influence of the concentrator optics was not taken into account. Therefore, in this study, we incorporate the Fresnel lens dependency in order to achieve a more realistic procedure. The accuracy of the method is examined for four CPV configurations: (1) a lattice-matched (LM) triple-junction (3J) solar cell; (2) a LM 3J solar cell with a poly(methyl methacrylate) (PMMA) Fresnel lens; (3) a metamorphic (MM) 3J solar cell; and (4) a MM 3J solar cell with a silicon-on-glass (SoG) Fresnel lens. The spectral factor (SF) is used to quantify the spectral effects on the performance of the four MJ-based CPV devices that are considered. The description of the methodology used to extract the equations and information on the experimental set-up used to evaluate the proposed equations of all systems is also provided.

2. Materials and Methods

2.1. The Spectral Factor in MJ-Based CPV Devices

The short-circuit current density (J_sc,i) of each subcell of a MJ solar cell in a concentrator can be expressed as:

$$J_{sc,i}=CR·{{\displaystyle \int }}_{{\lambda }_{i,min}}^{{\lambda }_{i,max}}S{R}_i\left(\lambda \right)·{\eta }_{opt}\left(\lambda \right)·E_b\left(\lambda \right)d\lambda$$

(1)

where CR is the geometrical concentration ratio, λ_i,min and λ_i,max the wavelength range of the corresponding subcell, SR_i the spectral response, η_opt the optical efficiency, E_b(λ) the spectrally resolved direct normal irradiance and the i-index corresponds to the specific junction of the MJ solar cell.

Due to the series connection of different junctions, the current density of the whole MJ solar cell is given by the minimum current:

$$J_{sc,cell}=\min \left(J_{sc,i}\right)$$

(2)

The impact of the spectrum is quantified using the SF of each individual subcell, which is expressed as:

$$f_{s,i}=S{F}_i=\frac{\int \text{}{E}_b\left(\lambda \right)·{\eta }_{opt}\left(\lambda \right)·S{R}_i\left(\lambda \right)d\lambda }{\int \text{}{E}_b\left(\lambda \right)d\lambda }·\frac{\int \text{}{E}_{b,ref}\left(\lambda \right)d\lambda }{\int \text{}{E}_{b,ref}\left(\lambda \right)·{\eta }_{opt}\left(\lambda \right)·S{R}_i\left(\lambda \right)d\lambda }=\frac{J_{sc,i}}{E_b}·\frac{E_{b,ref}}{J_{sc,i}^{ref}}$$

(3)

where $f_s$ is the spectral function and the index ref indicates the reference conditions.

Bearing the above in mind, the SF of the whole MJ solar cell can be expressed by means of the following equation:

$$f_s=SF=min\left(S{F}_i·\frac{J_{sc,i}^{ref}}{J_{sc,cell}^{ref}}\right)$$

(4)

This index quantifies the spectral impact on the performance of a MJ CPV device as a function of the input spectral distribution. In this sense, a value greater than 1 indicates spectral gains, a value lower than 1 indicates spectral losses and a value equal to 1 indicates spectral conditions equivalent to the reference spectrum. This index has been experimentally demonstrated to be valid for approximating the spectral impact on the power or energy output of MJ CPV systems under real operating conditions [11].

2.2. Proposed Analytical Equations

The detailed procedure used to extract the analytical equations evaluated in this work can be found in [10]. The Simple Model of the Atmosphere Radiative Transfer of Sunshine version 2 (SMARTS2) [12] was initially used to simulate the following spectra:

• 1 ≤ AM ≤ 5, step 0.25
• 0.05 ≤ AOD ≤ 0.6, step 0.05
• 0.25 ≤ PW ≤ 4 cm, step 0.25 cm

Hence, a total of 3264 spectra were generated, covering a wide range of spectral conditions. The SF of each subcell and for the whole multi-junction cell was calculated for every simulated spectrum using the equations discussed in the previous sub-section. The analysis of the impact of these spectra on each subcell of a lattice-matched GaInP/GaInAs/Ge MJ solar cell leads to the following analytical equations:

$$f_{s,i}=S{F}_i=f{\left(AM,AOD,PW\right)}_i$$

(5)

$$f{\left(AM,AOD,PW\right)}_i=f{\left(AM\right)}_i+f{\left(AOD\right)}_i+f{\left(PW\right)}_i$$

(6)

$$f{\left(AOD\right)}_i=f{\left(AOD coeff.\right)}_i·\left(AOD-AO{D}_{ref}\right)$$

(7)

$$f{\left(PW\right)}_i=f{\left(PW coeff.\right)}_i·\left(PW-P{W}_{ref}\right)$$

(8)

where f(AM), f(AOD coeff.) and f(PW coeff.) are the corresponding functions of each subcell and the subscript “coeff.” refers to the coefficients. The AOD_ref and PW_ref reference values are 0.084 and 1.42 cm respectively. The proposed spectral corrections for each subcell are given in

Table 1. Proposed spectral corrections for each subcell. SF: spectral factor; AM: air mass; AOD coeff.: aerosol optical depth coefficients; PW coeff.: precipitable water coefficients.

SF	f(AM)	f(AOD coeff.)	f(PW coeff.)
top	ax4 + bx3 + cx2 + dx + e *	aln(x) + b *	aln(x) + b *
middle		ax2 + bx + c *	Ax + b *
bottom		aln(x) + b *	aln(x) + b *

* where x = AM.

.

2.3. Experimental Campaign

The experimental validation of the proposed equations was carried out at the CEAEMA of the University of Jaén [13]. The Centre is equipped with a weather station and irradiance sensors such as pyrheliometers and pyranometers that measure different components of the irradiance (i.e., global horizontal and normal, direct normal and diffuse horizontal), see Figure 1-left. III-V component solar cells (or isotypes) from Black Photon and a solar spectral irradiance metre (SolarSIM-D2) from Spectrafy Inc. are used to characterise the spectral composition and also measure the spectrally resolved direct normal irradiance and the atmospheric parameters that influence the spectrum, i.e., AOD at 500 nm and PW. The AM is also calculated from the sun’s zenith angle.

It is important to note that all the sensors are within the calibration period and are cleaned once a week and also after rainy days to ensure quality of measurements.

As mentioned in the introduction, the following CPV configurations are considered in this study:

• LM: a device based on a lattice-matched GaInP/GaInAs/Ge solar cell
• LM + PMMA: a device based on a LM solar cell and a poly(methyl methacrylate) (PMMA) Fresnel lens
• MM: a device based on a metamorphic GaInP/GaInAs/Ge solar cell
• MM + SoG: a device based on a MM solar cell and a silicone-on-glass (SoG) Fresnel lens.

Further information about the external quantum efficiency (EQE) of the MJ solar cells and transmittance of the Fresnel lenses can be found in [14].

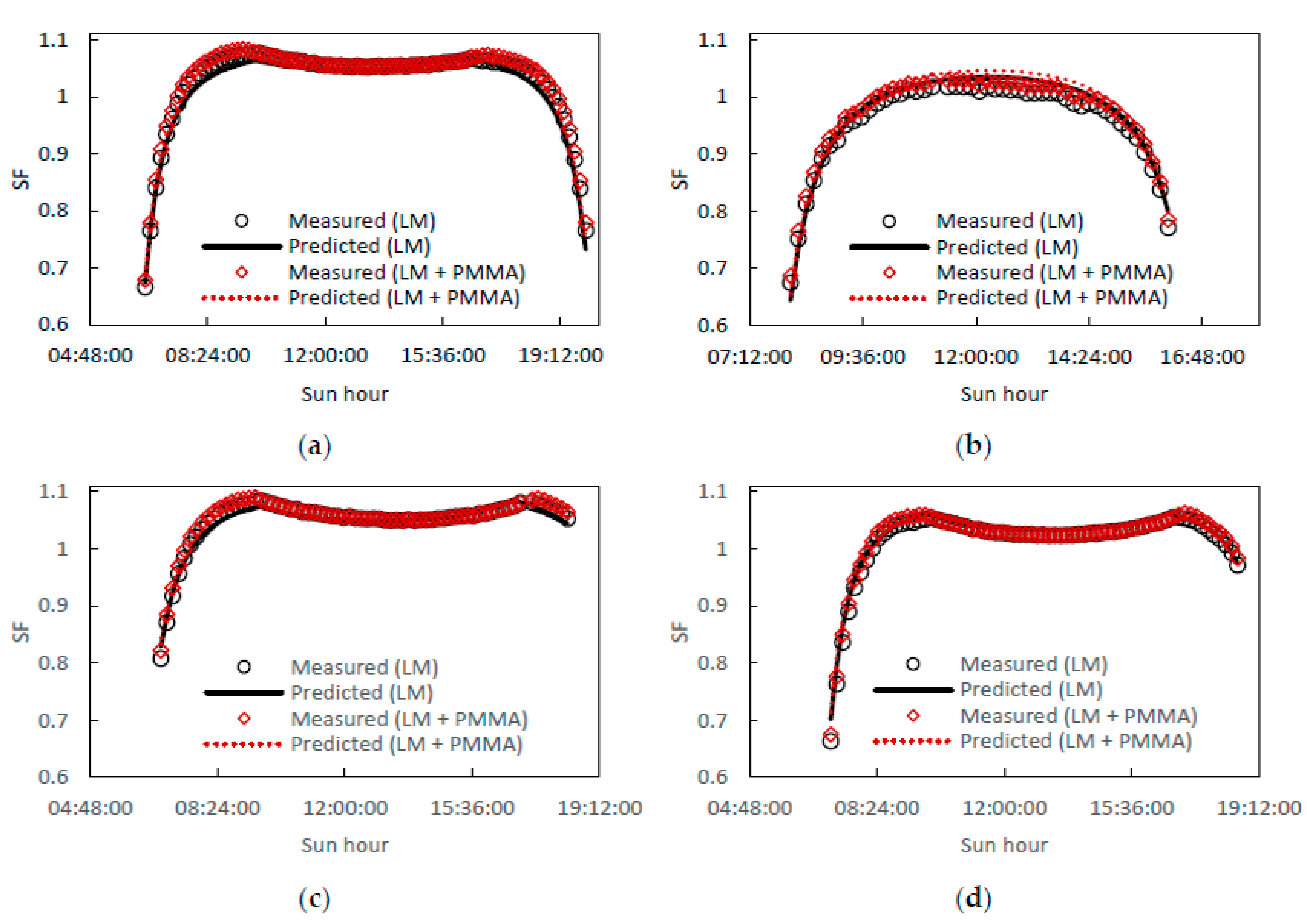
3. Analysis of Results

In order to evaluate the proposed equations for the four CPV devices under study, four days with different atmospheric characteristics were selected and therefore the following were considered:

• 21 June 2016—clear atmosphere with low AM ($\overline{AM}$= 2.0, $\overline{AOD}$ = 0.06, $\overline{PW}$ = 2.34 cm)
• 23 December 2016—clear atmosphere with high AM ($\overline{AM}$= 3.4, $\overline{AOD}$ = 0.04, $\overline{PW}$ = 1.35 cm)
• 29 June 2016—relatively hazy atmosphere ($\overline{AM}$= 2.0, $\overline{AOD}$ = 0.28, $\overline{PW}$ = 2.50 cm)
• 18 August 2016—relatively wet atmosphere ($\overline{AM}$ = 2.1, $\overline{AOD}$ = 0.12, $\overline{PW}$ = 3.62 cm)

These days exhibit different spectral conditions and, therefore, can allow the procedure’s evaluation. Figure 2 shows an example of the measured and predicted SF of LM and LM + PMMA CPV devices during the selected days. It can be seen that both configurations exhibit a good fit during the four days. In order to quantify the accuracy of the procedure, different statistical metrics were calculated such as the mean percentage absolute error (MAPE) and the mean relative error (MRE). The LM and LM + PMMA present almost the same MAPE with values ranging from 0.7% to 1.0% and a MRE ranging from −1.1% to 0.4%. The MM and MM + SoG devices also present similar results with a MAPE ranging from 0.5% to 0.6% and a MRE from −0.7% to 0.2%. It is also important to remark that the accuracy of the method did not show any particular trend with the spectral conditions of the day considered. As such, it can be concluded that the proposed equations show a high accuracy for all the CPV devices during all the different days.

Table 2. Mean absolute percentage error (MAPE) and mean relative error (MRE) for the four CPV devices and days considered. CPV: concentrating photovoltaic; MM: a device based on a metamorphic GaInP/GaInAs/Ge solar cell; MM + SoG: a device based on a MM solar cell and a silicone-on-glass (SoG) Fresnel lens; MAPE: the mean percentage absolute error; MRE: the mean relative error.

Device	MAPE (%)	MRE (%)
LM	0.91	−0.32
LM + PMMA	0.92	−0.32
MM	0.64	−0.19
MM + SoG	0.56	−0.17

summarizes the results of each CPV configuration, obtained during the selected days.

4. Summary and Conclusions

The accuracy of a new set of analytical equations was analysed in this work in order to evaluate the spectral impact of air mass (AM), aerosol optical depth (AOD) and precipitable water (PW) variations. To achieve this, a long term experimental campaign was conducted at the CEAEMA of the University of Jaén, located in southern Spain. The proposed equations were evaluated for four CPV configurations: (1) a lattice-matched (LM) triple-junction (3J) solar cell, (2) a lattice-matched (LM) triple-junction (3J) solar cell with a PMMA Fresnel lens, (3) a metamorphic (MM) 3J solar cell, and (4) a metamorphic (MM) 3J solar cell with a silicon-on-glass (SoG) Fresnel lens.

The equations exhibited a similar behaviour for all the CPV configurations. A MAPE ranging from 0.56% to 0.91% and a MRE ranging from −0.17% to −0.32% were found. In addition, the method showed a similar performance during days with different spectral conditions. Based on this work, it can be concluded that the proposed equations showed a high accuracy in the prediction of SF for different concentrator PV devices under a range of spectral conditions.