On the Delayed Scaled Consensus Problems
Abstract
:1. Introduction
2. Preliminaries
3. Undelayed Scaled Consensus Process
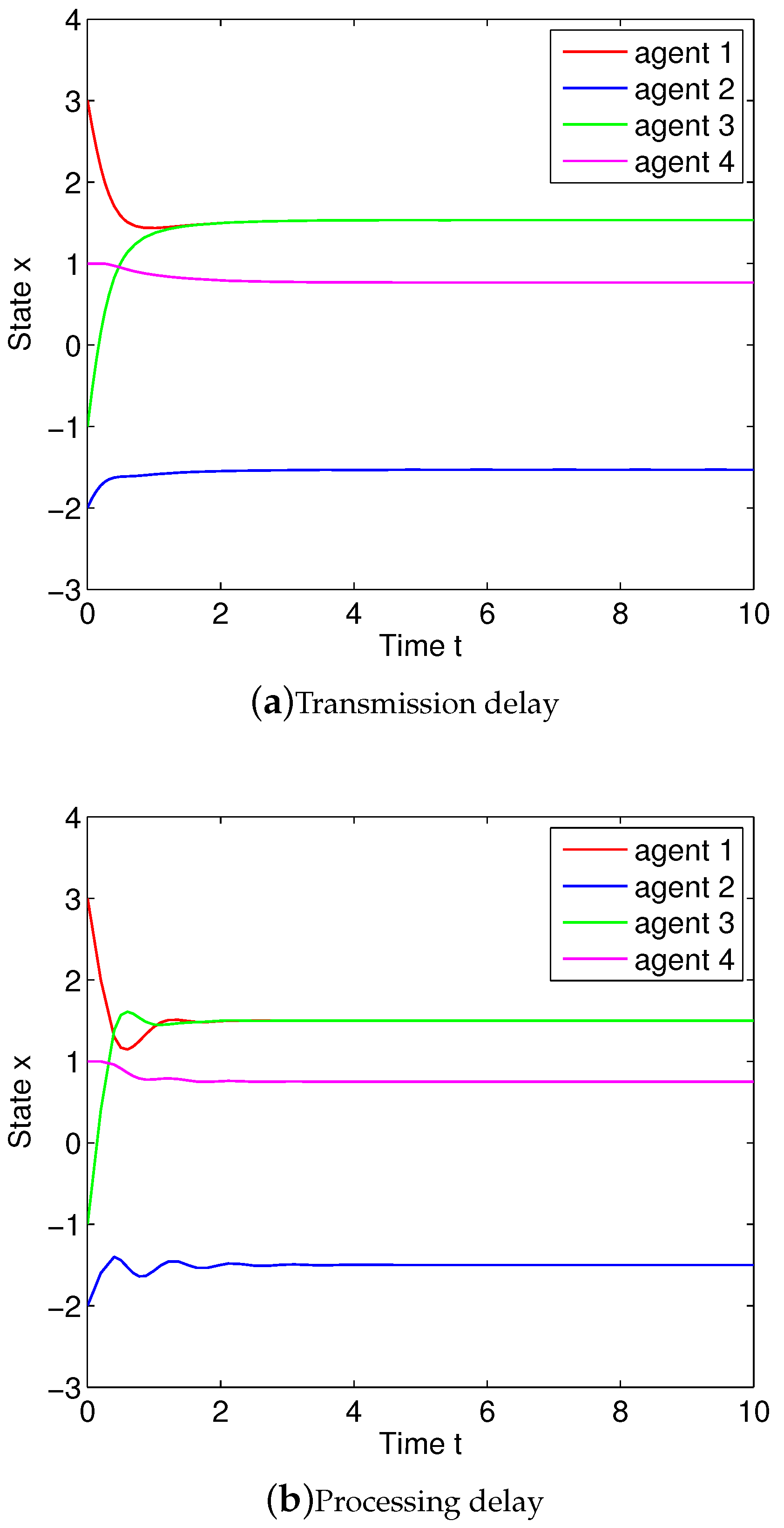
4. Scaled Consensus with Signal Transmission Delays
5. Scaled Consensus with Signal Processing Delays
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans. Ind. Inf. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Haddad, W.M.; Chellaboina, V.; Hui, Q. Nonnegative and Compartmental Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Guglieri, G.; Maroglio, F.; Pellegrino, P.; Torre, L. Design and development of guidance navigation and control algorithms for spacecraft rendezvous and docking experimentation. Acta Astronaut. 2014, 94, 395–408. [Google Scholar] [CrossRef]
- Roy, S. Scaled consensus. Automatica 2015, 51, 259–262. [Google Scholar] [CrossRef]
- Shang, Y. A combinatorial necessary and sufficient condition for cluster consensus. Neurocomputing 2016, 216, 611–616. [Google Scholar] [CrossRef]
- Altafini, C. Consensus problems on networks with antagonistic interactions. IEEE Trans. Autom. Control 2013, 58, 935–946. [Google Scholar] [CrossRef]
- Li, J.; Dong, W.; Xiao, H. Signed consensus problems on networks of agents with fixed and switching topologies. Int. J. Control 2017, 90, 148–160. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y. Robust consensus algorithms for multiscale coordination control of multivehicle systems with disturbances. IEEE Trans. Ind. Electron. 2016, 63, 1107–1119. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y. Scaled consensus problems on switching networks. IEEE Trans. Autom. Control 2016, 61, 1664–1669. [Google Scholar] [CrossRef]
- Hou, B.; Sun, F.; Li, H.; Chen, Y.; Liu, G. Scaled cluster consensus of discrete-time multi-agent systems with general directed topologies. Int. J. Control 2016, 47, 3839–3845. [Google Scholar] [CrossRef]
- Shang, Y. Finite-time scaled consensus through parametric linear iterations. Int. J. Syst. Sci. 2017, 48, 2033–2040. [Google Scholar] [CrossRef]
- Atay, F.M. On the duality between consensus problems and Markov processes, with application to delay systems. Markov Process. Relat. Field. 2016, 22, 537–553. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Merris, R. Laplacian matrices of graphs: A survey. Linear Algebra Appl. 1994, 197–198, 143–176. [Google Scholar] [CrossRef]
- Atay, F.M. The consensus problem in networks with transmission delays. Phil. Trans. R. Soc. A 2013, 371. [Google Scholar] [CrossRef] [PubMed]
- Haken, H. Synergetics; Springer: Berlin, Germany, 1978. [Google Scholar]
- Chu, T.; Zhang, C.; Zhang, Z. Necessary and sufficient condition for absolute stability of normal neural networks. Neural Netw. 2003, 16, 1223–1227. [Google Scholar] [CrossRef]
- Hayes, H.D. Roots of the transcendental equation associated with a certain differential difference equation. J. Lond. Math. Soc. 1950, 25, 226–232. [Google Scholar] [CrossRef]
- Shang, Y. Consensus in averager-copier-voter networks of moving dynamical agents. Chaos 2017, 27. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Y. On the Delayed Scaled Consensus Problems. Appl. Sci. 2017, 7, 713. https://doi.org/10.3390/app7070713
Shang Y. On the Delayed Scaled Consensus Problems. Applied Sciences. 2017; 7(7):713. https://doi.org/10.3390/app7070713
Chicago/Turabian StyleShang, Yilun. 2017. "On the Delayed Scaled Consensus Problems" Applied Sciences 7, no. 7: 713. https://doi.org/10.3390/app7070713
APA StyleShang, Y. (2017). On the Delayed Scaled Consensus Problems. Applied Sciences, 7(7), 713. https://doi.org/10.3390/app7070713