Lévy Statistics and the Glassy Behavior of Light in Random Fiber Lasers
Abstract
:1. Introduction
2. Materials and Methods
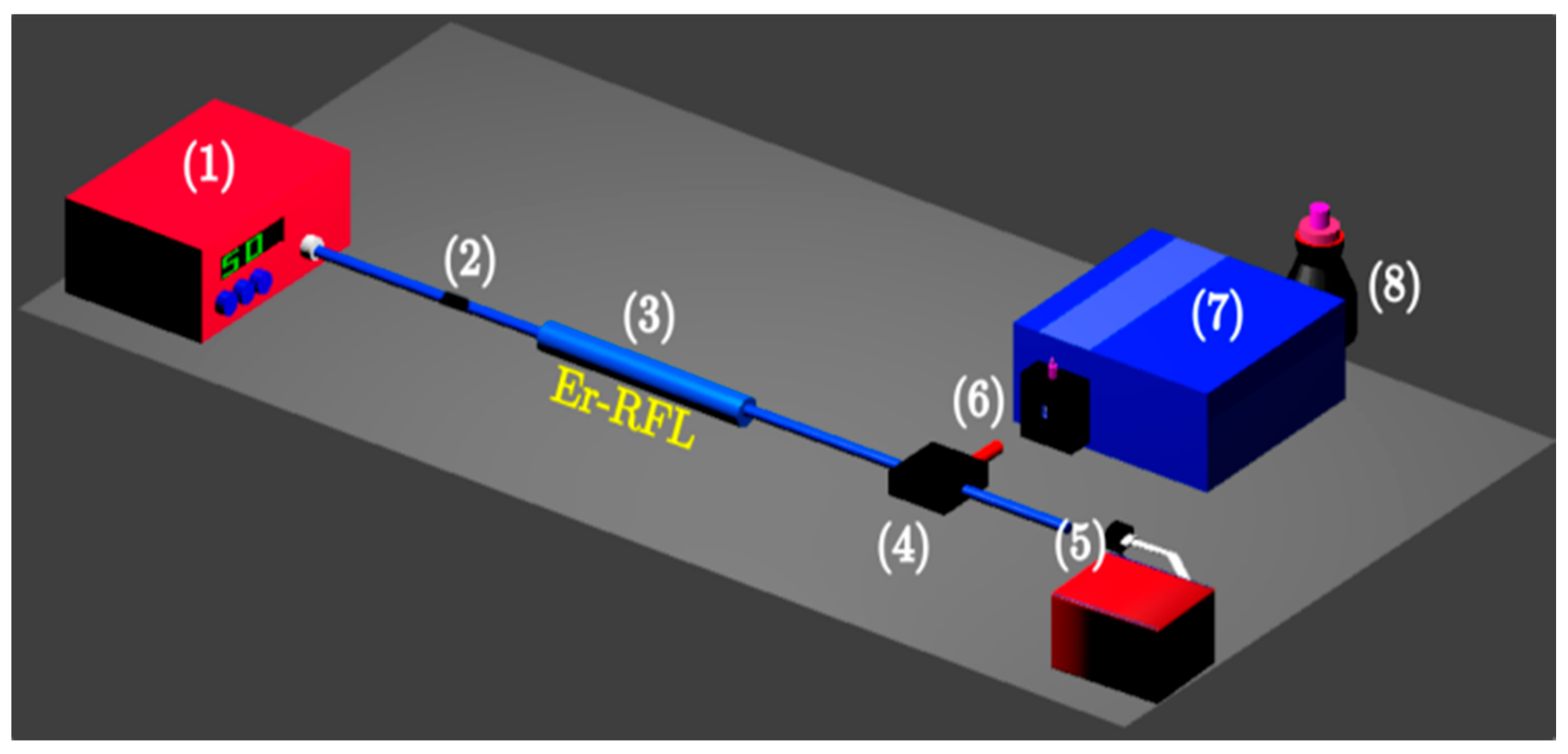
2.1. Random Fiber Lasers
2.2. Fiber Bragg Grating-Based Random Fiber Lasers
3. Results
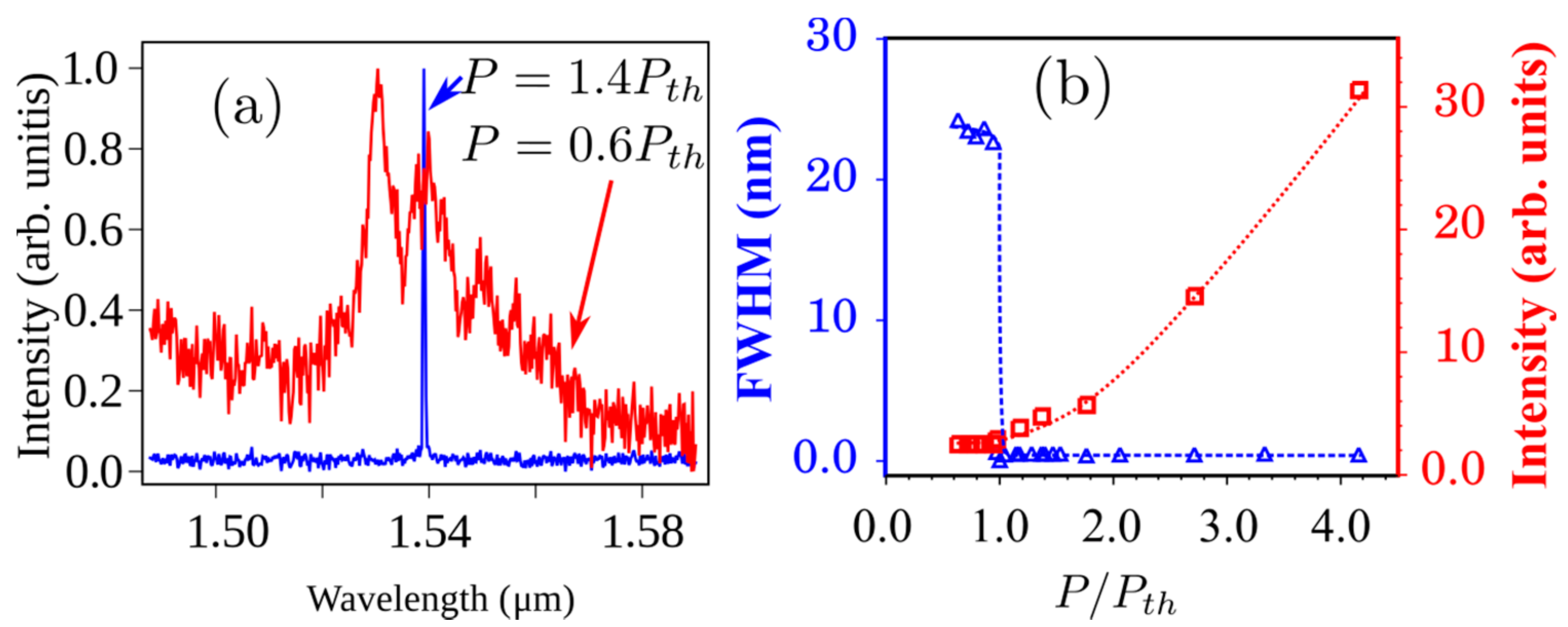
3.1. Characterization of the FBG-Based Er-RFL Explored as a Statistical-Physics Experimental Platform
3.2. Theoretical Framework
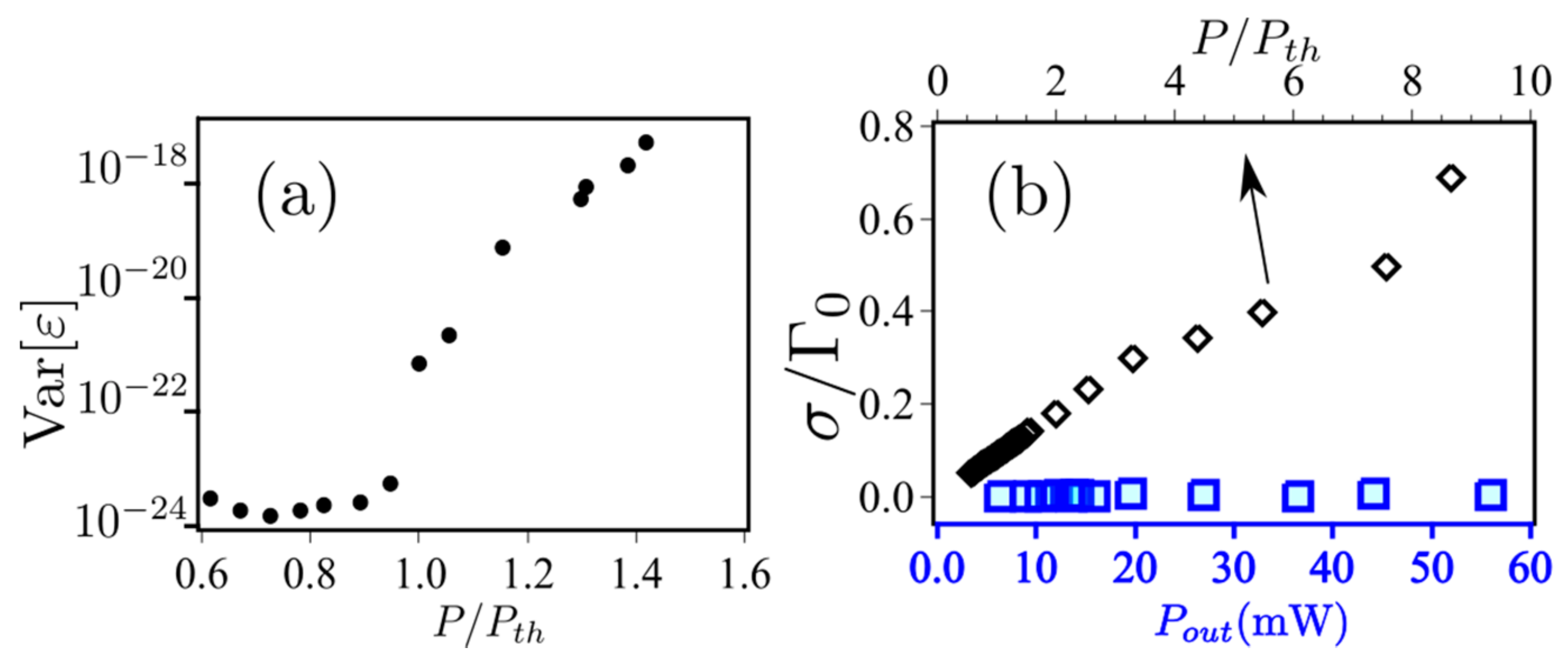
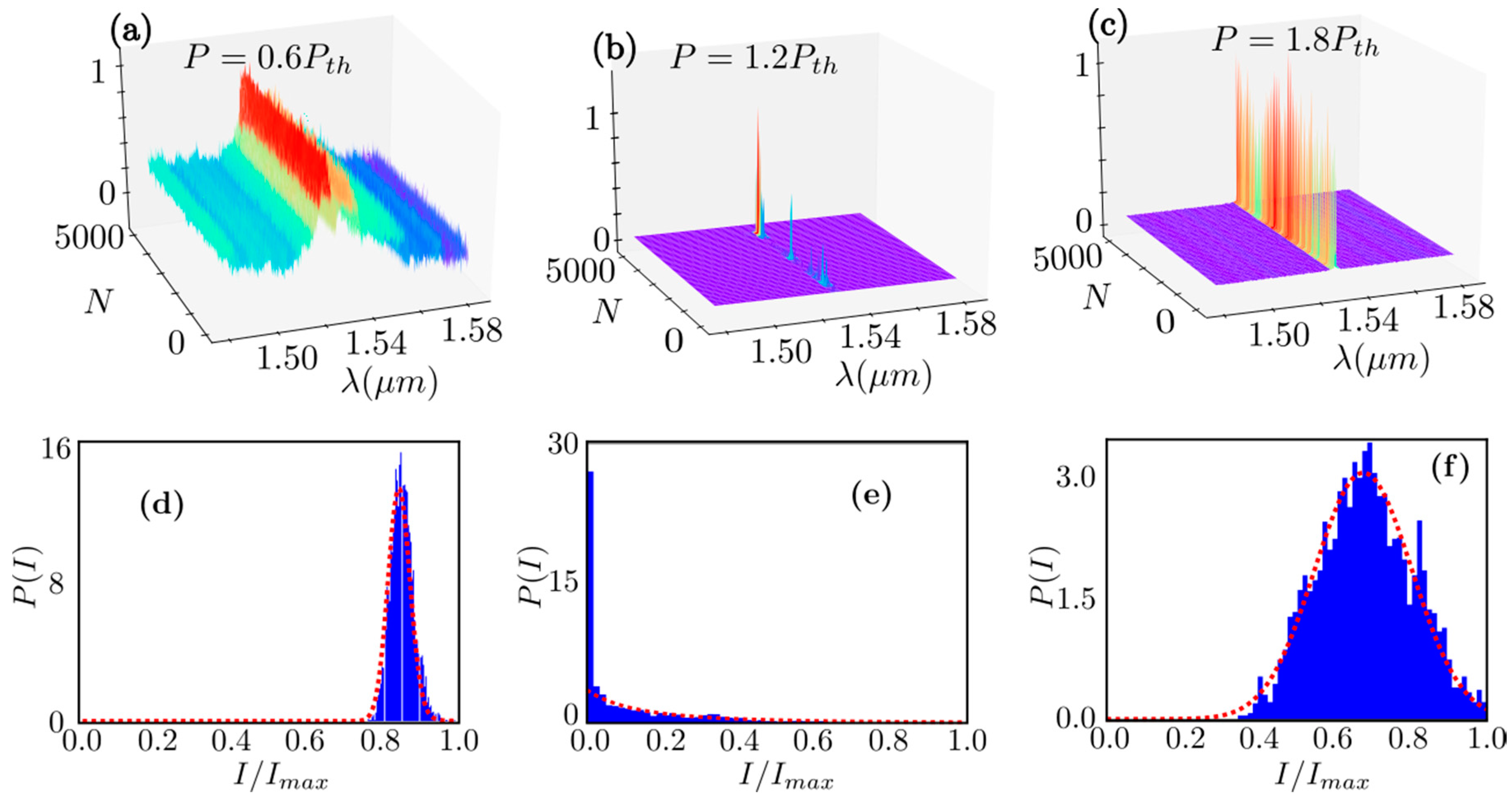
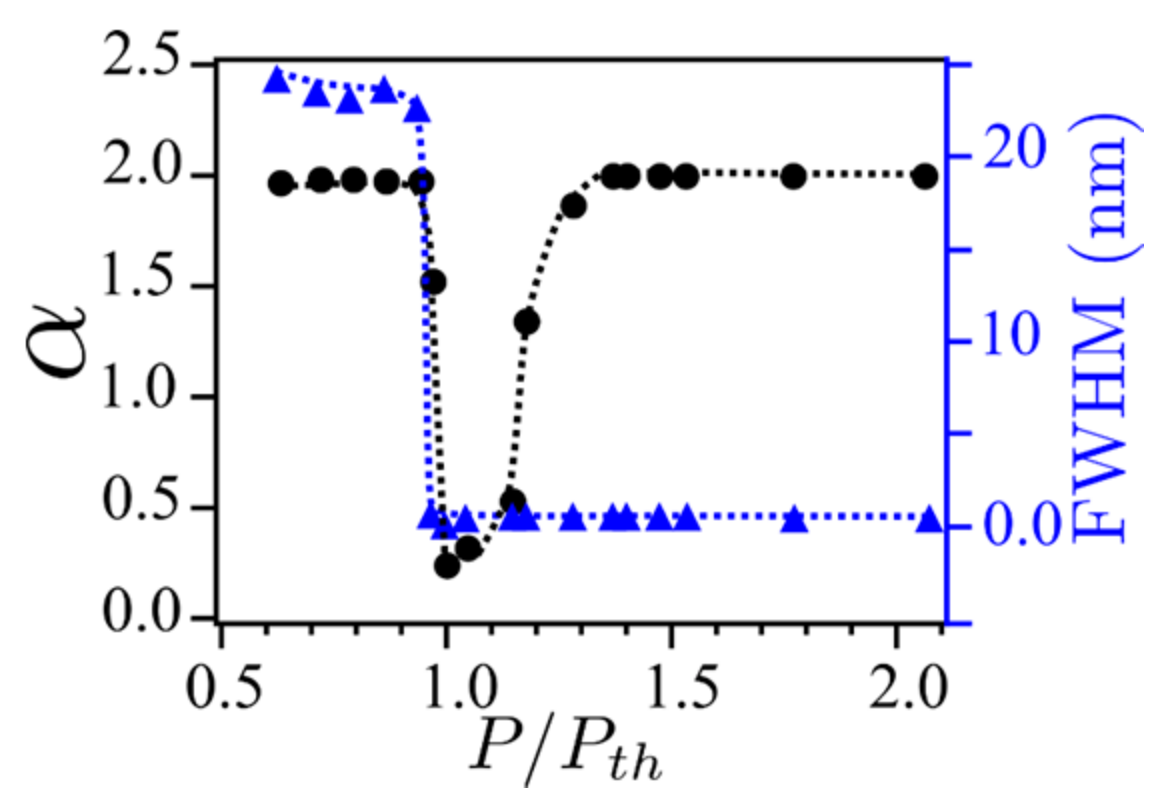
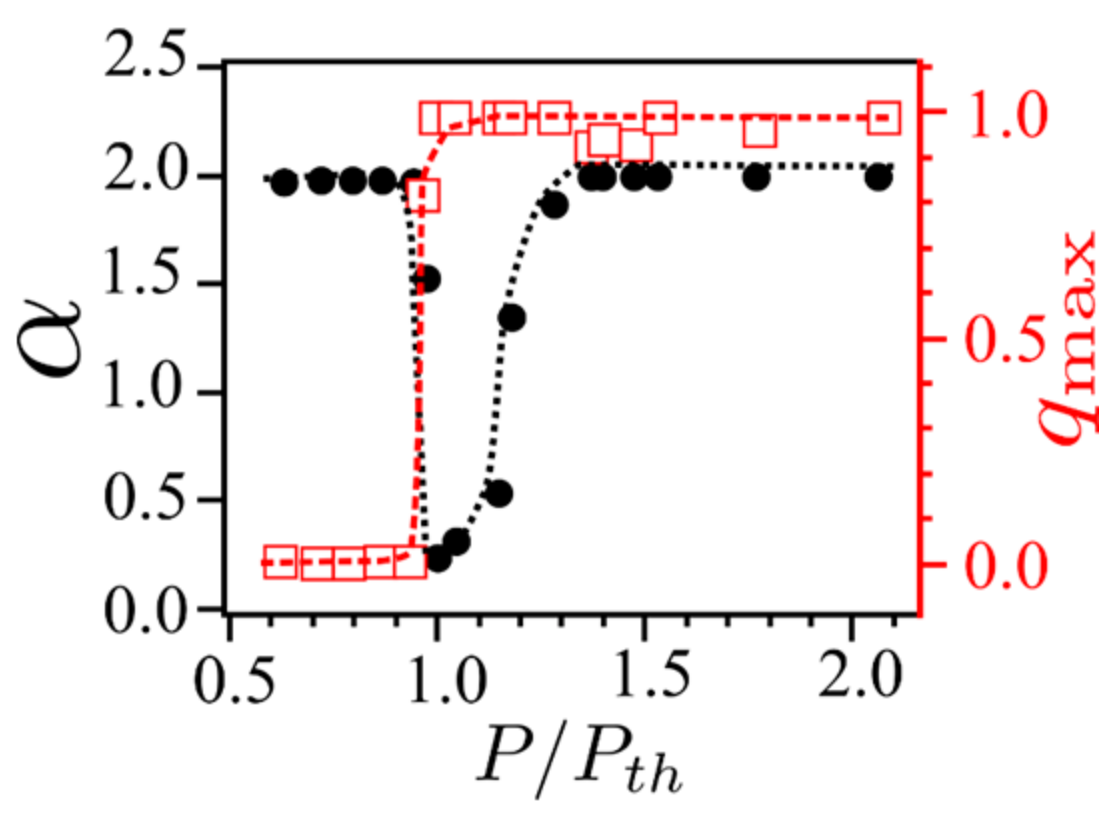
3.3. Lévy Statistics and Glassy Behavior in Er-RFL
4. Summary and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ambartsumyan, R.V.; Basov, N.G.; Kryukov, P.G.; Letokhov, V.S. Laser with nonresonant feedback. JETP Lett. 1966, 3, 167–169. [Google Scholar]
- Letokhov, V.S. Generation of light by a scattering medium with negative resonance absorption. Sov. Phys. JETP 1968, 26, 835–840. [Google Scholar]
- Ambartsumyan, R.V.; Kryukov, P.G.; Letokhov, V.S. Dynamics of emission line narrowing for a laser with nonresonant feedback. Sov. Phys. JETP 1967, 24, 1129–1134. [Google Scholar]
- Ambartsumyan, R.V.; Basov, N.G.; Letokhov, V.S. Frequency stability of a HeNe laser with nonresonant feedback. IEEE Trans. Instrum. Meas. 1968, 17, 338–343. [Google Scholar]
- Ambartsumyan, R.V.; Kryukov, P.G.; Letokhov, V.S.; Matveets, Y.A. Emission statistics of a laser with nonresonant feedback. JETP Lett. 1967, 5, 312–314. [Google Scholar]
- Letokhov, V.S. Stimulated radio emission of the interstellar medium. JETP Lett. 1966, 4, 321–323. [Google Scholar]
- Lavrinovich, N.N.; Letokhov, V.S. The possibility of laser effect in stellar atmospheres. Sov. Phys. JETP 1975, 40, 800–805. [Google Scholar]
- Letokhov, V.S. Astrophysical lasers. Quantum Electron. 2002, 32, 1065–1079. [Google Scholar] [CrossRef]
- Johansson, S.; Letokhov, V.S. Astrophysical lasers operating in optical Fe II lines in stellar ejecta of Eta Carinae. Astron. Astrophys. 2004, 428, 427–509. [Google Scholar] [CrossRef]
- Noginov, M.A. Solid State Random Lasers; Springer Series in Optical Sciences; Springer: New York, NY, USA, 2005. [Google Scholar]
- Lawandy, N.M.; Balachandran, R.M.; Gomes, A.S.L.; Sauvian, E. Laser action in strongly scattering medium. Nature 1994, 368, 436–438. [Google Scholar] [CrossRef]
- Ye, L.; Zhao, C.; Feng, Y.; Gu, B.; Cui, Y.; Lu, Y. Study on the polarization of random lasers from dye-doped nematic liquid crystals. Nanoscale Res. Lett. 2017, 12, 27. [Google Scholar] [CrossRef] [PubMed]
- Abegão, L.M.G.; Manoel, D.S.; Otuka, A.J.G.; Ferreira, P.H.D.; Vollet, D.R.; Donatti, D.A.; De Boni, L.; Mendonça, C.R.; de Vicente, F.S.; Rodrigues, J.J., Jr.; et al. Random laser emission from a rhodamine B-doped GPTS/TEOS-derived organic/sílica monolithic xerogel. Laser Phys. Lett. 2017, 14, 065801. [Google Scholar] [CrossRef]
- Shasti, M.; Coutino, P.; Mukherjee, S.; Varanytsia, A.; Smith, T.; Luchette, A.P.; Sukhomlinova, L.; Kosa, T.; Munoz, A.; Taheri, B. Reverse mode switching of the random laser emission in dye doped liquid crystals under homogeneous and inhomogeneous electric fields. Photonics Res. 2016, 4, 7–12. [Google Scholar] [CrossRef]
- Anderson, B.R.; Gunawidjaja, R.; Eilers, H. Self-healing organic-dye-based random lasers. Opt. Lett. 2015, 40, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Gomes, A.S.L.; Carvalho, M.T.; Dominguez, C.T.; de Araújo, C.B.; Prasad, P.N. Direct three-photon excitation of upconversion random laser emission in a weakly scattering organic colloidal system. Opt. Express 2014, 22, 14305–14310. [Google Scholar] [CrossRef] [PubMed]
- Knitter, S.; Kues, M.; Fallnich, C. Emission polarization of random lasers in organic dye solutions. Opt. Lett. 2012, 37, 3621–3623. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Herrnsdorf, J.; Guilhabert, B.; Zhang, Y.; Watson, I.M.; Gu, E.; Laurand, N.; Dawson, M.D. Colloidal quantum dot random laser. Opt. Express 2011, 19, 2996–3003. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, C.T.; Gomes, M.A.; Macedo, Z.S.; de Araújo, C.B.; Gomes, A.S.L. Multi-photon excited coherent random laser emission in ZnO powders. Nanoscale 2015, 7, 317–323. [Google Scholar] [CrossRef] [PubMed]
- Moura, A.L.; Jerez, V.; Maia, L.J.Q.; Gomes, A.S.L.; de Araújo, C.B. Multi-wavelength emission through self-induced second-order wave-mixing processes from a Nd3+ doped crystalline powder random laser. Sci. Rep. 2015, 5, 13816. [Google Scholar] [CrossRef] [PubMed]
- Moura, A.L.; Carreño, S.J.M.; Pincheira, P.I.R.; Fabris, Z.V.; Maia, L.J.Q.; Gomes, A.S.L.; de Araújo, C.B. Tunable ultraviolet and blue light generation from Nd:YAB random laser bolstered by second-order nonlinear processes. Sci. Rep. 2016, 6, 27107. [Google Scholar] [CrossRef] [PubMed]
- Polson, R.C.; Chipouline, A.; Vardeny, Z.V. Random lasing in π-conjugated films and infiltrated opals. Adv. Mater. 2001, 13, 760–764. [Google Scholar] [CrossRef]
- Meng, X.; Fujita, K.; Murai, S.; Tanaka, K. Coherent random lasers in weakly scattering polymer films containing silver nanoparticles. Phys. Rev. A 2009, 79, 053817. [Google Scholar] [CrossRef]
- Costela, A.; Garcia-Moreno, I.; Cerdan, L.; Martin, V.; Garcia, O.; Sastre, R. Dye-doped POSS solutions: Random nanomaterials for laser emission. Adv. Mater. 2009, 21, 4163–4166. [Google Scholar] [CrossRef]
- Tulek, A.; Polson, R.C.; Vardeny, Z.V. Naturally occurring resonators in random lasing of π-conjugated polymer films. Nat. Phys. 2010, 6, 303–310. [Google Scholar] [CrossRef]
- Polson, R.C.; Raikh, M.E.; Vardeny, Z.V. Random lasing from weakly scattering media; Spectrum universality in DOO–PPV polymer films. Phys. E 2002, 13, 1240–1242. [Google Scholar] [CrossRef]
- Dos Santos, M.V.; Dominguez, C.T.; Schiavon, J.V.; Barud, H.S.; de Melo, L.S.A.; Ribeiro, S.J.L.; Gomes, A.S.L.; de Araújo, C.B. Random laser action from flexible biocellulose-based device. J. Appl. Phys. 2014, 115, 083108. [Google Scholar] [CrossRef]
- Yu, S.F.; Yuen, C.; Lau, S.P.; Park, W.I.; Yi, G.-C. Random laser action in ZnO nanorod arrays embedded in ZnO epilayers. Appl. Phys. Lett. 2004, 84, 3241–3243. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, X.; Wei, S.; Sun, Y.; Wang, Y.; Zhou, J.; Shi, J.; Liu, D. Two-threshold silver nanowire-based random laser with different dye concentrations. Laser Phys. Lett. 2014, 11, 095002. [Google Scholar] [CrossRef]
- Gao, F.; Morshed, M.M.; Bashar, S.B.; Zheng, Y.; Shi, Y.; Liu, J. Electrically pumped random lasing based on an Au–ZnO nanowire Schottky junction. Nanoscale 2015, 7, 9505–9509. [Google Scholar] [CrossRef] [PubMed]
- Bashar, S.B.; Suja, M.; Morshed, M.; Gao, F.; Liu, J. An Sb-doped p-type ZnO nanowire based random laser diode. Nanotechnology 2016, 27, 065204. [Google Scholar] [CrossRef] [PubMed]
- Baudouin, Q.; Mercadier, N.; Guarrera, V.; Guerin, W.; Kaiser, R. A cold-atom random laser. Nat. Phys. 2013, 9, 357–360. [Google Scholar] [CrossRef]
- Van der Molen, K.L.; Mosk, A.P.; Lagendijk, A.D. Intrinsic intensity fluctuations in random lasers. Phys. Rev. A 2006, 74, 053808. [Google Scholar] [CrossRef]
- Van der Molen, K.L.; Tjerkstra, R.W.; Mosk, A.P.; Lagendijk, A.D. Spatial extent of random laser modes. Phys. Rev. Lett. 2007, 98, 143901. [Google Scholar] [CrossRef] [PubMed]
- Wiersma, D.S. The physics and applications of random lasers. Nat. Phys. 2008, 4, 359–367. [Google Scholar] [CrossRef]
- Leonetti, M.; Conti, C.; Lopez, C. The mode-locking transition of random lasers. Nat. Photonics 2011, 5, 615–617. [Google Scholar] [CrossRef]
- Ignesti, E.; Tommasi, F.; Fini, L.; Martelli, F.; Azzali, N.; Cavalieri, S. A new class of optical sensors: A random laser based device. Sci. Rep. 2016, 6, 35225. [Google Scholar] [CrossRef] [PubMed]
- Bhaktha, B.N.S.; Bachelard, N.; Noblin, X.; Sebbah, P. Optofluidic random laser. Appl. Phys. Lett. 2012, 101, 151101. [Google Scholar] [CrossRef]
- Bachelard, N.; Gigan, S.; Noblin, X.; Sebbah, P. Adaptive pumping for spectral control of random lasers. Nat. Phys. 2014, 10, 426–431. [Google Scholar] [CrossRef]
- Redding, B.; Choma, M.A.; Cao, H. Speckle-free laser imaging using random laser illumination. Nat. Photonics 2012, 6, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Luan, F.; Gu, B.B.; Gomes, A.S.L.; Yong, K.T.; Wen, S.C.; Prasad, P.N. Lasing in nanocomposite random media. Nano Today 2015, 10, 168–192. [Google Scholar] [CrossRef]
- Ghofraniha, N.; Viola, I.; Di Maria, F.; Barbarella, G.; Gigli, G.; Leuzzi, L.; Conti, C. Experimental evidence of replica symmetry breaking in random lasers. Nat. Commun. 2015, 6, 6058. [Google Scholar] [CrossRef] [PubMed]
- De Mattos, C.J.S.; Menezes, L.S.; Brito-Silva, A.M.; Gámez, M.A.M.; Gomes, A.S.L.; de Araújo, C.B. Random fiber laser. Phys. Rev. Lett. 2007, 99, 153903. [Google Scholar] [CrossRef] [PubMed]
- Lizárraga, N.; Puente, N.P.; Chaikina, E.I.; Leskova, T.A.; Méndez, E.R. Single-mode Er-doped fiber random laser with distributed Bragg grating feedback. Opt. Express 2009, 17, 395–404. [Google Scholar] [CrossRef] [PubMed]
- Gagné, M.; Kashyap, R. Demonstration of a 3 mW threshold Er-doped random fiber laser based on a unique fiber Bragg grating. Opt. Express 2009, 17, 19067–19074. [Google Scholar] [CrossRef] [PubMed]
- Turitsyn, S.K.; Babin, S.A.; El-Taher, A.E.; Harper, P.; Churkin, D.V.; Kablukov, S.I.; Ania-Castanon, J.D.; Karalekas, V.; Podivilov, E.V. Random distributed feedback fibre laser. Nat. Photonics 2010, 4, 231–235. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; Churkin, D.V.; Vatnik, I.D.; Nikulin, M.; Podivilov, E.V. Random distributed feedback fibre lasers. Phys. Rep. 2014, 542, 133–193. [Google Scholar] [CrossRef]
- Churkin, D.V.; Sugavanam, S.; Vatnik, I.D.; Wang, Z.; Podivilov, E.V.; Babin, S.A.; Rao, Y.; Turitsyn, S.K. Recent advances in fundamentals and applications of random fiber lasers. Adv. Opt. Photonics 2015, 7, 516–569. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, H.; Fan, M.; Zhang, L.; Rao, Y.; Zhang, W.; Jia, X. High power random fiber laser with short cavity length: Theoretical and experimental investigations. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 0900506. [Google Scholar]
- Li, S.W.; Ma, R.; Rao, Y.J.; Zhu, Y.Y.; Wang, Z.N.; Jia, X.H.; Li, J. Random distributed feedback fiber laser based on combination of Er-doped fiber and single-mode fiber. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 0900406. [Google Scholar]
- Wu, H.; Wang, Z.; Fan, M.; Zhang, L.; Zhang, W.; Ra, Y. Role of the mirror’s reflectivity in forward-pumped random fiber laser. Opt. Express 2015, 23, 1421–1427. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhou, P.; Wang, X.; Du, X.; Xiao, H.; Xu, X. Hundred-watt-level high power random distributed feedback Raman fiber laser at 1150 nm and its application in mid-infrared laser generation. Opt. Express 2015, 23, 17138–17144. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.L.; Ma, R.; Tang, C.H.; Rao, Y.J.; Zeng, X.P.; Yang, Z.J.; Wang, Z.N.; Gong, Y.; Wang, Y.S. All optical mode controllable Er-doped random fiber laser with distributed Bragg gratings. Opt. Lett. 2015, 40, 3181–3184. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dong, X.; Shum, P.P.; Liu, X.; Su, H. Random laser with multiphase-shifted Bragg grating in Er/Yb-codoped fiber. J. Lightwave Technol. 2015, 33, 95–99. [Google Scholar] [CrossRef]
- Du, X.; Zhang, H.; Wang, X.; Zhou, P.; Liu, Z. Investigation on random distributed feedback Raman fiber laser with linear polarized output. Photonics Res. 2015, 3, 28–31. [Google Scholar] [CrossRef]
- Tang, Y.; Xu, J. A random Q-switched fiber laser. Sci. Rep. 2015, 5, 9338. [Google Scholar] [CrossRef] [PubMed]
- Yao, B.C.; Rao, Y.J.; Wang, Z.N.; Wu, Y.; Zhou, J.H.; Wu, H.; Fan, M.Q.; Cao, X.L.; Zhang, W.L.; Chen, Y.F.; et al. Graphene based widely-tunable and singly-polarized pulse generation with random fiber lasers. Sci. Rep. 2015, 5, 18526. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Jiang, H.; Yang, X.; Pan, W.; Feng, Y. Ultra-wide wavelength tuning of a cascaded Raman random fiber laser. Opt. Lett. 2016, 41, 215–218. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Zhang, H.; Wang, X.; Zhou, P.; Liu, Z. Short cavity-length random fiber laser with record power and ultrahigh efficiency. Opt. Lett. 2016, 41, 571–574. [Google Scholar] [CrossRef] [PubMed]
- Dontsova, E.I.; Kablukov, S.I.; Vatnik, I.D.; Babin, S.A. Frequency doubling of Raman fiber lasers with random distributed feedback. Opt. Lett. 2016, 41, 1439–1442. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Liang, Y.; Qian, X.; Gao, P.; Xie, K.; Jiang, H. Polarized random laser emission from an oriented disorder polymer optical fiber. Opt. Lett. 2016, 41, 2584–2587. [Google Scholar] [CrossRef] [PubMed]
- Ardakani, A.G.; Rafieipour, P. Investigation of one-dimensional Raman random lasers based on the finite-difference-time-domain method: Presence of mode competition and higher-order Stokes and anti-Stokes modes. Phys. Rev. A 2016, 93, 023833. [Google Scholar] [CrossRef]
- Zhang, W.L.; Song, Y.B.; Zeng, X.P.; Ma, R.; Yang, Z.J.; Rao, Y.J. Temperature-controlled mode selection of Er-doped random fiber laser with disordered Bragg gratings. Photonics Res. 2016, 4, 102–105. [Google Scholar] [CrossRef]
- Wu, H.; Wang, Z.; Rao, Y. Tailoring the properties of cw random fiber lasers. In Proceedings of the Advanced Photonics Congress 2016 (IPR, NOMA, Sensors, Networks, SPPCom, SOF), Vancouver, NA, Canada, 18–20 July 2016. [Google Scholar]
- Babin, S.A.; Zlobina, E.A.; Kablukov, S.I.; Podivilov, E.V. High-order random Raman lasing in a PM fiber with ultimate e efficiency and narrow bandwidth. Sci. Rep. 2016, 6, 22625. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.L.; Zheng, M.Y.; Ma, R.; Gong, C.Y.; Yang, Z.J.; Peng, G.D.; Rao, Y.J. Fiber-type random laser based on a cylindrical waveguide with a disordered cladding layer. Sci. Rep. 2016, 6, 26473. [Google Scholar] [CrossRef] [PubMed]
- González, I.R.R.; Lima, B.C.; Pincheira, P.I.R.; Brum, A.A.; Macêdo, A.M.S.; Vasconcelos, G.L.; Menezes, L.S.; Raposo, E.P.; Gomes, A.S.L.; Kashyap, R. Turbulence hierarchy in a random fibre laser. Nat. Commun. 2017, 8, 15731. [Google Scholar] [CrossRef] [PubMed]
- Lima, B.C.; Gomes, A.S.L.; Pincheira, P.I.R.; Moura, A.L.; Gagné, M.; Raposo, E.P.; de Araújo, C.B.; Kashyap, R. Observation of Lévy statistics in one-dimensional erbium-based random fiber laser. J. Opt. Soc. Am. B 2017, 34, 293–299. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Lima, B.C.; Pincheira, P.I.R.; Moura, A.L.; Gagné, M.; Raposo, E.P.; de Araújo, C.B.; Kashyap, R. Glassy behavior in a one-dimensional continuous-wave erbium-doped random fiber laser. Phys. Rev. A 2016, 94, 011801. [Google Scholar] [CrossRef]
- Hokr, B.H.; Cerjan, A.; Thompson, J.V.; Yuan, L.; Liew, S.F.; Bixler, J.N.; Noojin, G.D.; Thomas, R.J.; Cao, H.; Stone, A.D.; et al. Evidence of Anderson localization effects in random Raman lasing. SPIE Proc. 2016, 9731, 973110. [Google Scholar]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications; Roberts & Company: Englewood, CO, USA, 2007. [Google Scholar]
- Zhu, G.; Gu, L.; Noginov, M.A. Experimental study of instability in a random laser with immobile scatterers. Phys. Rev. A 2012, 85, 043801. [Google Scholar] [CrossRef]
- Angelani, L.; Conti, C.; Ruocco, G.; Zamponi, F. Glassy behavior of light in random lasers. Phys. Rev. B 2006, 74, 104207. [Google Scholar] [CrossRef]
- Angelani, L.; Conti, C.; Ruocco, G.; Zamponi, F. Glassy behavior of light. Phys. Rev. Lett. 2006, 96, 065702. [Google Scholar] [CrossRef] [PubMed]
- Leuzzi, L.; Conti, C.; Folli, V.; Angelani, L.; Ruocco, G. Phase diagram and complexity of mode-locked lasers: From order to disorder. Phys. Rev. Lett. 2009, 102, 083901. [Google Scholar] [CrossRef] [PubMed]
- Conti, C.; Leuzzi, L. Complexity of waves in nonlinear disordered media. Phys. Rev. B 2011, 83, 134204. [Google Scholar] [CrossRef]
- Antenucci, F.; Conti, C.; Crisanti, A.; Leuzzi, L. General phase diagram of multimodal ordered and disordered lasers in closed and open cavities. Phys. Rev. Lett. 2015, 114, 043901. [Google Scholar] [CrossRef] [PubMed]
- Antenucci, F.; Crisanti, A.; Leuzzi, L. Complex spherical 2 + 4 spin glass: A model for nonlinear optics in random media. Phys. Rev. A 2015, 91, 053816. [Google Scholar] [CrossRef]
- Antenucci, F.; Crisanti, A.; Leuzzi, L. The glassy random laser: Replica symmetry breaking in the intensity fluctuations of emission spectra. Sci. Rep. 2015, 5, 16792. [Google Scholar] [CrossRef] [PubMed]
- Antenucci, F.; Crisanti, A.; Ibáñez-Berganza, M.; Marruzzo, A.; Leuzzi, L. Statistical mechanics models for multimode lasers and random lasers. Philos. Mag. 2016, 96, 704–731. [Google Scholar] [CrossRef]
- Raposo, E.P.; Gomes, A.S.L. Analytical solution for the Lévy-like steady-state distribution of intensities in random lasers. Phys. Rev. A 2015, 91, 043827. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Raposo, E.P.; Moura, A.L.; Fewo, S.I.; Pincheira, P.I.R.; Jerez, V.; Maia, L.J.Q.; de Araújo, C.B. Observation of Lévy distribution and replica symmetry breaking in random lasers from a single set of measurements. Sci. Rep. 2016, 6, 27987. [Google Scholar] [CrossRef] [PubMed]
- Crisanti, A.; Sommers, H.-J. The spherical p-spin interaction spin glass model: The statics. Z. Phys. B 1992, 87, 341–354. [Google Scholar] [CrossRef]
- Mézard, M.; Parisi, G.; Virasoro, M.A. Spin Glass Theory and Beyond; World Scientific: Singapore, 1987. [Google Scholar]
- Pincheira, P.I.R.; Silva, A.F.; Carreño, S.J.M.; Moura, A.L.; Fewo, S.I.; Raposo, E.P.; Gomes, A.S.L.; de Araújo, C.B. Observation of photonic to paramagnetic spin-glass transition in specially-designed TiO2 particles-based dye-colloidal random laser. Opt. Lett. 2016, 41, 3459–3462. [Google Scholar] [CrossRef] [PubMed]
- O’Bryan, I.C.L.; Sargent, I.M. Theory of multimode laser operation. Phys. Rev. A 1973, 8, 3071–3092. [Google Scholar] [CrossRef]
- Schenzle, A.; Brand, H. Multiplicative stochastic processes in statistical physics. Phys. Rev. A 1979, 20, 1628–1647. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes; Chapman and Hall: London, UK, 1994. [Google Scholar]
- Uppu, R.; Mujumdar, S. Exponentially tempered Lévy sums in random lasers. Phys. Rev. Lett. 2015, 114, 183903. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. Stochastic process with ultraslow convergence to a Gaussian: The truncated Lévy flight. Phys. Rev. Lett. 1994, 73, 2946–2949. [Google Scholar] [CrossRef] [PubMed]
- Bartumeus, F.; Raposo, E.P.; Viswanathan, G.M.; da Luz, M.G.E. Stochastic optimal foraging: Tuning intensive and extensive dynamics in random searches. PLoS ONE 2014, 9, e106373. [Google Scholar] [CrossRef] [PubMed]
- Lepri, S.; Cavalieri, S.; Oppo, G.-L.; Wiersma, D.S. Statistical regimes of random laser fluctuations. Phys. Rev. A 2007, 75, 063820. [Google Scholar] [CrossRef]
- Uppu, R.; Mujumdar, S. Lévy exponents as universal identifiers of threshold and criticality in random lasers. Phys. Rev. A 2014, 90, 025801. [Google Scholar] [CrossRef]
- McCulloch, J.H. Simple consistent estimators of stable distribution parameters. Commun. Stat. Simul. 1986, 15, 1109–1136. [Google Scholar] [CrossRef]
- Uppu, R.; Tiwari, A.K.; Mujumdar, S. Identification of statistical regimes and crossovers in coherent random laser emission. Opt. Lett. 2012, 37, 662–664. [Google Scholar] [CrossRef] [PubMed]
- Uppu, R.; Mujumdar, S. Dependence of the Gaussian-Lévy transition on the disorder strength in random lasers. Phys. Rev. A 2013, 87, 013822. [Google Scholar] [CrossRef]
- Tommasi, F.; Ignesti, E.; Lepri, S.; Cavalieri, S. Robustness of replica symmetry breaking phenomenology in random laser. Sci. Rep. 2016, 6, 37113. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araújo, C.B.d.; Gomes, A.S.L.; Raposo, E.P. Lévy Statistics and the Glassy Behavior of Light in Random Fiber Lasers. Appl. Sci. 2017, 7, 644. https://doi.org/10.3390/app7070644
Araújo CBd, Gomes ASL, Raposo EP. Lévy Statistics and the Glassy Behavior of Light in Random Fiber Lasers. Applied Sciences. 2017; 7(7):644. https://doi.org/10.3390/app7070644
Chicago/Turabian StyleAraújo, Cid B. de, Anderson S. L. Gomes, and Ernesto P. Raposo. 2017. "Lévy Statistics and the Glassy Behavior of Light in Random Fiber Lasers" Applied Sciences 7, no. 7: 644. https://doi.org/10.3390/app7070644





