Polarization Properties of Laser Solitons

Abstract

The objective of this paper is to summarize the results obtained for the state of polarization in the emission of a vertical-cavity surface-emitting laser with frequency-selective feedback added. We start our research with the single soliton; this situation presents two perpendicular main orientations, connected by a hysteresis loop. In addition, we also find the formation of a ring-shaped intensity distribution, the vortex state, that shows two homogeneous states of polarization with very close values to those found in the soliton. For both cases above, the study shows the spatially resolved value of the orientation angle. It is important to also remark the appearance of a non-negligible amount of circular light that gives vectorial character to all the different emissions investigated.

1. Introduction

The appearance of stable structures, solitons, in laser emission is an important topic in the field of nonlinear optics. Depending on their nature, they can be classified as temporal [1] and spatial solitons [2].

The spatial solitons are self-localized states of light capable of beating diffraction through nonlinearities; this attribute makes them useful for potential application in all optical processing and switching operations [3,4]. Among them, cavity solitons (CS) are bistable spatially self-localized waves that exist in the transverse aperture of broad-area nonlinear optical resonators. Examples of spatial CS have been found in many different experiments, e.g., laser with a saturable absorber [5], Kerr media [6], liquid crystal light valve [7] or vertical-cavity surface-emitting laser (VCSEL) [8].

The VCSEL is one of the most used and investigated kinds of solid state laser [9]. Since its development, it has been widely utilized in different applications [10]. In conditions of normal emission, above the threshold value for the injected current, a well characterized linear polarization is observed [11]. Depending on the state of polarization, the CS with only one component is called scalar; otherwise these structures are called vector CSs.

In this contribution, we create the solitonic structure in a very simple system—a VCSEL with a frequency-selective feedback setup as is shown in different publications of some of the authors [12,13]. In the aforementioned conditions, a rich collection of spatially self-localized intensity structures can be found, from the single spot CS to much more complex formations, i.e., the appearance of a ring-shaped structure, usually made by a circular intensity pattern with peaks—the vortex beam. In this particular experiment, a novel feature associated with the state of polarization of the single soliton is discovered, i.e., the existence of a hysteresis loop that connects two orthogonal orientations. Also remarkable is the discovery of a significant amount of circular light in all the cases studied, for the first time in this system, in accordance to other authors’ results [14] for the VCSEL emission, making it a full Poincare beam [15].

Our objective is to resolve the spatial distribution of the polarization in all these situations; starting from the case of homogeneous polarization found in the CS and applying also our analysis to the vortex.

The organization of the paper is as follows. In Section 2, the experimental setup and the method are included; in Section 3, the results are presented; in Section 4, we make an interpretation of the results and the future directions of our work.

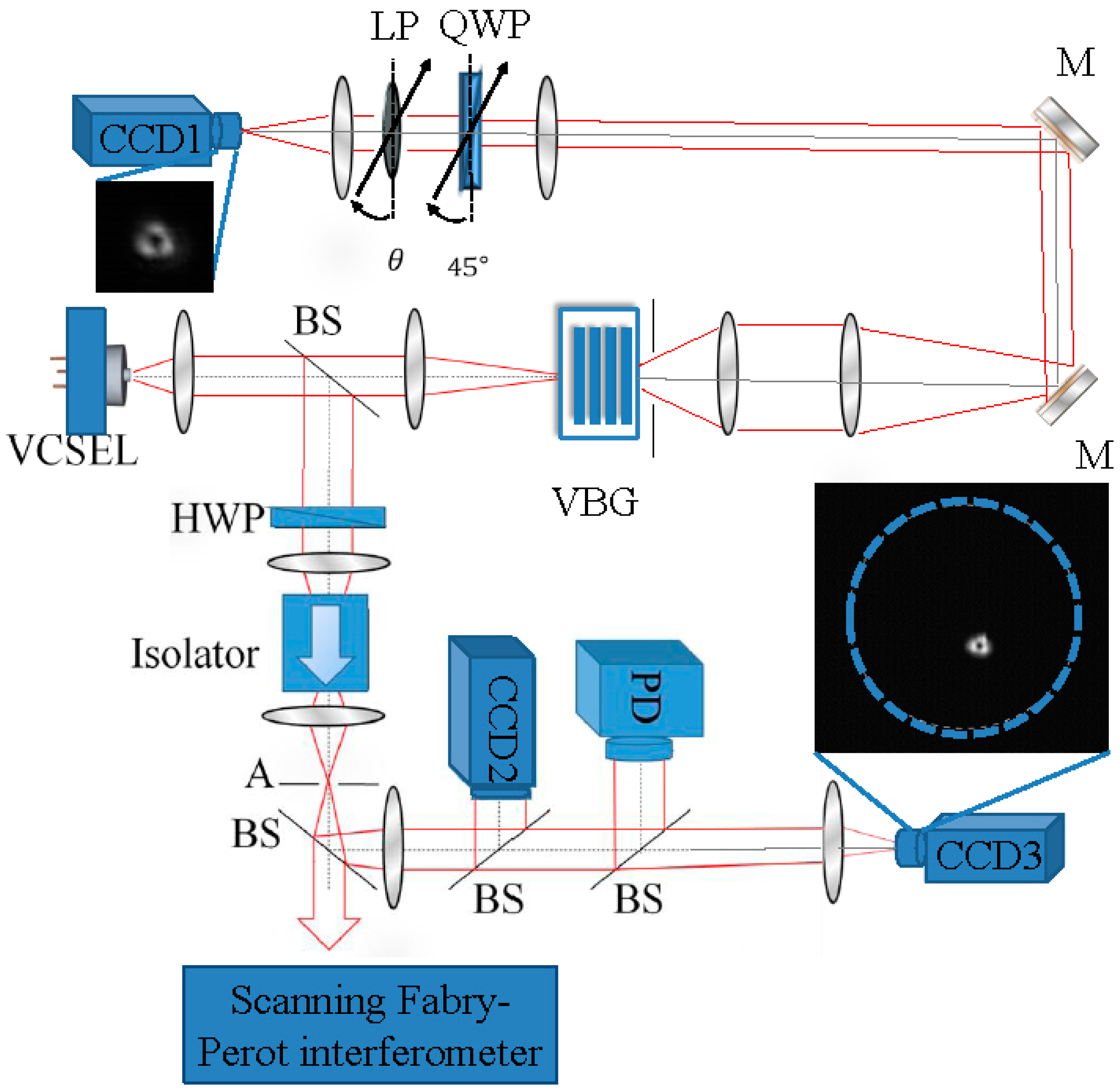
2. Materials and Method

The experimental setup and the instrumentation used in this experiment are very similar to those used in previous works on laser solitons in our group [8,12]. A detailed representation of this arrangement is shown in Figure 1. The VCSEL on this experiment is a large aperture device with a diameter of 200 mm. The emission takes place in the 975–980 nm region through the n-doped Bragg reflector and the transparent substrate, the so-called bottom emitter [16]. A Peltier element with a feedback circuit is utilized to stabilize the VCSEL temperature at $20{}^{\circ }$C.

The output of the VCSEL is collimated by an aspheric lens of $f_1=8$ mm focal length. A second lens with $f_2=50$ mm is used to focus the light onto the frequency-selective element, a volume Bragg grating (VBG). These two lenses are adjusted to form an a focal telescope, i.e., the external cavity is self-imaging after a round trip. The VBG has a narrow-band reflection peak of 95% at ${\lambda }_g=978.1$ nm, with a reflection bandwidth of $0.1$ nm full-width half-maximum (FWHM).

For monitoring the output, a wedged glass plate with an uncoated facet at the front and an anti-reflection coated facet at the back serves as an outcoupler or beam sampler (BS). The reflection is relying on Fresnel reflection and therefore is polarization dependent. The reflectivity is on the order of 10% for s-polarized light and 1% for p-polarized light. Note that the polarization asymmetry is much smaller (1:1.1) in transmission. Via a half-wave plate and an optical isolator, polarization resolved light-current (LI) characteristics as well as near and far field intensity distributions can be obtained with a photo-diode and CCD cameras, respectively.

The use of the intra-cavity BS also allows measurements without feedback. However, the main results for the polarization distributions are obtained by observation after the VBG, as the intra-cavity polarization state can be accessed directly from there. The light that goes through the VBG is re-imaged onto another CCD-camera (CCD1) by two telescopic systems, providing enough magnification to accurately resolve the different polarization zones. Within the collimated range between the two lenses of the second telescope, a linear polarizer (LP) and a quarter-wave plate (QWP) are used with different combinations in its orientation.

To analyze the state of polarization of the VCSEL’s emission, all our work relies on the spatially resolved measurement of the well-known Stokes parameters [17]. The data needed to accomplish this task are the different intensity patterns obtained for the different orientations of the polarizer’s axis. The polarization orientation is defined with respect to the propagation direction of the beam, i.e., in the plane orthogonal (x, y) to its wave vector.

The measurements necessary to determine the Stokes parameters are:

• $I_x$: Horizontally polarized component of the intensity.
• $I_y$: Vertically polarized component of the intensity
• $I_{45}$: Intensity component diagonally polarized.

Usually, this study is restricted to the linear components of the polarization but it is important to comment that in our case the results obtained confirm the existence of a non-negligible quantity of circular light. To measure this factor, a fourth value of the intensity is taken:

• $I_{circ}$: Circular component of the emission. In this case, a QWP is used in addition to the linear polarizer. including the $S_3$ factor associated with this component, the Stokes parameters are calculated from the following set of equations:

  $$\begin{array}{cc}\hfill S_0& =I_x+I_y\hfill \end{array}$$

  (1)

  $$\begin{array}{cc}\hfill S_1& =\frac{(I_x-I_y)}{S_0}\hfill \end{array}$$

  (2)

  $$\begin{array}{cc}\hfill S_2& =\frac{2·I_{45}}{S_0}-1\hfill \end{array}$$

  (3)

  $$\begin{array}{cc}\hfill S_3& =\frac{2·I_{circ}}{S_0}-1\hfill \end{array}$$

  (4)

  where $S_0$ represents the total intensity; $S_1$ the degree of horizontally (positive values of $S_1$) or vertically (negative values of $S_1$) polarized light; in the same way, $S_2$ accounts for the polarization degree across the diagonals (positive for ${45}^{\circ }$, negative for $-{45}^{\circ }$); and $S_3$ represents the degree of circular polarization (the sign denotes the direction of rotation). Furthermore, two additional calculations have been done—the fractional polarization (FP):

  $$FP=\sqrt[]{S_1^2+S_2^2+S_3^2}$$

  (5)

  in order to ensure the validity of our results, they are checked against the ideal value of 1, corresponding to the radius of the Poincare sphere.

The last parameter calculated is the value of the direction of polarization $\psi$, calculated with:

$$\psi =0.5·atan2\frac{S_2}{S_1}$$

(6)

Once the different intensity patterns for the VCSEL emission have been measured and recorded, the analysis is carried out using specific software developed in our group that allows us to have access to every individual pixel of the camera (CCD1 in Figure 1). This tool permits us to know not the mean value or average of the aforementioned parameters but the complete, spatially resolved description of these. In particular, we can obtain $\psi$(x, y) as the polarization state which is the main goal of our research.

3. Results

We start our experiment with a low value for the injection current, well below the lasing threshold, that places the device in the spontaneous emission regime. When the current applied to the VCSEL is increased, it switches up abruptly; then, we can observe the appearance of different bright single spots (CS) or the formation of more complicated structures.

From here on, the experiment is completed by decreasing the current again. In this part, two main aspects are observed in the L–I diagram: a significant grade of hysteresis in the emission and the existence of abrupt transitions; this last effect happens when the whole structure simplifies as shown in Figure 2.

In order to achieve a better understanding of the results, we split them in two parts. The first group deals with the treatment of the results obtained for the single soliton, its different polarization states and the transitions between them; the second part explains the polarization distribution obtained in the vortex pattern observed in the VCSEL’s emission. In both cases, a clear homogeneous polarization across all the intensity structure is found. The intensity characteristics for the soliton and vortex profile appear in Figure 3 .

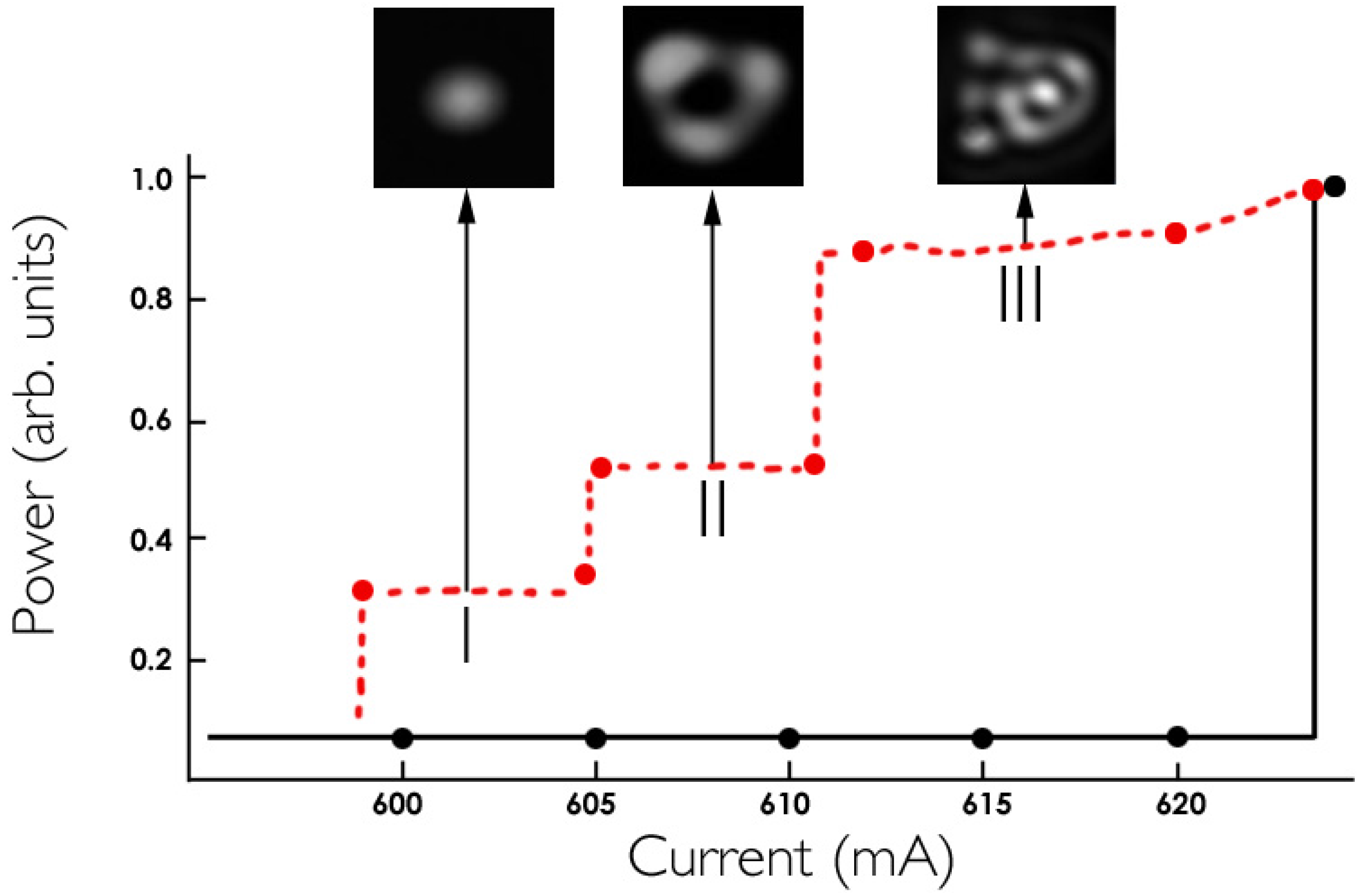
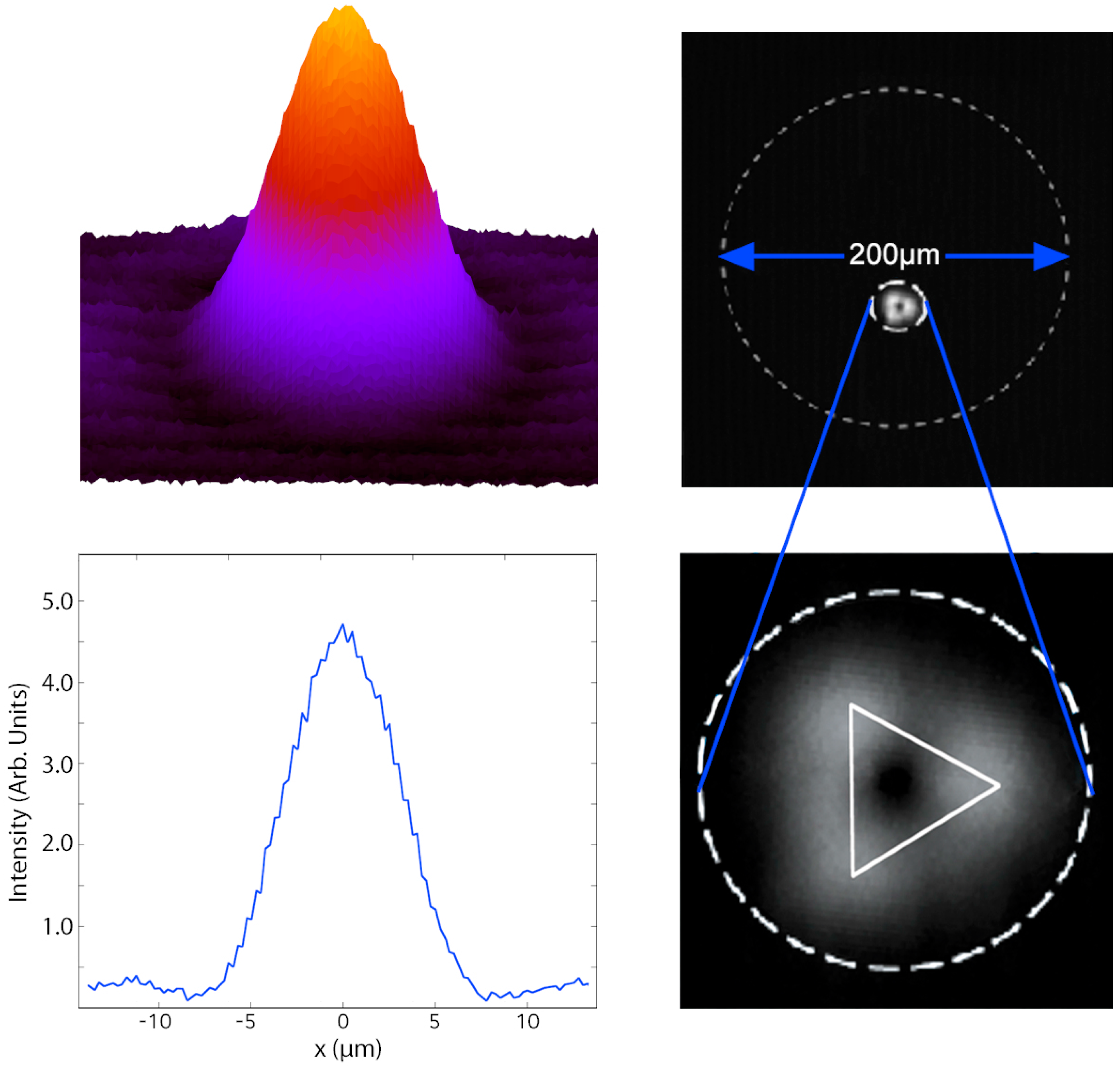
3.1. Single Soliton Case. The Cavity Soliton

To start with, in the analysis, we are going to focus on the simplest result obtained—the single soliton. The existence of CS in semiconductor microcavities has been predicted theoretically [18] and experimentally achieved in VCSEL’s below lasing threshold and proposed as pixels in all-optical systems [19].

Our case of study corresponds to those solitons formed in a cavity (CS) with a frequency-selective feedback term obtained from a VBG as is described in the second section. It is important to note that although it is possible for localized states to exist at any position of a homogeneous device, a strong pinning at preferred locations—traps—is found [20]. This effect is depicted in Figure 2; the complex cluster that appears for the highest value of the current evolves to the single soliton when the current decreases, but this behavior is restricted to a specific area on the VCSEL’s surface.

The intensity distribution of the single-peaked spots is reasonably Gaussian, with sizes ranging from 4.8 $\mathsf{\mu }$m to 5.8 $\mathsf{\mu }$m radius at $1/e^2$ point of intensity, as can be seen in the left column of Figure 3.

In this situation, two possible directions for the polarization are found, mutually orthogonal. Both orientations are homogeneous across all the soliton area, therefore we can assign just a single value to represent it, as is shown in Figure 4.

The aforementioned states are connected by a switch when the injection current makes a cycle for a particular range of values. The change between orthogonal polarization orientations in a VCSEL is a well-known topic [21]. In our work, this effect appears for the first time between CS through a hysteresis region, as can be seen in the right part of Figure 5, where this effect is analyzed for three different linear polarizer orientations. Another important element in this part of our experiment is the measurement of the frequency for both orientations. These data are taken out of the cavity by the BS and clearly exhibit the existence of two different modes, each one corresponding to the two polarizations observed, as is shown in the left part of Figure 5.

The amount of circular light in the emission is also studied by the analysis of the S3 parameter; in all the cases measured, this quantity represents about one-tenth of the total emitted intensity. The origin of this component is explained in the framework of the spin–flip model [22] in recent experiments for VCSELs [14]. For the polarization case investigated here, a theoretical treatment is currently under development in our group. Also remarkable is the association between the linear polarization and the circular component, i.e., the circular component changes its sense of rotation when the linear component flips, giving a complete vectorial character to both polarization states. This fact could be utilized in the aforementioned all-optical systems [19] to improve their performance by the use of the complete set of Stokes values as parameters in the information processing.

In order to verify the accuracy of our results, the FP factor is measured for both polarization orthogonal states. The results obtained are very close to the ideal value of one—radius of the Poincare sphere—ranging in the interval [0.96–0.98] for both orientations.

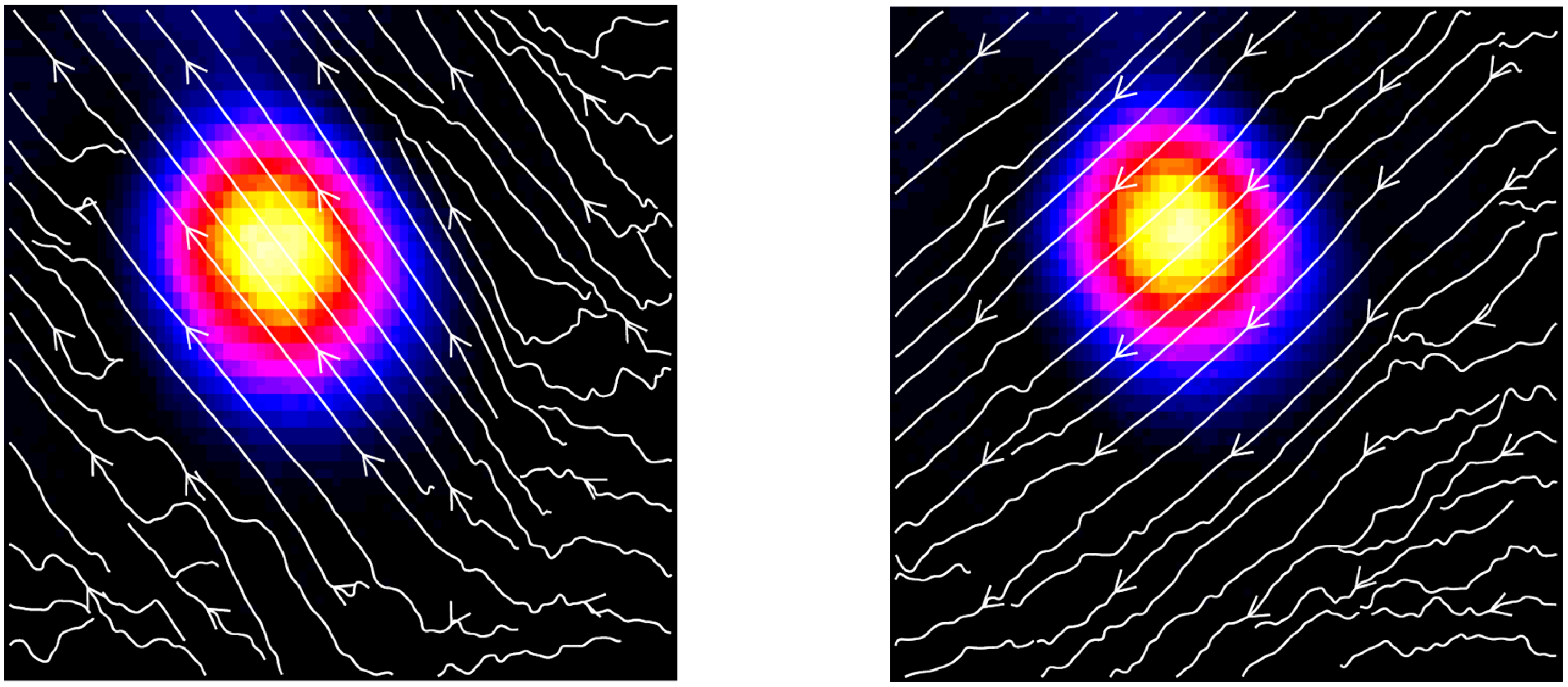
3.2. The Ring-Shaped Structure. The Optical Vortex Beam

A more complicated structure than the single soliton appears at higher values for the injection current, as can be seen in the picture corresponding to zone II in Figure 2. This emission pattern is normally made by a three-peak ring with a central hole in the middle and we can call it an optical vortex [23,24]. Its dimensions are of about ten microns for the distance between peaks; a plot of this structure is shown in Figure 3.

These were observed recently in coupled VCSELs—one operated as a gain device and one as a saturable absorber [25]. Vortices in self-focusing Ginzburg–Landau models were predicted [26]. References [27,28] investigate a nonlinear cavity with a saturable or cubic, i.e., Ginzburg–Landau-like nonlinearity, coupled to an additional linear filter which provides a minimal model for a VCSEL with frequency-selective feedback, similar to our experiment.

The homogeneous polarization, in the same way as in the previous section, describes a constant orientation for the whole area of the emission, obtaining one value or its orthogonal depending on the injection current value, with a very similar intensity pattern ($S_0$) in both cases. This structure is essentially identical to the vortex soliton observed in a prior work of our group [12], including a phase singularity in the dark center.

Corresponding generalized vortex solitons were predicted [29] and indications observed [30] in single-pass conservative systems and termed azimuthons. Theoretical predictions also exist for dissipative systems [31].

Figure 6 shows the states of polarization for the vortex. The angle takes again a very similar value to that already shown for the single soliton. In addition, the linear and circular components have the same behavior already seen in the soliton case, i.e., a particular sense of rotation is associated to one of the linear orientations.

4. Discussion

The observations presented establish the existence of solitons and vortex solitons in a cavity with a self-focusing medium. This phenomenon happens through a direct transition from the off-state, with only spontaneous emission, to the vortex appearance when we rise the injection current; this structure simplifies to the single soliton once we lower the current.

The setup described here is much simpler than the typical schemes to create vectorial vortex beams; this fact opens the possibility for the monolithic implementation of the external cavity in order to build a complete useful device to generate them.

In this work, the spatially resolved analysis of the polarization of single solitons and vortex structure is shown; it reveals two main directions for the polarization state in both cases. In addition, a relevant quantity of circular light is also found, which gives a full vectorial character to this light emission.

Another set of experiments, intended for the investigation of the polarization state for the soliton at different temperatures, is currently under way. Finally, the possible existence of more complex polarization structures for the vortex is another line of research in our group.