Adaptive Wavelet Threshold Denoising Method for Machinery Sound Based on Improved Fruit Fly Optimization Algorithm
Abstract
:1. Introduction
2. Literature Review
2.1. Wavelet Threshold Denoising
2.2. Fruit Fly Optimization Algorithm
2.3. Discussion
3. Basic Theory
3.1. Wavelet Threshold Denoising
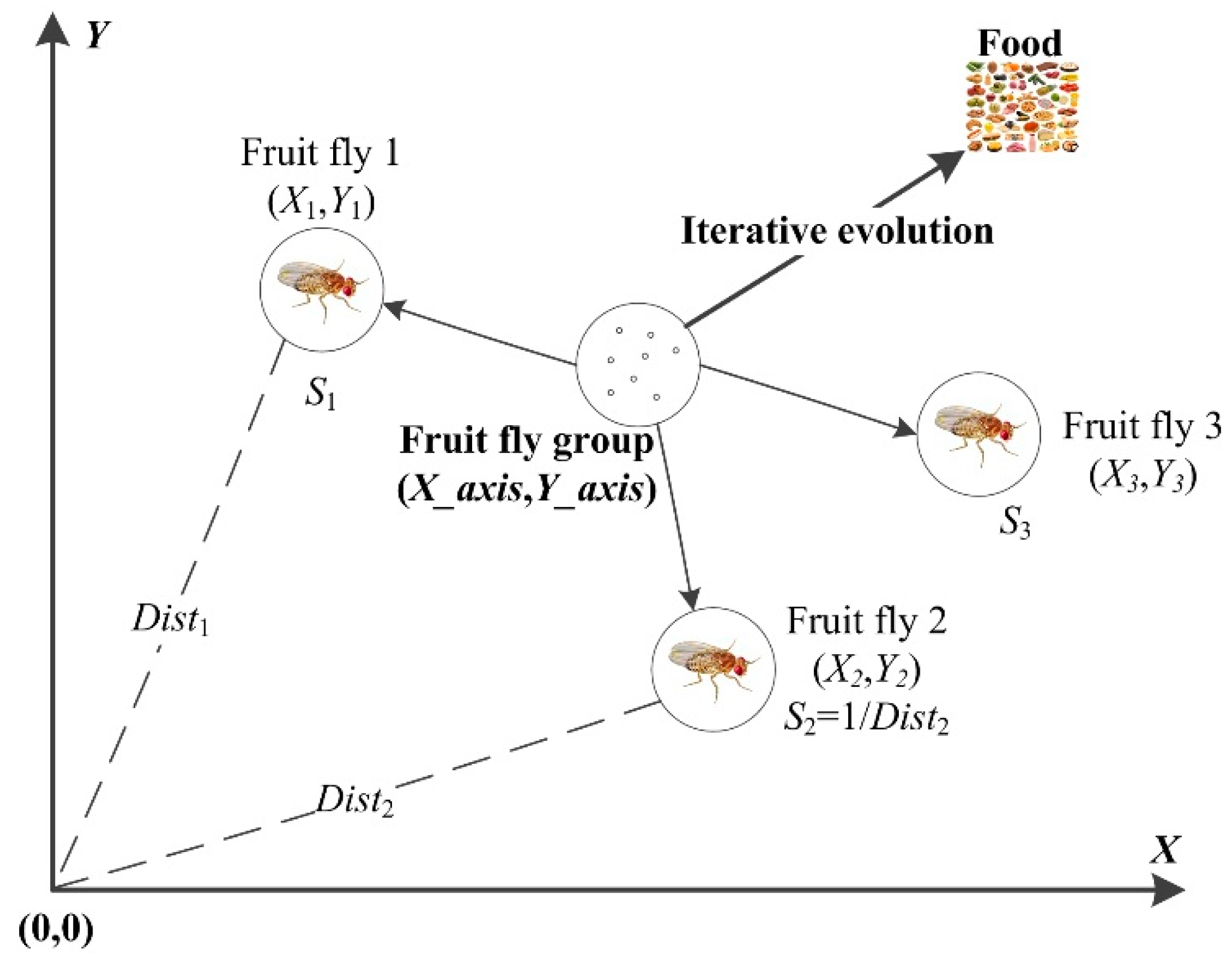
3.2. Fruit Fly Optimization Algorithm
4. The Proposed Method
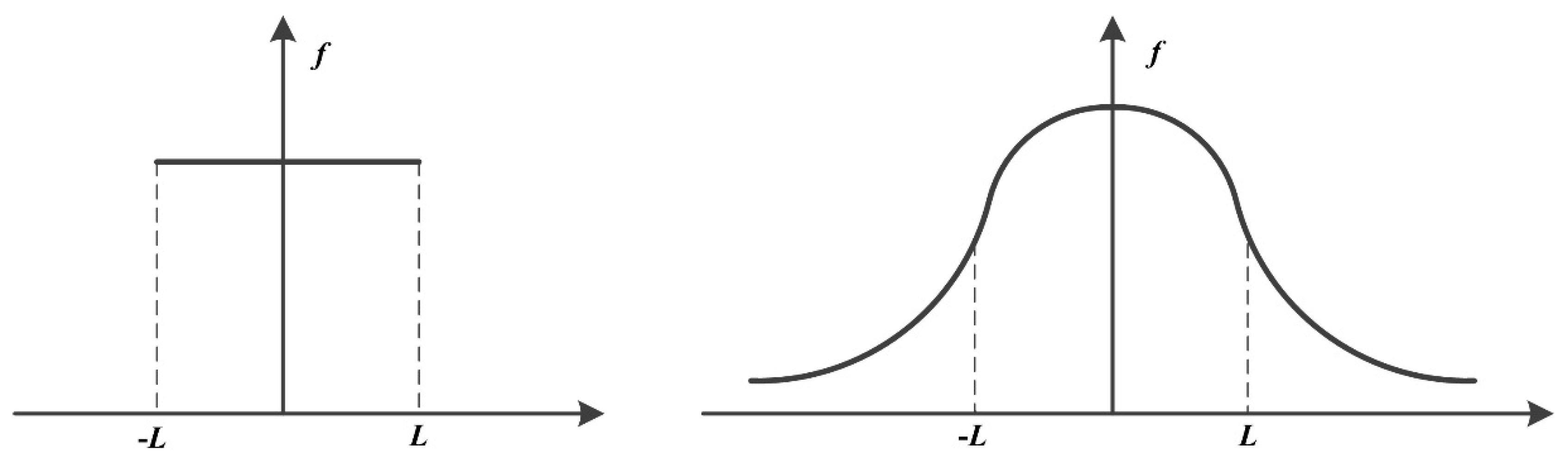
4.1. Improvement of FOA
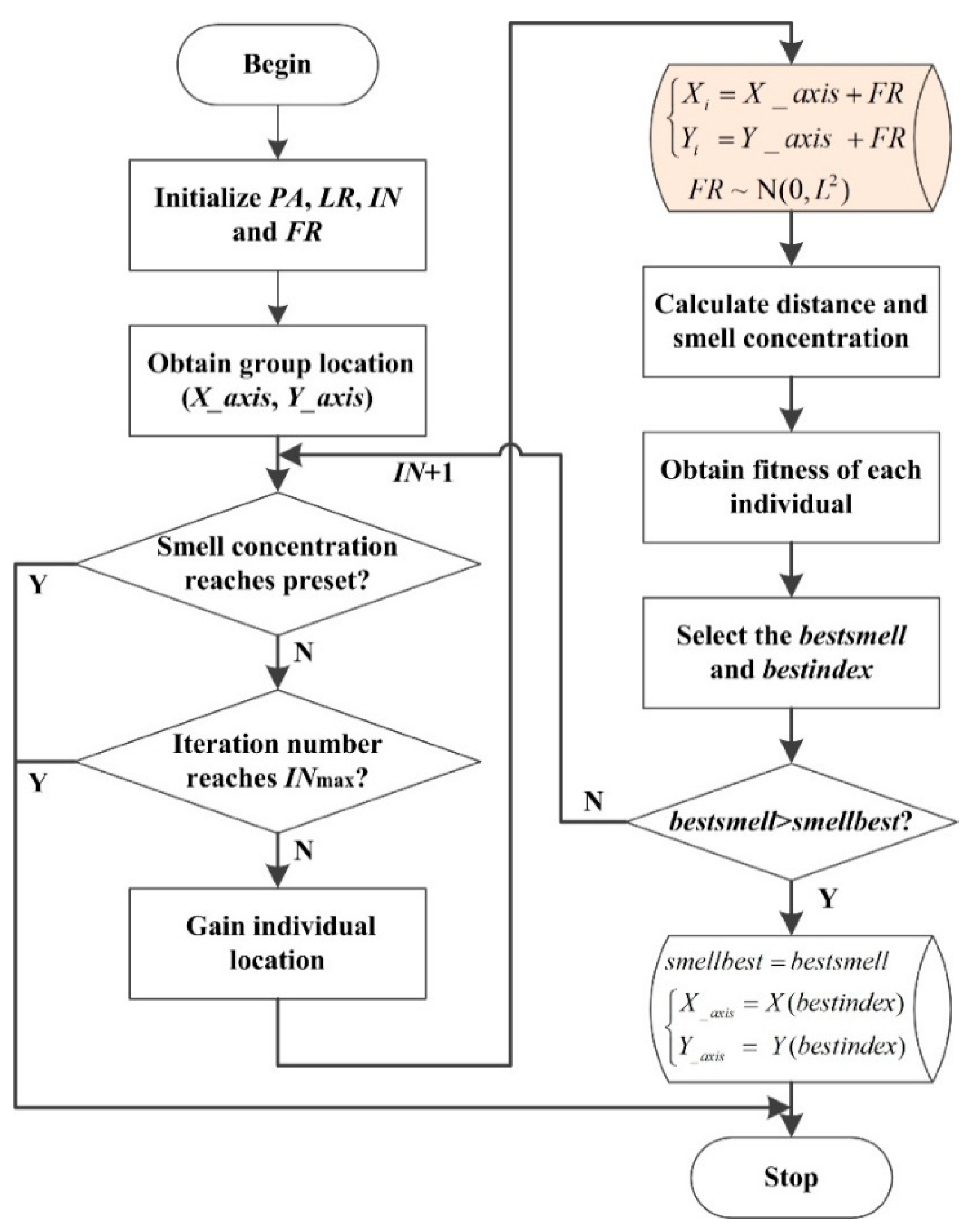
4.2. Flow of the Proposed Denosing Method
5. Simulation and Industrial Application
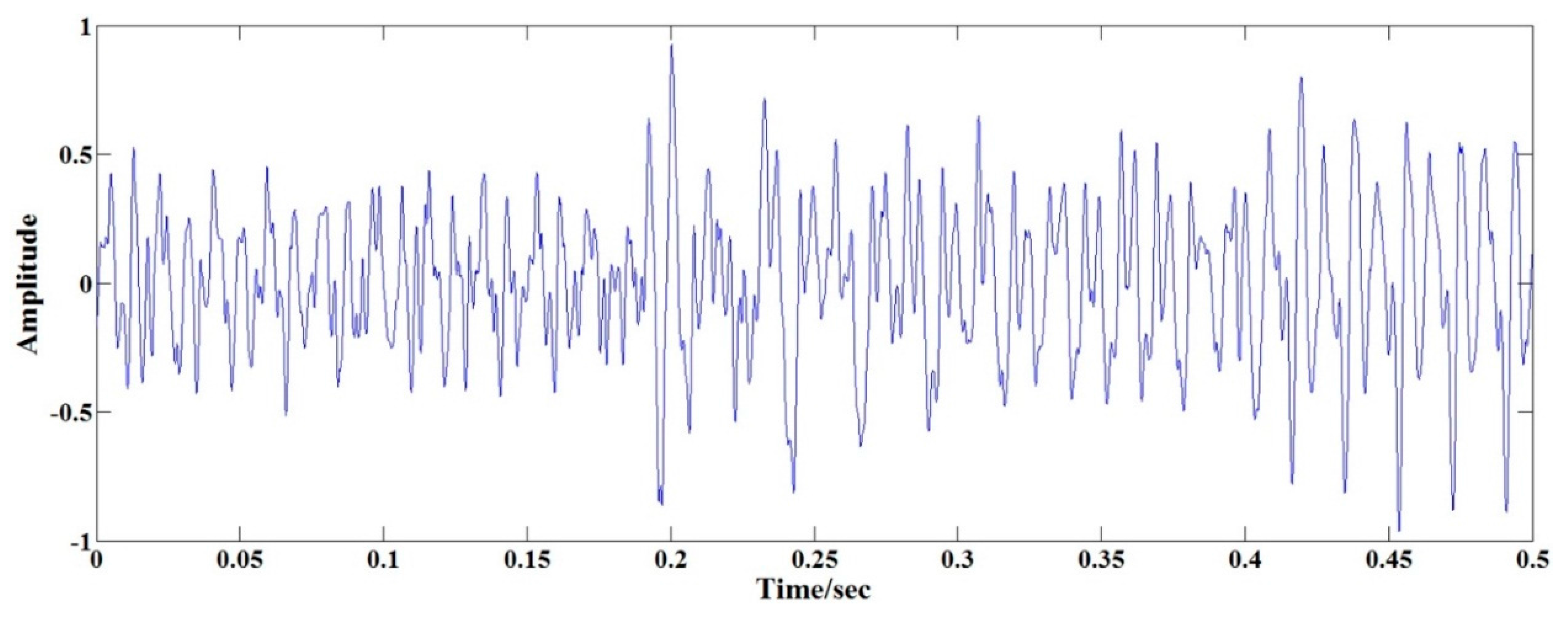
5.1. Signal Acquisition
5.2. Signal Denoising
- (1)
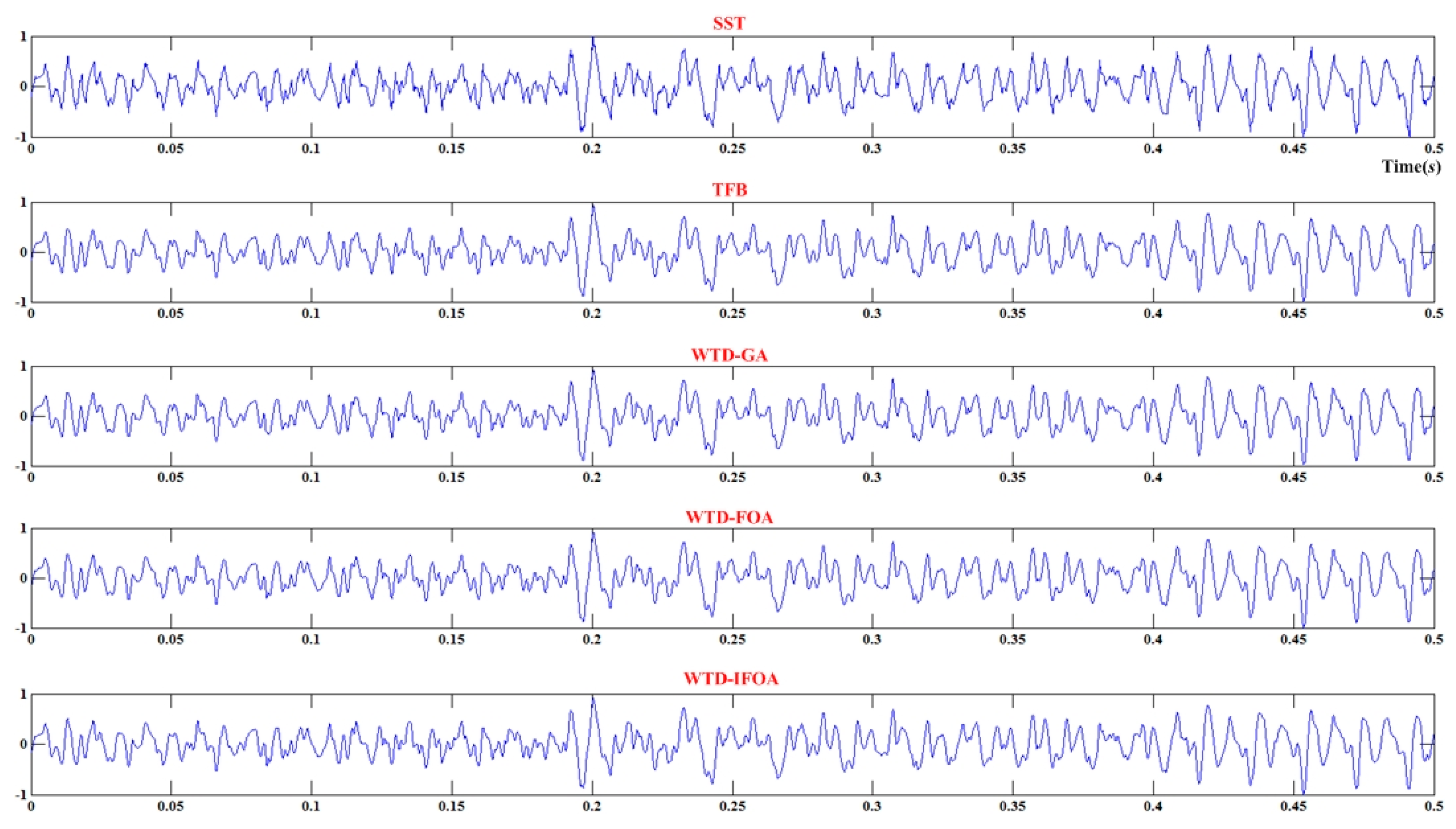
- Add Gaussian white noise into the original sound and conduct wavelet decomposition. A noisy signal with ζ = 5 dB was firstly analyzed and the synthesis was finished in Matlab 8.0 (MathWorks Inc., Natick, MA, USA, 2012). Then the synthetic signal was decomposed by wavelet decomposition with db2 wavelet at 5 levels [6]. The decomposition result is shown in Figure 7.
- (2)
- Denoise the noisy signal by SST. The value range of the wavelet threshold was firstly calculated according to Equation (3). The recommended threshold λrec was adopted according to Donoho, where q = 0.6745. The wavelet coefficients of each level were shrunk according to Equation (5). Then the signal was reconstructed by inverse WT.
- (3)
- Denoise the noisy signal by TFB. An improved threshold function with continuous first and second order derivative was introduced in [10], and is presented as follows:where λ is determined according to Equation (3) and k = 3.
- (4)
- Denoise the noisy signal by WTD-GA. The maximum λmax appeared at q = 1 and λmin obtained when q = 0.4, so . The population size was 100, each chromosome was a five-dimensional vector, the crossover probability was 0.7, the mutation probability was 0.01 and the most iteration generation was 100, as recommended by ref. [15].
- (5)
- Denoise the noisy signal by WTD-FOA. The parameters were set as follows: . λmin and λmax were calculated as previously. The fly distance obeys uniform distribution, FR ~ U(−0.2, 0.2). The population number was 5, each group contained 20 individuals and the iteration number was 100. The fitness of each fruit fly was calculated according to Equation (11).
- (6)
- Denoise the noisy signal by WTD-IFOA. The parameters were set as follows: , the fly distance obeys normal distribution, FR ~ N(0, 0.22). The population number was 5, each group contained 20 individuals and the iteration number was 100. The fitness of each fruit fly was calculated according to Equation (11).
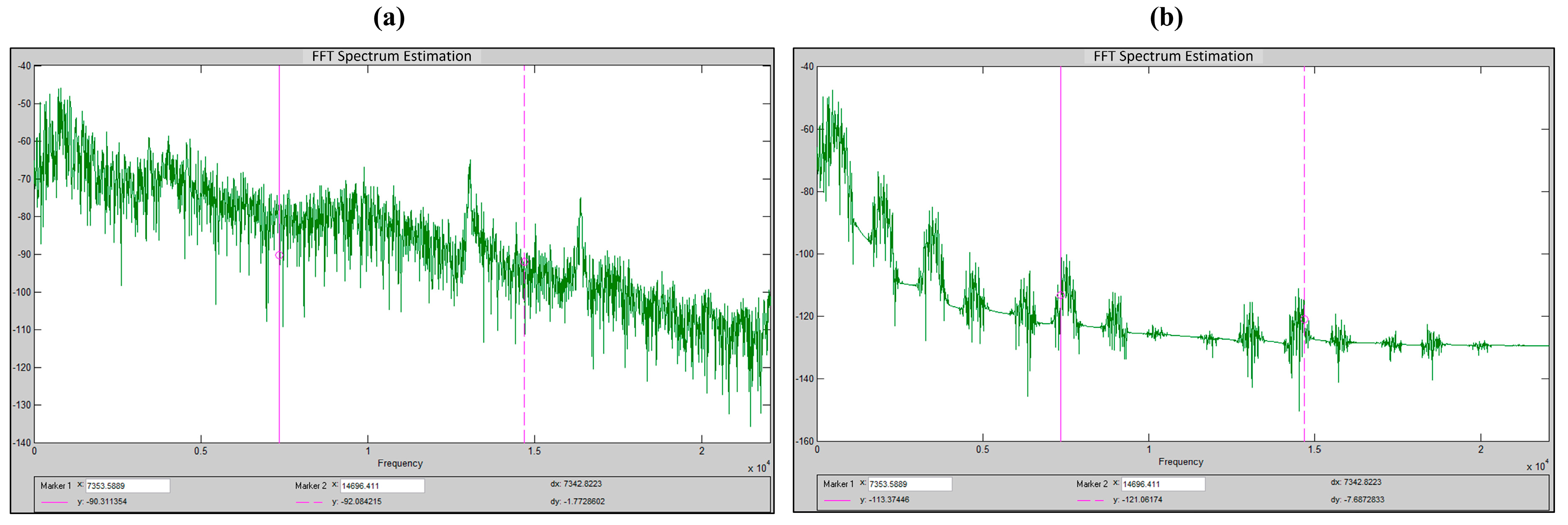
5.3. Application
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lin, J.; Qu, L.S. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Li, X.; Bassluny, A.M. Transient dynamical analysis of strain signals in sheet metal stamping processes. Int. J. Mach. Tool. Man. 2008, 48, 576–588. [Google Scholar] [CrossRef]
- Xue, W.F.; Chen, J.; Li, J.Q.; Liu, X.F. Acoustical feature extraction of rotating machinery with combined wave superposition and blind source separation. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2006, 220, 1423–1431. [Google Scholar] [CrossRef]
- Benko, U.; Petrovcic, J.; Juricic, D.; Tavcarb, J.; Rejec, J. An approach to fault diagnosis of vacuum cleaner motors based on sound analysis. Mech. Syst. Signal Process. 2005, 19, 427–445. [Google Scholar] [CrossRef]
- Ning, D.Y.; Gong, Y.J. Shocking fault component of abnormal sound signal in the fault engine extract method based on linear superposition method and cross-correlation analysis. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Abbasiona, S.; Rafsanjania, A.; Farshidianfarb, A.; Iranic, N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- White, D.J.; William, P.E.; Hoffman, M.W.; Balkir, S. Low-Power Analog Processing for Sensing Applications: Low-Frequency Harmonic Signal Classification. Sensors 2013, 13, 9604–9623. [Google Scholar] [CrossRef] [PubMed]
- Mallat, F.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Donoho, D.L. De-Noising by Soft-Thresholding. IEEE Trans. Inform. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Zhang, X.P.; Desai, M.D. Adaptive Denoising Based on SURE Risk. IEEE Signal Proc. Lett. 1998, 5, 265–267. [Google Scholar] [CrossRef]
- Nasri, M.; Nezamabadi-pour, H. Image denoising in the wavelet domain using a new adaptive thresholding function. Neurocomputing 2009, 72, 1012–1025. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, L.X.; Yu, H.B.; Xin, Y.; Cong, Z.B. A method for improving wavelet threshold denoising in laser-induced breakdown spectroscopy. Spectrochim. Acta B 2015, 107, 32–44. [Google Scholar] [CrossRef]
- Tian, J.; Yu, W.Y.; Ma, L.H. AntShrink: Ant colony optimization for image shrinkage. Pattern Recognit. Lett. 2010, 31, 1751–1758. [Google Scholar] [CrossRef]
- Bhutada, G.G.; Anand, R.S.; Saxena, S.C. PSO-based learning of sub-band adaptive thresholding function for image denoising. Signal Image Video Proc. 2012, 6, 1–7. [Google Scholar] [CrossRef]
- Li, J.; Cheng, C.; Jiang, T.; Grzybowski, S. Wavelet De-noising of Partial Discharge Signals Based on Genetic Adaptive Threshold Estimation. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 543–549. [Google Scholar]
- Pan, W.T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowl. Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Pan, W.-T. Using modified fruit fly optimisation algorithm to perform the function test and case studies. Connect. Sci. 2013, 25, 151–160. [Google Scholar] [CrossRef]
- Pan, W.-T. Mixed modified fruit fly optimization algorithm with general regression neural network to build oil and gold prices forecasting model. Kybernetes 2014, 43, 1053–1063. [Google Scholar] [CrossRef]
- Xu, W.J.; Deng, X.; Li, J. A New Fuzzy Portfolio Model Based on Background Risk Using MCFOA. Int. J. Fuzzy Syst. 2015, 17, 246–255. [Google Scholar] [CrossRef]
- Xing, Y.F. Design and optimization of key control characteristics based on improved fruit fly optimization algorithm. Kybernetes 2013, 42, 466–481. [Google Scholar] [CrossRef]
- Lin, S.M. Analysis of service satisfaction in web auction logistics service using a combination of Fruit fly optimization algorithm and general regression neural network. Neural Comput. Appl. 2013, 22, 783–791. [Google Scholar] [CrossRef]
- Wang, W.C.; Liu, X.G. Melt index prediction by least squares support vector machines with an adaptive mutation fruitfly optimization algorithm. Chemometr. Intell. Lab. 2015, 141, 79–87. [Google Scholar] [CrossRef]
- Wang, L.; Shi, Y.L.; Liu, S. An improved fruit fly optimization algorithm and its application to joint replenishment problems. Expert Syst. Appl. 2015, 42, 4310–4323. [Google Scholar] [CrossRef]
- Pan, Q.K.; Sang, H.Y.; Duan, J.H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl. Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Zhao, X.Y. Noise Smoothing for Structural Vibration Test Signals Using an Improved Wavelet Thresholding Technique. Sensors 2012, 12, 11205–11220. [Google Scholar] [CrossRef] [PubMed]
- Meng, B.; Li, Z.P.; Wang, H.H.; Li, Q.S. An improved wavelet adaptive logarithmic threshold denoising method for analysing pressure signals in a transonic compressor. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2015, 229, 2023–2030. [Google Scholar] [CrossRef]
- Soni, V.; Bhandari, A.K.; Kumar, A.; Singh, G.K. Improved sub-band adaptive thresholding function for denoising of satellite image based on evolutionary algorithms. IET Signal Process. 2013, 7, 720–730. [Google Scholar] [CrossRef]
- Li, H.Z.; Guo, S.; Zhao, H.R.; Su, C.B.; Wang, B. Annual Electric Load Forecasting by a Least Squares Support Vector Machine with a Fruit Fly Optimization Algorithm. Energies 2012, 5, 4430–4445. [Google Scholar] [CrossRef]
- Ramachandran, B.; Bellarmine, G.T. Improving observability using optimal placement of phasor measurement units. Int. J. Elec. Power 2014, 56, 55–63. [Google Scholar] [CrossRef]
- Yuan, X.F.; Dai, X.S.; Zhao, J.Y.; He, Q. On a novel multi-swarm fruit fly optimization algorithm and its application. Appl. Math. Comput. 2014, 233, 260–271. [Google Scholar] [CrossRef]
- Shan, D.; Cao, G.H.; Dong, H.J. LGMS-FOA: An Improved Fruit Fly Optimization Algorithm for Solving Optimization Problems. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Liu, C.C.; Sun, T.Y.; Tsai, S.J.; Yu, Y.H.; Hsieh, S.T. Heuristic wavelet shrinkage for denoising. Appl. Soft Comput. 2011, 2011, 256–264. [Google Scholar] [CrossRef]
- Lou, S.T.; Zhang, X.D. Fuzzy-based learning rate determination for blind source separation. IEEE Trans. Fuzzy Syst. 2003, 11, 375–383. [Google Scholar]
- Zhao, L.J.; Tian, Z. Vibration characteristics of thin coal seam shearer. Chin. J. Vib. Shock 2015, 34, 195–199. [Google Scholar]






| Operating System | Windows 7 (64 bits) |
|---|---|
| CPU | Intel Xeon E5-2690 (8 cores, 2.9 GHz) |
| Memory | 16 GB (DDR3) |
| Hard disk space | SSD (512 GB) |
| Matlab version | 8.0 |
| Method | SST | TFB | WTD-GA | WTD-FOA | WTD-IFOA | |
|---|---|---|---|---|---|---|
| Index | ||||||
| MSE (×10−4) | 12.19 | 9.61 | 11.78 | 8.53 | 7.88 | |
| PVE (%) | 10.56 | 7.39 | 2.18 | 2.28 | 1.16 | |
| CT (s) | 0.87 | 24.61 | 11.24 | 9.38 | 8.21 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Wang, Z.; Tan, C.; Si, L.; Zhang, L.; Liu, X. Adaptive Wavelet Threshold Denoising Method for Machinery Sound Based on Improved Fruit Fly Optimization Algorithm. Appl. Sci. 2016, 6, 199. https://doi.org/10.3390/app6070199
Xu J, Wang Z, Tan C, Si L, Zhang L, Liu X. Adaptive Wavelet Threshold Denoising Method for Machinery Sound Based on Improved Fruit Fly Optimization Algorithm. Applied Sciences. 2016; 6(7):199. https://doi.org/10.3390/app6070199
Chicago/Turabian StyleXu, Jing, Zhongbin Wang, Chao Tan, Lei Si, Lin Zhang, and Xinhua Liu. 2016. "Adaptive Wavelet Threshold Denoising Method for Machinery Sound Based on Improved Fruit Fly Optimization Algorithm" Applied Sciences 6, no. 7: 199. https://doi.org/10.3390/app6070199
APA StyleXu, J., Wang, Z., Tan, C., Si, L., Zhang, L., & Liu, X. (2016). Adaptive Wavelet Threshold Denoising Method for Machinery Sound Based on Improved Fruit Fly Optimization Algorithm. Applied Sciences, 6(7), 199. https://doi.org/10.3390/app6070199







