A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm
Abstract
:1. Introduction
2. Theoretical Descriptions
2.1. The Basic Principle of Second-Order Total Variation Denoising Algorithm
2.2. The Proposed Optimized Convex 1-D Second-Order Total Variation Denoising Algorithm
3. Simulation Signal Analysis
3.1. The Role of Permutation Entropy on Signal Randomness Detection
3.2. Numerical Simulation Analysis
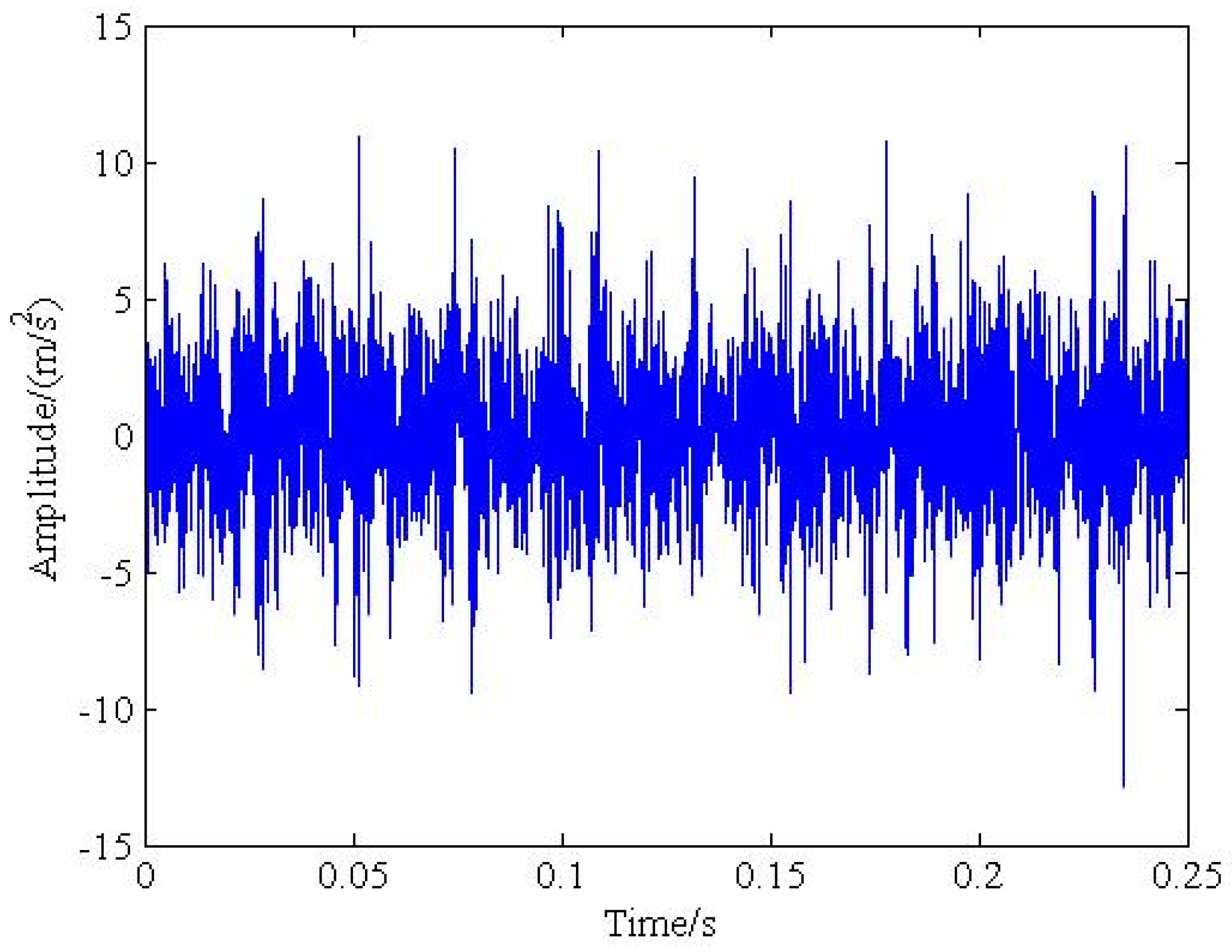
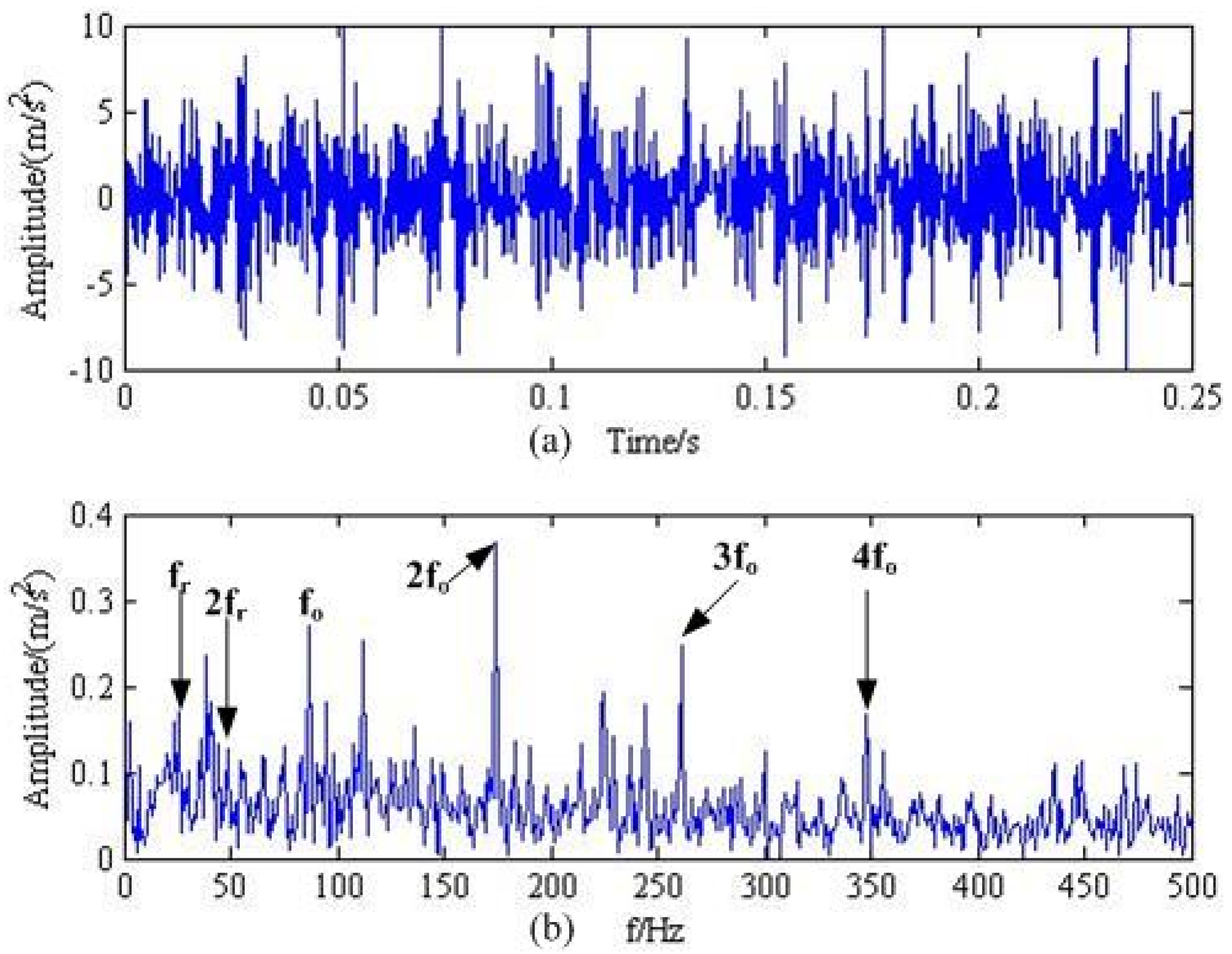
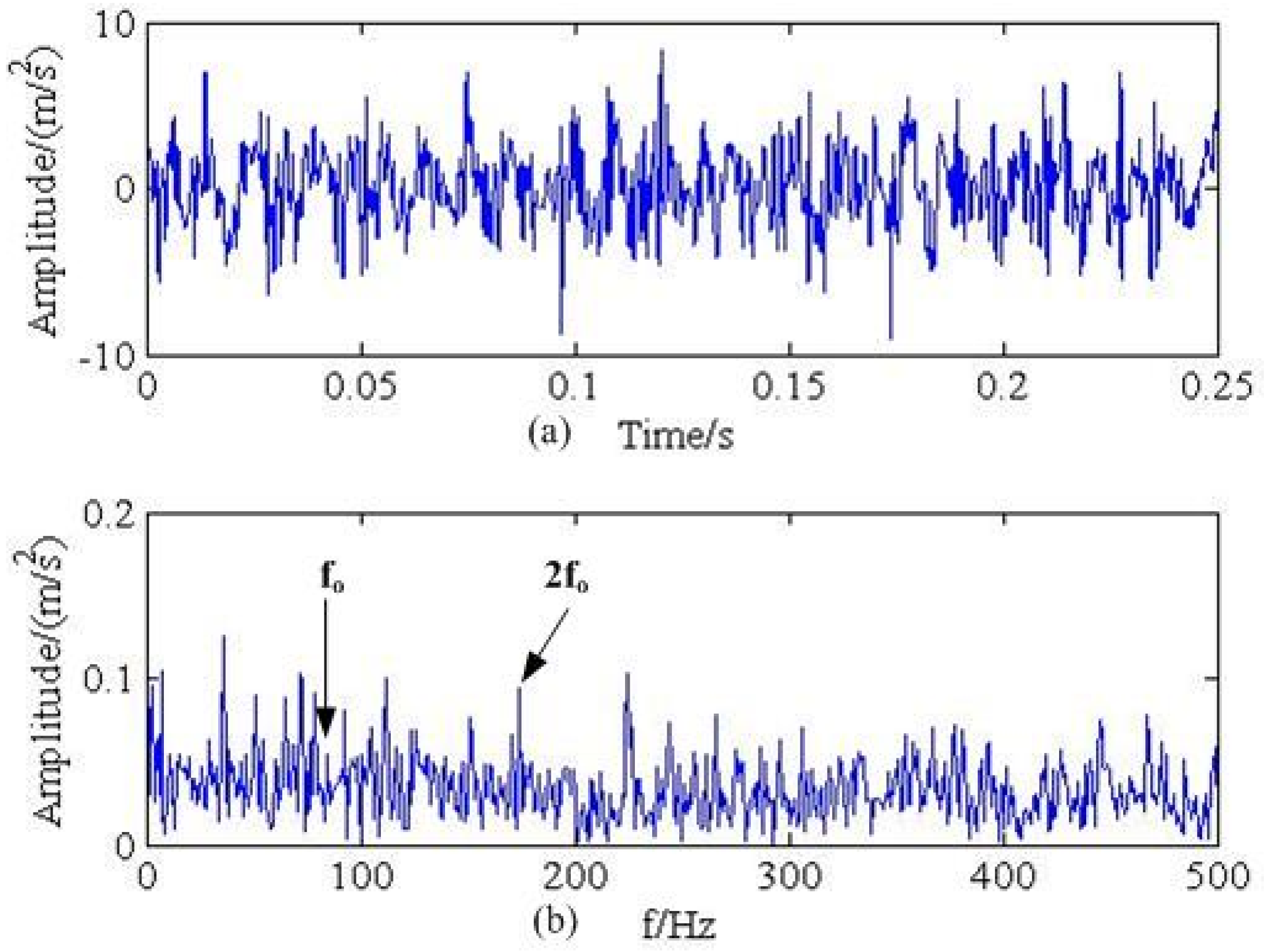
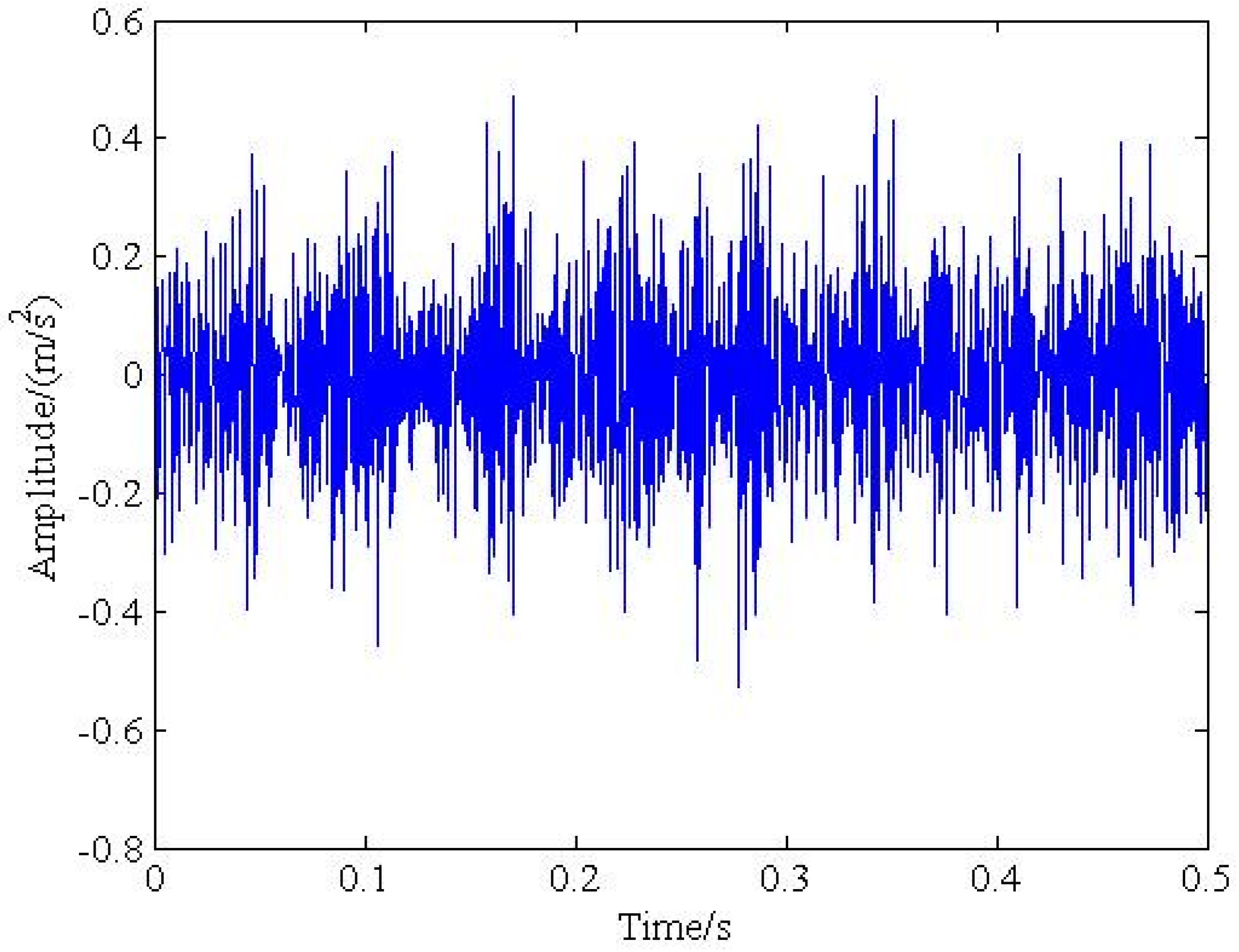
4. Experimental Verification
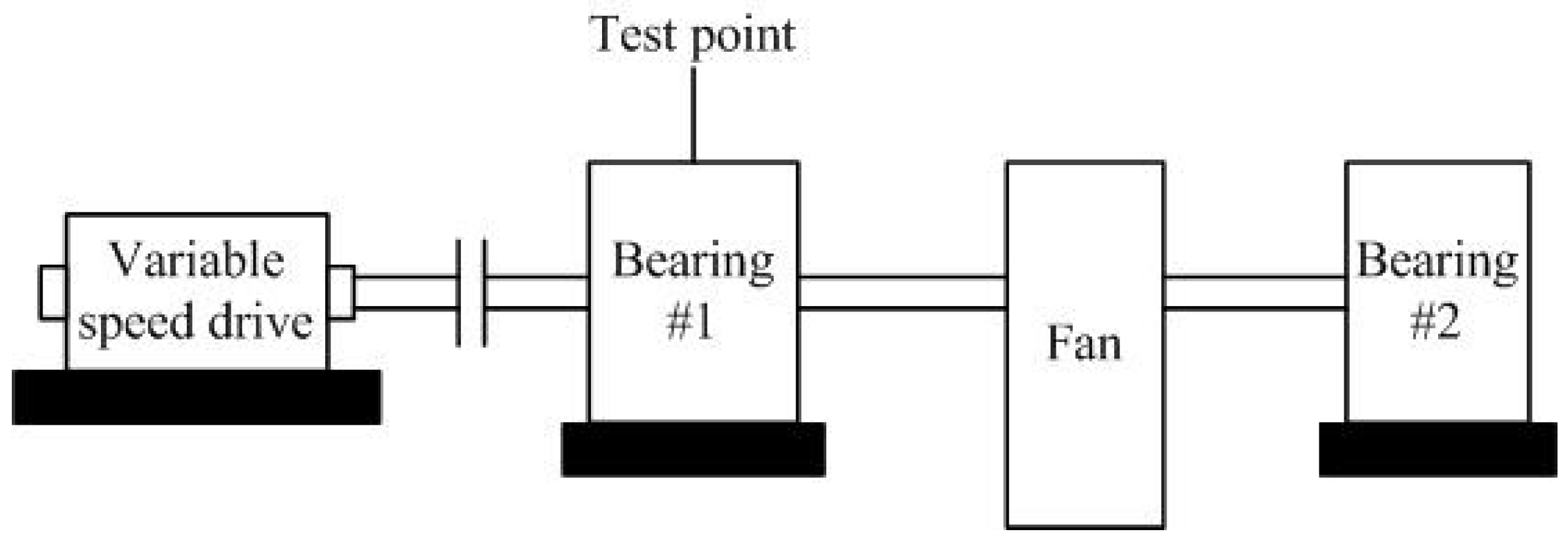
4.1. Experimental Setup
4.2. Experimental Results Analysis
5. Verification by Industrial Bearing Fault Signal
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Luo, H.; Lu, W.; Wang, Y.; Wang, L.; Zhao, X. A novel approach for analog fault diagnosis based on stochastic signal analysis and improved GHMM. Measurement 2016, 81, 26–35. [Google Scholar] [CrossRef]
- Dolenc, B.; Boškoski, P.; Juričić, Đ. Distributed bearing fault diagnosis based on vibration analysis. Mech. Syst. Signal Process. 2016, 66, 521–532. [Google Scholar] [CrossRef]
- Luo, S.; Cheng, J.; Zeng, M.; Yang, Y. An intelligent fault diagnosis model for rotating machinery based on multi-scale higher order singular spectrum analysis and GA-VPMCD. Measurement 2016, 87, 38–50. [Google Scholar] [CrossRef]
- Feng, Z.; Qin, S.; Liang, M. Time-frequency analysis based on Vold-Kalman filter and higher order energy separation for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Renew. Energy 2016, 85, 45–56. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66, 679–698. [Google Scholar] [CrossRef]
- An, X.; Jiang, D.; Liu, C.; Zhao, M. Wind farm power prediction based on wavelet decomposition and chaotic time series. Expert Syst. Appl. 2011, 38, 11280–11285. [Google Scholar] [CrossRef]
- Qu, J.; Zhang, Z.; Gong, T. A novel intelligent method for mechanical fault diagnosis based on dual-tree complex wavelet packet transform and multiple classifier fusion. Neurocomputing 2016, 171, 837–853. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Fan, G.; Peng, L.; Hong, W.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Hassan, A.R.; Bhuiyan, M.I.H. Computer-aided sleep staging using complete ensemble empirical mode decomposition with adaptive noise and bootstrap aggregating. Biomed. Signal Process. Control 2016, 24, 1–10. [Google Scholar] [CrossRef]
- Yan, X.G.; Edwards, C. Nonlinear robust fault reconstruction and estimation using a sliding mode observer. Automatica 2007, 43, 1605–1614. [Google Scholar] [CrossRef]
- Yan, X.G.; Edwards, C. Fault estimation for single output nonlinear systems using an adaptive sliding mode estimator. IET Control Theory Appl. 2008, 2, 841–850. [Google Scholar] [CrossRef]
- Condat, L. A Direct Algorithm for 1-D Total Variation Denoising. IEEE Signal Process. Lett. 2013, 20, 1054–1057. [Google Scholar] [CrossRef]
- Couprie, C.; Grady, L.; Najman, L.; Pesquet, J.-C.; Talbot, H. Dual constrained TV-based regularization on graphs. SIAM J. Imaging Sci. 2013, 6, 1246–1273. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, J.; Li, D.; Chen, H. Robust Kronecker product video denoising based on fractional-order total variation model. Signal Process. 2016, 119, 1–20. [Google Scholar] [CrossRef]
- Mila, N.; Ng, M.K.; Chi-Pan, T. Fast nonconvex nonsmooth minimization methods for image restoration and reconstruction. IEEE Trans. Image Process. 2010, 19, 3073–3088. [Google Scholar]
- Selesnick, I.W.; Parekh, A.; Bayram, I. Convex 1-D Total Variation Denoising with Non-convex Regularization. IEEE Signal Process. Lett. 2015, 22, 141–144. [Google Scholar] [CrossRef]
- He, W.; Yi, C.; Li, Y.; Xiao, H. Research on Mechanical Fault Diagnosis Scheme Based on Improved Wavelet Total Variation Denoising. Shock Vib. 2016, 2016, 3151802. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, L. Efficient multiplicative noise removal method using isotropic second order total variation. Comput. Math. Appl. 2015, 70, 2029–2048. [Google Scholar] [CrossRef]
- Bergmann, R.; Weinmann, A. A Second-Order TV-Type Approach for Inpainting and Denoising Higher Dimensional Combined Cyclic and Vector Space Data. J. Math. Imaging Vis. 2016, 55, 401–427. [Google Scholar] [CrossRef]
- Christoph, B.; Bernd, P. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar]
- Shi, W.; Shang, P.; Lin, A. The coupling analysis of stock market indices based on cross-permutation entropy. Nonlinear Dyn. 2015, 79, 2439–2447. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Wang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]







| The Variance of Noise | The SNR after Denoising by Different Methods | ||
|---|---|---|---|
| The Proposed Method | TV Denoising | Wavelet Denoising | |
| 0.1 | 18.66 | 9.06 | 15.59 |
| 0.2 | 16.52 | 8.41 | 12.44 |
| 0.3 | 15.15 | 7.07 | 11.57 |
| 0.4 | 12.13 | 4.69 | 10.28 |
| 0.5 | 11.31 | 3.31 | 9.20 |
| 0.6 | 10.28 | 2.17 | 8.31 |
| Rotation Speed r/min | Rotation Frequency/Hz | Sampling Rate/Hz | Sampling Time/s | Outer Fault/Hz |
|---|---|---|---|---|
| 1450 | 24.17 | 16384 | 1 | 87.01 |
| Rotation Speed r/min | Rotation Frequency/Hz | Sampling Rate/Hz | Sampling Time/s | Outer Fault/Hz |
|---|---|---|---|---|
| 993 | 16.5 | 2560 | 6.39 | 135.3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, C.; Lv, Y.; Dang, Z.; Xiao, H. A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm. Appl. Sci. 2016, 6, 403. https://doi.org/10.3390/app6120403
Yi C, Lv Y, Dang Z, Xiao H. A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm. Applied Sciences. 2016; 6(12):403. https://doi.org/10.3390/app6120403
Chicago/Turabian StyleYi, Cancan, Yong Lv, Zhang Dang, and Han Xiao. 2016. "A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm" Applied Sciences 6, no. 12: 403. https://doi.org/10.3390/app6120403
APA StyleYi, C., Lv, Y., Dang, Z., & Xiao, H. (2016). A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm. Applied Sciences, 6(12), 403. https://doi.org/10.3390/app6120403







