Distributed Optimal Economic Dispatch Based on Multi-Agent System Framework in Combined Heat and Power Systems
Abstract
:1. Introduction
2. Problem Formulation
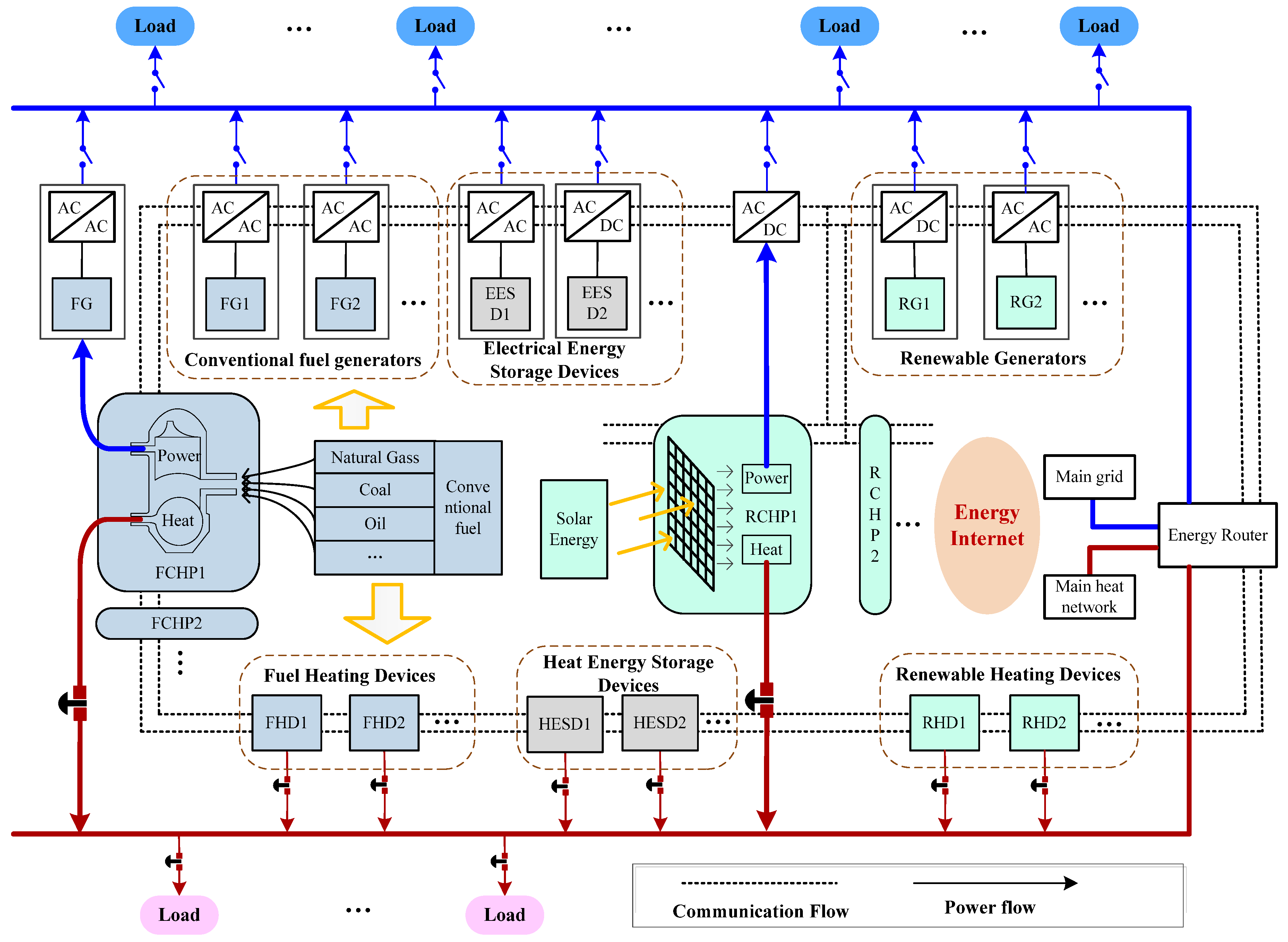
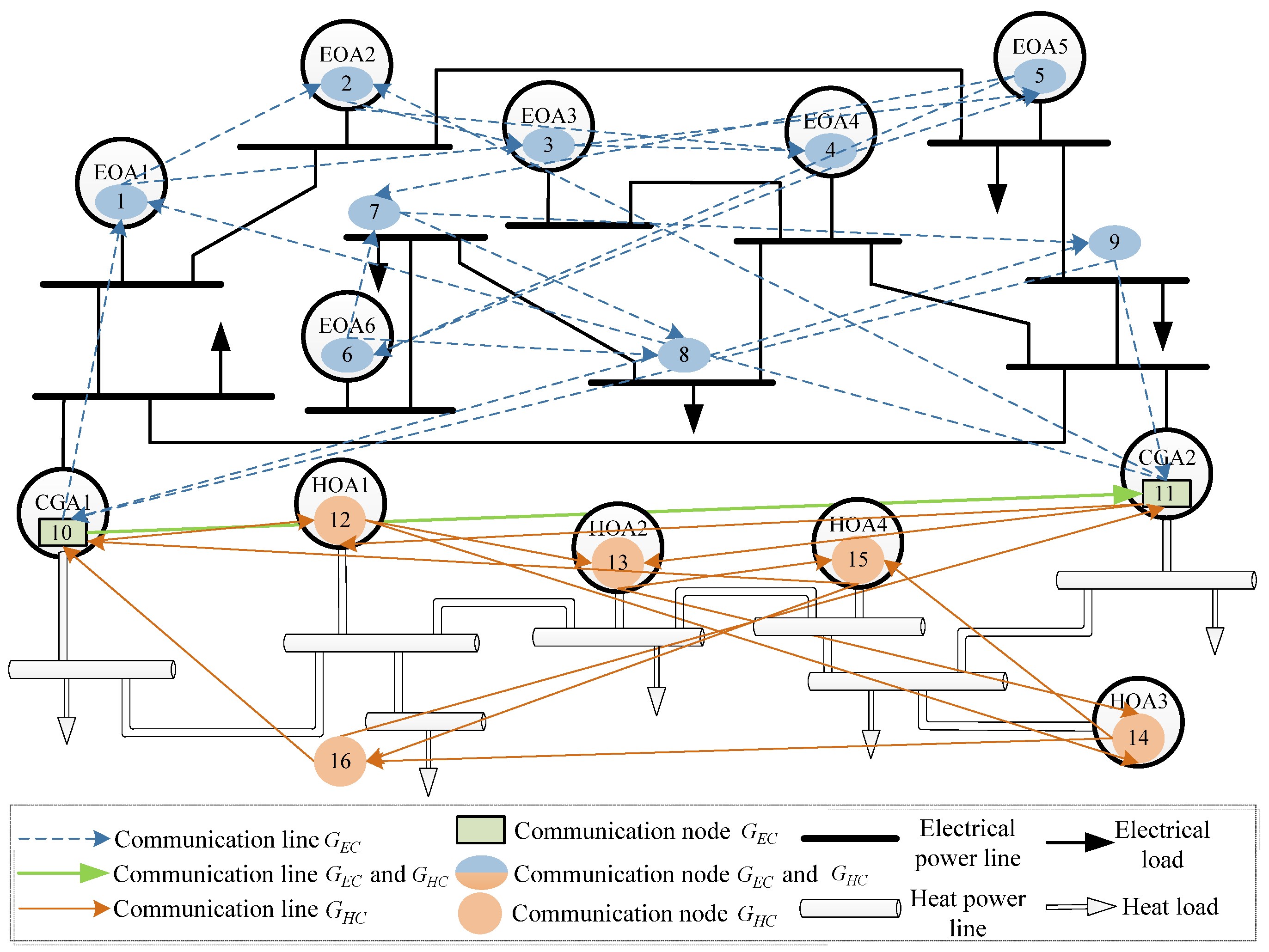
2.1. Structure and Agent Definitions
2.2. Modeling
2.3. Centralized Method
3. Distributed Method
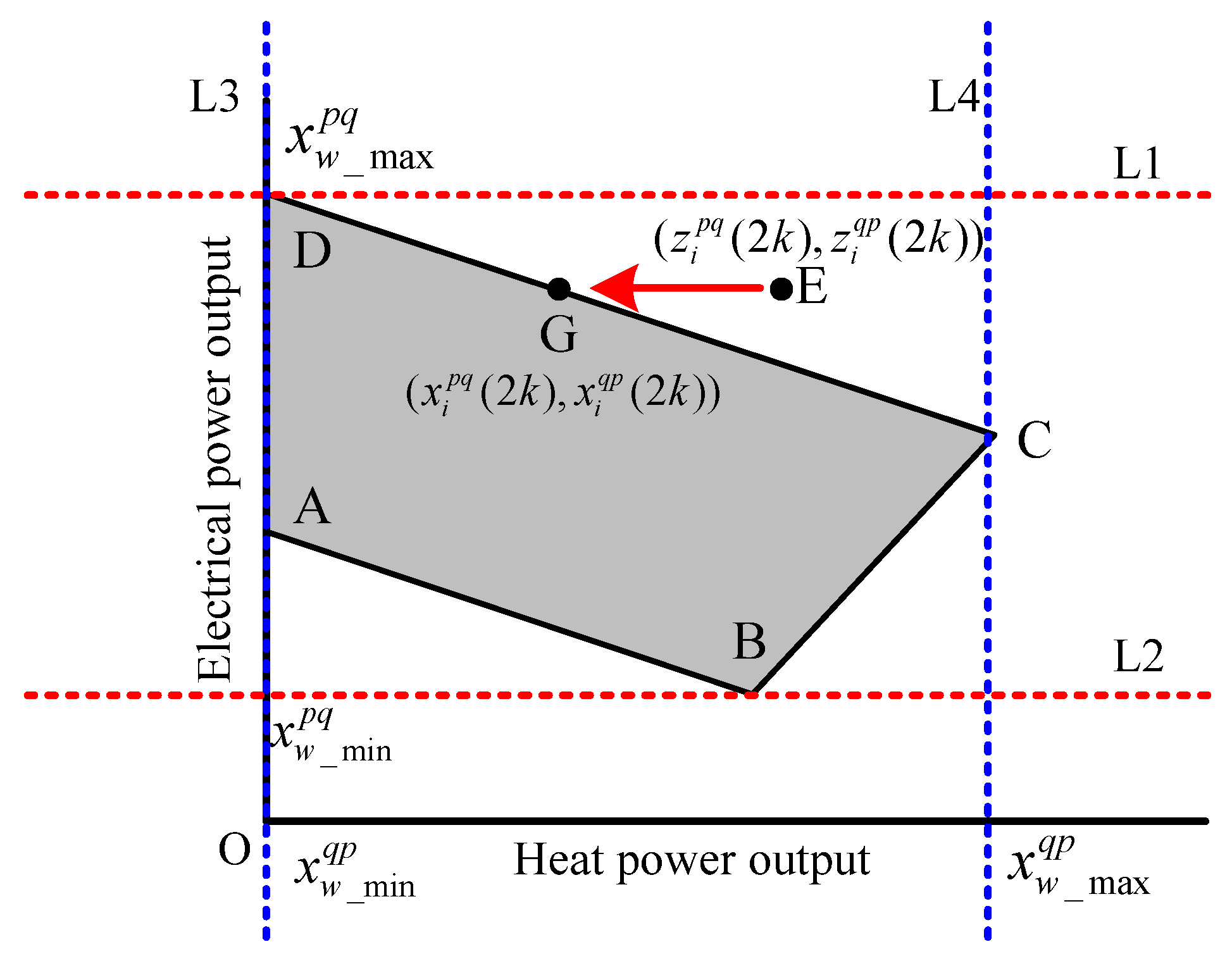
3.1. Basic Knowledge
3.2. Distributed Method
| Distributed Consensus-Based Method |
| Initialize: Each agent initializes all of variables based on Equation (13) |
| Iteration: () |
|
4. Simulation Results
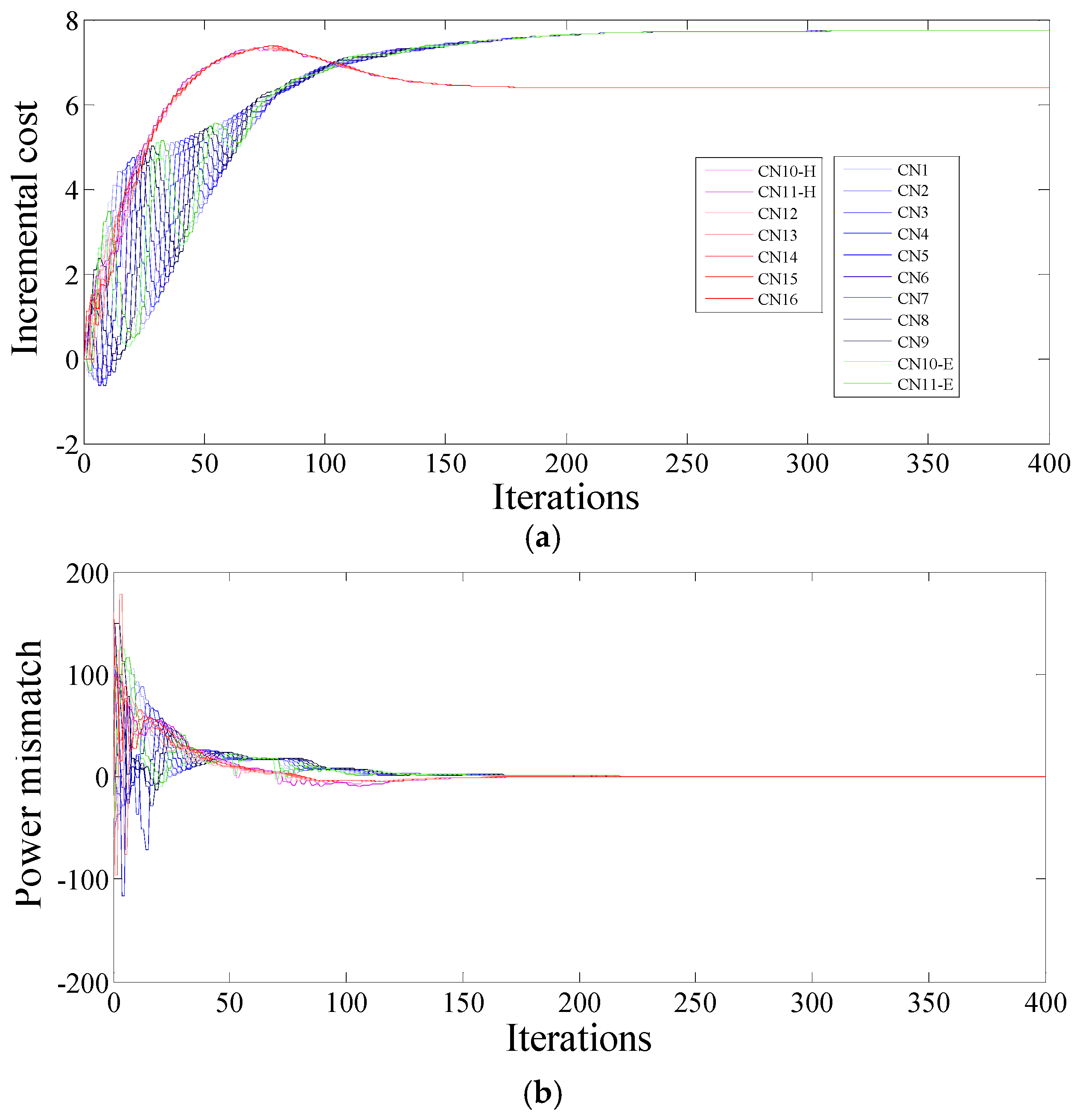
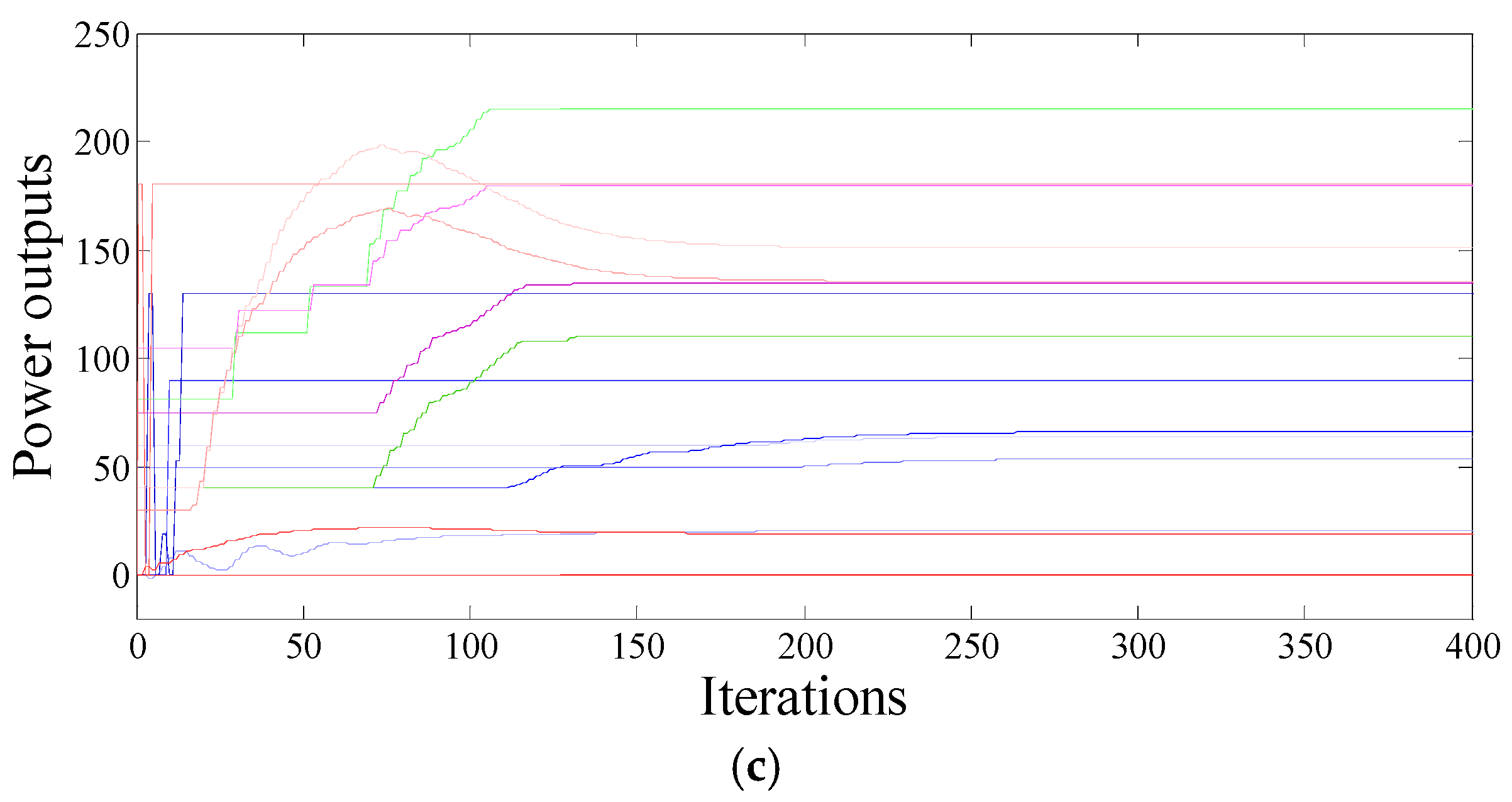
4.1. Case Study 1: Comparison with Centralized Method
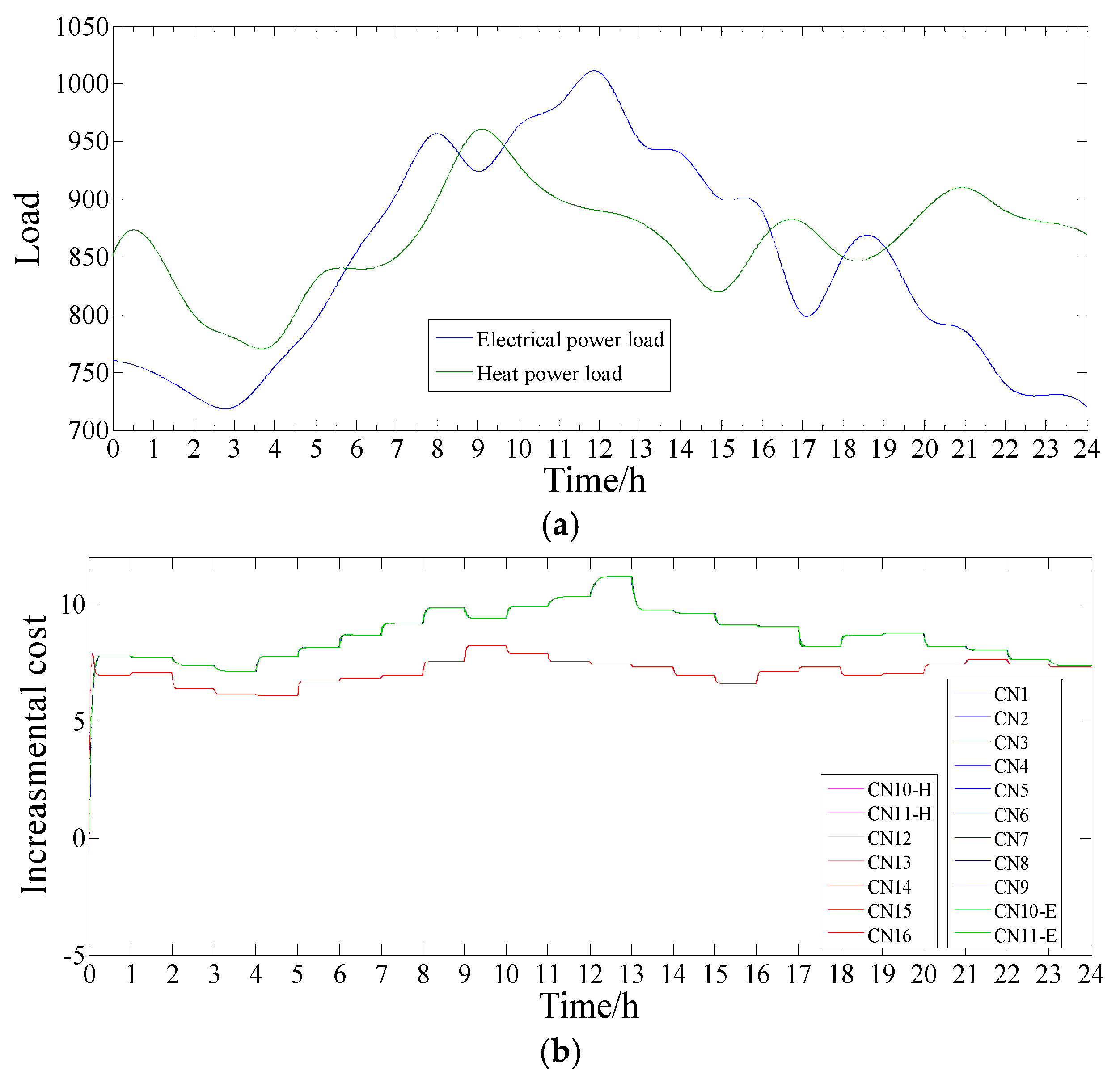
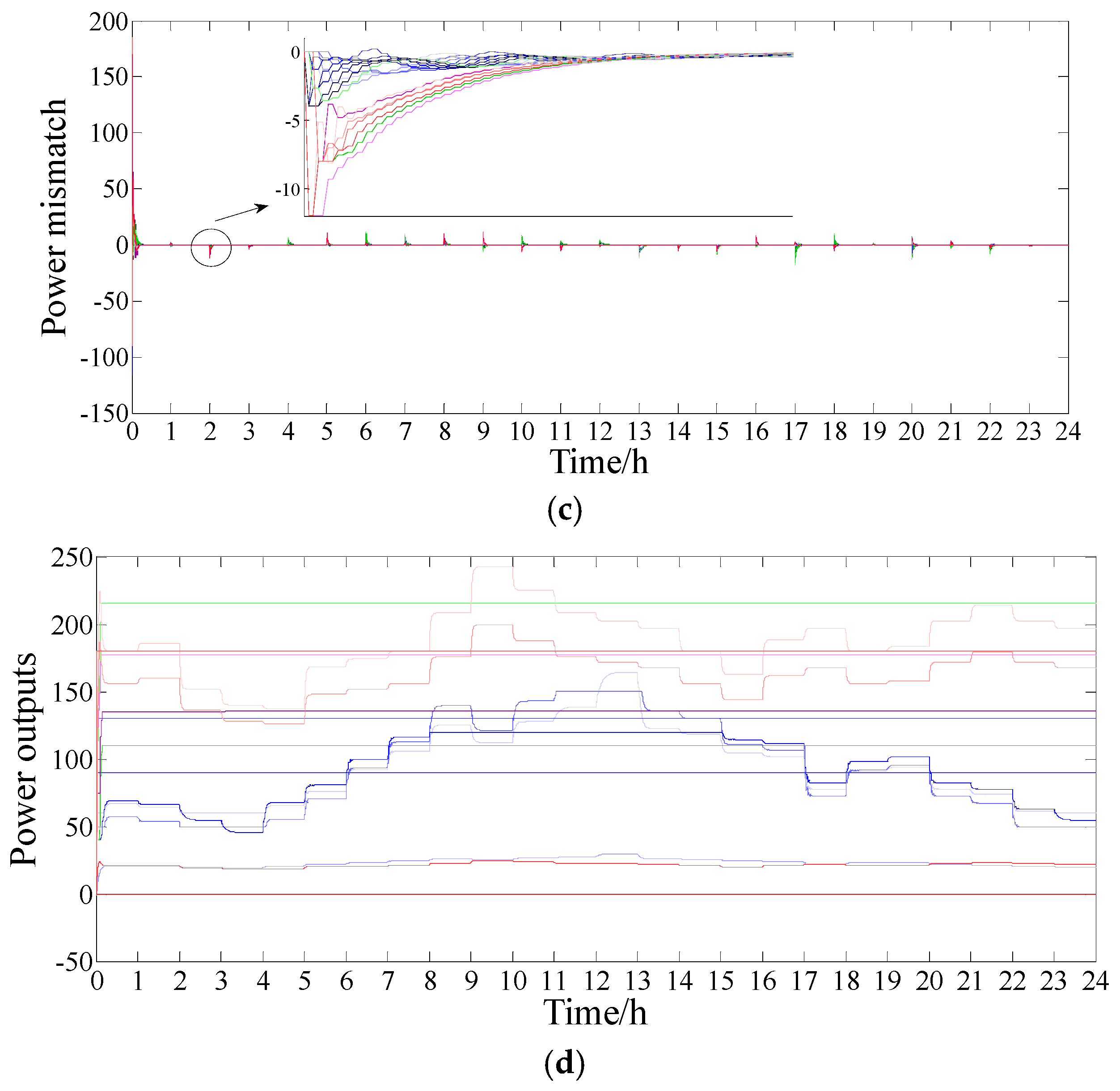
4.2. Case Study 2: Time-Varying Demand
4.3. Case Study 3: Plug and Play Test
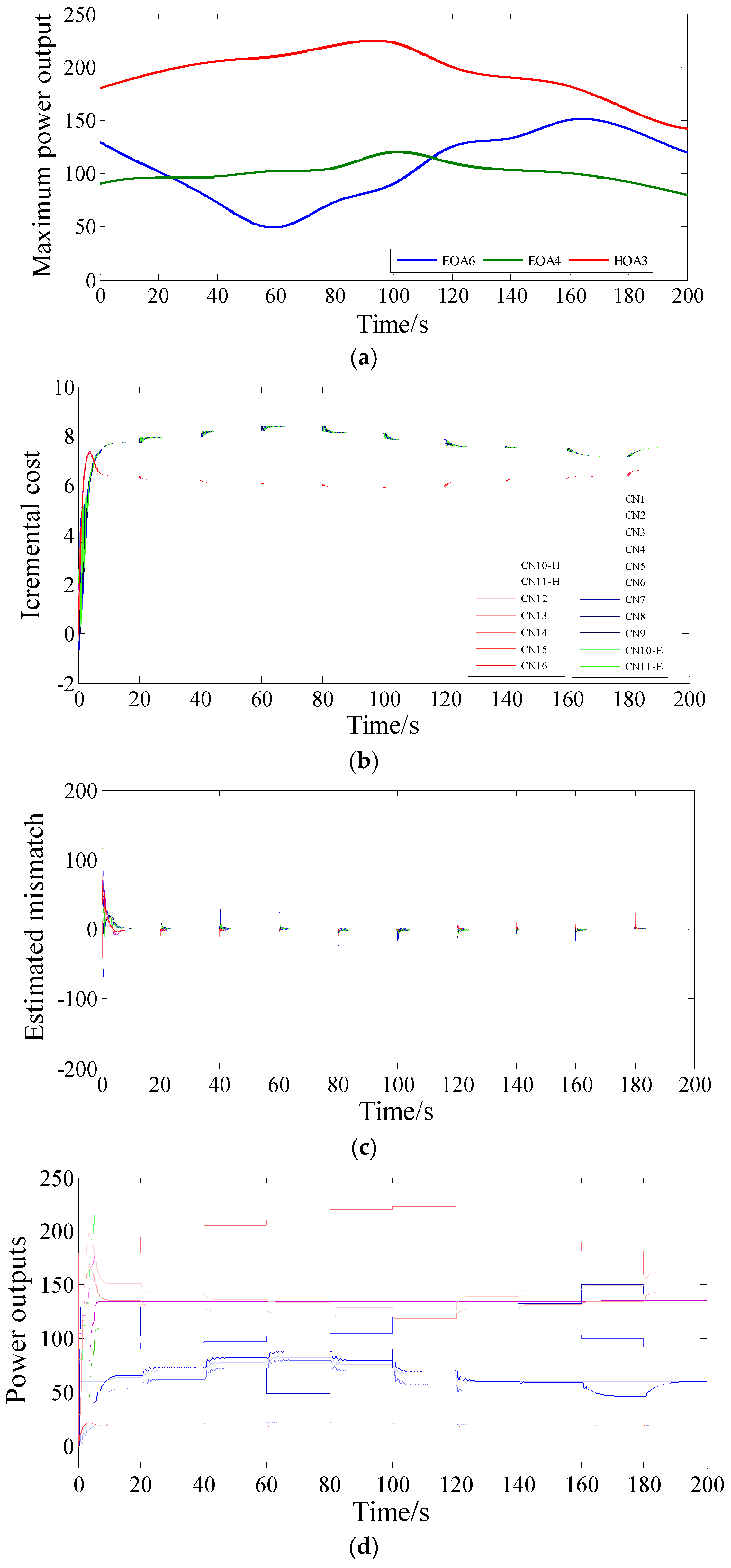
4.4. Case Study 4: Maximum-Power-Output-Varying Condition
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| CHP | Combined heat and power |
| EDP | Economic dispatch problem |
| DGs | Distributed generators |
| RGs | Renewable generators |
| FGs | Conventional fuel generators |
| DHDs | Distributed heating devices |
| RHDs | Renewable heating devices |
| FHDs | Conventional fuel heating devices |
| DESDs | Distributed energy storage devices |
| EESDs | Electrical energy storage devices |
| HESDs | Heat energy storage devices |
| RCHPs | Renewable combined heat and power |
| FCHPs | Fuel combined heat and power |
| EOAs | Electricity-only agents |
| CGAs | Co-generation agents |
| HOAs | Heat-only agents |
| , | Agent indices |
| , , | The number of EOAs, CGAs and HOAs, respectively |
| , | Iteration-step and step-size |
| , , , , and | Cost coefficients |
| , | Electrical power and heat power outputs of CGA |
| Electrical power output of EOA | |
| Heat power output of HOA | |
| , | Upper and lower bound functions of |
| , | Upper and lower bound functions of |
| , | Lower and upper bounds of |
| , , | Coefficients of the set of linear constraints of CGA |
| , | Lower and upper bounds of |
| , | Whole minimum and maximum values for all of |
| , | Whole minimum and maximum values for all of |
| , | Maximum peak power tracking point of RG and RHD |
| , | System maximum capacity of RG and RHDs |
| , | Values of point B |
| , | Total electrical power and heat power demands |
| , | Local electrical and heat load demands associated with agent |
| , | Lagrange multipliers for the equality constraints |
| , | Lagrange multipliers for inequality constraints. |
| , | The optimal electrical and heat incremental costs |
| One of state variable of agent | |
| The column stack vector of | |
| Normalized left eigenvector of R associated to the eigenvalue 1 | |
| , | Estimated electrical and heat incremental costs |
| , | Estimated electrical and heat power outputs before considering inequality constraints |
| , | Estimated electrical and heat power outputs after considering inequality constraints |
| , | Estimated electrical and heat power mismatches |
Appendix A
References
- Conti, S.; Faraci, G.; Corte, A.L.; Nicolosi, R.; Rizzo, S.A.; Schembra, G. Effect of islanding and telecontrolled switches on distribution system reliability considering load and green-energy fluctuations. Appl. Sci. 2016, 6, 1–26. [Google Scholar] [CrossRef]
- Peng, C.; Lei, S.; Hou, Y.; Wu, F. Uncertainty management in power system operation. CSEE J. Power Energy Syst. 2015, 1, 28–35. [Google Scholar] [CrossRef]
- Huang, C.; Yue, D.; Xie, J.; Li, Y.; Wang, K. Economic dispatch of power systems with virtual power plant based interval optimization method. CSEE J. Power Energy Syst. 2016, 1, 74–80. [Google Scholar] [CrossRef]
- Guo, T.; Henwood, M.I.; van Ooijen, M. An algorithm for combined heat and power economic dispatch. IEEE Trans. Power Syst. 1996, 11, 1778–1784. [Google Scholar] [CrossRef]
- Sashirekha, A.; Pasupuleti, J.; Moin, N.H.; Tan, C.S. Combined heat and power (CHP) economic dispatch solved using Lagrangian relaxation with surrogate subgradient multiplier updates. Int. J. Electr. Power Energy Syst. 2013, 44, 421–430. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Roosta, A.; Babak, A. A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch. Energy 2012, 42, 530–545. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, C.; Yuan, J. Hybrid energy scheduling in a renewable micro grid. Appl. Sci. 2015, 5, 516–531. [Google Scholar] [CrossRef]
- Huang, X.C.; Yang, Y.; Taylor, G.A. Service restoration of distribution systems under distributed generation scenarios. CSEE J. Power Energy Syst. 2016, 2, 43–50. [Google Scholar]
- Samimi, A.; Kazemi, A. Coordinated volt/var control in distribution systems with distributed generations based on joint active and reactive powers dispatch. Appl. Sci. 2016, 6, 1–17. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, T.; Yang, G.H.; Liang, H. Distributed cooperative optimal control for multiagent systems on directed graphs: An inverse optimal method. IEEE Trans. Cybern. 2015, 45, 1315–1326. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Zhang, Y.; He, H.; Ma, D.; Zhang, H. A Novel Energy Function-Based Stability Evaluation and Nonlinear Control Method for Energy Internet. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Zhang, H.; Qing, C.; Luo, Y. Neural-network-based constrained optimal control scheme for discrete-time switched nonlinear system using dual heuristic programming. IEEE Trans. Autom. Sci. Eng. 2014, 11, 839–849. [Google Scholar] [CrossRef]
- Samimi, A.; Kazemi, A. A new method to optimal allocation of reactive power ancillary service in distribution systems in the presence of distributed energy resources. Appl. Sci. 2015, 5, 1284–1309. [Google Scholar] [CrossRef]
- Zhang, H.; Kim, S.; Zhou, J. Distributed adaptive virtual impedance control for accurate reactive power sharing based on consensus control in microgrids. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Shi, W.; Xie, X.; Chu, C.C.; Gadh, R. Distributed optimal energy management in microgrids. IEEE Trans. Smart Grid 2015, 6, 1137–1146. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, T.; Liang, H.; Luo, Y. LQR-Based optimal distributed cooperative design for linear discrete-time multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2016. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Tan, S.; Xu, J.X. Consensus based method for economic dispatch problem in a smart grid. IEEE Trans. Power Syst. 2013, 28, 4416–4426. [Google Scholar] [CrossRef]
- Loia, V.; Vaccaro, A. Decentralized economic dispatch in smart grids by self-organizing dynamic agents. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 397–408. [Google Scholar] [CrossRef]
- Binetti, G.; Davoudi, A.; Lewis, F.L.; Naso, D.; Turchiano, B. Distributed consensus-based economic dispatch with transmission losses. IEEE Trans. Power Syst. 2014, 29, 1711–1720. [Google Scholar] [CrossRef]
- Rahbari-Asr, N.; Ojha, U.; Zhang, Z.; Chow, M.-Y. Incremental welfare consensus method for cooperative distributed generation/demand response in smart grid. IEEE Trans. Smart Grid 2014, 5, 2836–2845. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z. Distributed optimal resource management based on consensus method in a microgrid. IEEE Trans. Ind. Electron. 2015, 62, 2584–2592. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Liu, W. Distributed dynamic programming-based method for economic dispatch in smart grids. IEEE Trans. Ind. Inf. 2015, 11, 166–175. [Google Scholar] [CrossRef]
- Binetti, G.; Davoudi, A.; Naso, D.; Turchiano, B.; Lewis, F.L. A distributed auction-based method for the non-convex economic dispatch problem. IEEE Trans. Ind. Inf. 2014, 10, 1124–1132. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Y.; Liu, W.; Zhang, C.; Yu, H. Distributed Online optimal energy management for smart grids. IEEE Trans. Ind. Inf. 2015, 11, 717–727. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Loh, P.C.; Wang, P.; Blaabjerg, F. Cost-prioritized droop schemes for autonomous microgrids. IEEE Trans. Power Electron. 2015, 30, 1021–1025. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
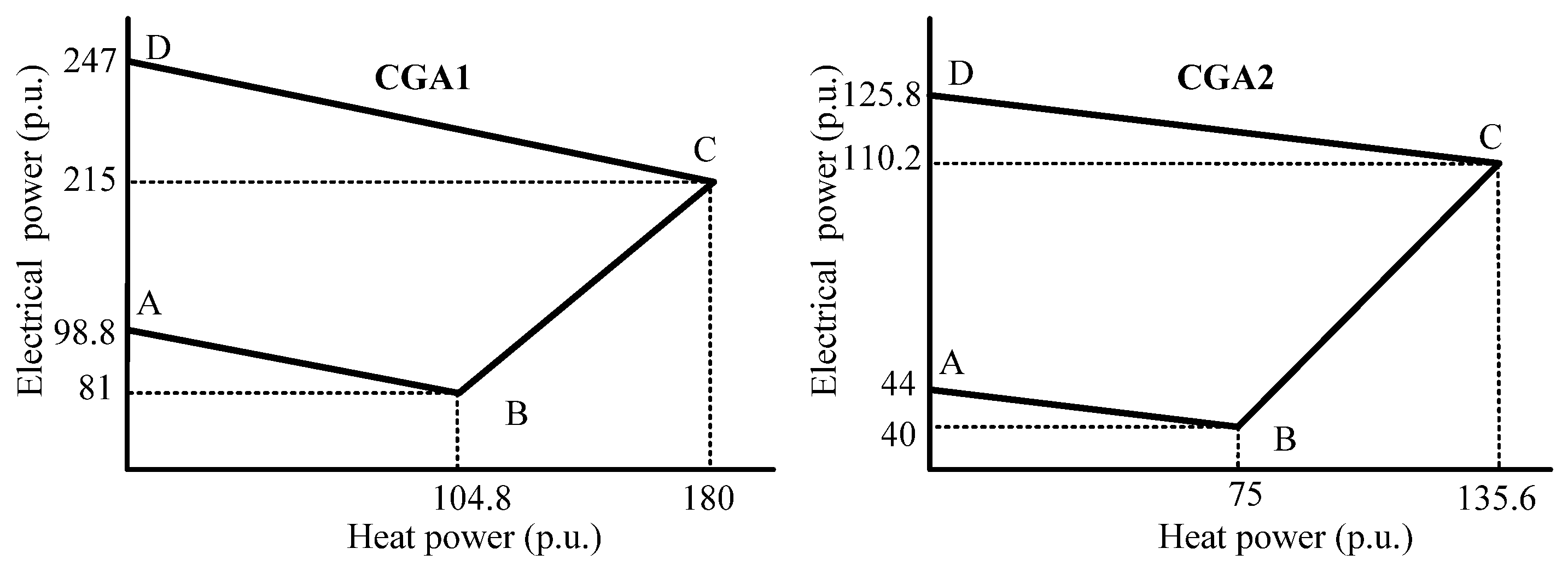

| Agent | Min | Max | |||||
|---|---|---|---|---|---|---|---|
| EOA1 | 0.0174 | 5.5 | - | - | - | 60 | 180 |
| EOA2 | 0.1880 | - | - | - | - | −75 | 75 |
| EOA3 | 0.0124 | 6.4 | - | - | - | 50 | 150 |
| EOA4 | 0.0004 | 0.106 | - | - | - | 0 | 140 |
| EOA5 | 0.0146 | 5.8 | - | - | - | 40 | 120 |
| EOA6 | 0.0009 | 0.02 | - | - | - | 0 | 180 |
| CGA1 | 0.0069 | 2.9 | 0.0060 | 0.84 | 0.0062 | - | - |
| CGA2 | 0.0087 | 5.0 | 0.0054 | 0.12 | 0.0022 | - | - |
| HOA1 | - | - | 0.0102 | 3.3 | - | 40 | 500 |
| HOA2 | - | - | 0.0146 | 2.42 | - | 30 | 300 |
| HOA3 | - | - | 0.0001 | 0.084 | - | 0 | 250 |
| HOA4 | - | - | 0.1660 | - | - | −200 | 200 |
| Agent | Case Study 1: Proposed Method | Case Study 1: Centralized Method | Case Study 2: Proposed Method |
|---|---|---|---|
| EOA1 | 64.1355 | 64.1987 | 64.1676 |
| EOA2 | 20.5636 | 20.5695 | 20.5666 |
| EOA3 | 53.7078 | 53.7950 | 53.7544 |
| EOA4 | 90.0000 | 90.0000 | 90.0000 |
| EOA5 | 66.1650 | 66.2368 | 66.2062 |
| EOA6 | 130.0000 | 130.0000 | 130.0000 |
| CGA1-E | 215.1412 | 215.0000 | 215.0399 |
| CGA2-E | 110.2749 | 110.2000 | 110.2529 |
| CGA1-H | 179.2058 | 180.0000 | 179.7754 |
| CGA2-H | 134.9488 | 135.6000 | 135.1400 |
| HOA1 | 150.9958 | 150.1772 | 150.5662 |
| HOA2 | 135.6291 | 135.0553 | 135.32714 |
| HOA3 | 180.0000 | 180.0000 | 180.0000 |
| HOA4 | 19.2180 | 19.1675 | 19.1914 |
| Total cost | 5811.3 | 5806.9 | 5809.3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-S.; Zhang, H.-G.; Huang, B.-N.; Teng, F. Distributed Optimal Economic Dispatch Based on Multi-Agent System Framework in Combined Heat and Power Systems. Appl. Sci. 2016, 6, 308. https://doi.org/10.3390/app6100308
Li Y-S, Zhang H-G, Huang B-N, Teng F. Distributed Optimal Economic Dispatch Based on Multi-Agent System Framework in Combined Heat and Power Systems. Applied Sciences. 2016; 6(10):308. https://doi.org/10.3390/app6100308
Chicago/Turabian StyleLi, Yu-Shuai, Hua-Guang Zhang, Bo-Nan Huang, and Fei Teng. 2016. "Distributed Optimal Economic Dispatch Based on Multi-Agent System Framework in Combined Heat and Power Systems" Applied Sciences 6, no. 10: 308. https://doi.org/10.3390/app6100308
APA StyleLi, Y.-S., Zhang, H.-G., Huang, B.-N., & Teng, F. (2016). Distributed Optimal Economic Dispatch Based on Multi-Agent System Framework in Combined Heat and Power Systems. Applied Sciences, 6(10), 308. https://doi.org/10.3390/app6100308









