Agent Based Fuzzy T-S Multi-Model System and Its Applications
Abstract
:1. Introduction
2. Concept Formulation
2.1. Dynamic Network of Agents
2.2. Consensus Protocol
2.3. Fuzzy T-S Model
3. Agent Based Fuzzy T-S Multi-Model System
4. Universal Approximation Characteristics of Agent Based Fuzzy T-S Mutil-Model Systems
5. Applications and Discussions
5.1. Chaotic Time Series Prediction
5.1.1. Description of the Equation
| Conditions | a | b | τ | |
|---|---|---|---|---|
| 1 | 0.2 | 0.1 | 17 | 1.2 |
| 2 | 0.2 | 0.09 | 19 | 1.0 |
| 3 | 0.2 | 0.12 | 16 | 0.7 |
5.1.2. Simulation Tests
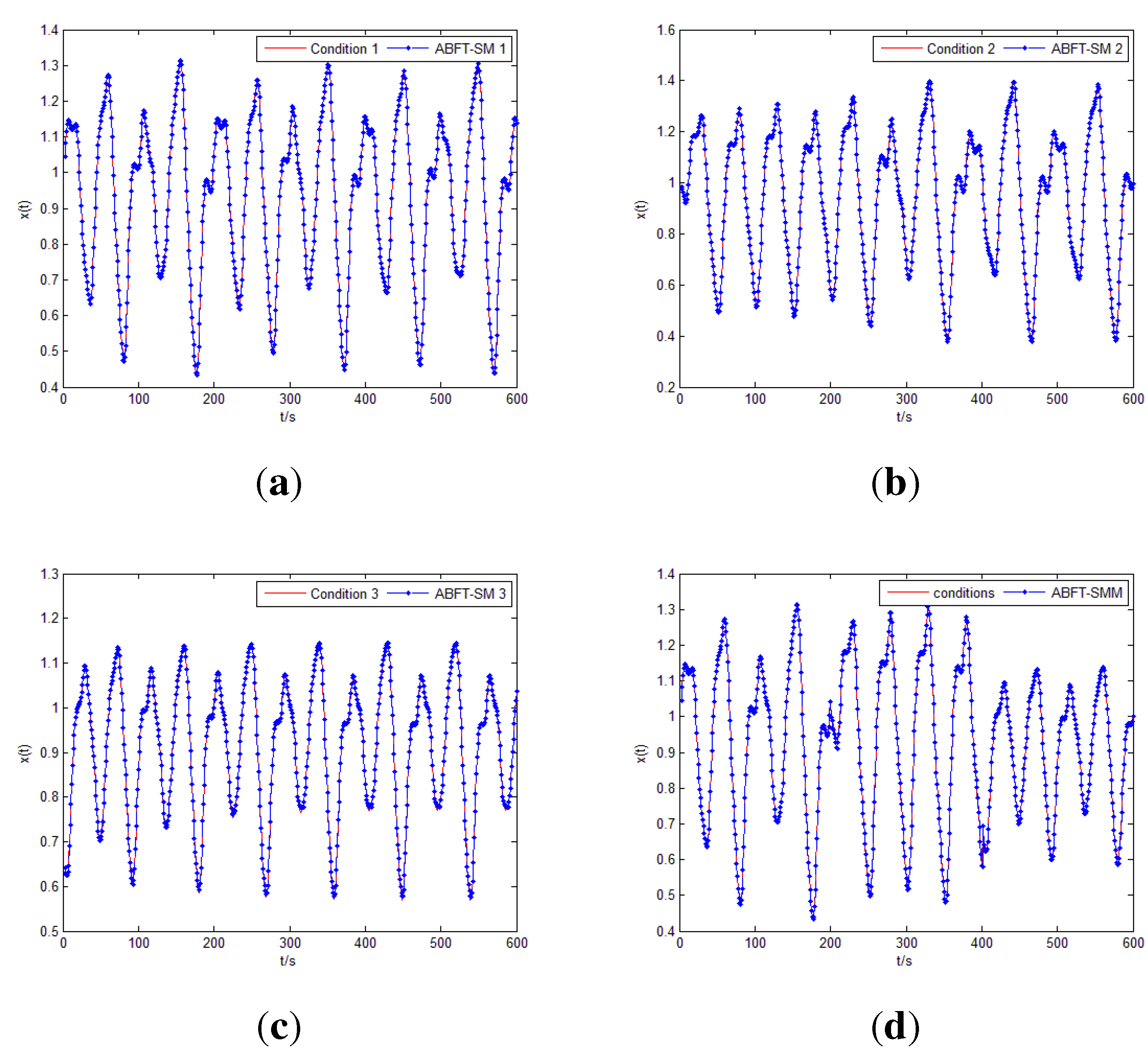
| Conditions | Centers | RMSE | ||
|---|---|---|---|---|
| 1 | 0.14 | 0.1 | 7 | 0.0037 |
| 2 | 0.1 | 0.1 | 6 | 0.0044 |
| 3 | 0.19 | 0.1 | 6 | 0.0040 |
5.1.3. Comparison and Discussion
5.2. Identification of Electrical Water Heater
5.2.1. Description of the System
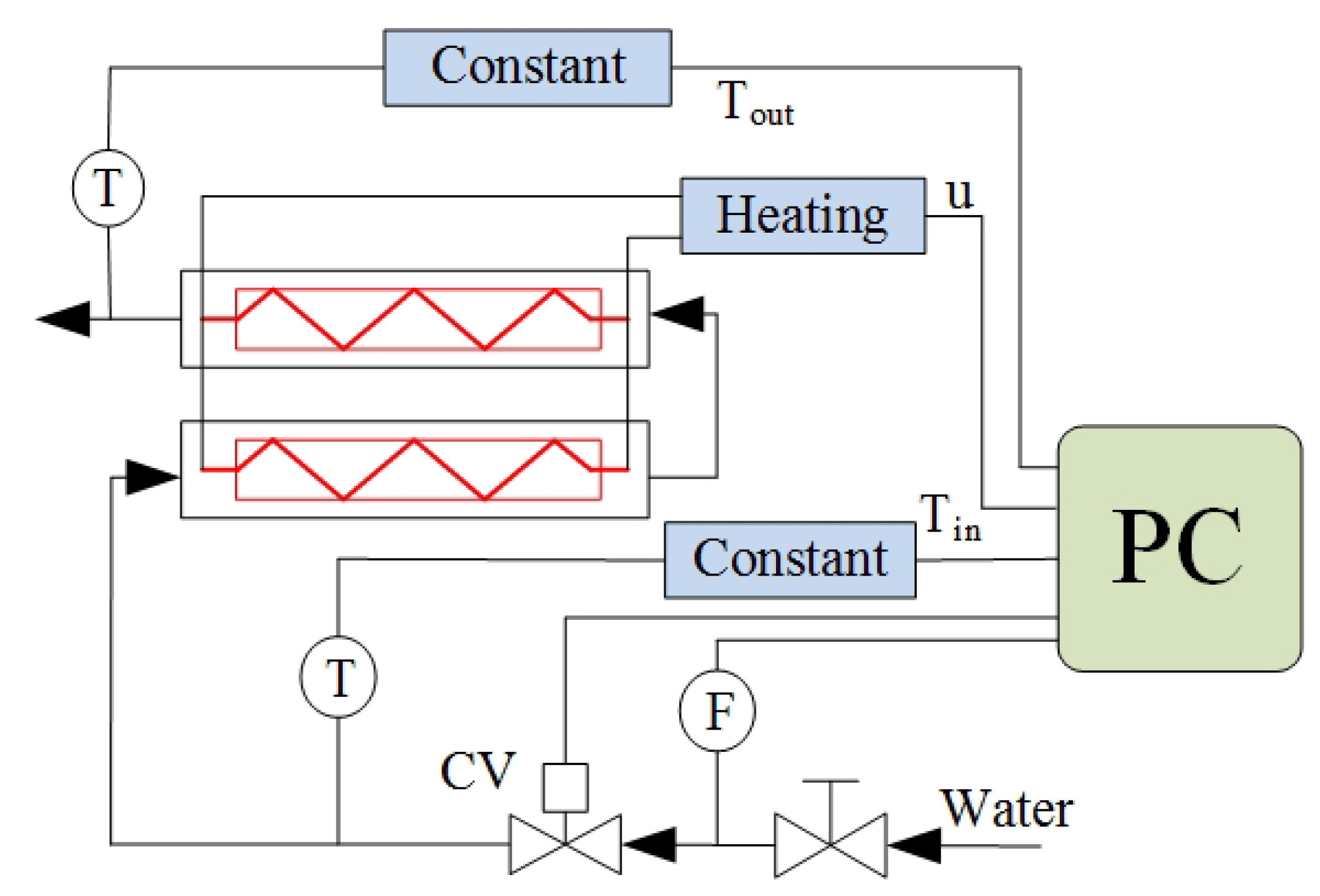
| Conditions | |||||
|---|---|---|---|---|---|
| 1 | 0.8112 | 0.0093 | 0.0019 | 20.83 | |
| 2 | 0.8302 | 0.0032 | 0.0086 | 21.35 |
5.2.2. Simulation and Discussion
| Conditions | Centers | RMSE | ||
|---|---|---|---|---|
| 1 | 0.18 | 1 | 21 | 0.01 |
| 2 | 0.2 | 1 | 17 | 0.0096 |
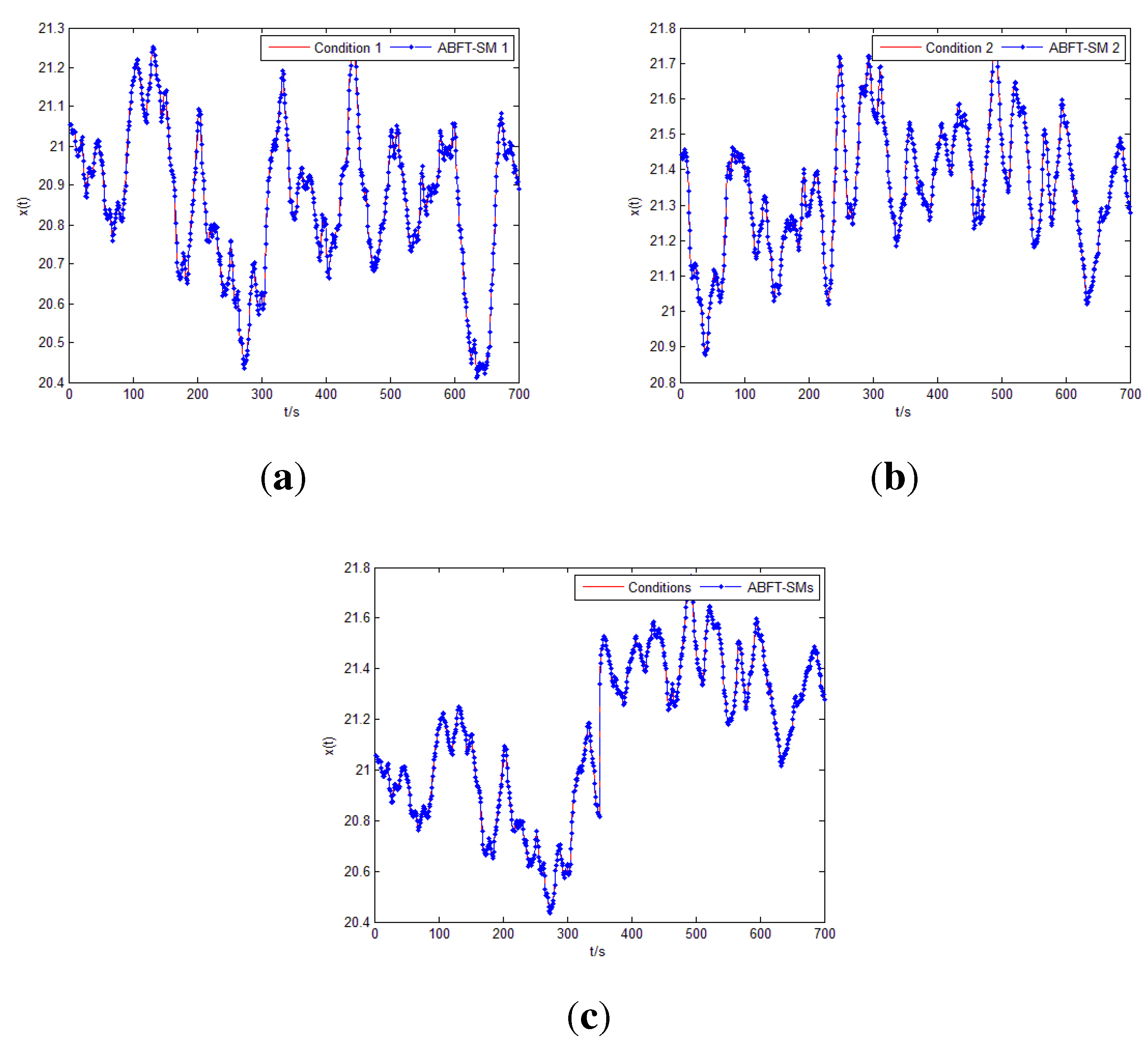
5.3. Waste Heat Utilizing System Modeling
5.3.1. System Description
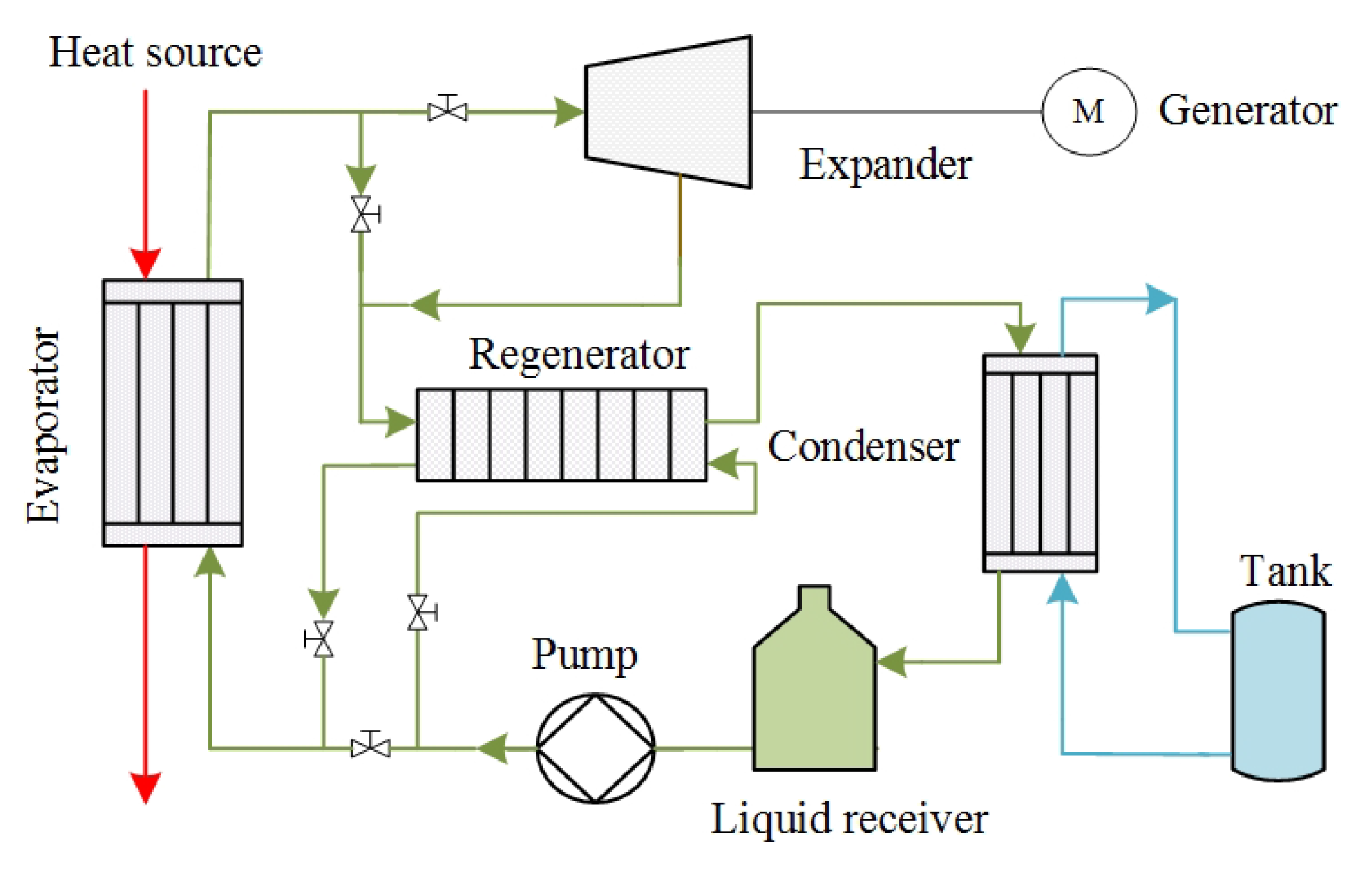
| Molecular Formula | CHCl2CF3 |
|---|---|
| Molecular weight | 152.931 g/mol |
| Critical pressure | 3.662 MPa |
| Critical temperature | 456.681 K |
| Critical density | 550.004 kg/m3 |
5.3.2. Simulation Tests
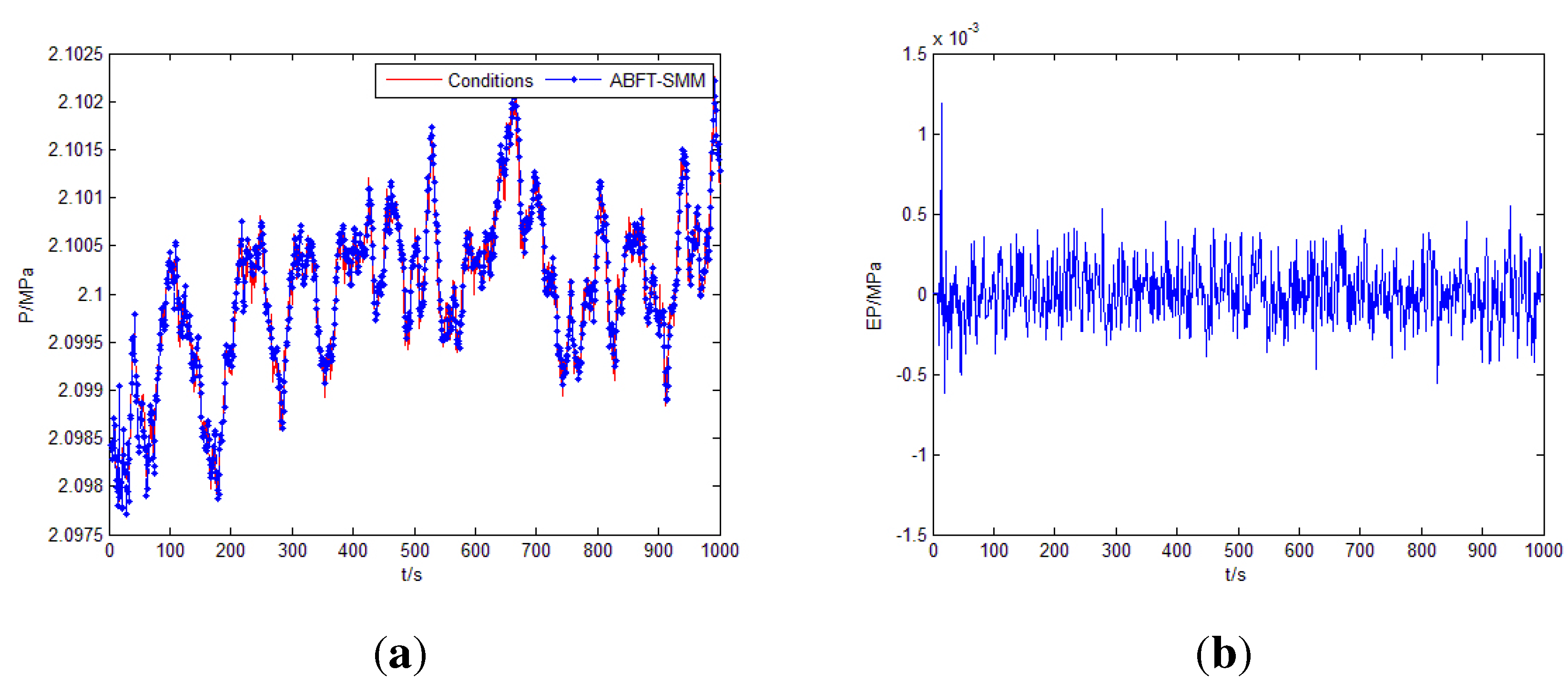
5.3.3. Comparison and Discussion of System Performances
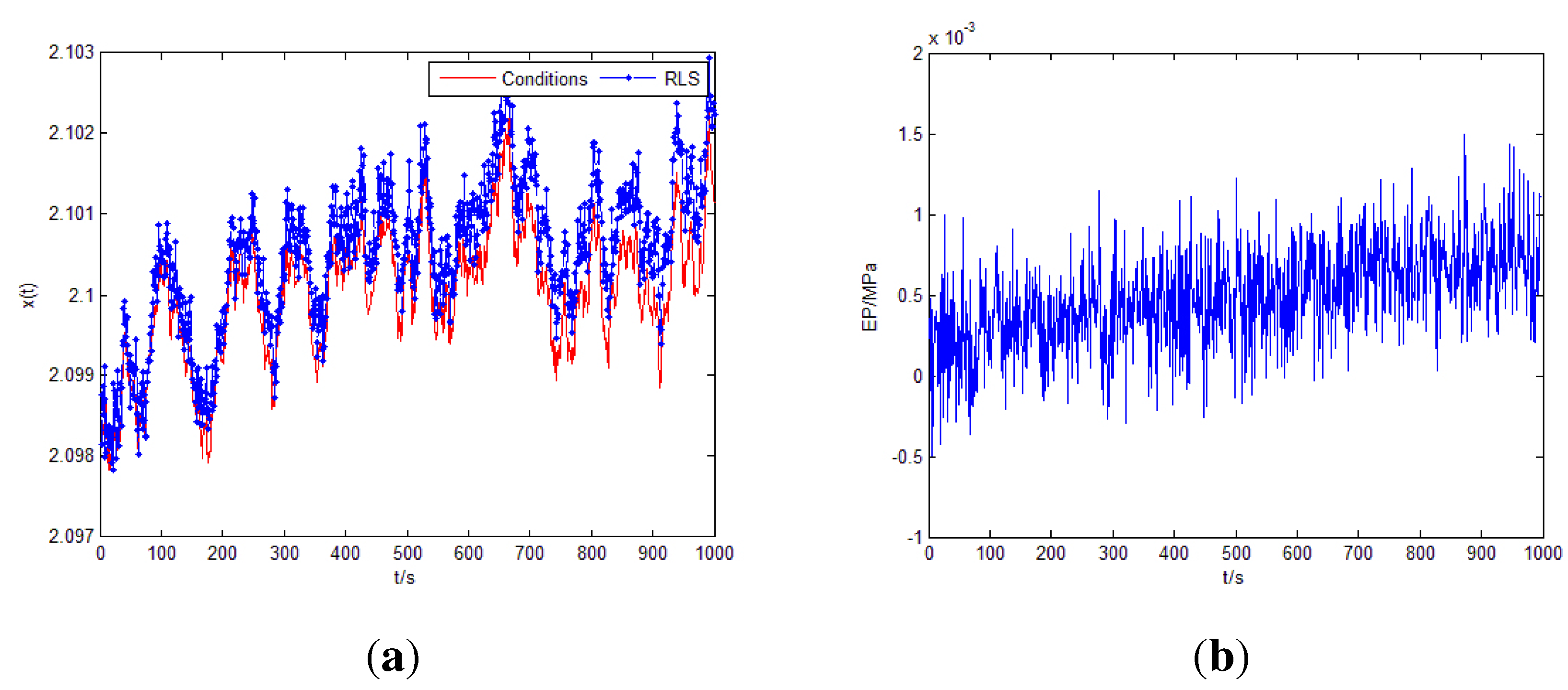
| Centers | RMSE | ||||||
|---|---|---|---|---|---|---|---|
| 8 |
6. Conclusions
- (1)
- The ABFT-SMM system is an h-consensus network.
- (2)
- The structure of the model can be adjusted by the number of the agents and their corresponding weights.
- (3)
- The proposed modelling method can approximate any linear or nonlinear system at arbitrary accuracy.
Acknowledgments
Conflicts of Interest
References
- McArthur, S.D.; Davidson, E.M.; Catterson, V.M. Multi-Agent Systems for Power Engineering Applications—Part I: Concepts, Approaches,and Technical Challenges. IEEE Trans. Power Syst. 2007, 22, 1743–1752. [Google Scholar] [CrossRef]
- Parker, J.; Epstein, J.M. A Distributed Platform for Global-Scale Agent-Based Models of Disease Transmission. ACM Trans. Model Comput. Simul. 2011, 22, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Romanovski, I.; Caines, P.E. On the supervisory control of multi-agent product systems: Controllability properties. Syst. Control Lett. 2007, 56, 113–121. [Google Scholar] [CrossRef]
- Muller, S.C.; Hager, U.; Rehtanz, C. A Multiagent System for Adaptive Power Flow Control in Electrical Transmission Systems. IEEE Trans. Ind. Informat. 2014, 10, 2290–2299. [Google Scholar] [CrossRef]
- Oh, H.S.; Thomas, R.J. Demand-Side Bidding Agents: Modeling and Simulation. IEEE Trans. Power Syst. 2008, 39, 1050–1056. [Google Scholar]
- Bristow, M.; Fang, L.P.; Hipel, K.W. Agent-Based Modeling of Competitive and Cooperative Behavior Under Conflict. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 834–850. [Google Scholar] [CrossRef]
- Cheng, Z.M.; Zhang, H.T.; Fan, M.C.; Chen, G.R. Distributed Consensus of Multi-Agent Systems With Input Constraints: A Model Predictive Control Approach. IEEE Trans. Circuits Syst. I 2015, 62, 1549–8328. [Google Scholar] [CrossRef]
- Doctor, F.; Iqbal, R.; Naguib, R.N.G. A fuzzy ambient intelligent agents approach for monitoring disease progression of dementia patients. J. Ambient Intell. Humaniz. Comput. 2014, 5, 147–158. [Google Scholar] [CrossRef]
- Dai, P.P.; Liu, C.L.; Liu, F. Consensus Problem of Heterogeneous Multi-agent Systems with Time Delay under Fixed and Switching Topologies. Int. J. Autom. Comput. 2014, 11, 340–346. [Google Scholar] [CrossRef]
- Hu, J.P.; Liu, Z.X.; Wang, J.H.; Lin, W.; Hu, X.M. Estimation, intervention and interaction of multi-agent systems. Acta Autom. Sin. 2013, 39, 1796–1804. [Google Scholar] [CrossRef]
- Hong, Y.G.; Chen, G.R.; Bushnell, L. Distributed observers design for leader-following control of multi-agent networks. Automatica 2008, 44, 846–850. [Google Scholar] [CrossRef]
- Wang, B.C.; Zhang, J.F. Distributed control of multi-agent systems with random parameters and a major agent. Automatica 2012, 48, 2093–2106. [Google Scholar] [CrossRef]
- Hong, Y.G.; Hu, J.P.; Gao, L.X. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar] [CrossRef]
- Su, Y.F.; Hong, Y.G.; Huang, J. A General Result on the Robust Cooperative Output Regulation for Linear Uncertain Multi-Agent Systems. IEEE Trans. Autom. Control 2013, 58, 1275–1279. [Google Scholar] [CrossRef]
- Xiong, W.J.; Yu, W.W.; Lv, J.H.; Yu, X.H. Fuzzy Modelling and Consensus of Nonlinear Multiagent Systems With Variable Structure. IEEE Trans. Circuits Syst. I 2014, 61, 1183–1191. [Google Scholar] [CrossRef]
- Ying, H. General SISO Takagi-Sugeno Fuzzy Systems with Linear Rule Consequent Are Universal Approximators. IEEE Trans. Fuzzy Syst. 1998, 6, 582–587. [Google Scholar] [CrossRef]
- Angelov, P.; Filev, D. An approach to online identification of Takagi-Sugeno fuzzy models. IEEE Trans. Syst. Man Cybern. 2004, 34, 484–498. [Google Scholar] [CrossRef]
- Narendra, K.S.; Xiang, C. Adaptive Control of Discrete-Time Systems Using Multiple Models. IEEE Trans. Autom. Control 2000, 45, 1669–1686. [Google Scholar] [CrossRef]
- Rosyadi, M.; Muyeen, S.M.; Takahashi, R.; Tamura, J. A Design Fuzzy Logic Controller for a Permanent Magnet Wind Generator to Enhance the Dynamic Stability of Wind Farms. Appl. Sci. 2012, 2, 780–800. [Google Scholar] [CrossRef]
- Wang, L.X. Fuzzy Systems are Universal Approximators. In Proceding of the IEEE International Conference on Fuzzy Sysystem, San Diego, CA, USA, 8–12 March 1992; pp. 1163–1170.
- Zhang, H.G.; Liu, D.R. Fuzzy Modeling and Fuzzy Control; Birkhauser: Basel, Switzerland, 2006. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis; Publishing House: McGraw-Hill, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Chiu, S.L. Fuzzy model identification based on cluster estimation. J. Int. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar]
- Abonyi, J.; Babuska, R.; Szeifert, F. Modified Gath-Geva Fuzzy Clustering for Identification of Takagi-Sugeno Fuzzy Models. IEEE Trans. Syst. Man Cybern. B Cybern. 2002, 32, 612–621. [Google Scholar] [CrossRef] [PubMed]
- Kalhor, A.; Araabia, B.N.; Lucasa, C. Evolving Takagi-Sugeno fuzzy model based on switching to neighboring models. Appl. Soft Comput. 2013, 13, 939–946. [Google Scholar] [CrossRef]
- Jang, J. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Crowder, R. Predicting the Mackey-Glass Time Series with Cascade-Correlation Learning. In Proceding of the 1990 Summer School, Carnegie Mellon University, Pittsburgh, PA, USA, January 1990; pp. 117–123.
- Angelov, P.; Xydeas, C.; Filev, D. Online identification of MIMO Evolving Takagi-Sugeno fuzzy models. IEEE Trans. Syst. Man Cybern. 2004, 1, 55–60. [Google Scholar]
- Castillo, O.; Castro, J.R.; Melin, P.; Diaz, A.R. Application of interval type-2 fuzzy neural networks in non-linear identification and time series prediction. Soft Comput. 2014, 18, 1213–1224. [Google Scholar] [CrossRef]
- Abonyi, J. Fuzzy Model Identification for Control; Birkhauser: Basel, Switzerland, 2003; pp. 243–245. [Google Scholar]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X. Agent Based Fuzzy T-S Multi-Model System and Its Applications. Appl. Sci. 2015, 5, 1235-1251. https://doi.org/10.3390/app5041235
Zhao X. Agent Based Fuzzy T-S Multi-Model System and Its Applications. Applied Sciences. 2015; 5(4):1235-1251. https://doi.org/10.3390/app5041235
Chicago/Turabian StyleZhao, Xiaopeng. 2015. "Agent Based Fuzzy T-S Multi-Model System and Its Applications" Applied Sciences 5, no. 4: 1235-1251. https://doi.org/10.3390/app5041235
APA StyleZhao, X. (2015). Agent Based Fuzzy T-S Multi-Model System and Its Applications. Applied Sciences, 5(4), 1235-1251. https://doi.org/10.3390/app5041235






