Imaging of Volume Phase Gratings in a Photosensitive Polymer, Recorded in Transmission and Reflection Geometry
Abstract
:1. Introduction
2. Experimental Section
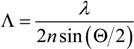
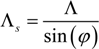
3. Results and Discussion
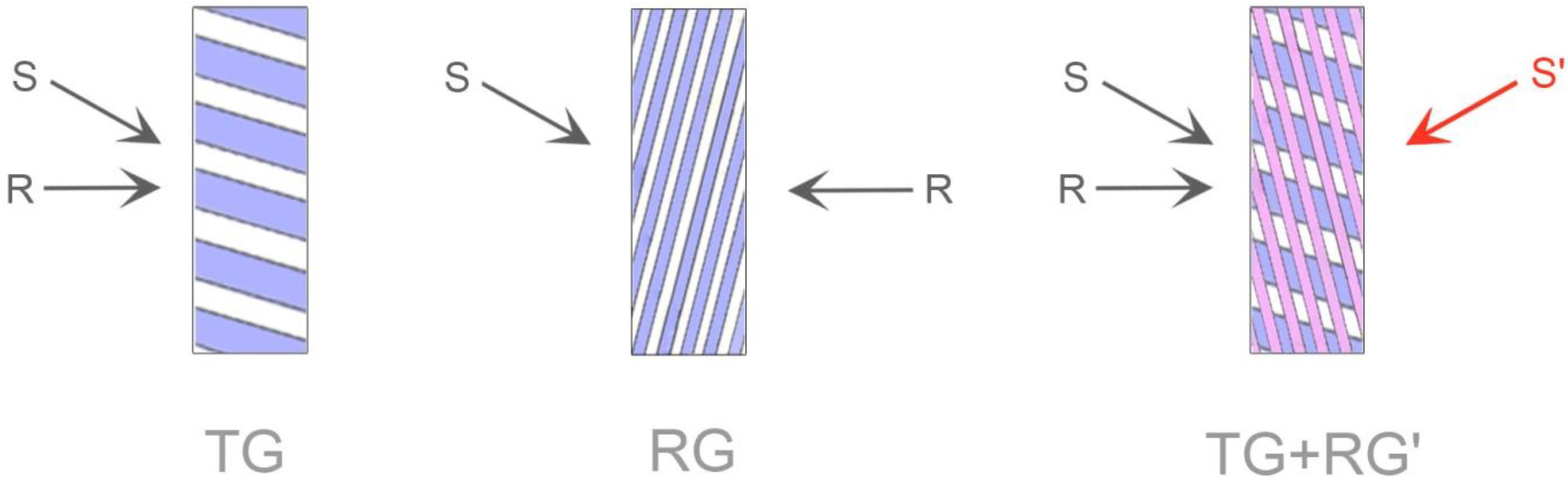
3.1. Secondary Reflection Gratings in Transmission Recording Geometry
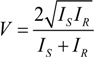

3.2. The Avoidance of Secondary Gratings
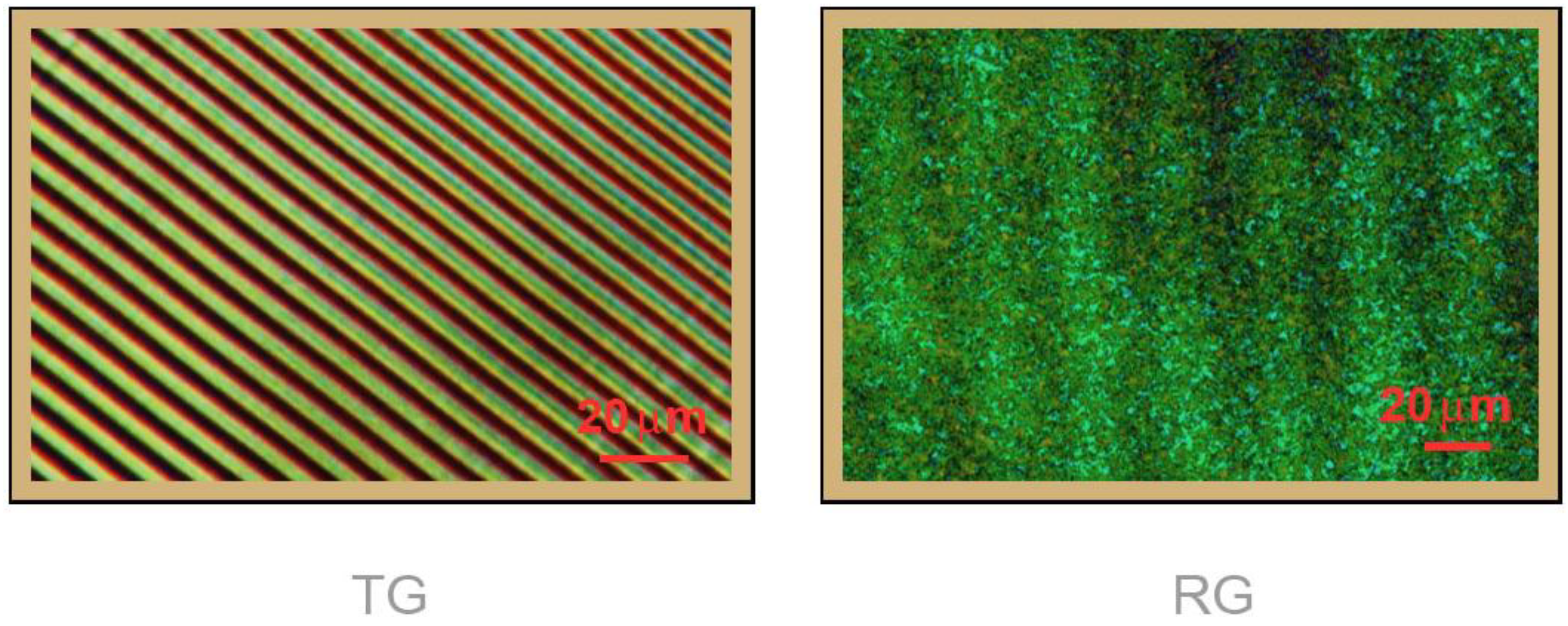
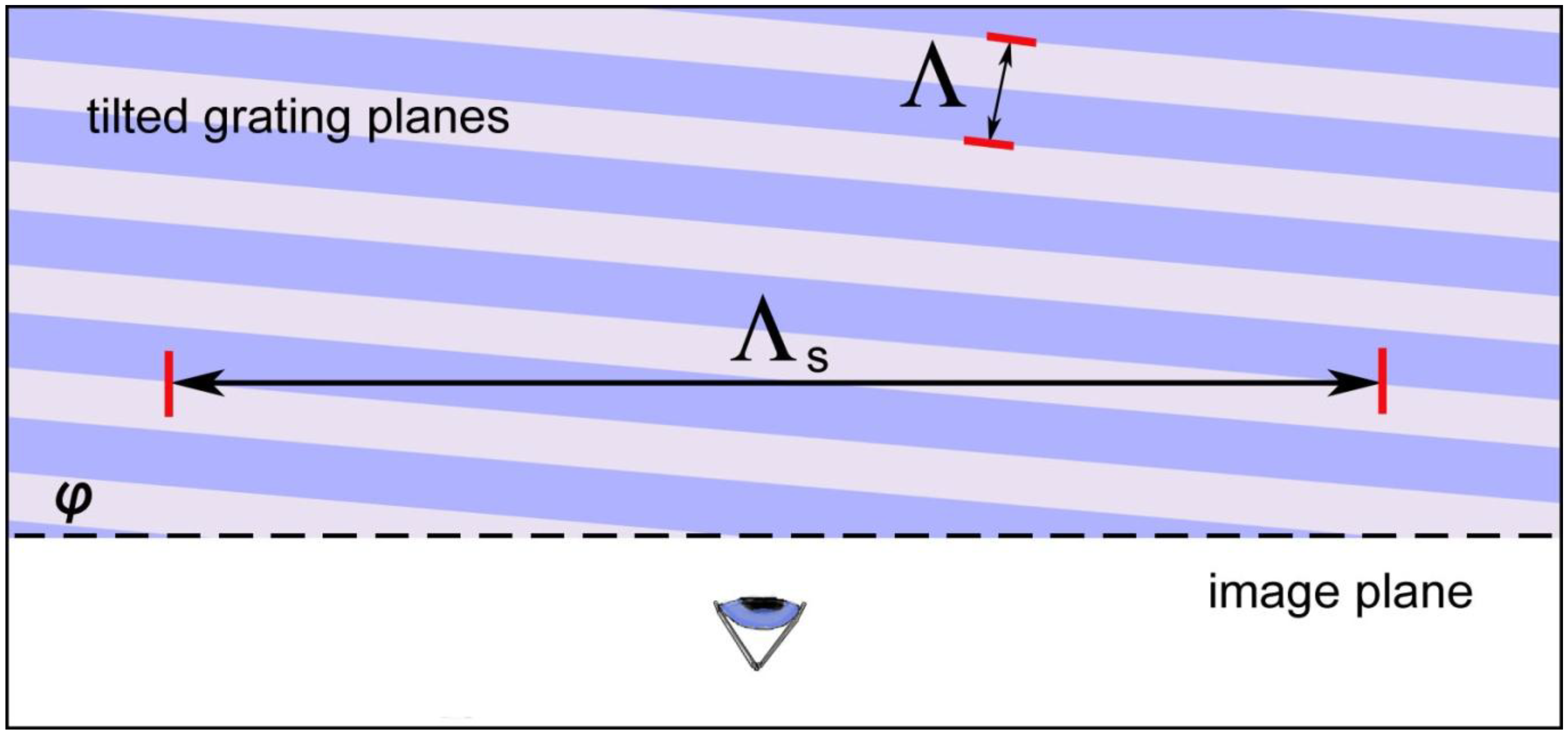
3.3. Refined Analysis of Spatial Characteristics

4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Trentler, T.J.; Boyd, J.E.; Colvin, V.L. Epoxy resin-photopolymer composites for volume holography. Chem. Mater. 2000, 12, 1431–1438. [Google Scholar] [CrossRef]
- Trout, T.J.; Schmieg, J.J.; Gambogi, W.J.; Weber, A.M. Optical photopolymers: Design and applications. Adv. Mater. 1998, 10, 1219–1224. [Google Scholar] [CrossRef]
- Hagen, R.; Bieringer, T. Photoaddressable polymers for optical data storage. Adv. Mater. 2001, 13, 1805–1810. [Google Scholar] [CrossRef]
- Ma, H.; Jen, A.K.Y.; Dalton, L.R. Polymer-based optical waveguides: Materials, processing, and devices. Adv. Mater. 2002, 14, 1339–1365. [Google Scholar] [CrossRef]
- Baylor, M.; Cerjan, B.; Pfiefer, C.; Boyne, R.; Couch, C.; Cramer, N.; Bowman, C.; McLeod, R. Monolithic integration of optical waveguide and fluidic channel structures in a thiol-ene/methacrylate photopolymer. Opt. Mater. Express 2012, 2, 1548–1555. [Google Scholar] [CrossRef]
- De Sio, L.; Ferjani, S.; Strangi, G.; Umeton, C.; Bartolino, R. Universal soft matter template for photonic applications. Soft Matter 2011, 7, 3739–3743. [Google Scholar] [CrossRef]
- Sabel, T.; Orlic, S.; Pfeiffer, K.; Ostrzinski, U.; Grützner, G. Free-surface photopolymerizable recording material for volume holography. Opt. Mater. Express 2013, 3, 329–338. [Google Scholar] [CrossRef]
- Orlic, S.; Bernstein, F.; Kratz, C.; Schlösser, A. Optical transfer function of three-dimensional photonic crystals by volume holographic recording. Appl. Phys. Lett. 2013, 103, 041106. [Google Scholar] [CrossRef]
- Guo, J.; Gleeson, M.R.; Sheridan, J.T. A review of the optimisation of photopolymer materials for holographic data storage. Phys. Res. Int. 2012, 2012, 803439. [Google Scholar] [CrossRef]
- Sabel, T.; Zschocher, M. Transition of refractive index contrast in course of grating growth. Sci. Rep. 2013, 3, 2552. [Google Scholar] [CrossRef]
- Sakhno, O.V.; Goldenberg, L.M.; Smirnova, T.N.; Stumpe, J. Holographic patterning of organic-inorganic photopolymerizable nanocomposites. Proc. SPIE 2009, 7487. [Google Scholar] [CrossRef]
- Sabel, T.; Zschocher, M. Dynamic Bragg angle shift in the course of volume hologram formation. Mater. Res. Lett. 2013, 2, 76–81. [Google Scholar] [CrossRef]
- Castagna, R.; Milner, A.; Zyss, J.; Prior, Y. Nanoscale Poling of Polymer Films. Adv. Mater. 2013, 25, 2234–2238. [Google Scholar] [CrossRef]
- Del Monte, F.; Martínez, O.; Rodrigo, J.A.; Calvo, M.L.; Cheben, P. A Volume Holographic Sol-gel material with large enhancement of dynamic range by incorporation of high refractive index species. Adv. Mater. 2006, 18, 2014–2017. [Google Scholar] [CrossRef]
- Orlic, S.; Müller, C.; Schlösser, A. All-optical fabrication of three-dimensional photonic crystals in photopolymers by multiplex-exposure holographic recording. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
- Smirnova, T.N.; Kokhtych, L.M.; Kutsenko, A.S.; Sakhno, O.V.; Stumpe, J. The fabrication of periodic polymer/silver nanoparticle structures: In situ reduction of silver nanoparticles from precursor spatially distributed in polymer using holographic exposure. Nanotechnology 2009, 20, 405301. [Google Scholar] [CrossRef]
- Juhl, A.T.; Busbee, J.D.; Koval, J.J.; Natarajan, L.V.; Tondiglia, V.P.; Vaia, R.A.; Bunning, T.J.; Braun, P.V. Holographically directed assembly of polymer nanocomposites. ACS Nano 2010, 4, 5953–5961. [Google Scholar] [CrossRef]
- Suzuki, N.; Tomita, Y. Real-time phase-shift measurement during formation of a volume holographic grating in nanoparticle-dispersed photopolymers. Appl. Phys. Lett. 2006, 88, 011105. [Google Scholar] [CrossRef]
- Criante, L.; Castagna, R.; Vita, F.; Lucchetta, D.E.; Simoni, F. Nanocomposite polymeric materials for high density optical storage. J. Opt. A Pure Appl. Opt. 2009, 11, 024011. [Google Scholar] [CrossRef]
- Lourtioz, J.-M. Photonic crystals: Writing 3D photonic structures with light. Nat. Mater. 2004, 3, 427–428. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sabel, T.; Zschocher, M. Imaging of Volume Phase Gratings in a Photosensitive Polymer, Recorded in Transmission and Reflection Geometry. Appl. Sci. 2014, 4, 19-27. https://doi.org/10.3390/app4010019
Sabel T, Zschocher M. Imaging of Volume Phase Gratings in a Photosensitive Polymer, Recorded in Transmission and Reflection Geometry. Applied Sciences. 2014; 4(1):19-27. https://doi.org/10.3390/app4010019
Chicago/Turabian StyleSabel, Tina, and Michael Zschocher. 2014. "Imaging of Volume Phase Gratings in a Photosensitive Polymer, Recorded in Transmission and Reflection Geometry" Applied Sciences 4, no. 1: 19-27. https://doi.org/10.3390/app4010019
APA StyleSabel, T., & Zschocher, M. (2014). Imaging of Volume Phase Gratings in a Photosensitive Polymer, Recorded in Transmission and Reflection Geometry. Applied Sciences, 4(1), 19-27. https://doi.org/10.3390/app4010019





