Double Relativistic Electron Accelerating Mirror
Abstract
:1. Introduction
2. Theoretical Model
2.1. The Equation of Motion of Electron Layer
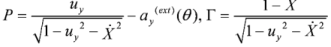 and being the constants of motion for a single electron in an electromagnetic wave down, where as ay(ext) = |e|Ay(ext)(θ)/mec2 is a dimensionless vector potential representing the incident wave; θ= ωt - kx, uy = vy / c is the dimensionless layer velocity component along the polarization direction (у); and,
and being the constants of motion for a single electron in an electromagnetic wave down, where as ay(ext) = |e|Ay(ext)(θ)/mec2 is a dimensionless vector potential representing the incident wave; θ= ωt - kx, uy = vy / c is the dimensionless layer velocity component along the polarization direction (у); and,  is the dimensionless layer velocity component along the wave vector (х). The equation of motion of the thin electron layer using these variables has the following form:
is the dimensionless layer velocity component along the wave vector (х). The equation of motion of the thin electron layer using these variables has the following form:
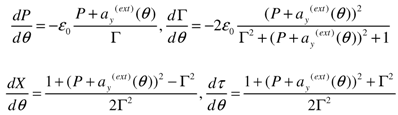
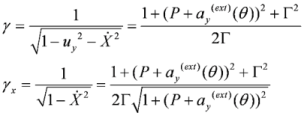
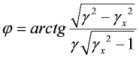
2.2. The Influence of a Second Plasma Layer on the Parameters of the Accelerated Electrons
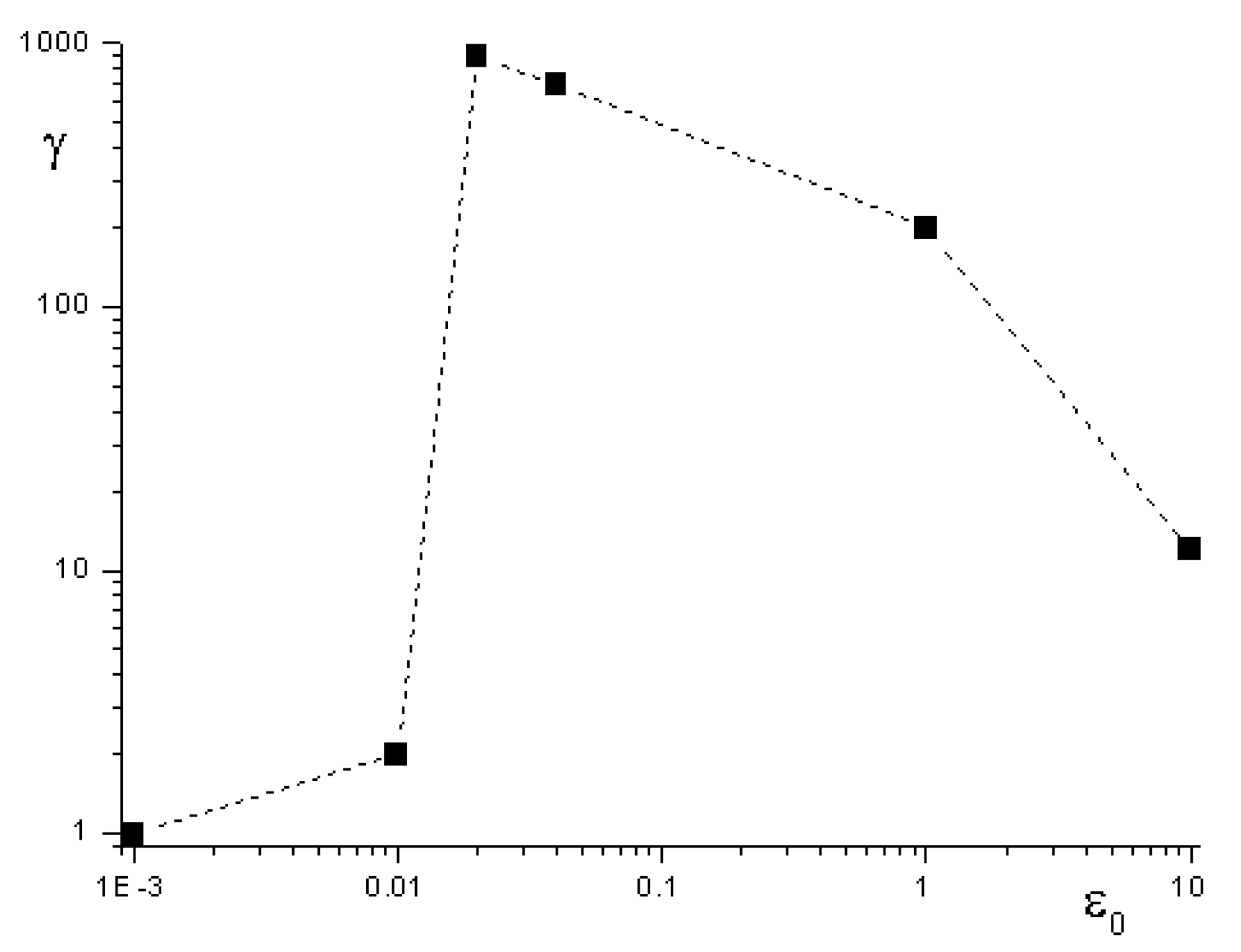
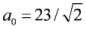 and ε0 = 0.02. Pulse duration is four laser periods for both cases.
and ε0 = 0.02. Pulse duration is four laser periods for both cases.
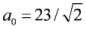 and ε0 = 0.02. Pulse duration is four laser periods for both cases.
and ε0 = 0.02. Pulse duration is four laser periods for both cases. 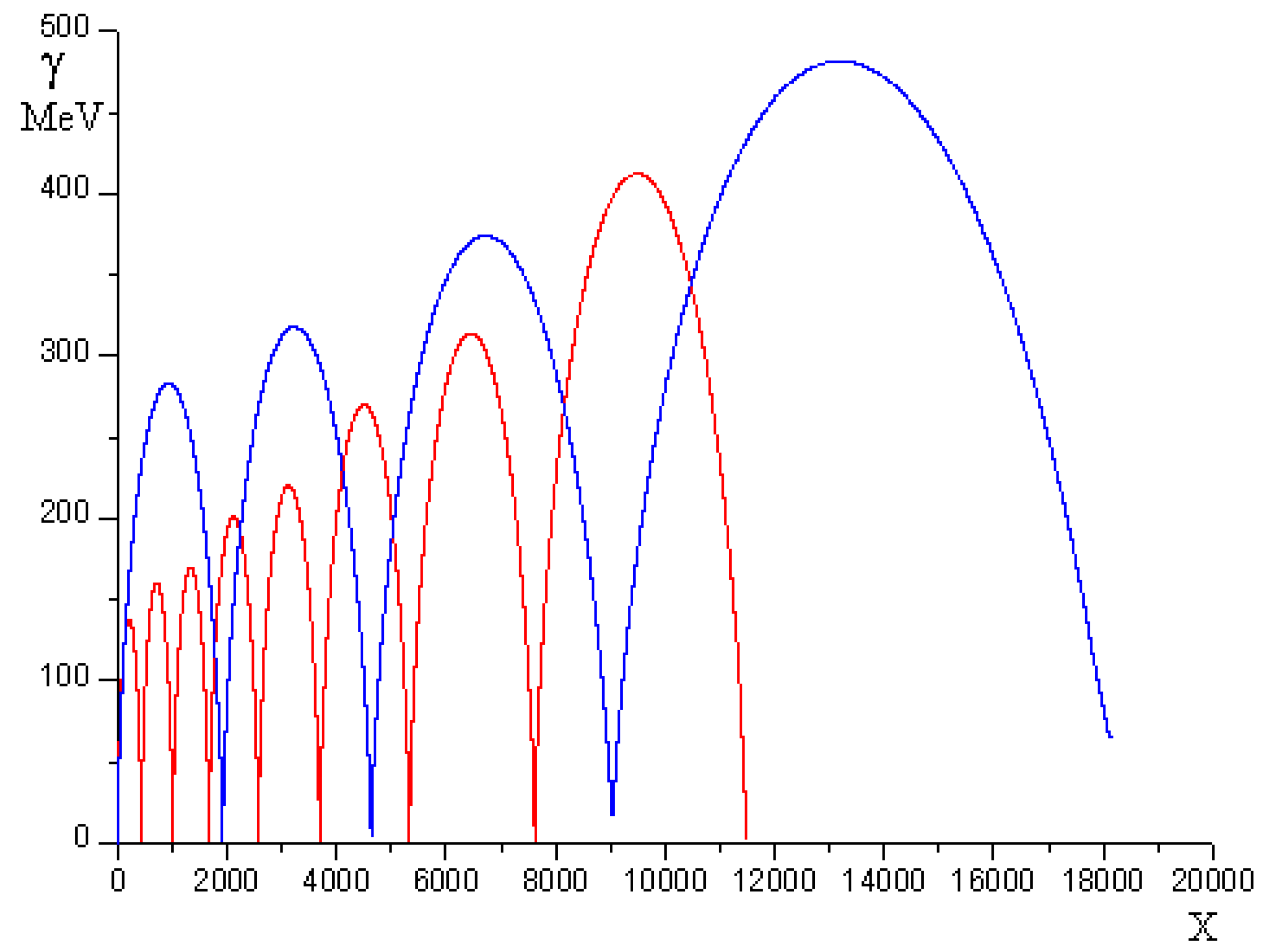
3. Results and Discussion
3.1. 2D Numerical Modeling of the Electron and Plasma Layers Interaction
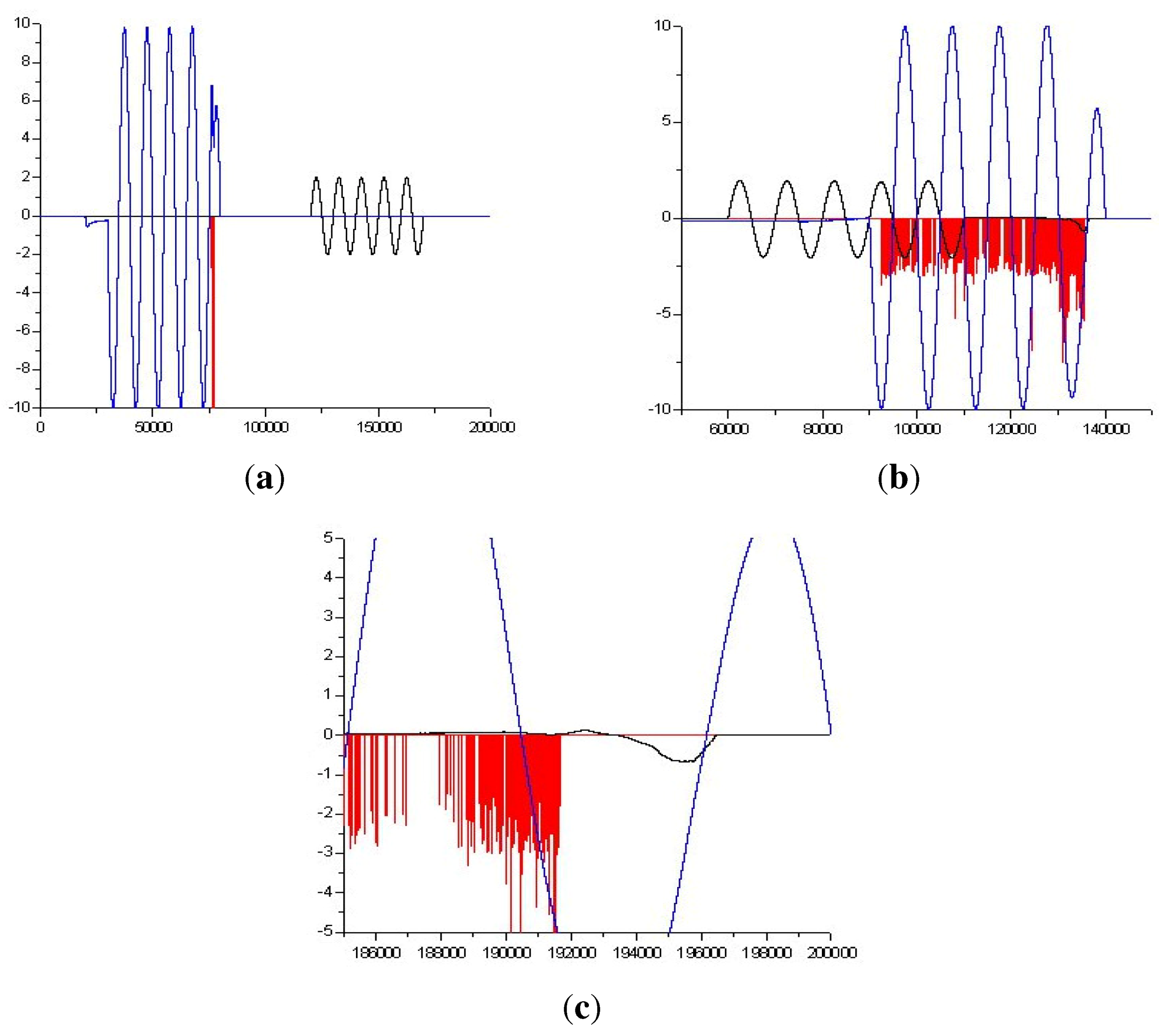
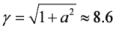 ) becomes ~4 MeV, correspondingly, the “tail” of the electron distribution function from the first target should not significantly change when passing through the second target. In Figure 4, the blue color illustrates the electron number density (with electrons energy > 15 MeV) at the time t = 57 fs when the electron layer from the first target reaches the second one. One can clearly see that the electron bunch has passed through the second target without any loss of energy and number of electrons. The laser pulse appears to be cut off by the dense plasma with 0.1 μm width. Thus, the plasma layer enables us to effectively separate the thin relativistic electron layer from the laser pulse without any loss of energy or number of electrons. It is noteworthy that the thickness of the electron bunch after propagation for the distance of 11 microns is about 60 nm in accordance with our calculations and estimations [8]. It is larger compared to the initial thickness, but is, in any case, still less than the laser wavelength.
) becomes ~4 MeV, correspondingly, the “tail” of the electron distribution function from the first target should not significantly change when passing through the second target. In Figure 4, the blue color illustrates the electron number density (with electrons energy > 15 MeV) at the time t = 57 fs when the electron layer from the first target reaches the second one. One can clearly see that the electron bunch has passed through the second target without any loss of energy and number of electrons. The laser pulse appears to be cut off by the dense plasma with 0.1 μm width. Thus, the plasma layer enables us to effectively separate the thin relativistic electron layer from the laser pulse without any loss of energy or number of electrons. It is noteworthy that the thickness of the electron bunch after propagation for the distance of 11 microns is about 60 nm in accordance with our calculations and estimations [8]. It is larger compared to the initial thickness, but is, in any case, still less than the laser wavelength.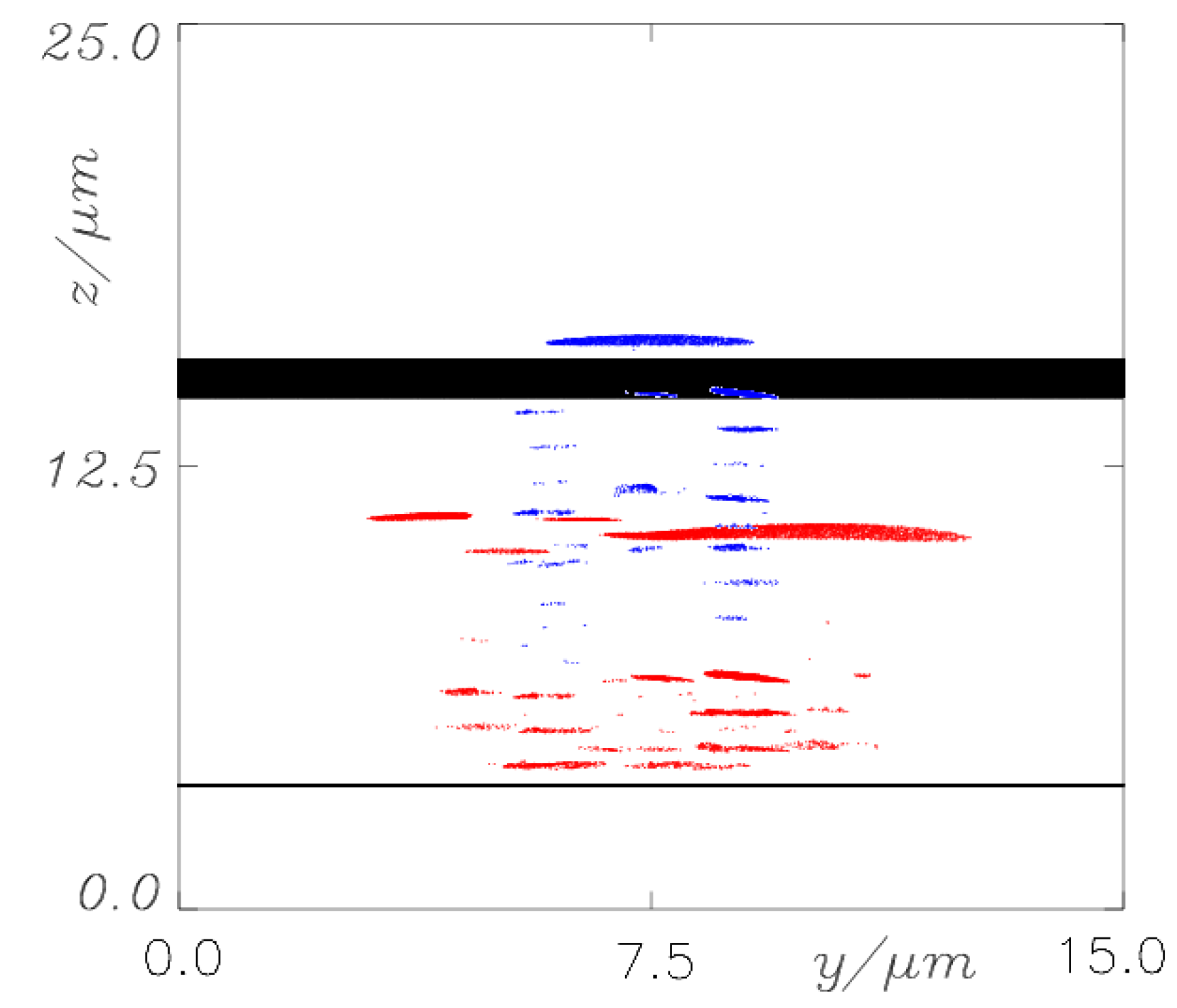
3.2. Scattering of a Counter-Propagating Laser Pulse from the Relativistic Electron Mirror
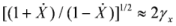 times. The scattering in the rest frame of reference occurs without frequency change. The following recalculation of the frequency of scattered radiation in the original laboratory frame of reference gives again the factor 2γx so that the reflected pulse has a quantum energy
times. The scattering in the rest frame of reference occurs without frequency change. The following recalculation of the frequency of scattered radiation in the original laboratory frame of reference gives again the factor 2γx so that the reflected pulse has a quantum energy 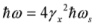 , with ωs being the frequency of the incident counter-propagating laser pulse. Note that a frequency shift is appearing not only due to Doppler’s effect of radiation reflected off a moving overdense electron layer, but also due to change of electron density inside a layer [14]. In our case, the number of electrons at laser front does not change after propagation out of the second target, and the effect connected with change of electron density is absent during the process of counter-propagating laser pulse reflection.
, with ωs being the frequency of the incident counter-propagating laser pulse. Note that a frequency shift is appearing not only due to Doppler’s effect of radiation reflected off a moving overdense electron layer, but also due to change of electron density inside a layer [14]. In our case, the number of electrons at laser front does not change after propagation out of the second target, and the effect connected with change of electron density is absent during the process of counter-propagating laser pulse reflection.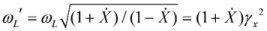 [9]. As a result, in the rest frame of reference of the electron layer, the reflection coefficient expressed using the variables in the laboratory frame of reference is equal to
[9]. As a result, in the rest frame of reference of the electron layer, the reflection coefficient expressed using the variables in the laboratory frame of reference is equal to 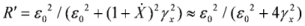 . In the rest frame of reference of the layer, the reflection occurs without frequency change, thus explaining why the number of reflected quanta Nh (hard quanta in the laboratory frame of reference) can be expressed through the number of incident laser quanta Ns as following Nh = R´NS. Since the absolute numbers of quanta are the relativistic invariants, then R´ is also the reflection coefficient with respect to the number of quanta (but not with respect to the pulses energies) in laboratory frame of reference. We would like to emphasize that the reflection coefficient R´ implies the non-relativistic (<1018 W/cm2) intensity Is´ of the incident radiation in the rest frame of reference of the layer. In the opposite case, as it was shown in [15], the decrease of the reflection coefficient occurs by Is´ / 1018 W/cm2 times (a more detailed and complex formula for R΄(ε0΄, IL΄)is given in this paper). The employment of the coefficient from the equation for the reflection coefficient R also implies the coherent character of the scattering process (this also follows from the fact that
. In the rest frame of reference of the layer, the reflection occurs without frequency change, thus explaining why the number of reflected quanta Nh (hard quanta in the laboratory frame of reference) can be expressed through the number of incident laser quanta Ns as following Nh = R´NS. Since the absolute numbers of quanta are the relativistic invariants, then R´ is also the reflection coefficient with respect to the number of quanta (but not with respect to the pulses energies) in laboratory frame of reference. We would like to emphasize that the reflection coefficient R´ implies the non-relativistic (<1018 W/cm2) intensity Is´ of the incident radiation in the rest frame of reference of the layer. In the opposite case, as it was shown in [15], the decrease of the reflection coefficient occurs by Is´ / 1018 W/cm2 times (a more detailed and complex formula for R΄(ε0΄, IL΄)is given in this paper). The employment of the coefficient from the equation for the reflection coefficient R also implies the coherent character of the scattering process (this also follows from the fact that 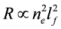 , i.e., the squared number of electrons in the layer) and the assumption of thinness of the layer (the width is less than the wavelength in the rest frame of reference). In order to validate these approximations, one needs to satisfy the inequality
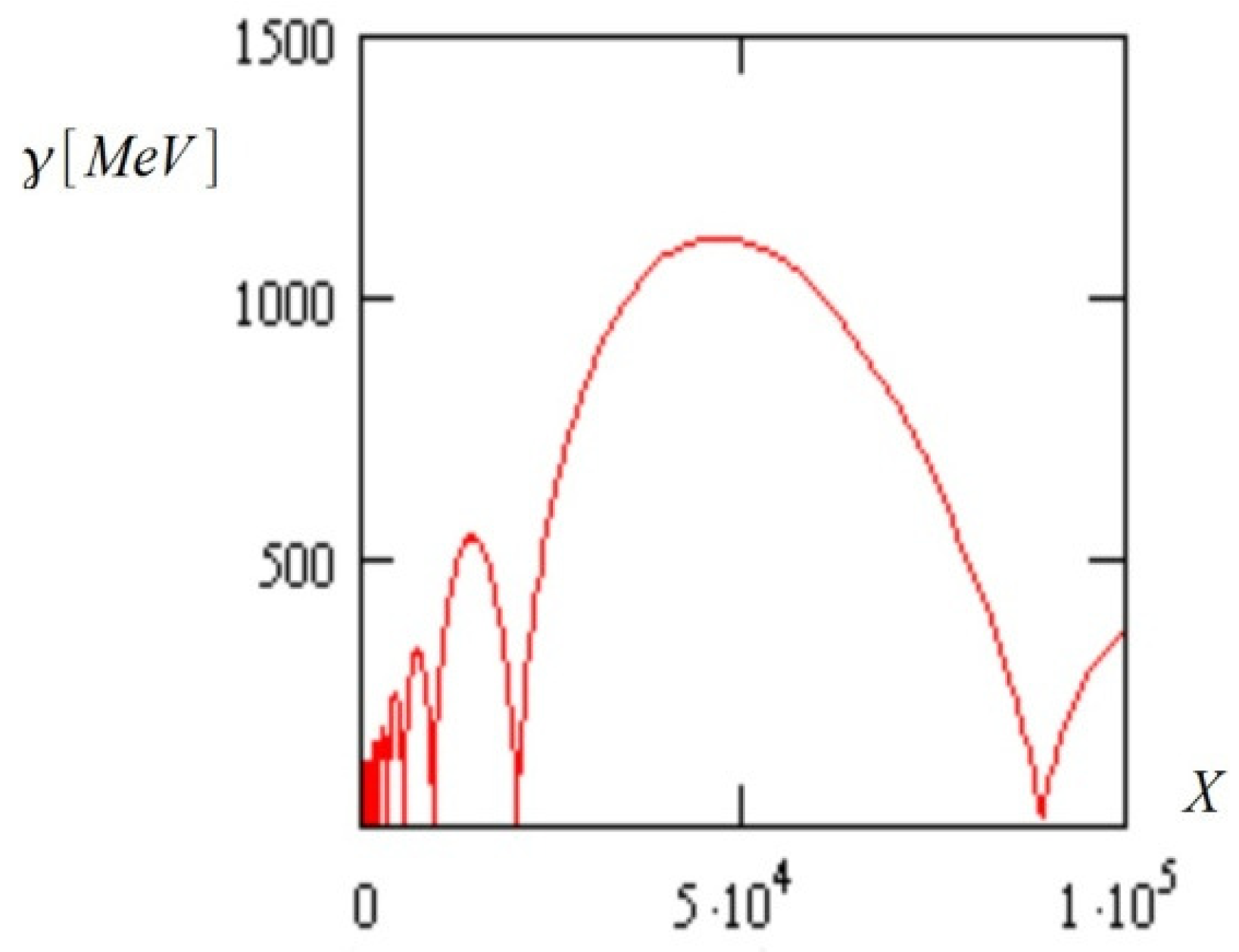
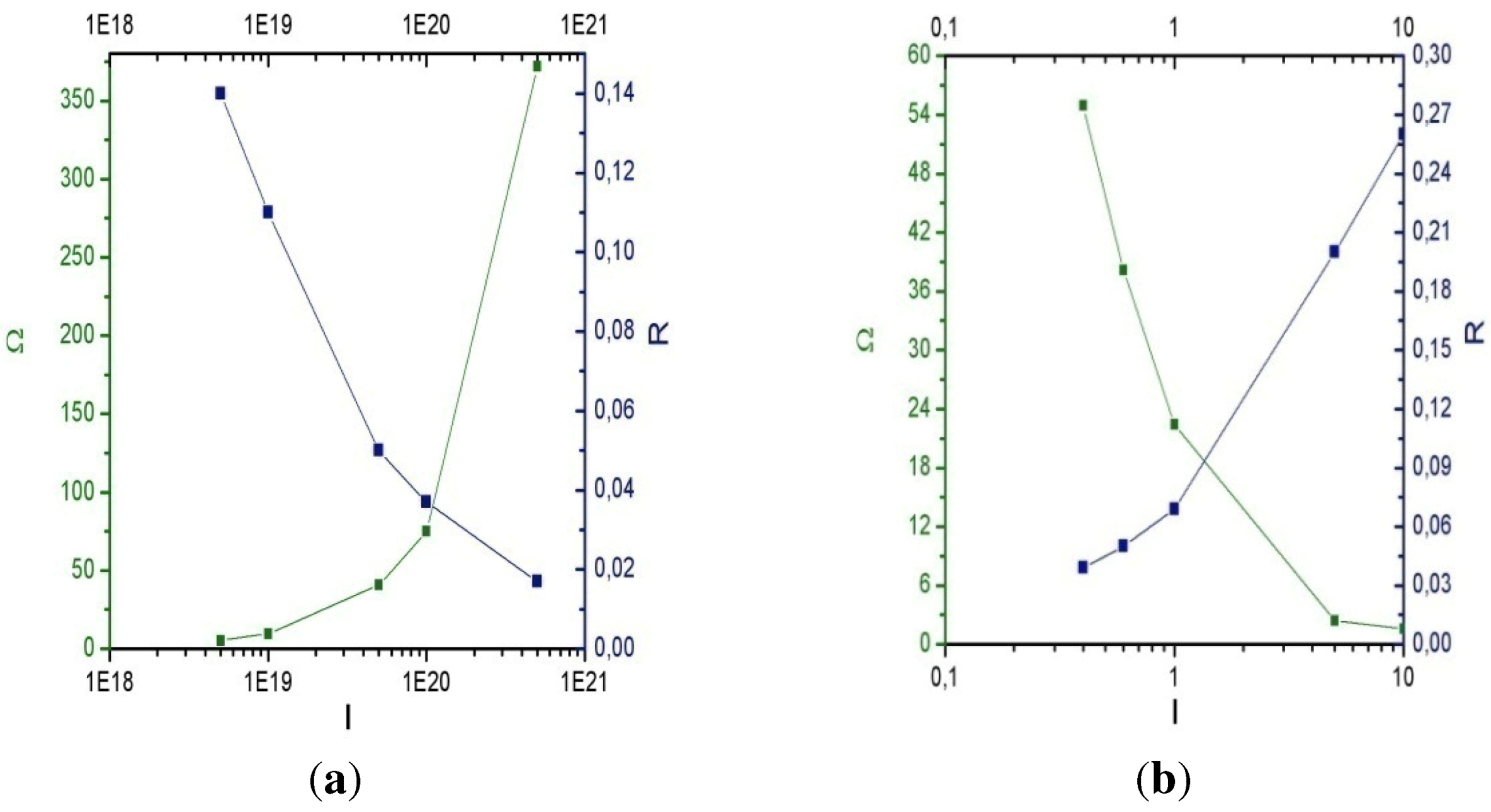
, i.e., the squared number of electrons in the layer) and the assumption of thinness of the layer (the width is less than the wavelength in the rest frame of reference). In order to validate these approximations, one needs to satisfy the inequality 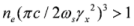 for the electron number density of the thin layer at the instant of reflection. In the numerical modeling, results of which are presented in Figure 5, the electron number density in the layer at t = 57 fs was estimated to 6 × 1021 cm−3, and this inequality was valid for the whole spectrum of electron energy. If, for some reason (e.g. durable movement of the electron layer), the electron number density will be low
for the electron number density of the thin layer at the instant of reflection. In the numerical modeling, results of which are presented in Figure 5, the electron number density in the layer at t = 57 fs was estimated to 6 × 1021 cm−3, and this inequality was valid for the whole spectrum of electron energy. If, for some reason (e.g. durable movement of the electron layer), the electron number density will be low 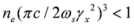 , then the coherent scattering will switch to the non-coherent Thomson scattering by single electrons. In this case, it is obvious that
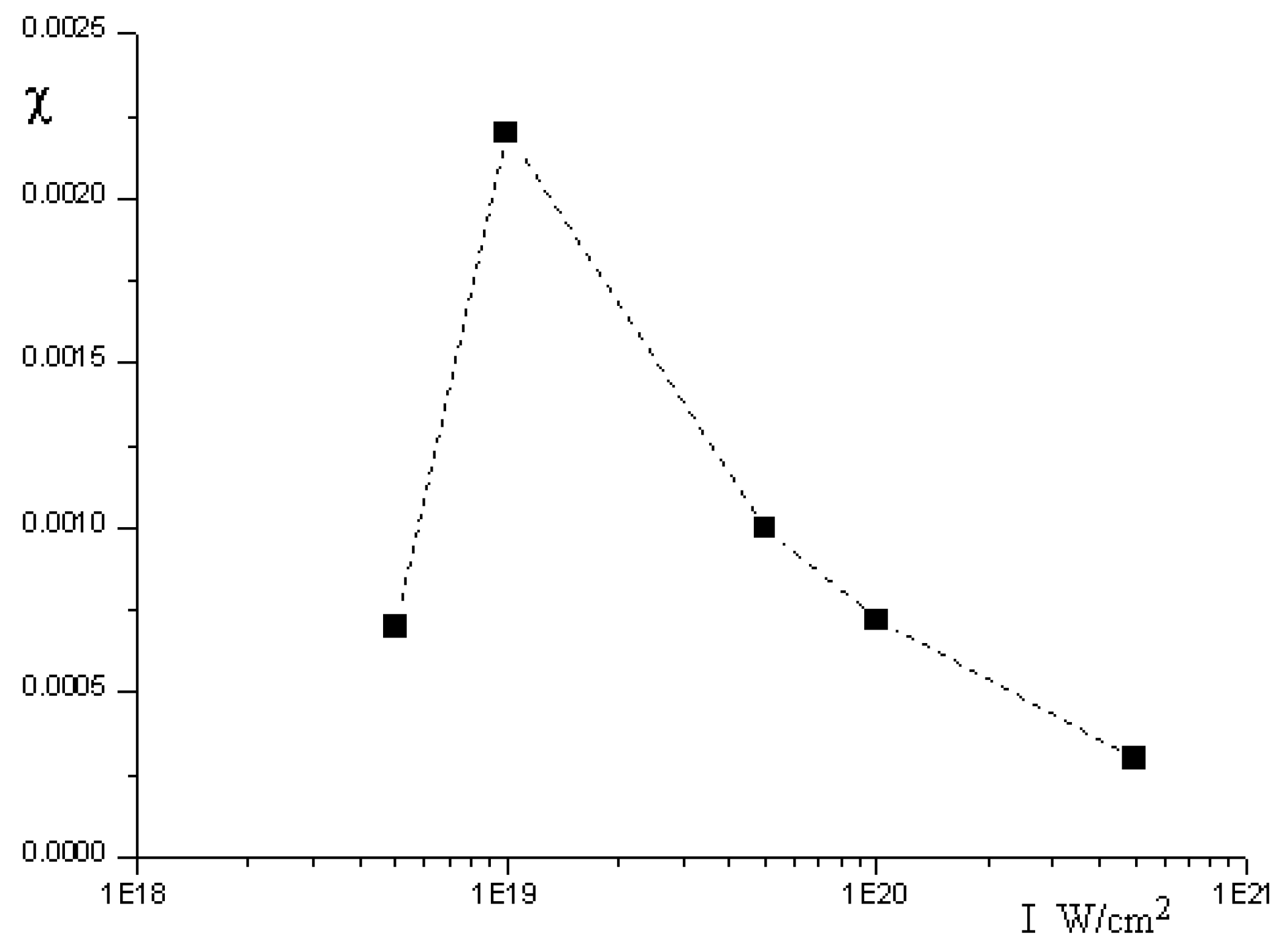
, then the coherent scattering will switch to the non-coherent Thomson scattering by single electrons. In this case, it is obvious that 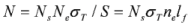 , where S is the scattering spot area, and σT = 6.6 × 10−25 cm2 is Thomson scattering cross-section. The reflection coefficient of non-coherent scattering is obviously equal to RT = σTnelf and its absolute magnitudes is substantially lower than R. The main important characteristic of the hard radiation source is its luminosity B (number of photons radiated from unit area per unit solid angle and per unit time). When the laser pulse is repeatedly irradiated with the frequency f (for the considered laser tens of Hz) the average flow (number of quanta per unit time) of the hard radiation will be Φ = fRNs. The average luminosity B of forward in the layer movement direction radiation is related to the flow Ф through the following relation:
, where S is the scattering spot area, and σT = 6.6 × 10−25 cm2 is Thomson scattering cross-section. The reflection coefficient of non-coherent scattering is obviously equal to RT = σTnelf and its absolute magnitudes is substantially lower than R. The main important characteristic of the hard radiation source is its luminosity B (number of photons radiated from unit area per unit solid angle and per unit time). When the laser pulse is repeatedly irradiated with the frequency f (for the considered laser tens of Hz) the average flow (number of quanta per unit time) of the hard radiation will be Φ = fRNs. The average luminosity B of forward in the layer movement direction radiation is related to the flow Ф through the following relation:
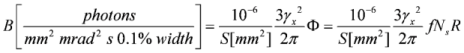
4. Conclusions
Acknowledgment
Conflict of Interest
References
- Bulanov, S.; Esirkepov, T.; Tajima, T. Light Intensification towards the Schwinger Limit. Phys. Rev. Lett. 2003, 91, 085001–085004. [Google Scholar]
- Pirozhkov, A.S.; Kando, J.; Ma, M.; Esirkepov, T.Z.; Fukuda, Y.; Chen, L.-M.; Daito, I.; Ogura, K.; Homma, T.; Hayashi, Y.; et al. Frequency multiplication of light back-reflected from a relativistic wake wave. Phys. Plasmas 2007, 14, 123106-1–123106-22. [Google Scholar] [CrossRef]
- Naumova, N.; Nees, J.A.; Sokolov, I.V.; Hou, B.; Mourou, G.A. Relativistic Generation of Isolated Attosecond Pulses in a λ3Focal Volume. Phys. Rev. Lett. 2004, 92, 063902–063904. [Google Scholar]
- Andreev, A. Generation of Ultrashort Electron Bunches from Overdense Mass Limited Target. In Proceedings of International Conference ICONO-LAT, St.Petersburg, Russia, 30 June 2005.
- Andreev, A.; Sonobe, R.; Kawata, S.; Miyazaki, S.; Sakai, K.; Miyauchi, K.; Kikuchi, T.; Platonov, K.; Nemoto, K. Effect of a laser prepulse on fast ion generation in the interaction of ultra-short intense laser pulses with a limited-mass foil target. Plasma Phys. Control. Fusion 2006, 48, 1605–1619. [Google Scholar]
- Kulagin, V.V.; Cherepenin, V.A.; Hur, M.S.; Suk, H. Flying mirror model for interaction of a super-intense nonadiabatic laser pulse with a thin plasma layer: Dynamics of electrons in a linearly polarized external field. Phys. Plasmas 2007, 14, 113101-1–113101-10. [Google Scholar]
- Kulagin, V.V.; Cherepenin, V.A.; Hur, M.S.; Suk, H. Theoretical Investigation of Controlled Generation of a Dense Attosecond Relativistic Electron Bunch from the Interaction of an Ultrashort Laser Pulse with a Nanofilm. Phys. Rev. Lett. 2007, 99, 124801-1–124801-4. [Google Scholar]
- Kulagin, V.V.; Cherepenin, V.A.; Hur, M.S.; Gulyaev, Y.V.; Kornienko, V.N.; Pae, K.H.; Valuev, V.V.; Lee, J.; Suk, H. Characteristics of relativistic electron mirrors generated by an ultrashort non adiabatic laser pulse from a nanofilm. Phys. Rev. E 2009, 80, 016404-1–016404-12. [Google Scholar]
- Landau, L.D. The Classical Theory of Fields, 4th ed; Butterworth-Heinemann: Oxford, UK, 1975; Volume 2, pp. 91–99. [Google Scholar]
- Miyauchi, K.; Miyazaki, S.; Sakai, K.; Kawata, S.; Kong, Q.; Andreev, A.A.; Kikuchi, T. Laser electron acceleration by a plasma separator. Phys. Plasmas 2004, 11, 4878–4881. [Google Scholar] [CrossRef]
- Wu, H.-C.; Meyer-ter-Vehn, J.; Fernandez, J.; Hegelich, B.M. Uniform Laser-Driven Relativistic Electron Layer for Coherent Thomson Scattering. Phys. Rev. Lett. 2010, 104, 23481–23484. [Google Scholar]
- Kemp, A.; Ruhl, H. Multispecies ion acceleration off laser-irradiated water droplets. Phys. Plasmas 2005, 12, 033105-1–033105-10. [Google Scholar]
- Esirkepov, T.Z.; Bulanov, S.V.; Kando, M.; Pirozhkov, A.S.; Zhidkov, A.G. Boosted high-harmonics pulse from double-sided relativistic mirror. Phys. Rev. Lett. 2009, 103, 025002-1–025002-4. [Google Scholar]
- Dias, J.M.; Lopes, N.C.; Silva, L.O.; Figueira, G.; Mendonca, T. Two-dimensional collision of probe photons with relativistic ionization fronts. Phys. Rev. E 2002, 65, 036404-1–036404-5. [Google Scholar] [CrossRef]
- Andreev, A.A.; Steinke, S.; Schnuerer, M.; Henig, A.; Nickles, P.V.; Platonov, K.Y.; Sokollik, T.; Sandner, W. Hybrid ion acceleration with ultrathin composite foils irradiated by high intensity circularly-polarized laser light. Phys. Plasmas 2010, 17, 123111-1–123111-11. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Andreev, A.; Platonov, K.; Sadykova, S. Double Relativistic Electron Accelerating Mirror. Appl. Sci. 2013, 3, 94-106. https://doi.org/10.3390/app3010094
Andreev A, Platonov K, Sadykova S. Double Relativistic Electron Accelerating Mirror. Applied Sciences. 2013; 3(1):94-106. https://doi.org/10.3390/app3010094
Chicago/Turabian StyleAndreev, Alexander, Konstantin Platonov, and Saltanat Sadykova. 2013. "Double Relativistic Electron Accelerating Mirror" Applied Sciences 3, no. 1: 94-106. https://doi.org/10.3390/app3010094



