Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases
Abstract
:1. Introduction
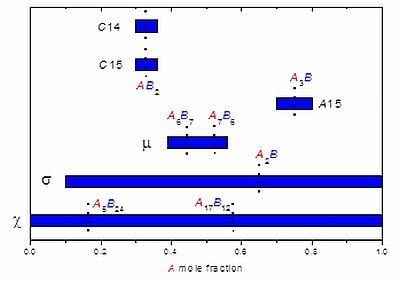
2. Generalities and Particular Features of FK Phases

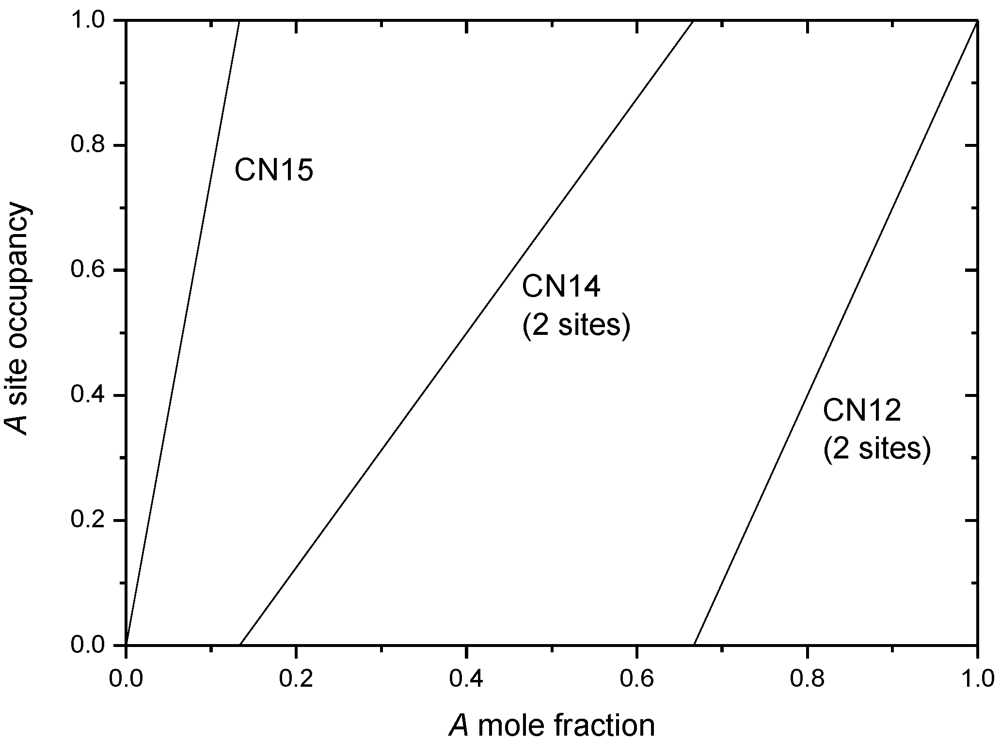
3. Studying Non-Stoichiometry Experimentally
3.1. Experimental Techniques
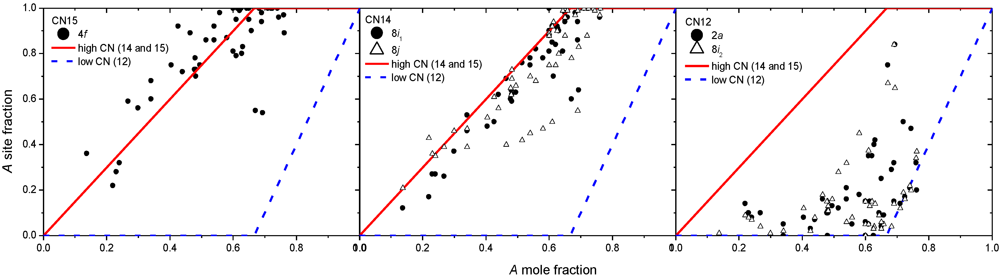
3.2. Results on Different FK Phases
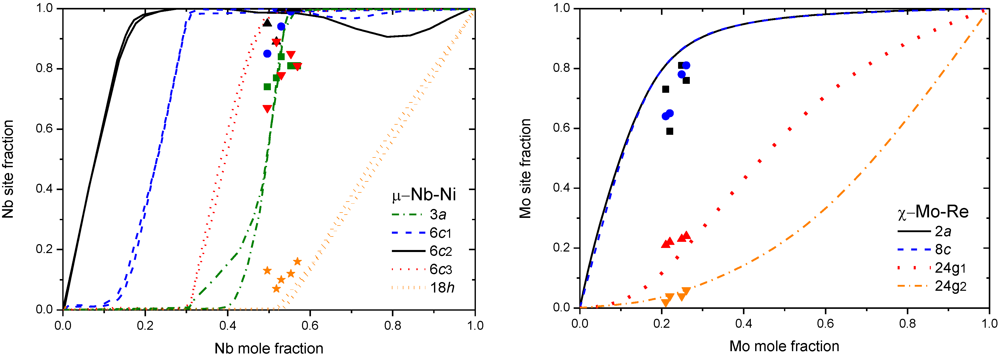
4. Non-Stoichiometry Studied by First Principle Calculations


5. Calphad Modeling of FK Phases
5.1. Basics of Calphad Modeling
5.2. Simple Models
| Phase | Site coordination and multiplicity per cell | Ideal composition(s) | Sublattice model |
|---|---|---|---|
| A15 | (CN14)6(CN12)2 | A3B | (A,B)3(A,B) |
| C15 | (CN16)8(CN12)16 | AB2 | (A,B)(A,B)2 |
| C14 | (CN16)4(CN12)2(CN12)6 | AB2 | (A,B)(A,B)2 or |
| (A,B)(A,B)0.5(A,B)1.5 | |||
| µ | (CN16)6(CN15)6(CN14)6(CN12)3(CN12)18 | A6B7 or A7B6 | (A)12(A,B)6(A,B)3(A,B)18 |
| σ | (CN15)4(CN14)8(CN14)8(CN12)8(CN12)2 | A2B | (A,B)2(A,B) |
| χ | (CN16)2(CN16)8(CN13)24(CN12)24 | A5B24 or A17B12 | (A,B)5(A,B)12(A,B)12 |
5.3. More Complex Models
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Fleischer, R.L. Miscellaneous novel intermetallics. In Intermetallic Compounds; Westbrook, J.H., Fleischer, R.L., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1994; Volume 2, pp. 237–256. [Google Scholar]
- Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. I. Definitions and basic principles. Acta Crystallogr. 1958, 11, 184–190. [Google Scholar] [CrossRef]
- Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures. Acta Crystallogr. 1959, 12, 483–499. [Google Scholar] [CrossRef]
- Sinha, A.K. Topologically close-packed structures of transition metal alloys. Prog. Mater. Sci. 1972, 15, 79–185. [Google Scholar]
- Cortella, L.; Vinet, B.; Desré, P.J.; Pasturel, A.; Paxton, A.T.; van Schilfgaarde, M. Evidences of transitory metastable phases in refractory metals solidified from highly undercooled liquids in a drop tube. Phys. Rev. Lett. 1993, 70, 1469–1472. [Google Scholar] [CrossRef]
- Moseley, P.T.; Seabrook, C.J. The crystal structure of β-tantalum. Acta Crystallogr. 1973, B29, 1170–1171. [Google Scholar]
- Kasper, J.S. Atomic and Magnetic Ordering in Transition Metal Structures. In Proceedings of the Theory of Alloy PhasesNational Metal Congress and Exposition, Philadelphia, PA, USA, 15–21 October 1955; American Society for Metals: Materials Park, OH, USA, 1956; pp. 264–278. [Google Scholar]
- Kasper, J.S.; Waterstrat, R.M. Ordering of atoms in the σ phase. Acta Crystallogr. 1956, 9, 289–295. [Google Scholar] [CrossRef]
- Van der Kraan, A.M.; de Mooij, D.B.; Buschow, K.H.J. Magnetic properties and 57Fe Mössbauer effect in V1-xFex alloys. Phys. Status Solidi (a) 1985, 88, 231–237. [Google Scholar] [CrossRef]
- Cieslak, J.; Reissner, M.; Steiner, W.; Dubiel, S.M. Magnetic moments and Curie temperatures of σ-FeCr alloys. J. Magn. Magn. Mater. 2004, 272–276, 534–535. [Google Scholar] [CrossRef]
- Cieslak, J.; Costa, B.F.O.; Dubiel, S.M.; Reissner, M.; Steiner, W. Magnetic ordering above room temperature in the sigma-phase of Fe66V34. J. Magn. Magn. Mater. 2009, 321, 2160–2165. [Google Scholar] [CrossRef]
- Vilar, R.; Cizeron, G. Evolutions structurales développées au sein de la phase σ Fe-Cr. Acta Metall. 1987, 35, 1229–1236. [Google Scholar] [CrossRef]
- Petrov, Y.I.; Shafranovsky, E.A.; Krupyanskii, Y.F.; Essine, S.V. Structure and Mössbauer spectra for the Fe-Cr system: From bulk alloy to nanoparticules. J. Appl. Phys. 2002, 91, 352–361. [Google Scholar]
- Cieslak, J.; Reissner, M.; Steiner, W.; Dubiel, S.M. Site occupation and local hyperfine fields in σ Fe-Cr alloys. J. Magn. Magn. Mater. 2007, 310, e613–e615. [Google Scholar] [CrossRef]
- Dubiel, S.M.; Tozoni, J.R.; Cieslak, J.; Braz, D.C.; Vidoto, E.L.G.; Bonagamba, T.J. Sublattice magnetism in σ-phase Fe100-xVx (x = 34.4, 39.9, and 47.9) studied via zero-field 51V NMR. Phys. Rev. 2010, B81, 184407:1–184407:5. [Google Scholar]
- Joubert, J.-M. Contribution of the Rietveld method to non-stoichiometric phase modeling. Part I: Generalities. Calphad 2002, 26, 419–425. [Google Scholar] [CrossRef]
- Joubert, J.-M.; Feutelais, Y. Contribution of the Rietveld method to non-stoichiometric phase modeling. Part II: Experimental examples. Calphad 2002, 26, 427–438. [Google Scholar] [CrossRef]
- Joubert, J.-M.; Cerný, R.; Emerich, H. Mixed site occupancies in µ-Zr-Nb-Al by resonant powder diffraction. Z. Krist. Suppl. 2007, 26, 311–316. [Google Scholar]
- Tobola, J.; François, M.; Elkaim, E.; Joubert, J.-M.; Vilasi, M. Resonant X-ray diffraction study and electronic structure calculations of three Mo-Ru-Si ternary phases. Intermetallics 2009, 18, 781–790. [Google Scholar]
- Yaqoob, K.; Crivello, J.-C.; Joubert, J.-M. Comparison of the site occupancies determined by combined Rietveld refinement and by DFT calculations: The example of the ternary Mo-Ni-Re σ phase. Inorg. Chem. 2012, 51, 3071–3078. [Google Scholar] [CrossRef]
- Joubert, J.-M.; Dupin, N. Mixed site occupancies in the μ phase. Intermetallics 2004, 12, 1373–1380. [Google Scholar] [CrossRef]
- Joubert, J.-M. Crystal chemistry and Calphad modelling of the σ phase. Prog. Mater. Sci. 2008, 53, 528–583. [Google Scholar] [CrossRef]
- Joubert, J.-M.; Phejar, M. The crystal chemistry of the χ phase. Prog. Mater. Sci. 2009, 54, 945–980. [Google Scholar] [CrossRef]
- Turchi, P.E.A.; Finel, A. Ordering phenomena in A15-based alloys. Phys. Rev. B 1992, 46, 702–725. [Google Scholar]
- Ducastelle, F.; Gautier, F. Generalized perturbation theory in disordered transitional alloys: Applications to the calculation of ordering energies. J. Phys. F Metal Phys. 1976, 6, 2039–2062. [Google Scholar] [CrossRef]
- Kikuchi, R. A theory of cooperative phenomena. Phys. Rev. 1951, 81, 988–1003. [Google Scholar] [CrossRef]
- Sanchez, J.; Ducastelle, F.; Gratias, D. Generalized cluster description of multicomponent systems. Physica 1984, A128, 334–350. [Google Scholar]
- Sluiter, M.H.F.; Esfarjani, K.; Kawazoe, Y. Site occupation reversal in the Fe-Cr σ·phase. Phys. Rev. Lett. 1995, 75, 3142–3146. [Google Scholar] [CrossRef]
- Berne, C.; Sluiter, M.; Kawazoe, Y.; Hansen, T.; Pasturel, A. Site occupancies in the Re-W sigma phase. Phys. Rev. B 2001, 64, 144103:1–144103:8. [Google Scholar]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. 1975, B12, 3060–3083. [Google Scholar]
- Connolly, J.W.D.; Williams, A.R. Density-functional theory applied to phase transformations in transition-metal alloys. Phys. Rev. 1983, B27, 5169–5172. [Google Scholar]
- Fries, S.G.; Sundman, B. Using Re-W sigma phase first-principles results in the Bragg-Williams approximation. Phys. Rev. B 2002, 66, 012203:1–012203:4. [Google Scholar]
- Bragg, W.L.; Williams, E.J. The effect of thermal agitation on atomic arrangement in alloys. Proc. R. Soc. (London) 1934, A145, 699–730. [Google Scholar]
- Ansara, I.; Dupin, N.; Sundman, B. Reply to the paper: “When is a compound energy not a compound energy? A critique of the 2-sublattice order/disorder model” of Nigel Saunders, Calphad 20 (1996) 491-499. Calphad 1997, 21, 535–542. [Google Scholar] [CrossRef]
- Dupin, N.; Fries, S.G.; Joubert, J.-M.; Sundman, B.; Sluiter, M.; Kawazoe, Y.; Pasturel, A. Using Nb-Ni μ phase first principles results in the Bragg-Williams approximation to calculate finite temperature thermodynamic properties. Philos. Mag. 2006, 86, 1631–1641. [Google Scholar] [CrossRef]
- Crivello, J.-C.; Joubert, J.-M. First principles calculations of the σ and χ phases in the Mo-Re and W-Re systems. J. Phys. Condens. Matter 2010, 22, 035402. [Google Scholar] [CrossRef]
- Farzadfar, S.-A.; Levesque, M.; Phejar, M.; Joubert, J.-M. Thermodynamic assessment of the Molybdenum-Rhenium System. Calphad Comput. Coupling Phase Diagr. Thermochem. 2009, 33, 502–510. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Sundman, B.; Selleby, M.; Johansson, B. Atomic, electronic, and magnetic structure of iron-based sigma-phases. Mater. Res. Soc. Symp. Proc. 2005, 842, 517–522. [Google Scholar]
- Pavlu, J.; Vrestal, J.; Sob, M. Ab initio study of formation energy and magnetism of sigma phase in Cr-Fe and Cr-Co systems. Intermetallics 2010, 18, 212–220. [Google Scholar] [CrossRef]
- Singh, D.J.; Nordström, L. Planewaves, Pseudopotentials and the LAPW Method; Springer: Berlin, Germany, 2006. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Cieslak, J.; Tobola, J.; Dubiel, S.M.; Sikora, W. Magnetic properties of σ-FeCr alloys as calculated with the charge- and spin-self-consistent KKR(CPA) method. Phys. Rev. 2010, B82, 224407:1–224407:9. [Google Scholar]
- Kabliman, E.; Blaha, P.; Schwarz, K.; Ruban, A.V.; Johansson, B. Ab initio-based mean-field theory of the site occupation in the Fe-Cr σ-phase. Phys. Rev. 2011, B83, 092201:1–092201:4. [Google Scholar]
- Yakel, H.L. Atom distribution in sigma phases. I. Fe and Cr atom distribution in a binary sigma phase equilibrated at 1063, 1013 and 923 K. Acta Crystallogr. 1983, B39, 20–28. [Google Scholar]
- Crivello, J.-C.; Palumbo, M.; Abe, T.; Joubert, J.-M. Ab initio ternary s-phase diagram: The Cr-Mo-Re system. Calphad Comput. Coupling Phase Diagr. Thermochem. 2010, 34, 487–494. [Google Scholar]
- Palumbo, M.; Abe, T.; Fries, S.G.; Pasturel, A. First-principles approach to phase stability for a ternary σ phase: Application to Cr-Ni-Re. Phys. Rev. 2011, B83, 144109:1–144109:7. [Google Scholar]
- Parlinski, K.; Li, Z.Q.; Kawazoe, Y. First-principles determination of the soft mode in cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063–4066. [Google Scholar] [CrossRef]
- Dubiel, S.M.; Cieslak, J.; Sturhahn, W.; Sternik, M.; Piekarz, P.; Stankov, S.; Parlinski, K. Vibrational properties of α- and σ-phase Fe-Cr alloy. Phys. Rev. Lett. 2010, 104, 155503:1–15503:4. [Google Scholar]
- Sundman, B.; Ågren, J. A regular solution model for phases with several components and sublattices, suitable for computer applications. J. Phys. Chem. Solids 1981, 42, 297–301. [Google Scholar] [CrossRef]
- Ferro, R.; Cacciamani, G. Remarks on crystallochemical aspects in thermodynamic modelling. Calphad 2002, 26, 439–458. [Google Scholar] [CrossRef]
- Du, Y.; Liu, S.; Chang, Y.A.; Yang, Y. A thermodynamic modeling of the Cr-Nb-Ni system. Comput. Coupling Phase Diagr. Thermochem. 2005, 29, 140–148. [Google Scholar] [CrossRef]
- De Keyzer, J.; Cacciamani, G.; Dupin, N.; Wollants, P. Thermodynamic modelling and optimization of the Fe-Ni-Ti system. Calphad Comput. Coupling Phase Diagr. Thermochem. 2009, 33, 109–123. [Google Scholar] [CrossRef]
- Frisk, K. A thermodynamic evaluation of the Mo-Ni system. Calphad 1990, 14, 311–320. [Google Scholar] [CrossRef]
- Zhou, S.H.; Wang, Y.; Jiang, C.; Zhu, J.Z.; Chen, L.-Q.; Liu, Z.-K. First-principles calculations and thermodynamic modeling of the Ni-Mo system. Mater. Sci. Eng. A 2005, 397, 288–296. [Google Scholar] [CrossRef]
- Bolcavage, A.; Kattner, U.R. A reassessment of the calculated Ni-Nb phase diagram. J. Phase Equilibria 1996, 17, 92–100. [Google Scholar] [CrossRef]
- Davydov, A.; Kattner, U.R. Thermodynamic assessment of the Co-Mo system. J. Phase Equilibria 1999, 20, 5–16. [Google Scholar] [CrossRef]
- Joubert, J.-M.; Sundman, B.; Dupin, N. Assessment of the niobium-nickel system. Comput. Coupling Phase Diagr. Thermochem. 2004, 28, 299–306. [Google Scholar] [CrossRef]
- Xiong, W.; Hedström, P.; Selleby, M.; Odqvist, J.; Thuvander, M.; Chen, Q. An improved thermodynamic modeling of the Fe-Cr system down to zero kelvin coupled with key experiments. Calphad Comput. Coupling Phase Diagr. Thermochem. 2011, 35, 355–366. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Joubert, J.-M.; Crivello, J.-C. Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases. Appl. Sci. 2012, 2, 669-681. https://doi.org/10.3390/app2030669
Joubert J-M, Crivello J-C. Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases. Applied Sciences. 2012; 2(3):669-681. https://doi.org/10.3390/app2030669
Chicago/Turabian StyleJoubert, Jean-Marc, and Jean-Claude Crivello. 2012. "Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases" Applied Sciences 2, no. 3: 669-681. https://doi.org/10.3390/app2030669