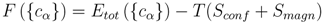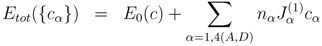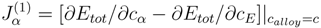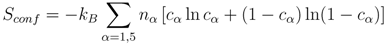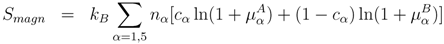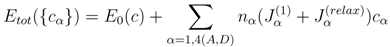1. Introduction
In 1923 the
σ-phase was first observed by Bain as a hard non-magnetic intermediate phase which was formed during a long-time high-temperature annealing in the Fe-Cr alloy with a nearly equiatomic composition. Being extremely brittle, the
σ-phase substantially degrades the mechanical properties of different types of alloys, mainly stainless steels, Fe-and Ni-based superalloys. The precipitation of this phase decreases ductility and corrosion resistance, while it increases brittleness and promotes the formation of cracks leading to high temperature failure, metal dusting and loss of toughness during heat treatment or welding [
1].
The
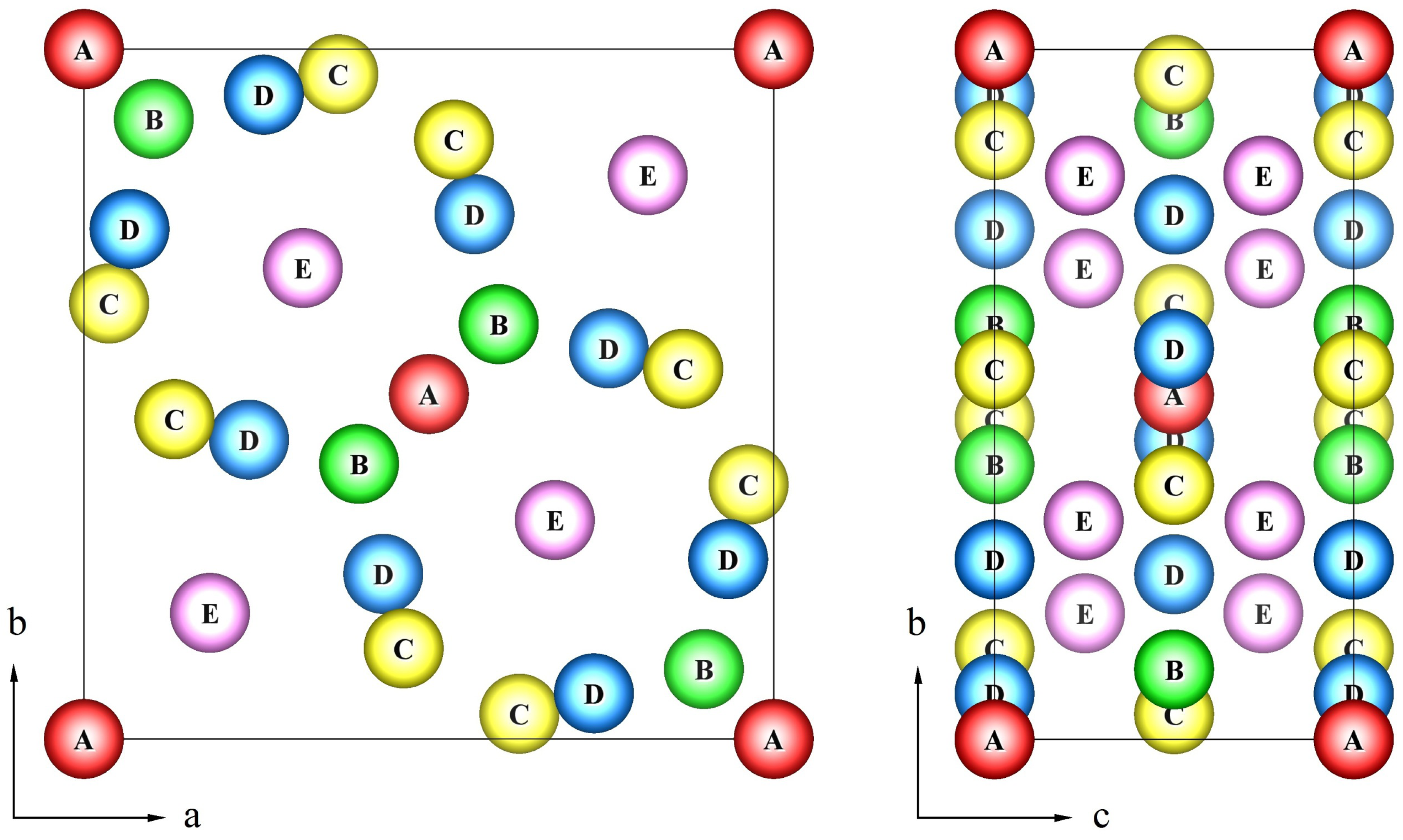
σ-phase has a topologically closed packed structure, which is defined by a tetragonal unit cell (space group
P 4
2/
mnm) containing 30 atoms. These atoms are located in five nonequivalent groups of sites or sublattices (A, B, C, D, E) [
2,
3]. One often uses the following formula
A212B415C814D812E814 to describe the
σ-phase structure, where bottom and top indices denote the site multiplicities and coordination numbers for each sublattice, respectively. The crystal structure of the
σ-phase can be determined as a stacking of the kagomé tiles with the A(0,0,0), B(
x,
x,0), C(
x,
y,0) and D(
x,
y,0) atoms lying in the tile plane and the E(
x,
x,
z) atoms placed between the pseudo-hexagonal rings of kagomé tile [
3] as shown in
Figure 1.
Figure 1.
The tetragonal unit cell of the σ-phase structure with 5 crystallographically inequivalent sites (A, B, C, D, E).
Figure 1.
The tetragonal unit cell of the σ-phase structure with 5 crystallographically inequivalent sites (A, B, C, D, E).
It is known that the nonequivalent
σ-phase sites are partially occupied by all the alloy components, but with certain preferences. Already in 1955 using neutron and X-ray diffraction studies in Fe-V, Ni-V and Mn-Cr alloys Kasper and Waterstrat suggested a general scheme for the ordering in binary
σ-phases of first row transition metal elements and those containing Mo [
4]. They found that the highly coordinated B sites are predominately occupied by the elements to the left of Mn in the periodic table (V, Cr, Mo), whereas the A and D sublattice with an icosahedral environment are almost exclusively occupied by elements to the right of manganese (Fe, Co, Ni). In contrast, the C and E sites are partially occupied by both components and the proportions depend on the alloy composition and external conditions. Although some preferences in the site occupation could be estimated for some binary
σ-phases, the knowledge of the atomic site distribution in a wide temperature and composition range is still missing. Such information is useful for studying the
σ-phase stability and its precipitation. However, it is quite hard to obtain these data experimentally due to sluggish kinetics of the transformation, difficulties in getting high purity samples and satisfying some other technological requirements.
In this context, an accurate theoretical study based on state-of-the-art first-principles methods combined with a proper statistical model can be used in order to determine the site preferences of the alloy components in the
σ-phase. Recently the site occupation in the
σ-phase has been widely studied by such methods [
5,
6,
7,
8,
9,
10,
11,
12,
13]. However, most of these methods were based on a formalism, which is quite computationally demanding. Alternatively, we have recently proposed a simpler approach to calculate the site preference in the binary
σ-phases [
14,
15,
16]. It is based on a simple single-site mean-field model, which recently has demonstrated to be able to produce quite accurate results for the site occupancy of Fe and Cr in the Fe-Cr
σ-phase. In this paper we briefly describe this method and apply it to study the distribution of alloy components in other binary
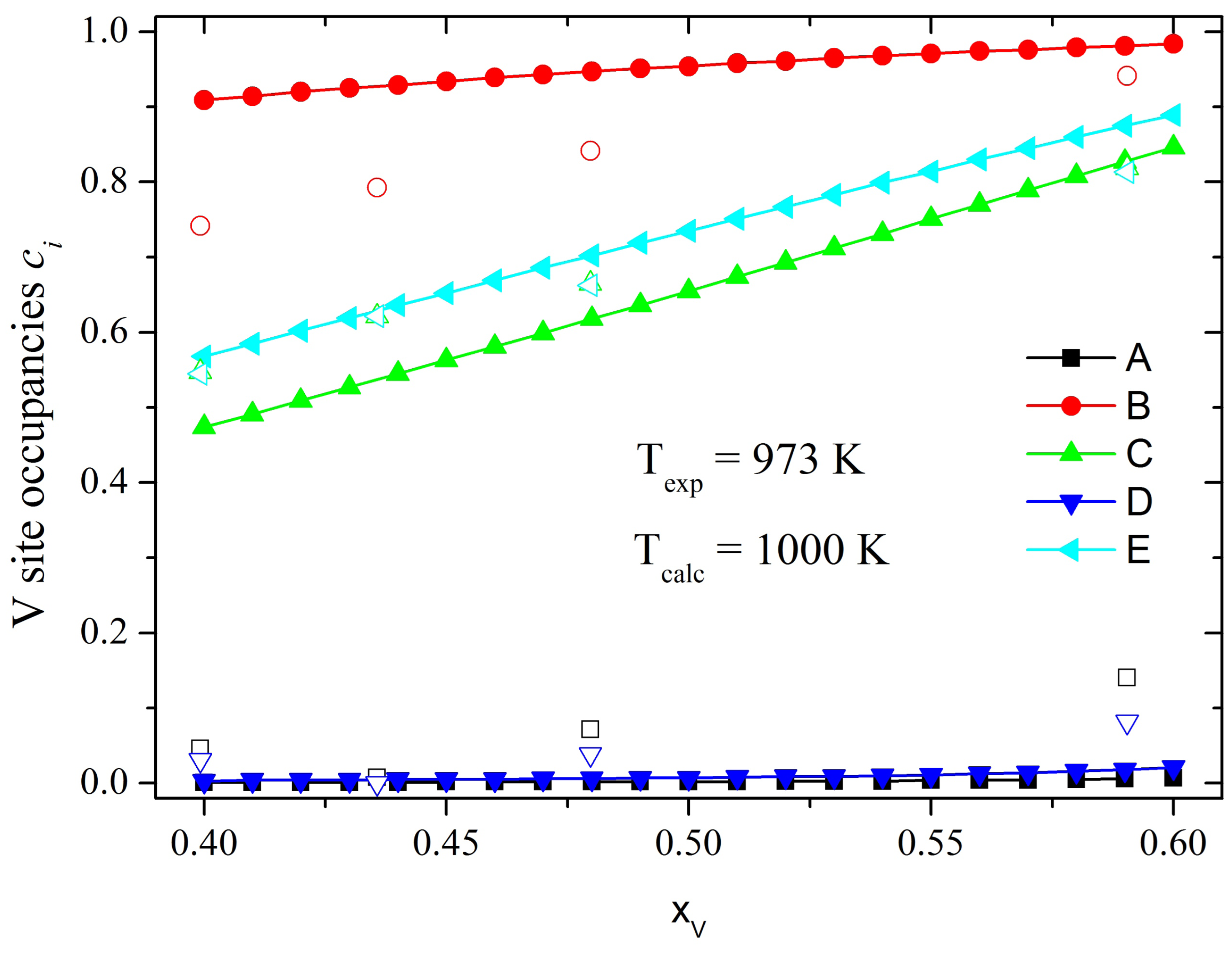
σ-phase, namely, Co-Cr, Re-W and Fe-V, for which experimental and theoretical information is available.
2. Single-Site Model for the Free Energy
In order to find the atomic occupancies of the
σ-phase sublattices, we minimize the Helmholtz free energy
F , which can be written in the following form for a given composition and temperature [
14,
15,
16]:
Here
Etot({
cα}) is the total energy of the
σ-phase,
cα the concentration of the reference component (e.g., Cr in the Fe-Cr alloy), and
α is the A, B, C, D, or E site. We assume here that the alloy components are distributed randomly on each site and there is no mutual correlation between them on different sublattices. As has been demonstrated in [
16], this is a valid approximation at high temperatures at least in the case of the Fe-Cr
σ-phase. Thus, the total energy (per unit cell),
Etot({
cα}), can be written in a simplified form as
where nα is the number of sites at sublattice α, and Jα(1) are the on-site interaction parameters, defined as
They are in fact the effective chemical potentials at 0 K, and determine the preference of the alloy components to occupy site
α relative to that of sublattice E. In general, the pair and higher order interaction parameters could also be taken into account. However, as we have shown in [
16], the on-site interaction parameters are dominant in the total energy expansion. The summation in Equation (3) runs only over four sublattices, since the occupation at the fifth sublattice is determined by the alloy composition
c and the concentrations at the other four sublattices
cα.
E0(
c) is the total energy of a homogeneous random alloy (
cα =
c) and
Jα(1) are the on-site interaction parameters.
The second term in Equation (1) contains the configurational and magnetic entropy correspondingly given by:
and
Here µα are the local magnetic moments of the alloy components (A, B) in the A-B σ-phase, which are found by minimizing the corresponding magnetic free energy in the first-principles calculations at a given temperature.
Although the
σ-phase forms at high temperatures in the paramagnetic state, the local magnetic moments do not disappear on the Fe atoms, as has been shown by Korzhavyi
et al. [
7] for the FeCr
σ-phase, and they significantly contribute to the energetics of the
σ-phase. Furthermore, as has already been discussed in our previous works [
14,
16], longitudinal spin fluctuations should exist at high temperature. These are thermal Stoner-like many-body excitations which lead to fluctuations of the magnitude of the local magnetic moments. In order to calculate these high temperature magnetic excitations we adopt a simple model [
17], which implies that longitudinal spin fluctuations (LSF) contribute to the magnetic entropy of the paramagnetic state. The LSFs induce modified spin magnetic moments on the alloy components, while for instance the Cr atoms would have zero magnetic moments in the disordered local moment (DLM) state.
In present work we assume that the lattice vibrations do not play a decisive role in the distribution of the alloy components between the sublattices and therefore neglect their contribution in Equation (1). Furthermore, since the σ-phase forms at relatively high temperatures and there is no experimental evidence of being close to any kind of phase transition (ordering or magnetic), we also neglect contributions from short-range order effects in the configurational part.
3. First-Principles Calculations
The total energies of random alloys and the on-site interaction parameters in Equation (3) have been obtained by the exact muffin-tin orbital (EMTO) method using the full charge density formalism (FCD) [
18,
19]. The EMTO method is considered as an improved screened Korringa–Kohn–Rostoker method, which implies large overlapping potential spheres for a sufficiently accurate description of the exact single-electron potential, while the FCD method was devised to perform with high efficiency as well as with an accuracy close to full potential total energy methods [
20]. In the present work the exchange-correlation functional was evaluated within the generalized gradient approximation [
21].
The electronic structure of the random alloy in the
σ-phase has been calculated using the coherent potential approximation (CPA) [
22]. We have demonstrated in [
16] that the density of states and the average magnetic moments are well reproduced by the CPA. The screened Coulomb interactions have been chosen to be
αscr = 0.67 and
βscr = 1.05 for all the
σ-phase sublattices. These values are approximate, but the corresponding supercell calculations, which would be needed to evaluate all screening constants, are impractical.
Local Lattice Relaxations
In our previous calculations for the FeCr
σ-phase, we have neglected the effect of local atomic relaxations. As has been shown in [
14], the contribution from local lattice relaxations to the formation enthalpy is about 2.5 mRy / 30 at. cell in the FeCr case, which was expected due to small size mismatch of Fe and Cr. In case of the CoCr, ReW and FeV
σ-phases we show in
Table 1 the results for the energy of local lattice relaxations
Erelax, which have been obtained for the room temperature values of an unit cell volume
V and a ratio of the lattice cell constants
c/a by the full-potential linearized augmented plane wave method [
23], implemented in the WIEN2k code [
24]. Obviously,
Erelax is small in the case of the CoCr and ReW
σ-phases, but not negligible in the case of the FeV
σ-phase.
Table 1.
The room temperature lattice parameters (V, c/a), the corresponding size (atomic radii) mismatch of the alloy components ΔAR and the energy of the local atomic relaxations Erelax in the Re0.5W0.5, Co0.5Cr0.5 and Fe0.5V0.5 σ-phases.
Table 1.
The room temperature lattice parameters (V, c/a), the corresponding size (atomic radii) mismatch of the alloy components ΔAR and the energy of the local atomic relaxations Erelax in the Re0.5W0.5, Co0.5Cr0.5 and Fe0.5V0.5 σ-phases.
| System | Volume | c/α | ΔAR | Erelax |
|---|
| Re0.5W0.5 | 0.46482 nm3 a | 0.521 a | 0.002 nm | 5 mRy/30 at. cell |
| Co0.5Cr0.5 | 0.35235 nm3 b | 0.517 b | 0.003 nm | 6 mRy/30 at. cell |
| Fe0.5V0.5 | 0.37074 nm3 c | 0.517 c | 0.008 nm | 30 mRy/30 at. cell |
In order to account for the effects of the lattice relaxations in the Fe-V system, we introduce in our model an additional term, called Jα(relax) , such that the total energy has the following form:
These Jα(relax) parameters can be interpreted as the energy gain due to the atomic relaxations with respect to substitution of one Fe atom by one V atom in each sublattice α. To calculate these energies we use the WIEN2k code and simulate a cell of 30 atoms, in which we exchange one Fe atom from each of the A, B, C and D sublattices with one V atom from the E sublattice. Thus the relaxation parameter is defined as Jα(relax) = Eα(relax) – EE(relax), where Eα(relax) is the energy of relaxation of α = A, B, C and D site with respect to substitution of one Fe atom and EE(relax)is the energy of relaxation of the E site with respect to substitution of one V atom.