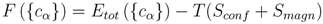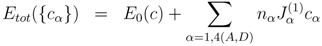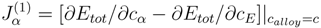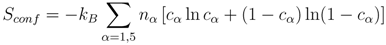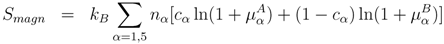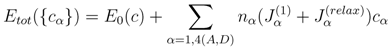Ab Initio Study of Lattice Site Occupancies in Binary Sigma Phases Using a Single-Site Mean Field Model

Abstract

The site occupation of binary Fe-Cr, Co-Cr, Re-W and Fe-V sigma phases is studied in the present work with a first-principles-based single-site mean field theory. We show that the alloy components in these systems exhibit similar site preferences except for the Re-W system, where the occupation of two sites is reversed in agreement with previously published works. In case of the FeV sigma phase, for which the size mismatch between the alloy components is large, we also include into our consideration the effect of local lattice relaxations. The obtained results are found in good agreement with the experimental data and previous theoretical studies.

1. Introduction

In 1923 the σ-phase was first observed by Bain as a hard non-magnetic intermediate phase which was formed during a long-time high-temperature annealing in the Fe-Cr alloy with a nearly equiatomic composition. Being extremely brittle, the σ-phase substantially degrades the mechanical properties of different types of alloys, mainly stainless steels, Fe-and Ni-based superalloys. The precipitation of this phase decreases ductility and corrosion resistance, while it increases brittleness and promotes the formation of cracks leading to high temperature failure, metal dusting and loss of toughness during heat treatment or welding [1].

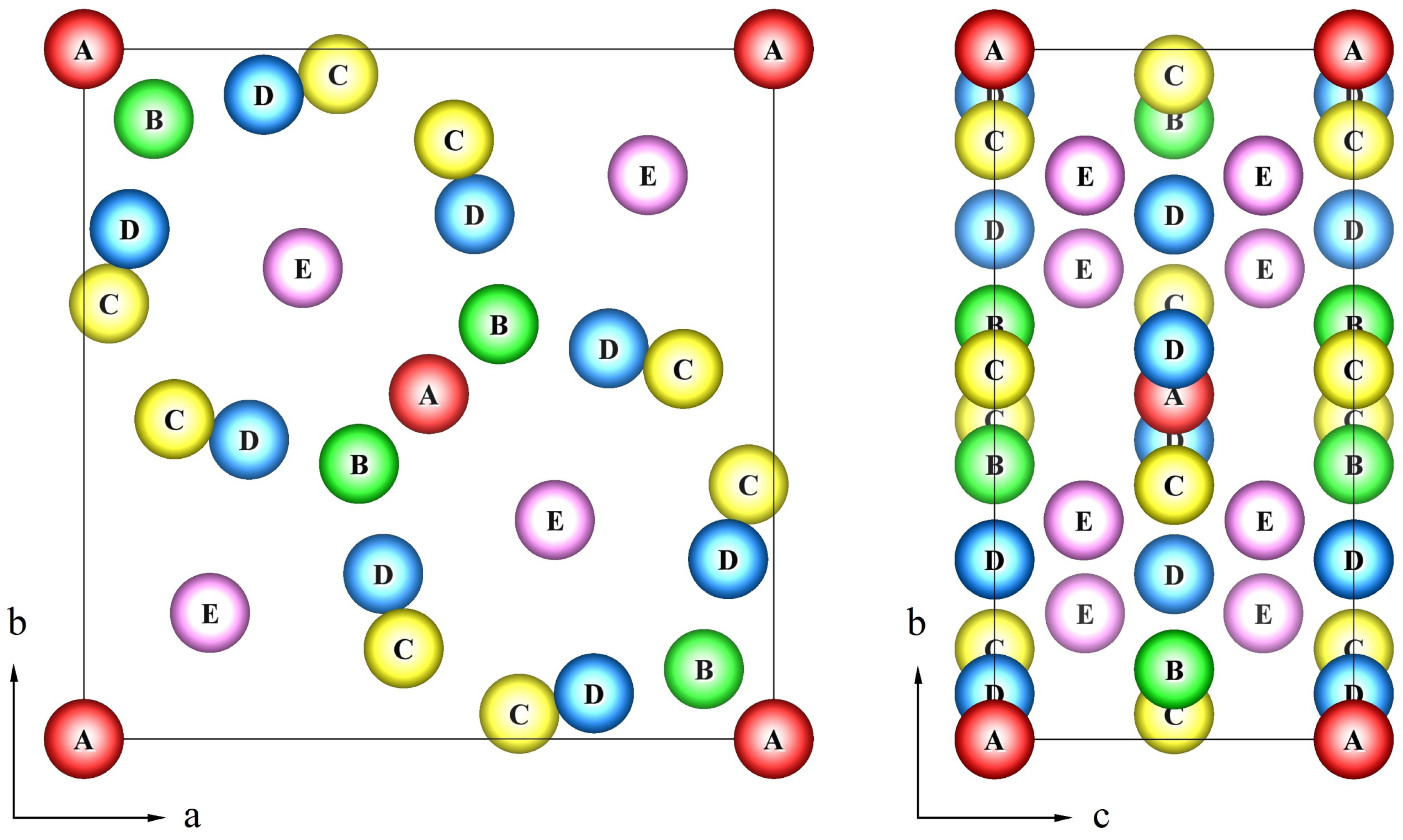
The σ-phase has a topologically closed packed structure, which is defined by a tetragonal unit cell (space group P 4₂/mnm) containing 30 atoms. These atoms are located in five nonequivalent groups of sites or sublattices (A, B, C, D, E) [2,3]. One often uses the following formula A₂¹²B₄¹⁵C₈¹⁴D₈¹²E₈¹⁴ to describe the σ-phase structure, where bottom and top indices denote the site multiplicities and coordination numbers for each sublattice, respectively. The crystal structure of the σ-phase can be determined as a stacking of the kagomé tiles with the A(0,0,0), B(x, x,0), C(x, y,0) and D(x, y,0) atoms lying in the tile plane and the E(x, x, z) atoms placed between the pseudo-hexagonal rings of kagomé tile [3] as shown in Figure 1.

Figure 1. The tetragonal unit cell of the σ-phase structure with 5 crystallographically inequivalent sites (A, B, C, D, E).

Figure 1. The tetragonal unit cell of the σ-phase structure with 5 crystallographically inequivalent sites (A, B, C, D, E).

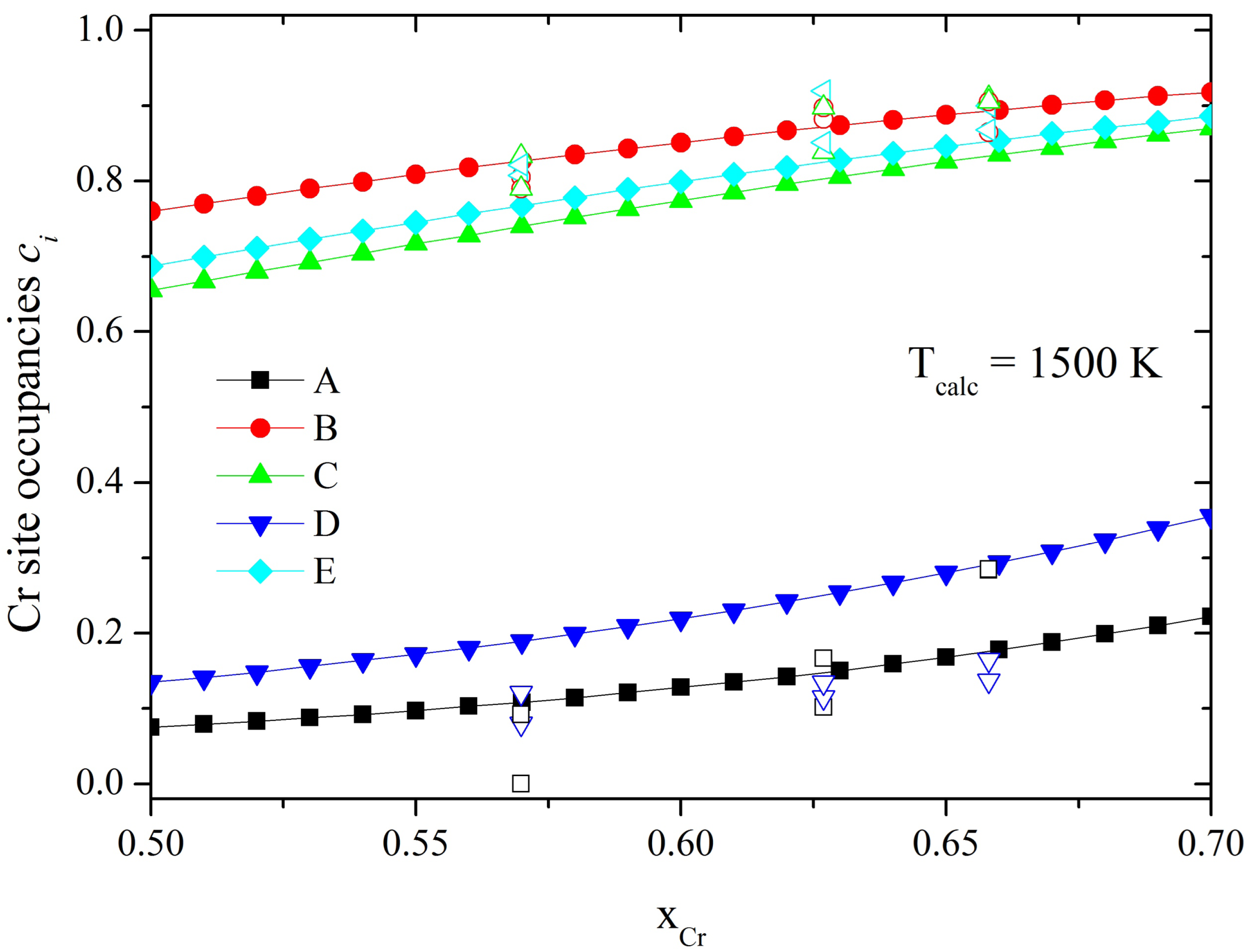
It is known that the nonequivalent σ-phase sites are partially occupied by all the alloy components, but with certain preferences. Already in 1955 using neutron and X-ray diffraction studies in Fe-V, Ni-V and Mn-Cr alloys Kasper and Waterstrat suggested a general scheme for the ordering in binary σ-phases of first row transition metal elements and those containing Mo [4]. They found that the highly coordinated B sites are predominately occupied by the elements to the left of Mn in the periodic table (V, Cr, Mo), whereas the A and D sublattice with an icosahedral environment are almost exclusively occupied by elements to the right of manganese (Fe, Co, Ni). In contrast, the C and E sites are partially occupied by both components and the proportions depend on the alloy composition and external conditions. Although some preferences in the site occupation could be estimated for some binary σ-phases, the knowledge of the atomic site distribution in a wide temperature and composition range is still missing. Such information is useful for studying the σ-phase stability and its precipitation. However, it is quite hard to obtain these data experimentally due to sluggish kinetics of the transformation, difficulties in getting high purity samples and satisfying some other technological requirements.

In this context, an accurate theoretical study based on state-of-the-art first-principles methods combined with a proper statistical model can be used in order to determine the site preferences of the alloy components in the σ-phase. Recently the site occupation in the σ-phase has been widely studied by such methods [5,6,7,8,9,10,11,12,13]. However, most of these methods were based on a formalism, which is quite computationally demanding. Alternatively, we have recently proposed a simpler approach to calculate the site preference in the binary σ-phases [14,15,16]. It is based on a simple single-site mean-field model, which recently has demonstrated to be able to produce quite accurate results for the site occupancy of Fe and Cr in the Fe-Cr σ-phase. 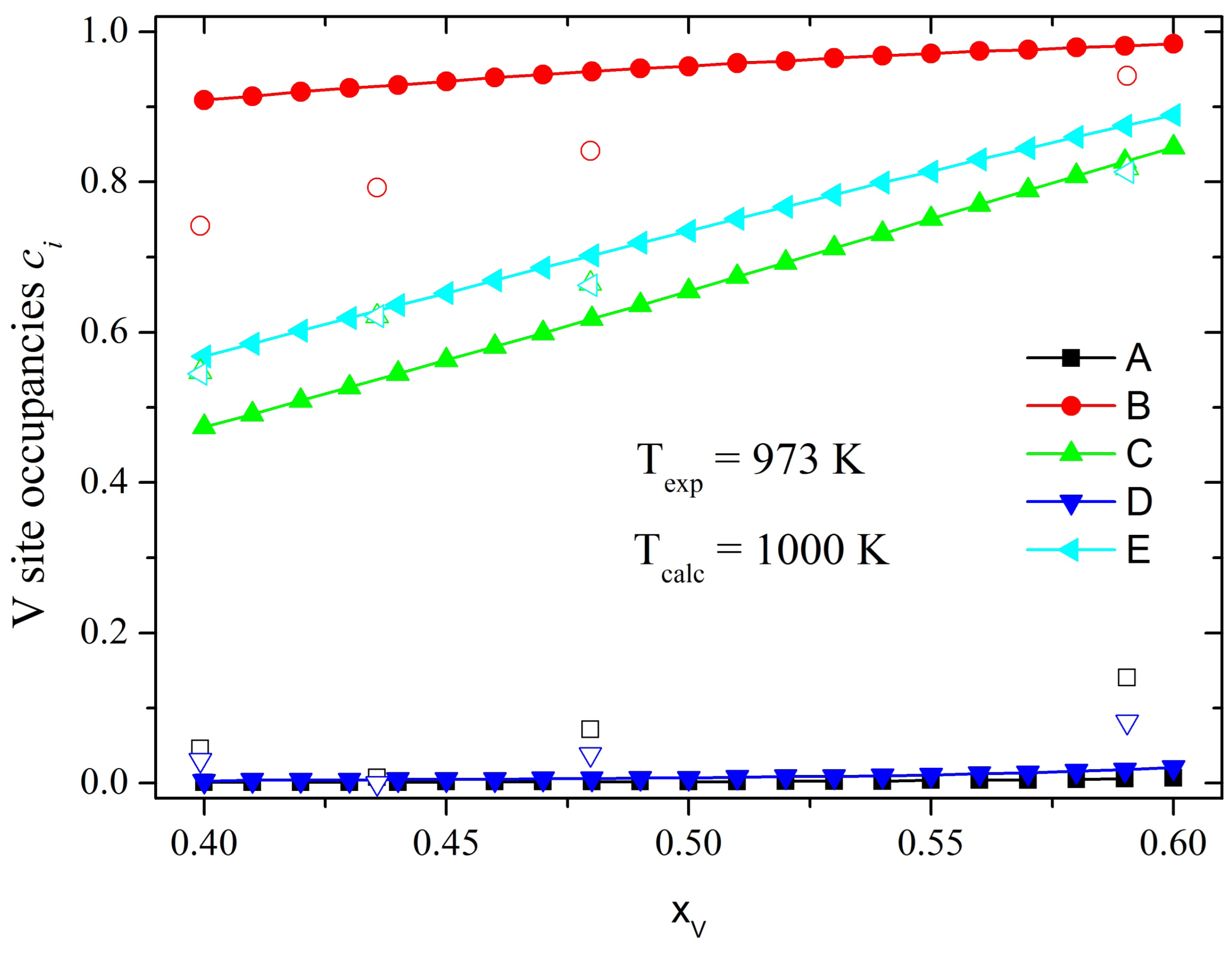In this paper we briefly describe this method and apply it to study the distribution of alloy components in other binary σ-phase, namely, Co-Cr, Re-W and Fe-V, for which experimental and theoretical information is available.

2. Single-Site Model for the Free Energy

In order to find the atomic occupancies of the σ-phase sublattices, we minimize the Helmholtz free energy F , which can be written in the following form for a given composition and temperature [14,15,16]:

(1)

Here E_tot({c_α}) is the total energy of the σ-phase, c_α the concentration of the reference component (e.g., Cr in the Fe-Cr alloy), and α is the A, B, C, D, or E site. We assume here that the alloy components are distributed randomly on each site and there is no mutual correlation between them on different sublattices. As has been demonstrated in [16], this is a valid approximation at high temperatures at least in the case of the Fe-Cr σ-phase. Thus, the total energy (per unit cell), E_tot({c_α}), can be written in a simplified form as

(2)

where n_α is the number of sites at sublattice α, and J_α⁽¹⁾ are the on-site interaction parameters, defined as

(3)

They are in fact the effective chemical potentials at 0 K, and determine the preference of the alloy components to occupy site α relative to that of sublattice E. In general, the pair and higher order interaction parameters could also be taken into account. However, as we have shown in [16], the on-site interaction parameters are dominant in the total energy expansion. The summation in Equation (3) runs only over four sublattices, since the occupation at the fifth sublattice is determined by the alloy composition c and the concentrations at the other four sublattices c_α. E0(c) is the total energy of a homogeneous random alloy (c_α = c) and J_α⁽¹⁾ are the on-site interaction parameters.

The second term in Equation (1) contains the configurational and magnetic entropy correspondingly given by:

(4)

and

(5)

Here µ_α are the local magnetic moments of the alloy components (A, B) in the A-B σ-phase, which are found by minimizing the corresponding magnetic free energy in the first-principles calculations at a given temperature.

Although the σ-phase forms at high temperatures in the paramagnetic state, the local magnetic moments do not disappear on the Fe atoms, as has been shown by Korzhavyi et al. [7] for the FeCr σ-phase, and they significantly contribute to the energetics of the σ-phase. Furthermore, as has already been discussed in our previous works [14,16], longitudinal spin fluctuations should exist at high temperature. These are thermal Stoner-like many-body excitations which lead to fluctuations of the magnitude of the local magnetic moments. In order to calculate these high temperature magnetic excitations we adopt a simple model [17], which implies that longitudinal spin fluctuations (LSF) contribute to the magnetic entropy of the paramagnetic state. The LSFs induce modified spin magnetic moments on the alloy components, while for instance the Cr atoms would have zero magnetic moments in the disordered local moment (DLM) state.

In present work we assume that the lattice vibrations do not play a decisive role in the distribution of the alloy components between the sublattices and therefore neglect their contribution in Equation (1). Furthermore, since the σ-phase forms at relatively high temperatures and there is no experimental evidence of being close to any kind of phase transition (ordering or magnetic), we also neglect contributions from short-range order effects in the configurational part.

3. First-Principles Calculations

The total energies of random alloys and the on-site interaction parameters in Equation (3) have been obtained by the exact muffin-tin orbital (EMTO) method using the full charge density formalism (FCD) [18,19]. The EMTO method is considered as an improved screened Korringa–Kohn–Rostoker method, which implies large overlapping potential spheres for a sufficiently accurate description of the exact single-electron potential, while the FCD method was devised to perform with high efficiency as well as with an accuracy close to full potential total energy methods [20]. In the present work the exchange-correlation functional was evaluated within the generalized gradient approximation [21].

The electronic structure of the random alloy in the σ-phase has been calculated using the coherent potential approximation (CPA) [22]. We have demonstrated in [16] that the density of states and the average magnetic moments are well reproduced by the CPA. The screened Coulomb interactions have been chosen to be α_scr = 0.67 and β_scr = 1.05 for all the σ-phase sublattices. These values are approximate, but the corresponding supercell calculations, which would be needed to evaluate all screening constants, are impractical.

Local Lattice Relaxations

In our previous calculations for the FeCr σ-phase, we have neglected the effect of local atomic relaxations. As has been shown in [14], the contribution from local lattice relaxations to the formation enthalpy is about 2.5 mRy / 30 at. cell in the FeCr case, which was expected due to small size mismatch of Fe and Cr. In case of the CoCr, ReW and FeV σ-phases we show in Table 1 the results for the energy of local lattice relaxations E_relax, which have been obtained for the room temperature values of an unit cell volume V and a ratio of the lattice cell constants c/a by the full-potential linearized augmented plane wave method [23], implemented in the WIEN2k code [24]. Obviously, E_relax is small in the case of the CoCr and ReW σ-phases, but not negligible in the case of the FeV σ-phase.

Table 1. The room temperature lattice parameters (V, c/a), the corresponding size (atomic radii) mismatch of the alloy components Δ_AR and the energy of the local atomic relaxations E_relax in the Re_0.5W_0.5, Co_0.5Cr_0.5 and Fe_0.5V_0.5 σ-phases.

System	Volume	c/α	ΔAR	Erelax
Re0.5W0.5	0.46482 nm3 a	0.521 a	0.002 nm	5 mRy/30 at. cell
Co0.5Cr0.5	0.35235 nm3 b	0.517 b	0.003 nm	6 mRy/30 at. cell
Fe0.5V0.5	0.37074 nm3 c	0.517 c	0.008 nm	30 mRy/30 at. cell

^a Ref. [25]; ^b Ref. [26]; ^c Ref. [27].

Table 1. The room temperature lattice parameters (V, c/a), the corresponding size (atomic radii) mismatch of the alloy components Δ_AR and the energy of the local atomic relaxations E_relax in the Re_0.5W_0.5, Co_0.5Cr_0.5 and Fe_0.5V_0.5 σ-phases.

System	Volume	c/α	ΔAR	Erelax
Re0.5W0.5	0.46482 nm3 a	0.521 a	0.002 nm	5 mRy/30 at. cell
Co0.5Cr0.5	0.35235 nm3 b	0.517 b	0.003 nm	6 mRy/30 at. cell
Fe0.5V0.5	0.37074 nm3 c	0.517 c	0.008 nm	30 mRy/30 at. cell

^a Ref. [25]; ^b Ref. [26]; ^c Ref. [27].

In order to account for the effects of the lattice relaxations in the Fe-V system, we introduce in our model an additional term, called J_α^(relax) , such that the total energy has the following form:

(6)

These J_α^(relax) parameters can be interpreted as the energy gain due to the atomic relaxations with respect to substitution of one Fe atom by one V atom in each sublattice α. To calculate these energies we use the WIEN2k code and simulate a cell of 30 atoms, in which we exchange one Fe atom from each of the A, B, C and D sublattices with one V atom from the E sublattice. Thus the relaxation parameter is defined as J_α^(relax) = E_α^(relax) – E_E^(relax), where E_α^(relax) is the energy of relaxation of α = A, B, C and D site with respect to substitution of one Fe atom and E_E^(relax)is the energy of relaxation of the E site with respect to substitution of one V atom.

4. Results and Discussion

4.1. The Fe-Cr σ-Phase

In [14,16] we analyzed the possible effects, which may play a role in the behaviour of the atomic site distribution in the σ-phase. These are the magnetic state, structural variations (volume and c/a), which might be present in the system due to effects of the neutron irradiation or thermal expansion, and temperature effects. It was found that the magnetic entropy contributes mainly to the icosahedral coordinated (A, D) and highly coordinated B sites. Usually these sites are predominantly occupied by only one sort of the alloy components. At the same time the structural variations lead to an additional atomic redistribution. In particular, a volume expansion promotes an accumulation of more Cr in the A and D sublattices, while the c/a ratio affects the occupation of the C sites.

Taking these effects into account, we have calculated the Cr site occupancies in the Fe_0.5Cr_0.5σ-phase for the low and high temperature values that were obtained for the experimental room temperature lattice parameters and temperature expanded ones. The results are shown in Figure 2 and agree quite well with the available experimental data [2,28]. At very high temperatures the configurational entropy drives the system to a highly disordered distribution of the alloy components on the five σ-phase sublattices. By decreasing the temperature, Fe and Cr atoms exhibit a clear preference for different inequivalent sites. At temperatures of about 700 K, which is the lower border of the σ-phase stability range, the (A, D) sites become occupied only by Fe atoms (i.e., nearly no Cr atoms), the (B, E) sites mostly by Cr atoms, while the occupation of the C site remains almost unchanged and mixed. It is interesting to note that the preference of the Cr atoms between the B and E sites crosses around 650–700 K, at a temperature where the σ-phase formation starts. The occupation behavior for other sites also changes at this temperature as discussed above. This effect might be due to structural variations with temperature in our model, whereas no experimental data on thermal expansion of the σ-phase in any system is found in literature.

Figure 2. The Cr site occupancies of the (A, B, C, D, E) sublattices versus temperature including the magnetic and temperature effects in the Fe_0.5Cr_0.5σ-phase. The empty symbols denote the available experimental data (error bars within the symbol sizes) [2,28]. The vertical lines indicate the temperature range of the σ-phase formation in the Fe-Cr alloy. (Reprinted figure with permission from [16] as follows: Kabliman, E.; Blaha, P.; Schwarz, K.; Peil, O.E.; Ruban, A.V.; Johansson, B. Phys. Rev. B 2011, 84, 184206. Copyright (2011) by the American Physical Society. http://link.aps.org/abstract/PRB/v84/p184206).

Figure 2. The Cr site occupancies of the (A, B, C, D, E) sublattices versus temperature including the magnetic and temperature effects in the Fe_0.5Cr_0.5σ-phase. The empty symbols denote the available experimental data (error bars within the symbol sizes) [2,28]. The vertical lines indicate the temperature range of the σ-phase formation in the Fe-Cr alloy. (Reprinted figure with permission from [16] as follows: Kabliman, E.; Blaha, P.; Schwarz, K.; Peil, O.E.; Ruban, A.V.; Johansson, B. Phys. Rev. B 2011, 84, 184206. Copyright (2011) by the American Physical Society. http://link.aps.org/abstract/PRB/v84/p184206).

4.2. The Re-W and Co-Cr σ-Phase

In order to test the applicability of our model to other binary σ-phases we first chose the Re-W and Co-Cr systems, which have a small mismatch between the atomic radii similar to the Fe-Cr system. The calculated effective on-site interactions and magnetic moments of these two systems are given in Table 2. According to [29] the Co-Cr system is a possible third candidate for a magnetic σ-phase in addition to the Fe-Cr and Fe-V σ-phases. The magnetism of the Co-Cr σ-phase at 0 K was theoretically studied in [10]. In present work it was found that both the Co and Cr atoms in the Co-Cr σ-phase have finite magnetic moments, even at the relevant high temperatures. In contrary the Re-W system is non-magnetic. Using these parameters the distributions of the alloy components in the Re_0.5W_0.5 and Co_0.5Cr_0.5 alloys were calculated and the corresponding results are shown in Figure 3 in comparison with the Fe_0.5Cr_0.5σ-phase. Taking into account the small mismatch between the atomic radii of the alloy components in the Re-W and Co-Cr systems and the absence of corresponding experimental data, in the present work we neglect structural changes with respect to the alloy composition and temperature within the range of the σ-phase formation. Nevertheless these effects can be approximately estimated based on the corresponding study of the Fe-Cr σ-phase.

Table 2. On-site parameters J_α⁽¹⁾ (mRy/cell) calculated for the Re_0.5W_0.5 and Co_0.5Cr_0.5 systems within the DLM-LSF model at T = 1,400 K and T = 1,500 K respectively. µ_α^Co and µ_α^Cr are the local magnetic moments of the Co and Cr atoms in the Co_0.5Cr_0.5σ-phase, while the Re-W σ-phase is nonmagnetic.

		A	B	C	D	E
Jα(1) (mRy/cell)	ReW	15.188	–8.156	–1.594	12.656	0.0
	CoCr	15.656	–1.500	0.563	12.656	0.0
μαCo (μB)	Co	0.802	1.167	1.064	0.854	0.875
μαCr (μB)	Cr	0.491	0.903	0.673	0.570	0.564

Table 2. On-site parameters J_α⁽¹⁾ (mRy/cell) calculated for the Re_0.5W_0.5 and Co_0.5Cr_0.5 systems within the DLM-LSF model at T = 1,400 K and T = 1,500 K respectively. µ_α^Co and µ_α^Cr are the local magnetic moments of the Co and Cr atoms in the Co_0.5Cr_0.5σ-phase, while the Re-W σ-phase is nonmagnetic.

		A	B	C	D	E
Jα(1) (mRy/cell)	ReW	15.188	–8.156	–1.594	12.656	0.0
	CoCr	15.656	–1.500	0.563	12.656	0.0
μαCo (μB)	Co	0.802	1.167	1.064	0.854	0.875
μαCr (μB)	Cr	0.491	0.903	0.673	0.570	0.564

As can be seen from Figure 3 the site occupancies in the Re_0.5W_0.5 system behave similarly to the Fe_0.5Cr_0.5 alloy. However, one can notice that at low temperatures the C and E sites in the Re_0.5W_0.5σ-phase are occupied by the W atoms in reverse order in comparison to the Cr atoms in the Fe_0.5Cr_0.5σ-phase. This is in agreement with earlier published results [30,31]. Both theoretical results agree well with the experimental data from [30]. The reversed occupation of the C and E sites seems to be caused by the big difference between the Cr and W atomic radii. Thus the occupation of these sites (C and E) can change with respect to each other depending on the alloy component.

For the Co_0.5Cr_0.5σ-phase the values of the Cr site occupancies are almost the same as in the Fe_0.5Cr_0.5 system, but the slightly pronounced dominance of a particular alloy component in the occupation of a particular site occurs and can be explained by the slightly larger size mismatch between the alloy components in the Co-Cr than in Fe-Cr system. The Co-Cr σ-phase forms more on the right hand side of the phase diagram (larger Cr content) and is usually observed for a concentration range 54%–67% of Cr in a temperature interval 600–1,280 °C [29]. As in the Fe-Cr system (see [14,16]), one can use the parameters obtained for the Co_0.5Cr_0.5 in order to predict the Cr site occupancies in the full composition range of the σ-phase formation. In Figure 4 the Cr site distribution calculated versus the alloy composition is displayed together with the experimental data from [29] measured at various temperatures. Taking into account the scattering of the experimental data, good agreement is found between the present calculated results and the experimental measurements (probabilities), justifying our theoretical model also for this case.

Figure 3. The site occupancies of the (A, B, C, D, E) sublattices for the reference components in the Re_0.5W_0.5, Co_0.5Cr_0.5 and Fe_0.5V_0.5 alloys in comparison with the results for the Fe_0.5Cr_0.5σ-phase from [14] (without temperature effects).

Figure 3. The site occupancies of the (A, B, C, D, E) sublattices for the reference components in the Re_0.5W_0.5, Co_0.5Cr_0.5 and Fe_0.5V_0.5 alloys in comparison with the results for the Fe_0.5Cr_0.5σ-phase from [14] (without temperature effects).

Figure 4. The Cr site occupancies of the (A, B, C, D, E) sublattices in the Co-Cr system versus the Cr composition, x_Cr, at fixed T = 1,500 K. The full symbols denote the calculated results, the empty symbols represent the experimental site occupancies (error bars are less than 0.5%) [29].

Figure 4. The Cr site occupancies of the (A, B, C, D, E) sublattices in the Co-Cr system versus the Cr composition, x_Cr, at fixed T = 1,500 K. The full symbols denote the calculated results, the empty symbols represent the experimental site occupancies (error bars are less than 0.5%) [29].

4.3. The Fe-V Sigma-Phase

The formation probability of the σ-phase in the Fe-V alloy is many times larger than in the Fe-Cr system due to a much wider temperature and compositional ranges, where this phase is stable [32]. Despite the fact that the σ-phase in the Fe-V system was found many years ago, the concentration and temperature ranges of its existence are still not precisely known. In general it is difficult to accurately determine the phase boundaries due to several factors such as: the slow kinetics of the transformation, the dependence on the purity of the alloys, the mechanical state (strained or strain-free state) and the annealing temperature. According to the phase diagrams analyzed in [32] the upper temperature limit for the σ-phase stability equals to 1, 321 °C for an alloy composition x_V = 46.5%, and it depends rather strongly on composition: ∼ 1, 000 °C for x_V = 34% and ∼ 1, 050 °C for x_V = 63%. On the other hand, the lower temperature limit of formation does not depend too much on the concentration and is around 647–650 °C.

Local Atomic Relaxations

As mentioned above, the quite large size mismatch of the alloy components in the Fe-V system causes that the effect of local atomic relaxations might not be negligible in contrast to the other studied systems (Fe-Cr, Re-W and Co-Cr) (see Table 1). In order to account for these effects we introduced a new parameter in our model, namely J_α^(relax) , which we calculated for each sublattice in the Fe_0.5V_0.5 σ-phase (assuming the experimental lattice parameters V = 0.37074 nm³ and c/a = 0.517) and list them in Table 3. As can be seen, the local lattice relaxations change the effective on-site interactions only moderately and consequently the corresponding site occupancies will be hardly affected. Therefore one might expect that the effect of local atomic relaxations in binary σ-phases near the equiatomic composition is negligible for all binary systems, for which the component size mismatch is less than that in the Fe-V system.

Table 3. On-site interaction parameters J_α⁽¹⁾ (mRy/cell) calculated for the Fe0.5V0.5 alloy with/without taking into account local lattice relaxations J_α^(relax) for the experimental lattice parameters V = 0.37074 nm³ and c/a = 0.517 within the DLM-LSF model at T = 1,000 K.

	A	B	C	D	E
Jα(1) (mRy/cell)	24.750	-7.594	0.656	20.344	0.0
Jα(1) + Jα(relax) (mRy/cell)	22.594	-7.219	0.656	18.656	0.0

Table 3. On-site interaction parameters J_α⁽¹⁾ (mRy/cell) calculated for the Fe0.5V0.5 alloy with/without taking into account local lattice relaxations J_α^(relax) for the experimental lattice parameters V = 0.37074 nm³ and c/a = 0.517 within the DLM-LSF model at T = 1,000 K.

	A	B	C	D	E
Jα(1) (mRy/cell)	24.750	-7.594	0.656	20.344	0.0
Jα(1) + Jα(relax) (mRy/cell)	22.594	-7.219	0.656	18.656	0.0

Site Occupancies (x_V = 0.50)

Let us start from the equiatomic composition x_V = 0.50 and consider a possible increase in volume from V_exp = 0.37074 nm³ to the high temperature value V = 0.38319 nm³ due to thermal expansion. The calculated effective on-site interactions and corresponding local magnetic moments of Fe and V atoms are given in Table 4 at three different temperatures.

Table 4. On-site parameters J_α⁽¹⁾ (mRy/cell) and local magnetic moments of Fe and V atom µ_α^Fe and µ_α^V calculated for the lattice parameters V = 0.38319 nm³ and c/a = 0.517 within the DLM-LSF model at three different temperatures T = 500, 1,000 and 1,500 K.

	T (K)	A	B	C	D	E
Jα(1) (mRy/cell)	500	25.406	–7.125	1.031	21.000	0.0
	1,000	24.750	–7.594	0.656	20.344	0.0
	1,500	24.094	–7.781	0.375	19.875	0.0
μαFe (μB)	500	0.841	1.768	1.445	1.089	0.895
	1,000	1.047	1.790	1.518	1.240	1.079
	1,500	1.169	1.804	1.571	1.334	1.187
μαV (μB)	500	0.091	0.119	0.108	0.098	0.091
	1,000	0.170	0.217	0.200	0.183	0.171
	1,500	0.240	0.303	0.280	0.257	0.242

Table 4. On-site parameters J_α⁽¹⁾ (mRy/cell) and local magnetic moments of Fe and V atom µ_α^Fe and µ_α^V calculated for the lattice parameters V = 0.38319 nm³ and c/a = 0.517 within the DLM-LSF model at three different temperatures T = 500, 1,000 and 1,500 K.

	T (K)	A	B	C	D	E
Jα(1) (mRy/cell)	500	25.406	–7.125	1.031	21.000	0.0
	1,000	24.750	–7.594	0.656	20.344	0.0
	1,500	24.094	–7.781	0.375	19.875	0.0
μαFe (μB)	500	0.841	1.768	1.445	1.089	0.895
	1,000	1.047	1.790	1.518	1.240	1.079
	1,500	1.169	1.804	1.571	1.334	1.187
μαV (μB)	500	0.091	0.119	0.108	0.098	0.091
	1,000	0.170	0.217	0.200	0.183	0.171
	1,500	0.240	0.303	0.280	0.257	0.242

Using the J_α⁽¹⁾ parameters and the corresponding Fe and V magnetic moments (obtained at T = 1,000 K), we calculated the distribution of the V atoms among the five σ-phase sublattices in the Fe_0.5V_0.5 alloy with respect to temperature and alloy composition (see Figure 5). The results obtained at high temperatures agree reasonably well with the experimental values measured for an alloy composition x_V = 0.48. At the low temperature we find that for example the C sublattice is equally occupied by both alloy components. Using the WIEN2k code we also calculated the equilibrium atomic distribution at T = 0 K. In contrast to the Fe_0.5Cr_0.5 alloy (see Figure 3), the E sublattice of the Fe_0.5V_0.5σ-phase has a partial site occupancy by V atoms. There are 7 V + 1 Fe atoms in the E sublattice, while the C sublattice has an equal occupancy by both alloy components, i.e., 4 V + 4 Fe atoms. Thus the atomic site occupancies estimated within our model at low temperatures are found in good agreement with the ground state equilibrium distribution obtained at T = 0 K by the WIEN2k code.

Figure 5. The V site occupancies of the (A, B, C, D, E) sublattices versus the V composition, x_V , at fixed T = 1,000 K. The full symbols denote the calculated results, the empty symbols represent the available experimental data (error bars within the symbol sizes) [28,32]. J_α⁽¹⁾ and µ_α^(Fe,V) are obtained for Fe_0.5V_0.5 at T = 1,000 K.

Figure 5. The V site occupancies of the (A, B, C, D, E) sublattices versus the V composition, x_V , at fixed T = 1,000 K. The full symbols denote the calculated results, the empty symbols represent the available experimental data (error bars within the symbol sizes) [28,32]. J_α⁽¹⁾ and µ_α^(Fe,V) are obtained for Fe_0.5V_0.5 at T = 1,000 K.

Site Occupancies (x_V = 0.40, 0.60)

Let us now consider the atomic site distribution in the Fe-V σ-phase with respect to the alloy composition, x_V (see Figure 5). The predicted site occupancies as function of the alloy composition reproduce well the experimental values for the C and E sublattices, while they differ in slope for the B and (A, D) sublattices. Due to the large size mismatch between the Fe and V atoms, the lattice parameters of the Fe-V σ-phase should depend significantly on the alloy composition. According to experimental measurements [27] an increase of the vanadium content by 10% from the equiatomic composition, Fe_0.5V_0.5, linearly increases the volume of the unit cell from 0.37074 nm³ (for x_V = 0.5) to 0.37634 nm³ (for x_V = 0.6), while the c/a values decrease from 0.517 to 0.516, respectively. On the other hand, with a decrease of the vanadium content by 10% to x_V = 0.4, the volume and c/a ratio change to 0.36514 nm³ and 0.518, correspondingly. Assuming a linear dependence, one can extrapolate the expanded volumes as V = 0.37747 nm³ for x_V = 0.4 and V = 0.38892 nm³ for x_V = 0.6. The optimization of the c/a ratio in the Fe-V σ-phase within the EMTO-CPA method is not really reliable due to the large size mismatch of the Fe and V atoms. Therefore, we stay at a constant c/a ratio, but keep in mind that the site occupancies might vary due to a change of c/a, as has been discussed for the Fe-Cr σ-phase.

The corresponding effective interactions J_α⁽¹⁾and magnetic moments µ_α^(Fe,V) obtained for x_V = 0.40 and x_V = 0.60 are given in Table 5. One can see that for x_V = 0.40 all four effective interactions are different (smaller in absolute values) from those obtained for x_V = 0.50, while for x_V = 0.60 only the changes for the B and C sublattices are remarkable. Nevertheless, when we compare the site occupancies for the parameters obtained for x_V = 0.40 and x_V = 0.60 with those predicted from the parameters obtained for x_V = 0.50, only small differences can be observed. The corresponding values of the site occupancies calculated at T = 1,000 K are given in Table 6. As can be seen only the B, C and E site occupancies change noticeably (those, which have predominant occupancy by V atoms) for x_V = 0.40, while for x_V = 0.60 all values are nearly the same. For x_V = 0.40 the C and E sublattices now have almost an equal occupation in accord with the experimental data (see Figure 5). The occupancy of the B site is a bit smaller, but still higher than the corresponding experimental value. This discrepancy could be due to several reasons: additional structural variations with respect to the alloy composition, temperature expansion, or local atomic relaxations. Particularly the latter might not be negligible for alloy compositions different from the equiatomic composition, especially for those sublattices with small deviations from integer occupation, e.g., the A and D sublattices for x_V = 0.60 or the B sublattice for x_V = 0.40. These effects could be taken into account similiar as for the equiatomic composition (see Equation (6)), but such calculations are not presented in this work.

Table 5. On-site parameters J_α⁽¹⁾ (mRy/cell) and local magnetic moments of Fe and V, µ_α^Fe and µ_α^V, calculated for different alloy compositions x_V = {0.40; 0.50; 0.60} in the Fe-V system with the corresponding lattice parameters V = {0.37747; 0.38319; 0.38892} nm³ and c/a = {0.518; 0.517; 0.516} within the DLM-LSF model at T = 1,000 K.

	xV	A	B	C	D	E
Jα(1) (mRy/cell)	0.40	23.625	–7.031	–0.094	19.406	0.0
	0.50	24.750	–7.594	0.656	20.344	0.0
	0.60	24.938	–8.625	0.844	20.531	0.0
μαFe (μB)	0.40	1.158	1.908	1.659	1.337	1.265
	0.50	1.047	1.790	1.518	1.240	1.079
	0.60	0.947	1.644	1.355	1.148	0.908
μαV (μB)	0.40	0.168	0.221	0.199	0.181	0.172
	0.50	0.170	0.217	0.200	0.183	0.171
	0.60	0.171	0.213	0.210	0.184	0.169

Table 5. On-site parameters J_α⁽¹⁾ (mRy/cell) and local magnetic moments of Fe and V, µ_α^Fe and µ_α^V, calculated for different alloy compositions x_V = {0.40; 0.50; 0.60} in the Fe-V system with the corresponding lattice parameters V = {0.37747; 0.38319; 0.38892} nm³ and c/a = {0.518; 0.517; 0.516} within the DLM-LSF model at T = 1,000 K.

	xV	A	B	C	D	E
Jα(1) (mRy/cell)	0.40	23.625	–7.031	–0.094	19.406	0.0
	0.50	24.750	–7.594	0.656	20.344	0.0
	0.60	24.938	–8.625	0.844	20.531	0.0
μαFe (μB)	0.40	1.158	1.908	1.659	1.337	1.265
	0.50	1.047	1.790	1.518	1.240	1.079
	0.60	0.947	1.644	1.355	1.148	0.908
μαV (μB)	0.40	0.168	0.221	0.199	0.181	0.172
	0.50	0.170	0.217	0.200	0.183	0.171
	0.60	0.171	0.213	0.210	0.184	0.169

Table 6. The V site occupancies in the Fe-V system calculated for different alloy compositions x_V = {0.40; 0.60} with parameters obtained for the fixed Fe_0.5V_0.5 composition or taking into account concentration and structural effects as described in the text within the DLM-LSF model at T = 1,000 K.

xV	(V; c/α)	A	B	C	D	E
0.40	(0.38319 nm3; 0.517)	0.001	0.917	0.473	0.002	0.567
0.40	(0.37747 nm3; 0.518)	0.001	0.897	0.511	0.002	0.538
0.50	(0.38319 nm3; 0.517)	0.001	0.959	0.656	0.004	0.735
0.60	(0.38319 nm3; 0.517)	0.003	0.986	0.851	0.013	0.893
0.60	(0.38892 nm3; 0.516)	0.003	0.990	0.846	0.012	0.896

Table 6. The V site occupancies in the Fe-V system calculated for different alloy compositions x_V = {0.40; 0.60} with parameters obtained for the fixed Fe_0.5V_0.5 composition or taking into account concentration and structural effects as described in the text within the DLM-LSF model at T = 1,000 K.

xV	(V; c/α)	A	B	C	D	E
0.40	(0.38319 nm3; 0.517)	0.001	0.917	0.473	0.002	0.567
0.40	(0.37747 nm3; 0.518)	0.001	0.897	0.511	0.002	0.538
0.50	(0.38319 nm3; 0.517)	0.001	0.959	0.656	0.004	0.735
0.60	(0.38319 nm3; 0.517)	0.003	0.986	0.851	0.013	0.893
0.60	(0.38892 nm3; 0.516)	0.003	0.990	0.846	0.012	0.896

5. Summary

In present work we gave a short overview of a single-site mean field theory for calculating of the atomic site occupancies in the σ-phase. This method was applied to the Fe-Cr, Re-W, Co-Cr and Fe-V systems. It was shown that the chosen binary σ-phases have similar preferences in occupation of the particular lattice sites except for the Re-W system, where a reversal occupation of two sites was observed in agreement with previously published works. For one system, namely Fe-V, which has a large atomic mismatch between the alloy components, we included into our model an additional parameter, which describes the effects of local atomic relaxations. The results obtained in the present work were found in a good agreement with the experimental data and previously published theoretical works. The suggested model can in principle be generalized for multicomponent systems.