The Capacitated Location-Allocation Problem Using the VAOMP (Vector Assignment Ordered Median Problem) Unified Approach in GIS (Geospatial Information Systam)

Abstract

The Vector Assignment Ordered Median Problem (VAOMP) is a new unified approach for location-allocation problems, which are one of the most important forms of applied analysis in GIS (Geospatial Information System). Solving location-allocation problems with exact methods is difficult and time-consuming, especially when the number of objectives and criteria increases. One of the most important criteria in location-allocation problems is the capacity of facilities. Firstly, this study develops a new VAOMP approach by including capacity as a criterion, resulting in a new model known as VAOCMP (Vector Assignment Ordered Capacitated Median Problem). Then secondly, the results of applying VAOMP, in scenario 1, and VAOCMP, in scenario 2, for the location-allocation of fire stations in Tehran, with the objective of minimizing the arrival time of fire engines to an incident site to no more than 5 min, are examined using both the Tabu Search and Simulated Annealing algorithms in GIS. The results of scenario 1 show that 52,840 demands were unable to be served with 10 existing stations. In scenario 2, given that each facility could not accept demand above its capacity, the number of demands without service increased to 59,080, revealing that the number of stations in the study area is insufficient. Adding 35 candidate stations and performing relocation-reallocation revealed that at least three other stations are needed for optimal service. Thirdly, and finally, the VAOMP and VAOCMP were implemented in a modest size problem. The implementation results for both algorithms showed that the Tabu Search algorithm performed more effectively.

1. Introduction

Location-allocation is one of the most important analyses in GIS science, identifying optimal facility locations for optimal services to specific demands [1]. Demands can be allocated to facilities based on factors, such as minimum distance, minimum cost, the capacity of facilities, etc. The best location for each facility depends on such criteria as optimal distance, capacity, population density, and optimal cost. An unsuitable location for a facility would adversely affect that facility in providing an effective service. If the location of a facility is far from an appropriate demographic space, then it will not service it well [2]. Similarly, the capacity of facilities is a factor in the effectiveness of their service. The location of the facilities must be well-defined and distributed in such a way that they can respond to the demand, in terms of their capacity. For example, if the capacity of a hospital is 10,000 beds, it means that the hospital is not able to provide more than this number and should not accept more patients than this capacity. As is clear, capacity is a main criterion in location-allocation problems, because each facility in the real world can serve only a specified demand.

The location-allocation problem has four main models, namely, the P-Median model, the Simple Plant Location Problem (SPLP), P-Center, and Coverage problem [3]. The Median problem approach introduces the median points into the candidate points, with the objective of minimizing the total cost [4]. The Maximal Covering Location model aims to maximize demand coverage with the predetermined number of facilities [5]. The Center problem covers all the points, its goal being to minimize the maximum distance between demand points and the closest service center [6]. The objective of SPLP is to minimize the combined transportation costs and fixed costs for setting up and operating facilities. Improvements in optimization methods, computer programming, computational theory, algorithms, and computer hardware have resulted in a wide range of well-developed location analysis approaches [7]. Many models have been developed, with various criteria and constraints, to solve the complexity of real-world problems. Although these models are different from each other in their objective and structure, they are, in fact, derived from the same four main models [7]. Many research studies have been undertaken using these models: Yu and Liu, for example, have studied min-max cover problems, while Ding and Qiu [8,9] applied an algorithm for the facility location problem with the goal of minimizing total cost. Xu and et al. [10] examined the mixed center location problem, developing three heuristics to solve it. Because of the complexity of these models, which belong to the NP-hard problem category [11], employing exact methods to solve them is very time-consuming. Consequently, metaheuristic algorithms are used. Unifying these location-allocation main models would make the problem still more complicated, but this unification is important for two reasons: (1) it helps us to categorize and understand the relationship between different problems; and (2) it can be a tool for introducing and constructing new models that satisfy human needs [1].

In 1984, Hillsman [12] used the median structure to solve many location problems by changing distance or cost matrix. Church and Weaver also introduced the Vector Assignment P-Median Problem (VAPMP). The VAPMP allows each demand to be assigned several facilities [13]. In 2014, Lei and Church presented a model called the Vector Assignment Ordered Median Problem (VAOMP), which generalizes both the VAPMP and OMP models. This model is used to solve many problems. They used the Integer Linear Programming method to solve their developed model, which requires expensive software, and its computational time is long [7]. To reduce the computational time of the model, Lei et al. [1] applied the VAOMP unified approach and Tabu Search algorithm in 2016. The unified approach mentioned above led to a significant reduction in the computational time required to solve various problems. Applying some algorithms and changing their parameters may reduce computational time.

The objective of this paper, given the importance of capacity as a criterion in various problems and in constructing realistic conditions, is to develop the VAOMP model with a capacity criterion, so that this model becomes the VAOCMP (Vector Assignment Ordered Capacitated Median Problem). This is because, in the real world, each facility has a specific capacity that must be considered in the simulation of objects. This study then investigates the application of the VAOMP and VAOCMP models to the specific study area of fire stations in Tehran (in new areas with large populations), with a demand capacity of 50,000 people and the goal of minimizing the arrival time of fire engines to the incident site to 5 min. Using the Tabu Search and Simulated Annealing algorithms in a GIS environment (previously examined by Aghamohammadi et al. and Kovacevic-Vujcic et al. [14,15]), this paper compares VAOMP with VAOCMP and evaluates the implementation of the two different algorithms in solving large-size problems and then it tests the models in a larger set to make sure that the models on the big data also deliver acceptable results. GIS is also used in this study to collect and organize data, to introduce the candidate locations, and to produce the graphical outputs.

The rest of this paper is organized as follows. The following section defines the problem definition, before the subsequent section reviews the literature, to identify which similar studies have already been undertaken. Section 4 presents the development of the VAOMP model, considering the capacity criterion and the formulation of VAOCMP. Section 3 presents the methodology or the workflow of the VAOCMP model with the Tabu and Simulated Annealing algorithms, and Section 4 presents the implementation of the model in two case study scenarios (with and without the capacity criterion). We then conclude with a summary of findings and a discussion of necessary future work.

1.1. Problem Definition

Location-allocation is a long-established research problem. The overall objective of this problem is to position a certain number of facilities in optimal locations, so that they are able to serve specific demands or customers in an optimal manner. The location-allocation of emergency facilities, such as fire stations, is even more important among public facilities. Because these facilities are responsible for protecting the lives and property of people, these facilities must be in the optimal location to effectively meet demand in any region. According to National Fire Protection Association (NFPA) international standard, each fire station has a capacity of 50,000 people; that is, it has to serve up to 50,000 people [16,17].

If the capacity criterion for these facilities is not taken into account, too many demands may be allocated to the fire stations, which they will not be able to meet, threatening lives and property in the event of an incident. Many studies on location-allocation have not considered the capacity condition, such as Lei and Church, 2014, Lei et al., 2016, etc. This makes the problem space unrealistic because, in general, according to the NFPA, each station is considered for 50,000 people, and a fire station with its equipment and forces are unable to serve more than this population. So more than this population needs to create new stations, although the improper location of the stations will also disrupt their operation. Therefore, the capacity criterion is a very important one for the location-allocation model. At the same time, the fire service must be able to reach the scene of an incident in less than 5 min to be able to contain it. Hence, the purpose of the location-allocation model in this research is to minimize the arrival time of fire engines to demand sites. To this end, the present study uses the new unified VAOMP model, which can solve various location-allocation problems, to solve the specific problem of locating fire stations and with the aim of minimizing response time. Taking into account the importance of capacity in locating emergency facilities, this study also develops the VAOMP model with the added criterion of capacity.

Location-allocation problems are NP-hard problems, so that metaheuristic methods need to be used for problem-solving to save valuable time. Thus, in this study, two algorithms are used: Tabu Search and Simulated Annealing algorithms. If there are not enough fire stations to serve the demand in an area, i.e., several demands remain without stations, then new candidate locations for stations need to be created. In this case, relocation-reallocation is performed to select the appropriate stations to serve all the demands. In a large city with a dense texture as a case study, it is necessary to check the status of its existing fire stations. If there are insufficient existing fire stations, it is necessary to create additional stations for optimal service. It is solving this problem for which location-allocation models are required.

1.2. Literature Review

The problem of location-allocation was raised by Weber. He determined the location of a market by minimizing the total distance between the markets and their demands [18]. This was a Median problem. With the evolution of hardware and software, several other location-allocation problems were developed and tested with different target functions and constraints. Location-allocation problems belong to the category of NP-hard issues [11] and are a subset of combinatorial optimization problems. Solving various location-allocation problems using exact methods is very time-consuming. For this reason, most research is undertaken using metaheuristic algorithms.

For example, Arostegui et al compared the Genetic, Simulated Annealing, and Tabu Search algorithms in determining the location of various facilities under time constraints, solution constraints, and unconstrained criteria. They found that implementation of the Simulated Annealing and Genetic algorithms depended on the type of problem, as well as the problem conditions [19]. For this reason, the authors used the two algorithms Simulated Annealing and Tabu Search, to solve their location-allocation problem. Vecihi et al. developed an evolutionary Simulated Annealing algorithm to determine the location of uncapacitated facilities on a large scale [20]. The Simulated Annealing method is simple in terms of execution and yields results comparable with the Genetic algorithm. Torrent et al. applied the Simulated Annealing algorithm to a location-allocation problem, thereby reducing the solving time [21]. The results of this research show that Simulated Annealing algorithm is a simple and good algorithm in solving location-allocation problems.

Aghamohammadi et al. [14] developed a hybrid algorithm for solving allocation problems of emergency evacuation based on Tabu search algorithm. The results of this research show that metaheuristic algorithms are good ones in solving emergency location-allocation problems. Mahmoodpour et al. compared Genetic, Tabu Search and Simulated Annealing algorithms in location problem and network modeling in thermal energy generation. The effectiveness of each algorithm was examined, and the results showed the efficiency of the Simulated Annealing algorithm in solving this type of problem [22]. Bolouri et al. solved the problem of multi-objective location-allocation of fire stations in Tehran using the P-Median model and two Genetic and Simulated Annealing algorithms. The results showed the efficiency of the Genetic algorithm in a great number of demands [23]. All of these investigations were done with the same four location-allocation models.

In 2014, Lei and Church developed the VAOMP unified approach that can solve various location-allocation problems with a target function. This model can identify and construct new models that satisfy human needs. Too, the VAOMP problem is NP-hard, since it encompasses NP-hard problems, such as the P-Center problem and the P-Median problem as special cases. Lei and Church showed that using ILP takes a long computation time in finding optimal solutions [7]. The authors used the developed Lei and Church model to solve their problem, which lacks the capacity condition. Therefore, Lei et al. solved the VAOMP problem for the same case study using the Tabu Search algorithm. Their Computational results showed that the Tabu Search algorithm can often find the solutions in seconds, the solutions that are better than those obtained using the ILP method in hours or a day [1]. They proposed using a Simulated Annealing algorithm to solve different location-allocation problems with the VAOMP model. Hitherto, no research has been undertaken with the newly developed VAOMP model. Bolouri et al. from the perspective of spatial justice, examined the condition of fire stations using two algorithms, Simulated Annealing and Tabu Search, using VAOMP in solving location-allocation problem. The results showed that the location of some of the existing facilities for service is not suitable [24].

First, the present study uses from VAOMP model for the location-allocation of fire stations in Tehran. Since fire stations have a particular capacity to service demand, the capacity criterion needs to be considered in the VAOMP model. Therefore, the VAOMP model must be developed with capacity as a criterion (VAOCMP). Then, Tabu Search, and Simulated Annealing algorithms will be used to solve the VAOMP and VAOCMP problem in two scenarios for fire stations, with the aim of minimizing the total weighted time required to service their demand centers. The contribution of this paper is in developing the VAOMP model with a capacity criterion and then applying this in a case study for fire stations. Finally, the results of the VAOMP and VAOCMP models with two algorithms will be examined, and the impact of considering the capacity criterion on emergency facilities (fire stations) will be determined.

1.3. Developing the VAOMP Model Considering the Capacity Criterion (VAOCMP)

Capacity will be considered as one of the most important factors in each facility. If capacity is ignored in these facilities, the number of allocations for each facility would be unknown, and sometimes there would be a facility with a large number of allocations or sometimes one without any allocation in the problem. In the real world, every facility has a specific capacity for servicing its allocations, so the VAOMP model, which does not consider capacity, has been developed with a capacity criterion to make the problem more realistic. In this newly developed model, which we call the Vector Assignment Ordered Capacitated Median Problem (VAOCMP), all the conditions of the VAOMP model are established, such as the assignment of one demand to multiple facilities, levels of order, etc. Meanwhile, each facility has a particular capacity, which ensures that each facility will not operate over its capacity. The mathematical function of the model developed will be:

$$Minimize Z={{\displaystyle \sum }}_{k=1}^n{\lambda }_k{w}_k$$

(1)

$${{\displaystyle \sum }}_{k=1}^n{w}_k={{\displaystyle \sum }}_{i \in I}{{\displaystyle \sum }}_{j ϵ J}{{\displaystyle \sum }}_{i=1}^L{a}_i{\theta }_{il}{d}_{ij}{x}_{ij}^l{c}_{ij}^l for each i ϵ I$$

(2)

The variables and parameters of this model are:

• I is the set of demands
  J is the set of facilities
  $a_i$ the population or the number of demands in each building block or at location i
• k = 1, 2,…n is an index for the relative rank of service time, one assigned to each demand.
  ${\lambda }_k$ the weight on the kth rank of service
  $d_{ij}$ the distance or time (or generalized cost) between i and j.
  L the maximum number of levels of closeness being considered in the model for any demand (in this research is equal to 1)
  ${\theta }_{il}$ the fraction of the time demand at i is served by its lth closest facility
• $C_j$ capacity of each facility or fire station that is equal to 50,000 people
• $c_{ij}^l=\{1\begin{array}{c} \mathrm{if} \mathrm{demandIi} \mathrm{assigns} \mathrm{to} \mathrm{facility} \mathrm{j} \mathrm{as} \mathrm{the} \mathrm{lth} \mathrm{closest} \mathrm{open} \mathrm{facility}\\ 0 otherwise\end{array}$

The constraints of this model are:

$$w_k\ge {{\displaystyle \sum }}_{j ϵ J}{{\displaystyle \sum }}_{i=1}^L{a}_i{\theta }_{il}{d}_{ij}{x}_{ij}^l-M.\left(1-u_i^k \right) for each i ϵ I,k=1,2,\dots n$$

(3)

$${{\displaystyle \sum }}_{k=1}^n{u}_i^k=1 for each i ϵ I$$

(4)

$${{\displaystyle \sum }}_{i ϵ I}{u}_i^k=1for each \mathrm{k}=1, 2, \dots , \mathrm{n}$$

(5)

$$w_k\le w_{k+1} for each k=1, 2, \dots , n-1$$

(6)

$${{\displaystyle \sum }}_{j \in J}^L{x}_{ij}^l\le y_j for each i ϵ I, l=1,2,\dots L$$

(7)

$${{\displaystyle \sum }}_{L=1}^L{x}_{ij}^l\le y_j for each i ϵ I, j ϵ J$$

(8)

$${{\displaystyle \sum }}_{q ϵ C_{ij}}{x}_{iq}^l+ {{\displaystyle \sum }}_{s=1}^l{x}_{ij}^s \ge y_j for each i ϵ I , j ϵ J, l=1, 2, \dots , L$$

(9)

$$P_2 \le {{\displaystyle \sum }}_{j ϵ J}{y}_j \le P_1$$

(10)

$$0 \le x_{ij}^l \le 1 y_j and u_i^k \left\{0,1\right\}$$

(11)

$${{\displaystyle \sum }}_{j=1}{{\displaystyle \sum }}_{k=1}^n{c}_{ij}^l=L for each i ϵ I$$

(12)

$${{\displaystyle \sum }}_{i=1}{{\displaystyle \sum }}_{k=1}^n{c}_{ij}^l\le C_j for each j ϵ J$$

(13)

Before presenting the VAOCMP model, it is necessary to obtain the cost matrix between all the points of demand and the selected facilities by Origin-Destination Cost Matrix (OD Cost Matrix) analysis in GIS. The OD Cost Matrix is a matrix that specifies the cost between each facility and each demand point. In this research, the cost is defined as the arrival time for fire engines to the demand point. Then, all the arrays in the OD Cost Matrix are ranked according to the lowest cost (or time), so it can be determined which facility is closest to which demand, and which demand will be the closest demand to each facility. Based on the number of allocation levels, or l and then by considering the capacity at each level of the order, it will be determined which facility will be served by which demand. Applying the ranking, any demand closer to a facility is likely to be allocated earlier than demands which are further away, and therefore, the capacity of the facility will be filled up with closer, rather than more distant, demands. If two arrays or demands have the same cost for a facility (while the facility has spare capacity), the array with the smaller demand index will be allocated for the capacity. Then the partial sum ($w_k)$ is calculated for each facility, based on the ranking level. The OD Cost Matrix seems to be highly effective in quickly reaching the solution: as it is possible to find the lowest cost between facilities and demands, each demand point will be allocated to its closest adjacent facility, and every facility will also be served by its closest adjacent demand. For example, a demand may be serviced by different facilities based on its ranked level, but the capacity of the facility can only serve the closest demands around it. However, the intended demand may not be the closest demand to the facility, so the capacity of the facility will not be allocated to the demand further away, and that more distant demand must use capacity from another facility, which is not necessarily the closest facility to the intended demand. The constraints of this model are described as follows:

Equation (2) also considers capacity as a factor: if a demand is allowed to be allocated to a facility, the value of $c_{ij}^l$ will be equal to 1. Constraint (3) requires a large coefficient value, M; this constraint establishes that when i has the kth smallest partial sum, the unconditional partial sum should be equal to the actual partial sum of the costs. Constraints (4) and (5) define that each partial sum should be assigned only one rank and that each rank should be assigned to only one partial sum. Constraint (6) stated that the partial sum of the kth rank should be less than, or equal to, the partial sum at the next rank. Constraint (7) is a constraint, ensuring that each demand is assigned to a facility as its lth closest. Constraint (8) is a Balinski-like constraint, where an assignment to a site at j can be made only if that site has been selected for a facility. Constraints (9) stated that a given demand i is assigned to facility j as the lth closest facility, when j is actually the lth closest facility to i. Constraint (10) stated that the number of open facilities should be from p2 to p1. Constraint (11) defines the appropriate values and constraints for the decision variables [1]. Constraint (12) states that each demand can only be allocated to L facilities according to the ranked level. Constraint (13) states that the sum of allocations for each facility should be less than, or equal to, its capacity. The pseudo-code of this function is as follows:

• The required number of facilities is selected as the initial solution using spatial analysis. This solution will speed up the time required to reach the optimal solution.
• The OD Cost Matrix is created for all demands and facilities selected at the previous step.
• All the arrays in the OD Cost Matrix are arranged or ranked based on the minimum cost.
• Based on the order of matrix arrays, which was created in the previous step, and considering the capacity of each facility, the closest demand to each facility is allocated according to the type and the number of service levels.
• According to Equation (2), the partial sum for each demand is calculated based on the allocations of each demand to each facility and the possibility of allocating the demand to a facility according to the capacity criterion and the ranked level of each demand to any facility.
• Then, all the demands are sorted according to their minimum partial sum: the minimum value will be the lowest weight ${\lambda }_k$.
• In the last step by Equation (1), the minimum value of the function will be obtained for the selected facilities.

2. Material and Methods

Firstly, using the VAOMP model, the status of the fire stations in the study area will be investigated. This is to minimize the arrival time of the fire trucks to the accident site, using the Simulated Annealing (1.2.0.0) and Tabu Search (1.0.0.0) algorithms. Then, to evaluate the model, the VAOMP is executed in a larger area. Secondly, the VAOCMP model is developed by adding the capacity criterion to the VAOMP model. Then, the model developed for the study area will be used with the same algorithms to determine the location-allocation of fire stations with the VAOCMP model, to minimize the arrival time of fire trucks to the demand point at no more than 5 min and again the developed VAOCMP model runs in a larger area (as in the previous step).

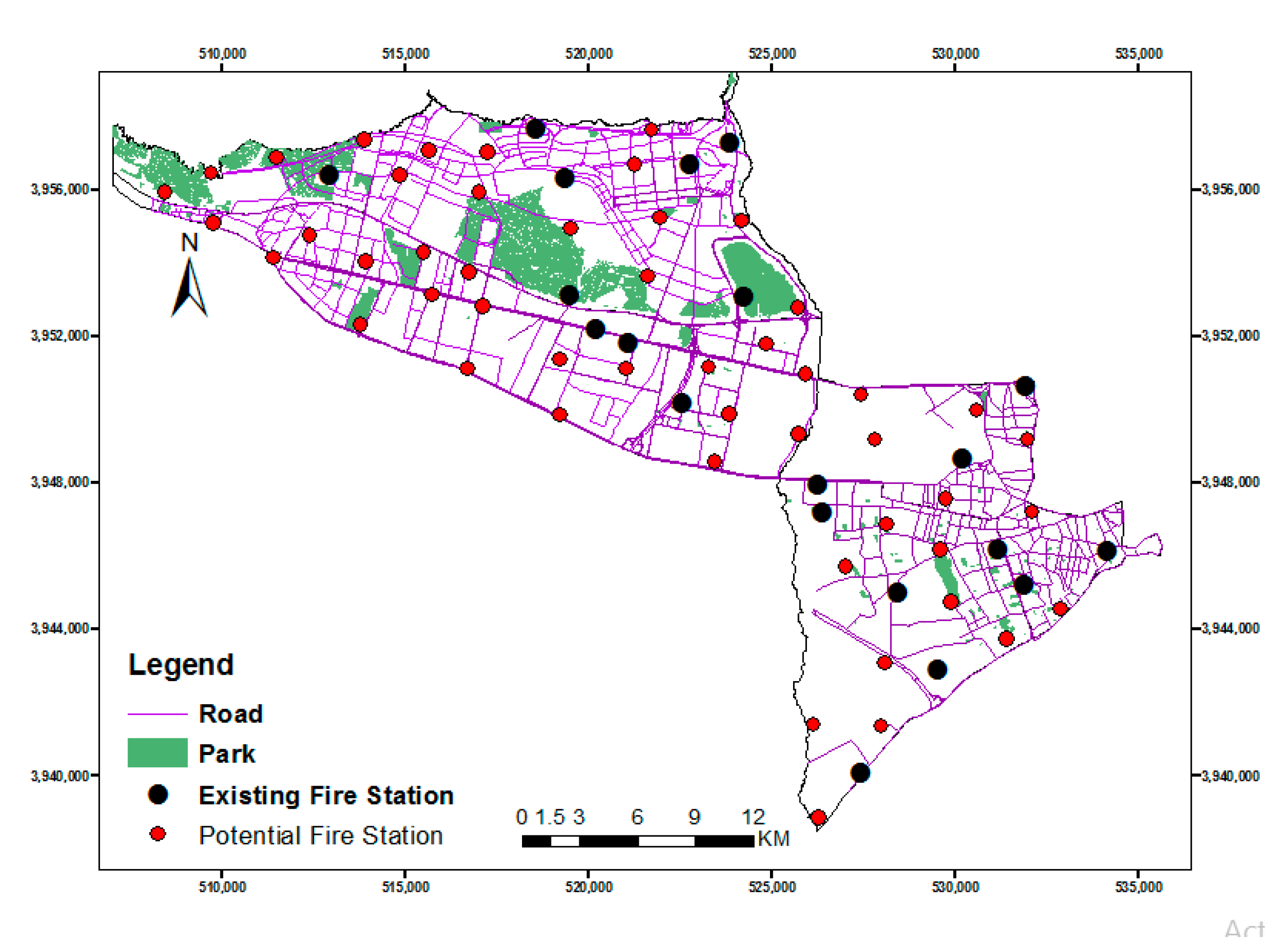
In both steps, if the existing stations were not able to service all the demands, some new stations would be created as candidates from the positioning of candidate fire stations (checking different parameters for locating and overlaying different layers). Then, using the VAOMP and VAOCMP models, we will relocate and reallocate candidate stations for the predefined aim, and investigate the allocation number for each station. Consequently, an optimal algorithm will be identified for solving this type of problem. Then the status of location and allocation will be compared using VAOMP and VAOCMP in the case study. Figure 1 shows the main steps of implementation in the study area.

It should be noted that the VAOMP approach is converted to a Median problem, if ${\lambda }_1={\lambda }_2=\cdots ={\lambda }_n=1$, the assignment vector is θ = [1] and the number of assignment levels is also one. In addition, it must fit in Constraint (10) $p_1=p_2=p$ [7]. The Median problem is one of the problems that automatically generate the closest assignment. The function in the studied problem is Median, and its cost is the arrival time of fire engines to demand points.

3. Result

In this study, the required data include: the statistical zones and the existing population in the 21st and 22nd districts of Tehran; the existing and candidate fire stations; and the road network and information about the roads, including the average traffic on each section of the road, traffic speed, location of one-way or two-way roads and location of U-turns. In today’s world, human life is accompanied by high mobility. Modern web mapping services, such as OpenStreetMap, an example of Volunteered Geographic Information (VGI), and Google Maps provide fairly accurate geographic information at no cost. In the era of smartphones and mobile internet, these map distributors can be used virtually everywhere [25]. Novack, Wang, and Zipf presented how the greenness, sociability, and quietness factors are defined and extracted from OSM. OSM data is sufficiently accessible and reliable. Different researchers are aware of the benefits of using OSM as a data set for different applications [26,27,28].

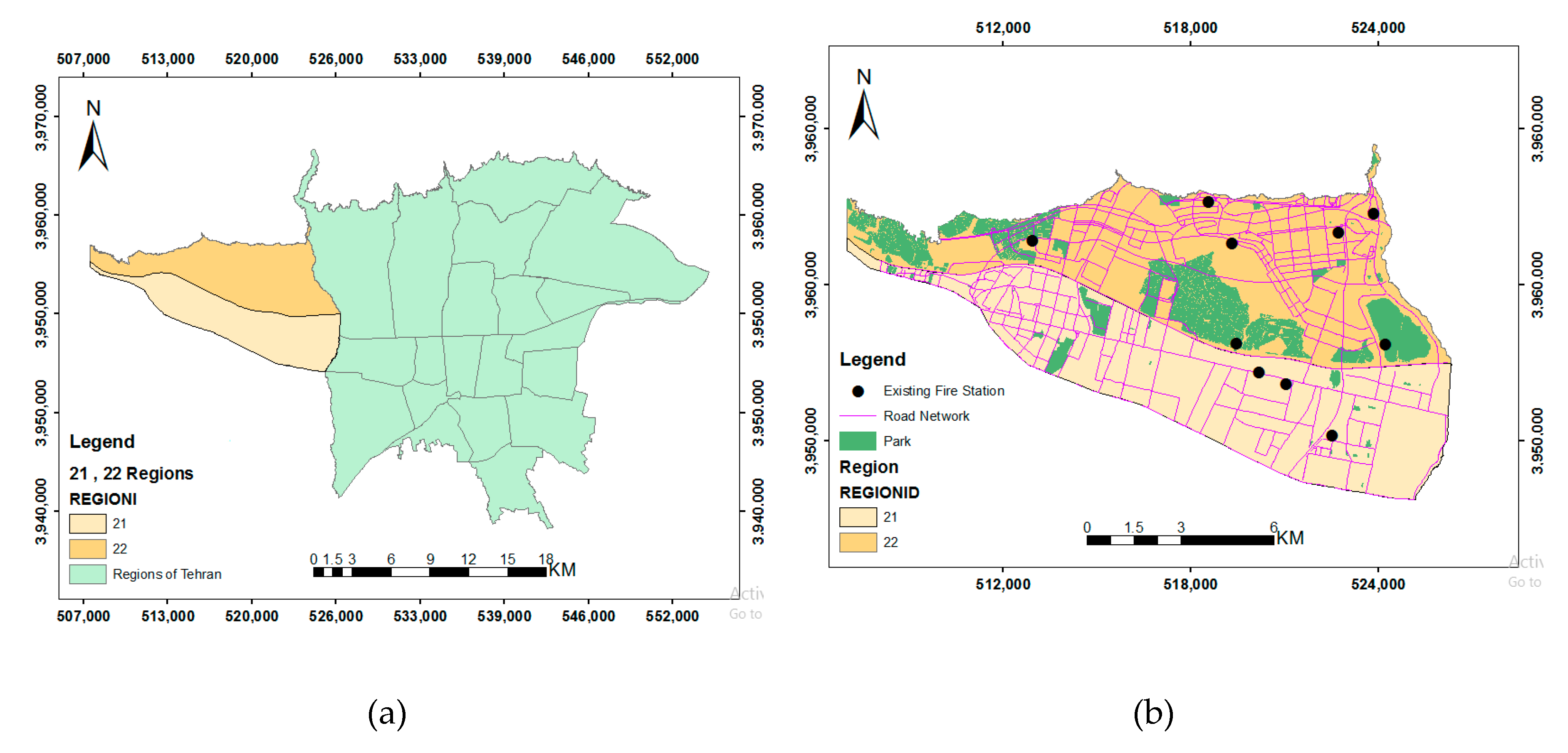
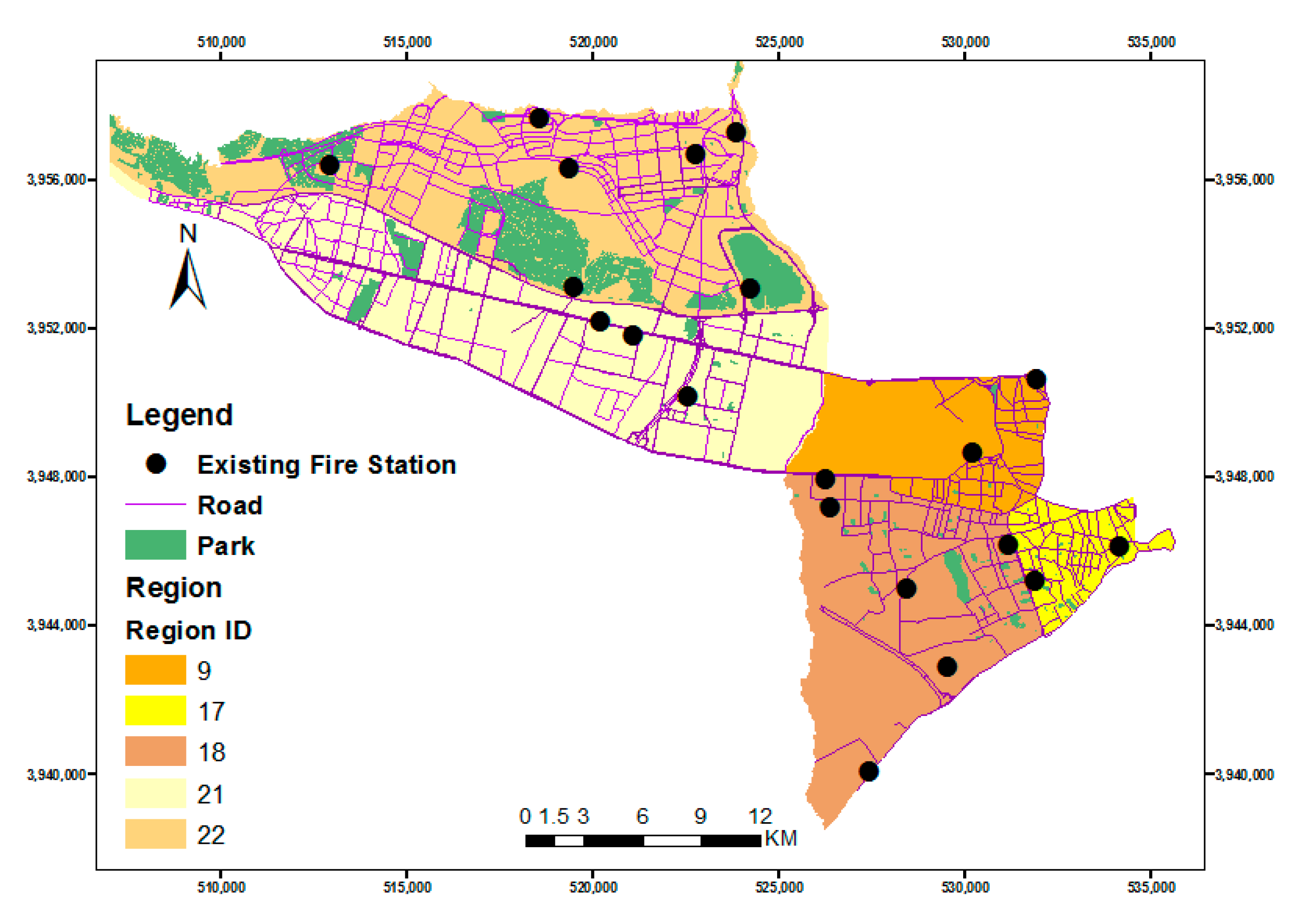
The metropolis of Tehran has witnessed disastrous incidents in recent years. The 22nd district is located in the northwest of Tehran with many tall buildings. The area of this district is about 6200 hectares. District 22 is geographically the largest part of the capital. Due to its size and increasing population, this district requires greater attention. According to the latest census in 2015, the population of this district is over 150,000, and it will reach 450,000 persons by the year 1404 based on the Detailed Plan. District 21 measures about 5156 hectares. This is 7.8% of the total area of Tehran, and in comparison with other areas, it is one of the largest areas of the Tehran municipality. The population of this district is 186,600, according to the latest census, which is more than 8% of Tehran’s population.

These areas selected in Tehran are among the new and emerging areas in Tehran in which the population density has increased in recent years and is still increasing. In addition, these areas have very tall buildings and towers that require proper service to them. Moreover, due to the population and size of the study areas, these areas do not have emergency facilities, including a sufficient number of fire stations to serve. The total number of road sections is 1585. The population of these two districts is 336,600, according to the latest census. To evaluate the function of the model in a larger size, three areas 9, 17, and 18, which have a large area and population, are added to the study area. Then the statistical zones and demand data (or existing population in the region) were converted to a shape file for GIS input. Then, for each 40 people (which is equal to the average population of the building blocks), in the study area, 1 point is placed to facilitate the processing. GIS technology is used in this research for display, outputting, and performing some analysis.

The facilities are service providers, and in this study, the facilities are fire stations. To implement this location-allocation model, the fire station locations in Tehran’s 21st and 22nd districts will be required. There are 10 fire stations in these areas. By international standards, each fire station has a capacity of about 50,000 people, which is also stored in the shape file of fire stations. For the road network, the main road network is that in the 21st and 22nd districts of Tehran. 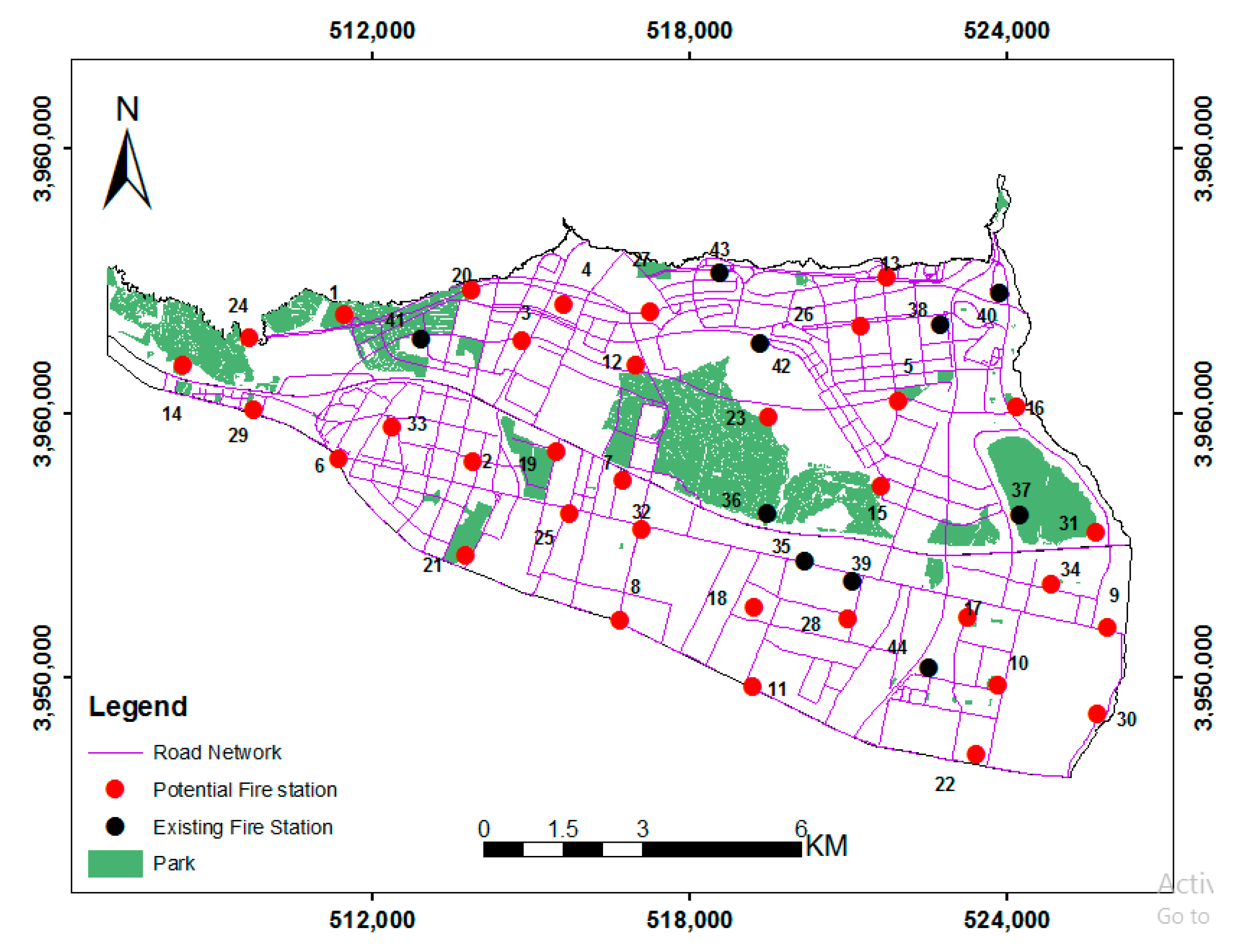Figure 2 shows the location of existing fire stations, potential stations (which are derived from the positioning of the candidate fire stations), and the main road network in Tehran’s 21st and 22nd districts. 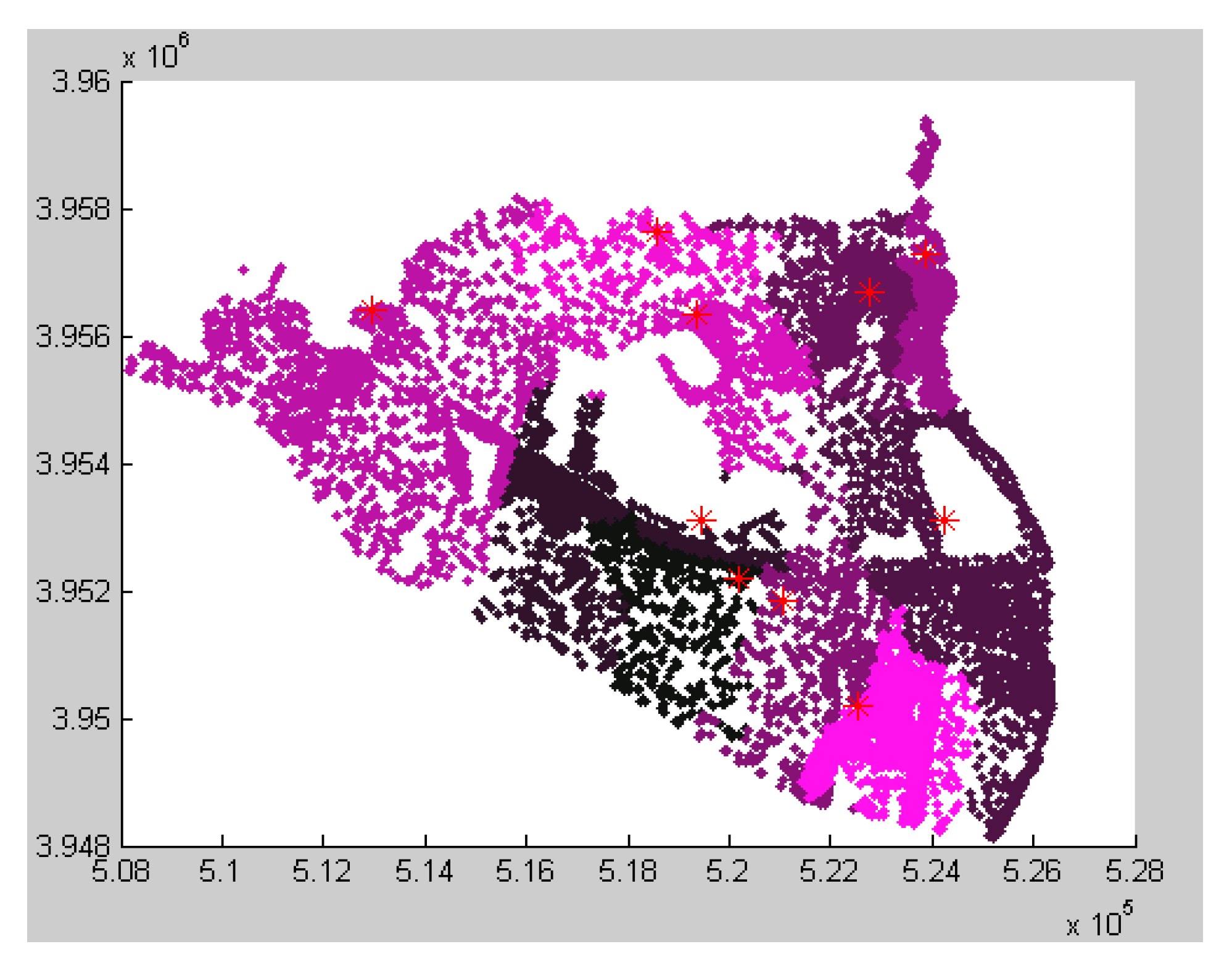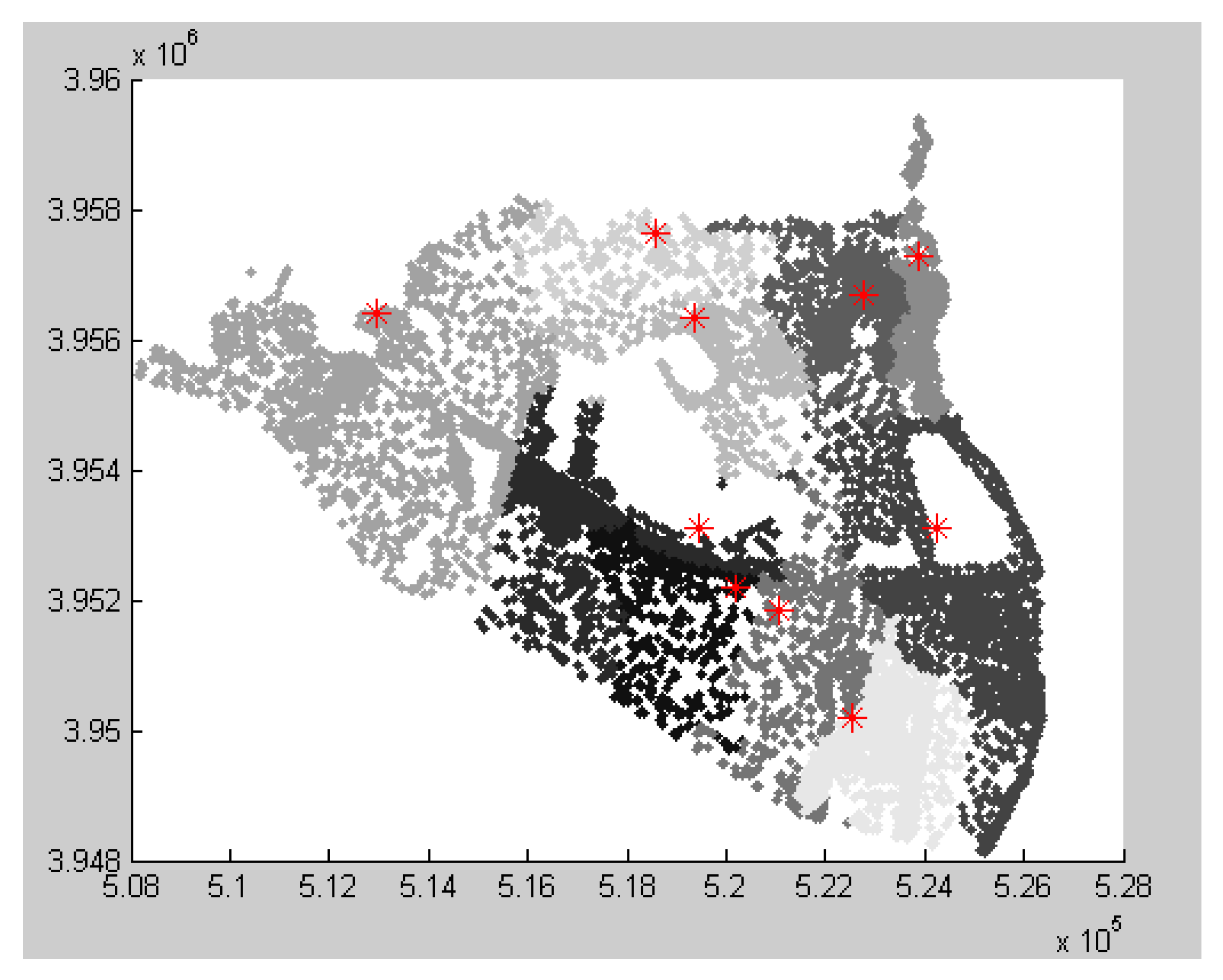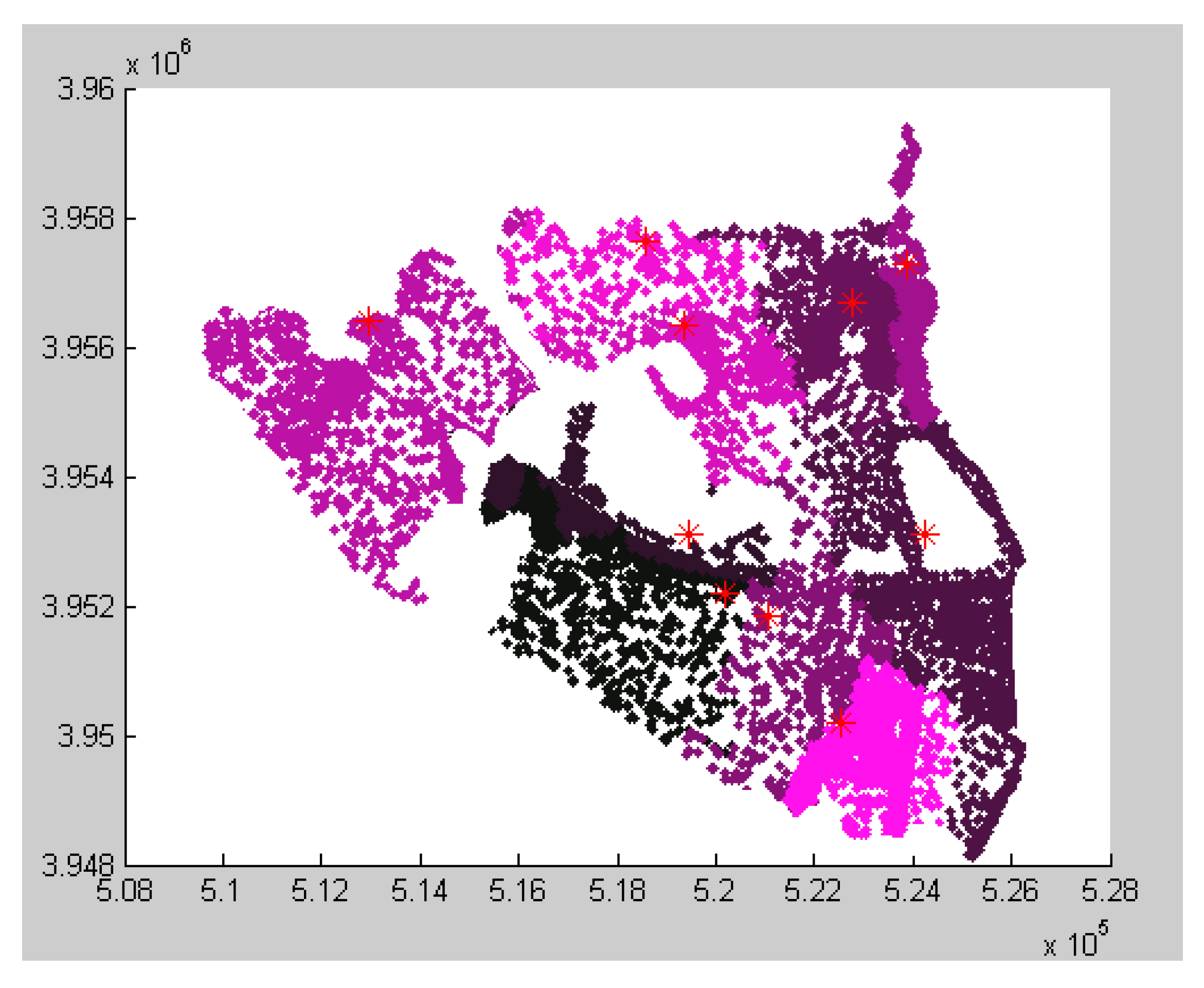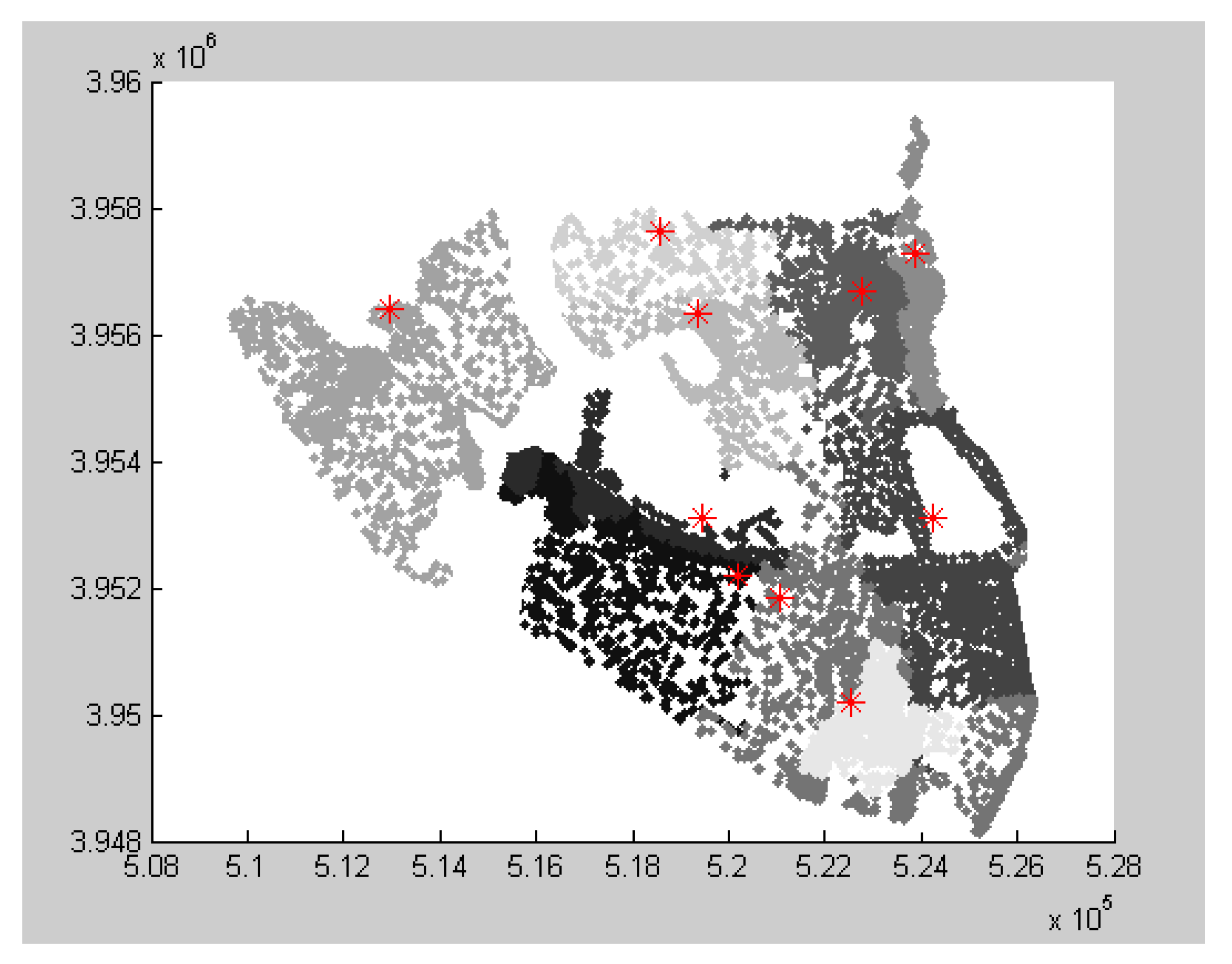Figure 3 shows the population or demand distribution in the statistical zones. Each point shows 40 people. The programming of the model is done in the MATLAB environment.

4. Discussion

4.1. Scenario 1: Implementation of the VAOMP Model Aiming to Minimize Arrival Time for Existing Stations in the Study Area

Minimizing the arrival time from fire stations to an incident site is also a Median problem: as mentioned earlier, the VAOMP model can be turned into a Median problem and can be used to examine the allocation status of existing stations. Therefore, both algorithms will be used separately to solve this problem. To obtain the best results with these models, the parameters of both algorithms are tuned by sensitivity analysis.

4.1.1. Implementation of the Tabu Search Algorithm

A Tabu Search algorithm is used to minimize the arrival time of fire engines to 8415 demand points at no less than 5 min from 10 existing fire stations; the VAOMP model is used to check the demand allocation of the area. To get better solutions in a shorter time, it is necessary to tune the parameters of this algorithm using sensitivity analysis. Performing the sensitivity analysis, the parameters of the algorithm to be adjusted include the number of generations, the Tabu tenures, and the number of neighbors. These were tuned as 15 Tabu tenures, 50 generations, and 90 neighborhoods. The allocation results are shown in Figure 4 (unallocated demands are not shown in this figure). The allocation of each station and unallocated demand are also shown in

Table 1. The number of allocations for each station, runtime, and the optimal value of the function using the Tabu Search algorithm.

No. Stations	1	2	3	4	5	6	7	8	9	10
Number of allocations	25,760	18,200	35,840	33,240	21,960	17,520	51,240	17,760	9880	52,360
Runtime (sec)	394.648
Optimal value	143,478,895.2
Number of demands	336,600
Number of unallocated demands	52,840

.

4.1.2. Implementation of the Simulated Annealing

The allocation results following the implementation of the Simulated Annealing algorithm to minimize time with the VAOMP model are shown in Figure 5. The parameters of this algorithm are similarly optimized by sensitivity analysis. The optimized parameters include the initial temperature, absolute temperature, and cooling rate. According to much research, the absolute temperature is 0.001 [29,30,31]. The best cooling rate for this problem was 0.9, and the initial temperature was 200° F.

Table 2. The number of allocations for each station, runtime, and the optimal value of the function using the Simulated Annealing algorithm.

No. Stations	1	2	3	4	5	6	7	8	9	10
Number of allocations	25,760	18,200	35,840	33,240	21,960	17,520	51,240	17,760	9880	52,360
Runtime (sec)	466.285
Optimal value	143,478,895.2
Number of demands	336,600
Number of unallocated demands	52,840

shows the number of allocations for each station.

4.1.3. Comparison of Algorithms and Validation of Models

By comparing Table 1 and Table 2, we see that both algorithms generate the same optimal value (the best result of Equation 1 is obtained from the iteration of each algorithm), as expected, because the minimum time of each demand with each station is obtained with the OD Cost Matrix. Therefore, it is clear which demand is allocated to which station. Thus, it is expected that even the number of allocations for each station will be similar in both algorithms. These results also show similarity, which is the reason for validating the implementation of the algorithms. However, the run time of the algorithms is different, and of these, it is the Tabu Search algorithm that has a lower run time. Moreover, with the goal of minimizing arrival time, the number of demands remaining without a station is 52,840. Hence, in the next section, this problem will be resolved by adding candidate stations and through relocation-reallocation.

4.1.4. Relocation-Reallocation with the VAOMP Model to Service All Demands Using Both Algorithms

Considering that the number of stations to minimize response time yields 52,840 demands with no service, several new stations will be selected using relocation and reallocation. This means that existing stations stay constant, and some new stations are selected from among the candidate stations produced by location analysis. The number of stations in the area is 10. The purpose of relocation-reallocation is to select 11 stations (10 existing stations, and 1 new station from 35 candidate stations), 12 stations, and then 13 stations. Figure 6 shows the location of the candidate stations.

Since, with metaheuristic algorithms, each execution of the algorithm has a different solution from the others, it is necessary to use a repeatability test to evaluate the robustness of solutions. In this way, the results obtained from a certain number of successive performances with the same parameters are compared in terms of convergence. If the solutions obtained do not differ significantly, we can say that the algorithm is robust in solving the problems.

To investigate the robustness of the methods developed and the average time of problem-solving for each, experiments were designed involving different numbers of fire stations, namely, 11, 12, and 13 stations, respectively. Each of these modes was solved 10 times with the two algorithms. Then, the normalized standard deviation of solutions obtained for the target function for both methods was calculated for each set of experiments. The accuracy obtained for the different modes has been shown in

Table 3. The normalized standard deviation of solutions obtained using the VAOMP model with both algorithms.

Number of Fire Stations	Normalized Standard Deviation Solutions of Obtained Based on Tabu Search	Normalized Standard Deviation of Solutions Obtained Based on Simulated Annealing
11	0.0277	0.0288
12	0.0498	0.0618
13	0.0903	0.1041

.

Table 4. Average of optimal values for 10 iterations of the model using both algorithms.

Number of Fire Stations	Average of Optimal Values Based on Tabu Search	Average of Optimal Values Based on Simulated Annealing
11	110,336,112.9	110,905,133.8
12	106,997,363.5	107,456,433.3
13	104,312,426.7	104,614,621.7

shows the average of the optimal values with 10 independent implementation of the model.

As Table 4 shows, the increase in the number of stations generates complexity in the problem. As a result, the average value of the target functions when the model is implemented on 10 occasions independently has fallen, because, by increasing the number of stations, the demands can be allocated to their optimal stations. Since the final output of these models indicates the number of demands allocated to each station, the third parameter, which is examined to establish the robustness of the solutions, is the difference in the allocations between the various iterations. The proportion of total demands that are assigned in the same way in the 10 iterations of the experiment is considered the evaluation parameter. The values obtained for the two methods are shown in

Table 5. Comparison of the accuracy of allocation results.

Number of Fire Stations	Accuracy of Allocation Based on Tabu Search	Accuracy of Allocation Based on Simulated Annealing
11	89	85
12	85	80
13	82	77

.

As can be seen, the increase in the number of stations, due to the complexity of the space, and reduced the accuracy of allocation in both methods. The fourth parameter is the average percentage of demand allocated by the two algorithms. Its results are shown in

Table 6. The average percentage of demand allocated using both algorithms.

Number of Fire Stations	Average Percentage of All Demand Allocated Based on Tabu Search	Average Percentage of All Demand Allocated Based on Simulated Annealing
11	85.924	84.418
12	97.799	96.546
13	99.999	99.989

.

The last parameter examined is the time taken for the problem-solving, which is measured during the test. In

Table 7. Comparison of the average problem-solving time in seconds.

Number of Fire Stations	Solving Time Based on Tabu Search	Solving Time Based on Simulated Annealing
11	412.773	571.245
12	452.994	618.081
13	472.297	653.392

, the average runtime in each of the implementations has been shown for the two methods.

Regarding the parameters studied, it can be said that the Tabu Search method has greater stability and strength than the Simulated Annealing method. The Simulated Annealing algorithm produces a worse result in solving this type of problem, while its solving time for the Median problem is higher than Tabu.

4.1.5. Evaluating the VAOMP Model in a Larger Set

Three more districts are added to the process. The total population of five districts is 1,250,796 persons. The number of existing fire stations in these five districts is 20. Figure 7 shows the whole of the case study. First, the location-allocation analysis for existing fire stations is done in the case study. The results are outlined in

Table 8. Runtime and the optimal value of the VAOMP for existing stations using both algorithms.

Algorithm	Tabu Search	Simulated Annealing
Runtime (sec)	612.51	735.33
Optimal value	425,884,271.54	425,884,271.54
Number of demands	1,250,796	1,250,796
Number of unallocated demands	104,200	104,200

.

Considering that the number of stations to minimize response time yields 104,200 demands with no service, 50 potential fire stations are added to the processing. The number of existing stations in the area is 20. Therefore, the purpose of relocation-reallocation is to select 26 (20 existing stations and 6 new stations from 50 candidate stations), 27 and 28 stations. Figure 8 shows the location of candidate stations. The results of relocation-reallocation are shown in

Table 9. The normalized standard deviation of solutions obtained using the VAOMP model with both algorithms.

Number of Fire Stations	Normalized Standard Deviation Solutions of Obtained Based on Tabu Search	Normalized Standard Deviation of Solutions Obtained Based on Simulated Annealing
26	0.0691	0.0745
27	0.0913	0.1144
28	0.1327	0.1599

,

Table 10. Average of optimal values for 10 iterations of the model using both algorithms.

Number of Fire Stations	Average of Optimal Values Based on Tabu Search	Average of Optimal Values Based on Simulated Annealing
26	391,081,355.14	400,233,479.26
27	387,451,662.22	393,846,782.62
28	384,991,646.11	389,329,631.14

,

Table 11. Comparison of the accuracy of allocation results.

Number of Fire Stations	Accuracy of Allocation Based on Tabu Search	Accuracy of Allocation Based on Simulated Annealing
26	86	81
27	81	78
28	79	75

,

Table 12. The average percentage of demand allocated using both algorithms.

Number of Fire Stations	Average Percentage of All Demand Allocated Based on Tabu Search	Average Percentage of All Demand Allocated Based on Simulated Annealing
26	84.332	82.540
27	95.212	94.571
28	99.720	98.885

and

Table 13. Comparison of the average problem-solving time in seconds.

Number of Fire Stations	Solving Time Based on Tabu Search	Solving Time Based on Simulated Annealing
26	632.315	749.219
27	651.103	768.320
28	695.514	800.107

.

Regarding the above tables, it can be said that the Tabu Search method has greater stability and strength than the Simulated Annealing method in modest size problems.

4.2. Scenario 2: Implementation of the VAOCMP Model Aiming to Minimize Arrival Time for Existing Stations in the Study Area

This scenario is similar to scenario 1, except that the VAOCMP is used in this case.

4.2.1. Implementation of the Tabu Search Algorithm

To achieve optimal results, it is necessary to reset the parameters of this algorithm for the VAOCMP model. The most appropriate parameters for this algorithm are identified by sensitivity analysis as follows: 25 Tabu tenures, 70 generation, and 90 neighborhoods. Allocation results for 10 existing fire stations are shown in Figure 9 (unallocated demands have not been shown in the figure). The allocations for each station and unallocated demands are also shown in

Table 14. The number of allocations for each station, runtime, and the optimal value of the function using the Tabu Search algorithm in the VAOCMP model.

No. Stations	1	2	3	4	5	6	7	8	9	10
Number of allocations	25,960	18,200	34,960	31,240	21,960	17,520	50,000	17,780	9880	50,000
Runtime (sec)	525.36
Optimal value	142,474,495.67
Number of demands	336,600
Number of unallocated demands	59,080

.

To minimize the arrival time for fire engines to the location of an incident using the VAOCMP model with the Tabu Search algorithm, the value of the objective function falls, because, as expected, when a demand cannot be allocated to a station according to the capacity criterion, it must be allocated to the next adjacent station that has a distance of less than 5 min. However, in many cases, the time interval to the next station is more than 5 min. As a result, the demand cannot be allocated to any station. Therefore, the value of the objective function has fallen in this case compared to the VAOMP model. In this method, since each array of the OD Cost Matrix is ranked from the minimum to maximum value, a closer demand is assigned to each station, so that each station cannot exceed its capacity. At the same time, the surplus capacity of each station can be transferred to other stations.

4.2.2. Implementation of the Simulated Annealing Algorithm

The parameters of this algorithm are readjusted to solve the VAOCMP model. The parameters are the absolute temperature of 0.001, the initial temperature of 300 ° F, and the cooling rate of 0.95. Allocation results for 10 existing fire stations have been shown in Figure 10.

Table 15. The number of allocations for each station, runtime, and the optimal value of the function using the Simulated Annealing algorithm in the VAOCMP model.

No. Stations	1	2	3	4	5	6	7	8	9	10
Number of allocations	25,960	18,200	35,960	33,240	21,960	17,520	50,000	17,800	9880	50,000
Runtime (sec)	598.444
Optimal value	142,474,495.67
Number of demands	336,600
Number of unallocated demands	59,080

shows the number of allocations for each station.

4.2.3. Comparison of Algorithms and Validation of Models

By comparing Table 14 and Table 15, it is possible to see that, as expected, both algorithms produce the same optimal value, because, with the OD Cost Matrix, the minimum time is obtained for each demand and each station. Thus, it is clear that which demand should be assigned to which station. Hence, it is expected that even the number of allocations for each station will be similar in the two algorithms, and this is clear from the results. This is the reason for validating the algorithms. Only the runtime of algorithms differs: the Tabu Search algorithm has a shorter runtime than the Simulated Annealing algorithm.

However, by comparing Table 14 and Table 15 with Table 1 and Table 2 (minimizing arrival time taking into account the capacity of each station, and then, regardless of the capacity of each station), we conclude that the number of allocations at some stations has changed: the stations which had more than 50,000 people allocated to them in the incapacitated criterion have their capacity reduced to 50,000 people with VAOCMP model. As a result, the surplus capacity of each station has been allocated to the closest adjacent station, but, in most cases, the surplus capacity of each station was not able to be allocated to any other station, so that the value of the target function has dramatically decreased. In this case (minimizing arrival time with the capacity criterion), 59,080 demands remain without the station. Hence, in the following section, we will solve the problem by adding the same candidate stations and performing relocation-reallocation.

4.2.4. Relocation-Reallocation with the VAOVMP Model to Service All Demands Using Both Algorithms

Similar to scenario 1, the insufficient number of stations to minimize arrival time and the 59,080 demands remaining without service in this scenario means that we select new stations by relocation and reallocation. The number of existing stations in the region is 10. The purpose of relocation and reallocation to select 11 stations (10 existing stations, and 1 new station from 35 candidate stations) and then 12 and 13 stations. Checking the solution strength yields similar results as in the first scenario.

Table 16. The normalized standard deviation of solutions obtained using the VAOCMP model with both algorithms.

Number of Fire Stations	Normalized Standard deviation Solutions of Obtained Based on Tabu Search	Normalized Standard Deviation of Solutions Obtained Based on Simulated Annealing
11	0.0351	0.0398
12	0.0727	0.0841
13	0.1489	0.1855

shows the accuracy obtained for different states.

Table 17. Average of optimal values for 10 iterations of the model using both algorithms.

Number of Fire Stations	Average of Optimal Values Based on Tabu Search	Average of Optimal Values Based on Simulated Annealing
11	105,982,411.3	106,227,122.4
12	102,113,345.1	102,446,657.6
13	100,142,011.0	100,815,312.2

shows the average of optimal values for 10 iterations.

As the table shows, the increase in the number of stations leads to an improvement in the average value of the target function for 10 independent implementations of the model. The value is reduced because, with an increase in the number of stations, the demands can be allocated to their optimal stations. In

Table 18. Comparison of the accuracy of allocation results.

Number of Fire Stations	Accuracy of Allocation Based on Tabu Search	Accuracy of Allocation Based on Simulated Annealing
11	88	84
12	83.5	80
13	81	76

, the accuracy value for allocation obtained from different states is shown for the two methods. The average percentage of all demands allocated with the two algorithms is shown in

Table 19. The average percentage of all demand allocated using both algorithms.

Number of Fire Stations	Average Percentage of All Demand Allocated Based on Tabu Search	Average Percentage of All Demand Allocated Based on Simulated Annealing
11	84.483	83.222
12	96.959	95.435
13	99.999	99.510

.

In

Table 20. Comparison of the average problem-solving time in seconds.

Number of Fire Stations	Solving Time Based on Tabu Search	Solving Time Based on Simulated Annealing
11	565.310	605.778
12	613.585	632.112
13	649.947	670.661

, a comparison of the average problem-solving time, in seconds, has been shown for the two methods.

Regarding the parameters studied, it can be said that the Tabu Search method has greater stability and strength than the Simulated Annealing method in the two scenarios. The Simulated Annealing algorithm produces a poorer result in solving the Median problem, while the solving time for the Median problem is higher than with the Tabu algorithm.

4.2.5. Evaluating the VAOCMP Model in a Larger Set

In this section, the VAOCMP model is evaluated using two algorithms for a larger data set, similar to Section 4.1.5. The results of location-allocation for existing stations are outlined in

Table 21. Runtime and the optimal value of the function by Tabu Search and Simulated Annealing algorithm for existing stations.

Algorithm	Tabu Search	Simulated Annealing
Runtime (sec)	653.18	791.25
Optimal value	341,431,239.22	341,431,239.22
Number of demands	1,250,796	1,250,796
Number of unallocated demands	163,800	163,800

.

One hundred sixty-three thousand eight hundred demands in the case study are without services. Because, taking into account the capacity of each station, each facility cannot allocate more than 50,000 persons, and surplus demands may not be allocated to any other station. Similar to Section 4.1.5, relocation-reallocations are done, but using the VAOCMP model. The results of relocation-reallocation are shown in

Table 22. The normalized standard deviation of solutions obtained using the VAOCMP model with both algorithms.

Number of Fire Stations	Normalized Standard Deviation Solutions of Obtained Based on Tabu Search	Normalized Standard Deviation of Solutions Obtained Based on Simulated Annealing
26	0.0812	0.1008
27	0.1258	0.1399
28	0.1739	0.2073

,

Table 23. Average of optimal values for 10 iterations of the model using both algorithms.

Number of Fire Stations	Average of Optimal Values Based on Tabu Search	Average of Optimal Values Based on Simulated Annealing
26	303,661,932.10	306,327,182.44
27	298,551,847.41	301,688,805.25
28	294,853,029.37	296,971,302.57

,

Table 24. Comparison of the accuracy of allocation results.

Number of Fire Stations	Accuracy of Allocation Based on Tabu Search	Accuracy of Allocation Based on Simulated Annealing
26	84	79
27	79	77
28	78	73

,

Table 25. The average percentage of all demand allocated using both algorithms.

Number of Fire Stations	Average Percentage of All Demand Allocated Based on Tabu Search	Average Percentage of All Demand Allocated Based on Simulated Annealing
26	82.676	81.009
27	93.103	90.338
28	98.990	97.730

and

Table 26. Comparison of the average problem-solving time in seconds.

Number of Fire Stations	Solving Time Based on Tabu Search	Solving Time Based on Simulated Annealing
26	715.228	852.210
27	782.140	901.825
28	840.371	949.414

.

So, the VAOCMP model can also solve the modest size problem efficiently. As it is known, the Tabu Search algorithm provides better solutions to this problem.

5. Conclusions

Location-allocation models are one of the most important forms of GIS analysis and are used in many applications. To simulate the real world more effectively, it is necessary to add the objectives and criteria required to solve the problem into the problem space to obtain optimal solutions. One of these criteria is the criterion of capacity. Adding this condition to the problem of locating and allocating emergency facilities, such as fire stations, will lead to the optimal selection of stations in relation to the capacity of each station, thereby allowing for optimal service. First, the VAOMP model was developed to include the capacity criterion, and then the results of the VAOMP model were investigated with the VAOCMP model to examine the status of the existing fire stations in the study area, with the aim of minimizing arrival time using the Tabu Search and Simulated Annealing algorithms. The result in scenario 1 shows that 10 existing stations in the area were not enough to serve 336,600 existing demands and that 52,840 demands remained without service. Thus, 35 candidate stations were added to the analytical processes by locating potential fire stations. The processes showed that 13 stations are able to serve all demands, while the Tabu Search algorithm produces better results. This research used the VAOMP model developed by “Lei and Church, 2014”, and the research results showed that the model could produce good and close results with exact methods with a huge amount of data. Too, the results of this study are consistent with the results of Lei et al. [1], who sought to optimize airports with the VAOMP model using the Tabu search algorithm. This new model can find optimal positions well, and like Lei et al. [1] Tabu algorithm show good results. According to Aghamohammadi et al. [14], the Tabu algorithm works better than the Simulated Annealing algorithm in solving location-allocation problems and has a better speed in achieving optimal solutions. With the larger data set, the VAOMP model was used, and results showed with 28 fire stations, 99.30% of demands can be allocated.

Again, the results of using the VAOCMP model in Scenario 2 showed that 10 stations in the study area were not able to service 59,080 demands in the area. Therefore, the candidate stations generated in Scenario 1 were used again, and the results showed that the 13 stations (10 existing stations and 3 candidate stations) were able to service to 99.5% of the region’s demand. Again, with the larger data set (1,250,796 persons), the VAOCMP model was used, and results showed with 28 fire stations, 98.36% of demands can be allocated. In this scenario, the Tabu Search algorithm produces better results than the Simulated Annealing algorithm in solving this kind of Median problem. Other researchers can use this unified approach to solve different problems with other algorithms, above all in large-scale problems. Future research will also be able to develop the model by adding other objectives and criteria, such as multi capacity facilities, user preferences, and multi objectives.