Limited Power Point Tracking for a Small-Scale Wind Turbine Intended to Be Integrated in a DC Microgrid
Abstract
:1. Introduction
- To propose a strategy in order to limit the power provided from an SSWT that will be integrated in a DC MG.
- To propose two LPPT algorithms based on the P&O principle to overcome drawbacks of the conventional P&O method.
- To test the impact of a sudden variation of the power and the wind speed on the performances of the selected LPPT methods.
2. Related Work
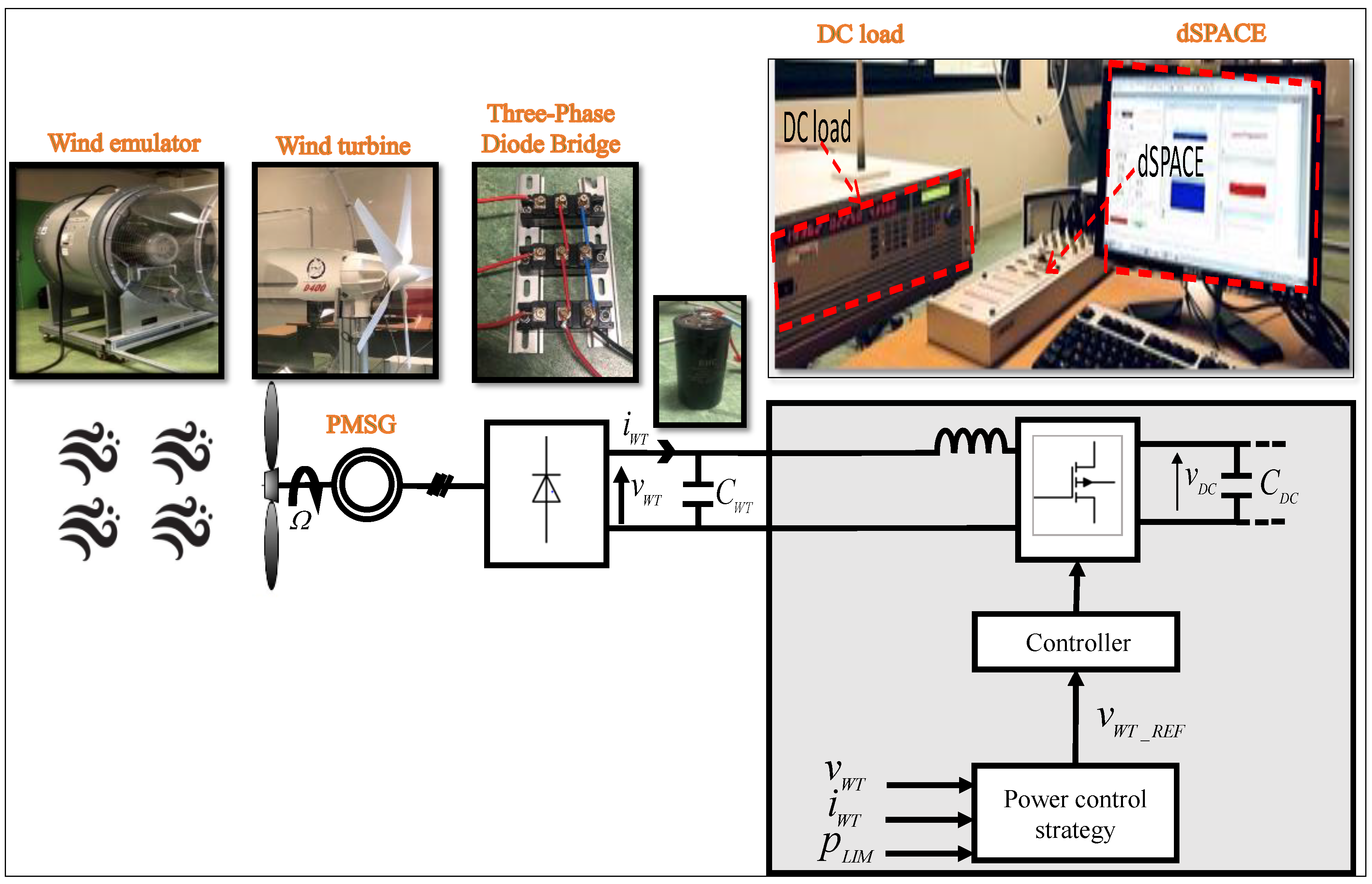
3. MG Overview and Experimental Test Bench
3.1. MG Overview
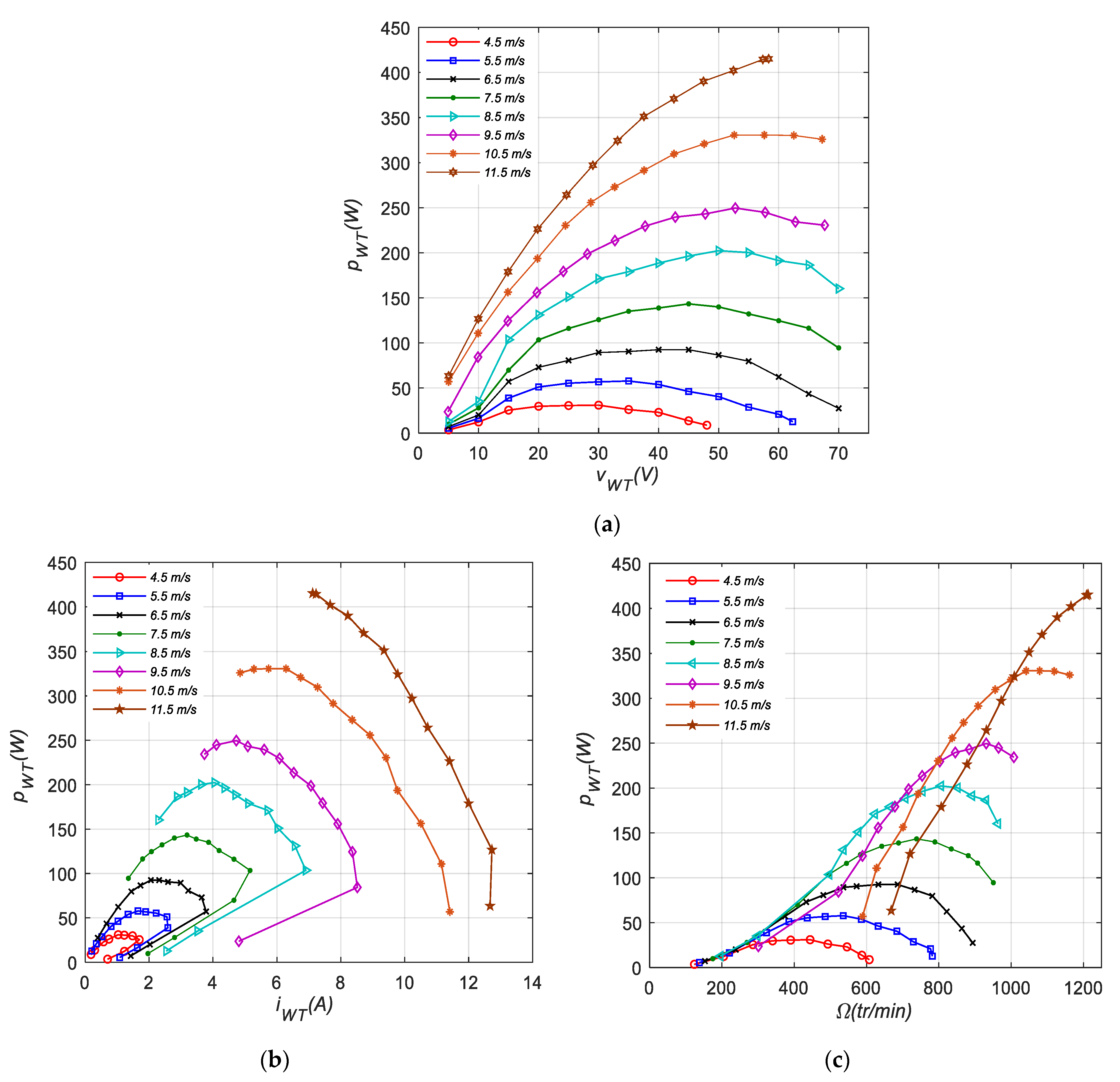
3.2. Experimental Setup for the SSWT
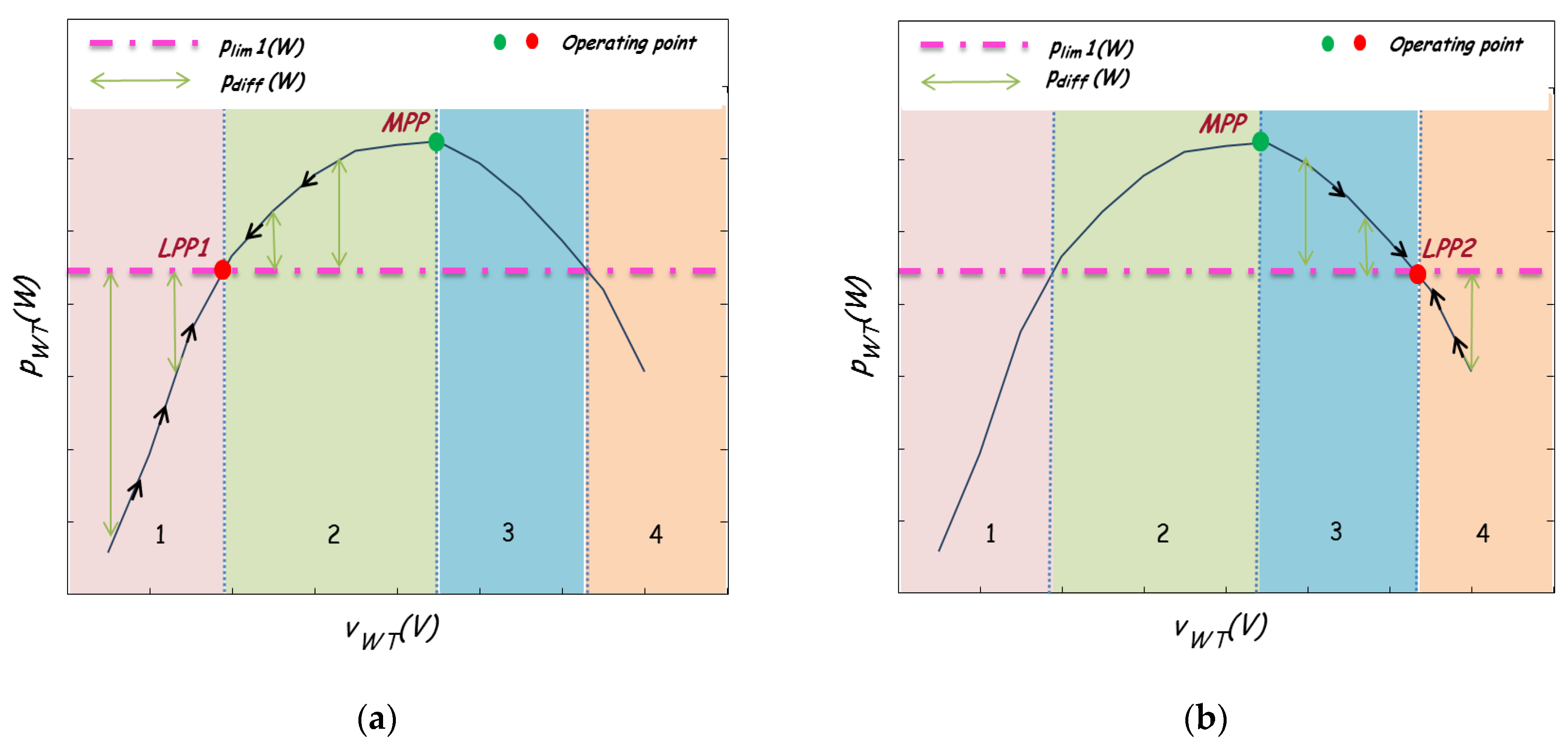
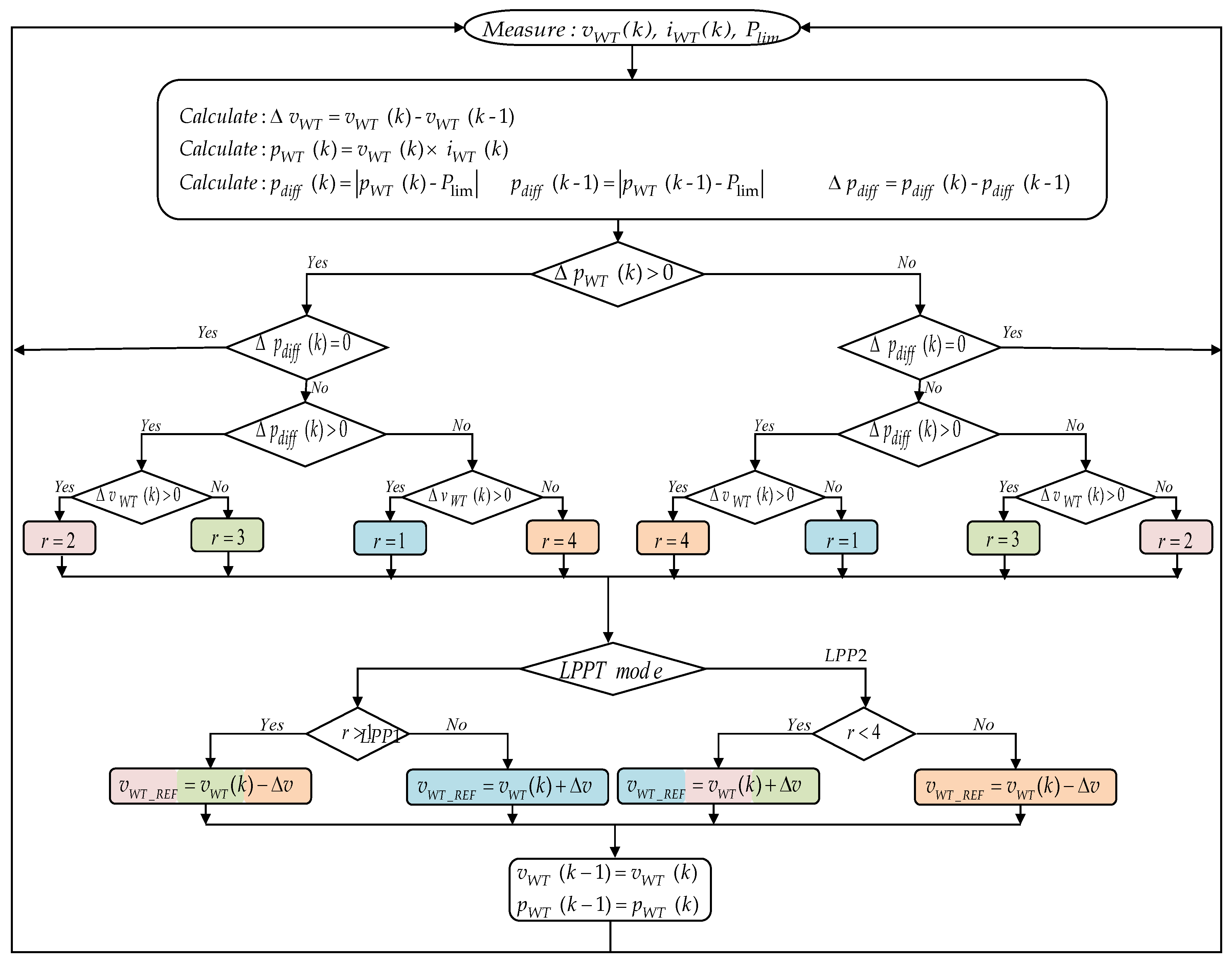
3.3. LPPT Control Strategies
3.3.1. P&O with Fixed Step Size
3.3.2. P&O with Variable Step Size Based on Newton’s Method
3.3.3. P&O with Variable Step Size Based on FL
4. Experimental Results and Discussion
4.1. Performance of Proposed Power Control Strategies
4.1.1. P&O with Fixed Step Size
4.1.2. P&O with Variable Step Sizes Based on Newton’s Algorithm
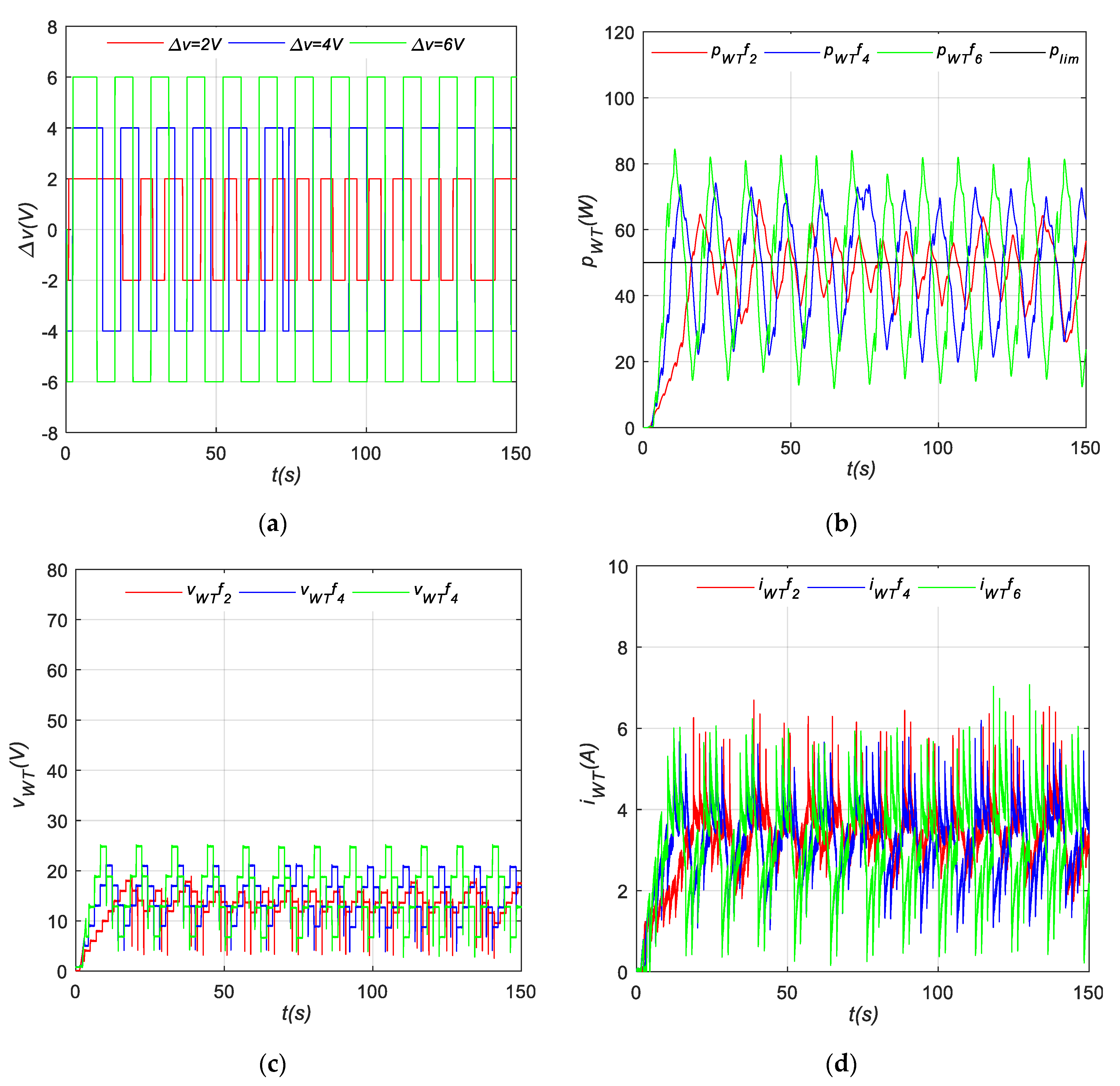
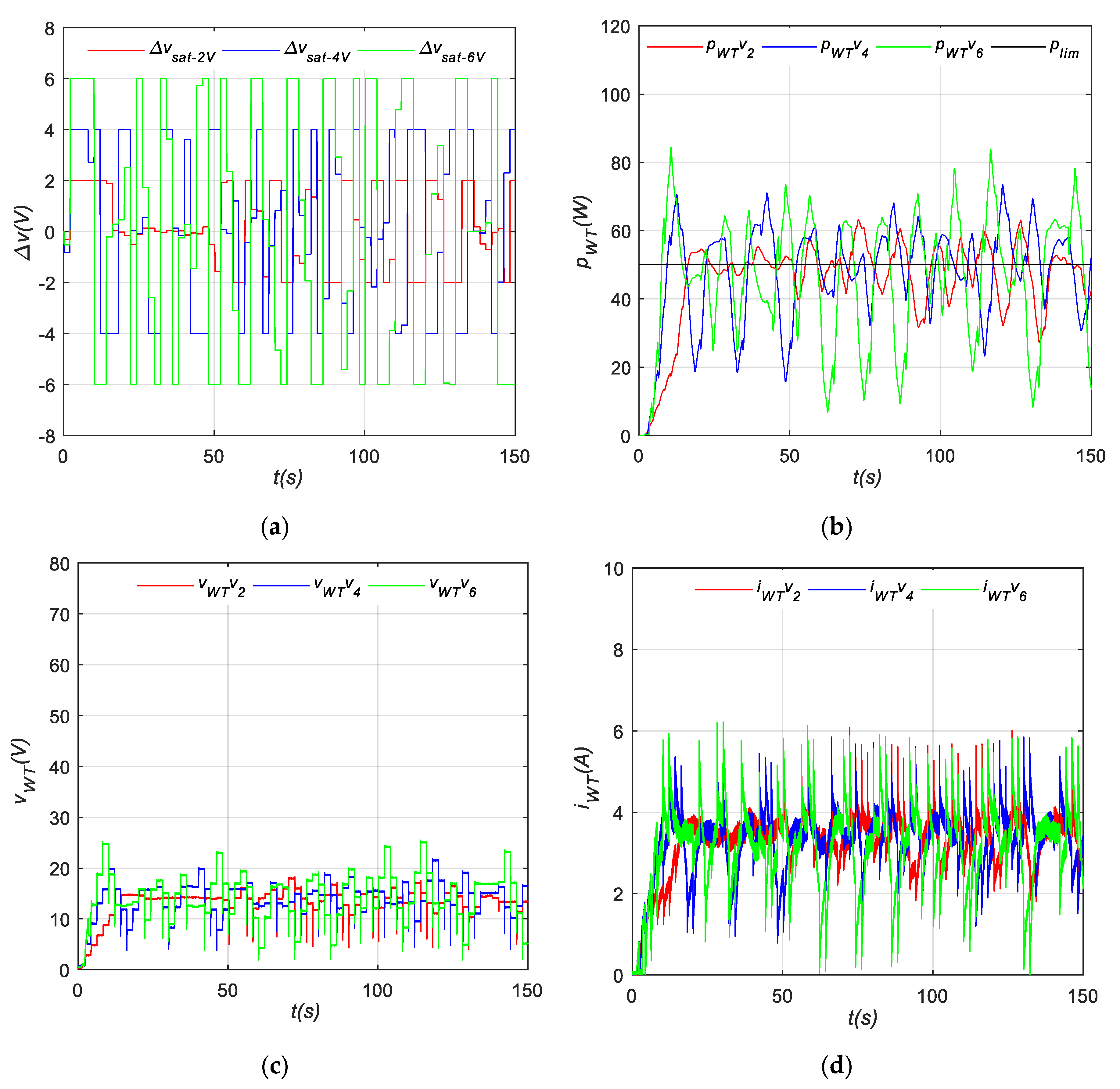
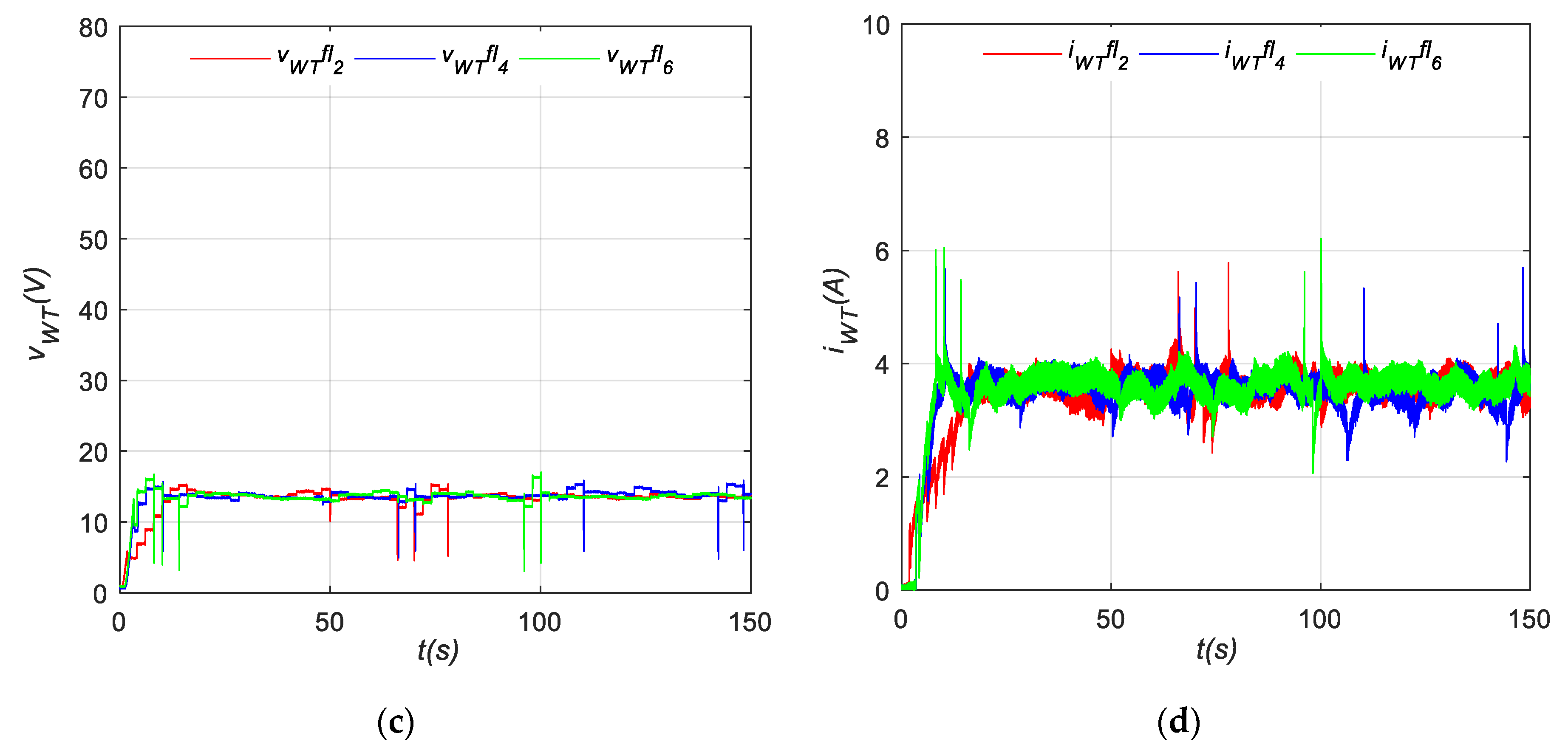
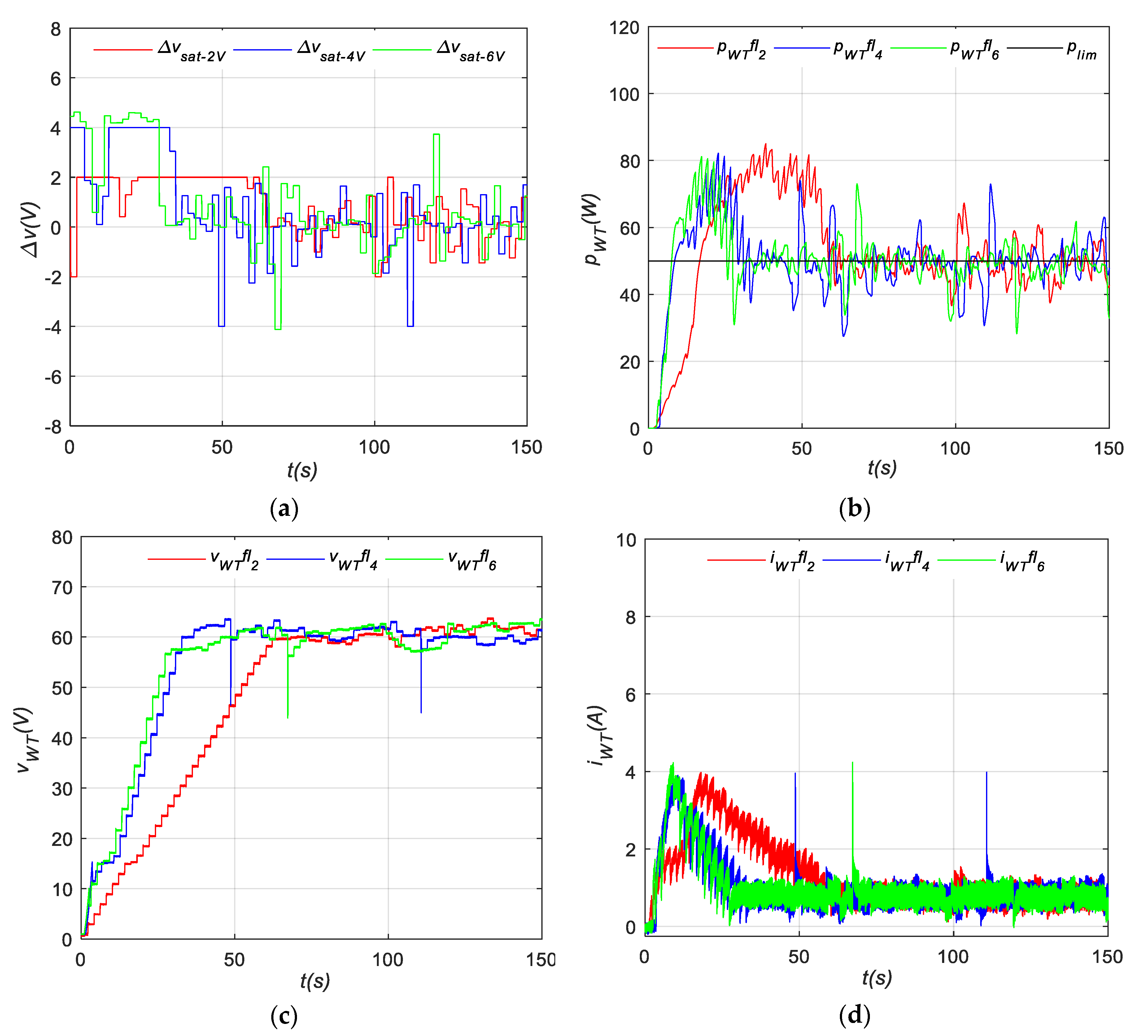
4.1.3. P&O Based on FL
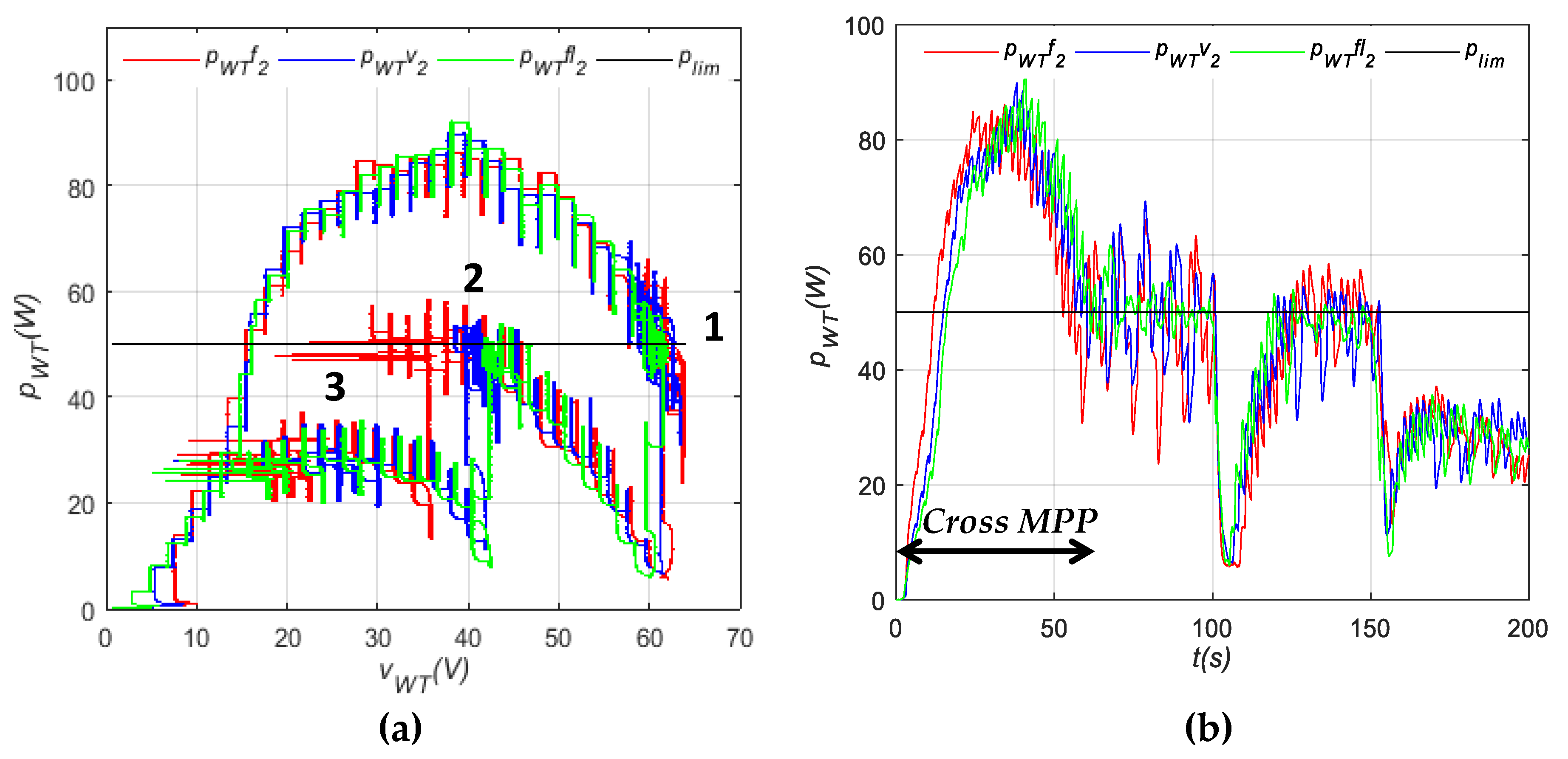
4.1.4. Comparison of the Power Control Methods
4.2. Impact of Sudden Variations on the Performance of the WT System
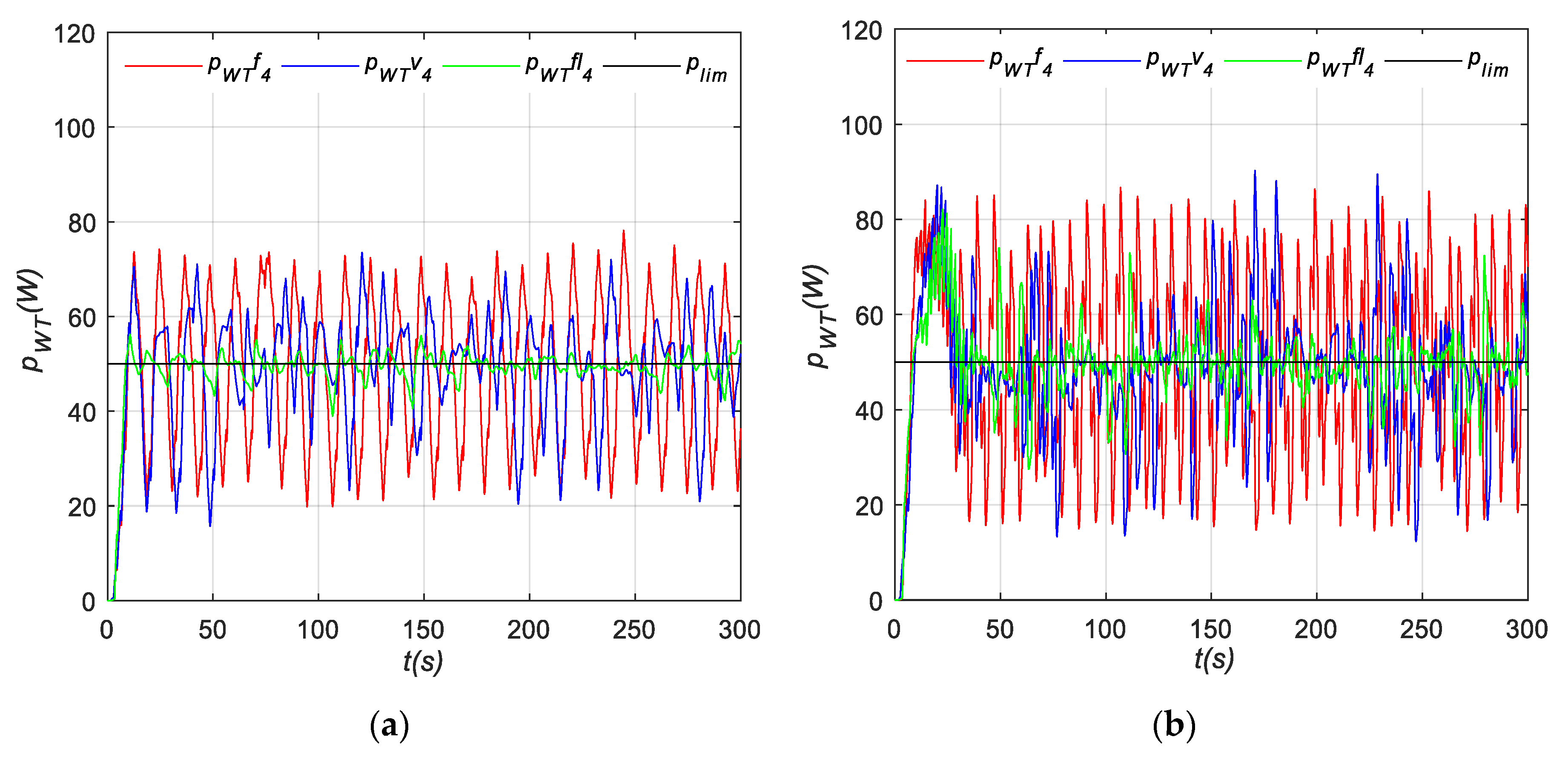
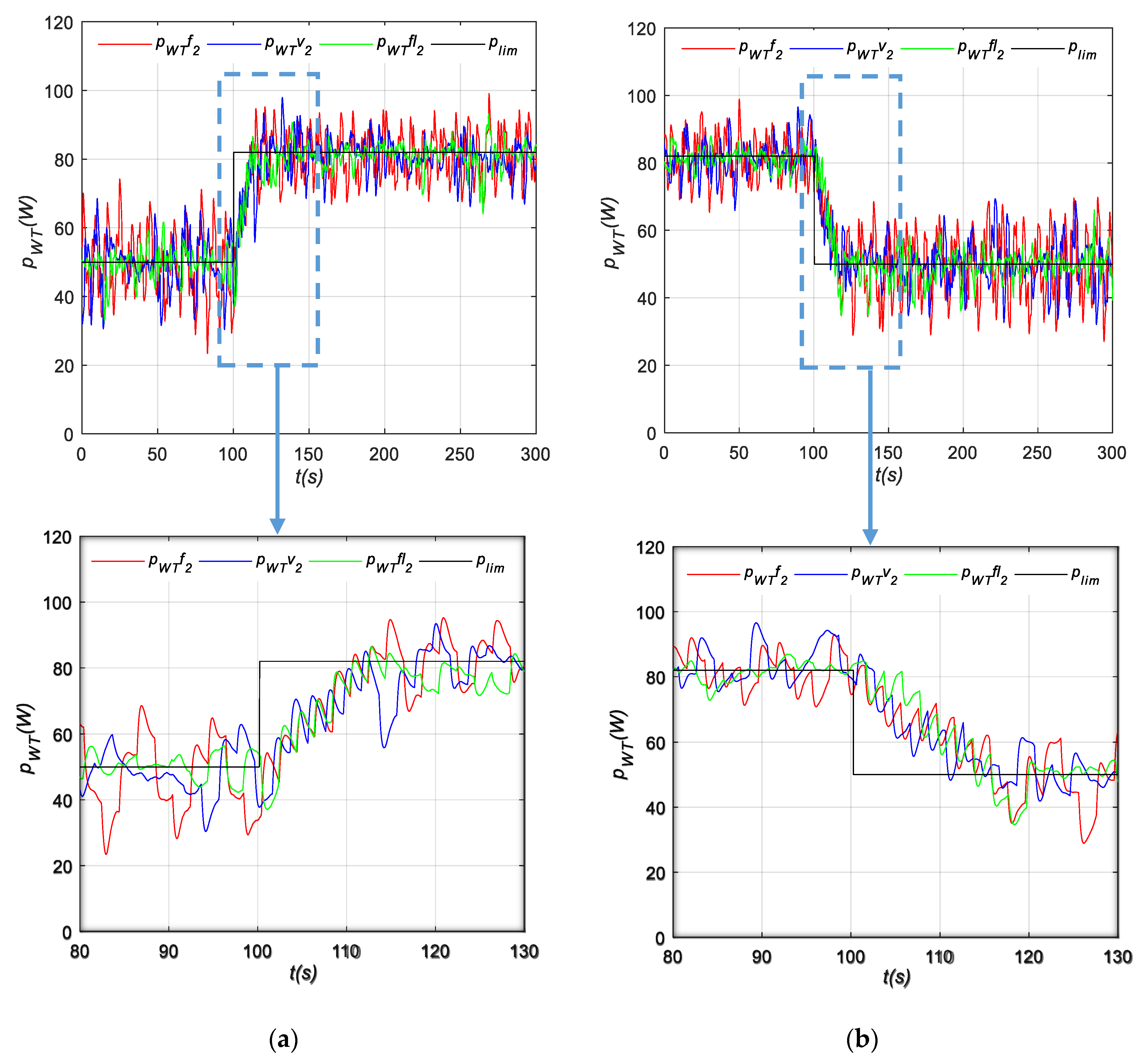
4.2.1. Power Variation
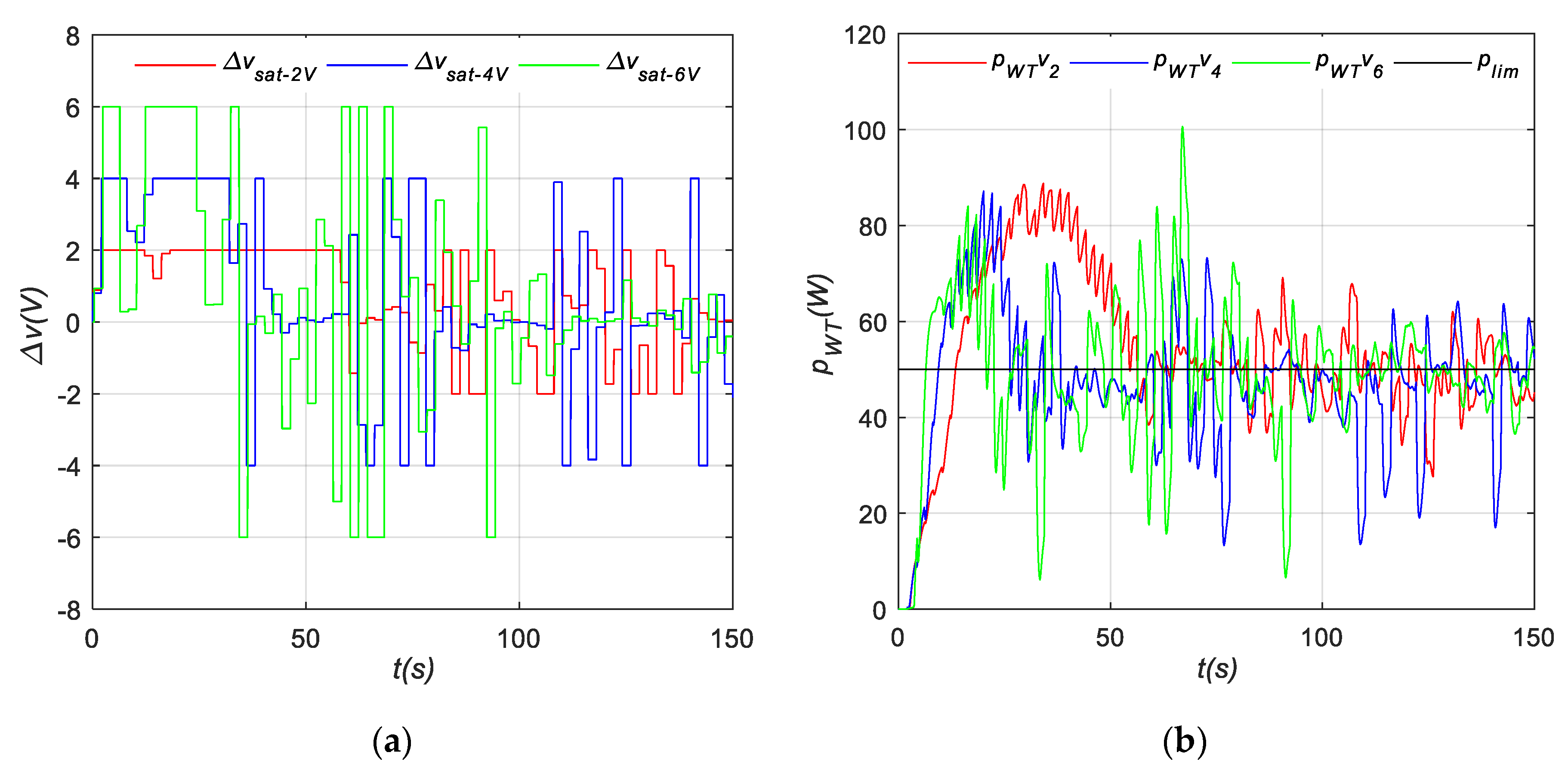
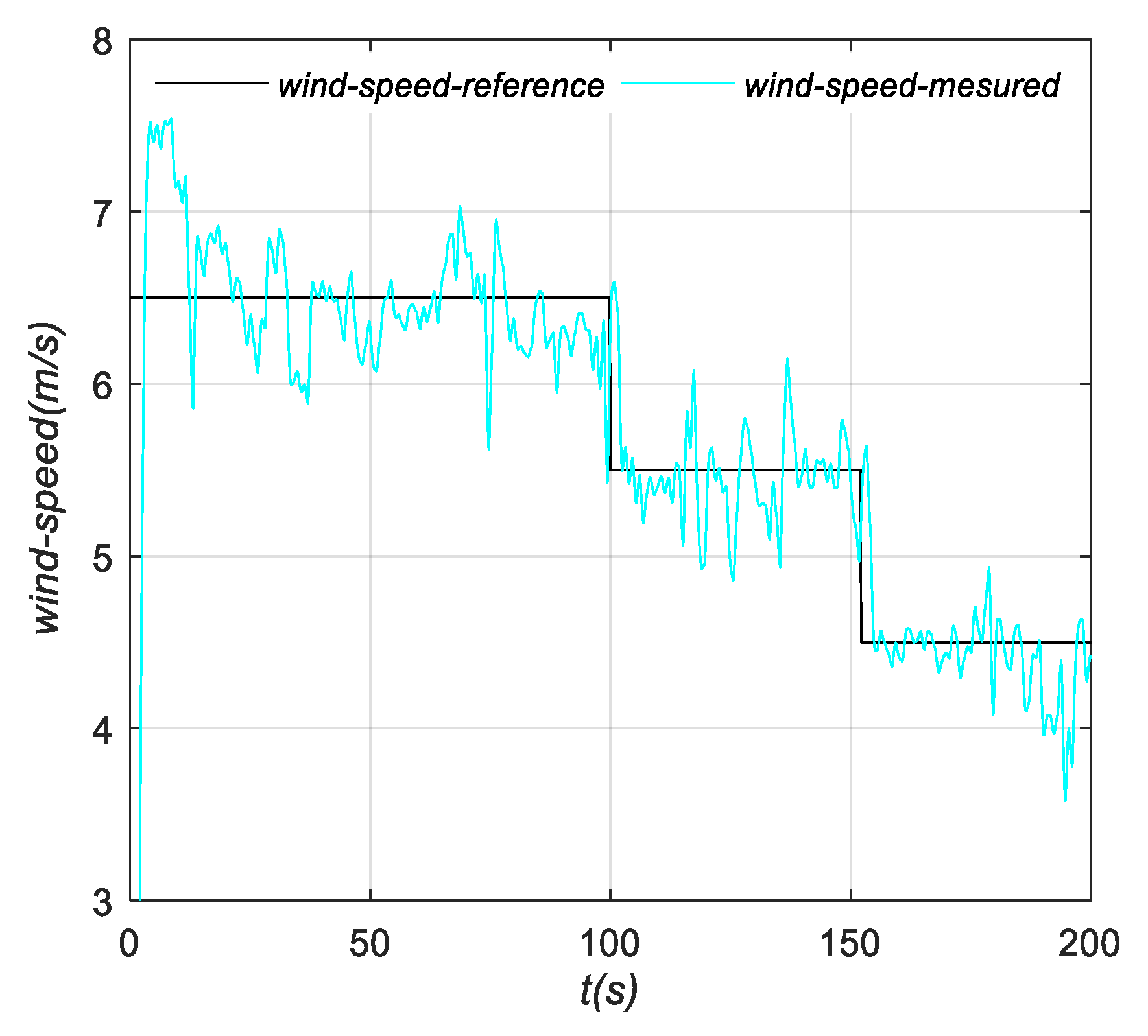
4.2.2. Wind Speed Variation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Owusu, P.A.; Asumadu-Sarkodie, S. A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 2016, 3, 1–14. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel high efficient speed sensorless controller for maximum power extraction from wind energy conversion systems. Energy Convers. Manag. 2016, 123, 392–401. [Google Scholar] [CrossRef]
- Sechilariu, M.; Wang, B.C.; Locment, F.; Jouglet, A. DC microgrid power flow optimization by multi-layer supervision control. Design and experimental validation. Energy Convers. Manag. 2014. [Google Scholar] [CrossRef]
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef] [Green Version]
- Al-Ghossini, H.; Locment, F.; Sechilariu, M.; Gagneur, L.; Forgez, C. Adaptive-tuning of extended Kalman filter used for small scale wind generator control. Renew. Energy 2016. [Google Scholar] [CrossRef]
- Hussain, J.; Mishra, M.K. Adaptive Maximum Power Point Tracking Control Algorithm for Wind Energy Conversion Systems. IEEE Trans. Energy Convers. 2016, 31, 697–705. [Google Scholar] [CrossRef]
- Daili, Y.; Gaubert, J.P.; Rahmani, L. New control strategy for fast-efficient maximum power point tracking without mechanical sensors applied to small wind energy conversion system. J. Renew. Sustain. Energy 2015, 7. [Google Scholar] [CrossRef]
- Liu, H.; Locment, F.; Sechilariu, M. Integrated control for small power wind generator. Energies 2018, 11, 1217. [Google Scholar] [CrossRef] [Green Version]
- Orlando, N.A.; Liserre, M.; Mastromauro, R.A.; Dell’Aquila, A. A survey of control issues in pmsg-based small wind-turbine systems. IEEE Trans. Ind. Inform. 2013, 9, 1211–1221. [Google Scholar] [CrossRef]
- Daili, Y.; Gaubert, J.P.; Rahmani, L. Implementation of a new maximum power point tracking control strategy for small wind energy conversion systems without mechanical sensors. Energy Convers. Manag. 2015, 97, 298–306. [Google Scholar] [CrossRef]
- Syahputra, R.; Soesanti, I. Performance improvement for small-scale wind turbine system based on maximum power point tracking control. Energies 2019, 12, 3938. [Google Scholar] [CrossRef] [Green Version]
- Vijay Babu, A.R.; Suresh, K.; Umamaheswara Rao, C.; Saida Reddy, C. Design and implementation of high gain power converter for wind energy conversion system. J. Adv. Res. Dyn. Control Syst. 2018, 10, 307–317. [Google Scholar]
- Liu, H.; Locment, F.; Sechilariu, M. Maximum Power Point Tracking Method for Small Scale Wind Generator Experimental validation. In Proceedings of the 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, 28–30 July 2015; pp. 87–101. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Chatterjee, K. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 55, 957–970. [Google Scholar] [CrossRef]
- Amir, A.; Amir, A.; Selvaraj, J.; Rahim, N.A. Study of the MPP tracking algorithms: Focusing the numerical method techniques. Renew. Sustain. Energy Rev. 2016, 62, 350–371. [Google Scholar] [CrossRef]
- Nasiri, M.; Milimonfared, J.; Fathi, S.H. Modeling, analysis and comparison of TSR and OTC methods for MPPT and power smoothing in permanent magnet synchronous generator-based wind turbines. Energy Convers. Manag. 2014, 86, 892–900. [Google Scholar] [CrossRef]
- Tiwari, R.; Babu, N.R. Fuzzy logic based MPPT for permanent magnet synchronous generator in wind energy conversion system. IFAC-PapersOnLine 2016, 49, 462–467. [Google Scholar] [CrossRef]
- Urtasun, A.; Sanchis, P.; Marroyo, L. Limiting the power generated by a photovoltaic system. In Proceedings of the 10th International Multi-Conferences on Systems, Signals & Devices 2013 (SSD13), Hammamet, Tunisia, 18–21 March 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Rezk, H.; Eltamaly, A.M. A comprehensive comparison of different MPPT techniques for photovoltaic systems. Sol. Energy 2015, 112, 1–11. [Google Scholar] [CrossRef]
- Belmokhtar, K.; Doumbia, M.L.; Agbossou, K. Novel fuzzy logic based sensorless maximum power point tracking strategy for wind turbine systems driven DFIG (doubly-fed induction generator). Energy 2014, 76, 679–693. [Google Scholar] [CrossRef]
- Meghni, B.; Dib, D.; Azar, A.T. A second-order sliding mode and fuzzy logic control to optimal energy management in wind turbine with battery storage. Neural Comput. Appl. 2017, 28, 1417–1434. [Google Scholar] [CrossRef]
- Calabrese, D.; Tricarico, G.; Brescia, E.; Cascella, G.L.; Monopoli, V.G.; Cupertino, F. Variable structure control of a small ducted wind turbine in the whole wind speed range using a luenberger observer. Energies 2020, 13, 4647. [Google Scholar] [CrossRef]
- Lin, C.-H. Wind Turbine Driving a PM Synchronous Generator Using Novel Recurrent Chebyshev Neural Network Control with the Ideal Learning Rate. Energies 2016, 9, 441. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, L.; Liu, Y. Implementation of maximum power point tracking based on variable speed forecasting for wind energy systems. Processes 2019, 7, 158. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.H.; Hsu, Y.Y. Effect of rotor excitation voltage on steady-state stability and maximum output power of a doubly fed induction generator. IEEE Trans. Ind. Electron. 2011, 58, 1096–1109. [Google Scholar] [CrossRef]
- Belhadji, L.; Bacha, S.; Munteanu, I.; Rumeau, A.; Roye, D. Adaptive MPPT applied to variable-speed microhydropower plant. IEEE Trans. Energy Convers. 2013, 28, 34–43. [Google Scholar] [CrossRef]
- Harrag, A.; Messalti, S. Variable step size modified P&O MPPT algorithm using GA-based hybrid offline/online PID controller. Renew. Sustain. Energy Rev. 2015, 49, 1247–1260. [Google Scholar] [CrossRef]
- Messalti, S.; Harrag, A.; Loukriz, A. A new variable step size neural networks MPPT controller: Review, simulation and hardware implementation. Renew. Sustain. Energy Rev. 2017, 68, 221–233. [Google Scholar] [CrossRef]
- Hui, J.C.Y.; Bakhshai, A.; Jain, P.K. An Energy Management Scheme with Power Limit Capability and an Adaptive Maximum Power Point Tracking for Small Standalone PMSG Wind Energy Systems. IEEE Trans. Power Electron. 2016, 31, 4861–4875. [Google Scholar] [CrossRef]
- Bai, W.; Sechilariu, M. DC Microgrid System Modeling and Simulation Based on a Specific Algorithm for Grid-Connected and Islanded Modes with Real-Time Demand-Side Management Optimization. Appl. Sci. 2020, 10, 2544. [Google Scholar] [CrossRef] [Green Version]
- Tiang, T.L.; Ishak, D. Novel MPPT Control in Permanent Magnet Synchronous Generator System for Battery Energy Storage. Appl. Mech. Mater. 2011, 110–116, 5179–5183. [Google Scholar] [CrossRef]
- Papadopoulos, T.; Tatakis, E.; Koukoulis, E. Improved active and reactive control of a small wind turbine system connected to the grid. Resources 2019, 8, 54. [Google Scholar] [CrossRef] [Green Version]
- Kesraoui, M.; Korichi, N.; Belkadi, A. Maximum power point tracker of wind energy conversion system. Renew. Energy 2011, 36, 2655–2662. [Google Scholar] [CrossRef]
- Lazarov, V.; Roye, D.; Spirov, D.; Zarkov, Z. Study of control strategies for variable speed wind turbine under limited power conditions. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, North Macedonia, 6–8 September 2010; pp. 125–130. [Google Scholar] [CrossRef]
- Linus, R.M.; Damodharan, P. Maximum power point tracking method using a modified perturb and observe algorithm for grid connected wind energy conversion systems. IET Renew. Power Gener. 2015, 9, 682–689. [Google Scholar] [CrossRef]
- Vijayakumar, K.; Kumaresan, N.; Ammasaigounden, N. Speed sensor-less maximum power point tracking and constant output power operation of wind-driven wound rotor induction generators. IET Power Electron. 2015, 8, 33–46. [Google Scholar] [CrossRef]


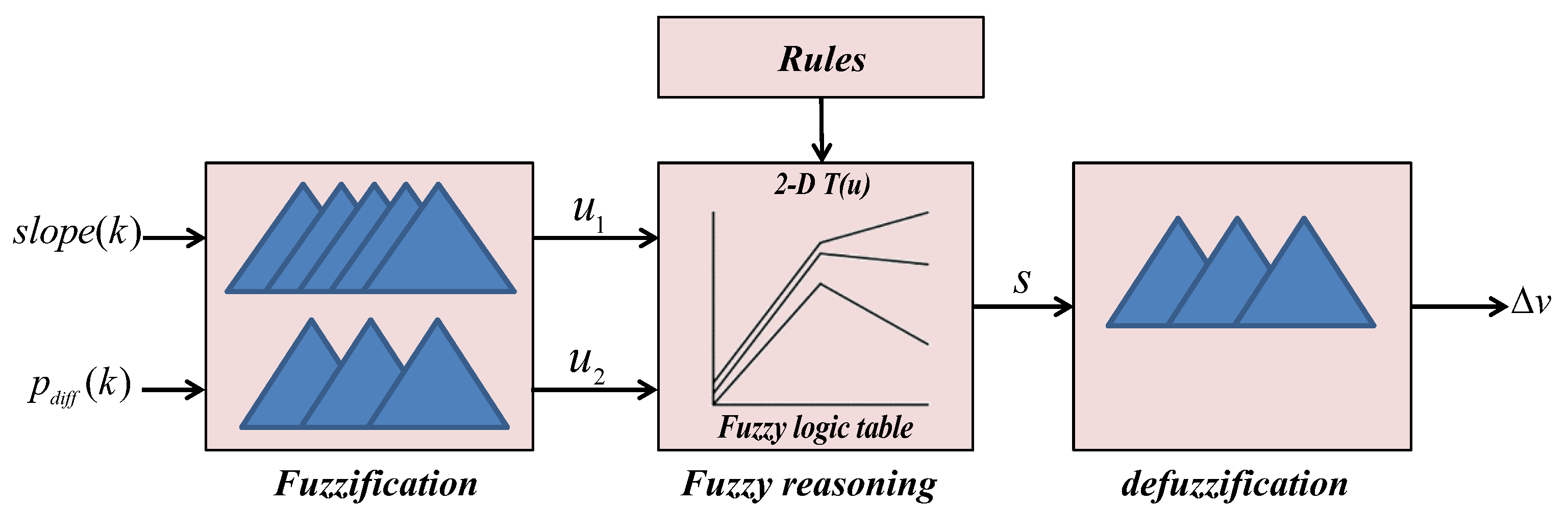





| N | Z | P | ||
|---|---|---|---|---|
| NB | z | z | z | |
| NS | p | z | n | |
| ZE | p | z | n | |
| PS | p | z | n | |
| PB | z | z | z | |
| Control Strategy Method | LPP1 (Mean ± SD) | LPP2 (Mean ± SD) |
|---|---|---|
| Fix step size | 48.6 ± 15.4 | 49.8 ± 19.3 |
| Newton’s method | 49.5 ± 10.0 | 48.3 ± 12.7 |
| Fuzzy logic | 49.6 ± 2.4 | 49.3 ± 5.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aourir, J.; Locment, F. Limited Power Point Tracking for a Small-Scale Wind Turbine Intended to Be Integrated in a DC Microgrid. Appl. Sci. 2020, 10, 8030. https://doi.org/10.3390/app10228030
Aourir J, Locment F. Limited Power Point Tracking for a Small-Scale Wind Turbine Intended to Be Integrated in a DC Microgrid. Applied Sciences. 2020; 10(22):8030. https://doi.org/10.3390/app10228030
Chicago/Turabian StyleAourir, Jamila, and Fabrice Locment. 2020. "Limited Power Point Tracking for a Small-Scale Wind Turbine Intended to Be Integrated in a DC Microgrid" Applied Sciences 10, no. 22: 8030. https://doi.org/10.3390/app10228030





