Wind Turbines Optimal Operation at Time Variable Wind Speeds
Abstract
:1. Introduction
2. Wind Turbine’s Mathematical Model
3. PMSG’s Optimal Power Determination based on the Kinetic Motion Equation
- the first term, which is dependent on the moment of total inertia, is called the “inertial power”,
- the second term, , which is dependent on the PMSG’s angular speed, , and on the wind speed, , as depicted by Equation (1), represents the “wind turbine’s power”.
- the third term, which is dependent on the PMSG’s angular speed, , and on the load resistance, represents the PMSG’s power, .
- the first term, , represents the wind energy captured by the wind turbine during the time interval, ,
- the second term, , represents the energy delivered by the PMSG to the main grid,
- the third term, , represents the kinetic energy,where the variation of the kinetic energies, , can be determined very precisely by measuring the PMSG’s angular speed, .
4. PMSG’s Optimal Power Control Based on the PI-type Regulator
5. PMSG’s Optimal Power Control Based on the PID-type Regulator
6. Case Study
6.1. PMSG’s Optimal Power Determination
6.2. PI-Based Control of the PMSG’s Optimal Power
6.3. PID-Based Control of the PMSG’s Optimal Power
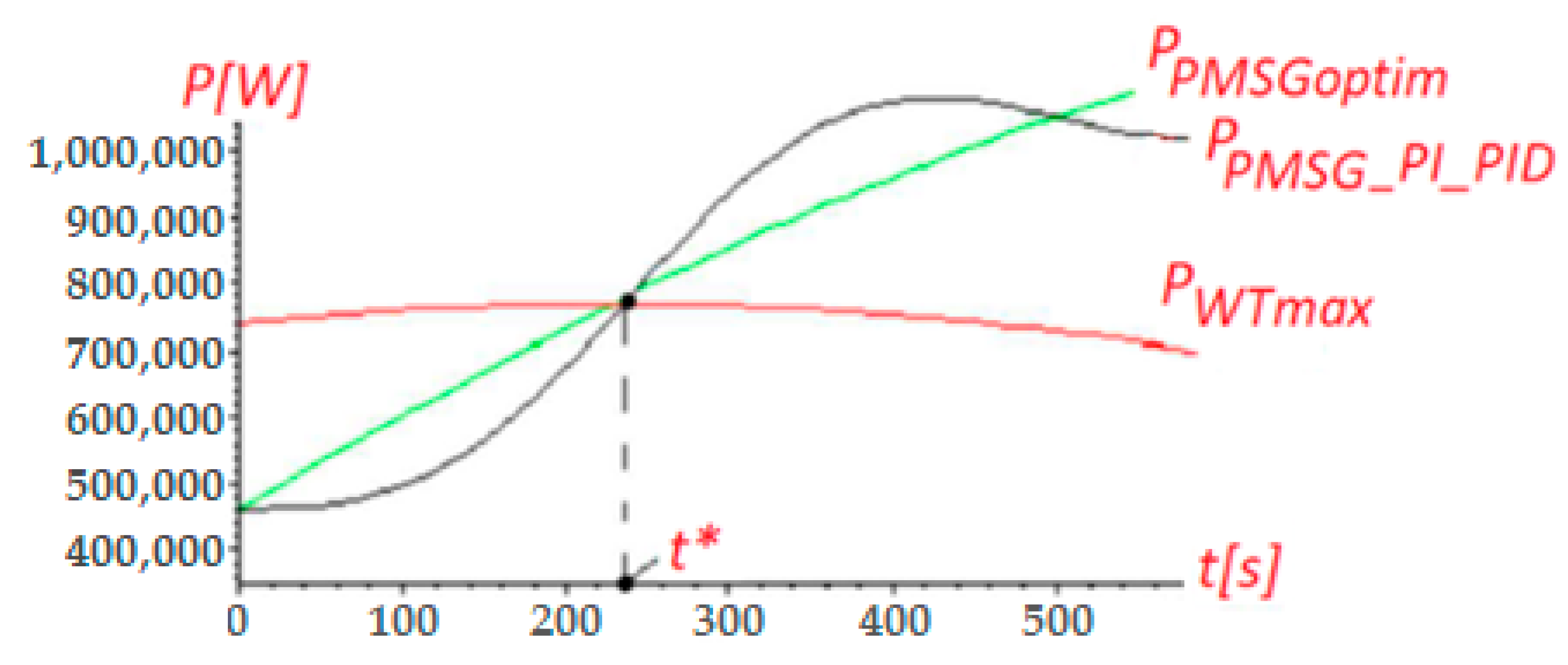
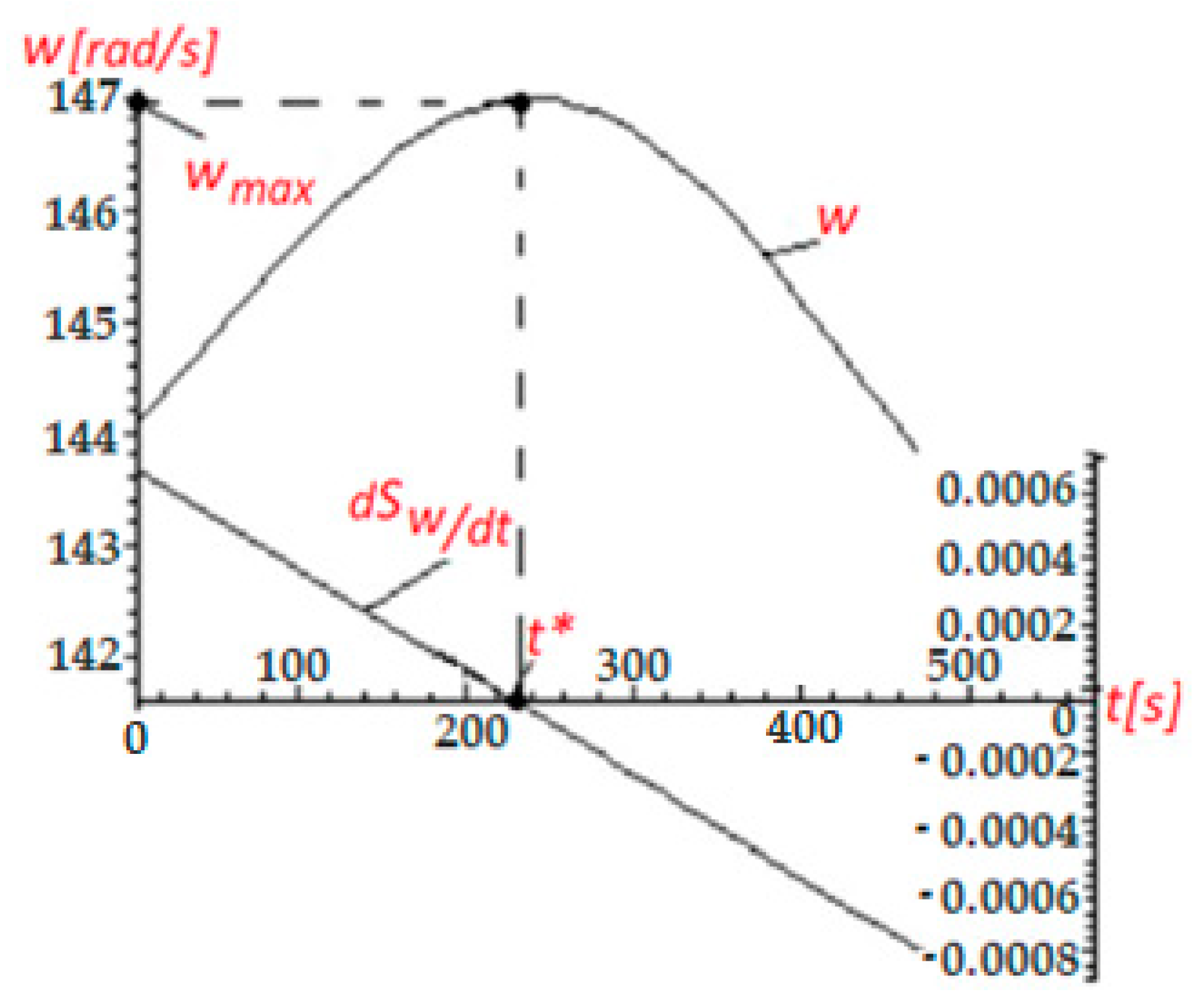
- the maximum wind turbine’s power when operating at MPP, defined in Equation (47) ()
- the PMSG’s optimal power calculated from the kinetic motion equation, defined in Equation (49) ()
- the PMSG’s power obtained by using either the PI- or PID-type regulators, , resulting from either Equation (62) or Equation (67).
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
Appendix A
| Type | Horizontal Axis Wind Turbine with Variable Rotor Speed |
|---|---|
| Rotor diameter | 100 m |
| Power regulation | Independent electromechanical pitch system for each blade |
| Rated power | 2500 kW |
| Hub height | 100 m |
| Rated rotational speed | 14.05 rpm |
| Operating range rotational speed | 3.83–15.61 rpm |
| Cut-in wind speed | 3 m/s |
| Rated wind speed | 12 m/s |
| Cut-out wind speed (10-min mean) | 25 m/s |
| Extreme wind speed (50-year mean) | 37.5 m/s |
| Annual average wind speed | 7.5 m/s |
| Design life time | 20 years |
| IEC 61400-1, class | IIIA |
| Variable | Description | Units |
|---|---|---|
| delivered energy | (J) | |
| captured wind energy | (J) | |
| kinetic energy | (J) | |
| total moment of inertia | () | |
| inertial power | (W) | |
| PMSG’s power | (W) | |
| PMSG’s average power | (W) | |
| PMSG’s optimal power | (W) | |
| PMSG’s power obtained by using either the PI- or PID-type regulators | (W) | |
| PMSG’s power in the case of PI control | (W) | |
| PMSG’s power in the case of PID control | (W) | |
| wind turbine’s power | (W) | |
| wind turbine’s average power | (W) | |
| wind turbine’s maximum power | (W) | |
| PMSG’s torque | (Nm) | |
| wind turbine’s torque | (Nm) | |
| wind speed | (m/s) | |
| measured wind speed | (m/s) | |
| PMSG’s angular speed | (rad/s) | |
| PMSG’s maximum angular speed | (rad/s) | |
| PMSG’s optimal angular speed | (rad/s) | |
| the PMSG’s angular speed at time instant | (rad/s) | |
| the PMSG’s angular speed at time instant | (rad/s) |
References
- Qi, L.; Zheng, L.; Bai, X.; Chen, Q.; Chen, J.; Chen, Y. Chen Nonlinear Maximum Power Point Tracking Control Method for Wind Turbines Considering Dynamics. Appl. Sci. 2020, 10, 811. [Google Scholar] [CrossRef] [Green Version]
- Sorandaru, C.; Musuroi, S.; Ancuti, M.-C.; Erdodi, G.-M.; Petrescu, D.-I. Equivalent power for a wind power system. In Proceedings of the 2016 IEEE 11th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 12–14 May 2016; pp. 225–228. [Google Scholar] [CrossRef]
- Sorandaru, C.; Musuroi, S.; Frigura-Iliasa, F.M.; Vatau, D.; Dordescu, M. Analysis of the Wind System Operation in the Optimal Energetic Area at Variable Wind Speed over Time. Sustainability 2019, 11, 1249. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, M.; Yatim, A.H.; Tan, C.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Hussein, M.M.; Senjyu, T.; Orabi, M.; Wahab, M.A.A.; Hamada, M.M. Control of a Stand-Alone Variable Speed Wind Energy Supply System. Appl. Sci. 2013, 3, 437–456. [Google Scholar] [CrossRef] [Green Version]
- Yin, M.; Li, W.; Chung, C.Y.; Zhou, L.; Chen, Z.; Zou, Y. Optimal torque control based on effective tracking range for maximum power point tracking of wind turbines under varying wind conditions. IET Renew. Power Gener. 2017, 11, 501–510. [Google Scholar] [CrossRef]
- Yang, Z.; Yin, M.; Xu, Y.; Zou, Y.; Dong, Z.Y.; Zhou, Q. Inverse Aerodynamic Optimization Considering Impacts of Design Tip Speed Ratio for Variable-Speed Wind Turbines. Energies 2016, 9, 1023. [Google Scholar] [CrossRef] [Green Version]
- Seo, S.; Oh, S.-D.; Kwak, H.-Y. Wind turbine power curve modeling using maximum likelihood estimation method. Renew. Energy 2019, 136, 1164–1169. [Google Scholar] [CrossRef]
- Marčiukaitis, M.; Žutautaitė, I.; Martišauskas, L.; Jokšas, B.; Gecevičius, G.; Sfetsos, A. Non-linear regression model for wind turbine power curve. Renew. Energy 2017, 113, 732–741. [Google Scholar] [CrossRef]
- Taslimi-Renani, E.; Delshad, M.M.; Elias, M.F.M.; Rahim, N.A. Development of an enhanced parametric model for wind turbine power curve. Appl. Energy 2016, 177, 544–552. [Google Scholar] [CrossRef]
- Linus, R.M.; Damodharan, P. Maximum power point tracking method using a modified perturb and observe algorithm for grid connected wind energy conversion systems. IET Renew. Power Gener. 2015, 9, 682–689. [Google Scholar] [CrossRef]
- Karabacak, M.; Fernández-Ramírez, L.M.; Kamal, T.; Kamal, S. A New Hill Climbing Maximum Power Tracking Control for Wind Turbines With Inertial Effect Compensation. IEEE Trans. Ind. Electron. 2019, 66, 8545–8556. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Jokar, M.A.; Kalhor, A. Using artificial neural networks for temporal and spatial wind speed forecasting in Iran. Energy Convers. Manag. 2016, 115, 17–25. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, Z.; Qiao, W.; Qu, L. An Adaptive Network-Based Reinforcement Learning Method for MPPT Control of PMSG Wind Energy Conversion Systems. IEEE Trans. Power Electron. 2016, 31, 7837–7848. [Google Scholar] [CrossRef]
- Navarrete, E.C.; Trejo-Perea, M.; Correa, J.C.J.; Carrillo-Serrano, R.V.; Ríos-Moreno, J.G. Expert Control Systems for Maximum Power Point Tracking in a Wind Turbine with PMSG: State of the Art. Appl. Sci. 2019, 9, 2469. [Google Scholar] [CrossRef] [Green Version]
- Zuluaga, C.; Álvarez, M.A.; Giraldo, E. Short-term wind speed prediction based on robust Kalman filtering: An experimental comparison. Appl. Energy 2015, 156, 321–330. [Google Scholar] [CrossRef]
- Beltran, O.; Peña, R.; Ramírez, J.S.; Esparza, A.; Muljadi, E.; Gao, W. Inertia Estimation of Wind Power Plants Based on the Swing Equation and Phasor Measurement Units. Appl. Sci. 2018, 8, 2413. [Google Scholar] [CrossRef] [Green Version]
- Shang, L.; Hu, J.; Yuan, X.; Chi, Y. Understanding Inertial Response of Variable-Speed Wind Turbines by Defined Internal Potential Vector. Energies 2016, 10, 22. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Dong, J.; Jiang, L. Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Appl. Energy 2018, 210, 711–723. [Google Scholar] [CrossRef]
- Liu, X.; Han, Y.; Wang, C. Second-order sliding mode control for power optimisation of DFIG-based variable speed wind turbine. IET Renew. Power Gener. 2017, 11, 408–418. [Google Scholar] [CrossRef]
- Available online: http://www.monsson.eu (accessed on 10 December 2019).
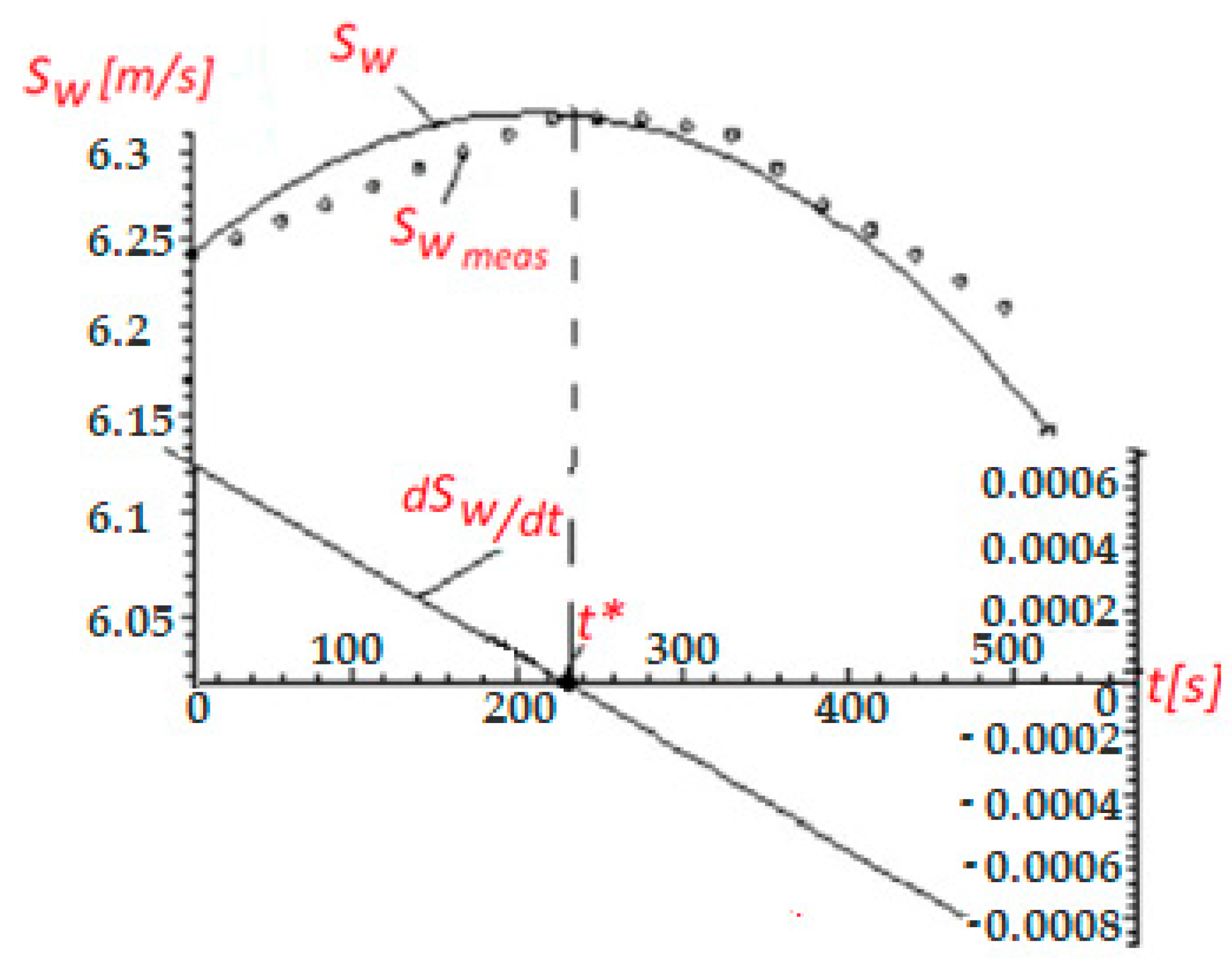
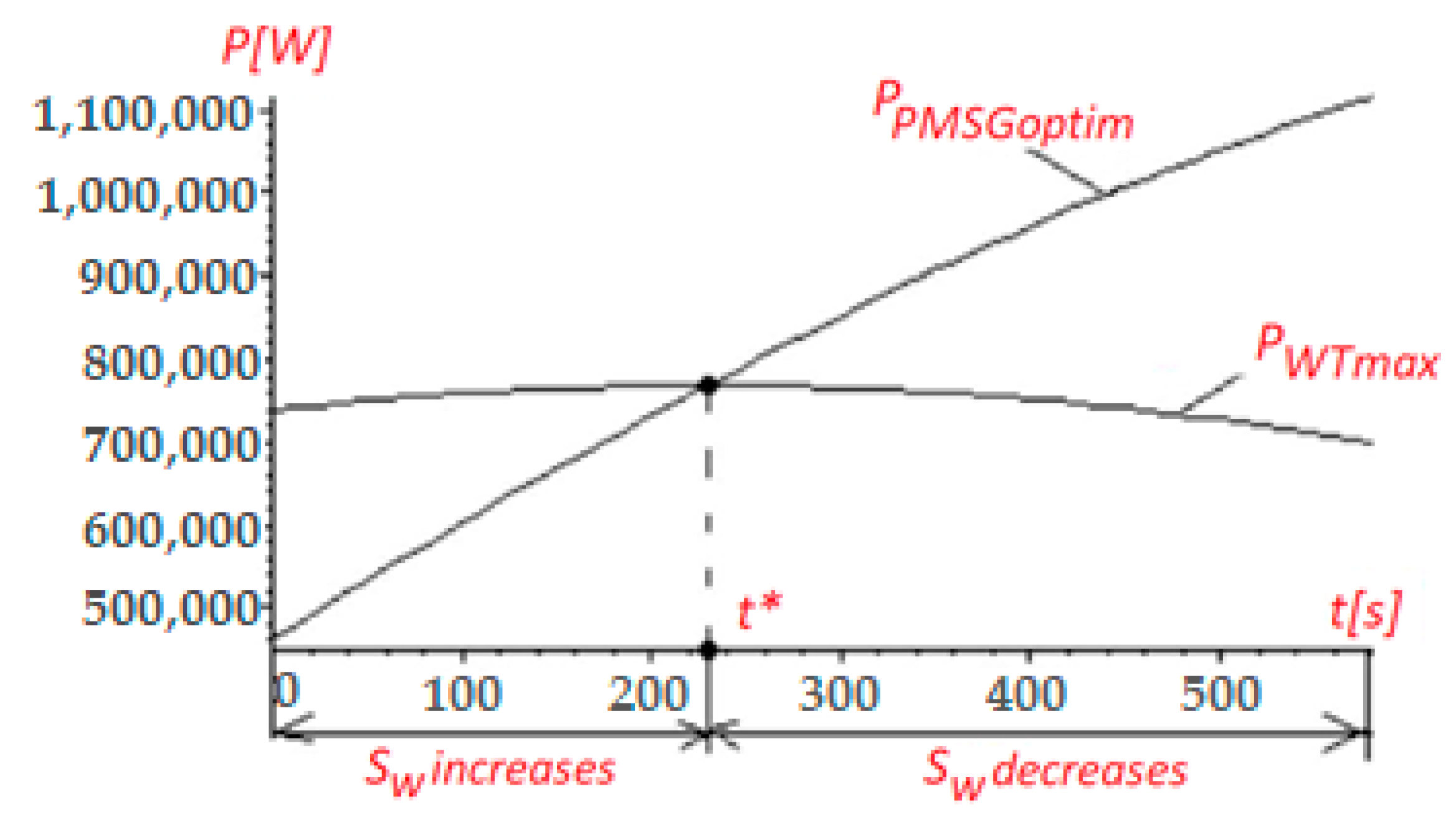

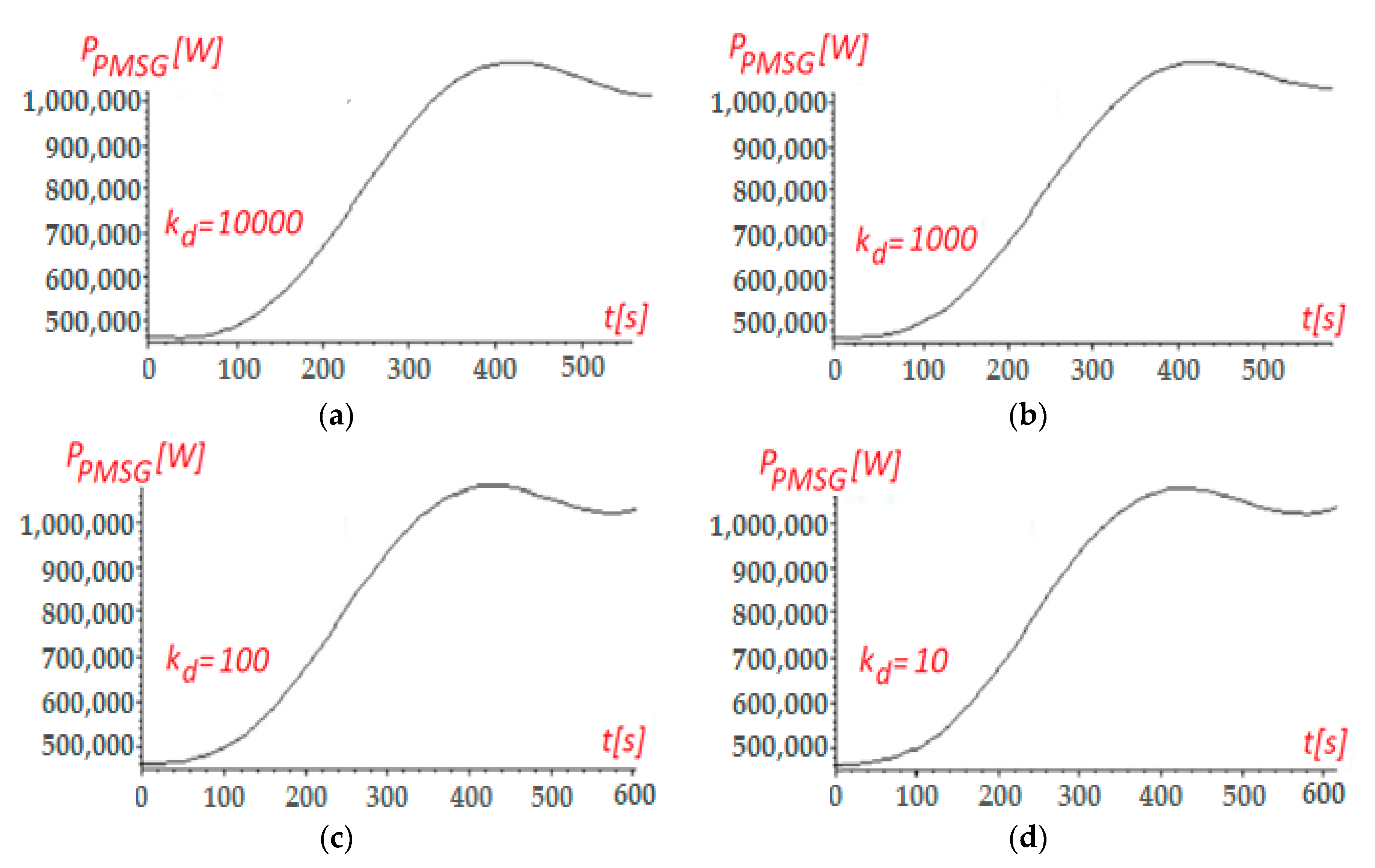
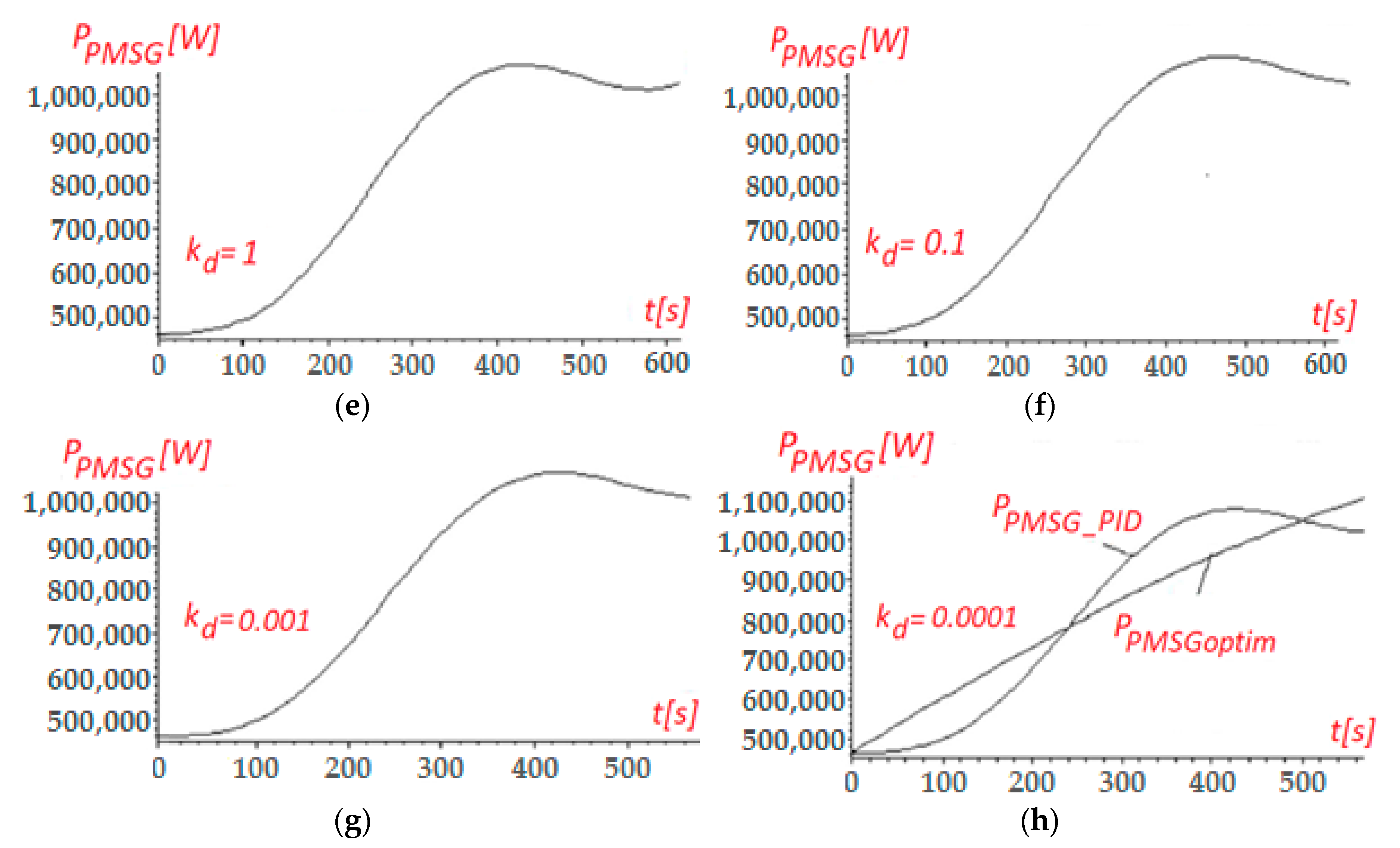
| t (s) | Swmeas(t) (m/s) |
|---|---|
| 0 | 6.24 |
| 30 | 6.25 |
| 60 | 6.26 |
| 90 | 6.27 |
| 120 | 6.28 |
| 150 | 6.29 |
| 180 | 6.3 |
| 210 | 6.31 |
| 240 | 6.32 |
| 270 | 6.32 |
| 300 | 6.32 |
| 330 | 6.315 |
| 360 | 6.31 |
| 390 | 6.29 |
| 420 | 6.27 |
| 450 | 6.255 |
| 480 | 6.24 |
| 510 | 6.225 |
| 540 | 6.21 |
| 570 | 6.14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ancuti, M.-C.; Musuroi, S.; Sorandaru, C.; Dordescu, M.; Erdodi, G.M. Wind Turbines Optimal Operation at Time Variable Wind Speeds. Appl. Sci. 2020, 10, 4232. https://doi.org/10.3390/app10124232
Ancuti M-C, Musuroi S, Sorandaru C, Dordescu M, Erdodi GM. Wind Turbines Optimal Operation at Time Variable Wind Speeds. Applied Sciences. 2020; 10(12):4232. https://doi.org/10.3390/app10124232
Chicago/Turabian StyleAncuti, Mihaela-Codruta, Sorin Musuroi, Ciprian Sorandaru, Marian Dordescu, and Geza Mihai Erdodi. 2020. "Wind Turbines Optimal Operation at Time Variable Wind Speeds" Applied Sciences 10, no. 12: 4232. https://doi.org/10.3390/app10124232






