There are six parameters in our model. The task is defined by its size, N, and its complexity, K. Environmental turbulence is captured by μ. The organization is characterized by the number of agents, M, the frequency of knowledge sharing among them, p, and the degree of autonomy, λ. In all the simulations, we fix N and M at 100 and 20, respectively, and vary other parameters to investigate the effect of autonomy/conformity and frequency of communications on the performance of organizations under various degrees of complexity and turbulence. Appendix shows the results from and , which are similar to the results from .
To summarize the performance of an organization over time, we mainly focus on present discounted values (PDVs) of organizational performance over these 1,000 periods: namely, , where δ is a discount factor. Below, we will set the discount factor at . This discount factor gives the payoff for the last period a weight that is 0.37 of that for the first period. If we set the discount factor too low, the payoff at will be given a negligible weight compared to those for earlier periods. For example, if , the weight for the payoff at will be less than of the payoff at . Since performance can take a long time to level off, we want the weight of payoff at to compare favorably with the initial payoffs. We will discuss the effect of changing the value of δ in light of the dynamics of organizational performance below. We also take an average over 500 simulation runs based on varying random seeds, to ensure that our results are not driven by a few special realizations of our simulation.
Before turning to the outcomes of the model simulation, let us briefly discuss the basic property of the NK landscape. It has been shown by Kauffman [
4] that when
and
, the performance function defined by the NK landscape has a unique locally-best configuration (thus, it is also the globally best configuration). Furthermore, it has been shown that local search processes, such as the one we consider in our individual search process, will eventually find the best configuration. Thus, for
and
, differences in performance among organizations with varying values of
p and
are simply due to their speed in finding the best configuration. When
, on the other hand, the NK performance landscape has various local maxima, and local search processes can get stuck with a configuration that corresponds to one of these local maxima and, therefore, fail to find the globally best configuration. When
, the best (locally, as well as globally) configuration changes from time to time. Thus, how fast the right configuration can be found in a changing environment becomes crucial. Keeping this basic property of the NK landscape in mind will help clarify the results that we turn to now.
3.1. Effect of p and λ
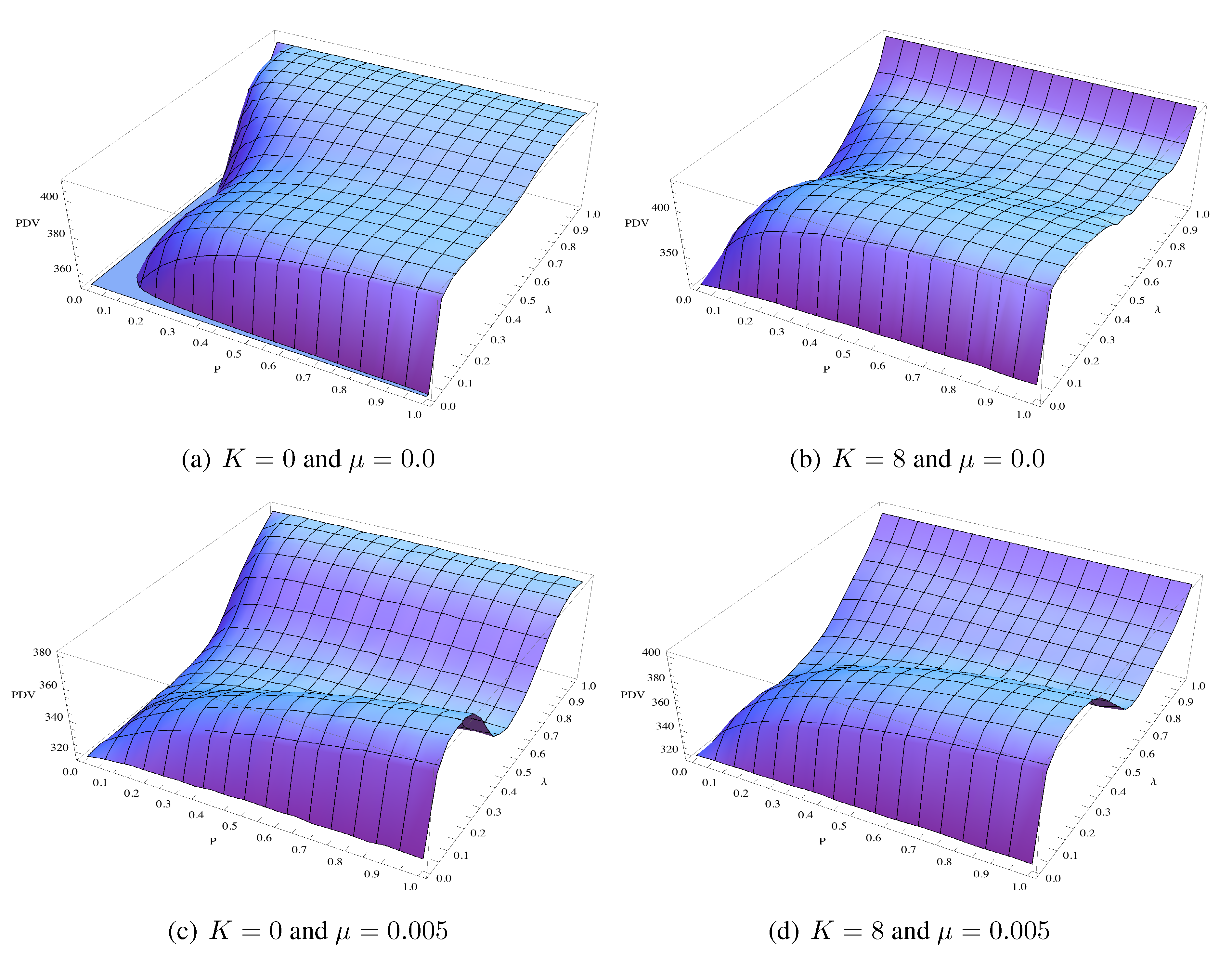
Figure 1 shows the PDV (by height) for various degrees of activeness of communication,
p (the horizontal axis), and of autonomy,
λ (the vertical axis), under four combinations of complexities,
, and uncertainties,
. Recall that a higher
λ represents weaker organizational conformity.
Figure 1.
Average present discounted values (PDVs) of organizational performances for various p and λ in four combinations of task complexity ( (left) and (right)) and environmental turbulence ( (top) and (bottom)). Discount factor is . Data are generated by taking an average over 500 simulation runs for each set of parameter values.
Figure 1.
Average present discounted values (PDVs) of organizational performances for various p and λ in four combinations of task complexity ( (left) and (right)) and environmental turbulence ( (top) and (bottom)). Discount factor is . Data are generated by taking an average over 500 simulation runs for each set of parameter values.
All four panels in
Figure 1 show that organizational performance as measured by PDV improves as the communication becomes more active (
i.e., as we move along the horizontal axis from low to high
p). That is, the more frequently individuals engage in knowledge sharing, the higher their organizational performance, regardless of task complexity and environmental uncertainty.
While the figure exhibits a monotonic relationship between PDV and frequency of knowledge sharing,
p, the relationship between PDV and autonomy,
λ, is not monotonic in three out of four cases shown in
Figure 1. When the task is complex or the environment is turbulent (Panel (b)-(d)), the optimal parameter choices for
λ are bimodal—either full autonomy or a high level of organizational conformity.
Let us first consider the case in which there is a monotonic relationship between PDV and λ. This is true when the task is simple () and the environment stable () (Panel (a)). In this case, a higher λ leads to a higher PDV, although PDV quickly levels off beyond when p is sufficiently high. This result comes from the the property of the NK landscape for and : all individuals in the organization eventually find the unique locally-best (as well as globally best) configuration through their individual search. Forcing them to confirm to organizational knowledge by choosing low λ slows down the search at the individual level (because agents search less often), but the loss from the slow search is limited when organizational knowledge is improved sufficiently rapidly (i.e., when p is high enough). Since the agents’ knowledge becomes homogeneous even without any information sharing (i.e., all approach the unique best configuration), the knowledge heterogeneity in the initial state does not greatly impede organizational learning.
In the remaining three cases shown in Panel (b), (c) and (d), the relationship between PDV and
λ is non-monotonic when the level of knowledge sharing in the organization,
p, is sufficiently high. In these cases, the performance of the organization has two peaks: (1) when autonomy is very high, i.e,
(the
high-autonomy organization); and (2) when there is a substantial, but not overly-strong, organizational conformity,
(the
high-conformity organization). When
λ is very small (so that individual searches are seldom conducted) or has intermediate values of around 0.5 or 0.6, performance becomes low. See
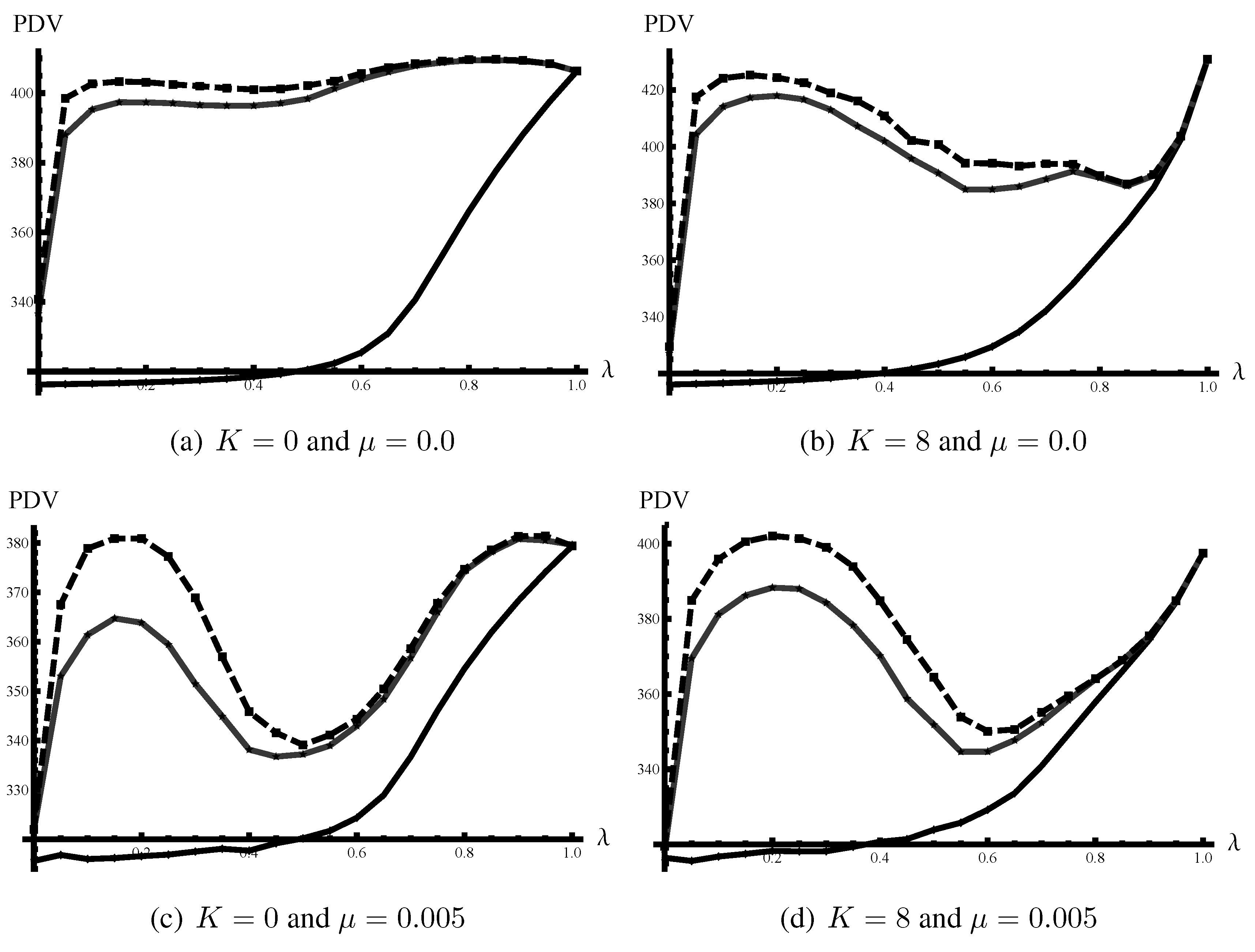
Figure 2 for cross section views of
Figure 1 at
,
and
where the locations of peaks are better illustrated. It can also be seen from the figure that for
to generate as high a level of performance as
, the knowledge-sharing efforts must be persistent (
i.e., sufficiently close to
).
Why do successful organizations, in the face of complex tasks and turbulent environments, bifurcate into two types? In other words, why do we obtain non-monotonic relationships between λ and organizational performance? To answer this question, we turn to the dynamics of performance in the next subsection.
Figure 2.
Average PDVs of organizational performances for various λ in four combinations of task complexity ( (left) and (right)) and environmental turbulence ( (top) and (bottom)). In each figure, results for three distinct ps are reported: (solid black), (solid gray) and (dashed black). The discount factor is . Data are generated by taking an average over 500 simulation runs.
Figure 2.
Average PDVs of organizational performances for various λ in four combinations of task complexity ( (left) and (right)) and environmental turbulence ( (top) and (bottom)). In each figure, results for three distinct ps are reported: (solid black), (solid gray) and (dashed black). The discount factor is . Data are generated by taking an average over 500 simulation runs.
3.2. Dynamics
In this subsection, we show that when the task is complex or the environment turbulent, (1) choosing the intermediate level of
λ substantially slows down both individual and organizational learning; and (2) high-autonomy organizations tend to outperform high-conformity organizations, initially, although the latter eventually outperform the former.
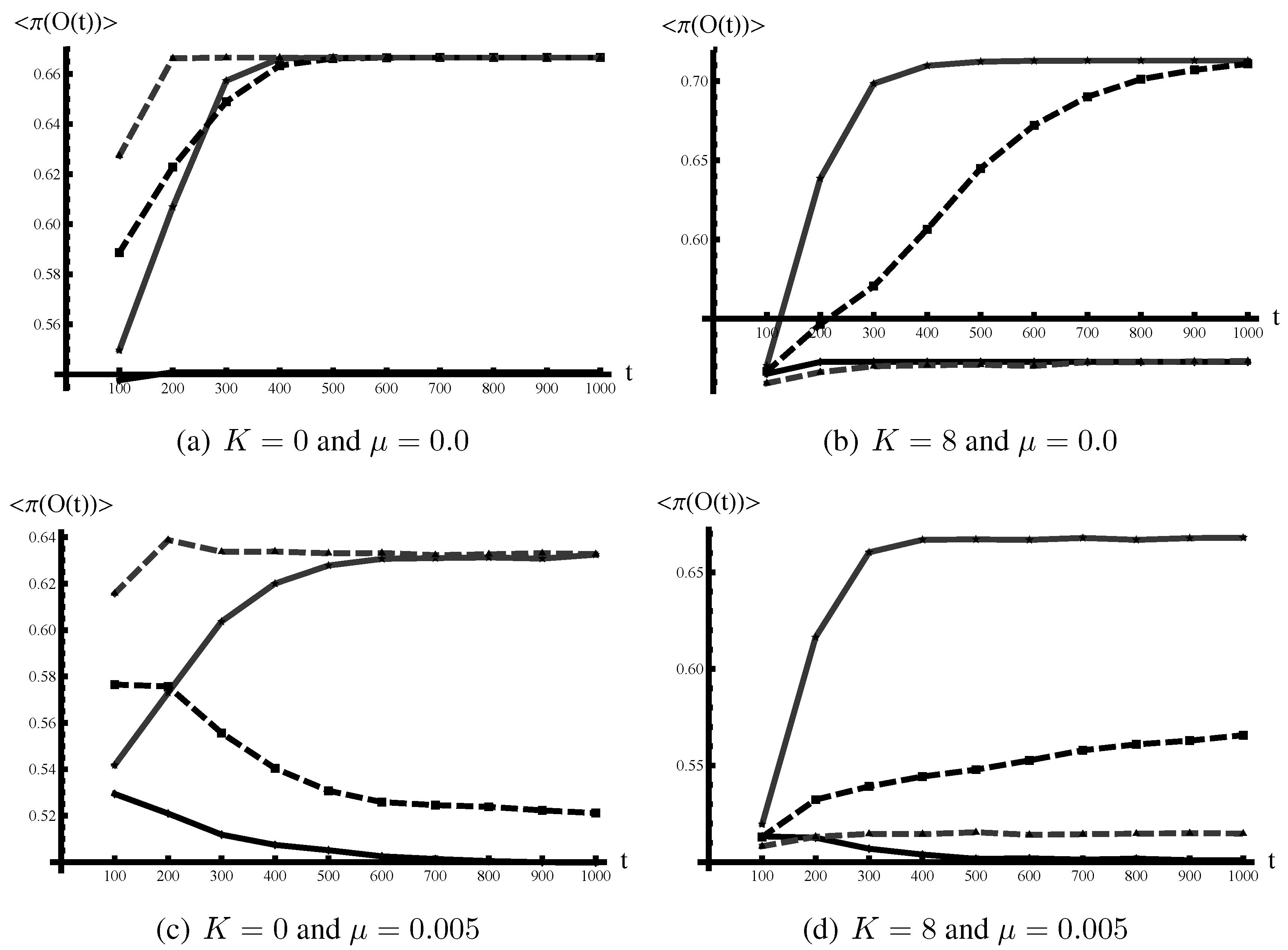
Figure 3 shows the evolution of organizational performance over time for four values of
λ,
(shown in solid black, solid gray, dashed black and dashed gray, respectively) and for the four combinations of
and
. These four
λs are chosen, because they correspond approximately to the local maxima and minima of organizational performance measured by PDV. Knowledge sharing within an organization is assumed to be very frequent,
. As we have seen above, a lower value of
p results in lower performance for an organization with
λ lower than one.
Figure 3 reports the average per-period organizational performance for each block of 100 periods,
i.e., for
,
, and so on.
Figure 3.
Average performance over time for two levels of complexity, (left) and (right) and two degrees of environmental turbulence, (top) and (bottom). Four values of λ are considered: (solid black), (solid gray), (dashed black) and (dashed gray). The communication is active (). The data is generated by taking the average per period organizational performance for each block of 100 periods. The average from 500 simulation runs is reported.
Figure 3.
Average performance over time for two levels of complexity, (left) and (right) and two degrees of environmental turbulence, (top) and (bottom). Four values of λ are considered: (solid black), (solid gray), (dashed black) and (dashed gray). The communication is active (). The data is generated by taking the average per period organizational performance for each block of 100 periods. The average from 500 simulation runs is reported.
When the task is simple and the environment stable (i.e., and ), organizations with high autonomy (i.e., higher λs) improve their performance faster (Panel (a)). As discussed above, the best configuration for the task can be found through the particular local search process considered in this paper. Therefore, all the agents in an organization will eventually find the unique best configuration as long as . (Note that when , there is no individual search, so agents never find the best configuration). Once everyone in an organization has found the best configuration, there is no further improvement in organizational performance. Organizations with the highest autonomy that conduct only individual searches () do not necessarily outperform organizations with higher levels of conformity (), because the latter organizations can achieve very good performance, provided knowledge sharing takes place frequently enough. As knowledge sharing becomes less frequent (i.e., lower p), however, the higher conformity imposed on individuals (i.e., lower λ) does tend to hinder individual searches and impair organizational performance.
When the task is complex, the results are quite different, even in the complete absence of environmental turbulence. Panel (b) of the
Figure 3 shows that a higher value of
λ corresponds to a higher performance only in the early periods, namely the first 100 periods. In later periods, for example, for
, while
(dashed gray) exhibits the highest performance, the performance of
(dashed black) is lower than that of
(solid gray). Eventually,
outperforms
. This case demonstrates the possible trade-off between performance in earlier periods and performance in later periods. This reversal in relative performance between high-autonomy organizations and high-conformity organizations during 1,000 periods makes it clear that we should not set
δ too low. If we set
δ too low, the better performance of high-conformity organizations in the later periods will not be captured in PDV. On the other hand, we want to avoid
, because if the simulation were much longer, this would hide the high performance in early periods when computing PDV. It should also be noted that the average performances in all three cases, except for
, converge to the same level in the final 100 periods of our simulations, as shown in Panel (b) of the figure.
In turbulent environments (Panels (c) and (d)), the performances of the organizations with
and
exhibit a similar pattern to that shown in Panel (b). That is, initially, the organization with
demonstrates higher performance than the organization with
, but in the later periods, the latter outperforms the former. However, the dynamics of performance for
(solid black) is quite different in turbulent environments from that in stable environments. That is, when the environment is sufficiently turbulent, performance does not improve much over time (in the case of a complex task, Panel (d)) or can even deteriorate (in the case of a simple task, Panel (c)). Note that, due to environmental turbulence, organizational performance in an individual simulation run demonstrates high temporal variations. Such volatilities are hidden, however, in
Figure 3, where we plot the averaged performance in each block of 100 periods and further take averages across 500 simulation runs. Nonetheless, deterioration of average performance appears for
after period 200 for
and
(Panel (c)). This puzzling outcome deserves more careful analysis.
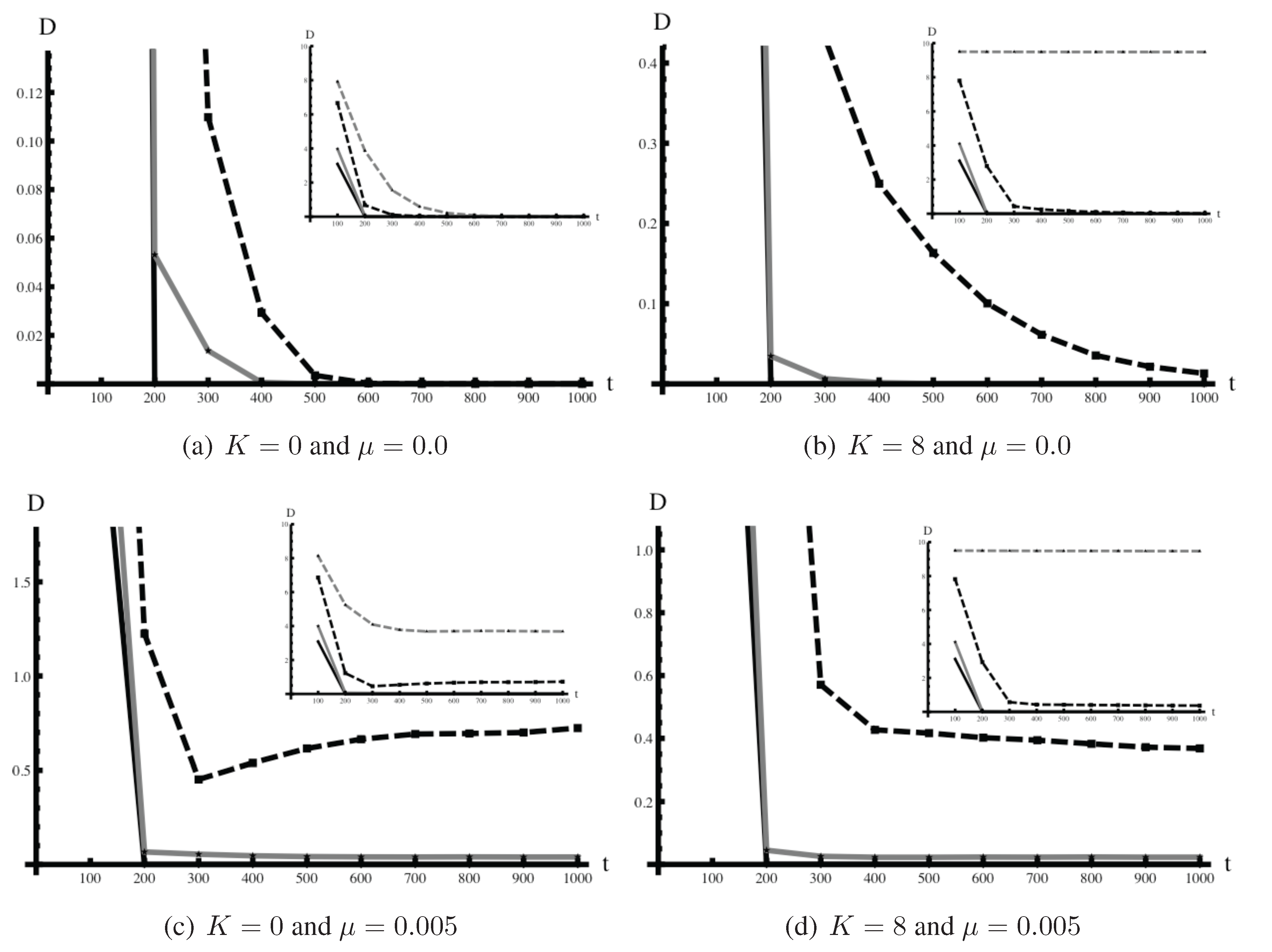
How could the performance for in a turbulent environment with a simple task deteriorate after an initial improvement? Looking at the dynamics of diversity of individual configurations, measured by the average distance between individual configurations and their means, and the dynamics of the value of organizational knowledge, , helps us to answer this question. Let us first define the diversity of individual configurations more precisely. The mean configuration of dimension, j, at period, t, is . The distance between configurations of individual, i, and the mean configurations at period, t, is therefore . The diversity for an organization in period, t, is .
The dynamics of diversity of individual configurations is plotted in
Figure 4, and the dynamics of the value of organizational knowledge in
Figure 5, for four combinations of task complexity,
, and environmental turbulence,
.
is assumed.
Figure 4.
The diversity within an organization for two levels of complexity, (left) and (right), and two degrees of environmental turbulence, (top) and (bottom). The communication is active (). Four values of λ are considered: (solid black), (solid gray), (dashed black), (dashed gray). For clarity of exposition, only are shown in the main figure. See the insets for all four λs. The extent of diversity is measured based on the discrepancy between individual configurations and their means. The data is generated by taking the average per-period diversity for each block of 100 periods. The average from 500 simulation runs is reported.
Figure 4.
The diversity within an organization for two levels of complexity, (left) and (right), and two degrees of environmental turbulence, (top) and (bottom). The communication is active (). Four values of λ are considered: (solid black), (solid gray), (dashed black), (dashed gray). For clarity of exposition, only are shown in the main figure. See the insets for all four λs. The extent of diversity is measured based on the discrepancy between individual configurations and their means. The data is generated by taking the average per-period diversity for each block of 100 periods. The average from 500 simulation runs is reported.
As in the case of organizational performance shown in
Figure 3, we took the average over each block of 100 periods.
Figure 3 reports the results obtained from taking the average of these averaged per-period performance results across 500 simulations. For clarity of exposition, in each panel of
Figure 4, the diversity measures of individual configurations for
are shown in the main figure and the diversity for
is shown only in the in-set (together with the other three)
When the task is simple and the environment stable, the diversity measure converges to zero for all types of organizations plotted in
Figure 4 (Panel (a)). The lower
λ is, the faster the convergence. The reason why even an organization with
(dashed gray, shown only in the in-sets) shows zero diversity in the later period is that, as discussed above, when
and
, every agent in the organization eventually finds the unique best configuration through individual searches. Moreover, since everyone eventually agrees on the best configuration, the value of organizational knowledge shows rapid improvement, as shown in
Figure 5 (Panel (a)).
Figure 5.
The dynamics of the average value of organizational knowledge for two levels of task complexity, (left) and (right), and two degrees of environmental turbulence, (top) and (bottom). Four values of λ are considered: (solid black), (solid gray), (dashed black), (dashed gray). The communication is active (). The data is generated by taking the average per-period value of organizational knowledge for each block of 100 periods. The average from 500 simulation runs is reported.
Figure 5.
The dynamics of the average value of organizational knowledge for two levels of task complexity, (left) and (right), and two degrees of environmental turbulence, (top) and (bottom). Four values of λ are considered: (solid black), (solid gray), (dashed black), (dashed gray). The communication is active (). The data is generated by taking the average per-period value of organizational knowledge for each block of 100 periods. The average from 500 simulation runs is reported.
When the environment is stable, but the task complex (
,
), as shown in
Figure 4 (Panel (b)), diversity remains high for organizations with
(dashed gray, shown only in the in-set) for long periods of time, while the diversity measures in the organizations with
and
quickly converge to zero. When
, the diversity measure declines much more slowly than with smaller values of
λ.
The high diversity found for organizations with
under the complex task is due to the existence of many distinct, but locally-best, configurations. Since such locally-best configurations vary, diversity among the individual configurations remains high and agents in the organizations do not agree on how to improve organizational knowledge. As a result of this dissonance in individual knowledge, the value of organizational knowledge remains low (
Figure 5, Panel (b)).
Panel (b) of
Figure 5 also shows that an organization with
is much slower at improving organizational knowledge than one with
. Recall that, in our model, in order to modify organizational knowledge, not only must new proposals be submitted, they must also be approved. In the model considered here, a proposal is approved when a majority of better-performing agents configure the dimension as proposed. Also, as discussed above for the case of
, when a task is complex, individual searches may lead to various distinct configurations that are local optima. If many agents search in different directions, it is more difficult for them to agree on how to modify organizational knowledge. The insufficient alignment of the individual knowledge base resulting from lower assimilation creates a bottleneck to improvement of organizational knowledge, which, in turn, slows down the improvement of organizational performance.
The inability to improve organizational knowledge can be detrimental when the environment is changing. As shown in Panel (c) of
Figure 5, an unstable environment, even in the absence of any interdependencies (
i.e., a task is not complex), could prevent organizational knowledge from improving. When
, an intermediate level of conformity, the quality of organizational knowledge deteriorates over time, especially after the first 100 periods. This lack of effective organizational learning is caused by the persistent diversity of individual knowledge—depicted in panel (c) of
Figure 4—that prevent agents from agreeing how to update the organizational knowledge. This explains why the average performance in organizations with
deteriorates, as can be seen in Panel (c) of
Figure 3. Interestingly, when organizations face both complex tasks and turbulent environments, a high-conformity organization (
i.e.,
) improves its organizational knowledge much faster than any other organization type, as shown in Panel (d) of
Figure 5. Although a high-autonomy organization (
i.e.,
) is incapable of improving organizational knowledge in this case, in marked contrast with Panel (c), such an organization does not suffer from poor organizational knowledge, because agents never adopt poor configurations of the organizational knowledge.
3.3. Optimal Degree of Conformity
So far, we have considered four combinations of task complexity (
) and environmental turbulence (
). We have seen that when the environment is turbulent or the task complex, successful organizations bifurcate into two types: high-autonomy
vs. high-conformity organizations. We have also noted that for the latter to be successful, very frequent knowledge sharing within the organization is required to improve and maintain the quality of organizational knowledge. We now seek to identify the conditions under which a high-conformity organization outperforms a high-autonomy one.
Figure 6 illustrates which organization, high-autonomy (
) or high-conformity (
), performs best under various levels of task complexity (
K) and various degrees of environmental turbulence (
μ). We assume very frequent knowledge sharing;
.
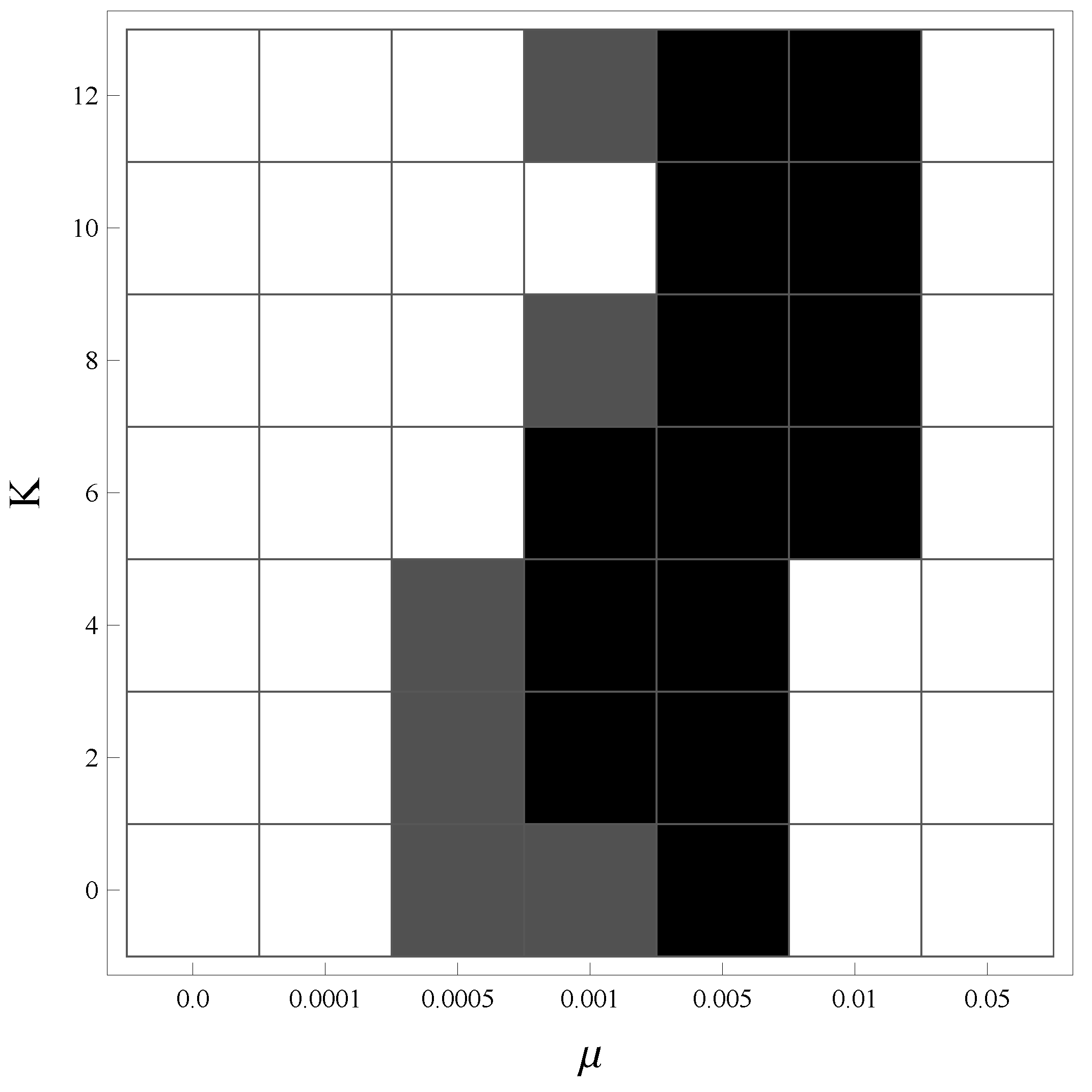
Figure 6.
Comparison of PDV between and for various degrees of complexity, K, and environmental turbulence, μ. and , in calculating PDVs. White (black) areas indicate that () performs better. Gray areas indicate that there is no difference between and .
Figure 6.
Comparison of PDV between and for various degrees of complexity, K, and environmental turbulence, μ. and , in calculating PDVs. White (black) areas indicate that () performs better. Gray areas indicate that there is no difference between and .
The white (black) cells in the figure show the combinations of K and μ, where an organization with () outperforms the other. The gray cells show the cases where and perform equally well. We performed a two-sample t-test based on PDVs generated by 500 simulations for each set of parameter values. Depending on the results of a variance comparison test, unequal variance or equal variance is assumed in performing a t-test. One organization is said to outperform the other if the mean PDV is significantly greater at a 5% significance level in a one-tailed test.
Interestingly, high-autonomy organizations (
) tend to perform better when either environment is stable or extremely turbulent, whereas high-conformity organizations tend to exceed the former in mildly turbulent environment. A well-aligned search process based on an assimilated knowledge base in the high-conformity organizations helps the organization to achieve a good balance between search and stability in a changing environment and improve the organizational knowledge increasingly faster than uncoordinated search in the high-autonomy organizations, as we discuss in
Section 3.2 (see
Figure 3). This mechanism does not work properly when the environment is excessively turbulent, because continuous improvement under assimilated knowledge becomes too slow to chase the “moving carrot.” In such an extreme situation, the value of developing organizational knowledge is low, as it becomes obsolete extremely quickly. In contrast, complexity of tasks does not seem to greatly affect the relative performance of high-conformity organizations
versus high-autonomy organizations.
There is a caveat regarding this finding. Note that we are measuring performance with PDVs that put higher weights on earlier periods than on later ones. As seen in the previous section, if we compare the average performance in later periods (or place more weight on the performance in later periods by using a higher discounting factor, δ), a high-conformity organization () outperforms a high-autonomy organization () for a greater range of parameters.