Structuring Nutrient Yields throughout Mississippi/Atchafalaya River Basin Using Machine Learning Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Data Processing
2.3. Principal Component Analysis (PCA)
2.4. t-Distributed Stochastic Neighbor Embedding (t-SNE)
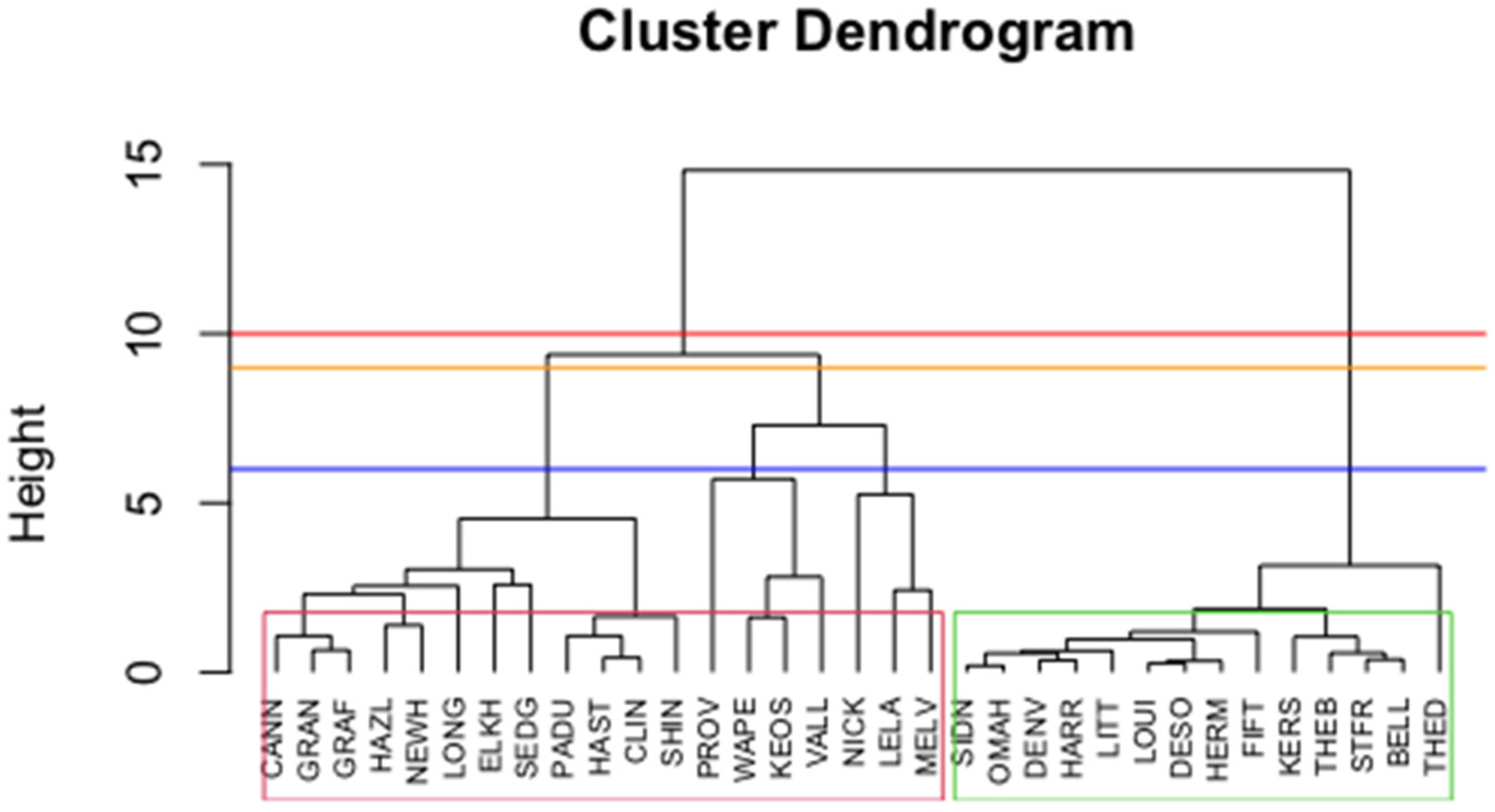
2.5. Clustering Analysis (CA)
3. Results
3.1. Distributions of Nutrient Yields (TN, TP, and SI)
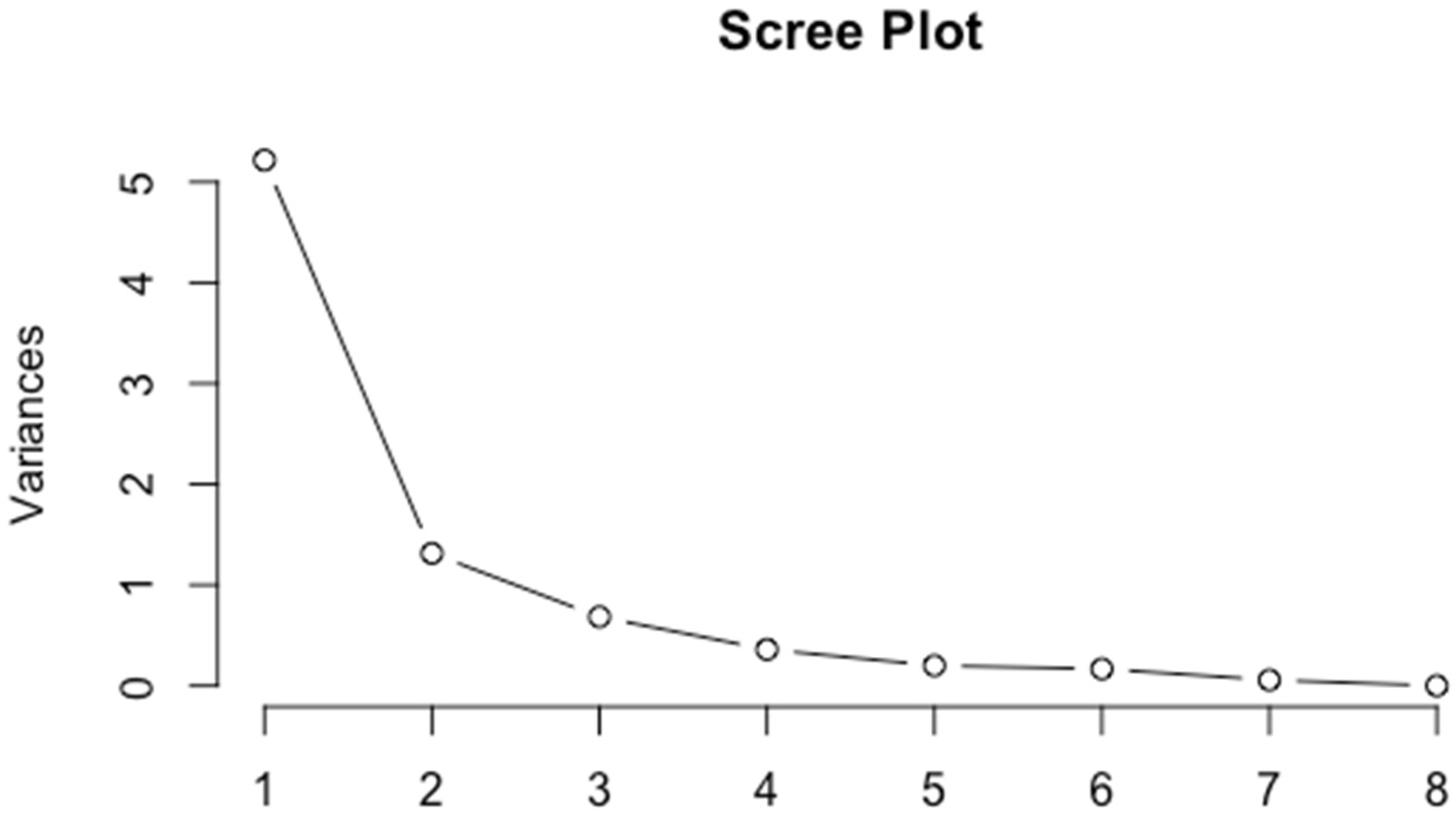
3.2. PCA Results
3.2.1. Correlation Matrix
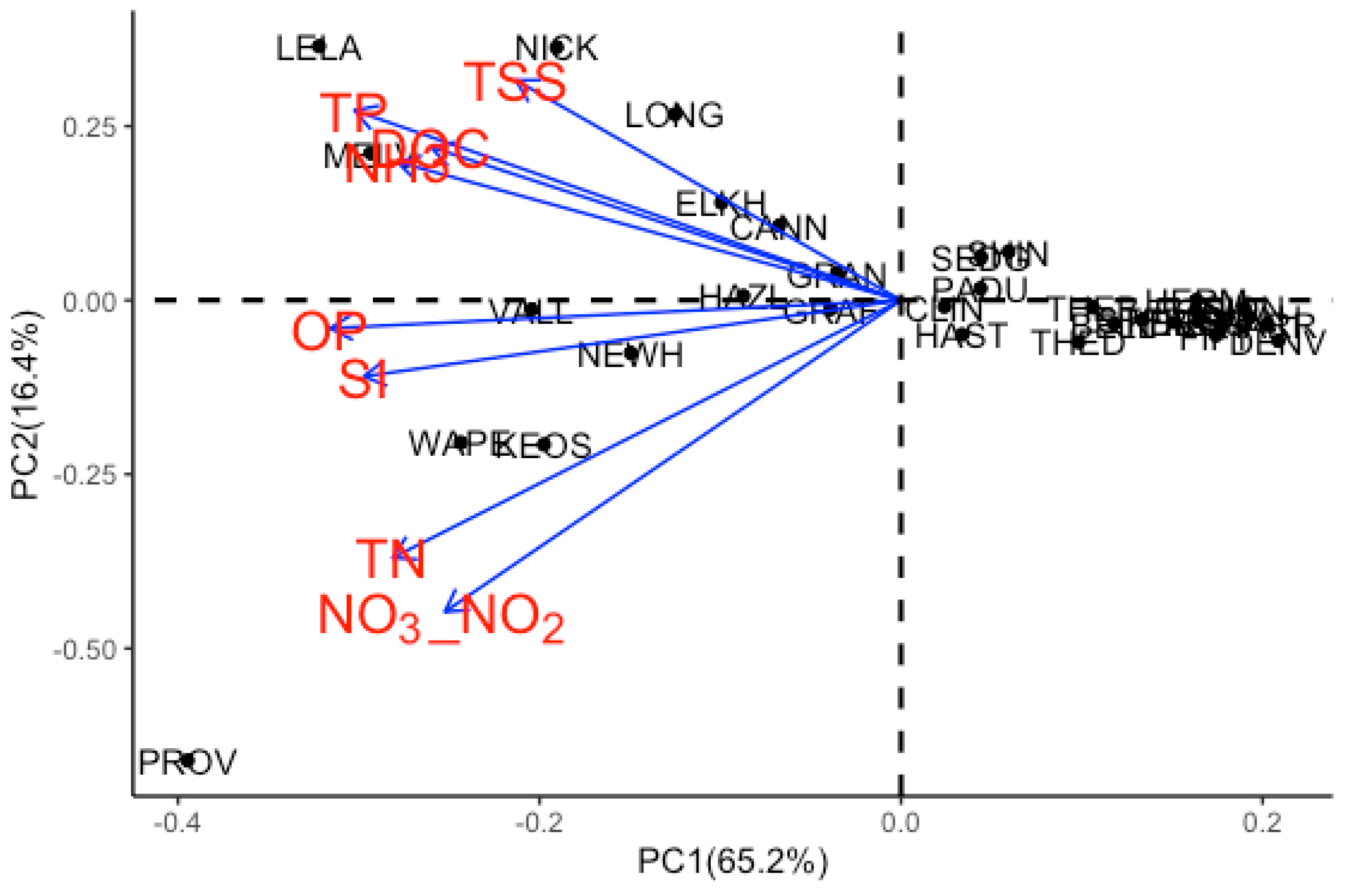
3.2.2. Factor Loadings
3.2.3. Factor Scores
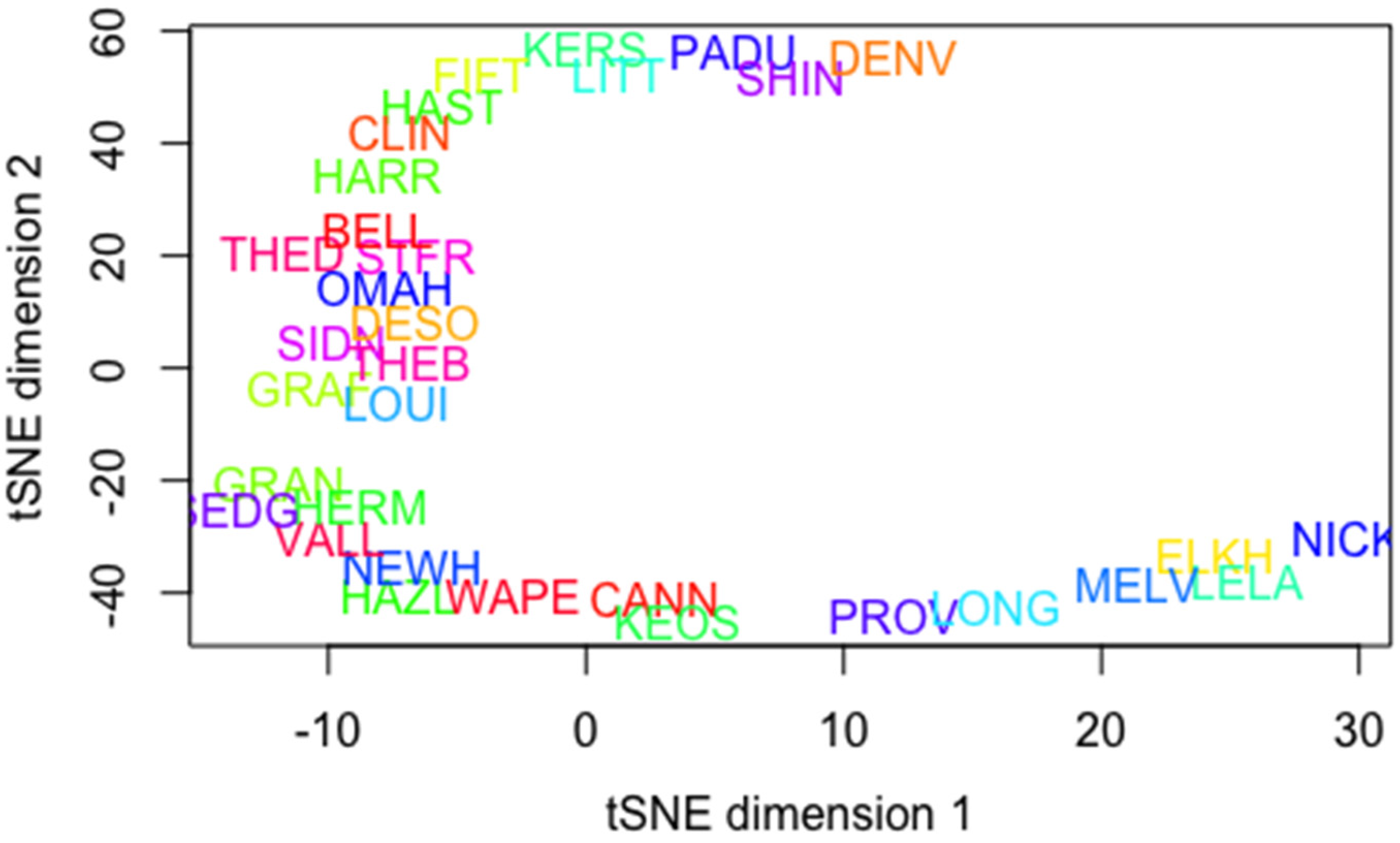
3.3. t-SNE Results
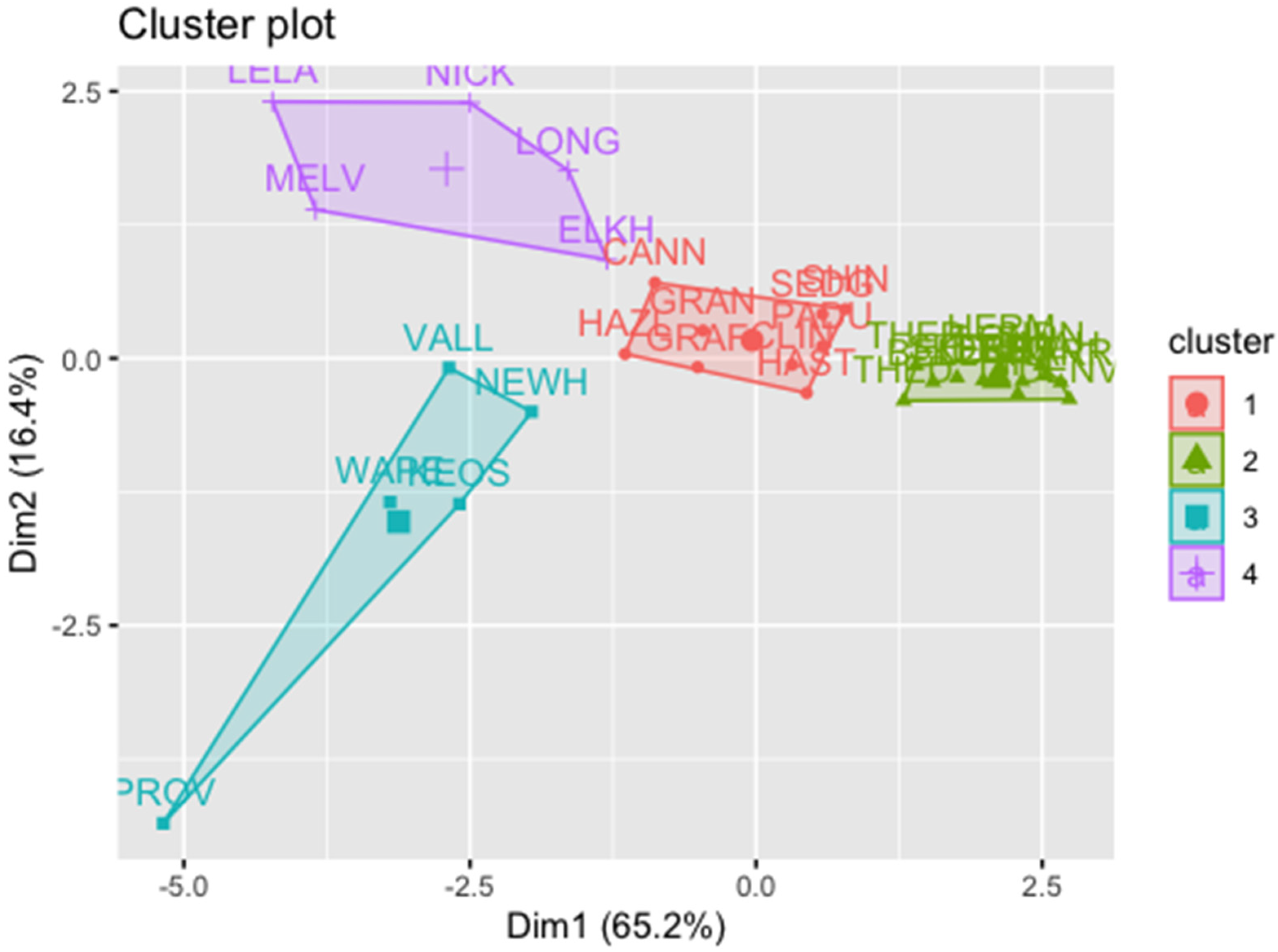
3.4. CA Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McKinney, L.D.; Shepherd, J.G.; Wilson, C.A.; Hogarth, W.T.; Chanton, J.; Murawski, S.A.; Sandifer, P.A.; Sutton, T.; Yoskowitz, D.; Wowk, K.; et al. The Gulf of Mexico AN OVERVIEW. Oceanography 2021, 34, 30. [Google Scholar] [CrossRef]
- USEPA (U.S. Environmental Protection Agency). Nutrient Criteria Technical Guidance Manual—Lakes and Reservoirs; U.S. Environmental Protection Agency, Office of Water: Washington, DC, USA, 2000; 232p.
- Robertson, D.M.; Schwarz, G.E.; Saad, D.A.; Alexander, R.A. Incorporating Uncertainty into the Ranking of SPARROW Model Nutrient Yields from Mississippi/Atchafalaya River Basin Watersheds. J. Am. Water Resour. Assoc. 2009, 45, 534. [Google Scholar] [CrossRef]
- Robertson, D.M.; Saad, D.A. Nitrogen and Phosphorus Sources and Delivery from the Mississippi/Atchafalaya River Basin: An Update Using 2012 SPARROW Models. J. Am. Water Resour. Assoc. 2021, 57, 406. [Google Scholar] [CrossRef]
- LIoyd, C.E.M.; Freer, J.E.; Johnes, P.J.; Collins, A.L. Using hysteresis analysis of high-resolution water quality monitoring data, including uncertainty, to infer controls on nutrient and sediment transfer in catchments. Sci. Total Environ. 2016, 543, 388. [Google Scholar] [CrossRef]
- Morales-Marín, L.A.; Chun, K.P.; Wheater, H.S.; Lindenschmidt, K.E. Trend analysis of nutrient loadings in a large prairie catchment. Hydrol. Sci. J. 2017, 62, 657. [Google Scholar] [CrossRef]
- Feng, H.; Qian, Y.; Cochran, J.K.; Zhu, Q.; Hu, W.; Yan, H.; Li, L.; Huang, X.; Chu, Y.S.; Liu, H.; et al. Nanoscale measurement of trace element distributions in Spartina alterniflora root tissue during dormancy. Sci. Rep. 2017, 7, 40420. [Google Scholar] [CrossRef] [PubMed]
- Nie, J.; Mirza, S.; Viteritto, M.; Li, Y.; Witherell, B.B.; Deng, Y.; Yoo, S.; Feng, H. Estimation of nutrient (N and P) fluxes into Newark Bay, USA. Mar. Pollut. Bull. 2023, 190, 114832. [Google Scholar] [CrossRef] [PubMed]
- Antonopoulos, V.Z.; Papamichail, D.M.; Mitsiou, K.A. Statistical and trend analysis of water quality and quantity data for the Strymon River in Greece. Hydrol. Earth Syst. Sci. 2001, 5, 679. [Google Scholar] [CrossRef]
- Alexander, R.B.; Smith, R.A. Trends in the nutrient enrichment of U.S. rivers during the late 20th century and their relation to changes in probable stream trophic conditions. Limnol. Oceanogr. 2006, 51, 639. [Google Scholar] [CrossRef]
- Fernández del Castillo, A.; Yebra-Montes, C.; Verduzco Garibay, M.; de Anda, J.; Garcia-Gonzalez, A.; Gradilla-Hernández, M.S. Simple Prediction of an Ecosystem-Specifific Water Quality Index and the Water Quality Classifification of a Highly Polluted River through Supervised Machine Learning. Water 2022, 14, 1235. [Google Scholar] [CrossRef]
- Du, J.L.; Feng, H.; Nie, J.; Li, Y.; Witherell, B.B. Characterisation and assessment of spatiotemporal variations in nutrient concentrations and fluxes in an urban watershed: Passaic River Basin, New Jersey, USA. Int. J. Environ. Pollut. 2018, 63, 154. [Google Scholar] [CrossRef]
- Goolsby, D.A.; Battaglin, W.A.; Lawrence, G.B.; Artz, R.S.; Aulenbach, B.T.; Hooper, R.P.; Keeney, D.R.; Stensland, G.J. Flux and Sources of Nutrients in the Mississippi-Atchafalaya River Basin: Topic 3 Report for the Integrated Assessment on Hypoxia in the Gulf of Mexico; NOAA Coastal Ocean Program Decision Analysis Series No. 17; NOAA Coastal Ocean Program: Silver Spring, MD, USA, 1999; 130p.
- David, M.B.; Drinkwater, L.E.; McIssac, G.F. Sources of Nitrate Yields in the Mississippi River Basin. J. Environ. Qual. 2010, 39, 1657. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, L.M.; David, M.B.; Drinkwater, L.E. A Spatial Analysis of Phosphorus in the Mississippi River Basin. J. Environ. Qual. 2011, 40, 931. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Qian, Y.; Cochran, J.K.; Zhu, Q.; Heilbrun, C.; Li, L.; Hu, W.; Yan, H.; Huang, X.; Ge, M.; et al. Seasonal differences in trace element concentrations and distribution in Spartina alterniflora root tissue. Chemosphere 2018, 204, 359. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, S.G.; Schreiber, S.; Tanna, R.N.; Roberts, D.R.; Arciszewski, T.J. Statistical tools for water quality assessment and monitoring in river ecosystems—A scoping review and recommendations for data analysis. Water Qual. Res. J. 2022, 57, 40. [Google Scholar] [CrossRef]
- de Andrade Costa, D.; Soares de Azevedo, J.P.; dos Santos, M.A.; dos Santos, R. Water quality assessment based on multivariate statistics and water quality index of a strategic river in the Brazilian Atlantic Forest. Sci. Rep. 2020, 10, 22038. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, Y.; Wang, D.; Wu, H.; Lin, A.; He, L. Using Principal Components Analysis and IDW Interpolation to Determine Spatial and Temporal Changes of Surface Water Quality of Xin’anjiang River in Huangshan, China. Int. J. Environ. Res. Public Health 2020, 17, 2942. [Google Scholar] [CrossRef]
- Singh, K.P.; Malik, A.; Mohan, D.; Sinha, S. Multivariate statistical techniques for the evaluation of spatial and temporal variations in water quality of Gomti River (India)—A case study. Water Res. 2004, 38, 3980. [Google Scholar] [CrossRef]
- Dutta, S.; Dwivedi, A.; SureshKumar, M. Use of water quality index and multivariate statistical techniques for the assessmentof spatial variations in water quality of a small river. Environ. Monit. Assess. 2018, 190, 718. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011.
- Worku, T.; Khare, D.; Tripathi, S. Modeling runoff–sediment response to land use/land cover changes using integrated GIS and SWAT model in the Beressa watershed. Environ. Earth Sci. 2017, 76, 550. [Google Scholar] [CrossRef]
- Robertson, D.M.; Saad, D.A. SPARROW Models Used to Understand Nutrient Sources in the Mississippi/Atchafalaya River Basin. J. Environ. Qual. 2013, 42, 1422. [Google Scholar] [CrossRef] [PubMed]
- Robertson, D.M.; Saad, D.A.; Schwarz, G.E. Spatial Variability in Nutrient Transport by HUC8, State, and Subbasin based on Mississippi/Atchafalaya River Basin SPARROW models. J. Am. Water Resour. Assoc. 2014, 50, 988. [Google Scholar] [CrossRef]
- Varis, O. Bayesian decision analysis for environmental and resource management. Environ. Model. Softw. 1997, 12, 177. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579. [Google Scholar]
- Tseng, H.-H.; Naqa, I.E.; Chien, J.-T. Power-law stochastic neighbor embedding. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2347–2351. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Cerny, B.A.; Kaiser, H.F. A study of a measure of sampling adequacy for factor-analytic correlation matrices. Multivar. Behav. Res. 1977, 12, 43. [Google Scholar] [CrossRef]
- Arsham, H.; Lovric, M. Bartlett’s Test. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, California, CA, USA, 21 June–18 July 1965, 27 December 1965–7 January 1966; Le Cam, L.M., Neyman, J., Eds.; University of California Press: California, CA, USA, 1967; Volume 1, p. 281. [Google Scholar]
- Nielsen, F. Hierarchical Clustering. In Introduction to HPC with MPI for Data Science; Springer: Berlin/Heidelberg, Germany, 2016; pp. 195–211. ISBN 978-3-319-21903-5. [Google Scholar]
- Saad, D.A.; Robertson, D.M. 2019 Midwest SPARROW Streamflow, Total Nitrogen, Total Phosphorus, and Suspended Sediment Models Inputs and Outputs; U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2019. [CrossRef]
- Saad, D.A.; Robertson, D.M. Long-Term Mean Annual Total Nitrogen and Total Phosphorus Loads Estimated Using Fluxmaster 5-Parameter Models and Detrended to 2012, Midwest Region of the United States, 1999–2014; U.S. Geological Survey Data Release; U.S. Geological Survey: Reston, VA, USA, 2020. [CrossRef]
- Schaller, J.; Faucherre, S.; Joss, H.; Obst, M.; Goeckede, M.; Planer-Friedrich, B.; Peiffer, S.; Gilfedder, B.; Elberling, B. Silicon increases the phosphorus availability of Arctic soils. Sci. Rep. 2019, 9, 449. [Google Scholar] [CrossRef]
- Yu, S.; Xu, Z.; Wu, W.; Zuo, D. Effect of land use types on stream water quality under seasonal variation and topographic characteristics in the Wei River basin, China. Ecol. Indic. 2016, 60, 202. [Google Scholar] [CrossRef]
- Mundorff, J.C. Sediment Discharge during Floods in Eastern Nebraska; US Department of the Interior, Geological Survey: Reston, VA, USA, 1962; Volume 470.
- Robertson, D.M.; Saad, D.A.; Benoy, G.A.; Vouk, I.; Schwarz, G.E.; Laitta, M.T. Spatially Referenced Models of Streamflow and Nitrogen, Phosphorus, and Suspended-Sediment Loads in Stream of the Midwestern United States. U.S. Geol. Surv. Sci. Investig. Rep. 2019, 5114, 74. [Google Scholar] [CrossRef]


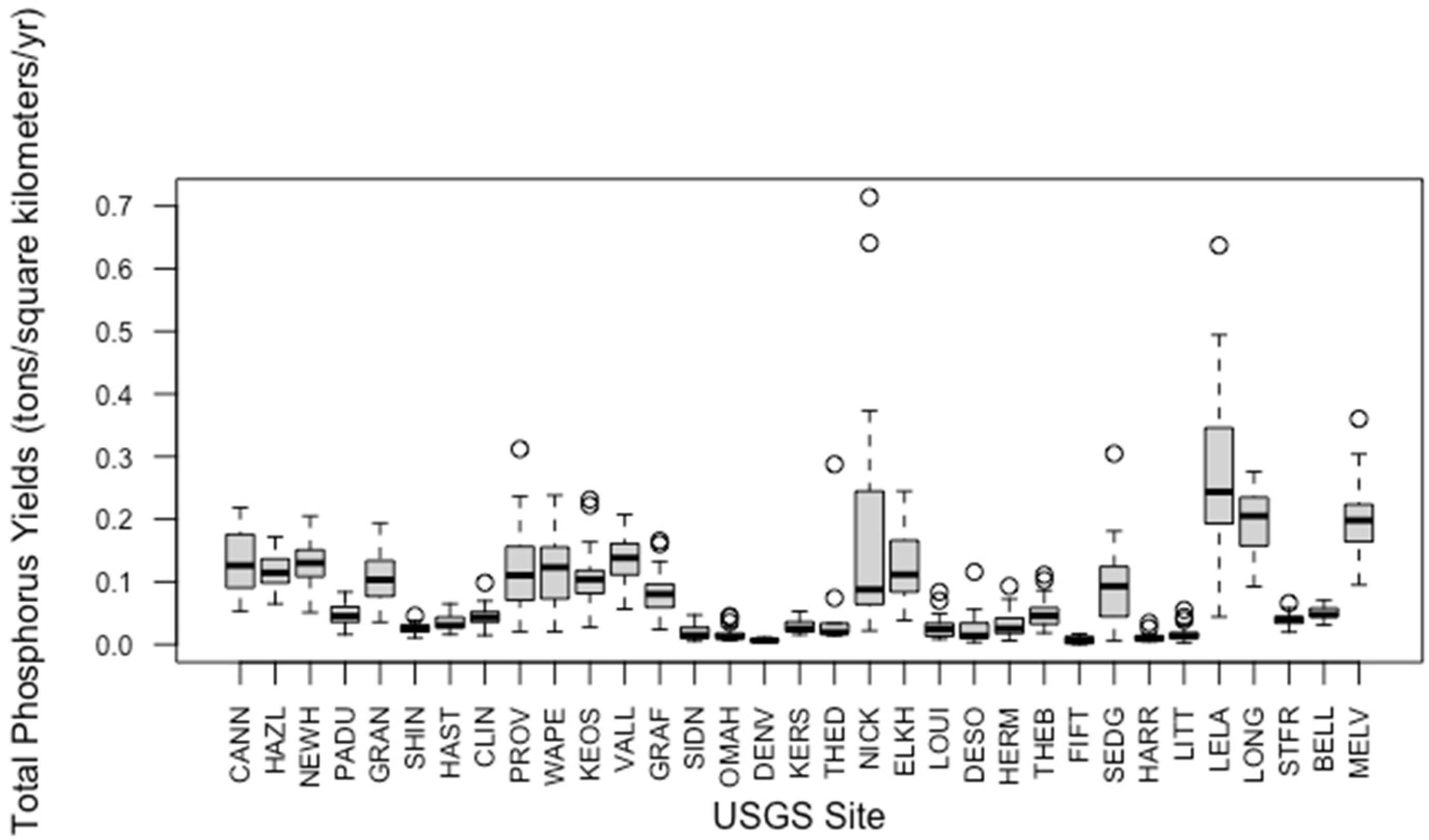
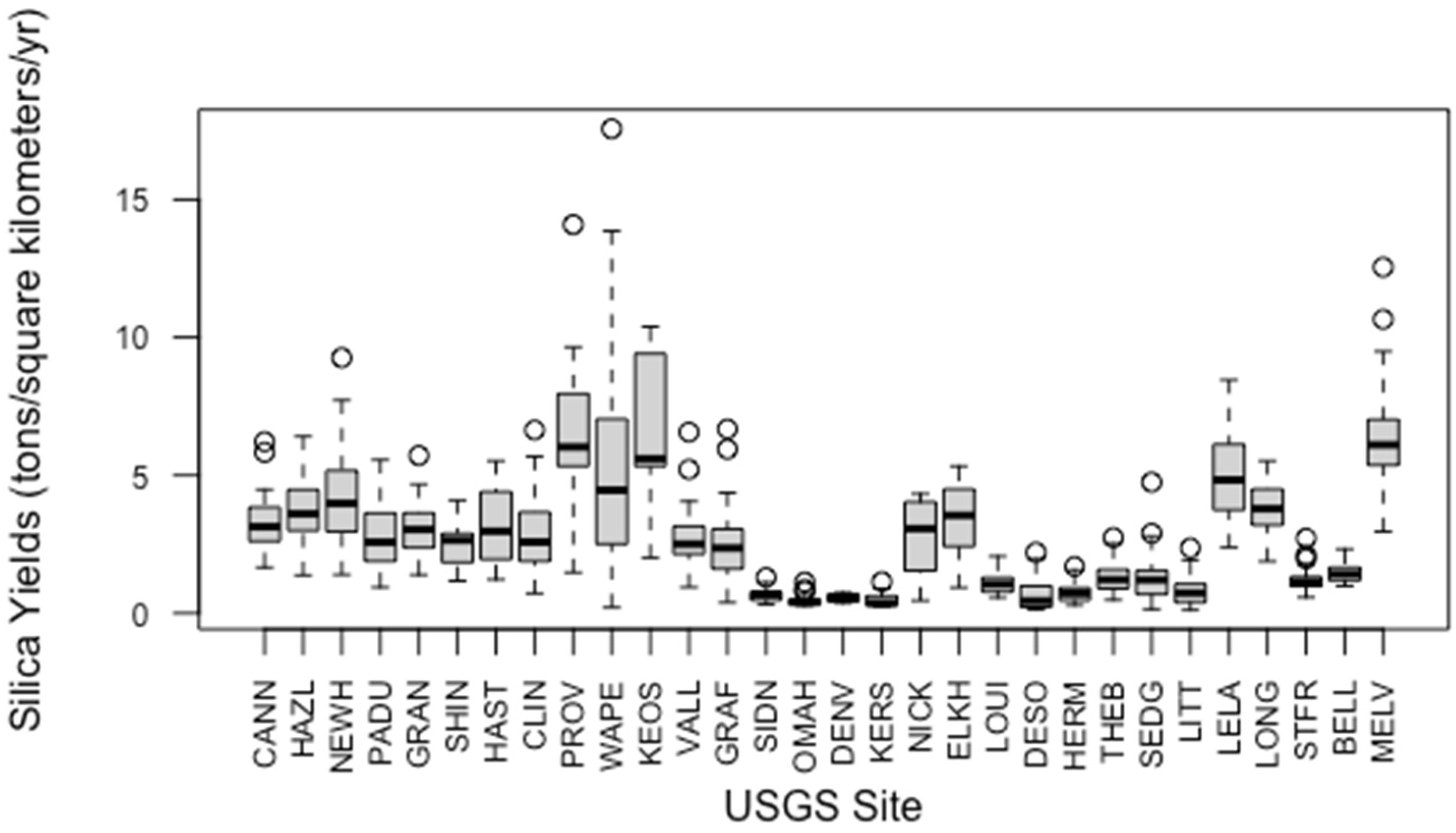
| SITE_ABB | SITE_QW_ID | Location |
|---|---|---|
| CANN | 3303280 | Ohio River at Cannelton Dam at Cannelton, IN |
| HAZL | 3374100 | White River at Hazleton, IN |
| NEWH | 3374100 | Wabash River at New Harmony, IN |
| PADU | 3609750 | Tennessee River at Highway 60 near Paducah, KY |
| GRAN | 3612500 | Ohio River at Dam 53 near Grand Chain, IL |
| SHIN | 5288705 | Shingle Creek at Queen Ave. in Minneapolis, MN |
| HAST | 5331580 | Mississippi River below L&D 2 at Hastings, MN |
| CLIN | 5420500 | Mississippi River at Clinton, IA |
| PROV | 5451210 | South Fork Iowa River NE of New Providence, IA |
| WAPE | 5465500 | Iowa River at Wapello, IA |
| KEOS | 5490500 | Des Moines River at Keosauqua, IA |
| VALL | 5586100 | Illinois River at Valley City, IL |
| GRAF | 5587455 | Mississippi River below Grafton, IL |
| SIDN | 6329500 | Yellowstone River near Sidney, MT |
| OMAH | 6610000 | Missouri River at Omaha, NE |
| DENV | 6713500 | Cherry Creek at Denver, CO |
| KERS | 6754000 | South Platte River near Kersey, CO |
| THED | 6775900 | Dismal River near Thed Ford, NE |
| NICK | 6800000 | Maple Creek near Nickerson, NE |
| ELKH | 6800500 | Elkhorn River at Waterloo, NE |
| LOUI | 6805500 | Platte River at Louisville, NE |
| DESO | 6892350 | Kansas R. at Desoto, KS |
| HERM | 6934500 | Missouri River at Hermann, MO |
| THEB | 7022000 | Mississippi River at Thebes, IL |
| FIFT | 7060710 | North Sycamore Creek near Fifty-Six, AR |
| SEDG | 7144100 | L. Arkansas R. NR Sedgwick, KS |
| HARR | 7241550 | North Canadian River near Harrah, OK |
| LITT | 7263620 | AR River David D. Terry L&D below Little Rock, AR |
| LELA | 7288650 | Bogue Phalia NR Leland, MS |
| LONG | 7288955 | Yazoo River BL Steele Bayou NR Long Lake, MS |
| STFR | 7373420 | Mississippi River NR St. Francisville, LA |
| BELL | 7374525 | Mississippi River at Belle Chasse, LA |
| MELV | 7381495 | Atchafalaya River at Melville, LA |
| DOC | NH3 | NO3_NO2 | OP | SI | TSS | TN | TP | |
|---|---|---|---|---|---|---|---|---|
| DOC | 1.00 | |||||||
| NH3 | 0.68 | 1.00 | ||||||
| NO3_NO2 | 0.31 | 0.42 | 1.00 | |||||
| OP | 0.62 | 0.72 | 0.70 | 1.00 | ||||
| SI | 0.68 | 0.57 | 0.69 | 0.77 | 1.00 | |||
| TSS | 0.35 | 0.55 | 0.23 | 0.52 | 0.40 | 1.00 | ||
| TN | 0.42 | 0.52 | 0.99 | 0.76 | 0.74 | 0.33 | 1.00 | |
| TP | 0.79 | 0.77 | 0.39 | 0.80 | 0.70 | 0.73 | 0.51 | 1.00 |
| Eigenvalues | 5.22 | 1.31 |
|---|---|---|
| Cumulative (%) | 65.2 | 16.4 |
| Principal Component(PC) | PC1 | PC2 |
| DOC | −0.33 | 0.28 |
| NH3 | −0.36 | 0.25 |
| NO3-NO2 | −0.32 | −0.57 |
| OP | −0.40 | −0.05 |
| SI | −0.37 | −0.14 |
| TSS | −0.27 | 0.40 |
| TN | −0.36 | −0.47 |
| TP | −0.39 | 0.35 |
| USGS Monitoring Site | PC1 | PC2 |
|---|---|---|
| CANN | −0.88 | 0.71 |
| HAZL | −1.15 | 0.04 |
| NEWH | −1.96 | −0.50 |
| PADU | 0.57 | 0.11 |
| GRAN | −0.46 | 0.26 |
| SHIN | 0.78 | 0.46 |
| HAST | 0.44 | −0.32 |
| CLIN | 0.31 | −0.06 |
| PROV | −5.18 | −4.35 |
| WAPE | −3.19 | −1.34 |
| KEOS | −2.59 | −1.36 |
| VALL | −2.68 | −0.08 |
| GRAF | −0.51 | −0.08 |
| SIDN | 2.49 | −0.06 |
| OMAH | 2.53 | −0.16 |
| DENV | 2.74 | −0.38 |
| KERS | 1.98 | −0.20 |
| THED | 1.28 | −0.40 |
| NICK | −2.50 | 2.39 |
| ELKH | −1.30 | 0.92 |
| LOUI | 2.14 | −0.09 |
| DESO | 2.16 | −0.20 |
| HERM | 2.15 | 0.003 |
| THEB | 1.39 | −0.07 |
| FIFT | 2.29 | −0.33 |
| SEDG | 0.58 | 0.41 |
| HARR | 2.66 | −0.22 |
| LITT | 2.32 | −0.22 |
| LELA | −4.23 | 2.40 |
| LONG | −1.64 | 1.76 |
| STFR | 1.76 | −0.18 |
| BELL | 1.55 | −0.22 |
| MELV | −3.85 | 1.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhen, Y.; Feng, H.; Yoo, S. Structuring Nutrient Yields throughout Mississippi/Atchafalaya River Basin Using Machine Learning Approaches. Environments 2023, 10, 162. https://doi.org/10.3390/environments10090162
Zhen Y, Feng H, Yoo S. Structuring Nutrient Yields throughout Mississippi/Atchafalaya River Basin Using Machine Learning Approaches. Environments. 2023; 10(9):162. https://doi.org/10.3390/environments10090162
Chicago/Turabian StyleZhen, Yi, Huan Feng, and Shinjae Yoo. 2023. "Structuring Nutrient Yields throughout Mississippi/Atchafalaya River Basin Using Machine Learning Approaches" Environments 10, no. 9: 162. https://doi.org/10.3390/environments10090162





