Quantifying Hydrothermal Alteration: A Review of Methods
Abstract
:1. Introduction
“A metamorphic process by which the chemical composition of a rock or rock portion is altered in a pervasive manner and which involves the introduction and/or removal of chemical components as a result of the interaction of the rock with aqueous fluids (solutions). During metasomatism the rock remains in a solid state.”
2. Theoretical Considerations
2.1. Alteration Types
Magnetite quartz fluid grunerite fluid
15Ca(Mg,Fe)(CO3)2 + 3SiO2 + 11H2O + 5O2
chlorite + calcite + fluid => white mica + ankerite − dolomite + quartz + fluid
albite fluid muscovite fluid quartz
orthoclase fluid muscovite fluid quartz
Alkali feldspar fluid albite muscovite quartz fluid
muscovite fluid chlorite fluid
2.2. Altered Rocks, Analysis, and Sampling
3. Presentation of the Data Sets
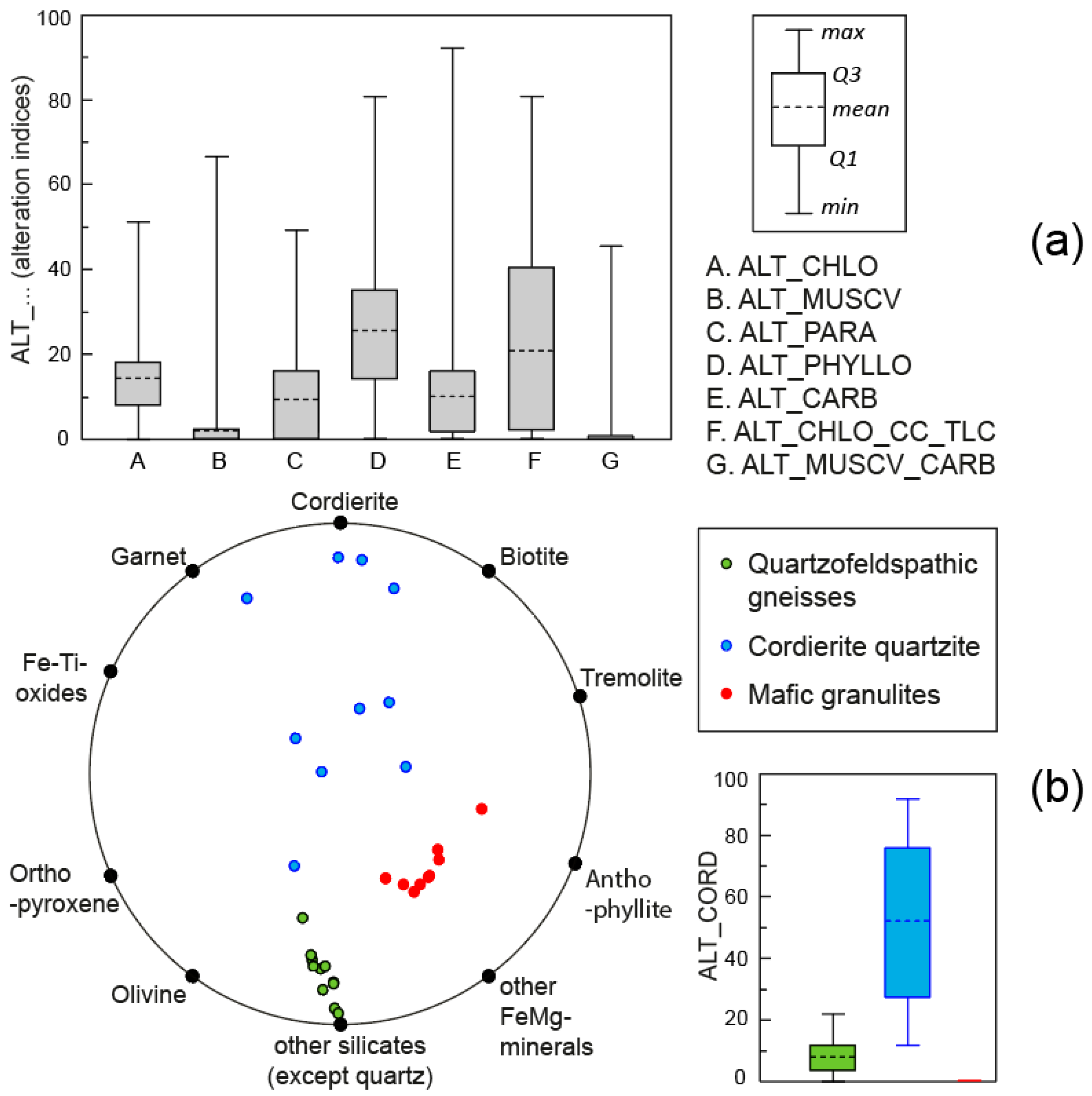
4. Alteration Indices
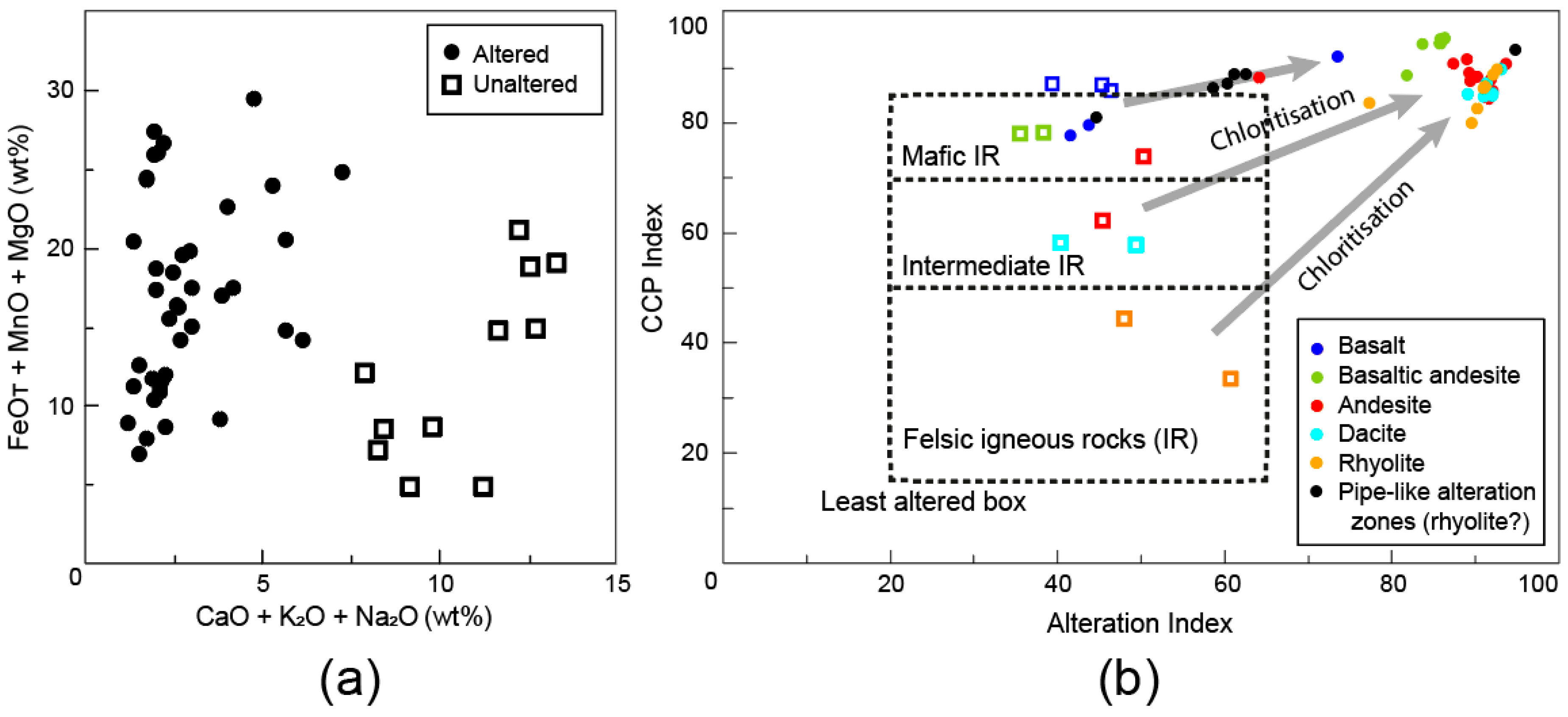
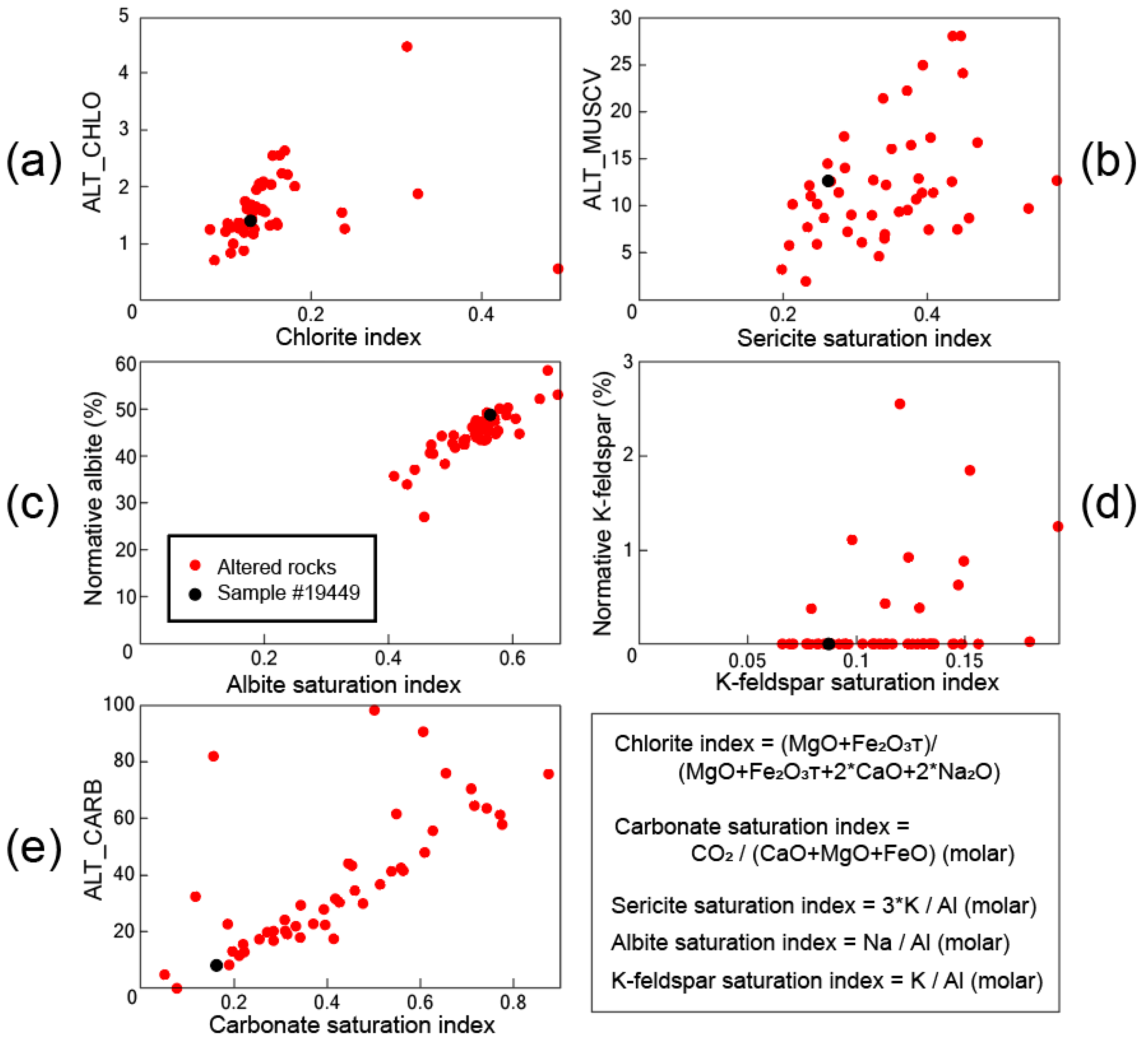
4.1. Major Element Ratios
4.2. Normative Mineral Ratios
- M1, M2, to Mn—proportions of the normative minerals displayed on the circle diagram;
- F1, F2, to Fn, and G1, G2, to Gn—factors (e.g., to locate cordierite, the factors used are Fcord = Cx cos(π/3) + R and Gcord = Cy sin(π/3) + R).
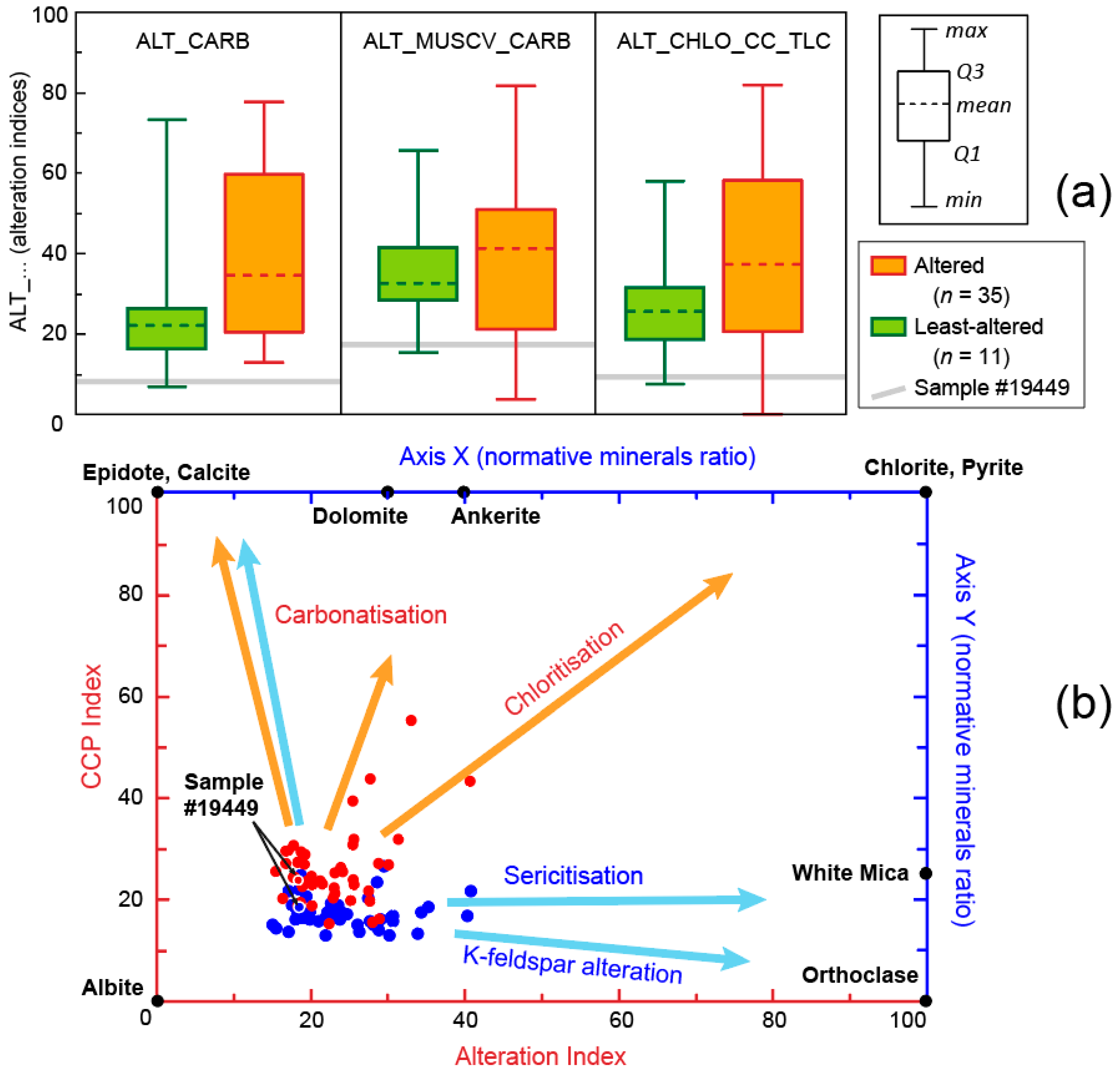
4.3. Comparison of the Alteration Indice
5. Mass Balance Methods
5.1. Mass Transfer Equation
- Xn—mass change of component n expressed in g per 100 g of precursor;
- WBn − WAn—weight of component n in the precursor (A) and in the altered rock (B);
- w—weight of precursor (=100 g usually);
- XAn, XBn—component n in rocks A and B;
- SB, SA—density of rocks A and B (often neglected);
- FV (volume ratio) = volumeA/volumeB = (massB/massA)*(SA/SB) ~ (massB/massA).
5.2. Errors, Precursors, and Immobile Elements
5.3. Three Mass Balance Methods
5.4. Interpretation of the Results
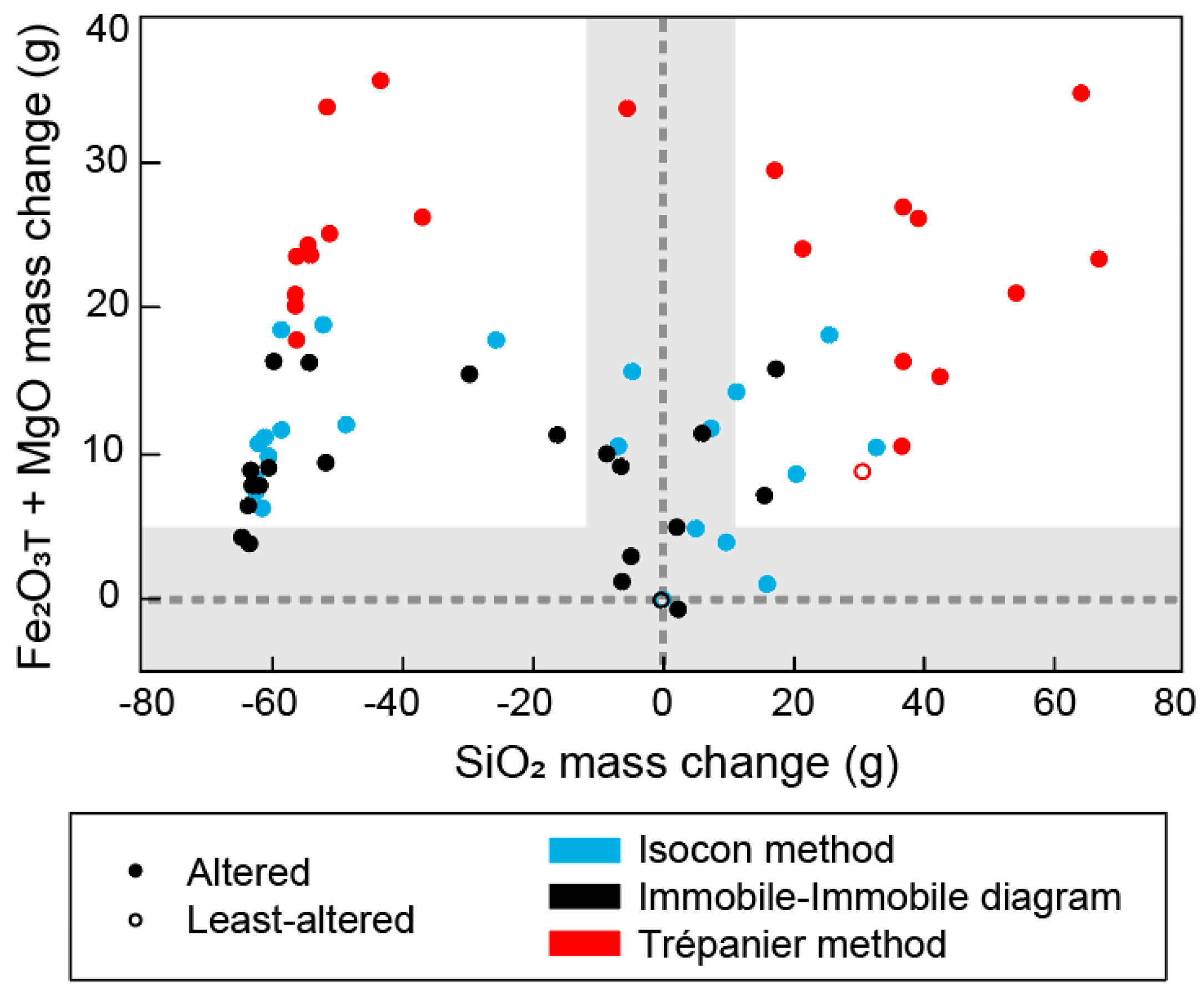
5.5. Natural Examples
6. Discussion
6.1. Requirements for the Presented Methods
6.2. A Method for each Alteration Process
6.3. Recommendations and Alternative Methods
7. Conclusions
- Major element ratios are alteration indices easy to calculate and best applied to well-documented areas;
- Normative mineral ratios provide a reliable quantification of carbonatisation and can help relate observed metamorphic minerals to chemical data;
- The isocon mass balance method is suitable for single precursor systems having well-documented precursors. It can be tedious in its application but has the advantage to rely on several immobile elements;
- The immobile element method is a more practical mass balance method that is particularly effective in multi-precursor systems; and
- The modelled precursor mass balance method solves the precursor sampling issue but can only be applied to common igneous rocks.
Funding
Acknowledgments
Conflicts of Interest
References
- Large, R.R.; McGoldrick, P.J. Lithogeochemical halos and geochemical vectors to stratiform sediment hosted Zn-Pb-Ag deposits, 1. Lady Loretta Deposit, Queensland. J. Geochem. Explor. 1998, 63, 37–56. [Google Scholar] [CrossRef]
- Eilu, P.; Groves, D.I. Primary alteration and geochemical dispersion haloes of Archaean orogenic gold deposits in the Yilgarn Craton: The pre-weathering scenario. Geochem. Explor. Environ. Anal. 2001, 1, 183–200. [Google Scholar] [CrossRef]
- Cooke, D.R.; Baker, M.; Hollings, P.; Sweet, G.; Chang, Z.; Danyushevsky, L.; Gilbert, S.; Zhou, T.; White, N.C.; Gemmell, J.B. New advances in detecting the distal geochemical footprints of porphyry systems-epidote mineral chemistry as a tool for vectoring and fertility assessments. In Building Exploration Capability for the 21st Century; Kelley, K.D., Golden, H.C., Eds.; Colt Print Services: Boulder, CO, USA, 2014; pp. 127–152. ISBN 978-1-629491-424. [Google Scholar]
- Phillips, G.N.; Powell, R. Formation of gold deposits: A metamorphic devolatilization model. J. Metamorph. Geol. 2010, 28, 689–718. [Google Scholar] [CrossRef]
- Morogan, V. Mass transfer and REE mobility during fenitization at Alno, Sweden. Contrib. Mineral. Petrol. 1989, 103, 25–34. [Google Scholar] [CrossRef]
- Sillitoe, R.H. Porphyry copper systems. Econ. Geol. 2010, 105, 3–41. [Google Scholar] [CrossRef]
- Robert, F. Syenite-associated disseminated gold deposits in the Abitibi greenstone belt, Canada. Miner. Depos. 2001, 36, 503–516. [Google Scholar] [CrossRef]
- Stanton, R.L. Magmatic evolution and the ore type-lava type affiliations of volcanic exhalative ores. Australas. Inst. Min. Metall. Monogr. 1990, 14, 101–108. [Google Scholar]
- Zharikov, V.A.; Pertsev, N.N.; Rusinov, V.L.; Callegari, E.; Fettes, D.J. Metasomatism and metasomatic rocks. In A Classification of Metamorphic Rocks and Glossary of Terms. Recommendations of the International Union of Geological Sciences Subcommission on the Systaematics of Metamorphic Rocks; IUGS: Paris, France, 2007; p. 17. [Google Scholar]
- Roden, M.F.; Murthy, V.R. Mantle metasomatism. Annu. Rev. Earth Planet. Sci. 1985, 13, 269–296. [Google Scholar] [CrossRef]
- Ferry, J.M.; Dipple, G.M. Fluid flow, mineral reactions, and metasomatism. Geology 1991, 19, 211–214. [Google Scholar] [CrossRef]
- Stanley, C.R.; Madeisky, H.E. Lithogeochemical exploration for hydrothermal ore deposits using Pearce element ratio analysis. In Alteration and Alteration Processes Associated with Ore-Forming Systems, Geological Association of Canada, Short Course Notes; Lentz, D.R., Ed.; GAC: Guangzhou, China, 1994; Volume 11, pp. 193–211. [Google Scholar]
- Gibson, H.L.; Allen, R.L.; Riverin, G.; Lane, T.E. The VMS model: Advances and application to exploration targeting. Proc. Explor. 2007, 7, 713–730. [Google Scholar]
- Mathieu, L.; Bouchard, R.-A.; Pearson, V.; Daigneault, R. The Coulon deposit: Quantifying alteration in volcanogenic massive sulphide systems modified by amphibolite-facies metamorphism. Can. J. Earth Sci. 2016, 53, 1443–1457. [Google Scholar] [CrossRef]
- Mathieu, L. Quantifying hydrothermal alteration with normative minerals and other chemical tools at the Beattie Syenite, Abitibi greenstone belt, Canada. Geochem. Explor. Environ. Anal. 2016, 16, 233–244. [Google Scholar] [CrossRef]
- Kishida, A.; Kerrich, R. Hydrothermal alteration zoning and gold concentration at the Kerr-Addison Archean lode gold deposit, Kirkland Lake, Ontario. Econ. Geol. 1987, 82, 649–690. [Google Scholar] [CrossRef]
- Piché, M.; Jébrak, M. Normative minerals and alteration indices developed for mineral exploration. J. Geochem. Explor. 2004, 82, 59–77. [Google Scholar] [CrossRef]
- MacLean, W.H.; Barrett, T.J. Lithogeochemical techniques using immobile elements. J. Geochem. Explor. 1993, 48, 109–133. [Google Scholar] [CrossRef]
- Gifkins, C.C.; Herrmann, W.; Large, R.R. Altered Volcanic Rocks: A Guide to Description and Interpretation; Centre for Ore Deposit Research, University of Tasmania: Hobart, Australia, 2005. [Google Scholar]
- Simmons, S.F.; Christenson, B.W. Origins of calcite in a boiling geothermal system. Am. J. Sci. 1994, 294, 361–400. [Google Scholar] [CrossRef]
- Guilbert, J.M.; Park, C.F., Jr. The Geology of Ore Deposits, Freeman and Company; W.H. Freeman and Co.: New York, NY, USA, 1986. [Google Scholar]
- Lawley, C.J.M.; Dubé, B.; Mercier-Langevin, P.; Kjarsgaard, B.; Knight, R.; Vaillancourt, D. Defining and mapping hydrothermal footprints at the BIF-hosted Meliadine gold district, Nunavut, Canada. J. Geochem. Explor. 2015, 155, 33–55. [Google Scholar] [CrossRef]
- Colvine, A.C. Archean Lode Gold Deposits in Ontario; OGS Miscellaneous Paper 139; Ontario Ministry of Northern Development and Mines: Greater Sudbury, ON, Canada, 1988; Volume 139, ISBN 077294105X.
- Leitch, C.H.B.; Lentz, D.R. The Gresens approach to mass balance constrains of the alteration systems: Methods, pitfalls, examples. In Alteration and Alteration Processes Associated with Ore-Forming Systems; Lentz, D.R., Ed.; Geological Assocociation of Canada: St. John’s, NL, Canada, 1994; Volume 11, pp. 161–192. [Google Scholar]
- Barrett, T.J.; MacLean, W.H. Chemostratigraphy and hydrothermal alteration in exploration for VHMS deposits in greenstones and younger volcanic rocks. In Alteration and Alteration Processes Associated with Ore-Forming Systems; Lentz, D.R., Ed.; Geological Association of Canada: St. John’s, NL, Canada, 1994; Volume 11, pp. 433–465. [Google Scholar]
- Large, R.R.; Gemmell, J.B.; Paulick, H.; Huston, D.L. The alteration box plot: A simple approach to understanding the relationship between alteration mineralogy and lithogeochemistry associated with volcanic-hosted massive sulfide deposits. Econ. Geol. 2001, 96, 957–971. [Google Scholar] [CrossRef]
- Embley, R.W.; Jonasson, I.R.; Perfit, M.R.; Franklin, J.M.; Tivey, M.A.; Malahoff, A.; Smith, M.F.; Francis, T.J.G. Submersible investigation of an extinct hydrothermal system on the Galapagos Ridge; sulfide mounds, stockwork zone, and differentiated lavas. Can. Mineral. 1988, 26, 517–539. [Google Scholar]
- Witt, W.K. Porphyry intrusions and albitites in the Bardoc-Kalgoorlie area, Western Australia, and their role in Archean epigenetic gold mineralization. Can. J. Earth Sci. 1992, 29, 1609–1622. [Google Scholar] [CrossRef]
- Sangster, D.F. The role of dense brines in the formation of vent-distal sedimentary-exhalative (SEDEX) lead-zinc deposits: Field and laboratory evidence. Miner. Depos. 2002, 37, 149–157. [Google Scholar] [CrossRef]
- Levesque, G. Duality of magmatism at Kirkland Lake, Ontario, Canada. Master’s Thesis, University of Ottawa, Ottawa, ON, Canada, 1994. [Google Scholar]
- Dominy, S.C. Sampling: A critical component to gold mining project evaluation. Proj. Eval. Conf. Melb. Aust. 2007, 23, 89–96. [Google Scholar]
- Sarbas, B.; Nohl, U. The GEOROC database as part of a growing geoinformatics network. In Geoinformatics Conference; GSA: Washington, DC, USA, 2008. [Google Scholar]
- Zheng, Y.C.; Gu, L.; Tang, X.; Wu, C.; Li, C.; Liu, S. Geology and geochemistry of highly metamorphosed footwall alteration zones in the Hongtoushan volcanogenic massive sulfide deposit, Liaoning Province, China. Resour. Geol. 2011, 61, 113–139. [Google Scholar] [CrossRef]
- Allard, G.O. Doré Lake Complex and Its Importance to Chibougamau Geology and Metallogeny; MERN Report DP-386; Ministère des richesses naturelles: Québec, QC, Canada, 1976.
- Guha, J. Hydrothermal systems and correlations of mineral deposits in the Chibougamau mining district-an overview. In Chibougamau, Stratigraphy and Mineralization; Guha, J., Chown, E., Eds.; Canadian Institute of Mining and Metallurgy: Westmount, QC, Canada, 1984; Volume 34, pp. 517–534. [Google Scholar]
- Magnan, M.; Pilote, P.; Daigneault, R. Minéralisations et Altérations à La MINE Copper Rand, Chibougamau; MERN Report ET-98-01; Ministère de l’Énergie et des Ressources Naturelles: Québec, QC, Canada, 1999. [Google Scholar]
- Jeffrey, W.G. The Geology of the Campbell Chibougamau Mine. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 1959. [Google Scholar]
- Pilote, P. Le camp minier de Chibougamau et le parautochtone grenvillien: Métallogénie, métamorphisme et aspects structuraux. In Livret-Guide D’excursion B1; Joined Anual Meeting; Geological Association of Canada–Mineralogical Association of Canada (GAC-MAC): Montreal, QC, Canada, 2006; p. 138. [Google Scholar]
- Warren, R.G.; Shaw, R.D. Volcanogenic Cu-Pb-Zn bodies in granulites of the central Arunta Block, central Australia. J. Metamorph. Geol. 1985, 3, 481–499. [Google Scholar] [CrossRef]
- Ravenelle, J.-F.; Dubé, B.; Malo, M.; McNicoll, V.; Nadeau, I.; Simoneau, J. Insights on the Geology of the World-Class Roberto Gold Deposit, Éléonore property, James Bay Area, Quebec; Current Research 2010-1; Geological Survey of Canada: Ottawa, ON, Canada, 2010; ISBN 1100145885.
- Ravenelle, J.-F. Amphibolite Facies Gold Mineralization: An Exemple from the Roberto Deposit, Eleonore Property, James Bay, Quebec. Ph.D. Thesis, Université du Québec, Institut National de la Recherche Scientifique, Montreal, QC, Canada, 2013. [Google Scholar]
- Fontaine, A.; Dubé, B.; Malo, M.; McNicoll, V.J.; Brisson, T.; Doucet, D.; Goutier, J. Geology of the metamorphosed Roberto gold deposit (Éléonore Mine), James Bay region, Quebec: Diversity of mineralization styles in a polyphase tectonometamorphic setting. In Targeted Geoscience Initiative 4: Contributions to the Understanding of Precambrian Lode Gold Deposits and Implications for Exploration; Dubé, B., Mercier-Langevin, P., Eds.; Geological Survey of Canada: Québec, QC, Canada, 2015; pp. 209–227. [Google Scholar]
- Mercier-Langevin, P. Les minéralisations auriféres au sein de la tonalite de La Grande-Sud, Baie-James, Québec. Master’s Thesis, Université du Québec à Chicoutimi, Chicoutimi, QC, Canada, 2000. [Google Scholar]
- Mercier-Langevin, P.; Daigneault, R.; Goutier, J.; Dion, C.; Archer, P. Geology of the Archean intrusion-hosted La-Grande-Sud Au-Cu prospect, La Grande Subprovince, James Bay region, Quebec. Econ. Geol. 2012, 107, 935–962. [Google Scholar] [CrossRef]
- MacLean, W.H.; Kranidiotis, P. Immobile elements as monitors of mass transfer in hydrothermal alteration; Phelps Dodge massive sulfide deposit, Matagami, Quebec. Econ. Geol. 1987, 82, 951–962. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Sawaguchi, T.; Iwaya, S.; Horiuchi, M. Delineation of prospecting targets for Kuroko deposits based on modes of volcanism of underlying dacite and alteration halos. Min. Geol. 1976, 26, 105–117. [Google Scholar]
- Hughes, C.J. Spilites, keratophyres, and the igneous spectrum. Geol. Mag. 1972, 109, 513–527. [Google Scholar] [CrossRef]
- Barth, T.F.W. Principles of classification and norm calculations of metamorphic rocks. J. Geol. 1959, 67, 135–152. [Google Scholar] [CrossRef]
- Riverin, G.; Hodgson, C.J. Wall-rock alteration at the Millenbach Cu-Zn mine, Noranda, Quebec. Econ. Geol. 1980, 75, 424–444. [Google Scholar] [CrossRef]
- Herrmann, W.; Berry, R.F. MINSQ-a least squares spreadsheet method for calculating mineral proportions from whole rock major element analyses. Geochem. Explor. Environ. Anal. 2002, 2, 361–368. [Google Scholar] [CrossRef]
- Trépanier, S.; Mathieu, L.; Daigneault, R. CONSONORM-LG: New normative minerals and alteration indexes for low-grade metamorphic rocks. Econ. Geol. 2015, 110, 2127–2138. [Google Scholar] [CrossRef]
- Mathieu, L.; Trépanier, S.; Daigneault, R. CONSONORM_HG: A new method of norm calculation for mid- to high-grade metamorphic rocks. J. Metamorph. Geol. 2016, 34, 1–15. [Google Scholar] [CrossRef]
- Middlemost, E.A.K. Iron oxidation ratios, norms and the classification of volcanic rocks. Chem. Geol. 1989, 77, 19–26. [Google Scholar] [CrossRef]
- Le Maitre, R.W. The chemical variability of some common igneous rocks. J. Petrol. 1976, 17, 589–598. [Google Scholar] [CrossRef]
- Warren, R.G. Metamorphic and tectonic evolution of granulites, Arunta Block, central Australia. Nature 1983, 305, 300–303. [Google Scholar] [CrossRef]
- Groves, D.I.; Goldfarb, R.J.; Gebre-Mariam, M.; Hagemann, S.G.; Robert, F. Orogenic gold deposits: A proposed classification in the context of their crustal distribution and relationship to other gold deposit types. Ore Geol. Rev. 1998, 13, 7–27. [Google Scholar] [CrossRef]
- Saeki, Y.; Date, J. Computer application to the alteration data of the footwall dacite lava at the Ezuri Kuroko deposits, Akita prefecture. Min. Geol. 1980, 30, 241–250. [Google Scholar]
- Gresens, R.L. Composition-volume relationships of metasomatism. Chem. Geol. 1967, 2, 47–65. [Google Scholar] [CrossRef]
- Babcock, R.S. Computational models of metasomatic processes. Lithos 1973, 6, 279–290. [Google Scholar] [CrossRef]
- Brimhall, G.H.; Dietrich, W.E. Constitutive mass balance relations between chemical composition, volume, density, porosity, and strain in metasomatic hydrochemical systems: Results on weathering and pedogenesis. Geochim. Cosmochim. Acta 1987, 51, 567–587. [Google Scholar] [CrossRef]
- Piercey, S.J. Modern analytical facilities 2. A review of quality assurance and quality control (QA/QC) procedures for lithogeochemical data. Geosci. Can. 2014, 41, 75–88. [Google Scholar] [CrossRef]
- Trépanier, S.; Mathieu, L.; Daigneault, R.; Faure, S. Precursors predicted by artificial neural networks for mass balance calculations: Quantifying hydrothermal alteration in volcanic rocks. Comput. Geosci. 2016, 89, 32–43. [Google Scholar] [CrossRef]
- Pearce, J.A.; Norry, M.J. Petrogenetic implications of Ti, Zr, Y, and Nb variations in volcanic rocks. Contrib. Mineral. Petrol. 1979, 69, 33–47. [Google Scholar] [CrossRef]
- MacLean, W.H. Rare earth element mobility at constant inter-REE ratios in the alteration zone at the Phelps Dodge massive sulphide deposit, Matagami, Quebec. Miner. Depos. 1988, 23, 231–238. [Google Scholar] [CrossRef]
- Rubin, J.N.; Henry, C.D.; Price, J.G. The mobility of zirconium and other “immobile” elements during hydrothermal alteration. Chem. Geol. 1993, 110, 29–47. [Google Scholar] [CrossRef]
- Grant, J.A. Isocon analysis: A brief review of the method and applications. Phys. Chem. Earth Parts A/B/C 2005, 30, 997–1004. [Google Scholar] [CrossRef]
- Grant, M. Étude du Métamorphisme et de la Distribution Verticale Des Teneurs en Au, As et Sb à la mine Sigma, Val-d’Or, Québec/Study of Metamorphism and Vertical Distribution of Au, As and Sb Grades at the Sigma mine, Val-d’Or, Québec. Master’s Thesis, École Polytechnique de Montréal, Montrea, QC, Canada, 1986. [Google Scholar]
- Leith, C.K.; Mead, W.J. Metamorphic Geology; Henry Holt: New York, NY, USA, 1915. [Google Scholar]
- Goldich, S.S. A study in rock-weathering. J. Geol. 1938, 46, 17–58. [Google Scholar] [CrossRef]
- Akella, J. Calculation of material transport in some metasomatic processes. Neues Jahrb. Mineral. Abh. 1966, 104, 316–329. [Google Scholar]
- Krauskopf, K.B. Introduction to Geochemistry; McGraw-Hill: New York, NY, USA, 1979; ISBN 0070354472. [Google Scholar]
- Finlow-Bates, T.; Stumpfl, E.F. The behaviour of so-called immobile elements in hydrothermally altered rocks associated with volcanogenic submarine-exhalative ore deposits. Miner. Depos. 1981, 16, 319–328. [Google Scholar] [CrossRef]
- Kranidiotis, P.; MacLean, W.H. Systematics of chlorite alteration at the Phelps Dodge massive sulfide deposit, Matagami, Quebec. Econ. Geol. 1987, 82, 1898–1911. [Google Scholar] [CrossRef]
- Barrett, T.J.; MacLean, W.H. Chemical, mass, and oxygen isotope changes during extreme hydrothermal alteration of an Archean rhyolite, Noranda, Quebec. Econ. Geol. 1991, 86, 406–414. [Google Scholar] [CrossRef]
- Barrett, T.J.; Cattalani, S.; Chartrand, F.; Jones, P. Massive sulfide deposits of the Noranda area, Quebec. II. The Aldermac mine. Can. J. Earth Sci. 1991, 28, 1301–1327. [Google Scholar] [CrossRef]
- Barrett, T.J.; MacLean, W.H.; Cattalani, S.; Hoy, L.; Riverin, G. Massive sulfide deposits of the Noranda area, Quebec. III. The Ansil mine. Can. J. Earth Sci. 1991, 28, 1699–1730. [Google Scholar] [CrossRef]
- Baumgartner, L.P.; Olsen, S.N. A least-squares approach to mass transport calculations using the isocon method. Econ. Geol. 1995, 90, 1261–1270. [Google Scholar] [CrossRef]
- Shriver, N.A.; MacLean, W.H. Mass, volume and chemical changes in the alteration zone at the Norbec mine, Noranda, Quebec. Miner. Depos. 1993, 28, 157–166. [Google Scholar] [CrossRef]
- Coggon, R.M.; Teagle, D.A.H.; Harris, M.; Davidson, G.J.; Alt, J.C.; Brewer, T.S. Hydrothermal contributions to global biogeochemical cycles: Insights from the Macquarie Island ophiolite. Lithos 2016, 264, 329–347. [Google Scholar] [CrossRef]
- Tomkins, A.G.; Mavrogenes, J.A. Mobilization of gold as a polymetallic melt during pelite anatexis at the Challenger deposit, South Australia: A metamorphosed Archean gold deposit. Econ. Geol. 2002, 97, 1249–1271. [Google Scholar] [CrossRef]
- Franklin, J.M.; Kasarda, J.; Poulsen, K.H. Petrology and chemistry of the alteration zone of the Mattabi massive sulfide deposit. Econ. Geol. 1975, 70, 63–79. [Google Scholar] [CrossRef]
- McQueen, K.G. Ore deposit types and their primary expressions. In Regolith Expression of Australian Ore Systems: A Compilation of Exploration Case Histories With Conceptual Dispersion, Process and Exploration Models; Butt, C.R.M., Robertson, I.D.M., Scott, K.M., Cornelius, M., Eds.; Cooperative Research Centre for Landscape Environments and Mineral Exploration: Millaa Millaa, Australia, 2005; pp. 1–14. [Google Scholar]
- Gaillard, N.; Williams-Jones, A.E.; Clark, J.R.; Lypaczewski, P.; Salvi, S.; Perrouty, S.; Piette-Lauziére, N.; Guilmette, C.; Linnen, R.L. Mica composition as a vector to gold mineralization: Deciphering hydrothermal and metamorphic effects in the Malartic District, Québec. Ore Geol. Rev. 2018, 789–820. [Google Scholar] [CrossRef]
- Nash, J.T. Fluid-Inclusion Petrology-Data from Porphyry Copper Deposits and Applications to Exploration; Professional Paper 907-D; U.S. Geological Survey: Reston, VA, USA, 1976.
- Brauhart, C.W.; Huston, D.L.; Andrew, A.S. Oxygen isotope mapping in the Panorama VMS district, Pilbara Craton, Western Australia: Applications to estimating temperatures of alteration and to exploration. Miner. Depos. 2000, 35, 727–740. [Google Scholar] [CrossRef]
- Beaudoin, G.; Pitre, D. Stable isotope geochemistry of the Archean Val-d’Or (Canada) orogenic gold vein field. Miner. Depos. 2005, 40, 59–75. [Google Scholar] [CrossRef]
- Pearce, T.H. A contribution to the theory of variation diagrams. Contrib. Mineral. Petrol. 1968, 19, 142–157. [Google Scholar] [CrossRef]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]



| Mass Changes | Examples of Assemblages | |
|---|---|---|
| Sulphidation | +S, +metals | Any minerals + sulphides |
| Silicification | +Si | Any minerals + quartz |
| Carbonatisation | +C, (+Ca) | Carbonates ± quartz-white mica-chlorite 1 Talc + chlorite + carbonate 2 |
| Sericitisation | +K or -K, -Na, -Ca, +H | White mica + quartz + pyrite 3 |
| Chloritisation | +Fe, +Mg, +H -Na, -Ca, -K | Chlorite + pyrite + white mica ± quartz 1 |
| Propylitisation | +H, +C | Epidote + chlorite + albite ± carbonate 3 |
| K-feldspar alteration | +K, -Na | K-feldspar + biotite + quartz 3 |
| Albitisation | +Na, -K | Albite + hornblende ± biotite-quartz 4 |
| Rhyolite | Dacite | Andesite | Basalt | |
|---|---|---|---|---|
| Samples (n) | 3423 | 3753 | 12,315 | 1360 |
| SiO2 (wt %) | 73.28 | 65.90 | 57.26 | 51.05 |
| TiO2 | 0.36 | 0.60 | 0.93 | 1.33 |
| Al2O3 | 13.24 | 15.72 | 16.67 | 15.46 |
| Fe2O3T | 2.71 | 4.75 | 8.58 | 11.73 |
| MgO | 0.49 | 1.70 | 4.08 | 6.41 |
| MnO | 0.07 | 0.09 | 0.14 | 0.18 |
| CaO | 1.32 | 3.86 | 7.11 | 9.64 |
| Na2O | 3.51 | 3.87 | 3.43 | 2.56 |
| K2O | 4.06 | 2.62 | 1.54 | 0.79 |
| P2O5 | 0.07 | 0.18 | 0.24 | 0.21 |
| LOI | 1.25 | 1.24 | 1.00 | 1.06 |
| Cr (ppm) | 18.29 | 36.27 | 90.68 | 191.54 |
| Zr | 297.85 | 174.84 | 137.55 | 109.75 |
| Y | 44.64 | 22.70 | 23.41 | 25.64 |
| Fe2O3/Fe2O3T 1 | 0.40 | 0.35 | 0.30 | 0.20 |
| FeO | 1.46 | 2.78 | 5.40 | 8.45 |
| Fe2O3 | 1.08 | 1.66 | 2.57 | 2.35 |
| AI | 48.51 | 35.85 | 34.78 | 37.11 |
| CCPI | 37.75 | 43.59 | 52.82 | 58.17 |
| ALT_CHLO | 3.59 | 8.78 | 10.36 | 10.68 |
| ALT_MUSCV | 5.61 | 0.69 | 0 | 0 |
| MB_CaO 2 | −0.01 | −0.34 | −0.72 | −0.23 |
| MB_Fe2O3T | −0.26 | 0.12 | 0.34 | −0.07 |
| MB_K2O | 0.78 | 0.04 | −0.08 | 0.07 |
| MB_MgO | 0.06 | −0.17 | −0.40 | −0.29 |
| MB_Na2O | −0.42 | 0.01 | −0.10 | −0.18 |
| MB_SiO2 | 8.68 | 3.04 | −1.35 | −0.84 |
| Method—Alteration Indices | |
|---|---|
| Advantage | Easy to calculate |
| Disadvantage | Strongly sensitive to the composition of the precursors |
| Requirements | Whole-rock chemical analyses (major elements), known precursors |
| Recommendation | To be used only in well-documented areas |
| Method—Normative Calculations and Related Indices | |
|---|---|
| Advantages | Accurate estimate of carbonatisation and other alterationsRelatively independent of the composition of precursors |
| Disadvantage | Silicification, albitisation, and K-feldspar alterations are hard to quantify because marker alteration minerals are abundant in unaltered rocks |
| Requirements | Whole-rock chemical analyses (major elements) and basic knowledge of metamorphic assemblages (to select the proper P-T model) |
| Recommendation | Can be used in a variety of contextsRecommended if carbonatisation needs to be quantified |
| Mass Balance Calculations—Generalities | |
| Advantage | Quantify mass gains and losses for each mobile element |
| Disadvantage | Chemical method that can be hard to reconcile with mineralogical observations, as alteration types bear the name of minerals, not chemical elements |
| Requirements | Whole-rock chemical analyses (at least major and minor elements); analysed and identified immobile elements |
| Method #1—Isocon Analysis | |
| Advantage | Precise mass balance calculation that can be used on all rock types |
| Disadvantages | Requires the sampling of a fresh rock that closely resembles the precursor of the studied altered rock Tedious in its application Only for rocks having similar precursors (single precursor systems) |
| Recommendation | To be used in well-documented areas |
| Method #2—Immobile Elements | |
| Advantages | Precise mass balance calculation for multiple precursor systems Simple to use |
| Disadvantages | Requires the sampling of a fresh rock that closely resembles the precursors of each rock type Mostly applied to co-magmatic igneous rocks, but it could be adapted to sedimentary rocks |
| Recommendation | To be used in well- to relatively well-documented areas |
| Method #3—Modelled Precursors | |
| Advantages | Designed for grassroots exploration (i.e., poorly documented areas) Does not require precise constraints on the composition of precursors |
| Disadvantages | Applies only to igneous rocks Complex, but software solutions are available [62] |
| Recommendation | Use in poorly to well-documented areas, as long as the precursor is an igneous rock and Zr is analysed |
| Data Set | Reported Alteration | Major Element Ratios | Normative Methods | Isocon Method | Immobile Element Method | Modelled Precursors |
|---|---|---|---|---|---|---|
| Hongtoushan | Chl 1 | Yes | Imprecise (A 2) | Imprecise (B, C) | No (B) | |
| Chibougamau | Si, Carb, Chl, Ser | Imprecise (C) | Yes | Imprecise (B, C) | Imprecise (D) | |
| Arunta | Chl | Imprecise (E) | Imprecise (E) | Imprecise (B, E) | No (B) | |
| Roberto | Calc, Si, K | Imprecise (C) | Imprecise (A, C) | Imprecise (B, C, D) | No (B, D) | |
| La Grande Sud | Si, Carb, K, Ser, Prop | Yes | Yes | Yes | Yes | Imprecise (D) |
| Phelps–Dodge | Chl, Si | No (F) | No (A, F) | Yes, for some major elements (F) | ||
| Major Element Ratios | Normative Methods | Isocon Method | Immobile Element Methods | Modelled Precursor | |
|---|---|---|---|---|---|
| Silicification, K-feldspar, albitisation | Hard to interpret if precursor is unavailable | Accurate quantification if precursor is representative | |||
| Carbonatisation, propylitic alteration | If CO2 analysed | Yes | If CO2 analysed | No | |
| Sericitisation | K-gains or losses are hard to discriminate | Precise quantification of alkali gains/losses; can be hard to relate to white mica proportions | |||
| Chloritisation | Yes | Yes, often better | Yes, and can distinguish Fe- from Mg-gains | ||
| Sedimentary precursor | Only if a representative precursor is identified | No | No | ||
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathieu, L. Quantifying Hydrothermal Alteration: A Review of Methods. Geosciences 2018, 8, 245. https://doi.org/10.3390/geosciences8070245
Mathieu L. Quantifying Hydrothermal Alteration: A Review of Methods. Geosciences. 2018; 8(7):245. https://doi.org/10.3390/geosciences8070245
Chicago/Turabian StyleMathieu, Lucie. 2018. "Quantifying Hydrothermal Alteration: A Review of Methods" Geosciences 8, no. 7: 245. https://doi.org/10.3390/geosciences8070245
APA StyleMathieu, L. (2018). Quantifying Hydrothermal Alteration: A Review of Methods. Geosciences, 8(7), 245. https://doi.org/10.3390/geosciences8070245





