Investigating the Effect of a Mechanism Combined with a Speed-Increasing Gear and a Pneumatic Artificial Muscle
Abstract
:1. Introduction
2. Methods
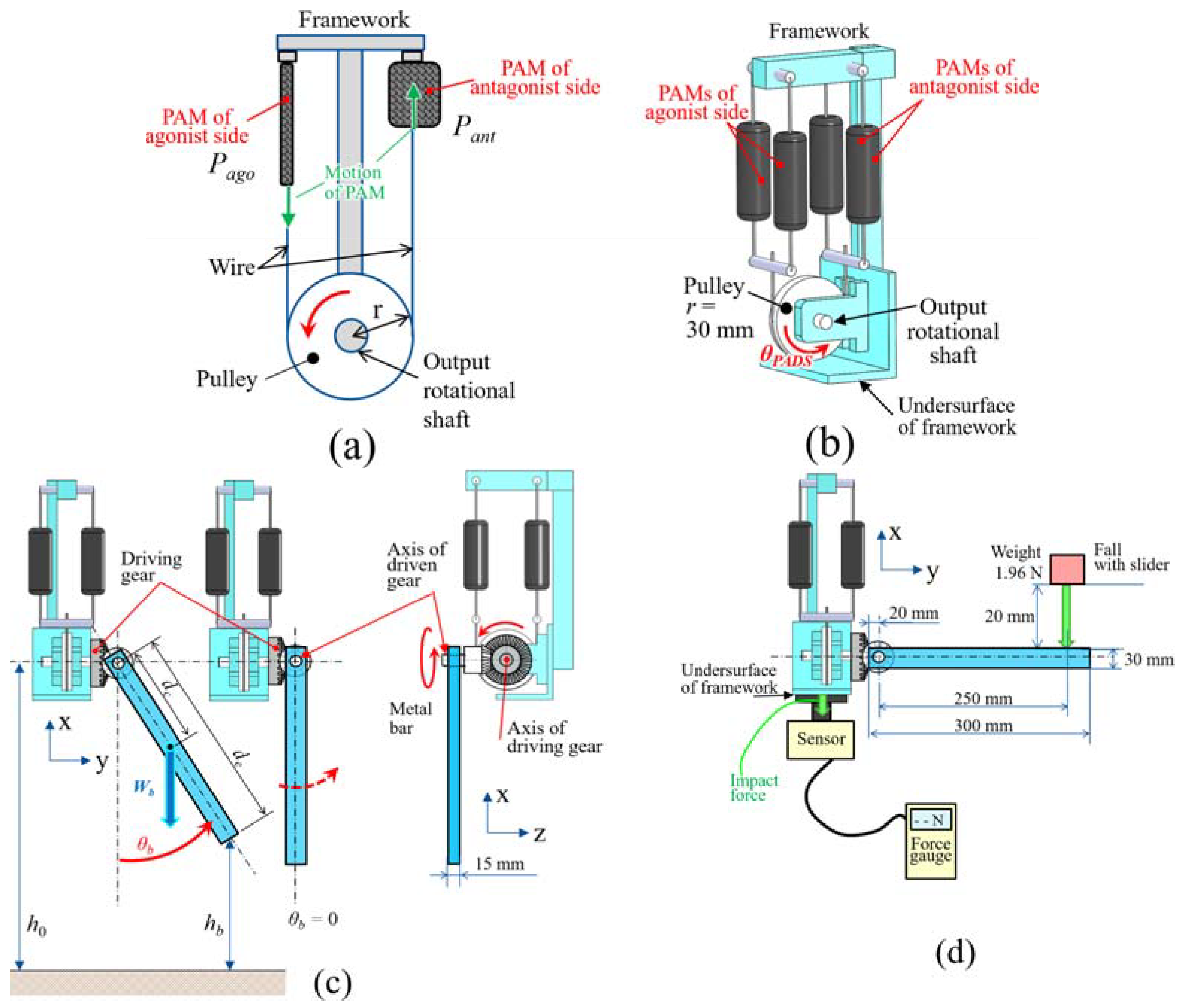
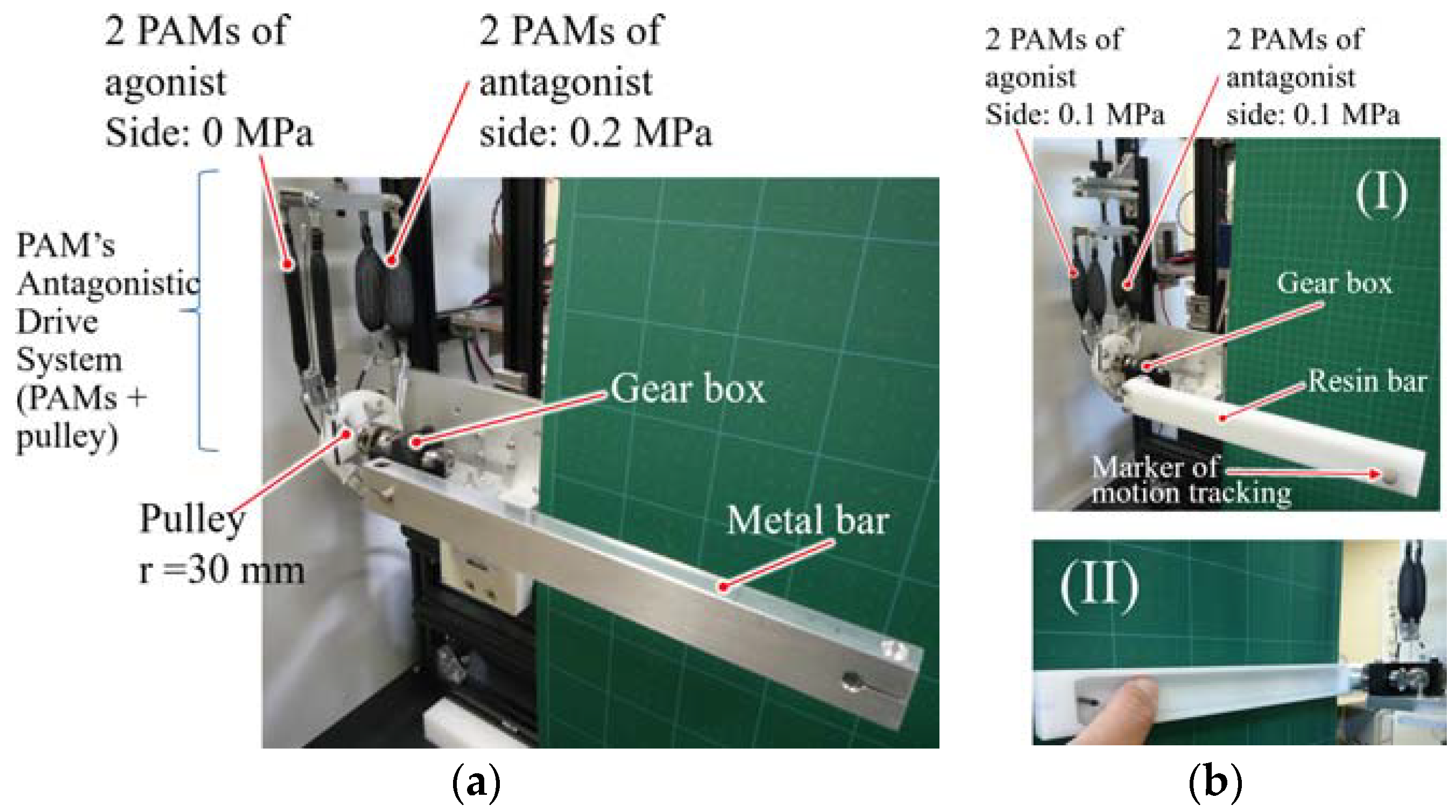
2.1. Overview
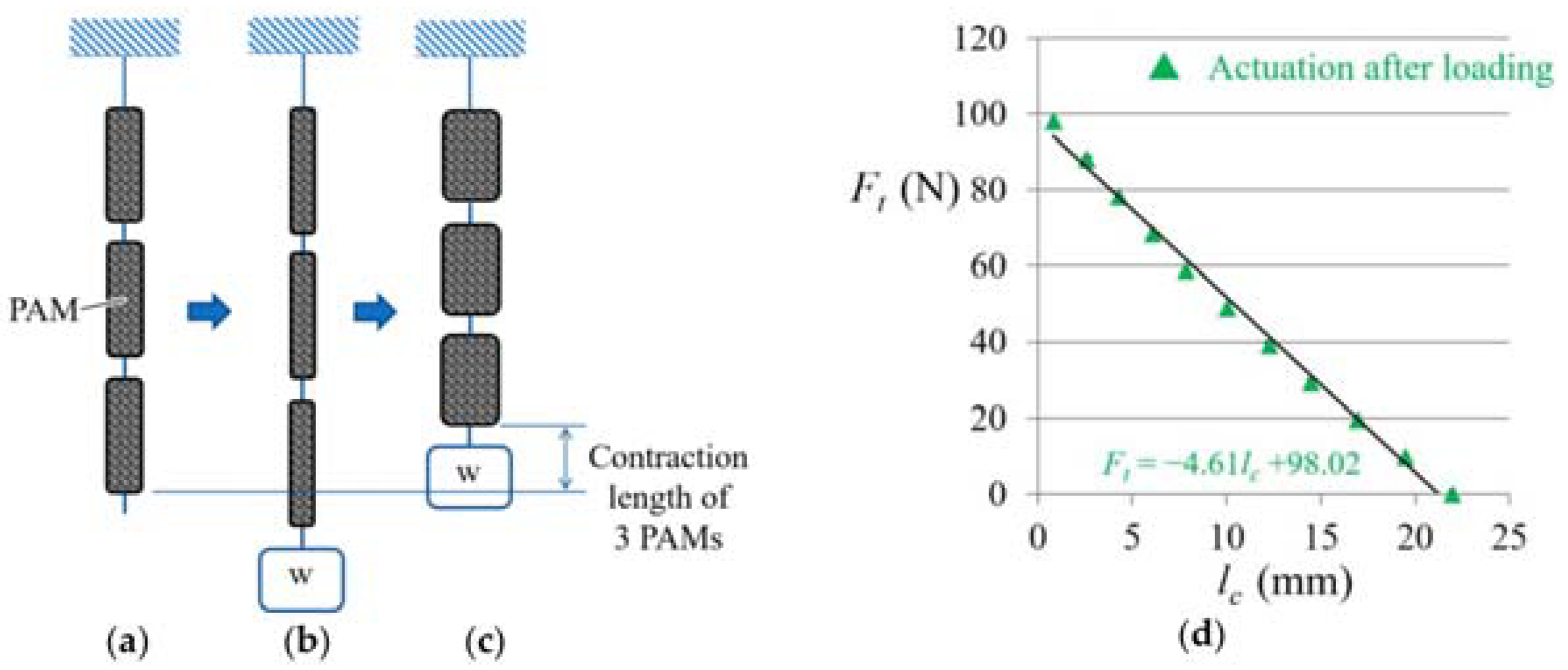
2.2. Pneumatic Artificial Muscle (PAM)
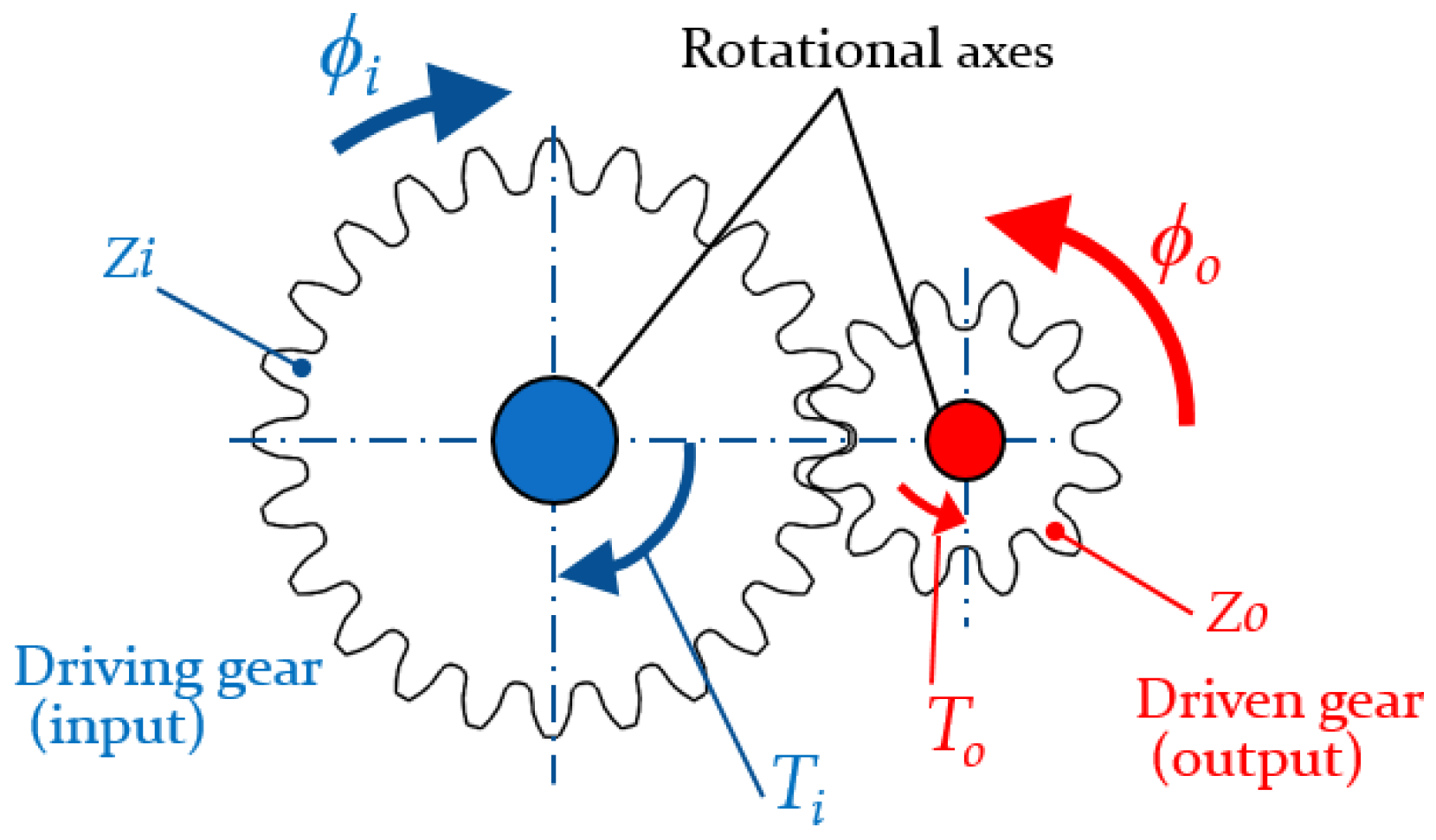
2.3. Gearbox
= RgCp(−4.61(2πrRgθb/360)/Cs + 98.02)r
2.4. Simulation
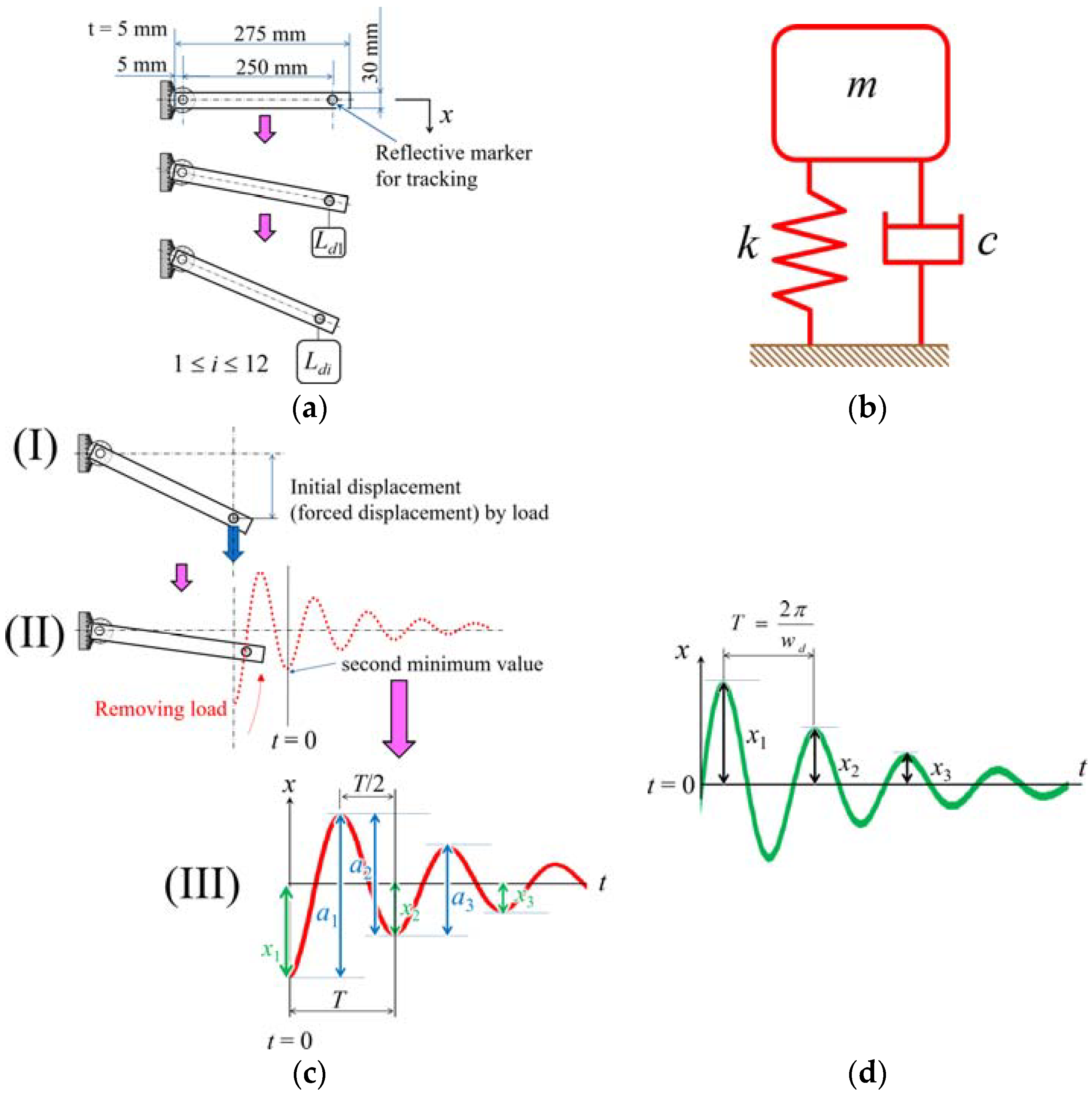
2.5. Experiment
3. Results
3.1. Prototype
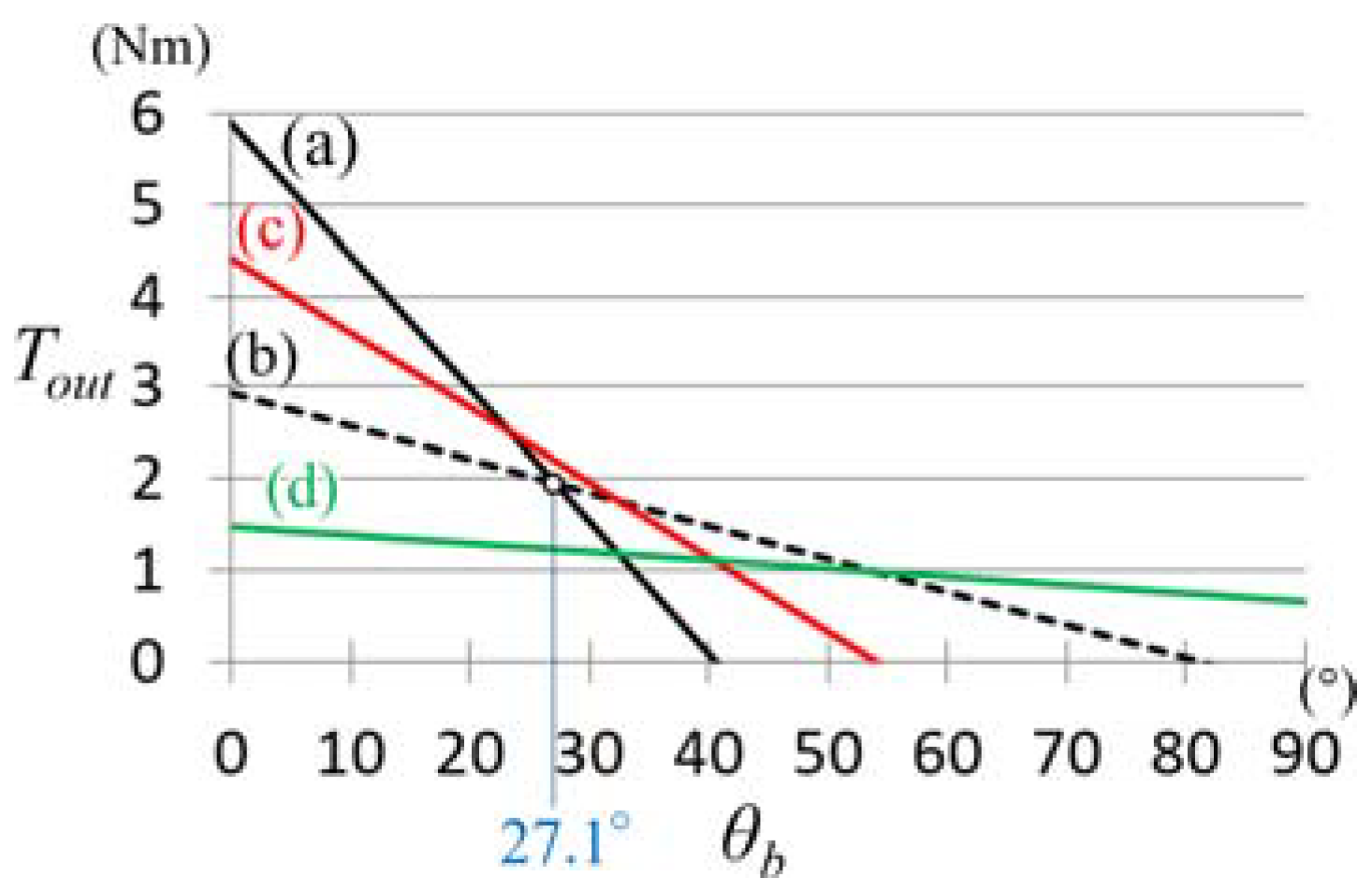
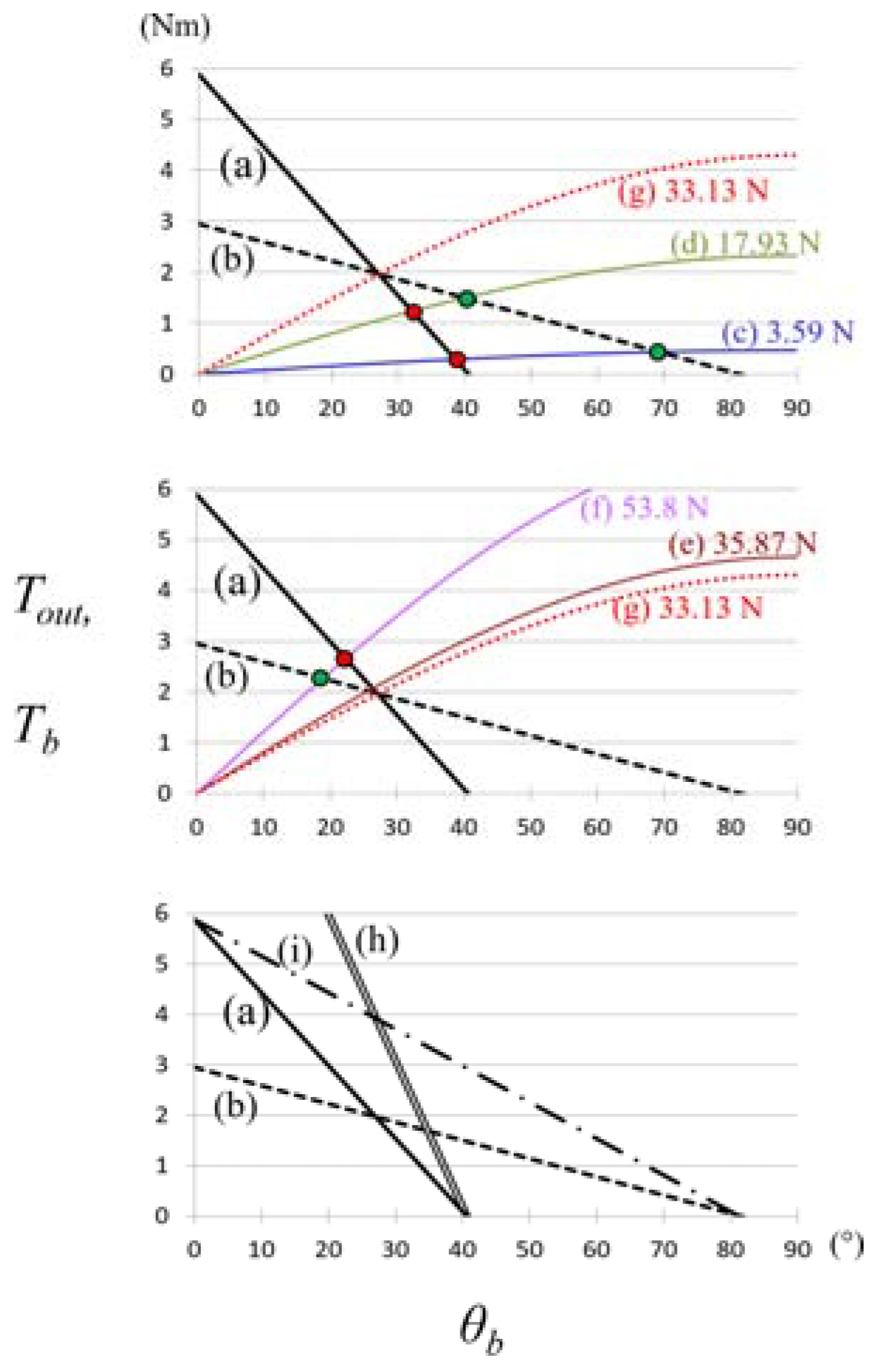
3.2. Simulation
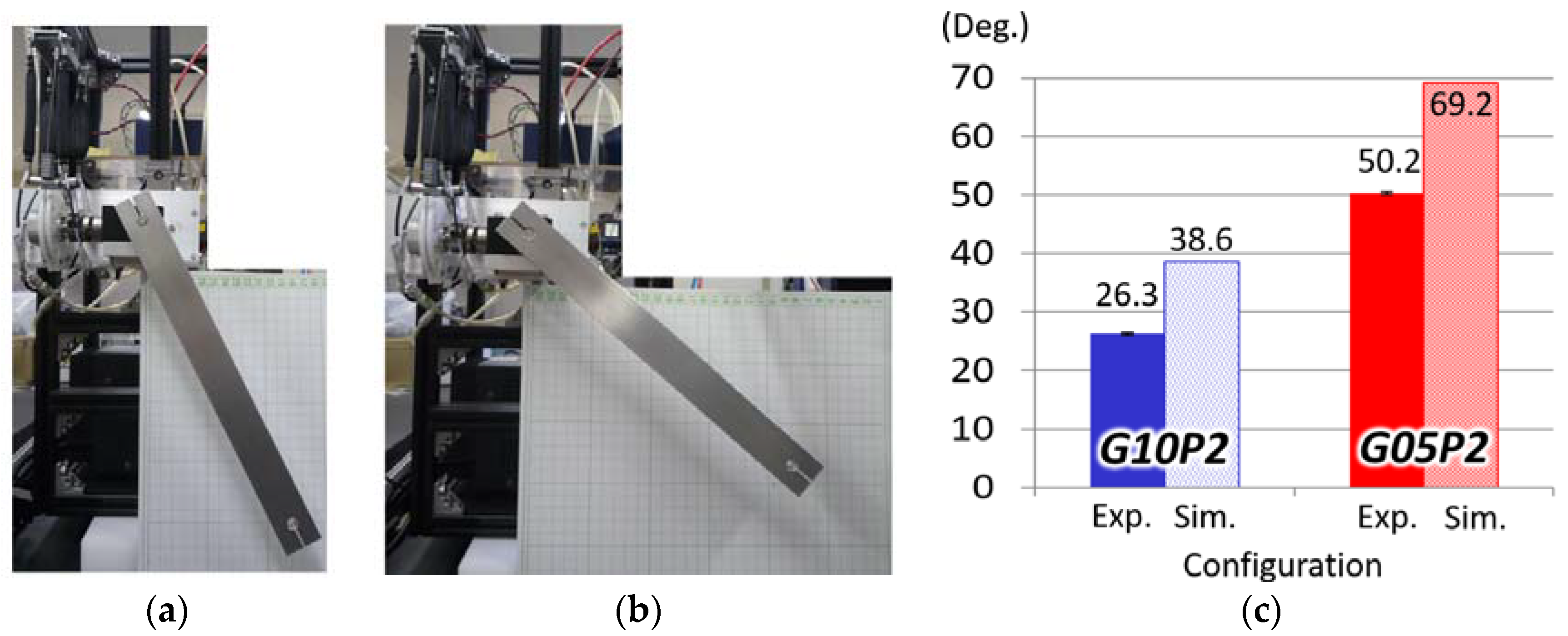
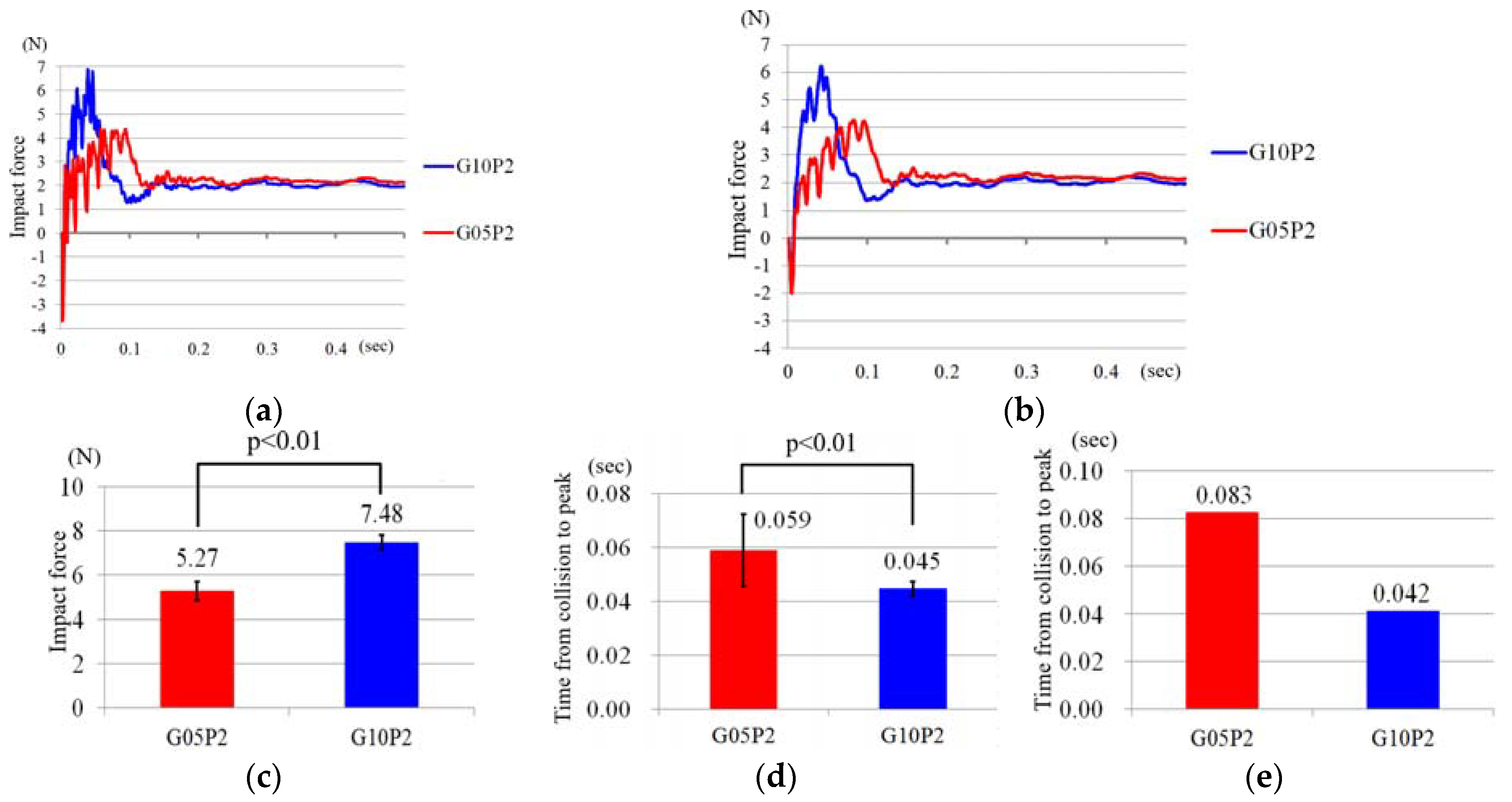
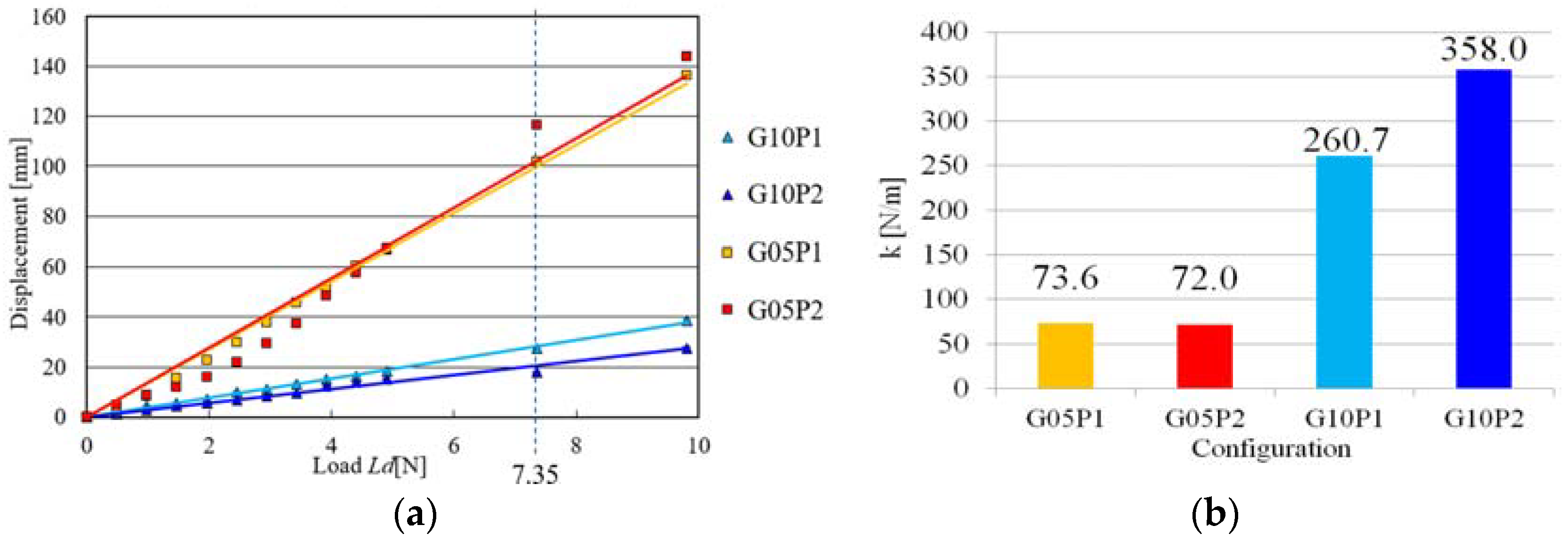
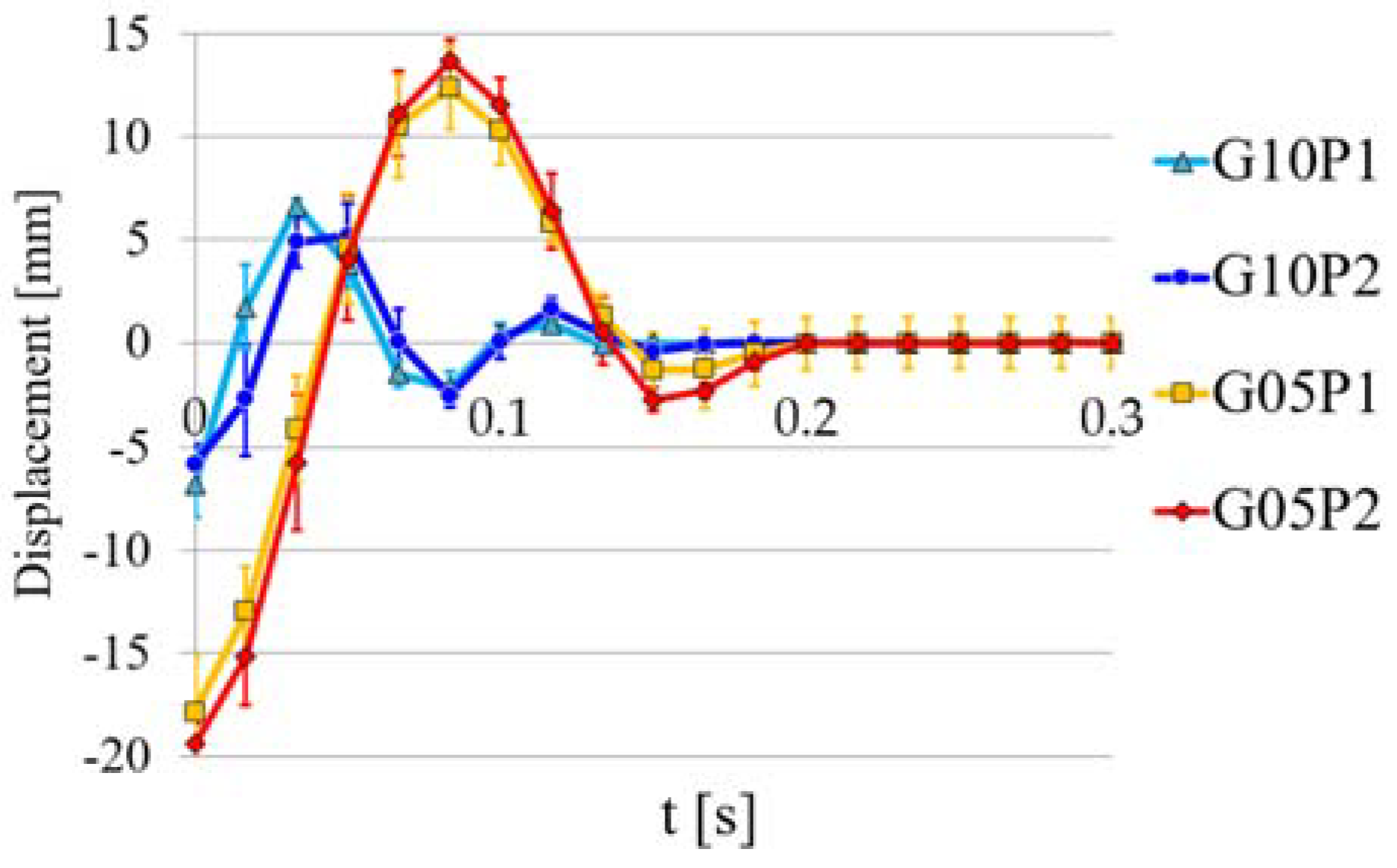
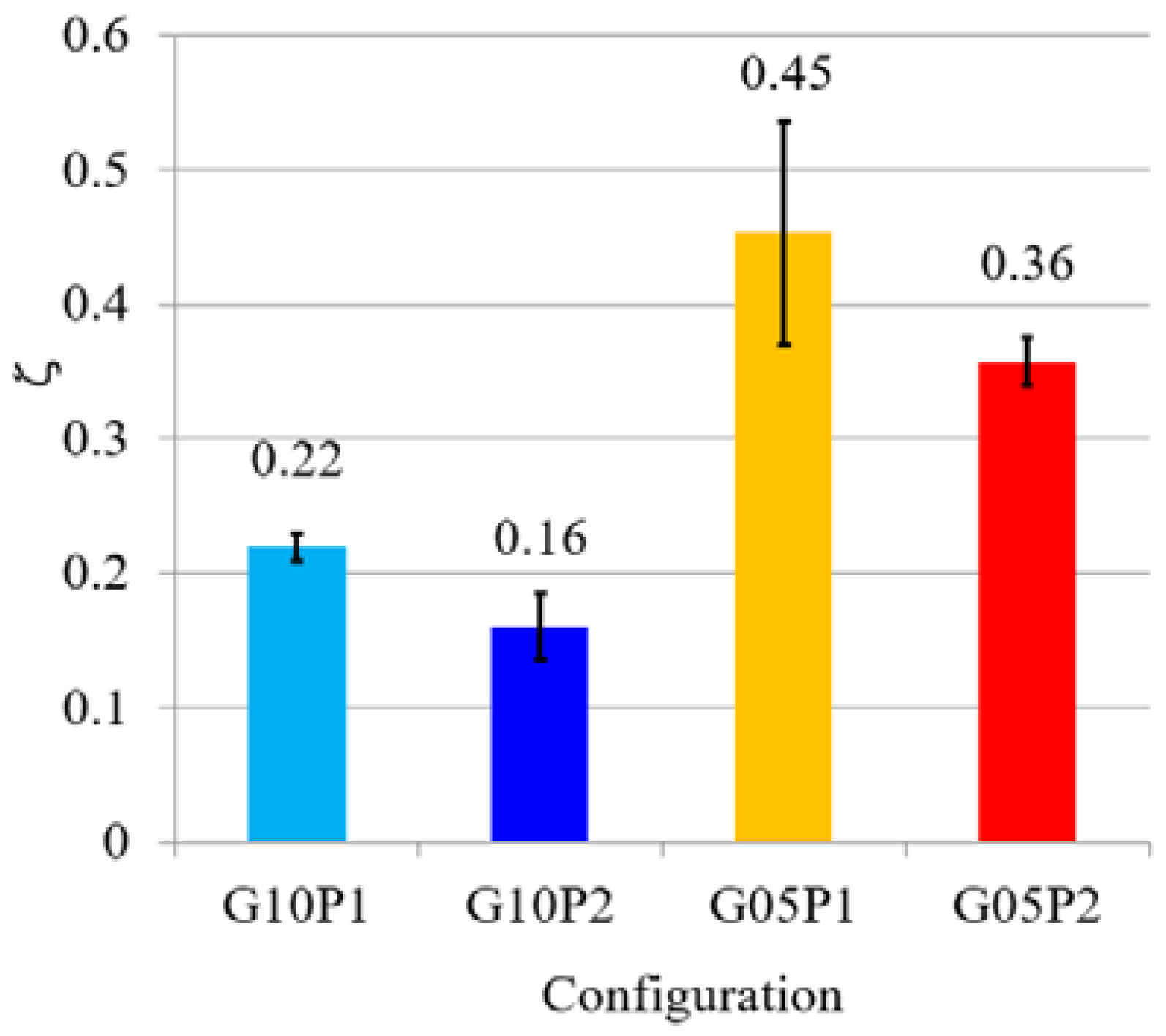
3.3. Experiments
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| PAM | Pneumatic artificial muscle |
| ROM | Range of motion |
| SMA | Shape memory alloys |
| PADS | PAM’s antagonistic drive system |
| PADS-gear mechanism | Mechanism combined with PADS and gearbox |
| Zi | Teeth number of input large gear |
| Zo | Teeth number of output small gear |
| Ti | Input torque of gear box |
| To | Output torque of gear box |
| ϕi | Input rotational angle of gear box |
| ϕo | Output rotational angle of gear box |
| Ft | Traction force |
| lc | Contraction length |
| Rg | Reduction ratio of gear |
| Tout | Output torque of PADS-gear mechanism |
| Cs | Number of PAM serial connections |
| Cp | Number of PAM parallel connections |
| r | Pulley radius |
| θPADS | Rotational angle of PADS (in degrees) |
| Wb | Weight of bar |
| dc | Distance between bar center and rotational axis |
| θb | Rotational angle of bar (in degrees) |
| Tb | Required torque for rotating bar |
| c | Viscous damping coefficient |
| k | Spring constant |
| Ld | Load |
| x | Displacement of bar end tip |
| Fs | Static load |
| t | Time |
| wn | Natural angular frequency |
| wd | Damped angular frequency |
| ζ | Damping ratio |
| C1 and σ | Arbitrary constants |
| δ | Logarithmic decrement |
| m | Mass |
| T | Cycle time |
| G05P1-2 | G05P1 and G05P2 |
| G10P1-2 | G10P1 and G10P2 |
References
- Jiang, F.; Tao, G.; Li, Q. Analysis and control of a parallel lower limb based on pneumatic artificial muscles. Adv. Mech. Eng. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Aguilar-Sierra, H.; Yu, W.; Salazar, S.; Lopez, R. Design and control of hybrid actuation lower limb exoskeleton. Adv. Mech. Eng. 2015, 76, 1–13. [Google Scholar] [CrossRef]
- Mizuno, T.; Tsujiuchi, N.; Koizumi, T.; Nakamura, Y.; Sugiura, M. Spring-damper model and articulation control of pneumatic artificial muscle actuators. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; pp. 1267–1272. [Google Scholar]
- Ahmad Sharbafi, M.; Shin, H.; Zhao, G.; Hosoda, K.; Seyfarth, A. Electric-Pneumatic Actuator: A New Muscle for Locomotion. Actuators 2017, 6, 30. [Google Scholar] [CrossRef]
- Martens, M.; Boblan, I. Modeling the Static Force of a Festo Pneumatic Muscle Actuator: A New Approach and a Comparison to Existing Models. Actuators 2017, 6, 33. [Google Scholar] [CrossRef]
- Davis, S.; Caldwell, D.G. pneumatic Muscle Actuators for Humanoid applications–Sensor and Valve Integration, Humanoid Robots. In Proceedings of the 6th IEEE-RAS International Conference, Genova, Italy, 4–6 December 2006; pp. 456–461. [Google Scholar]
- Zhong, J.; Fan, J.; Zhu, Y.; Zhao, J.; Zhai, W. One nonlinear PID control to improve the control performance of a manipulator actuated by a pneumatic muscle actuator. Adv. Mech. Eng. 2014, 6, 172782. [Google Scholar] [CrossRef]
- Zhong, J.; Fan, J.; Zhu, Y.; Zhao, J.; Zhai, W. Static modeling for commercial braided pneumatic muscle actuators. Adv. Mech. Eng. 2014, 6, 425217. [Google Scholar] [CrossRef]
- Erin, O.; Pol, N.; Valle, L.; Park, Y.L. Design of a bio-inspired pneumatic artificial muscle with self-contained sensing. In Proceedings of the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC’16), Orlando, FL, USA, 16–20 August 2016; pp. 2115–2119. [Google Scholar]
- Plettenburg, D. Pneumatic actuators: A comparison of energy-to-mass ratios. In Proceedings of the 2005 IEEE 9th International Conference on Rehabilitation Robotics (ICORR2005), Chicago, IL, USA, 28 June–1 July 2005; pp. 545–549. [Google Scholar]
- Peerdeman, B.; Smit, G.; Stramigioli, S.; Plettenburg, D.; Misra, S. Evaluation of pneumatic cylinder actuators for hand prostheses. In Proceedings of the 4th IEEE RAS EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 1104–1109. [Google Scholar]
- Garcia, E.; Arevalo, J.C.; Sanchez, F.; Sarria, J.F.; Gonzalez-de-Santos, P. Design and development of a biomimetic leg using hybrid actuators. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011; pp. 1507–1512. [Google Scholar]
- Oh, J.S.; Shin, Y.J.; Koo, H.W.; Kim, H.C.; Park, J.; Choi, S.B. Vibration control of a semi-active railway vehicle suspension with magneto-rheological dampers. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Xu, B.; Peng, S.; Song, A.; Yang, R.; Pan, L. Robot-aided upper-limb rehabilitation based on motor imagery EEG. Int. J. Adv. Robot. Syst. 2011, 8, 88–97. [Google Scholar] [CrossRef]
- Aggogeri, F.; Pellegrini, N. Design and experimental validation of a shape memory alloy actuator for linear motors. Appl. Mech. Mater. 2015, 783, 69–75. [Google Scholar] [CrossRef]
- Kaplanoglu, E. Design of shape memory alloy-based and tendon-driven actuated fingers towards a hybrid anthropomorphic prosthetic hand. Int. J. Adv. Robot. Syst. 2012, 9, 77. [Google Scholar] [CrossRef]
- Borboni, A.; Aggogeri, F.; Pellegrini, N.; Faglia, R. Innovative modular SMA actuator. Adv. Mater. Res. 2012, 590, 405–410. [Google Scholar] [CrossRef]
- Wang, T.; Ge, L.; Gu, G. Programmable design of soft pneu-net actuators with oblique chambers can generate coupled bending and twisting motions. Sens. Actuators A Phys. 2018, 271, 131–138. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, J.; Zhu, L.M.; Zhu, X. A survey on dielectric elastomer actuators for soft robots. Bioinspir. Biomim. 2017, 12, 1–22. [Google Scholar] [CrossRef]
- Marhanani, C.; Widyotriatmo, A.; Suprijanto. Free regressor adaptive impedance control for arm rehabilitation robot. In Proceedings of the 2016 International Conference on Instrumentation, Control and Automation (ICA), Bandung, Indonesia, 29–31 August 2016; pp. 76–80. [Google Scholar]
- Li, Z.; Huang, Z.; He, W.; Su, C.Y. Adaptive impedance control for an upper limb robotic exoskeleton using biological signals. IEEE Trans. Ind. Electron. 2017, 64, 1664–1674. [Google Scholar] [CrossRef]
- Morales, R.; Badesa, F.J.; García-Aracil, N.; Sabater, J.M.; Pérez-Vidal, C. Pneumatic robotic systems for upper limb rehabilitation. Med. Biol. Eng. Comput. 2011, 49, 1145–1156. [Google Scholar] [CrossRef] [PubMed]
- Ishida, T.; Takanishi, A. A robot actuator development with high backdrivability. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics (RAM2006), Bangkok, Thailand, 7–9 June 2006; pp. 1–6. [Google Scholar]
- IMADA Co. Ltd. ZTA-DPU-500N. Available online: http://www.forcegauge.net/en/new-products/20109.html (accessed on 3 April 2018).
- Sekine, M.; Kita, K.; Yu, W. Designing and testing lightweight shoulder prostheses with hybrid actuators for movements involved in typical activities of daily living and impact absorption. Med. Devices Evid. Res. 2015, 8, 279–294. [Google Scholar] [CrossRef] [PubMed]
- SQUSE. PM-10P. Available online: http://www.squse.co.jp/product/detail.php?id=9 (accessed on 3 April 2018). (In Japanese).
- Sekine, M.; Shiota, K.; Kita, K.; Namiki, A.; Yu, W. A lightweight shoulder prosthesis with antagonistic impact-absorbing hybrid actuation for bimanual activities of daily living. Adv. Mech. Eng. 2016, 8, 1–17. [Google Scholar] [CrossRef]
- Kyouiku Gear MFG Co., Ltd. Available online: http://www.kggear.co.jp/ (accessed on 11 May 2018). (In Japanese).
- Library Co., Ltd. Available online: http://www.library-japan.com/ (accessed on 3 April 2018).
- Thomson, W.T. Theory of Vibration with Applications; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Koay, L.K.; Ratnam, M.M.; Gitano-Briggs, H. An Approach for Nonlinear Damping Characterization for Linear Optical Scanner. Exp. Tech. 2015, 39, 38–46. [Google Scholar] [CrossRef]


| Configuration | Gear Ratio | Air Pressure (MPa) | ||
|---|---|---|---|---|
| No. | Name | Antagonist Side | Agonist Side | |
| 1 | G10P1 | 1 | 0.1 | 0.1 |
| 2 | G10P2 | 1 | 0.2 | 0 |
| 3 | G05P1 | 0.5 | 0.1 | 0.1 |
| 4 | G05P2 | 0.5 | 0.2 | 0 |
| Configuration | Initial Displacement (mm) | |
|---|---|---|
| No. | Name | |
| 1 | G10P1 | 27 |
| 2 | G10P2 | 18 |
| 3 | G05P1 | 102 |
| 4 | G05P2 | 117 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekine, M.; Kokubun, R.; Yu, W. Investigating the Effect of a Mechanism Combined with a Speed-Increasing Gear and a Pneumatic Artificial Muscle. Actuators 2018, 7, 22. https://doi.org/10.3390/act7020022
Sekine M, Kokubun R, Yu W. Investigating the Effect of a Mechanism Combined with a Speed-Increasing Gear and a Pneumatic Artificial Muscle. Actuators. 2018; 7(2):22. https://doi.org/10.3390/act7020022
Chicago/Turabian StyleSekine, Masashi, Ryohei Kokubun, and Wenwei Yu. 2018. "Investigating the Effect of a Mechanism Combined with a Speed-Increasing Gear and a Pneumatic Artificial Muscle" Actuators 7, no. 2: 22. https://doi.org/10.3390/act7020022




