Actuator Location and Voltages Optimization for Shape Control of Smart Beams Using Genetic Algorithms
Abstract
:1. Introduction
2. Formulation of the Problem
2.1. Strains and Electrical Fields
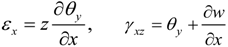
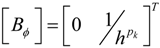
2.2. Constitutive Equations
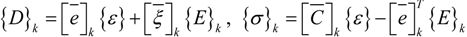
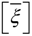 is the permittivity matrix. For non−piezoelectric layers, [e] and
is the permittivity matrix. For non−piezoelectric layers, [e] and 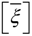 are reduced to zero matrices. The constitutive relations, given in Equation (4), are with reference to the global coordinate system (x, y, z).
are reduced to zero matrices. The constitutive relations, given in Equation (4), are with reference to the global coordinate system (x, y, z).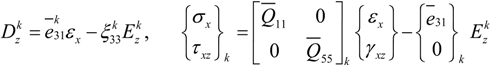
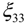 is the electric permittivity.
is the electric permittivity.2.3. Finite Element Formulation
3. Optimal Shape Control
3.1. The Fitness Function
 is the desired nodal transverse displacement value and r is the number of concerned displacements.
is the desired nodal transverse displacement value and r is the number of concerned displacements. 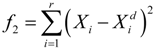
3.2. Design Optimization Problems
3.3. Genetic Algorithm and Great Deluge
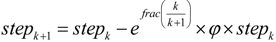

3.3.1. Chromosome Encoding

3.3.2. GA Implementation Issues
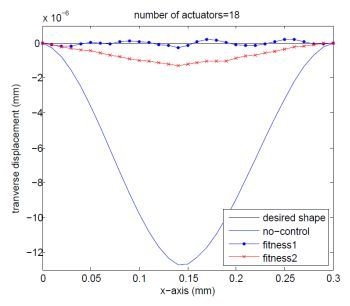
4. Numerical Results
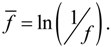
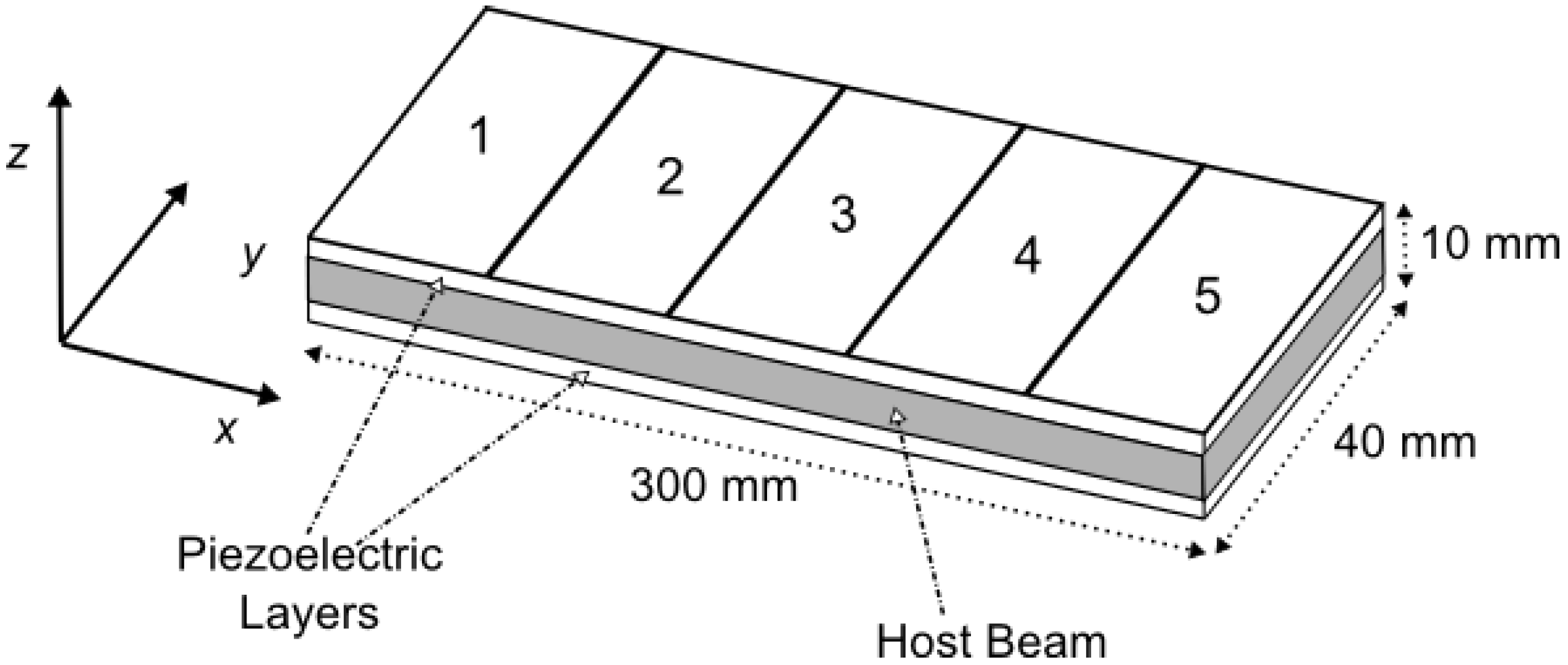
4.1. The Voltage Problem
4.2. The Location and Voltage Problem
| Number of used Actuator Groups | Method | Voltage of the Actuator Groups (V) | Fitness f2 | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||||
| 432.61 | 0.00 | 389.20 | 0.00 | 0.00 | 17.86 | |||
| Present (case 1) | 432.60 | 389.21 | 17.86 | |||||
| Present (case 2) | 438.87 | 400.55 | 17.76 | |||||
| (1,2,3) | [9] | 324.83 | 217.58 | 272.11 | 0.00 | 0.00 | 18.99 | |
| Present (case 1) | 324.91 | 217.41 | 272.20 | 18.99 | ||||
| Present (case 2) | 325.35 | 216.01 | 277.59 | 18.89 | ||||
| (1,2,3,4) | [9] | 320.15 | 243.17 | 169.88 | 122.44 | 0.00 | 22.14 | |
| Present (case 1) | 320.20 | 243.30 | 169.51 | 122.57 | 22.14 | |||
| Present (case 2) | 320.33 | 243.39 | 169.21 | 123.79 | 22.03 | |||
| (1,2,3,4,5) | [9] | 320.54 | 240.47 | 178.09 | 98.57 | 41.94 | 23.41 | |
| Present (case 1) | 321.06 | 241.18 | 173.58 | 107.45 | 30.37 | 23.61 | ||
| Present (case 2) | 320.18 | 243.09 | 171.98 | 107.91 | 31.20 | 23.56 | ||
4.2.1. Clamped−Free Beam
| Number of Actuators in Use | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 12 | 18 | 24 | 30 | ||||||
| f1 | f2 | f1 | f2 | f1 | f2 | f1 | f2 | f1 | f2 | |
| 1 | 240.00 | 240.00 | 72.88 | 170.6295 | 211.79 | 178.82 | 150.63 | 172.21 | 196.49 | 171.86 |
| 2 | 0 | 240.00 | 205.33 | 166.2474 | 137.64 | 240.00 | 181.99 | 164.26 | 135.51 | 165.25 |
| 3 | 240.00 | 240.00 | 57.59 | 239.5262 | 224.25 | 0 | 233.47 | 160.70 | 200.80 | 159.43 |
| 4 | 240.00 | 0 | 227.76 | 0 | 0 | 237.75 | 142.78 | 152.82 | 106.08 | 154.16 |
| 5 | 240.00 | 0 | 240.00 | 235.2183 | 236.74 | 150.84 | 62.97 | 148.71 | 172.72 | 147.67 |
| 6 | 240.00 | 240.00 | 240.00 | 240.00 | 157.88 | 141.92 | 153.98 | 141.55 | 134.09 | 142.17 |
| 7 | 240.00 | 240.00 | 240.00 | 0 | 144.00 | 136.04 | 133.83 | 137.12 | 175.95 | 136.62 |
| 8 | 240.00 | 0 | 0 | 240.00 | 101.20 | 131.17 | 202.06 | 129.91 | 77.37 | 130.25 |
| 9 | 240.00 | 0 | 240.00 | 0 | 111.33 | 124.13 | 82.88 | 125.06 | 133.95 | 125.01 |
| 10 | 0 | 240.00 | 0 | 240.00 | 154.75 | 179.14 | 155.75 | 118.98 | 147.23 | 118.82 |
| 11 | 0 | 240.00 | 0 | 240.00 | 124.40 | 0 | 20.06 | 113.21 | 89.92 | 112.97 |
| 12 | 0 | 0 | 240.00 | 0 | 138.96 | 220.14 | 142.41 | 107.06 | 88.79 | 107.72 |
| 13 | 0 | 240.00 | 240.00 | 0 | 0 | 0 | 215.45 | 101.73 | 163.93 | 101.21 |
| 14 | 0 | 0 | 0 | 240.00 | 232.81 | 149.81 | 0 | 95.90 | 54.65 | 95.94 |
| 15 | 0 | 0 | 0 | 0 | 0 | 89.29 | 0 | 89.52 | 66.10 | 89.88 |
| 16 | 0 | 0 | 240.00 | 0 | 0 | 84.59 | 223.23 | 84.19 | 137.71 | 84.19 |
| 17 | 0 | 0 | 0 | 240.00 | 180.02 | 116.37 | 54.80 | 78.72 | 16.61 | 78.05 |
| 18 | 0 | 0 | 0 | 0 | 126.31 | 0 | 50.74 | 71.97 | 126.12 | 72.91 |
| 19 | 0 | 0 | 0 | 240.00 | 0 | 167.23 | 135.11 | 99.19 | 72.24 | 66.33 |
| 20 | 0 | 0 | 0 | 0 | 118.10 | 0 | 0 | 0 | 17.67 | 61.24 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 87.00 | 79.27 | 54.98 |
| 22 | 0 | 0 | 240.00 | 0 | 0 | 132.40 | 133.63 | 72.41 | 27.59 | 49.26 |
| 23 | 0 | 0 | 0 | 0 | 194.29 | 0 | 28.23 | 0 | 60.20 | 43.54 |
| 24 | 0 | 0 | 0 | 0 | 0 | 124.34 | 36.36 | 77.41 | 55.35 | 37.67 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0.12 | 0 | 21.19 | 31.62 |
| 26 | 0 | 0 | 0 | 0 | 0 | 0 | 79.99 | 68.89 | 3.47 | 26.56 |
| 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 31.47 | 20.06 |
| 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 27.63 | 14.41 |
| 29 | 0 | 0 | 0 | 0 | 122.02 | 0 | 17.03 | 0 | 0.53 | 8.90 |
| 30 | 0 | 0 | 0 | 186.51 | 1.87 | 46.15 | 2.03 | 22.71 | 0.38 | 2.59 |
| Fitness | 22.00 | 16.11 | 25.60 | 19.09 | 30.65 | 20.88 | 31.29 | 23.12 | 33.66 | 26.77 |
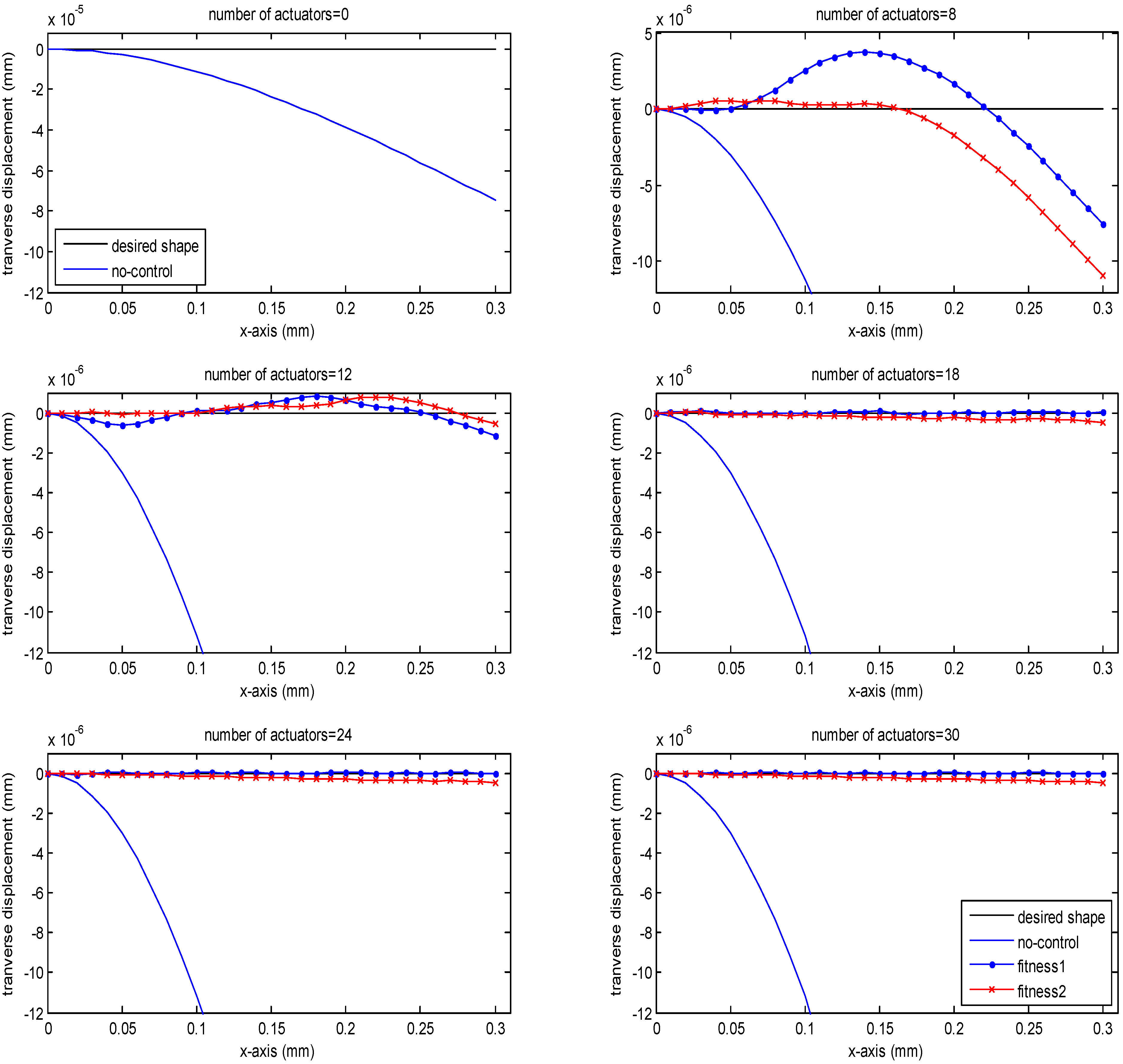
4.2.2. Clamped−Clamped Beam
5. Conclusions
| Number of Elements | Number of Actuators in Use | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 12 | 18 | 24 | 30 | ||||||
| f1 | f2 | f1 | f2 | f1 | f2 | f1 | f2 | f1 | f2 | |
| 1 | 240.00 | 240.00 | 239.98 | 240.00 | 240.00 | 240.00 | 240.00 | 235.43 | 239.95 | 211.92 |
| 2 | 240.00 | 240.00 | 0 | 0 | 240.00 | 240.00 | 240.00 | 205.09 | 196.47 | 180.26 |
| 3 | 0 | 0 | 239.97 | 0 | 240.00 | 213.31 | 240.00 | 174.19 | 141.02 | 149.30 |
| 4 | 0 | 0 | 0 | 0 | 240.00 | 157.75 | 99.60 | 143.31 | 33.89 | 118.34 |
| 5 | 0 | 0 | 0 | 240.00 | 0 | 169.21 | 70.087 | 112.43 | 72.03 | 87.38 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 3.87 | 108.23 | 72.32 | 56.42 |
| 7 | 0 | 0 | 0 | 0 | 157.35 | 91.23 | 93.21 | 0 | −51.29 | 25.46 |
| 8 | 0 | 0 | 0 | −168.77 | 65.58 | 0 | 46.64 | 46.47 | 48.25 | −5.51 |
| 9 | 0 | 0 | 0 | 0 | −172.58 | 0 | −59.20 | −11.14 | −162.20 | −36.47 |
| 10 | 0 | −240.00 | 0 | 0 | 0 | 0 | −240.00 | −42.00 | 1.25 | −67.42 |
| 11 | −240.00 | 0 | 0 | 0 | −240.00 | 131.61 | 0 | −72.92 | −151.25 | −98.38 |
| 12 | 0 | 0 | −239.96 | −240.00 | 0 | 121.53 | 0 | −103.80 | −144.01 | −129.35 |
| 13 | 0 | 0 | 239.97 | −240.00 | −240.00 | 156.44 | −240.00 | −134.69 | −230.12 | −160.31 |
| 14 | −240.00 | 0 | 239.98 | 0 | −240.00 | 191.35 | −240.00 | −165.58 | −239.98 | −191.27 |
| 15 | 0 | 0 | 239.99 | −240.00 | 0 | 197.23 | −240.00 | −167.45 | −239.93 | −193.21 |
| 16 | −240.00 | −240.00 | 239.98 | −240.00 | −240.00 | 174.10 | −240.00 | −140.27 | −222.46 | −166.13 |
| 17 | 0 | −240.00 | 0 | 0 | −240.00 | 150.97 | −191.31 | −158.49 | −186.16 | −139.05 |
| 18 | 0 | 0 | 0 | 0 | −192.47 | 230.14 | 0 | 0 | −106.64 | −111.97 |
| 19 | 0 | 0 | 239.93 | 0 | −199.99 | 0 | −143.09 | −125.64 | −115.69 | −84.89 |
| 20 | 0 | −240.00 | 0 | −240.00 | 0 | 0 | −96.15 | 0 | −54.88 | −57.80 |
| 21 | 0 | 0 | 0 | 0 | 0 | −184.05 | 13.02 | 0 | −67.16 | −30.72 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | −46.17 | 0 | −66.87 | −3.64 |
| 23 | 0 | 0 | 0 | 0 | 129.42 | 0 | 14.11 | 97.55 | 61.63 | 23.44 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5.15 | 50.52 |
| 25 | 0 | 0 | 0 | 240.00 | 0 | 98.34 | 139.55 | 144.69 | 45.88 | 77.61 |
| 26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 131.25 | 95.75 | 104.68 |
| 27 | 0 | 240.00 | 239.93 | 240.00 | 0 | 0 | 240.00 | 158.41 | 100.36 | 131.77 |
| 28 | 240.00 | 240.00 | 239.97 | 240.00 | 240.00 | 240.00 | 0 | 185.55 | 102.98 | 158.85 |
| 29 | 240.00 | 0 | 239.96 | 0 | 240.00 | 0 | 240.00 | 214.49 | 206.31 | 185.93 |
| 30 | 240.00 | 0 | 239.98 | 240.00 | 185.24 | 211.60 | 240.00 | 240.00 | 239.91 | 213.64 |
| Fitness | 22.24 | 16.92 | 24.31 | 18.17 | 28.46 | 20.79 | 30.26 | 22.37 | 31.90 | 24.97 |

Acknowledgements
References
- Chopra, I. Review of state of art of smart materials structures and integrated systems. AIAA J. 2002, 40, 2145–2187. [Google Scholar] [CrossRef]
- Srinivasan, A.V.; McFarland, D.M. Smart Structures: Analysis and Design; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Irschik, H. A review on static and dynamic shape control of structures by piezoelectric actuation. Eng. Struct. 2002, 24, 5–11. [Google Scholar] [CrossRef]
- Tong, D.; Williams, R.L.; Agrawal, S.K. Optimal shape control of composite thin plates with piezoelectric actuators. J. Intell. Mater. Syst. Struct. 1998, 9, 458–467. [Google Scholar] [CrossRef]
- Agrawal, B.N.; Treanor, K.E. Shape control of a beam using piezoelectric actuators. Smart Mater. Struct. 1999, 8, 729–740. [Google Scholar] [CrossRef]
- Chee, C.; Tong, L.; Steven, G.P. Piezoelectric actuator orientation optimization for static shape control of composite plates. Compos. Struct. 2002, 55, 169–184. [Google Scholar] [CrossRef]
- Onoda, J.; Hanawa, Y. Actuator placement optimization by genetic and improved simulated annealing algorithms. AIAA J. 1993, 31, 1167–1169. [Google Scholar] [CrossRef]
- Mota Silva, S.; Ribeiro, R.R.; Rodrigues, J.D.; Vaz, M.A.P.; Monteiro, J.M. The application of genetic algorithms for shape control with piezoelectric patches—An experimental comparison. Smart Mater. Struct. 2004, 13, 220–226. [Google Scholar]
- Hadjigeorgiou, E.P.; Stavroulakis, G.E.; Massalas, C.V. Shape control and damage identification of beams using piezoelectric actuation and genetic optimization. Int. J. Eng. Sci. 2006, 44, 409–421. [Google Scholar] [CrossRef]
- Frecker, M.I. Recent advances in optimization of smart structures and actuators. Int. J. Eng. Sci. 2003, 14, 207–216. [Google Scholar]
- Preumont, A. Vibration Control of Active Structures: An introduction; Springer-Verlag: Berlin Heidelberg, Germany, 2011. [Google Scholar]
- Thomas, O.; Deü, J.F.; Ducarne, J. Vibrations of an elastic structure with shunted piezoelectric patches: Efficient finite element formulation and electromechanical coupling coefficients. Int. J. Numer. Meth. Eng. 2009, 80.2, 235–268. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison−Wesley Professional: New York, NY, USA, 1989. [Google Scholar]
- Back, T.; Fogel, D.B.; Michalewicz, Z. Handbook of Evolutionary Computationl, 1st ed.; IOP Publishing Ltd.: Bristol, UK, 1997. [Google Scholar]
- Reddy, N.J. Mechanics of Laminated Composite Plates: Theory and Analysis; CRC: New York, NY, USA, 1997. [Google Scholar]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications. IEEE Trans. Ind. Electr. 1996, 43, 519–534. [Google Scholar]
- Dueck, G. New Optimization Heuristics the great deluge algorithm and the record−to−record travel. J. Comput. Phys. 1993, 104, 86–92. [Google Scholar] [CrossRef]
- McMullan, P. An extended implementation of the great deluge algorithm for course timetabling. Lect. Note. Comput. Sci. 2007, 4887, 538–545. [Google Scholar]
- Ozcan, E.; Misir, M.; Ochoa, G.; Burke, E.K. A Reinforcement learning−great−deluge hyper−heuristic for examination timetabling. Int. J. Appl. Metah. Comput. 2010, 1, 39–59. [Google Scholar]
- Kendall, G.; Mohamad, M. Channel Assignment in Cellular Communication Using a Great Deluge Hyper−Heuristic. In Proceedings of 12th IEEE International Conference on Networks, Berlin, Germany, 16–19 November 2004; pp. 769–773.
- Nahas, N.; Khatab, A.; Ait−Kadi, D.; Nourelfath, M. Extended great deluge algorithm for the imperfect preventive maintenance optimization of multi−state systems. Reliab. Eng. Syst. Safety 2008, 99, 1658–1672. [Google Scholar]
- Baykasoglu, A. Design optimization with chaos embedded great deluge algorithm. Appl. Soft Comput. 2012, 12, 1055–1067. [Google Scholar] [CrossRef]
Appendix
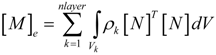
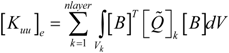
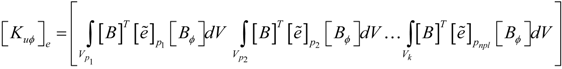
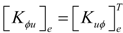
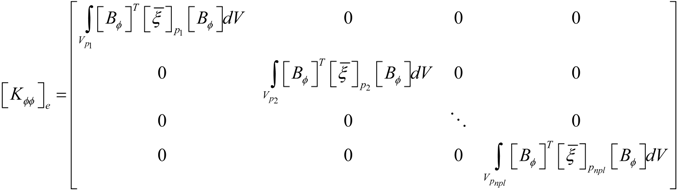
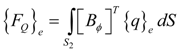
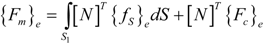
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Foutsitzi, G.A.; Gogos, C.G.; Hadjigeorgiou, E.P.; Stavroulakis, G.E. Actuator Location and Voltages Optimization for Shape Control of Smart Beams Using Genetic Algorithms. Actuators 2013, 2, 111-128. https://doi.org/10.3390/act2040111
Foutsitzi GA, Gogos CG, Hadjigeorgiou EP, Stavroulakis GE. Actuator Location and Voltages Optimization for Shape Control of Smart Beams Using Genetic Algorithms. Actuators. 2013; 2(4):111-128. https://doi.org/10.3390/act2040111
Chicago/Turabian StyleFoutsitzi, Georgia A., Christos G. Gogos, Evangelos P. Hadjigeorgiou, and Georgios E. Stavroulakis. 2013. "Actuator Location and Voltages Optimization for Shape Control of Smart Beams Using Genetic Algorithms" Actuators 2, no. 4: 111-128. https://doi.org/10.3390/act2040111