Analysis and Modeling of Linear-Switched Reluctance for Medical Application
Abstract
:1. Introduction
2. Proposed Concept of the LVAD
2.1. Presentation of the Actuator
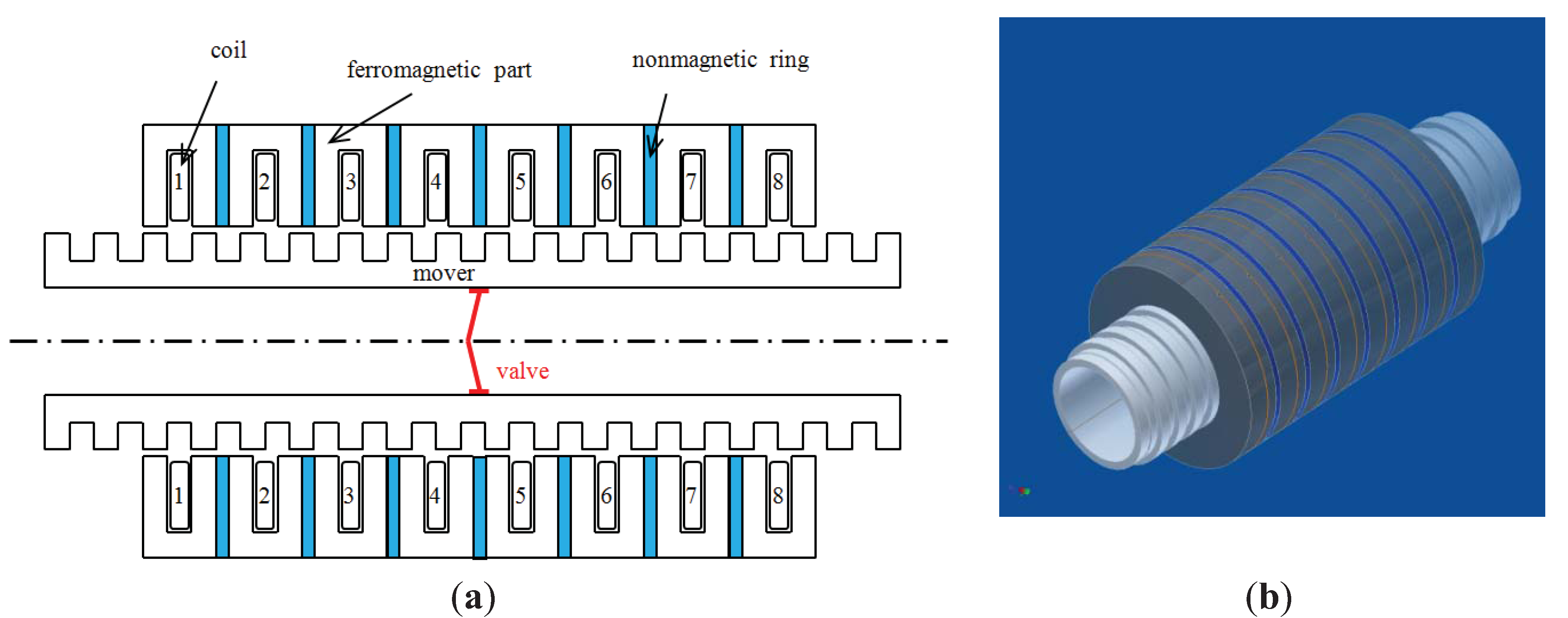
2.2. Kinetic Characteristics of the Motor
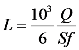
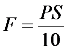
3. Dimensional Characteristics of the LVAD
3.1. Prototype Dimensions and Characteristics

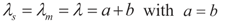
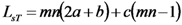
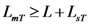
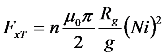

| Name | Abbreviation | Value (mm) |
|---|---|---|
| Valve radius | Rv | 12.5 |
| Mover yoke thickness | emy | 2 |
| Mover tooth length | hmt | 1.5 |
| Air gap length | g | 0.2 |
| Air gap radius | Rg | 16.1 |
| Stator tooth length | hst | 9 |
| Stator yoke thickness | esy | 1.5 |
| External radius | Rext | 26.7 |
| Tooth width | a | 2.9 |
| Slot width | b | 2.9 |
| Non-magnetic ring thickness | c | 1.45 |
| Total length of the stator | LsT | 80 |
| Total length of the mover | LmT | 140 |
| Name | Abbreviation | Value |
|---|---|---|
| Number of phases | m | 4 |
| Number of coils per phase | n | 2 |
| Number of turns per slot | N | 155 |
| Turn diameter | Фturn | 0.335 mm |
| Slot area | Aslot = bhst | 26.1 mm² |
| Coil area | Acoil = NπФturn2/4 | 13.66 mm² |
| Slot fill factor | kfill = Acoil/Aslot | 52.30% |
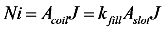
| Characteristic | Value |
|---|---|
| Mass of the mover | m = 270.8 g |
| Static dry friction force | fs = 1.75 N |
| Winding resistance (average value) | R = 8.5 Ω |
| Unaligned Position inductance (average value) | Lu = 34.1 mH |
| Aligned Position inductance (average value) | La = 44.6 mH |
| Winding inductance (average value) | L = 39.4 mH |
| Rate of change of inductance (average value) | ∆L/∆x = 10/2.9 |
3.2. Input-Output Characteristics
 , as:
, as:
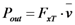
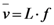
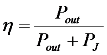
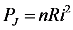
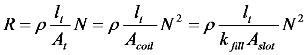
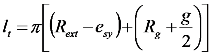
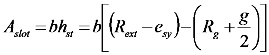
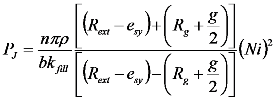
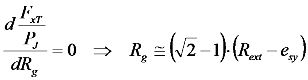
4. Control Principle
4.1. Open Loop Control of the Motor
4.1.1. Presentation
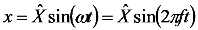
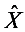 is equal to half the desired stroke and f is the operating frequency equal to the desired cardiac frequency (cf. Equation (1)).
is equal to half the desired stroke and f is the operating frequency equal to the desired cardiac frequency (cf. Equation (1)).
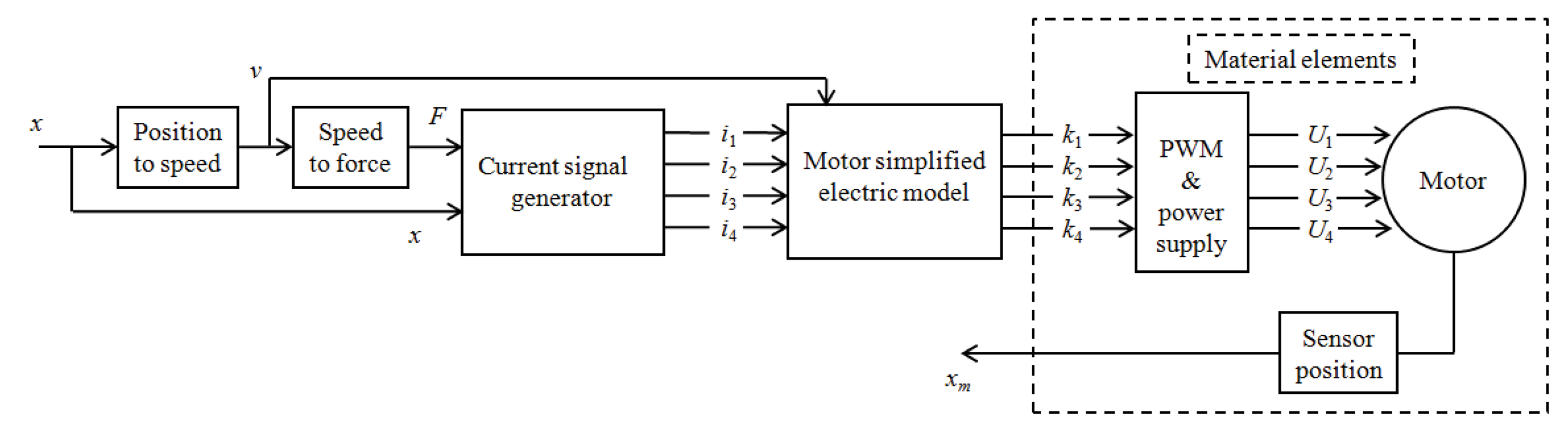
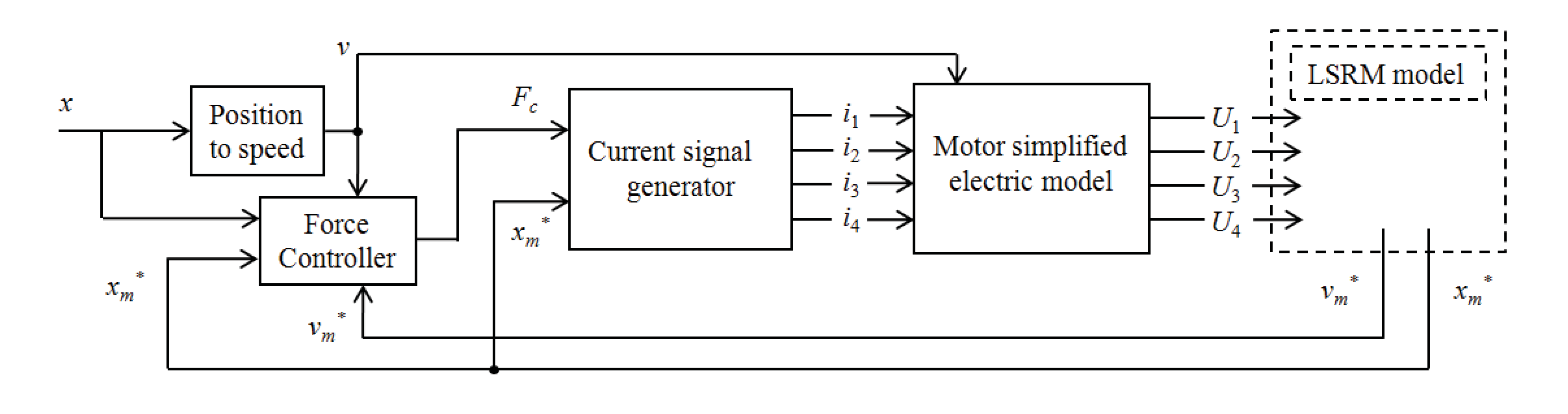
4.1.2. Determination of the Control Blocks
4.1.2.1. “Position to Speed” Block
4.1.2.2. “Motor Simplified Electric Motor” Block
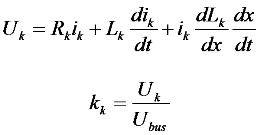
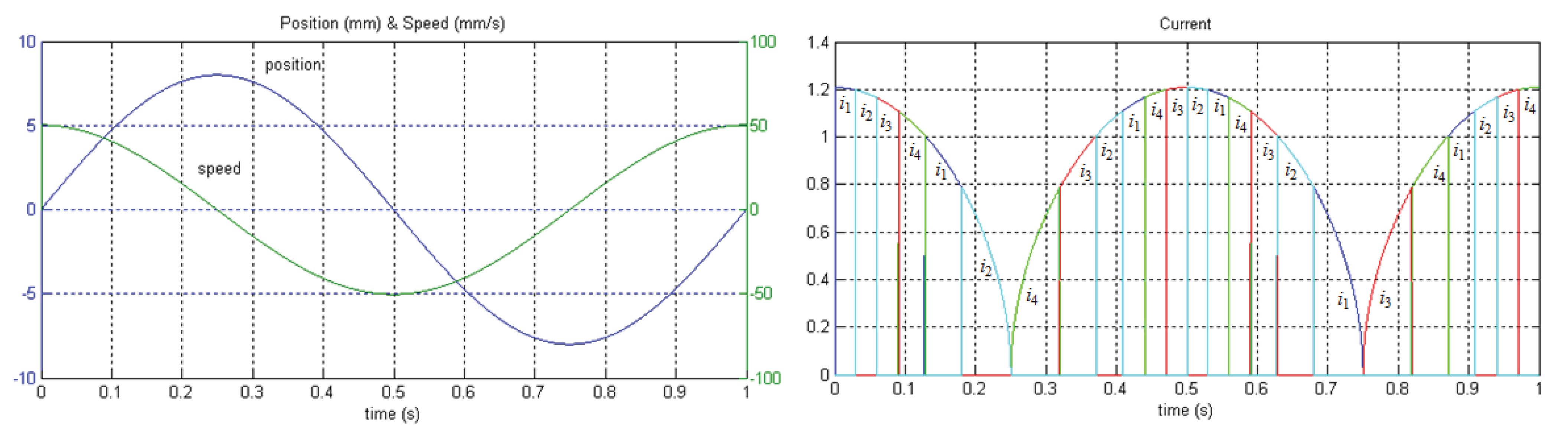
4.1.2.3. “Current Signal Generator” Block
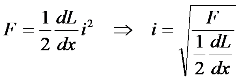
4.1.2.4. “Speed to Force” Block
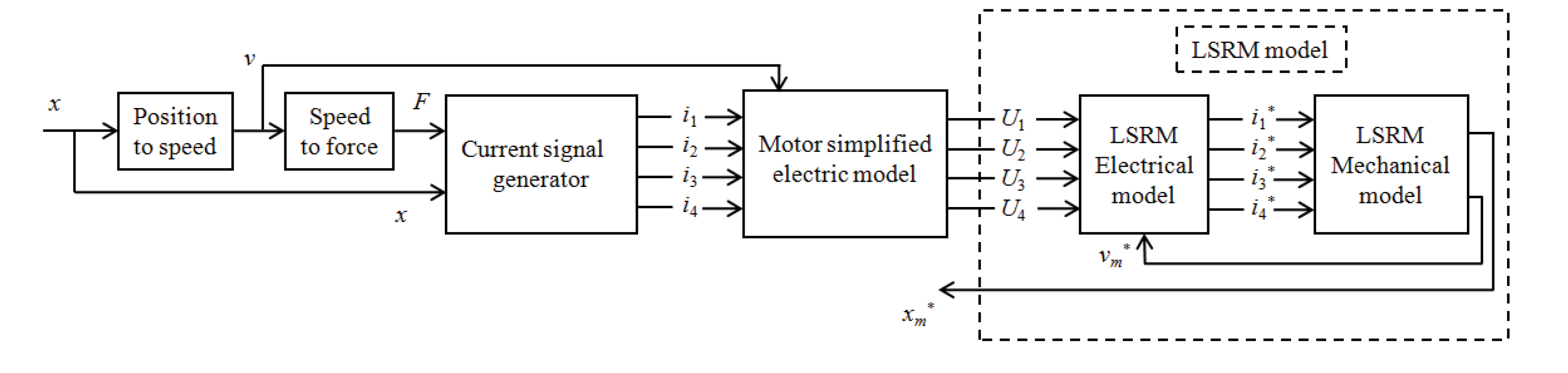
4.1.3. Modeling of the Motor with Matlab Simulink
4.1.3.1. Principle of Modeling
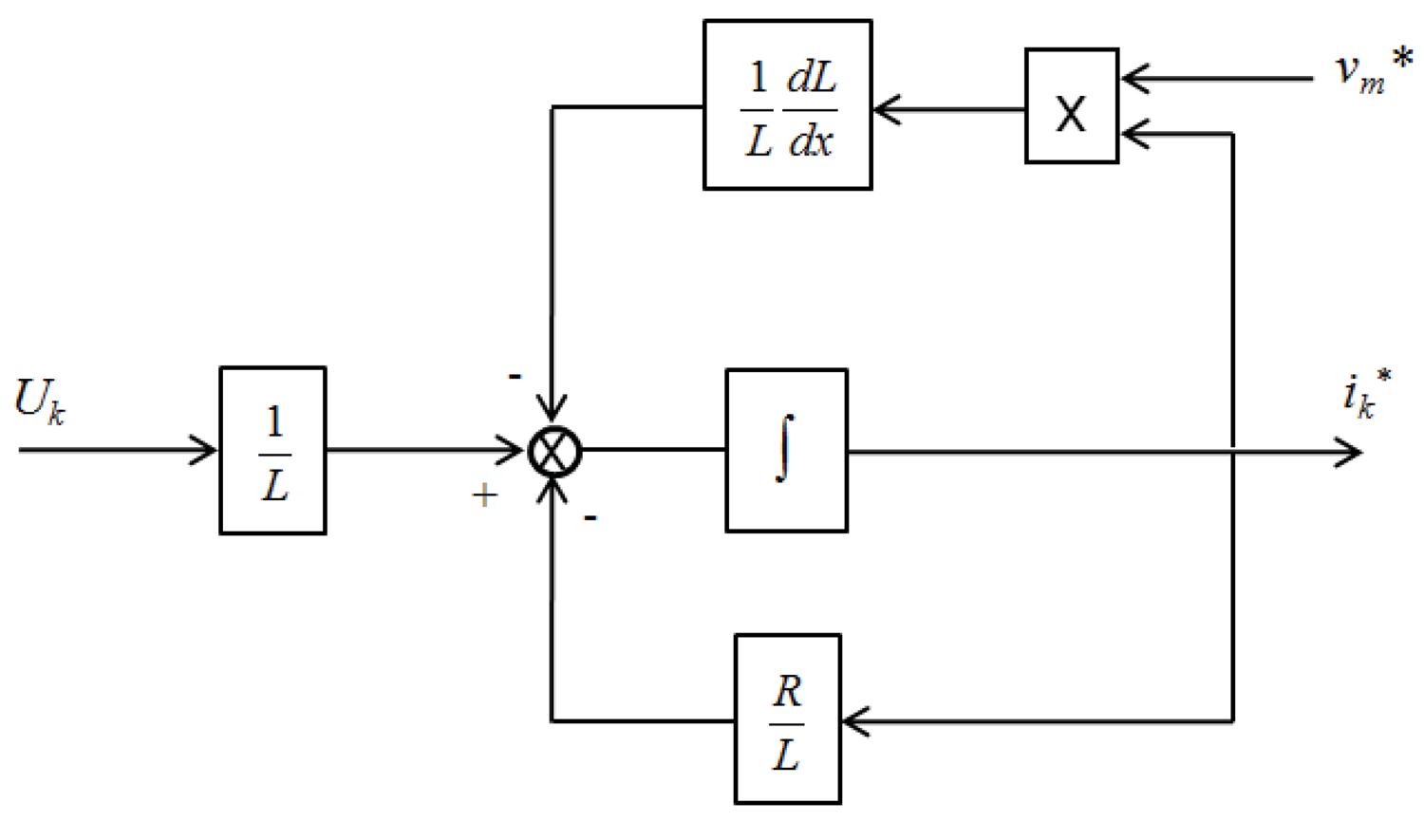
4.1.3.2. Electrical Modeling of the Motor
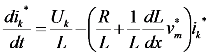
4.1.3.3. Mechanical Modeling of the Motor
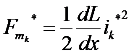
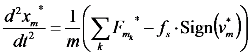
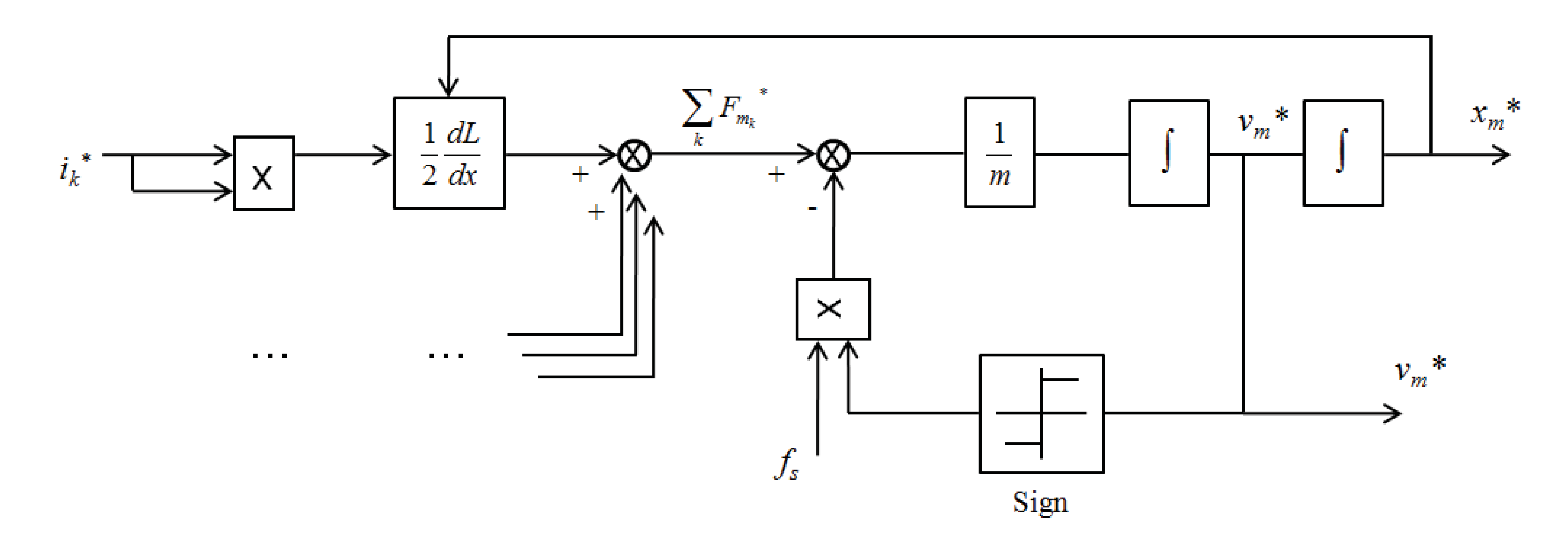
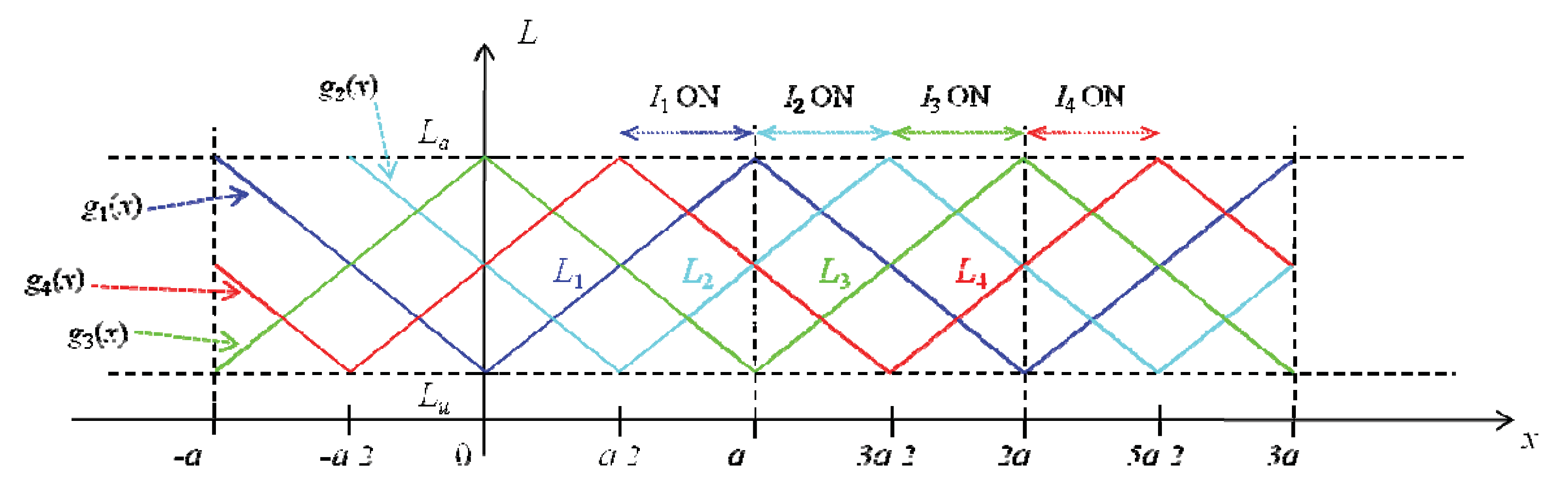
| −a < x < -a/2 | −a/2 < x < 0 | 0 < x < a/2 | a/2 < x < a | a < x < 3a/2 | 3a/2 < x < 2a | |
|---|---|---|---|---|---|---|
| g1(x) | −10/2.9 | −10/2.9 | 10/2.9 | 10/2.9 | −10/2.9 | −10/2.9 |
| g2(x) | 10/2.9 | −10/2.9 | −10/2.9 | 10/2.9 | 10/2.9 | −10/2.9 |
| g3(x) | 10/2.9 | 10/2.9 | −10/2.9 | -10/2.9 | 10/2.9 | 10/2.9 |
| g4(x) | −10/2.9 | 10/2.9 | 10/2.9 | -10/2.9 | −10/2.9 | 10/2.9 |

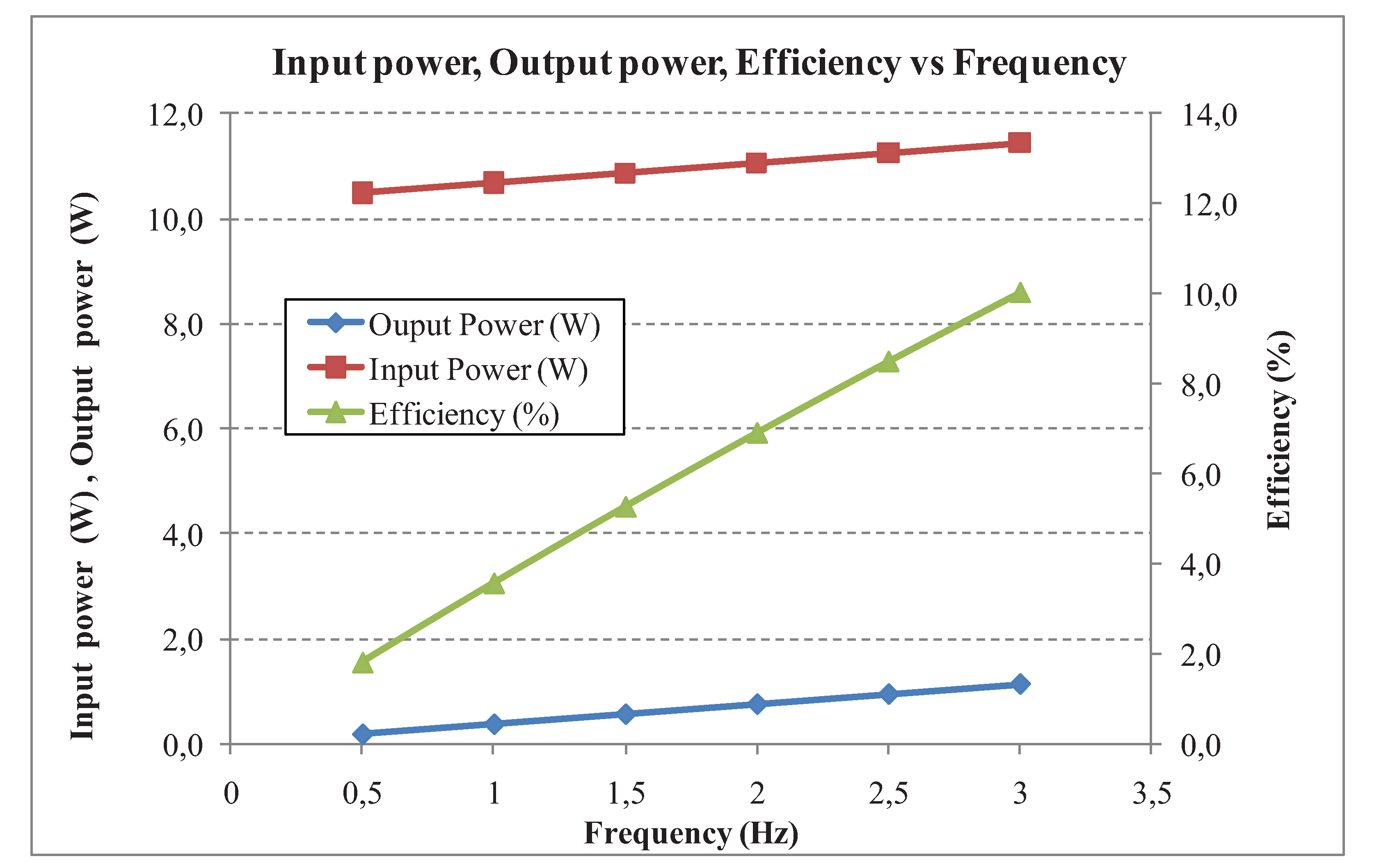
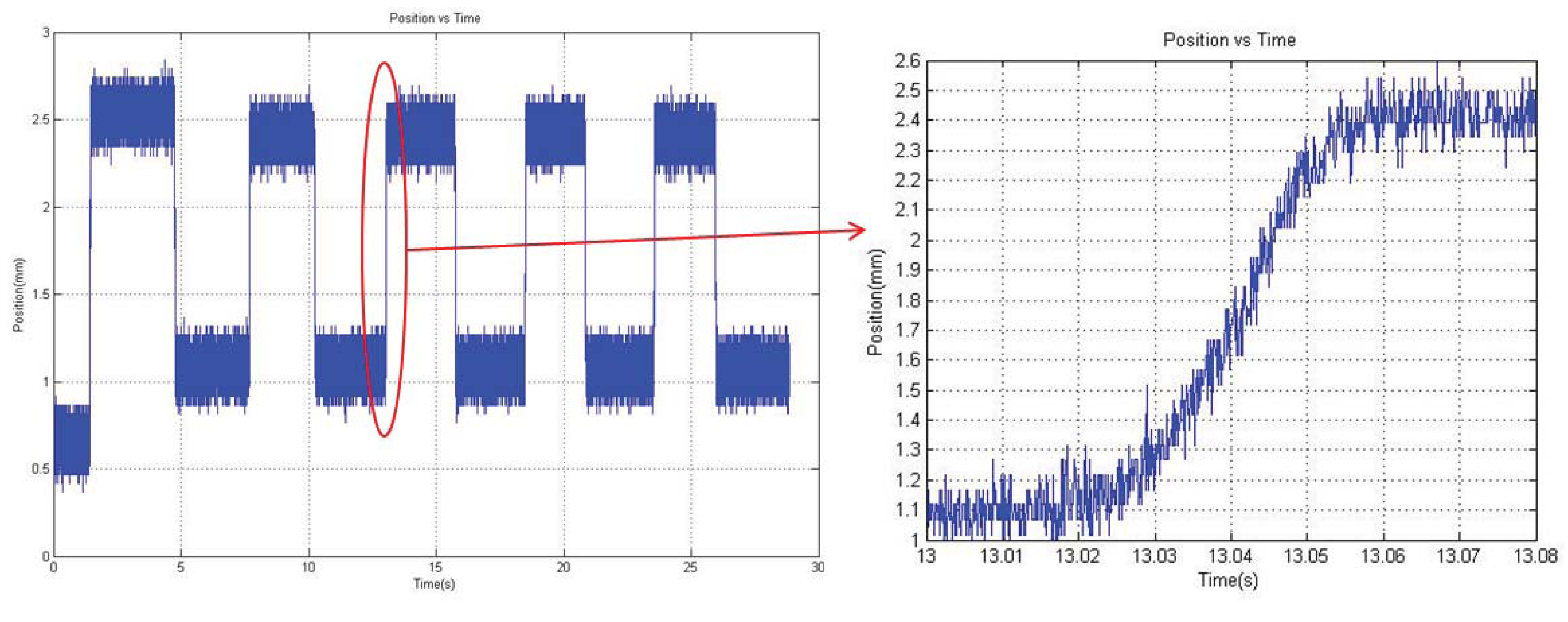
4.1.4. Results of the Open Loop Control
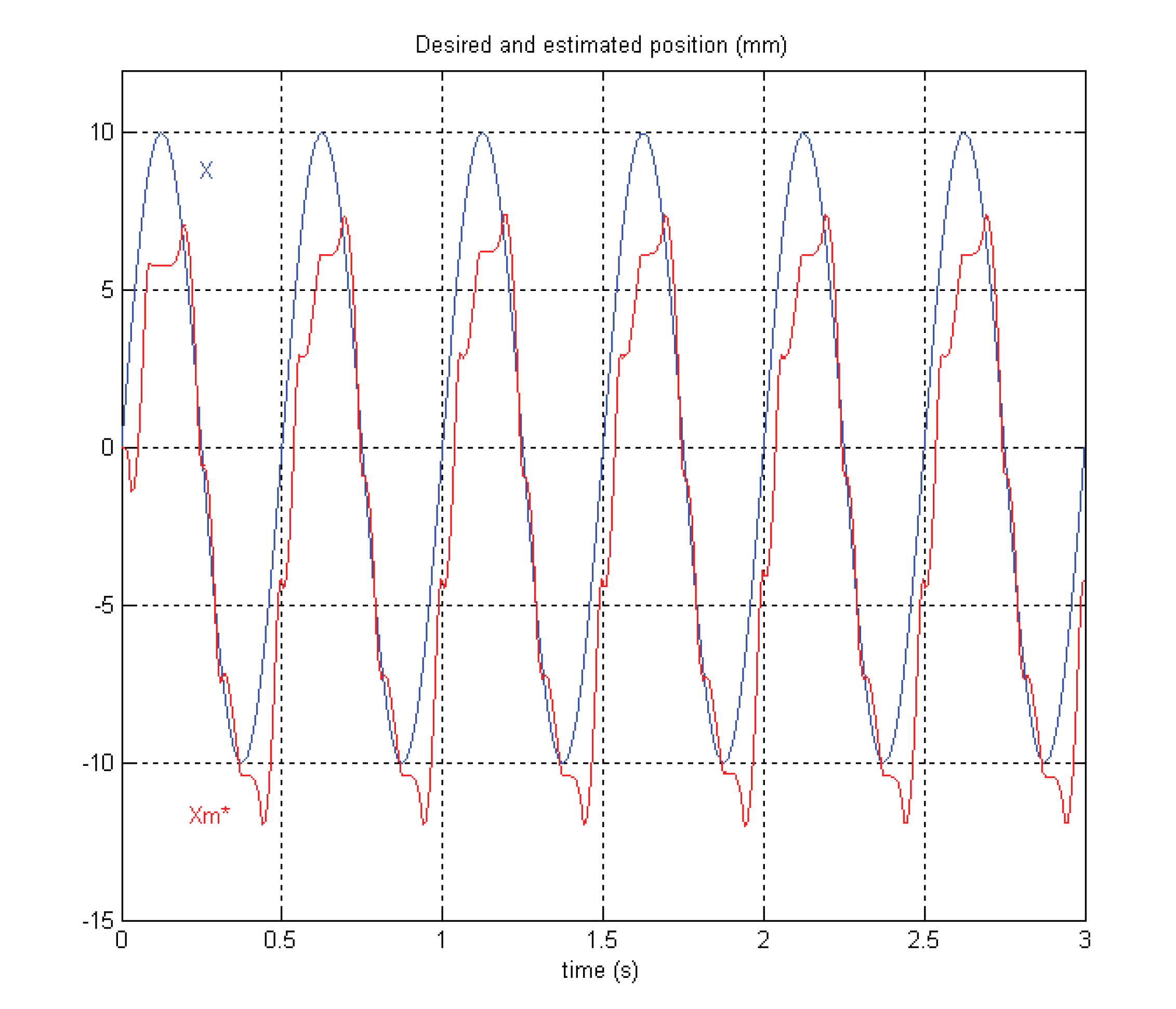
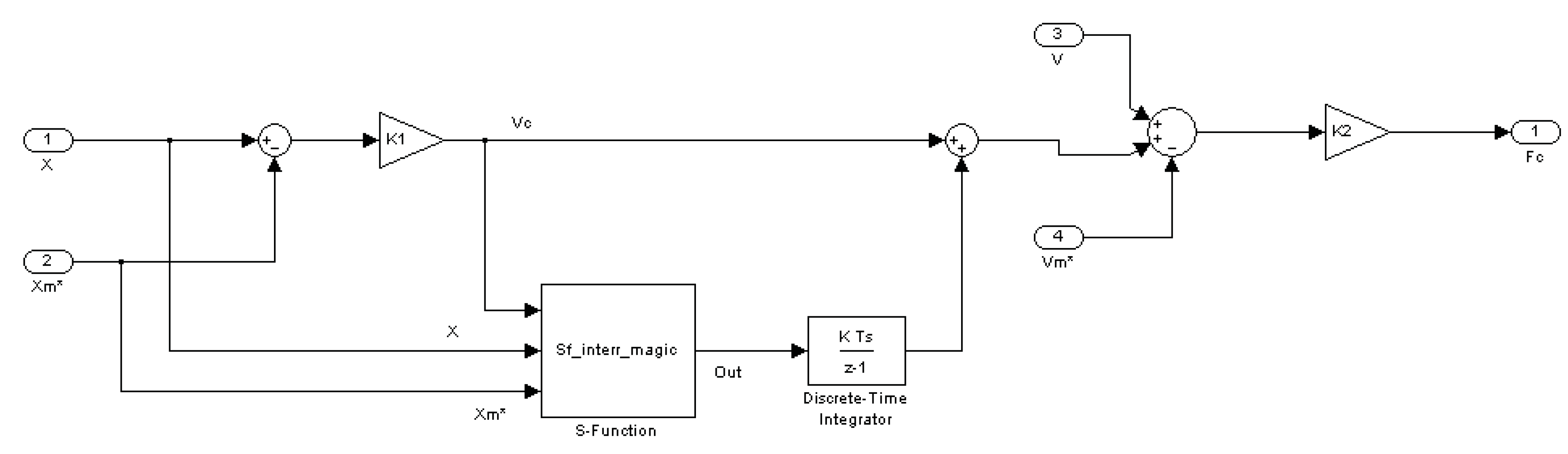
4.2. Closed Loop Control of the Motor
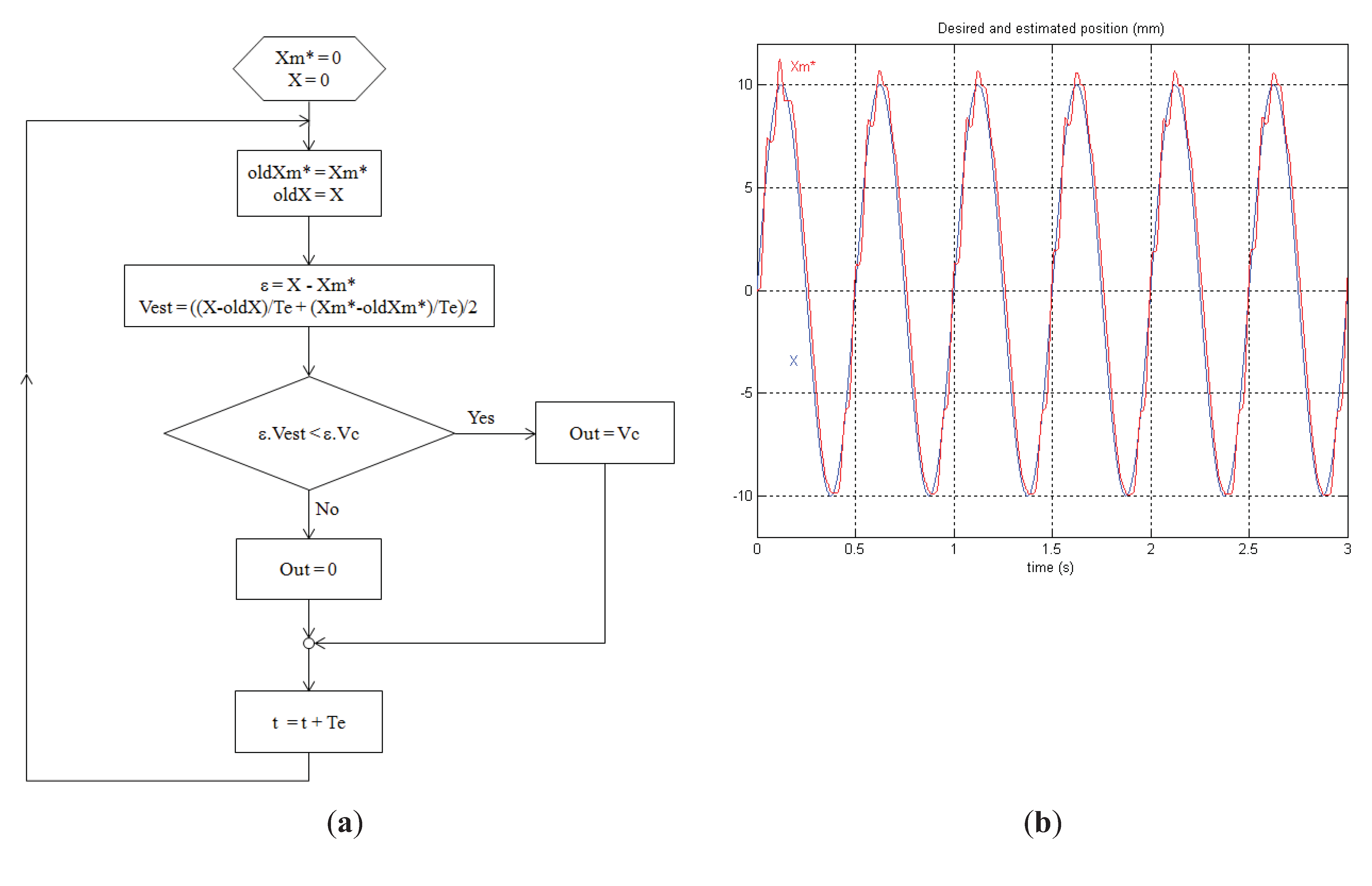
5. Conclusions
References
- DiGiorgi, P.L.; Naka, Y.; Oz, M.C. Left Ventricular Assist Devices. Contemporary Cardiology: Surgical Management of Congestive Heart Failure; Springer Humana Press: Totawa, NJ, USA, 2005; Chapter 7; pp. 155–189. [Google Scholar]
- Blitz, A.; Fang, J.C. Ventricular Assist Devices and Total Artificial Hearts. In Contemporary Cardiology: Device Therapy in Heart Failure; Springer Humana Press: Boston, MA, USA, 2009; Chapter 13; pp. 339–371. [Google Scholar]
- Allen, G.S.; Murray, K.D; Olsen, D.B. The importance of pulsatile and non pulsatile flow in the design of blood pumps. Artif. Organs 1997, 21, 922–928. [Google Scholar] [CrossRef]
- Corda, J.; Skopljak, E. Linear Switched Reluctance Actuator. In Proceedings of 6th International Conference on Electrical Machines and Drives; Inspec/IEE: London, UK, 1993; pp. 535–539. [Google Scholar]
- El Amraoui, L.; Gillon, F.; Vivier, S.; Brochet, P.; Benrejeb, M. Optimal Design Approach for Linear Tubular Machines. In Proceedings of IEEE International Conference on Systems Man and Cybernetics; IEEE: Danvers, MA, USA, 2002; Volume 5, pp. 1–6. [Google Scholar]
- Yamada, H.; Hamajima, T.; Xiang, S.; Nishizawa, N. Six-phase linear pulse motor as linear oscillatory actuator. IEEE Trans. Mag. 1987, MAG-23, 2841–2843. [Google Scholar]
- Llibre, J.F.; Martinez, N.; Nogarede, B.; Leprince, P. Linear Tubular Switched Reluctance Motor for heart assistance circulatory: Analytical and finite element modeling. In Proceedings of 10th International Workshop on Electronics, Control, Measurement and Signals (ECMS); IEEE: Danvers, MA, USA, 2011; pp. 1–6. [Google Scholar]
- Llibre, J.F.; Martinez, N.; Leprince, P.; Nogarède, B. Innovative Linear Pulsatile Pump for heart assistance circulatory. In Proceedings of The Eighth International Symposium on Linear Drives for Industry Applications (LDIA 2011), Eindhoven, The Netherlands, 3–6 July 2011.
- Lee, B.-S.; Bae, H.-K.; Vijayraghavan, P.; Krishnan, R. Design of a linear switched reluctance machine. IEEE Trans. Ind. Appl. 2000, 36, 1571–1580. [Google Scholar] [CrossRef]
- Viorel, I.-A.; Hameyer, K.; Strete, L. Transverse flux tubular switched reluctance motor. In Proceedings of 11th International Conference on Optimization of Electrical and Electronic Equipment, OPTIM'08; IEEE: Danvers, MA, USA, 2008; pp. 131–136. [Google Scholar]
- Vasquez, H.; Parker, J.K. A new simplified mathematical model for a switched reluctance motor in a variable speed pumping application. Mechatronics 2004, 14, 1055–1068. [Google Scholar] [CrossRef]
- Vasquez, H.; Parker, J.K.; Haskew, T. Control of a 6/4 switched reluctance motor in a variable speed pumping application. Mechatronics 2005, 15, 1061–1071. [Google Scholar] [CrossRef]
- Krishnan, R. Switched Reluctance Motor Drives, Modeling, Simulation, Analysis, Design, and Applications; CRC Press LCC: Boca Raton, FL, USA, 2001; pp. 21–22. [Google Scholar]
- Bae, H.-K.; Lee, B.-S.; Vijayraghavan, P.; Krishnan, R. A linear switched reluctance motor: converter and control. IEEE Trans. Ind. Appl. 2000, 36, 1351–1359. [Google Scholar] [CrossRef]
- Lim, H.S.; Krishnan, R.; Lobo, N.S. Design and control of a linear propulsion system for an elevator using linear switched reluctance motor drives. IEEE Trans. Ind. Appl. 2008, 55, 534–542. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Llibre, J.-F.; Martinez, N.; Leprince, P.; Nogarede, B. Analysis and Modeling of Linear-Switched Reluctance for Medical Application. Actuators 2013, 2, 27-44. https://doi.org/10.3390/act2020027
Llibre J-F, Martinez N, Leprince P, Nogarede B. Analysis and Modeling of Linear-Switched Reluctance for Medical Application. Actuators. 2013; 2(2):27-44. https://doi.org/10.3390/act2020027
Chicago/Turabian StyleLlibre, Jean-Francois, Nicolas Martinez, Pascal Leprince, and Bertrand Nogarede. 2013. "Analysis and Modeling of Linear-Switched Reluctance for Medical Application" Actuators 2, no. 2: 27-44. https://doi.org/10.3390/act2020027
APA StyleLlibre, J.-F., Martinez, N., Leprince, P., & Nogarede, B. (2013). Analysis and Modeling of Linear-Switched Reluctance for Medical Application. Actuators, 2(2), 27-44. https://doi.org/10.3390/act2020027





