Experimental and Numerical Analyses of New Massive Wooden Shear-Wall Systems

Abstract

Three innovative massive wooden shear-wall systems (Cross-Laminated-Glued Wall, Cross-Laminated-Stapled Wall, Layered Wall with dovetail inserts) were tested and their structural behaviour under seismic action was assessed with numerical simulations. The wall specimens differ mainly in the method used to assemble the layers of timber boards composing them. Quasi-static cyclic loading tests were carried out and then reproduced with a non-linear numerical model calibrated on the test results to estimate the most appropriate behaviour factor for each system. Non-linear dynamic simulations of 15 artificially generated seismic shocks showed that these systems have good dissipative capacity when correctly designed and that they can be assigned to the medium ductility class of Eurocode 8. This work also shows the influence of deformations in wooden panels and base connectors on the behaviour factor and dissipative capacity of the system.

1. Introduction

Structural systems with massive wooden shear-walls are becoming widespread in construction practice, particularly for pre-cast buildings. These structural systems have excellent thermal and acoustic insulation performance, due to the massiveness of the structure. However, their structural behaviour, especially under seismic action, is still required to be demonstrated, since their resistance, stiffness, ductility and dissipative properties must be fully assessed.

Numerical analyses, calibrated on experimental quasi-static tests on full-scale wall specimens, can be used to simulate the seismic behaviour of a complete case-study building and to evaluate its dissipative capacity, thus providing more detailed information on the main properties of new construction systems [1,2,3]. Much experimental research on low- and medium-rise massive timber shear-wall systems has aimed at examining the seismic behaviour of Cross Laminated Timber (CLT) buildings [4,5,6,7]. However, various systems can be obtained with massive walls and their mechanical characteristics can be experimentally and numerically evaluated.

Three massive wooden shear-wall systems (Cross-Laminated-Glued Wall, Cross-Laminated-Stapled Wall, Layered Wall with dovetail inserts) were analysed in this study. The results presented below are from non-linear numerical analyses with a simplified model of a three-storey building, and the seismic performance of the above wall systems was evaluated in terms of behaviour factor q, according to the definition given in Eurocode 8 [8].

2. Experimental Tests

Various types of tests were performed at the Laboratory of Mechanical Testing, CNR-IVALSA, at San Michele all’Adige (Trento, Italy), to verify the true characteristics and hysteretic behaviour of the structural systems tested.

2.1. Test Wall Configurations

The tests presented here were part of three experimental campaigns, partly commissioned by private companies for research and development projects. The test configurations and connection systems to the foundations were therefore not the same for the various walls, since the companies in question had used their own connection systems, in order to optimise the mechanical response.

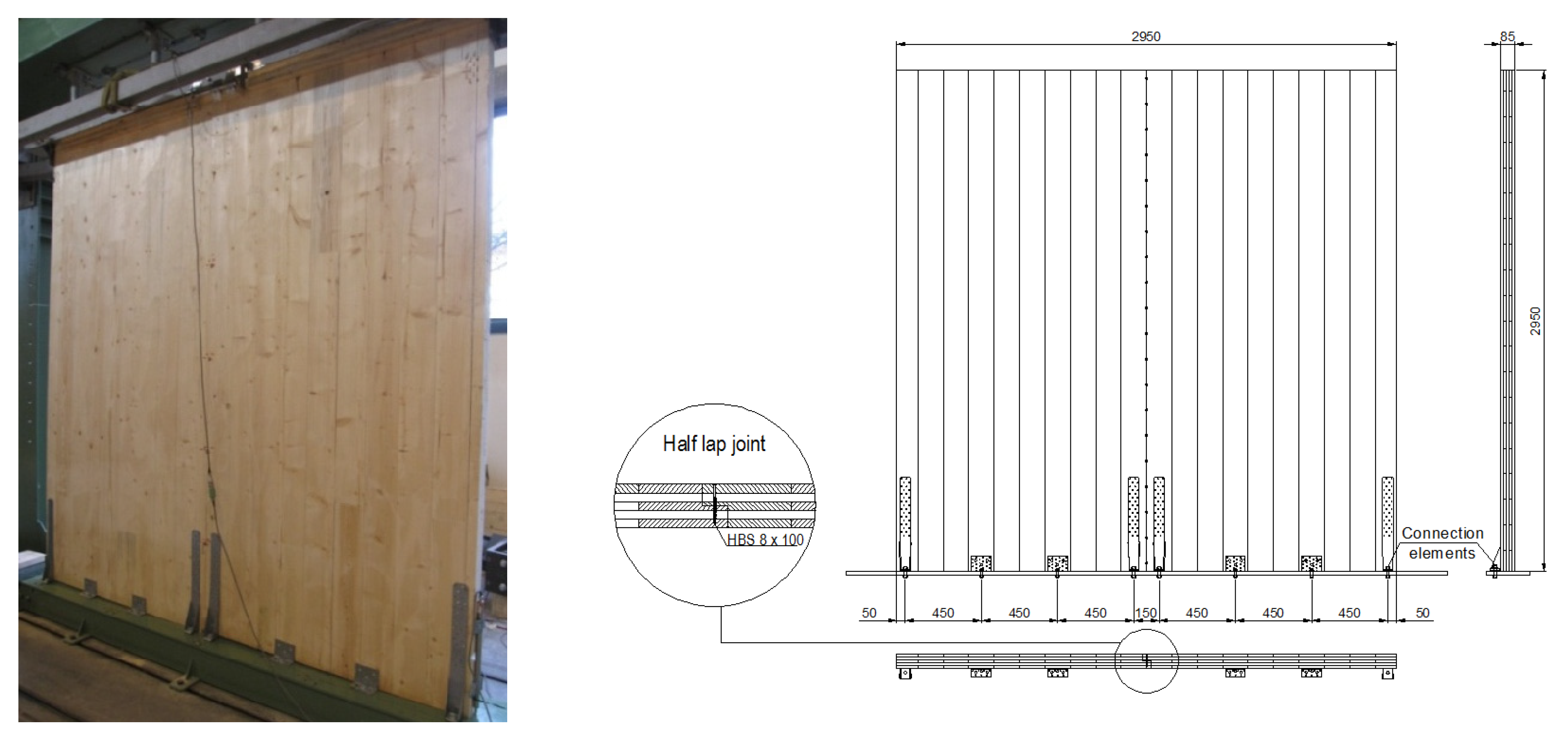
Three wall configurations corresponding to the three massive wooden shear-wall systems were studied: two Cross-Laminated-Glued (CLT) panels were used to create Wall A, Cross-Laminated-Stapled panels for Wall B, and Layered Panels with dovetail inserts for Wall C. The three types differ in both panel characteristics and the connection system linking walls to foundations. In CLT walls, the panels were composed of alternatively oriented perpendicular layers glued together. In Cross-Laminated-Stapled walls, glue was replaced by metal staples. In Layered Walls, the layers of vertically oriented boards were connected with perpendicular dovetail inserts. The massive walls were connected to the foundations with mechanical connectors, such as hold-downs and angle brackets, fastened with nails or screws. Wall A was assembled with two five-layer CLT panels, made of C24 timber boards, and with an overall thickness of 85 mm. The two panels were grooved symmetrically to half the depth of the panel at the edge, so that they could be coupled with screws inserted orthogonally to the joint, i.e., half-lap joint (Figure 1); Wall A was jointed with 10 HBS 8 × 100 screws (Rothoblaas).

Figure 1. Wall A: Geometric arrangement, connection systems and detail of half-lap joint.

Figure 1. Wall A: Geometric arrangement, connection systems and detail of half-lap joint.

Each panel composing Wall A was anchored at the base with two steel hold-downs HTT22 anchors and two BMF 90 mm × 48 mm × 3 mm × 116 mm angle brackets (Simpson Strong Tie) and screws (Rothoblaas). The hold-downs were connected to the CLT panels with 12 ringed Anker nails, nominal diameter 4 mm, and the angle brackets were connected with 11 Anker nails.

The Wall B specimens in Figure 2 were made of five crossed layers of C24 spruce boards, with a nominal thickness 28.5 mm. The panel was 142.5 mm thick, and the layers were stapled to each other.

Figure 2. Wall B: Geometric configuration.

Figure 2. Wall B: Geometric configuration.

Wall B was fixed to the foundation with seven angular steel elements (Titan TCN 240, Rothoblaas, Cortaccia (TN), Italy) positioned as shown in Figure 3. Two configurations were prepared: Titan Type A has a thick steel plate between the bolt head and the angle bracket, placed at the edge of the panel as a hold-down. Titan Type B was simply bolted to the foundation, like a regular shear-angle bracket. The brackets were anchored to the foundation with two M16 bolts and to the wall with 36 Anker nails.

Figure 3. Wall B: Connections to steel foundation.

Figure 3. Wall B: Connections to steel foundation.

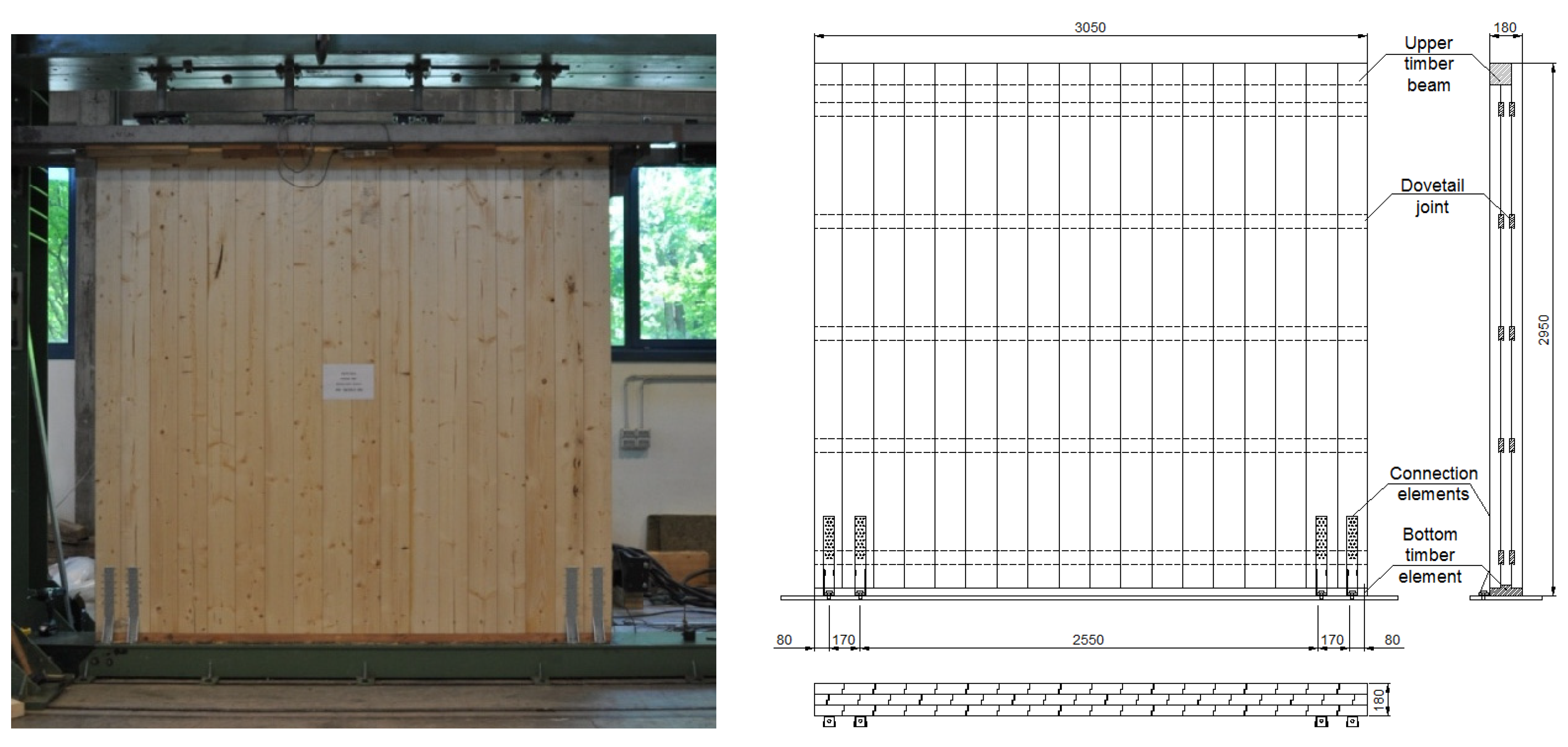
Wall C (Layered Wall with dovetail inserts) was made up of three layers of vertical sawn spruce boards, nominal thickness 60 mm, coupled with five pairs of horizontal spruce boards inserted dovetail-fashion. The panels measured 2950 (h) × 3050 (l) × 180 (w) mm (see Figure 4).

Figure 4. Wall C: Geometric configuration.

Figure 4. Wall C: Geometric configuration.

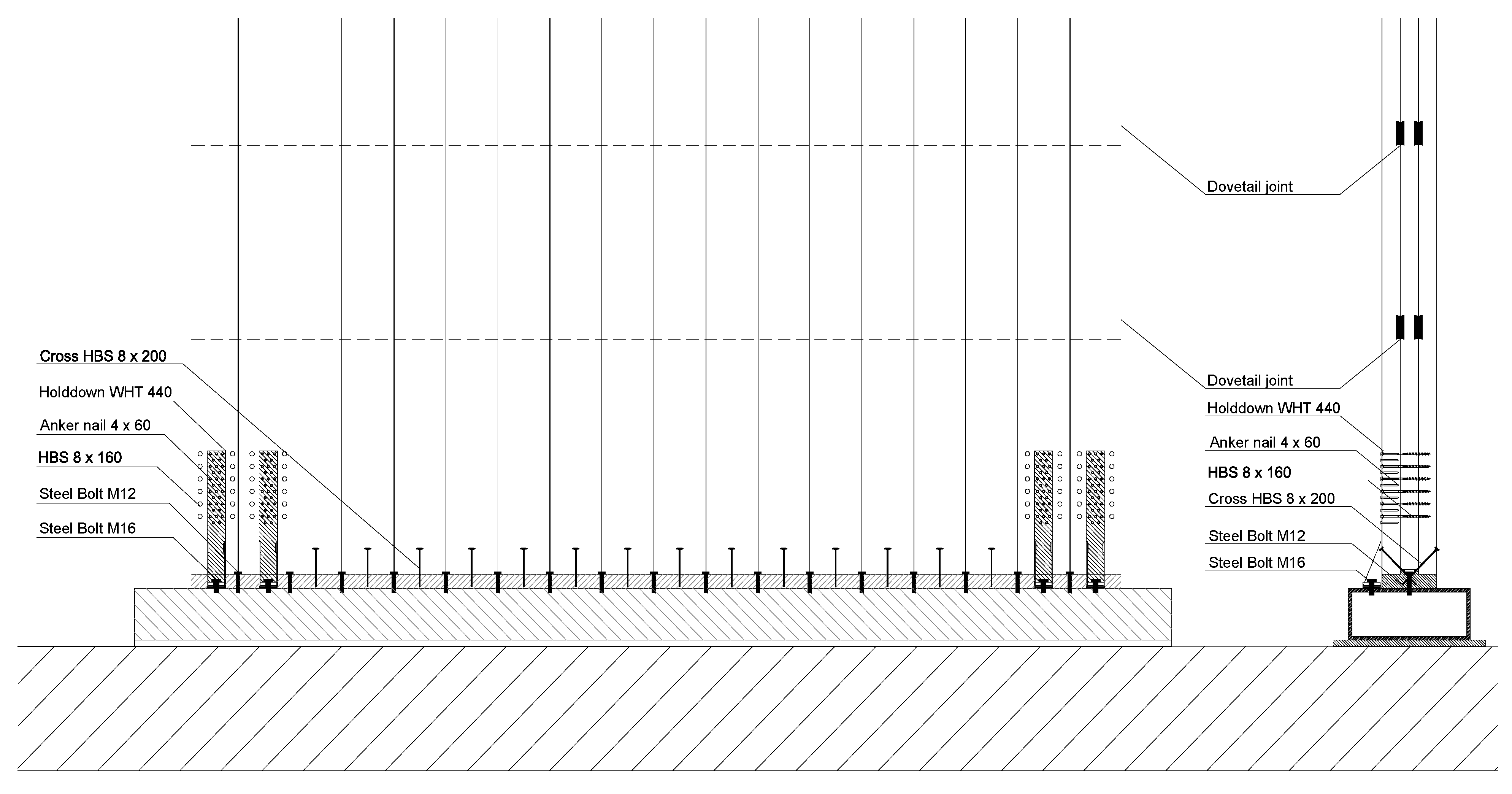
The timber panels were connected to the base larch beam with 18 pairs of cross-screws (HBS 8 mm × 200 mm), inclined 45° with respect to the vertical layer (Figure 5). The base beam was previously fixed to the portal’s foundation with seventeen 12 mm steel bolts. The panels were also connected directly to the foundation with two hold-downs on each side (WHT 440; Rothoblaas), each fastened with one M16 bolt to the foundation and 30 Anker nails to the wall. The vertical timber boards were reinforced with 12 HBS 8 mm × 160 mm screws at the edges of the hold-downs. The upper side of the wall was attached to a horizontal timber board (120 mm × 120 mm) with cross-screws (HBS 8 mm × 200 mm), inclined with respect to the vertical layer; the timber board was connected to the upper beam and firmly attached to the head of the jack, to ensure uniform distribution of both vertical and horizontal loads.

Figure 5. Wall C: Connections to foundation and dovetail joints.

Figure 5. Wall C: Connections to foundation and dovetail joints.

2.2. Test Set-Up

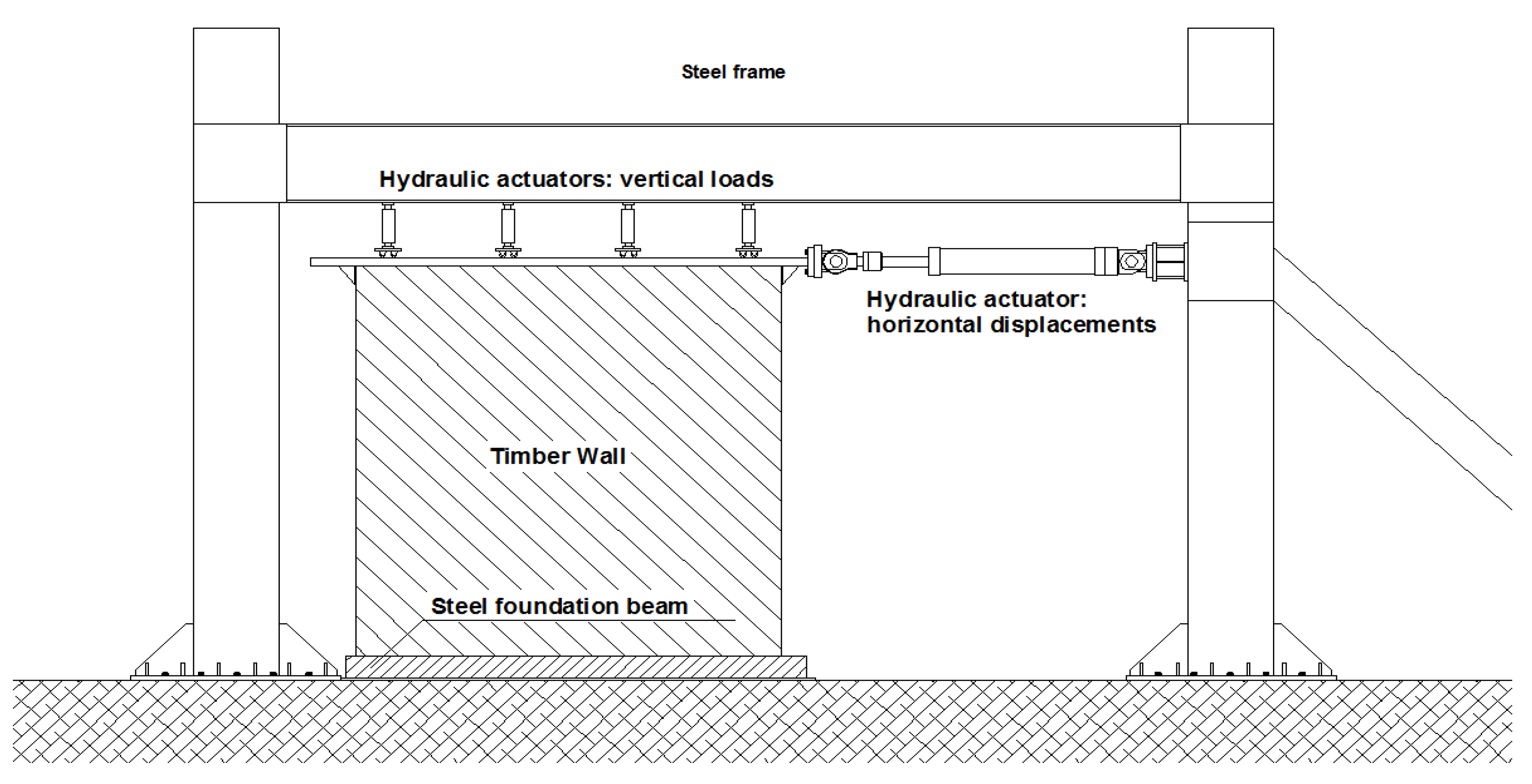
The 2.95 m × 2.95 m massive wooden walls were tested with the set-up shown in Figure 6. The panels were placed inside the steel frame and connected to the foundation. The steel frame was a rigid element in which the load system was linked to a hydraulic jack. The top of the actuator was rigidly connected to a steel beam placed above the specimen, in order to spread the vertical load of the four hydraulic jacks on the upper surface of the wall. The upper steel beam also had the function of imposing displacements generated by the horizontal hydraulic jack on the wall; horizontal loads were transmitted to the top ends of the wall by two rigid plates (100 mm × 100 mm). The specimens were linked by several kinds of systems to a steel beam rigidly fixed to the concrete floor of the laboratory.

Figure 6. Test set-up: steel frame, hydraulic actuator, vertical load system, and specimen.

Figure 6. Test set-up: steel frame, hydraulic actuator, vertical load system, and specimen.

2.3. Test Procedure

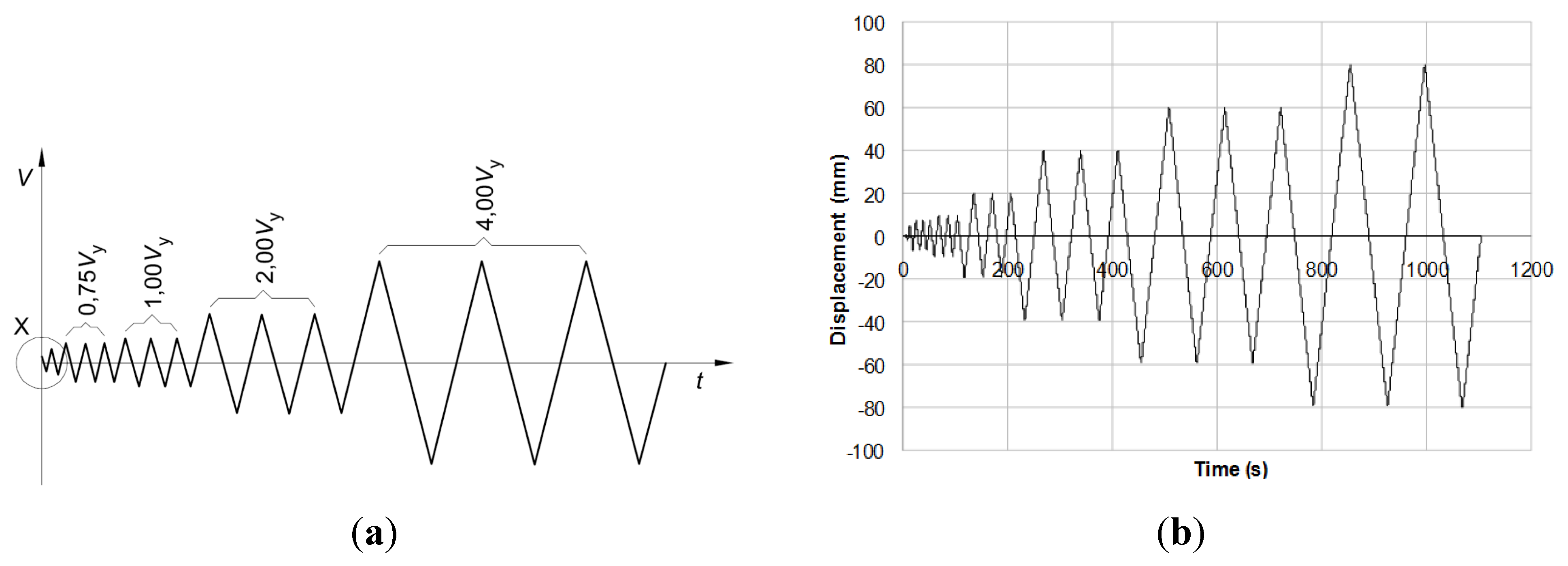
Three types of massive timber walls were tested: two specimens for each type, for a total of six tests. The specimens were tested with the quasi-static cyclic loading protocol recommended by EN 12512 [9] (Figure 7). This was done in order to impose on all the walls the reference displacement (yielding point) of 20 mm: according to EN 12512, this can be established starting from an estimated yielding point V_y,est deduced from test results, monotonic tests, or calculation [10]. The 20 mm value was chosen on the basis of tests previously conducted at IVALSA during the SOFIE project [1], and confirmed by the results of the present tests. The results could be properly compared, as the yielding point of 20 mm was fixed for all three wall types.

Figure 7. Loading protocol according to EN 12512 (V_y = reference slip).

Figure 7. Loading protocol according to EN 12512 (V_y = reference slip).

Testing involved cycle amplitude increases according to EN 12512, so that testing was stopped at a horizontal displacement of 80 mm, corresponding to 4V_y. This rate was determined because the technical limit of the set-up at 80 mm is a high level of displacement, in both absolute and relative terms, representing an inter-storey drift of 2.5%.

During cyclic testing, the walls were subjected to a constant vertical top load of 18.5 kN/m to simulate the vertical load which, in the real case of lightweight floors, loads the lowest wall [1].

2.4. Test Instrumentation

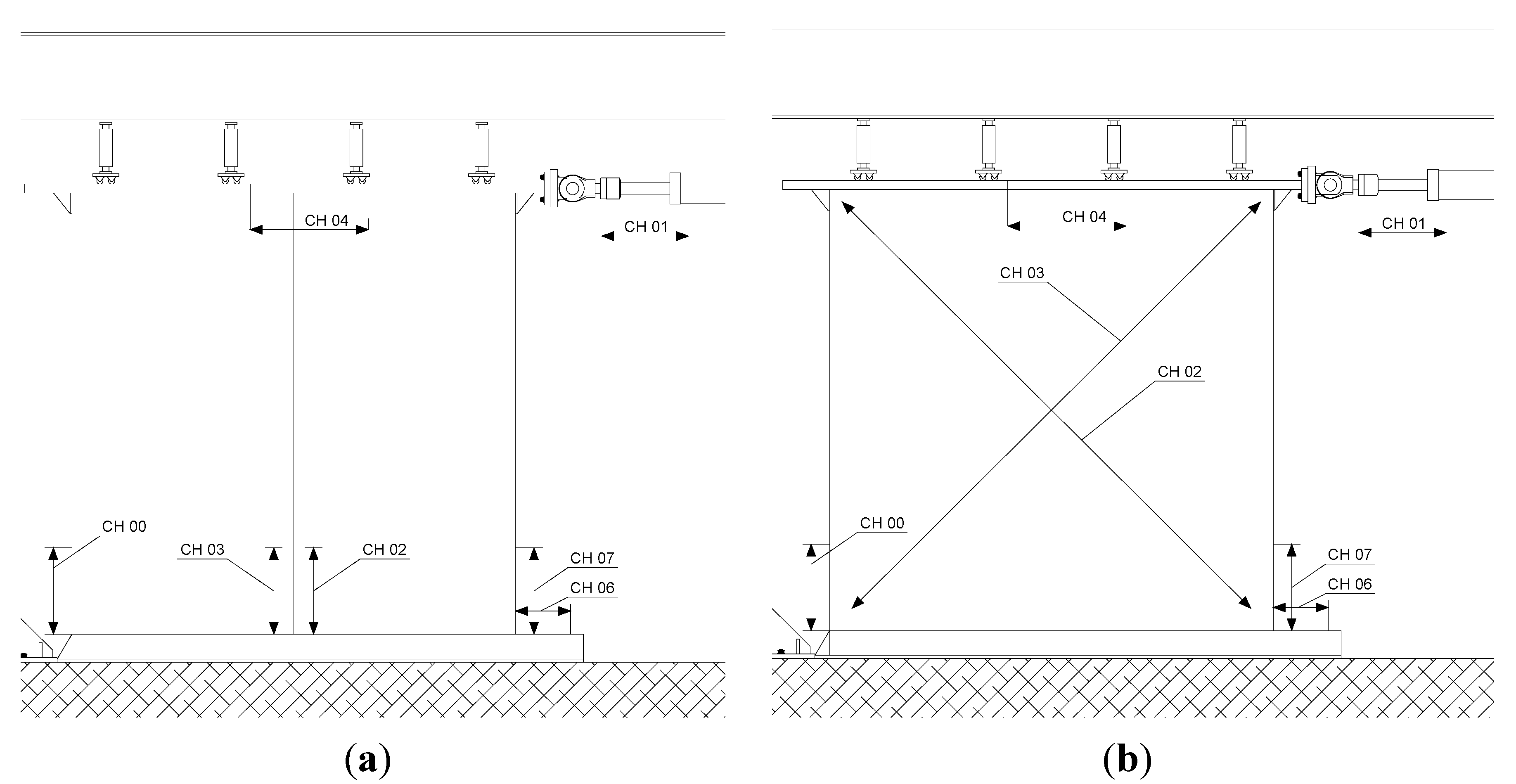
During cyclic testing, instruments on both sides of the walls measured the most significant movements of specimens, i.e., horizontal displacements at top and bottom, and vertical uplift due to rigid rocking (Figure 8; Table 1).

Racking displacement was assumed to be equal to that measured by the Linear Variable Differential Transducer (LVDT) of the hydraulic jack (CH01); CH04 measures displacements between the wall and the loading system, due to elastic deformation of the system itself and to plastic deformations by local compression on steel elements (100 mm × 100 mm) against the side of the wall (Figure 8). Two LVDTs, CH00 and CH07, were placed on the bottom edge of the wall to record vertical displacements due to rigid rocking. Wall A was monitored with two more vertical transducers, CH02 and CH03, placed on both sides of the half-lap joint, at 75 mm from the centre-line (Figure 8). As large shear deformations of Walls B and C were expected, two diagonal LVDTs were connected to the opposite corners of the wall with wires, and CH02 and CH03 were placed as shown in Figure 8.

Figure 8. Test instrumentation: (a) Wall A; (b) Walls B and C.

Figure 8. Test instrumentation: (a) Wall A; (b) Walls B and C.

Table 1. Test instrumentation.

ID	Measures	Wall A	Wall B	Wall C
CH00	Vertical displacements at edge of wall	X	X	X
CH01	Horizontal displacement of hydraulic actuator	X	X	X
CH02	Vertical displacements at half-lap joint—Panel A	X	–	–
CH02	Diagonal deformation due to shear deformation	–	X	X
CH03	Vertical displacements at half-lap joint—Panel B	X	–	–
CH03	Diagonal deformation due to shear deformation	–	X	X
CH04	Horizontal slip between wall and upper steel profile	X	X	X
CH06	Horizontal displacement at base of wall	X	X	X
CH07	Vertical displacements at edge of wall	X	X	X

Table 1. Test instrumentation.

ID	Measures	Wall A	Wall B	Wall C
CH00	Vertical displacements at edge of wall	X	X	X
CH01	Horizontal displacement of hydraulic actuator	X	X	X
CH02	Vertical displacements at half-lap joint—Panel A	X	–	–
CH02	Diagonal deformation due to shear deformation	–	X	X
CH03	Vertical displacements at half-lap joint—Panel B	X	–	–
CH03	Diagonal deformation due to shear deformation	–	X	X
CH04	Horizontal slip between wall and upper steel profile	X	X	X
CH06	Horizontal displacement at base of wall	X	X	X
CH07	Vertical displacements at edge of wall	X	X	X

3. Test Results

3.1. Failure Modes

At the end of testing, Wall A showed evident failure, due both to large deformations in the connection systems (hold-downs and angle brackets) and failure of the middle half-lap joint between the two panels making up the whole specimen (Figure 9 and Figure 10). This failure mode revealed rigid rotation of the two panels which, subjected to large displacements, behaved independently. Due to screw deformation, the middle joint could no longer transmit shear stresses between panels nor conform to the large deformations of the hold-downs, and failed with rotation and relative sliding between the panels along the mid-line.

Figure 9. Wall A: Shear deformation between panels at end of testing: (a) Rear face; (b) Front face.

Figure 9. Wall A: Shear deformation between panels at end of testing: (a) Rear face; (b) Front face.

Figure 10. Wall A: Details of connection system at end of testing: (a) uplift of hold-down; (b) nail and screw deformation; (c) deformation of shear bracket.

Figure 10. Wall A: Details of connection system at end of testing: (a) uplift of hold-down; (b) nail and screw deformation; (c) deformation of shear bracket.

At the end of testing, although Wall B did not show an evident failure mode, extensive large shear deformation occurred, with sliding between boards due to staple deformation and consequent failure (Figure 11). Rigid rotation of the entire panel due to uplift of the base connections after nail deformation was also noted (Figure 12).

Wall C showed a failure mode similar to that of Wall B: at the end of testing, shear deformation was evidenced as sliding between the vertical boards after plastic deformation of the dovetail inserts subjected to compressive stress perpendicular to the grain (Figure 13). A marked loss in shear stiffness between subsequent cycles was noted, together with rigid rotation of the entire panel, due to uplift of hold-downs after nail deformation (Figure 14).

Figure 11. Wall B: Shear deformation of panel at end of testing: (a) Front face; (b) Rear face.

Figure 11. Wall B: Shear deformation of panel at end of testing: (a) Front face; (b) Rear face.

Figure 12. Wall B: Detail of angle uplift at end of testing.

Figure 12. Wall B: Detail of angle uplift at end of testing.

Figure 13. Wall C: Shear deformation between vertical boards at end of testing: (a) Front face; (b) Rear face.

Figure 13. Wall C: Shear deformation between vertical boards at end of testing: (a) Front face; (b) Rear face.

Figure 14. Wall C: Details of connection system at end of testing: (a) uplift of hold-downs; (b)deformation on rear face.

Figure 14. Wall C: Details of connection system at end of testing: (a) uplift of hold-downs; (b)deformation on rear face.

3.2. Analysis of Hysteresis Cycles

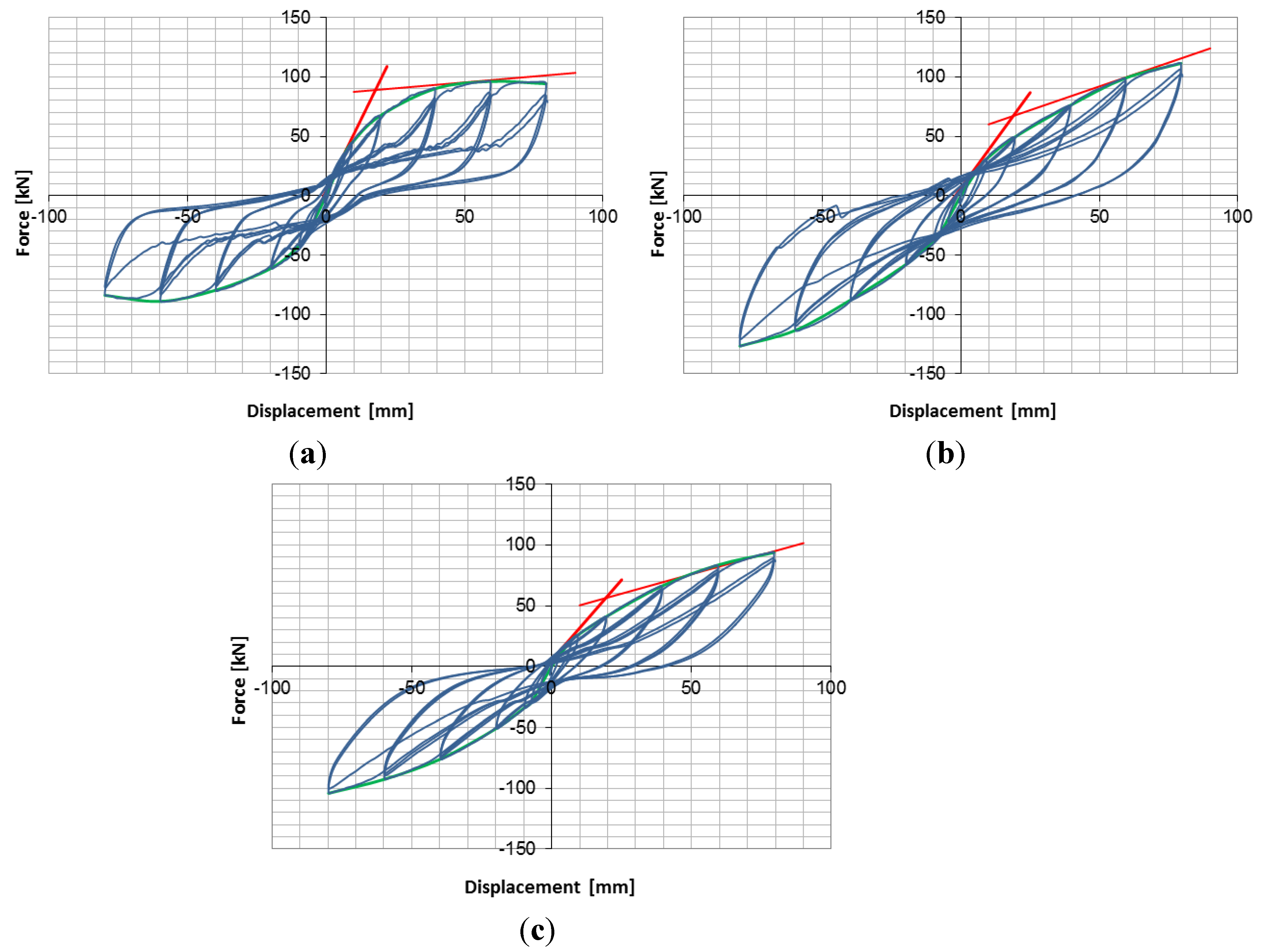
Data on recorded hysteresis loops are presented here. Figure 15 shows force-displacement graphs for the various tests. Wall A (two CLT panels connected at mid-line by screws with half-lap joints) showed very different mechanical behaviour with respect to Walls B and C, which were composed of a single panel. Wall A showed mechanical behaviour characterised by an almost horizontal post-elastic branch, due to the ductile behaviour of the joint, with plasticisation and deformation of nails. Conversely, Walls B and C revealed quite marked plastic hardening after initial elastic behaviour. Figure 15 also shows the bi-linearisation procedure of the hysteresis cycles, with two segments representing the tangents to the elastic and plastic branches of the envelope curves, as proposed in Method A of EN12512. The intersection of the two segments identifies the equivalent yielding point.

Interpretation of the bi-linear curves, according to EN 12512 in terms of stiffness, yielding point, ductility, residual strength and viscous damping ratio, are discussed in the following section and data are shown in Table 2 and Table 3.

Figure 15. Hysteresis cycle and definition of yielding point, according to EN 12512: (a) Wall A; (b) Wall B; (c) Wall C.

Figure 15. Hysteresis cycle and definition of yielding point, according to EN 12512: (a) Wall A; (b) Wall B; (c) Wall C.

Table 2. Interpretation of test results according to Method A of EN 12512.

Identification of Parameters		Wall A	Wall B	Wall C
Elastic stiffness	α [kN/mm]	4.76	3.21	2.64
Hardening stiffness	β [kN/mm]	0.21	0.82	0.64
Yielding displacement	Vy [mm]	17.83	18.88	19.29
Yielding force	Fy [kN]	88.97	67.10	56.27
Ductility ratio	μ  = Vu/Vy	4.48	4.23	4.14

Table 2. Interpretation of test results according to Method A of EN 12512.

Identification of Parameters		Wall A	Wall B	Wall C
Elastic stiffness	α [kN/mm]	4.76	3.21	2.64
Hardening stiffness	β [kN/mm]	0.21	0.82	0.64
Yielding displacement	Vy [mm]	17.83	18.88	19.29
Yielding force	Fy [kN]	88.97	67.10	56.27
Ductility ratio	μ  = Vu/Vy	4.48	4.23	4.14

Table 3. Strength degradation and equivalent viscous damping at each cyclic amplitude.

Cycle Amplitude (mm)	Wall A		Wall B		Wall C
	∆F = 1 − (F3/F1)	νeq = Ed/(2πEp)	∆F = 1 − (F3/F1)	νeq = Ed/(2πEp)	∆F = 1 − (F3/F1)	νeq = Ed/(2πEp)
20	5.44%	10.74%	4.19%	14.53%	3.08%	15.35%
40	12.31%	11.31%	1.92%	13.66%	5.41%	12.46%
60	12.56%	10.28%	5.96%	13.27%	7.98%	11.24%
80	12.05%	9.87%	10.23%	13.51%	7.52%	10.72%

F₁: Force at first cycle; F₃: Force at third cycle; E_d: Dissipated energy; E_p: Potential energy.

Table 3. Strength degradation and equivalent viscous damping at each cyclic amplitude.

Cycle Amplitude (mm)	Wall A		Wall B		Wall C
	∆F = 1 − (F3/F1)	νeq = Ed/(2πEp)	∆F = 1 − (F3/F1)	νeq = Ed/(2πEp)	∆F = 1 − (F3/F1)	νeq = Ed/(2πEp)
20	5.44%	10.74%	4.19%	14.53%	3.08%	15.35%
40	12.31%	11.31%	1.92%	13.66%	5.41%	12.46%
60	12.56%	10.28%	5.96%	13.27%	7.98%	11.24%
80	12.05%	9.87%	10.23%	13.51%	7.52%	10.72%

F₁: Force at first cycle; F₃: Force at third cycle; E_d: Dissipated energy; E_p: Potential energy.

3.3. Analysis of Experimental Results

The cyclic testing results were analysed to define the structural properties of these newly developed massive shear-walls. This section reports and critically discusses evaluation of the yielding limit, ultimate conditions, stiffness for elastic and hardening branches, maximum ductility achieved during testing, and strength degradation at each level of ductility.

3.3.1. Estimation of Ductility

The procedures for estimating ductility are extensively discussed by Muñoz et al. [11]. In this work, Method A of EN 12512 was adopted to define the ductility ratio of the test walls.

3.3.2. Wall Strength Degradation and Equivalent Viscous Damping

Wooden structures assembled with metal fasteners are sensitive to strength and stiffness degradation of connections when undergoing cyclic action. Their consequent reduction in strength is an important parameter in identifying their capacity to resist cyclic and therefore seismic action. Table 3 lists the strength degradation recorded between the first and third cycles at each displacement level. In accordance with Eurocode 8 [8], this parameter and the ductility ratio were used to define the Ductility Class of a timber structure.

As shown in Table 3, strength degradation increases with cyclic amplitude, but always remains lower than 15% in all walls, indicating that the structures perform well under cyclic action and are suitable for use in seismic areas.

3.3.3. Definition of Ductility Class

Eurocode 8 [8] lists three ductility classes, low, medium and high, according to the dissipative capacity of the timber building. The parameter identifying the most appropriate class is the ductility ratio, with a minimum value of 4 and 6 for Medium and High Ductility Class structures, respectively. In both cases, strength degradation must be under 20%. Following the procedure recommended by Eurocode 8 [8] and according to the results shown in Table 2 and Table 3, all test walls belonged to the Medium Ductility Class.

4. Numerical Evaluation of Behaviour Factor q

The Force-Based-Design method [12] is an engineering approach for seismic building design, referring to the inertial forces induced in structures by seismic action. Application of this method requires evaluation of the most suitable behaviour factor q, which summarises the post-elastic behaviour and ductility of a given structural system. According to code provisions, the q-factor may be estimated with reference to quasi-static tests, which define the hysteretic behaviour of single connectors or assembled wooden elements (e.g., an entire wall). These tests define characteristic features such as the ductility ratio and strength degradation at each ductility level [9]. To date, two methods have been used in Europe [1]. The first is based on the results of full-scale shake-table tests on whole buildings, and the second on fully realistic numerically simulated responses of whole buildings. Ceccotti and Sandhaas [1] did not carry out full-scale shaking tests but modelled buildings numerically and subjected them to seismic loading. The main feature of this method was the development of a numerical model which can reproduce the seismic response of an entire case-study building. The peak ground acceleration (PGA) approach was considered appropriate to evaluate the q-factor [13], defined as the ratio between the PGA which leads the structure to “near-collapse condition” (i.e., PGA_{u_eff}) and that conventionally used to design a building within an elastic approach (i.e., PGA_{u_code}), according to Equation (1).

q = PGA_{u_eff}/PGA_{u_code}

(1)

This method disregards the actual yielding limit of the structure and takes into account its over-design factor, defined as the ratio between yielding strength and design strength [14]. This definition of the q-factor is code-dependent, representing a conventional value based on the building's seismic design according to the seismic code in force. As reported in [13], the PGA-based method consists of several steps:

(1)

Choice of a case-study building and its design according to load-bearing capacity measured during tests and according to the appropriate seismic code [8], assuming q = 1, in order to resist the PGA_{u_code} value elastically.

(2)

Modelling of the test building with suitable finite-element models, capable of reproducing the hysteretic behaviour of shear walls and duly calibrated.

(3)

Definition of an ultimate or near-collapse condition of the building, which may coincide with the ultimate displacement recorded during tests. For timber buildings, definition of the near-collapse condition depends on the structural system used. Schädle and Blaß [2] report that the most suitable near-collapse condition is that of inter-storey drift.

(4)

Assessment of seismic intensity (PGA_{u_eff}), which leads to the near-collapse condition through a series of non-linear analyses in the time domain as PGA intensity gradually increases.

(5)

Determination of the most suitable q-factor according to the PGA-based approach.

The accepted simplification of this method is that PGA_{u_code} is constant, independently of seismic frequency content. Otherwise, near-collapse PGA, determined by non-linear analysis, is a function of the vibration period and seismic frequency content.

4.1. Seismic Design of Study Building

Earthquake action E_d for case-study buildings is calculated for a_g = 0.35 g (PGA_{u_code}), which is reached in the most earthquake-prone areas in Italy. The elastic response spectrum for building foundations resting on type A soil (rock soil, corresponding to S = 1.0, T_B = 0.15 s, T_C = 0.4 s, T_D = 2.0 s), behaviour factor q = 1, and building importance factor γ_I = 1 was assumed according to Eurocode 8 [8]. The seismic lateral force patterns to be used in an Equivalent Linear Static Design were calculated assuming the fundamental period of the shear walls within the plateau range. The unit lateral load-bearing capacity of the walls was deduced from the experimental load-displacement curves, i.e., the load corresponding to the ultimate displacement of 80 mm was assumed to be the conventional design strength of the walls. Design length B of the shear walls was then calculated by equating the design base shear force with their conventional shear strength, in order not to introduce design over-strength:

E_d = R_d

(2)

Note that the assumed overall seismic mass of 14 t respects Equation (2) for Wall B with linear static analysis and the elastic spectrum (120 kN). For Walls A and C, as their tested maximum shear force (R_{d_wall (d=du)}) was lower than E_d, their real length (3.00 m) had to be changed in order to obtain the design length of the walls fulfilling Equation (2) (see Table 4). The overall mass was then subdivided into nodal masses applied to each storey, giving a total storey mass of 4.66 t. A value of 80 mm as near-collapse condition was also chosen because no experimental data were available for higher displacements.

Table 4. Parameters used for wall design.

Parameters	Notations	Units	Jointed Clt Wall	Stapled Wall	Layered Wall
Design Peak Ground Acceleration	PGAu_code	–	0.35	0.35	0.35
Overall seismic mass	M	t	14.00	14.00	14.00
Earthquake base shear	Ed = Rd	kN	120.00	120.00	120.00
Near-collapse condition	du	mm	80.00	80.00	80.00
Height of shear wall	H	m	3.00	3.00	3.00
Near-collapse drift	du/H	–	2.67%	2.67%	2.67%
Experimental base shear strength	Rd_wall (d = du)	kN kN/m	90 90/3.00 = 30	120 120/3.00 = 40	95 95/3.00 = 31.67
Design length of shear wall	B	m	120/30 = 4.00	120/40 = 3.00	120/31.67 = 3.80
Principal period of structure	T1	s	0.37	0.40	0.37

The strength and stiffness of the base connections were recalculated according to the design base shear force.

Table 4. Parameters used for wall design.

Parameters	Notations	Units	Jointed Clt Wall	Stapled Wall	Layered Wall
Design Peak Ground Acceleration	PGAu_code	–	0.35	0.35	0.35
Overall seismic mass	M	t	14.00	14.00	14.00
Earthquake base shear	Ed = Rd	kN	120.00	120.00	120.00
Near-collapse condition	du	mm	80.00	80.00	80.00
Height of shear wall	H	m	3.00	3.00	3.00
Near-collapse drift	du/H	–	2.67%	2.67%	2.67%
Experimental base shear strength	Rd_wall (d = du)	kN kN/m	90 90/3.00 = 30	120 120/3.00 = 40	95 95/3.00 = 31.67
Design length of shear wall	B	m	120/30 = 4.00	120/40 = 3.00	120/31.67 = 3.80
Principal period of structure	T1	s	0.37	0.40	0.37

The strength and stiffness of the base connections were recalculated according to the design base shear force.

The adopted design method differs from the procedure recommended in available codes [8]. Code procedures refer to load-bearing capacity calculated by analytical formulas, whereas the procedure adopted here refers to experimental results. In addition, in the analytical procedure, partial resistance coefficient γ_m and load duration coefficient k_mod were used to change the characteristic 5% resistance to the design value. In this work, γ_m and k_mod were assumed as the unit. This procedure ensures that no design over-strength is introduced and therefore that the q-factor value is the lowest, representing the effective dissipative capacity, ductility and post-elastic resistance of the structure [15]. In other words, q-factor values are neither affected by design over-strength nor by safety, nor even modification coefficients. The same design strength of the three shear walls was thus ensured by increasing their base length. If this had not been done, in terms of dissipative capacity no comparisons could have been made among them.

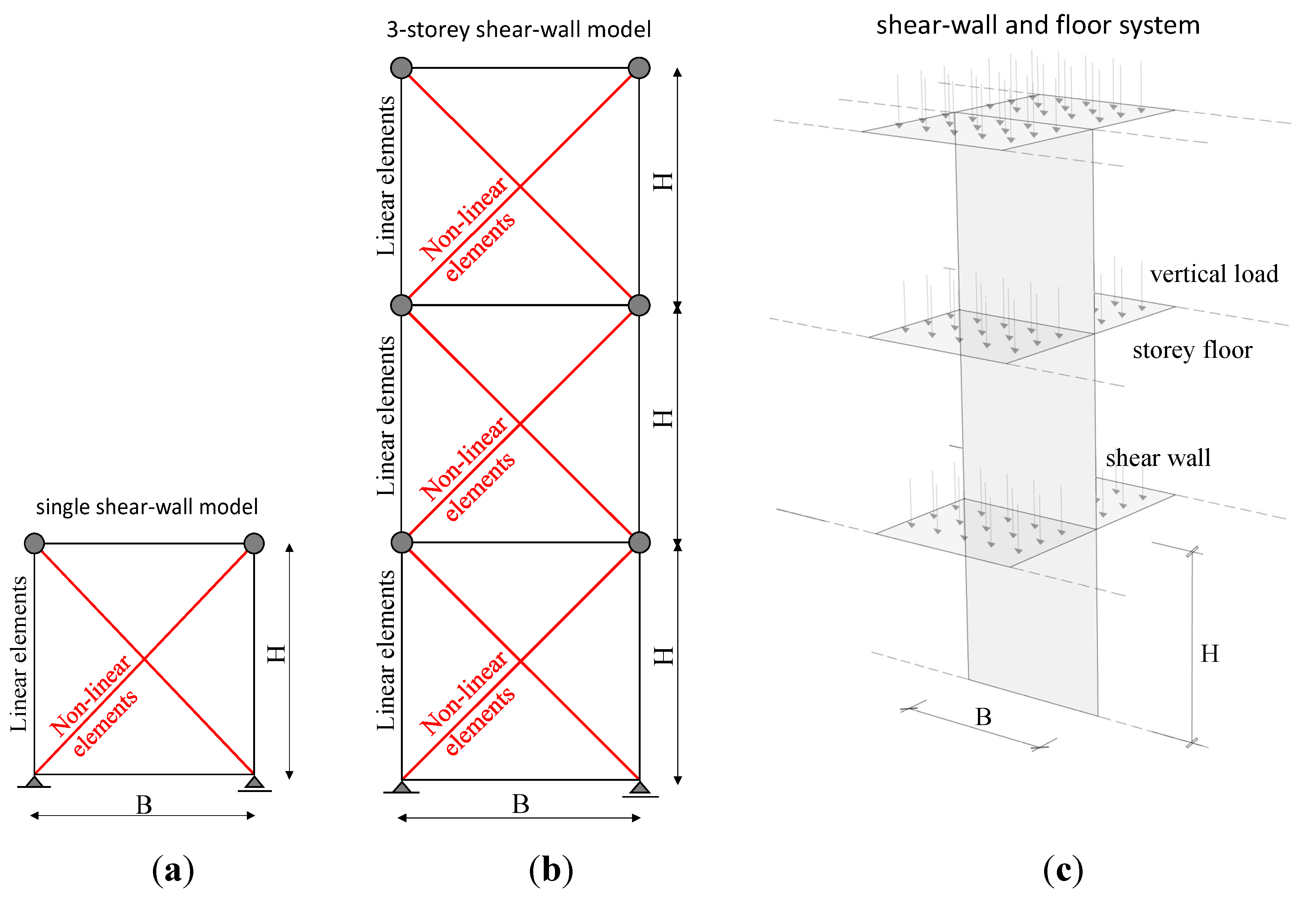
4.2. Numerical Model

Q-factor was evaluated in all studied wall systems from a simplified model of a three-storey building, with a procedure slightly modified from that of Ceccotti [13]. The model consists of a three-storey shear wall composed of three levels, with suitably assigned seismic masses for each floor (see Figure 16). Its geometrical characteristics and applied masses are listed in Table 4.

In detail, q-factor was numerically evaluated by previous calibration based on experimental hysteretic behaviour. All the walls showed pinched load-displacement responses and degradation under cyclic loading. In order to reproduce their true hysteretic response, the research-oriented numerical code “Open System for Earthquake Engineering Simulation—OPENSEES” [16] was used, with hysteresis model developed by Elwood [17]. Each finite-element model consisted of a perimeter frame with elastic trusses braced by non-linear springs, which faithfully reproduce the overall hysteresis response of the wall. Wall sub-models are shown in Figure 16. The numerical model is based on the simplified hypothesis that non-linear wall behaviour is completely assigned to the diagonal elements bracing the structure. This hypothesis was also adopted for the CLT wall model, in which dissipation capacity was mainly due to joint deformation. Comparisons among the three case studies were thus made possible, because the real hysteretic behaviour is simulated with the same modelling strategies. 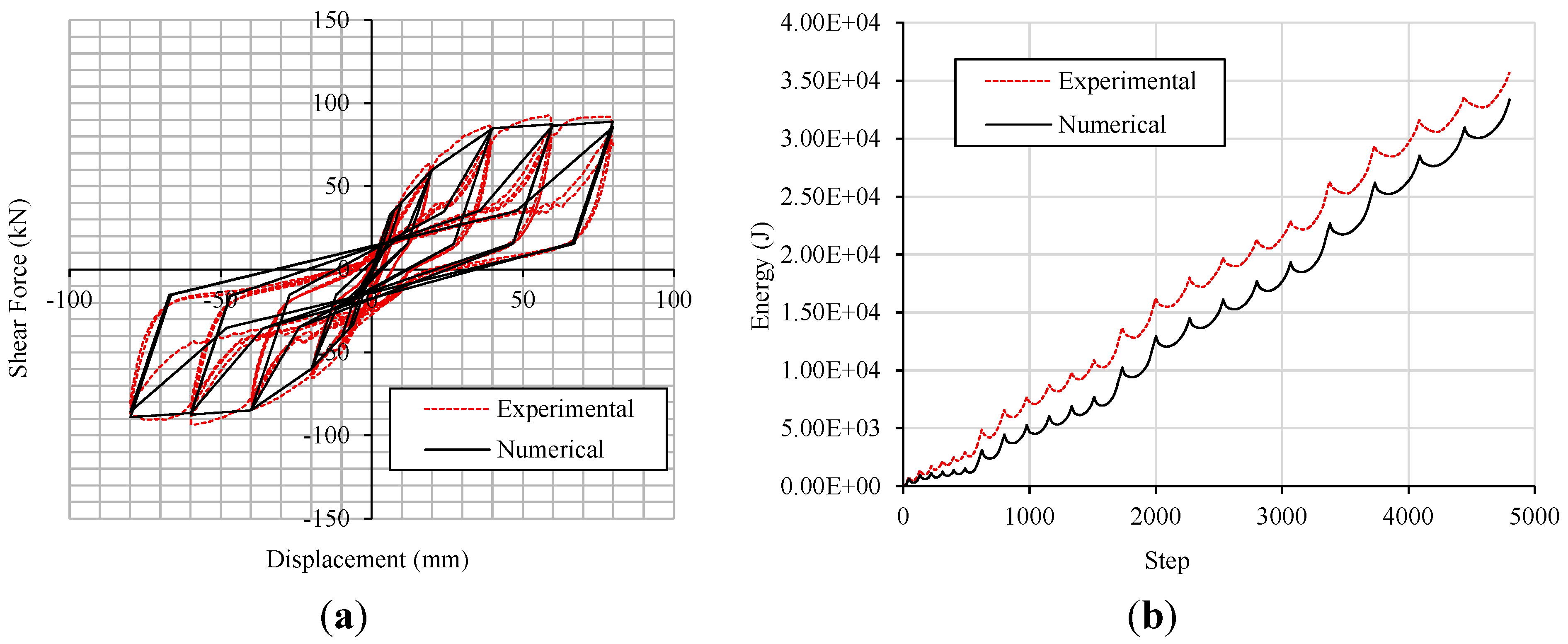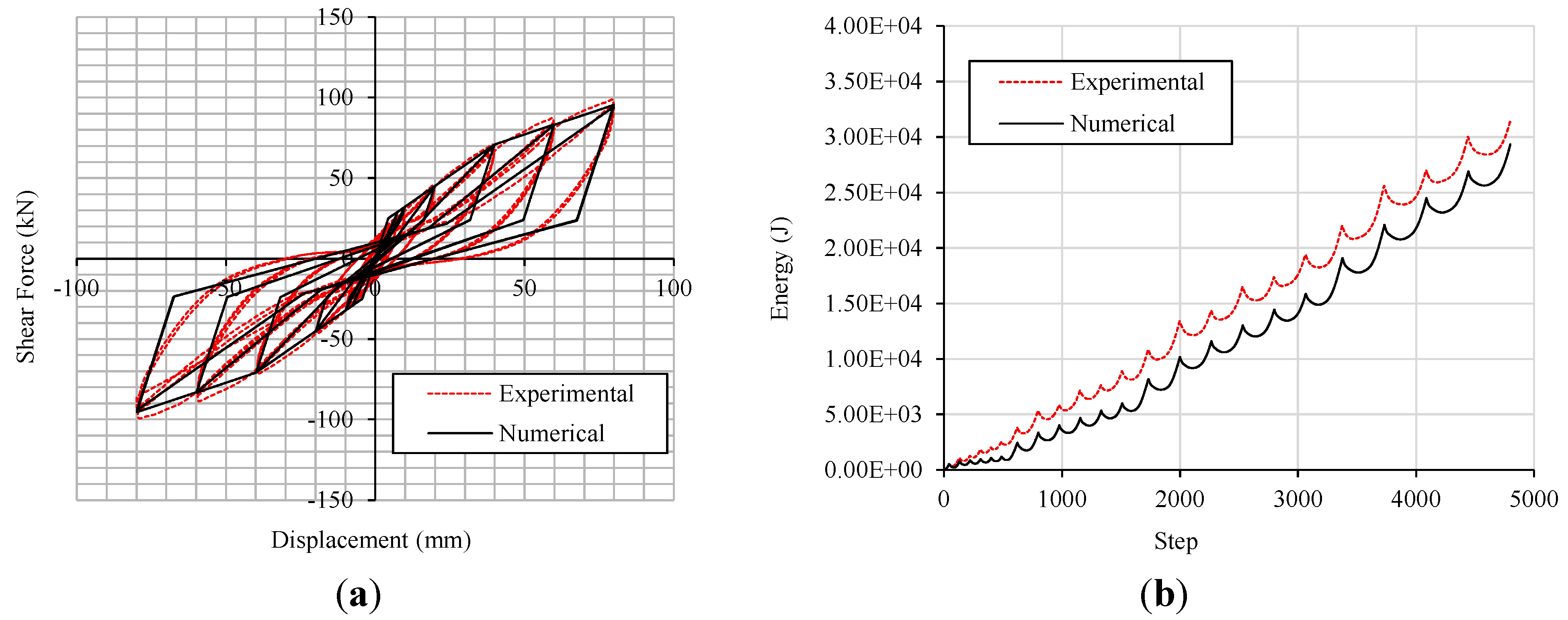The numerical models of all walls were calibrated according to the test results, shown in Figure 17 for jointed CLT wall, Figure 18 for Stapled wall, and Figure 19 for Layered wall.

The good accuracy of the models was ascertained by comparing the numerical data with test results. The dissipated energy graphs clearly show that the numerical model never over-estimates the experimental values, and that the difference between numerical model and test data in the near-collapse condition is always less than 10%.

Figure 16. Scheme of specimens used for: (a) calibration; (b) simulations; (c) design.

Figure 16. Scheme of specimens used for: (a) calibration; (b) simulations; (c) design.

Figure 17. Wall A: (a) Hysteresis loops; (b) Dissipated energy.

Figure 17. Wall A: (a) Hysteresis loops; (b) Dissipated energy.

Figure 18. Wall B: (a) Hysteresis loops; (b) Dissipated energy.

Figure 18. Wall B: (a) Hysteresis loops; (b) Dissipated energy.

Figure 19. Wall C: (a) Hysteresis loops; (b) Dissipated energy.

Figure 19. Wall C: (a) Hysteresis loops; (b) Dissipated energy.

4.3. Analyses and Results

Several non-linear dynamic analyses were performed with the calibrated model in order to evaluate the most suitable q-factor for each wall. To define the influence of the frequency content of seismic shocks on building responses, non-linear dynamic analyses were carried out on 15 artificially generated shocks, in order to meet the spectrum compatibility requirement. Two types of software were used to generate the shock signals: SIMQKE_GR [18] and SeismoArtif [19]. Dynamic equilibrium equations were integrated with time-steps of 0.001 s, with equivalent Rayleigh viscous damping of 2%, according to Ceccotti [13]. The test buildings were subjected to increasing levels of seismic intensity, from PGA_{u_code} to near-collapse condition (PGA_{u_eff}), i.e., when the ultimate inter-storey drift of 80 mm (2.67%) was reached. 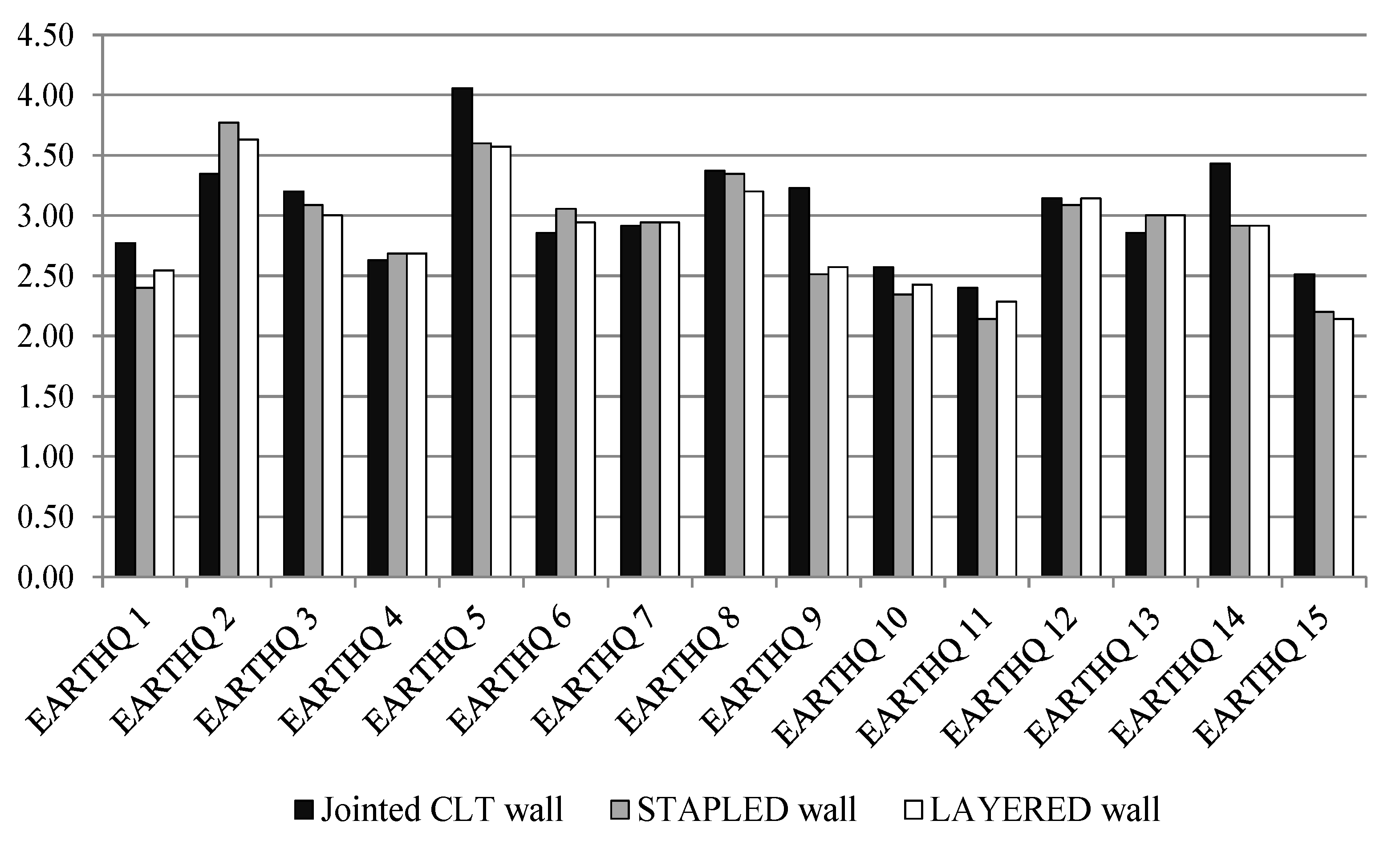Table 5 lists all the PGA_{u_eff} obtained and the related q-factor values (Figure 20).

Figure 20. Values for q-factor.

Figure 20. Values for q-factor.

Table 5. PGA_{u_eff} values and q-factor values for numerically analysed walls.

Shock signals	Wall A Jointed CLT		Wall B Stapled		Wall C Layered
	PGAu_eff	q	PGAu_eff	q	PGAu_eff	i
EARTHQUAKE 1	0.97	2.77	0.84	2.40	0.89	2.54
EARTHQUAKE 2	1.17	3.34	1.32	3.77	1.27	3.63
EARTHQUAKE 3	1.12	3.20	1.08	3.09	1.05	3.00
EARTHQUAKE 4	0.92	2.63	0.94	2.69	0.94	2.69
EARTHQUAKE 5	1.42	4.06	1.26	3.60	1.25	3.57
EARTHQUAKE 6	1.00	2.86	1.07	3.06	1.03	2.94
EARTHQUAKE 7	1.02	2.91	1.03	2.94	1.03	2.94
EARTHQUAKE 8	1.18	3.37	1.17	3.34	1.12	3.20
EARTHQUAKE 9	1.13	3.23	0.88	2.51	0.90	2.57
EARTHQUAKE 10	0.90	2.57	0.82	2.34	0.85	2.43
EARTHQUAKE 11	0.84	2.40	0.75	2.14	0.80	2.29
EARTHQUAKE 12	1.10	3.14	1.08	3.09	1.10	3.14
EARTHQUAKE 13	1.00	2.86	1.05	3.00	1.05	3.00
EARTHQUAKE 14	1.20	3.43	1.02	2.91	1.02	2.91
EARTHQUAKE 15	0.88	2.51	0.77	2.20	0.75	2.14
Average	1.06	3.02	1.01	2.87	1.00	2.87
Min	0.84	2.40	0.75	2.14	0.75	2.14
Max	1.42	4.06	1.32	3.77	1.27	3.63

Table 5. PGA_{u_eff} values and q-factor values for numerically analysed walls.

Shock signals	Wall A Jointed CLT		Wall B Stapled		Wall C Layered
	PGAu_eff	q	PGAu_eff	q	PGAu_eff	i
EARTHQUAKE 1	0.97	2.77	0.84	2.40	0.89	2.54
EARTHQUAKE 2	1.17	3.34	1.32	3.77	1.27	3.63
EARTHQUAKE 3	1.12	3.20	1.08	3.09	1.05	3.00
EARTHQUAKE 4	0.92	2.63	0.94	2.69	0.94	2.69
EARTHQUAKE 5	1.42	4.06	1.26	3.60	1.25	3.57
EARTHQUAKE 6	1.00	2.86	1.07	3.06	1.03	2.94
EARTHQUAKE 7	1.02	2.91	1.03	2.94	1.03	2.94
EARTHQUAKE 8	1.18	3.37	1.17	3.34	1.12	3.20
EARTHQUAKE 9	1.13	3.23	0.88	2.51	0.90	2.57
EARTHQUAKE 10	0.90	2.57	0.82	2.34	0.85	2.43
EARTHQUAKE 11	0.84	2.40	0.75	2.14	0.80	2.29
EARTHQUAKE 12	1.10	3.14	1.08	3.09	1.10	3.14
EARTHQUAKE 13	1.00	2.86	1.05	3.00	1.05	3.00
EARTHQUAKE 14	1.20	3.43	1.02	2.91	1.02	2.91
EARTHQUAKE 15	0.88	2.51	0.77	2.20	0.75	2.14
Average	1.06	3.02	1.01	2.87	1.00	2.87
Min	0.84	2.40	0.75	2.14	0.75	2.14
Max	1.42	4.06	1.32	3.77	1.27	3.63

The average q-factor was between 2.50 and 3.00, confirming the good dissipative capability of the tested systems.

Some comments may be made:

(1)

Numerical results confirm the estimates of q-factor, based on the definition of medium ductility class given by Eurocode 8 [8].

(2)

Although three different construction systems were examined, the difference in terms of q-factor was small, confirming the similarities of materials and connections among the walls.

(3)

The q-factor values ranged from 2.14 to 4.06; Wall A: minimum 2.40, maximum 4.06, average 3.02; Wall B: minimum 2.14, maximum 3.77, average 2.87; Wall C: minimum 2.14, maximum 3.63, average 2.87.

(4)

Clearly, the largest difference in terms of q-factor was found between walls in which the specimen underwent overall shear deformation (Stapled and Layered types) and the CLT wall, in which deformation capacity was entirely assigned to the connectors. This was due to specimen composition and the systems connecting the walls to the foundations. Wall A had the highest q-factor, because it consisted of two vertically jointed sub-walls, fixed to the foundation with correctly designed ductile connectors. The values of the other walls were slightly lower, because their energy dissipation capacity was exclusively due to the deformability of the shear wall panels, whereas the base connectors contributed only slightly to energy dissipation.

(5)

These results also show that:

• the energy dissipation capacity of the system is given mainly by shear deformation of wooden panels in stapled and layered walls, and by plastic deformation of base connectors in CLT walls;
• the dissipative capacity of massive CLT walls can be improved if smaller jointed panels are used and the number of steel connectors is increased [15].

Lastly, it must be stressed that the above results cannot be used to derive general conclusions about the most suitable q-factor to be used in designing the shear-wall systems examined here, since they were based on analysis of a single, conventional, three-storey case-study building. For more accurate and reliable evaluation of the variability of the q-factor with building characteristics (e.g., number of storeys, arrangement of resistant plated shear walls, etc.), more case studies must be numerically examined. In addition, three-dimensional numerical models could be used to explain the effects of irregularities in plan and intersections between shear walls.

5. Conclusions

Testing was carried out to characterise the mechanical properties and dissipative capacity of three types of massive shear walls commonly found in construction practice.

A numerical procedure based on time-history analyses was applied to determine the near-collapse PGA of three massive shear walls. The model used for analyses was calibrated on the results of quasi-static cyclic loading tests. The procedure yielded an estimate of the best behaviour factor q for these systems, exclusively due to wall dissipative capability. This result was achieved with a special design procedure characterised by no over-design factor and therefore based only on the ultimate shear force reached by the wall in the imposed near-collapse condition.

The results show that these systems have good dissipative capacity and can be used to good effect in seismically vulnerable areas. A q-factor of about 2.5 is suitable for construction types in the Medium Ductility Class of Eurocode 8 [8].

This work also shows that, for systems with low displacement capacity due to very stiff wooden panels, vertical joints should be introduced to subdivide the walls into smaller panels, to improve the seismic response. In CLT shear walls, dissipative capacity and ductility increase with the number of panels, i.e., with the number of steel connectors and fasteners used.

In shear walls made with stapled or layered panels, these positive characteristics are intrinsic to the massive timber panel itself, independently of the type of connections used. The use of such innovative materials is thus highly appropriate for building ductile shear walls.

Future studies must be planned to compare these systems with other shear-wall systems, examining various types of connections and design approaches, in order to generalise the results obtained here.