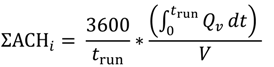1. Introduction
Air infiltration in buildings refers to the uncontrolled or unintentional flow of outside air to the internal space through leakages in the envelope, typically cracks and/or large leakage points. From the 1970s onwards, its impact on energy performance has been recognized in the literature, e.g., [
1]. Several studies have presented estimations of the heat load fraction in a building that takes place due to infiltration [
2,
3,
4,
5,
6,
7,
8,
9,
10]. In addition, infiltration has been verified as playing an important role in the internal environment and in the indoor air quality [
11,
12,
13,
14]. The heating, ventilation and air conditioning system (HVAC) is also most likely influenced by high infiltration rates, resulting in an offset from the designed inner climate as well as in waste of energy [
15]. Moisture problems have also been recorded due to leakage airflows (especially exfiltration) [
16].
Air infiltration in buildings can be driven either by the wind-induced pressure differences across the envelope or by the gradients between internal and external temperatures (buoyancy pressures) or by the mechanical ventilation [
17]. Analytical formulation of air infiltration caused by these mechanisms under steady state conditions has been investigated by Lyberg [
18]. A detailed summary of applicable single-zone and multi-zone models for air infiltration and ventilation calculations has been presented by Orme [
19]. In these models, the magnitude of wind as a driving force for infiltration is usually expressed by a typical value at a reference height (
i.e., at the height of the roof), excluding the dynamic nature of the phenomena [
20].
Physical models of the driving forces and their interaction with the building have been presented in order to estimate infiltration rates, based on the leakage numbers and climate indicators [
21]. The main scope of these models is to calculate the average seasonal natural infiltration rates from the leakage rates as quantified by an artificial (fan) pressurization test at 50 Pa pressure difference across the building envelope [
22]. The impact of wind is taken into account, but only in terms of mean wind speed.
However, especially in low-rise buildings, wind gustiness and the consequent pressure gradient on the facades seem to govern the air exchanges [
23]. In general, openings exposed to turbulent wind can have a large impact on the variation of the internal pressure distribution in a building, affecting the airflow [
24,
25]. Flows through small cracks (leakages) can potentially cause unacceptable situations from an energy point of view [
14]. Turbulence causing wind gustiness is recognized as one major factor that affects infiltration [
26]. Turbulent fluctuating wind causes unsteady flow effects that are linked with the instantaneous airflow rates across cracks and openings and differ from the mean ones [
27,
28,
29].
The dynamic characteristics of air infiltration was very early pointed out by Hill and Kusuda [
30] who studied the unsteady flow phenomena through cracks around a single window. The whole rooms used in their study were completely sealed (apart from the window), limiting the results to a single-side infiltration case. A simple theoretical pulsation flow model of an enclosure with a single opening, subjected to turbulent impinging air stream, has been presented by Cockroft and Robertson [
31]. In their study, the flow is caused by longitudinal fluctuations of wind and the compressibility of air within the enclosure. The study was focused on the single-side ventilation and it provided arguments on the percentage of the air flowing into the enclosure that contributes to the effective ventilation. Etheridge provided arguments in favor of the role of wind gustiness on the ventilation design field [
32]. He analyzed the connection between gust strength and duration on one side and the effects of inertia and compressibility on the other side for a study dealing with large opening (vents and ducts) in a purpose-designed naturally ventilated building. A power spectrum analysis linearization technique for modeling pulsating airflow due to turbulent wind-induced pressures was executed by Haghighat and Rao [
33]. They obtained good agreement between the model and their experimental results, but building crack geometries are not explicitly taken into account and the study deals with single-zone spaces.
In addition, leakage distribution has been mentioned as an important factor affecting the infiltration/ventilation rates [
34,
35,
36] and models have been developed towards the estimation of leakage distribution [
37]. In addition, the latter affects even the air pressure conditions in a building and the wind-induced internal pressure fluctuations [
38,
39]. In an analytical approach that allows the dynamic numerical simulation of infiltration and ventilation in buildings, based on Lyberg formulation and developed by Lowe, the assumption of uniformly distributed leakages on windward and leeward facades has been employed [
40]. Furthermore, in that study, as well as in many of those mentioned above, the space of interest is a single-compartment building. However, apart from the external leakages, the internal leakage paths have been recognized as an important element towards the leakage rates when undertaking a pressurization test [
41]. Recently, an analysis of infiltration rates in conjoined dwellings from the perspective of partition walls permeability was presented by Jones
et al. [
42]. The study provides arguments in favor of internal leakages consideration when the leakage-infiltration ratio is predicted, highlighting the significant variance the former can have. Clearly, predicting realistic air infiltration rates is a rather complex task, therefore assumptions and simplifications are usually employed in the models (e.g., steady-state conditions, mean wind speed, uniform leakage distribution, single-compartment spaces,
etc.). The current study deals with the dynamics of the building air exchanges, aiming to inter-link the elements mentioned above (wind gust frequency, leakage distribution and internal leakages) in a low-rise one-story building. The numerical methods could contribute to an estimation of the impact of turbulent wind on air exchanges, through the simulation of potentially critical variable parameters of building envelope.
The paper focuses on wind-driven infiltration (buoyancy pressures are neglected and no mechanical ventilation system has been applied). Its major objective is to ascertain the influence of wind unsteadiness in the instantaneous infiltration rates through a transient analysis. In particular, the impact of wind gust frequency on the air in- and exfiltration rates of a cross-ventilated building-model with variable leakage areas. The role of the internal leakages is also studied and for this reason five different compartmentalization/partition-wall-permeability scenarios are researched. A computational fluid dynamics (CFD) solver that has been widely used in estimation of cross ventilation rates (SST k-ω) is employed. The unsteady conditions (wind gust frequencies) are simulated as an additional sinusoidal factor in the wind profile formula. The accumulated infiltration rates over one hour (ΣACH) are calculated for the two wind gust frequencies cases, proving the potential of higher gustiness to create higher air exchange rates (ACH).
2. Case Study
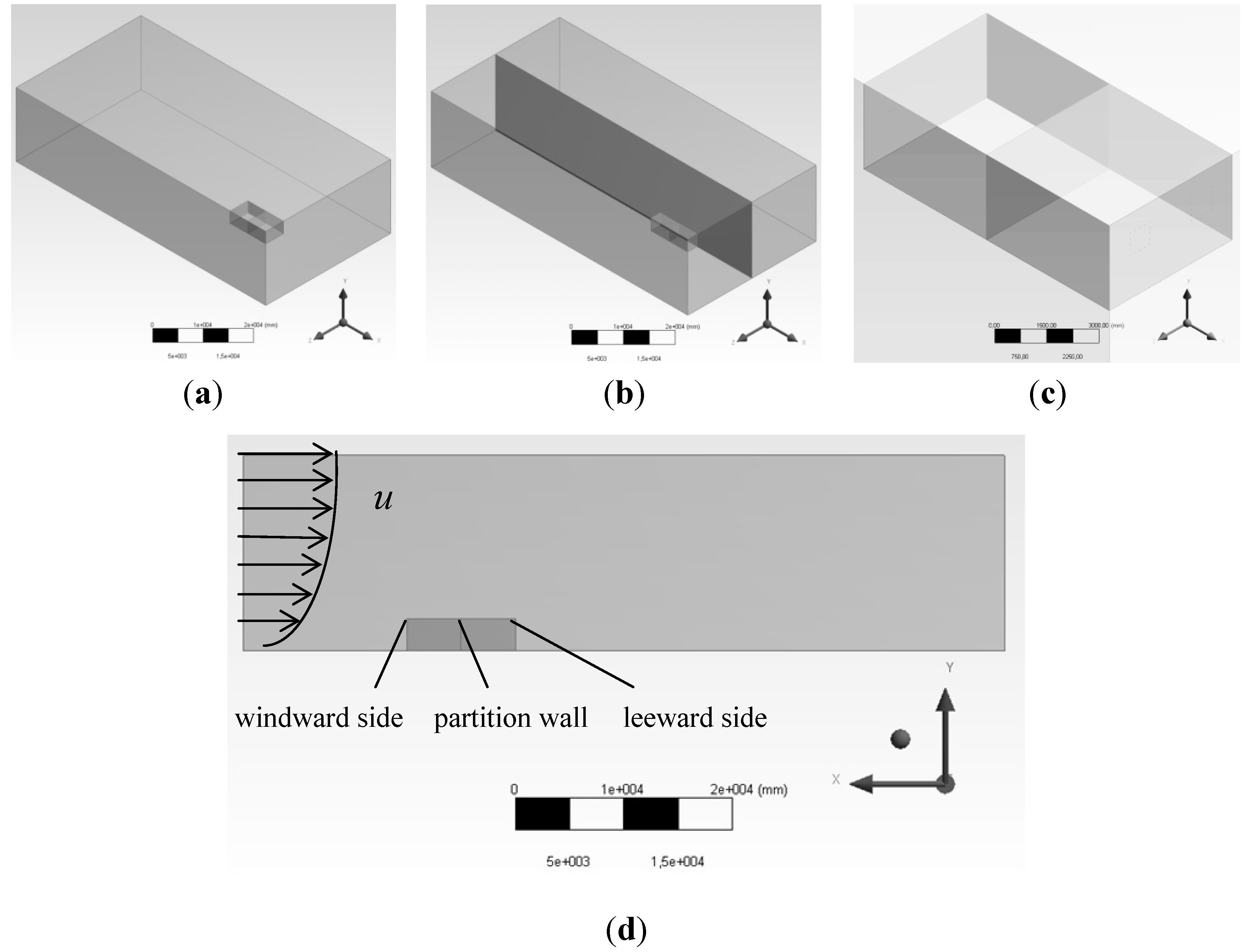
The current numerical study deals with the influence of unsteady wind to the instantaneous air exchange rates of a one-story low rise building. The geometry of the parallelepiped model is 10 m × 3 m × 5 m (
X, Y,
Z). Variable leakage areas are simulated in order to verify the impact of the leakage distribution on the infiltration rates. The leakages represent cracks around the window frames. The dimensions of each “window” are 0.8 m × 0.8 m. In total, four windows are assumed, all of them normal to the main wind direction, two on the windward and two on the leeward facade (
Figure 1).
Figure 1.
(a) The building-model and the domain; (b) A symmetry plane (XY) has been used in order to reduce the simulation expenses; (c) The external leakage areas (cracks around windows) and the internal leakage path representing the permeability of the partition wall; (d) Cross section of the domain and the building, the windward facade, the partition wall and the leeward facade are shown.
Figure 1.
(a) The building-model and the domain; (b) A symmetry plane (XY) has been used in order to reduce the simulation expenses; (c) The external leakage areas (cracks around windows) and the internal leakage path representing the permeability of the partition wall; (d) Cross section of the domain and the building, the windward facade, the partition wall and the leeward facade are shown.
As mentioned above, the main objective of this paper is to research the impact of the wind gust frequency. The investigation of the role of the latter is important towards the estimation of the wind-driven infiltration of a building in operation. In this context, two gust frequencies, Ω
high = 0.5 Hz and Ω
low = 0.1 Hz, are assumed, while they are implemented in the logarithmic wind profile formula as an additional sinusoidal factor. The wind speed fluctuates in all the frequencies between 0.0005 and 5 Hz [
43]; therefore, the choice of the wind gust frequencies in this study aims to study the middle-range wind frequencies in a logarithmic scale, excluding the extremes of very low or very high frequencies [
30,
43].
In order to study the role of the internal leakages, five scenarios (S
1–5) are employed (
Table 1). The scenario S
1 refers to a single-room model (without any partition wall), while in all the other cases refer to compartmentalized volume. The cases S
2, S
3, S
4 and S
5 represent different “permeability” of the partition wall in terms of internal leakages. In all the cases, the internal leakages are located on the lower level of the partition wall. In the scenarios S
2, S
3, and S
4, different amounts of leakages are simulated, while in the last one (S
5), the assumption of a completely tight wall is employed.
The total external leakage area of the building envelope is selected as 128 cm
2, which is approximately equal to 0.01% of the total exposed model surface. The leakages are located on the windward and on the leeward facade of the building, while no leakage paths are assumed to be on its sides. In order to research the influence of the leakage distribution under unsteady wind conditions and to see their physical connection to the internal leakages, seven cases of leakage distribution are solved. For the representation of the distribution of the external leakages on the windward and the leeward side, a ratio α is defined as follows:
where
Aleak,windward is the area of the leakages located on the windward side of the building and
Aleak,total the total leakage area, the sum of the leakages on the windward and the leeward side (=128 cm
2). In fact, the ratio α expresses the portion of the envelope leakages that is located on the windward side. The α takes the values: α = 5%, α = 15%, α = 30%, α = 50%, α = 70%, α = 85% and α = 95%.
The simulated building is surrounded by a fetch which plays the role of the domain. The size of the domain is 70 m × 18 m × 40 m. In order to deal with license constraints and to increase the number of the elements used in the mesh and consequently the accuracy of the solver, a symmetry plane has been used. An unstructured mesh of approximately 1.9 × 106 elements (1.4 × 106 tetrahedral, 1 × 104 pyramids, 4 × 105 prisms) and 4.6 × 105 nodes has been used.
Table 1.
Internal leakages scenarios (S1−5). Partition wall and internal leakages.
Table 1.
Internal leakages scenarios (S1−5). Partition wall and internal leakages.
| Scenario | Partition Wall | Internal Leakages |
|---|
| Scenario S1 | No | – |
| Scenario S2 | Yes | 8 cm2 (6.25%) * |
| Scenario S3 | Yes | 4 cm2 (3.125%) * |
| Scenario S4 | Yes | 2 cm2 (1.5625%) * |
| Scenario S5 | Yes | 0 |
3. Methodology
The computational fluid dynamics package ANSYS CFX was used for the numerical simulations. The Shear-Stress-Transport (SST) model, a two Equation k-ω based model [
44], has been employed. Pressure distribution around a building is in general important to get correct prediction of the pressure gradients and consequently of the air infiltration across the building envelope. A SST turbulence model has been shown to have good prediction accuracy for the indoor ventilation flow [
45]. In addition, other relevant studies on natural ventilation and flows in an enclosure have shown a good agreement between SST model and full scale data, which are better than standard k-ε and Re-Normalization Group (RNG) k-ε models [
46].
At the inlet of the domain, a logarithmic wind profile [
47] was assumed, while a sinusoidal term was added in the formula in order to describe the wind unsteadiness. Eventually, the wind profile used for this study is given by the following equation:
where
u is the wind velocity at height
z,
u* is the shear velocity,
κ von Karman’s constant,
z0 the roughness length and Ψ
m a stability function. The stability function can be evaluated directly from the Monin and Obukhov length
L, knowing the flux of sensible heat, or indirectly through simultaneous measurements of air temperature profiles [
47]. Under neutral stability conditions Ψ
m and
![Buildings 04 00027 i004]()
vanish.
The second term in the right side of the equation describes the “unsteadiness” of the wind, expressed by the gust frequency Ω. As mentioned above, two gust frequencies Ω have been simulated; Ω
high = 0.5 Hz (high frequency) and Ω
low = 0.1 Hz (low frequency). The periods
T of the two gust frequencies are shown in
Figure 2. The longitudinal wind velocity at the inlet of the domain varies from 3.27 to 7.27 m·s
−1. For the steady state (no gust) conditions, the wind velocity is 5.27 m·s
−1. The wind direction angle is normal to the windward side of the building, in all the simulated cases.
Figure 2.
Variation of velocity u (at the inlet of the domain and on height y = 1.5 m) in respect to time t.
Figure 2.
Variation of velocity u (at the inlet of the domain and on height y = 1.5 m) in respect to time t.
To obtain the dynamics of the building air exchange, the simulations are solved in transient mode. After a mesh sensitivity analysis, a time-step of 0.05 s has been investigated as sufficient for the length and time scale calculations. The instantaneous mass flow rate
Qm is solved numerically and consequently the instantaneous volumetric flow rates
Qv across the leakage areas are calculated, based on the transient, local density field for the interval run time. The equivalent air change rate ΣACH that represents the “accumulative” air exchanges over
ttot = 1 h is calculated:
where
trun is the total run time per case and
V the volume of the enclosure.
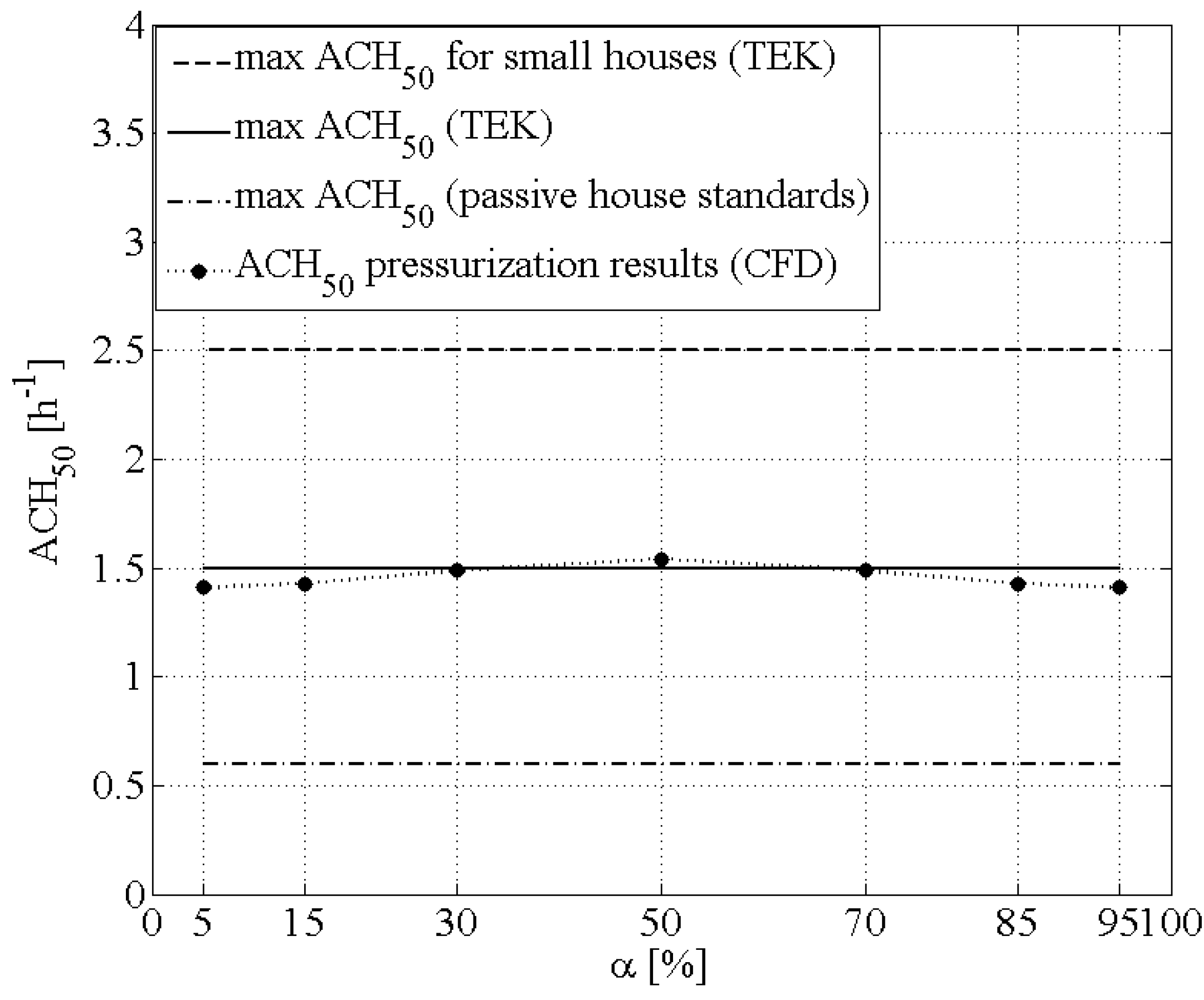
In order to have a magnitude of order of the airtightness level of the building-model, an additional case of simulating a 50 Pa pressure difference across the envelope was also performed. Establishing a pressure difference of 50 Pa across the envelope (e.g., using a fan), between indoors and outdoors, has been recognized as a simple and efficient way to characterize the global airtightness of a building, e.g., [
20]. The philosophy of the method is based on the rule that a leakier building requires higher airflow rates to pressurize the building to a certain level (e.g., 50 Pa), whereas a tighter building requires lower flow rates [
48]. The so-called “standard test method for determining air leakage rate by fan pressurization” is described in ASTM Standard E779 [
49] and has been widely employed by many national building regulations as a reference tool. The pressurization results at 50 Pa for the single-compartment building (Scenario S
1) are shown in the
Figure 3 and are compared to the relevant requirements as described in the current Norwegian Building Regulation TEK 10 [
50]. The building simulated seems that it would fulfill the airtightness criteria as set for steady-state pressurization conditions,
i.e.,
n50 ≤ 1.5 h
−1 or
n50,small ≤ 2.5 h
−1 for small houses). The CFD pressurization results vary with the leakage distribution ratio α because a change of the magnitude of the leakage area cause a change of the flow conditions (flow exponent, flow coefficient), resulting in a slightly different flow rate.
Figure 3.
The maximum allowed air exchanges per hour (ACH) at 50 Pa pressure difference for different kinds of buildings and the respective result from the CFD-simulated pressurization situation for the building-model of this study.
Figure 3.
The maximum allowed air exchanges per hour (ACH) at 50 Pa pressure difference for different kinds of buildings and the respective result from the CFD-simulated pressurization situation for the building-model of this study.
4. Results and Discussion
The equivalent air change rates ΣACH against the leakage ratio α for the scenarios S
1, S
2, S
3, S
4 and S
5 are shown in
Figure 4,
Figure 5,
Figure 6. In each graph, two lines appear, representing the rates under high and low wind gust frequency. The solid line shows the variation of the air exchanges because of the high frequency Ω
high, while the dashed one represents the cases under the low frequency Ω
low. It would be reasonable to claim that the gust frequency of the wind has a significant role, altering the infiltration rates of a building in operation. In addition, the leakage distribution seems that could potentially cause large differences in the ACH of an enclosure.
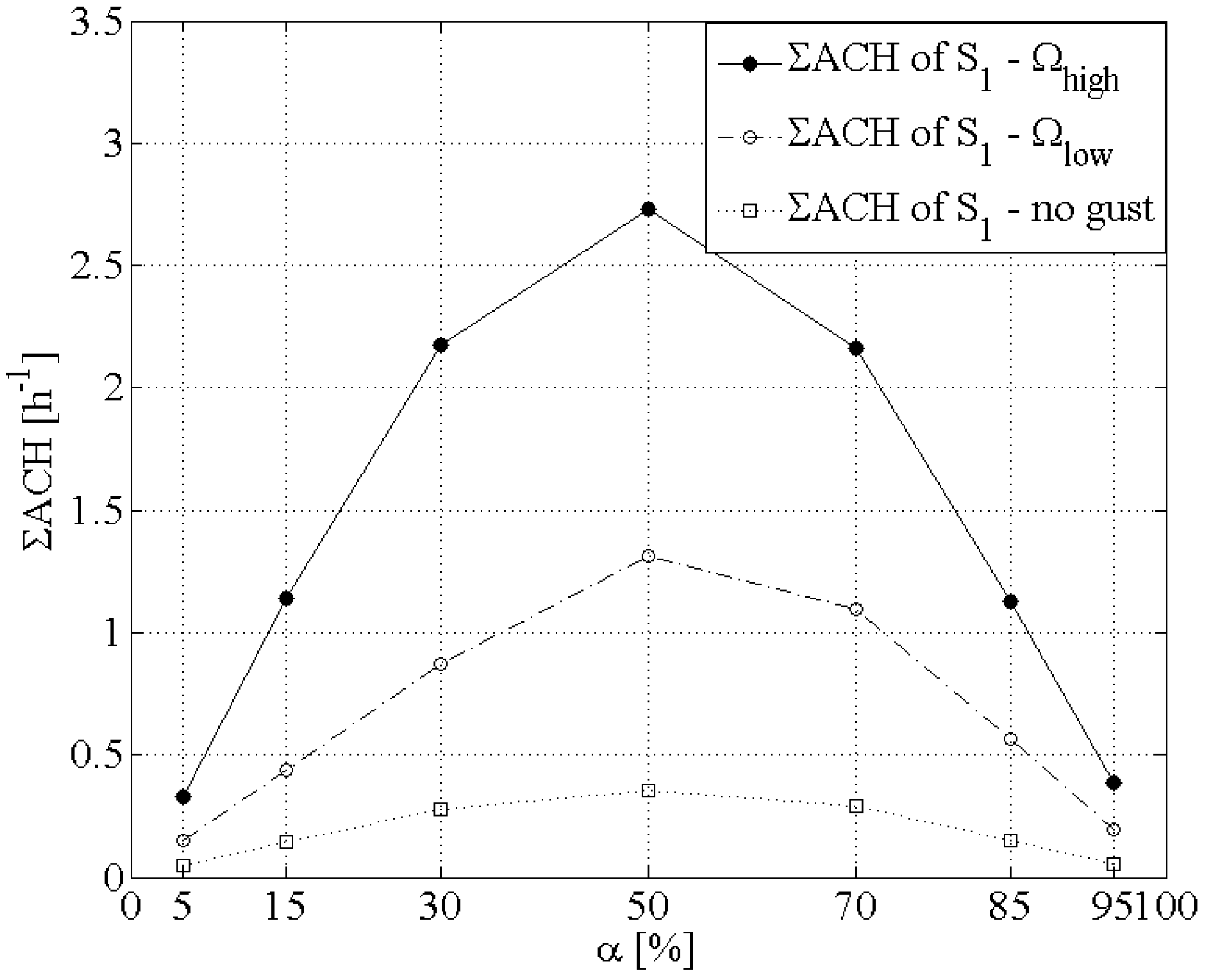
Figure 4.
The equivalent air change rate ΣACH respect to the leakage distribution α for the scenario of the single-room building (no partition wall, Scenario S1).
Figure 4.
The equivalent air change rate ΣACH respect to the leakage distribution α for the scenario of the single-room building (no partition wall, Scenario S1).
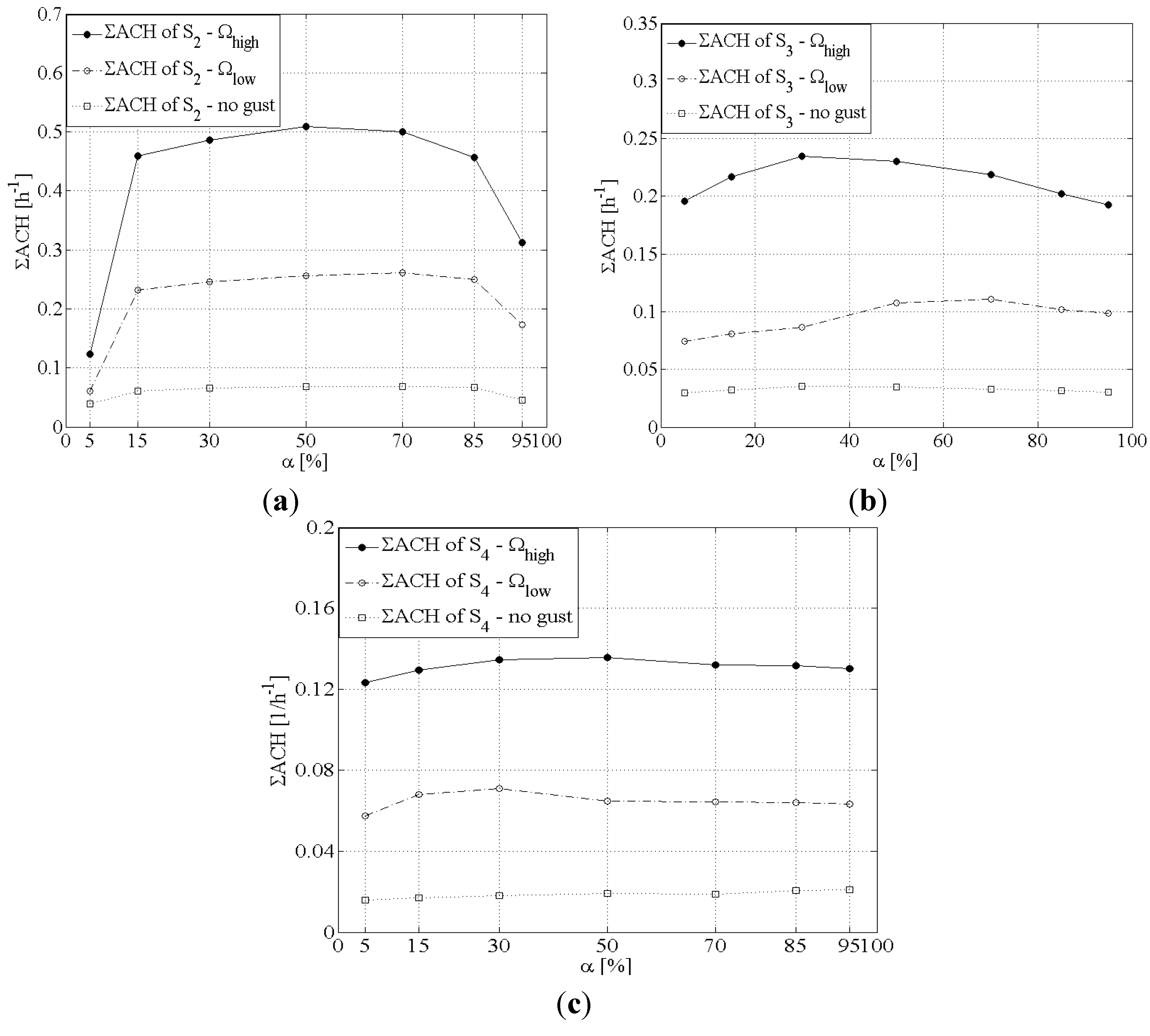
Figure 5.
The equivalent air change rate ΣACH respect to the leakage distribution α for the scenarios of compartmentalized volume and internal leakages on the partition wall. (a) 8 cm2 (Scenario S2); (b) 4 cm2 (Scenario S3); and (c) 2 cm2 (Scenario S4).
Figure 5.
The equivalent air change rate ΣACH respect to the leakage distribution α for the scenarios of compartmentalized volume and internal leakages on the partition wall. (a) 8 cm2 (Scenario S2); (b) 4 cm2 (Scenario S3); and (c) 2 cm2 (Scenario S4).
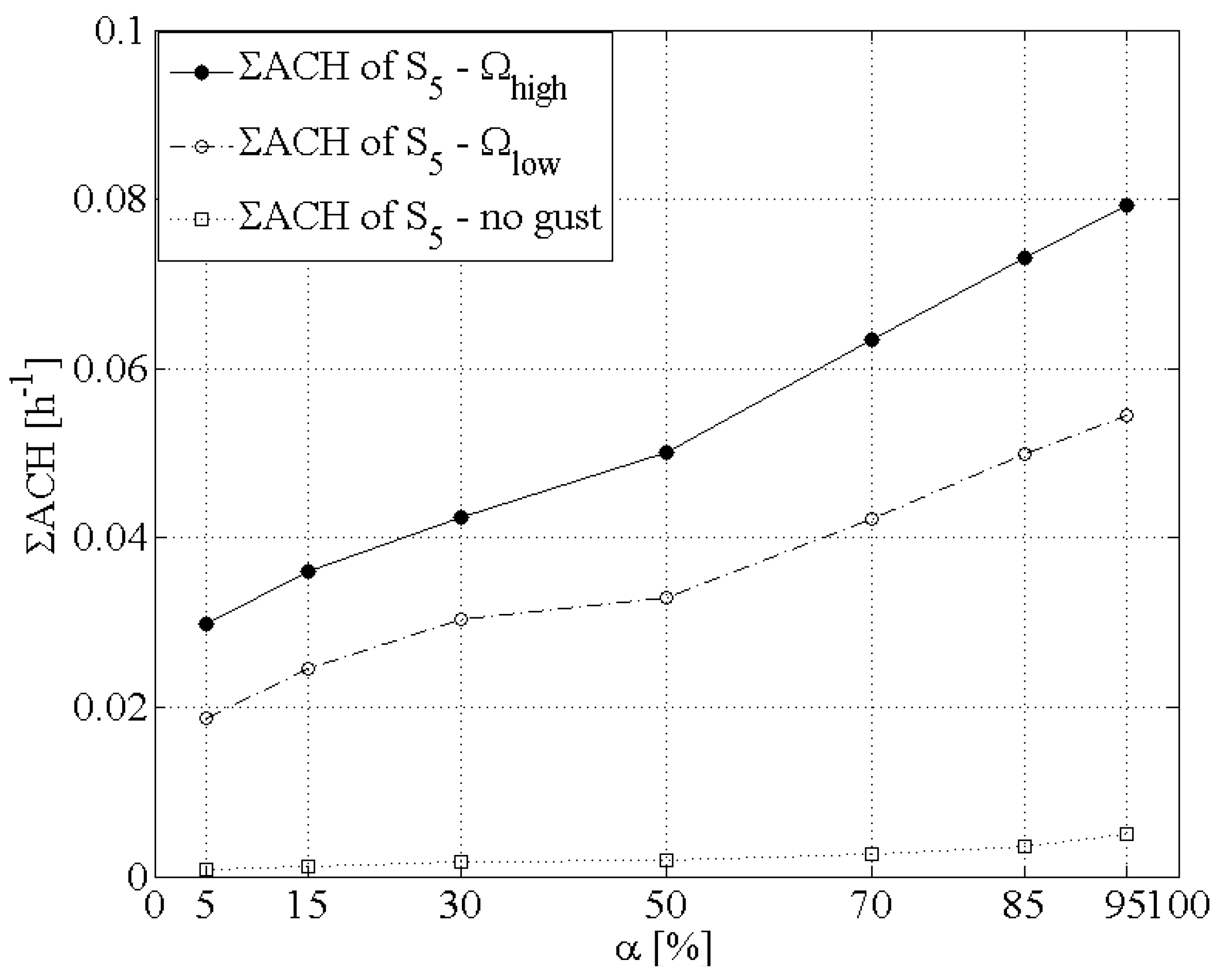
Figure 6.
The ΣACH of the two rooms for Scenario S5, when separated by a totally tight (impermeable) partition wall.
Figure 6.
The ΣACH of the two rooms for Scenario S5, when separated by a totally tight (impermeable) partition wall.
4.1. Single-Compartment Building—Internal Volume without Partition Wall (Scenario S1)
Employing the assumption that the internal volume is single-spaced,
Figure 4 shows that the infiltration rates are the highest among the cases studied. The absence of a partition wall leads to a strong air circulation within the one-room-enclosure. This “cross-ventilation” becomes even more dominant when the leakages are equally distributed on the two sides normal to the wind direction (windward and leeward),
i.e., α = 50%. For both the high and low gust frequency, the ACH takes the highest value when α = 50%. In particular, for the Ω
high the ACH is 2.73 h
−1, while for the low frequency Ω
low the rates are 1.31 h
−1. For the steady state conditions, the maximum ACH is 0.35 h
−1. In contrast, the air exchange rates appear to have the lowest values when the external leakages are located either on the windward (α = 95%) or on the leeward facade of the building (α = 5%). Again, the ΣACH increases in respect to the ratio α until it reaches the maximum value for α = 50% (5% ≤ α ≤ 50%) and then it is getting lower as α increases more (50% ≤ α ≤ 95%). The picture is similar for the steady state conditions (
Figure 4), but in this case the variation is clearly smaller. The role of the inertia forces of the mass of the enclosure appears to be, in general, weak in the scenario S
1. Employing the analogy between the air flow in the “enclosure” and a pneumatic spring system and based on the relatively high ACH rates, it would be reasonable to claim that the damping is relatively low. Nevertheless, based on the fairly symmetric picture of the
Figure 4, it could be extracted that the damping effect is growing more important when the leakages are mostly located either on the windward or on the leeward side, leading to a reduction of the actual infiltration rates. In those cases, the model behavior is getting more similar to the single-side-infiltration case. The results are consistent with the theoretical study of Etheridge on purpose-designed naturally ventilated buildings [
32]. Based on his mathematical model, the effects on the inertia and compressibility are inversely proportional to gust duration and, for a given gust strength, these effects will be more apparent for a gust with a higher amplitude and lower duration.
Moreover,
Figure 4 shows the significant impact of the wind unsteadiness on the air exchanges. The higher gust frequency Ω
high (0.5 Hz) results in higher equivalent air change rates ΣACH compared to the lower one (0.1 Hz) that was employed for this study. Again, when the period
T of the wind maxima (wind gusts) is reduced by five times (from
Tlow = 10 s to
Thigh = 2 s), the ACH increases.
Table 2 shows the impact of the increase of the wind gust frequency from 0.1 to 0.5 Hz on the ACH rates. In particular, for the scenario S
1, depending on how the leakages are distributed in the envelope, the rates alter in a range that varies between 97% (for α = 95%) and 160% (for α = 15%).
Table 2.
The increase of ΣACH for the different leakage-distribution cases when the gust frequency increases from 0.1 to 0.5 Hz.
Table 2.
The increase of ΣACH for the different leakage-distribution cases when the gust frequency increases from 0.1 to 0.5 Hz.
| Scenario | Increase of ΣACH |
|---|
| α = 5% | α = 15% | α = 30% | α = 50% | α = 70% | α = 85% | α = 95% |
|---|
| Scenario 1 | 119% | 160% | 150% | 108% | 97% | 99% | 97% |
| Scenario 2 | 103% | 98% | 97% | 99% | 91% | 82% | 80% |
| Scenario 3 | 163% | 170% | 171% | 114% | 98% | 98% | 96% |
| Scenario 4 | 114% | 90% | 90% | 109% | 104% | 105% | 105% |
| Scenario 5 | 59% | 47% | 40% | 52% | 50% | 46% | 46% |
The results show that the leakage distribution can cause large variations in ACH rates, especially under unsteady wind conditions.
Table 3 shows the standard deviation σ of the ΣACH for the five enclosure-scenarios studied under the two gust frequencies employed. In the Scenario S
1, the standard deviation is high, as σ = 0.936 and σ = 0.446 for the Ω
high and Ω
low, respectively, implying the important influence of the leakage distribution on the air exchange rates of a building in operation. Especially for the high gust frequency, it would be reasonable to claim that the leakage distribution raises an uncertainty issue for the estimation of the realistic infiltration rates of a building.
Table 3.
The standard deviation σ of ΣACH and the respective arithmetic mean when the ACH is considered in respect to the leakage distribution α.
Table 3.
The standard deviation σ of ΣACH and the respective arithmetic mean when the ACH is considered in respect to the leakage distribution α.
| Scenario | Standard Deviation σ (and the Arithmetic Mean) of ΣACH |
|---|
| Ωhigh | Ωlow | No Gust |
|---|
| Scenario 1 | 0.936 (1.435) | 0.446 (0.661) | 0.121 (0.188) |
| Scenario 2 | 0.141 (0.406) | 0.073 (0.211) | 0.012 (0.059) |
| Scenario 3 | 0.017 (0.213) | 0.014 (0.094) | 0.002 (0.032) |
| Scenario 4 | 0.004 (0.131) | 0.004 (0.065) | 0.002 (0.019) |
| Scenario 5 | 0.019 (0.053) | 0.013 (0.036) | 0.001 (0.002) |
4.2. Building with Partition Wall with Internal Leakages (Scenarios S2, S3 and S4)
Starting with Scenario S
2, all the cases presented hereinafter refer to a model in which a partition wall has been added. In total, there are four scenarios with compartmentalized models. In particular, in three of them (S
2, S
3 and S
4), internal leakages have been assumed on the partition wall. In
Figure 5a–c, the equivalent air change rates ΣACH for the Scenarios S
2, S
3 and S
4 are shown in respect to the leakage distribution ratio α.
It would be reasonable to claim that the existence of a relatively tight partition wall has a drastic impact (drop) on the air change rates (
Figure 5a–c). The ΣACH appear (for both the gust frequencies Ω
high and Ω
low) to be much lower compared to Scenario S
1). Although a “cross ventilation” takes place even in those cases (in analogy to S
1), the level of tightness of the wall in combination with the inertia forces of the mass of the internal volume increases the damping, resulting in significantly lower infiltration rates. Nevertheless, the impact of the wind gust frequency is important (as in Scenario S
1) in all the cases presented in this section (
Table 2). However, in general, the leakage distribution affects less the air exchanges in those three scenarios compared to Scenario S
1 (
Table 3).
As mentioned above, the partition wall and the compartmentalization of the initial enclosure reduces dramatically the ACH. Scenario S
2 represents the model with a partition wall on which internal leakages of 8 cm
2 have been simulated. The rates have been calculated as ΣACH = 0.51 h
−1 and ΣACH = 0.26 h
−1 for the Ω
high and the Ω
low, respectively, while for the steady state no-gust conditions ΣACH = 0.07 h
−1 (
Figure 5a). This corresponds to approximately a five-fold drop compared to the respective rates in Scenario S
1. The maximum values occur when α = 50% and α = 70% for the high and low gust frequencies, respectively. The internal leakages result in a similar symmetrical picture regarding the equivalent air exchanges; the lowest values of ΣACH occur when the external leakages are concentrated either on the windward or on the leeward facade of the building (α = 95% or α = 5%, respectively). However, the standard deviation is much smaller in this case, implying a more “mild” impact of the leakage distribution on the ACH (
Table 3). Especially, if the extreme sub-cases of α = 95% or α = 5% are excluded (
Figure 5a), the air infiltration rates vary relatively small in respect to the ratio α. In contrast, the influence of the wind gust frequency remains significant, as the change from 0.1 to 0.5 Hz results in an increase of ACH that increases from 80% (for α = 95%) to 103% (for α = 5%) (
Table 2).
A further reduction of the internal leakages on the partition wall results in an even larger drop of the ACH. In Scenario S
3 the internal leakages have been scaled down to 4 cm
2, half than in the previous Scenario S
2. Now the maximum values of the rates have been calculated as ΣACH = 0.23 h
−1 and ΣACH = 0.11 h
−1 for the Ω
high and the Ω
low, respectively, and ΣACH = 0.03 h
−1 for the no-gust wind conditions (
Figure 5b). The impact of the leakage distribution is getting even smaller in Scenario S
3, as shown in
Table 3. However, the influence of the gust frequency seems to be very important (
Table 2).
Finally, by controlling the internal leakages even more and reducing them to 2 cm
2, a further reduction of the ACH is achievable. In particular, in Scenario S
4, the maximum infiltration rates are ΣACH = 0.14 h
−1 and ΣACH = 0.07 h
−1 for the Ω
high and the Ω
low, respectively, while ΣACH = 0.02 h
−1 for the steady state conditions (
Figure 5c). The results appear to be quite “uniform” in respect to the leakage distribution ratio α, as reflected on the standard deviation σ, which is small for both the high and the low wind gust frequency (
Table 3). Under steady state conditions, the leakage distribution does not significantly alter the air exchanges, especially in Scenarios S
3 and S
4. Based on
Table 3, the standard deviation σ for the no-gust wind conditions is very small, showing that it is of no consequence whether the larger leakage area occurs on the windward or on the leeward side. These findings are in agreement with a study presented by Etheridge [
34]. Even for Scenario S
2, the infiltration rates do not vary significantly. An exception can be reported for the extreme cases of α = 95% and α = 5%, which are very close to a single-side ventilation situation and, hence, it is not now only the pressure difference between windward and leeward side that matters but also the absolute magnitude on each side.
In contrast, the frequency affects the air exchanges, as there is an increase in the ACH that increases from 96% to 114% when the frequency switches from 0.1 to 0.5 Hz. Under mild wind gust frequency conditions, the relatively tight partition element could potentially result in low air change rates. Thus, internal leakages and wind gust frequency seem to be critical parameters for the estimation of the operational wind-driven infiltration rates of a building.
4.3. Building with Impermeable Partition—Partition Wall without Internal Leakages (Scenario S5)
The role of the internal leakages on the air exchange rates estimation becomes even clearer in Scenario S
5. In this case, a hypothesis of a totally tight partition wall is employed. In
Figure 6, the calculated air exchanges over one hour are shown for the high and low wind gust frequency as well as for the steady state conditions. Controlling the internal leakages and assuming that the partition wall is completely tight, the air change rates become even lower compared to all the previous scenarios presented in the paper. The highest values are now ΣACH = 0.08 h
−1 and ΣACH = 0.05 h
−1 for the Ω
high and the Ω
low, respectively, while for the no-gust steady state conditions ΣACH = 0.005 h
−1 (
Figure 6). The impact of the gust frequency is now moderate in this scenario. As shown in
Table 2, the increase in the ACH varies between 40% and 59%, when the frequency alters from 0.1 to 0.5 Hz. The results are consistent with the airflow spectra of Haghighat
et al. [
33] showing that in a single-side infiltration case, a higher frequency might be necessary to cause a certain level of airflow that is possible with a lower frequency in a two “openings” scenario.
The rates increase in respect to the leakage distribution ratio α, so that the maximum values of ACH take place when the leakages are mostly located on the windward facade of the model (α = 95%). The latter is reflected in the standard deviations σ of the rates, which are higher than the respective ones in Scenario S
4 and fairly equal to those of Scenario S
3 (
Table 3).
The tight partition wall results in the total compartmentalization of the volume into two spaces. The inertia forces of the mass of the windward “room” are in this case higher because of the single-side infiltration and the compressibility of the volume decreases. The second “room” has gotten “isolated” in this case, so there is not significant air exchange through the leeward leakages. The combination of those facts leads to the dramatic drop of the rates as shown in the
Figure 6.
If the leakages are mostly located on the leeward facade or even equally distributed between the windward and the leeward side of the building, the operational air is exchanged, especially under the low gust frequency Ω
low. Nevertheless, even for the Ω
high the infiltration rates are now lower, implying that a high control of internal leakages can significantly contribute to eliminating the impact of the gust frequency. According to Jones
et al. [
42] assuming impermeable partition elements between dwellings (floor, ceiling and side walls) leads to higher estimated infiltration rates compared to when these elements are permeable. Their results are logical, because they show that the typical “cross ventilation” situation when assuming leakages only on the windward and leeward side is getting “disturbed” (and the airflow deviated) by the permeability of the partition elements resulting in smaller air exchanges through the leakages on the windward and the leeward sides. However, their findings cannot be straightforward comparable to the current study, as in the latter, the upper, lower and side elements are assumed to be completely tight in all the scenarios and only the airflow in the axis windward-leeward side is under investigation. A further extension of the current study in order to include internal leakages on more than one wall, different possible airflow patterns within an enclosure and leakages distributed on more elements than the ones normal to the wind direction would provide a more holistic perspective of infiltration rates and their connection with the internal leakage paths.
Finally,
Table 4 summarizes the highest and lowest values of the infiltration rates for the high wind gust frequency Ω
high, the low frequency Ω
low and the no-gust steady state conditions, in all the scenarios of compartmentalization/partition-wall-permeability. The values of the leakage distribution ratio α to that of when the max and min values occur are given in parenthesis.
Table 4.
The max and min values of ΣACH for Ωhigh, Ωlow and the steady state conditions.
Table 4.
The max and min values of ΣACH for Ωhigh, Ωlow and the steady state conditions.
| max and min ΣACH |
|---|
| Scenario | Ωhigh | Ωlow | Steady state, no gust |
|---|
| max | min | max | min | max | min |
|---|
| Scenario 1 | 2.73 (50%) | 0.33 (5%) | 1.31 (50%) | 0.15 (5%) | 0.35 (50%) | 0.05 (5%) |
| Scenario 2 | 0.51 (50%) | 0.12 (5%) | 0.26 (70%) | 0.06 (5%) | 0.07 (50%) | 0.04 (5%) |
| Scenario 3 | 0.23 (30%) | 0.19 (95%) | 0.11 (70%) | 0.07 (5%) | 0.04 (30%) | 0.03 (5%) |
| Scenario 4 | 0.14 (50%) | 0.12 (5%) | 0.07 (95%) | 0.06 (5%) | 0.02 (95%) | 0.015 (5%) |
| Scenario 5 | 0.08 (95%) | 0.03 (5%) | 0.05 (95%) | 0.02 (5%) | 0.005 (95%) | 0.001 (5%) |
5. Conclusions
A low rise building with variable leakage areas on the windward and the leeward side was simulated and studied numerically under unsteady wind conditions. The wind-driven infiltration rates under two different wind gust frequencies were calculated and compared to steady state conditions. The gust frequency seems to be a critical parameter, as it results in an increase of air exchanges of a building in operation.
The leakage distribution affects the infiltration rates especially in the single-compartment scenario, where strong cross “ventilation” takes place. The most severe situation appears when the leakage areas on the windward and the leeward facade are of the same magnitude of order. Again, the more equal the leakages are, the higher the distribution of air exchanges.
The existence of relatively tight internal walls in a double-compartment building decreases drastically the infiltration rates, compared to the single-space model. In particular, controlling the internal leakages, the drop of the ACH becomes significant, resulting in rates that could be considered as “acceptable” in a building-regulations context. In those cases, the influence of the gust frequency is still very important, while the role of the leakage distribution is moderate. By creating more tightness in the partition wall, the ACH decreases even more, constraining the impact of the gust frequency.
Leakage distribution creates uncertainty in the estimation of wind-driven infiltration. In addition, the wind gust frequency causes significant variations in the ACH of a building in operation. The paper also highlights that the control of the internal leakages should be a parameter more deeply studied. In decreasing the infiltration rates, the “component” of the internal leakage paths should also be considered as important, as well as the leakages of the envelope. Furthermore, fulfilling a sufficient airtightness level of the internal building elements could also moderate the impact of wind gust frequency.
The study raises issues regarding uncontrolled leakages in the building envelope. The detection of leakages and their distribution ought to be considered as critical factors, while wind unsteadiness results in significant variations in wind-driven infiltration. Furthermore, internal leakages seem to play an important role in the nearly zero-energy building target. Further research needs to be done in order to investigate the connection between internal and external leakages in a more detailed way.


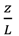 vanish.
vanish.