Evaluation of Rotation Capacity and Bauschinger Effect Coefficient of I-Shaped Beams Considering Loading Protocol Influences
Abstract
:1. Introduction
2. Cyclic Loading Tests on I-Shaped Steel Beams with Different Flange Width-to-Thickness Ratios, Shear Span Ratios, and Loading Histories
2.1. Outline of Experiment on I-Beams
2.2. Plastic Deformation Characteristics of I-Beam with Different Loading Protocols
2.3. Influence of Loading Protocols on Cyclic Behavior of I-Beams
3. Rotation Capacity and Energy Dissipation Capacity of I-Beams That Failed Due to Local Buckling under Different Loading Protocols
3.1. Parameters of Experiment
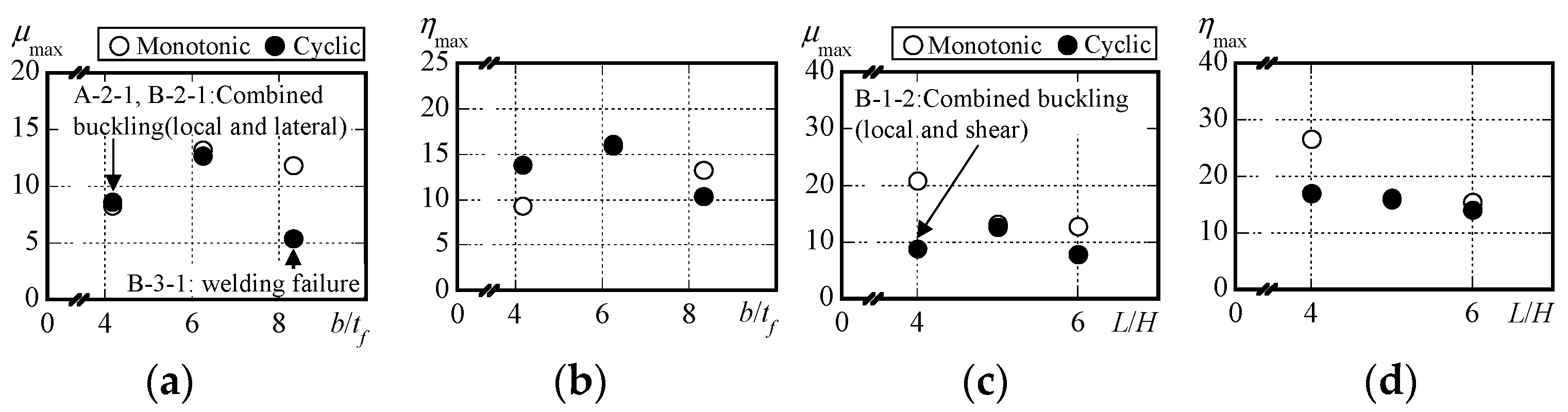
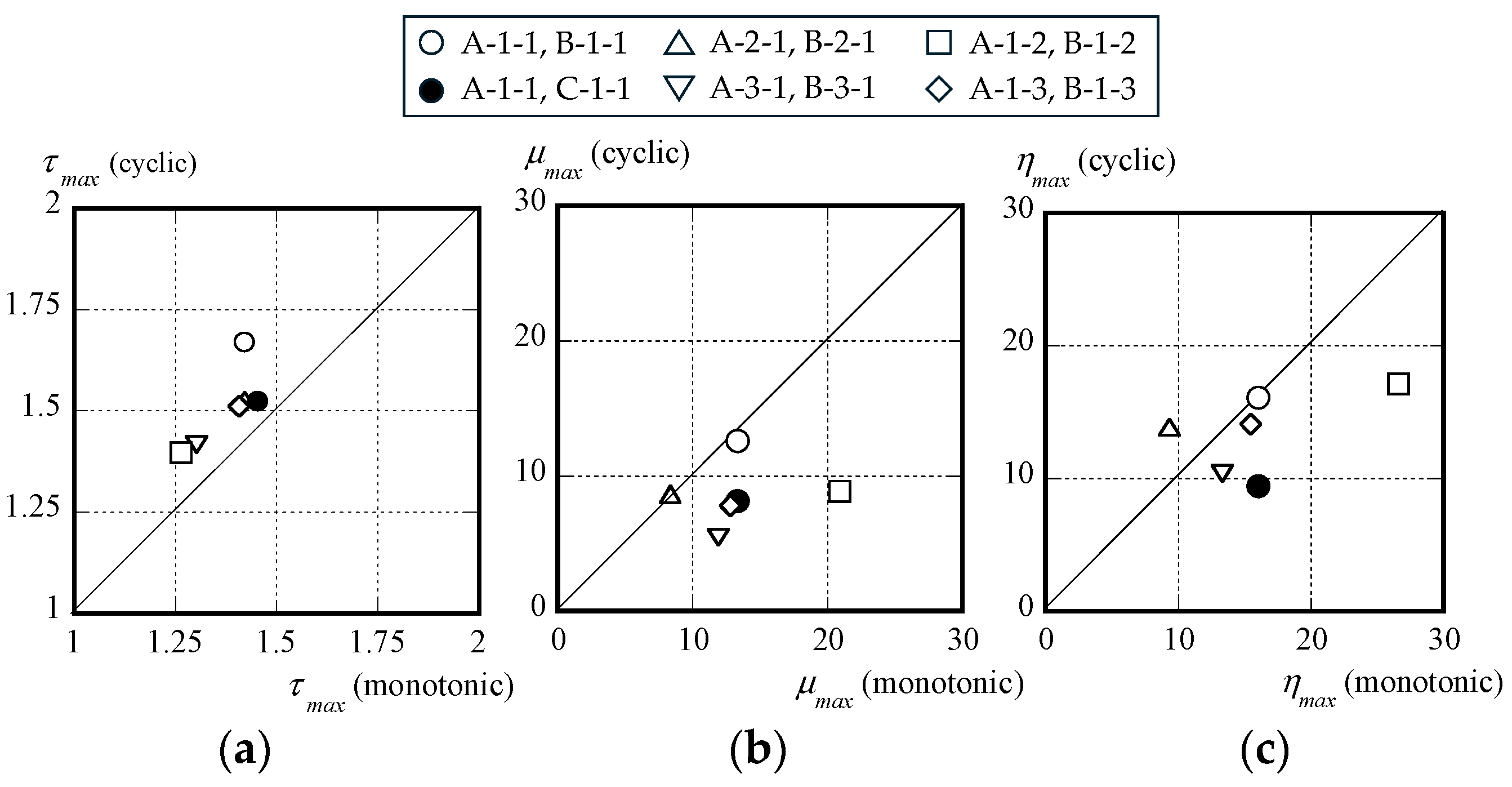
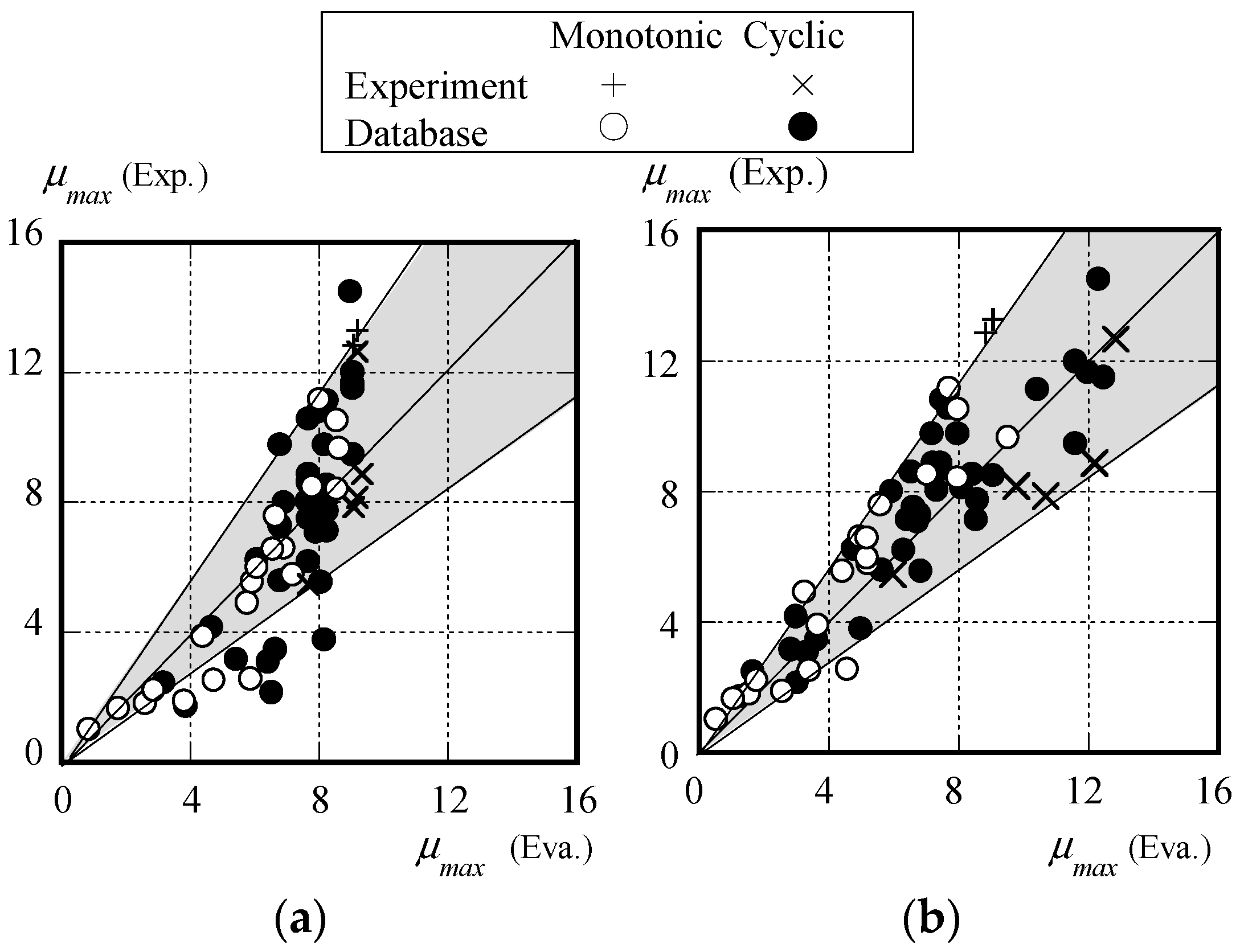
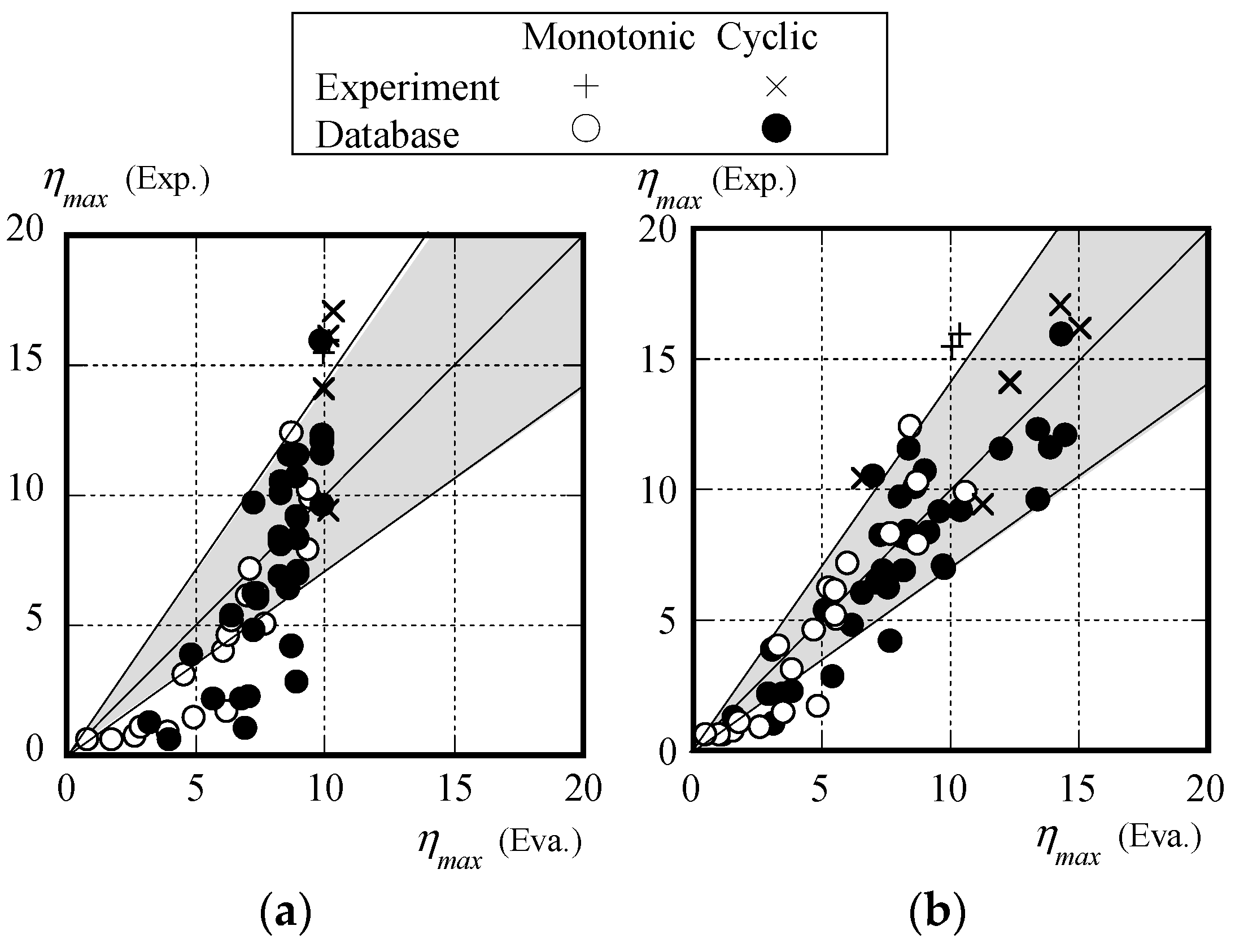
3.2. Rotation Capacity, Ultimate Strength Ratio, and Energy Dissipation Capacity of I-Beams with Different Loading Protocols
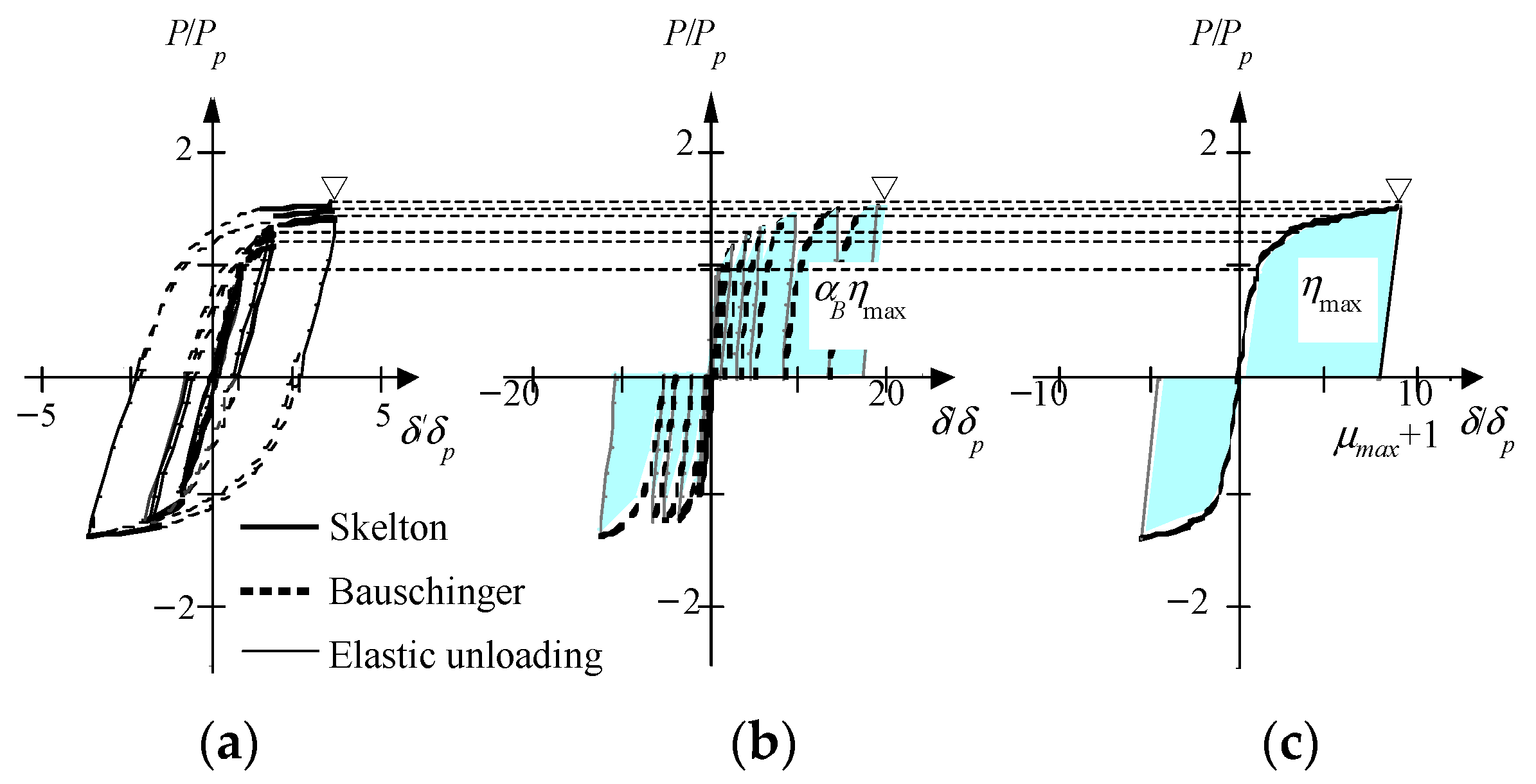
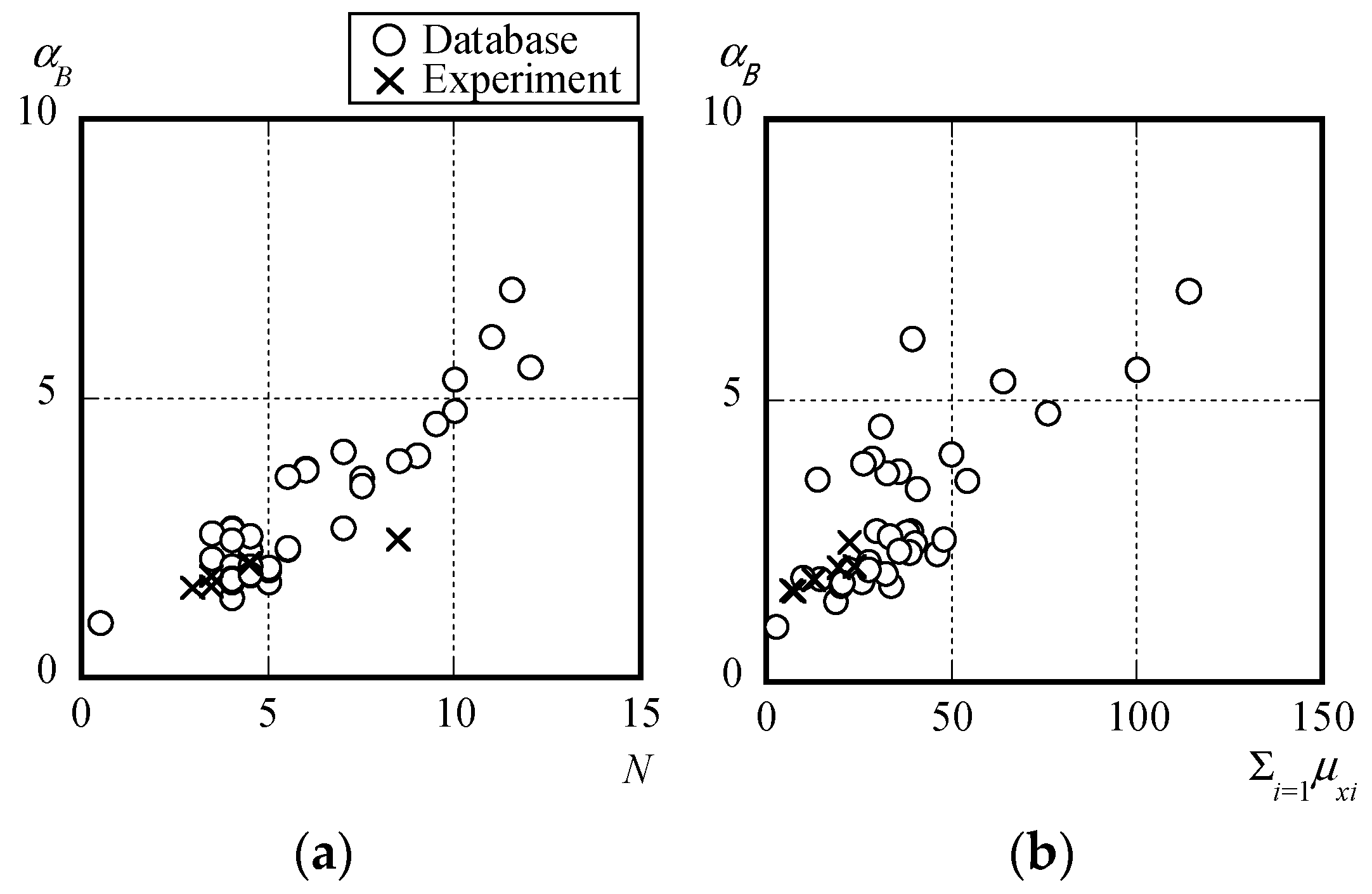
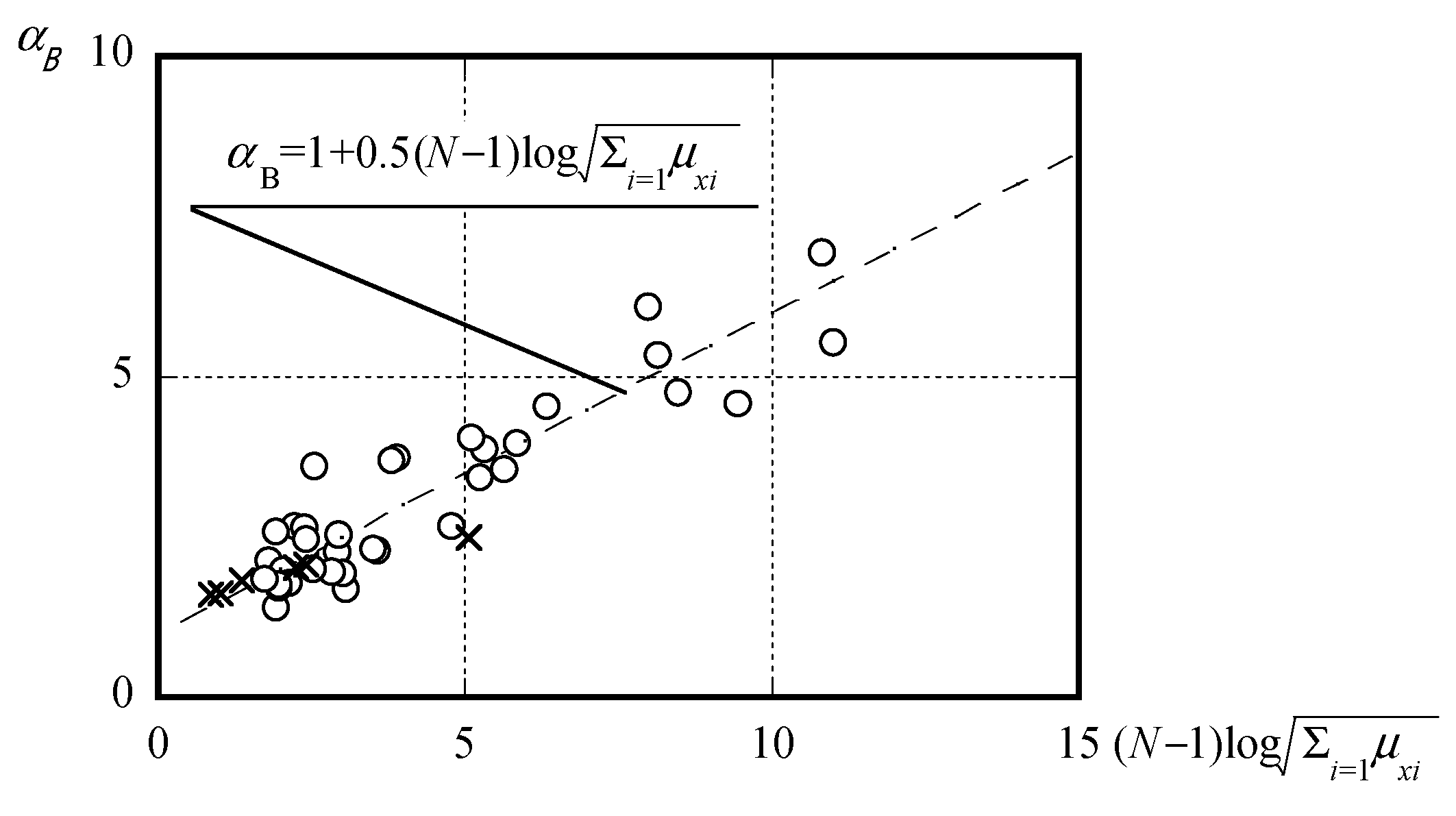
3.3. Influence of Bauschinger Effect Coefficient of I-Beams That Failed Due to Local Buckling under Cyclic Loading
4. Conclusion
- (1)
- When subjected to cyclic loading at the same amplitude in the plastic region where local buckling occurs in I-beams, it was confirmed that the strain values increase and plasticization progresses as the number of cycles increase. When subjected to cyclic loading, the rotation capacity and energy dissipation capacity obtained from the experimental results decrease with increasing cycles at the same amplitude in the skeleton curve.
- (2)
- For specimens of the same cross-section and length subjected to monotonic and cyclic loading, the rotation capacity and energy dissipation capacity are higher under monotonic loading if local buckling occurs.
- (3)
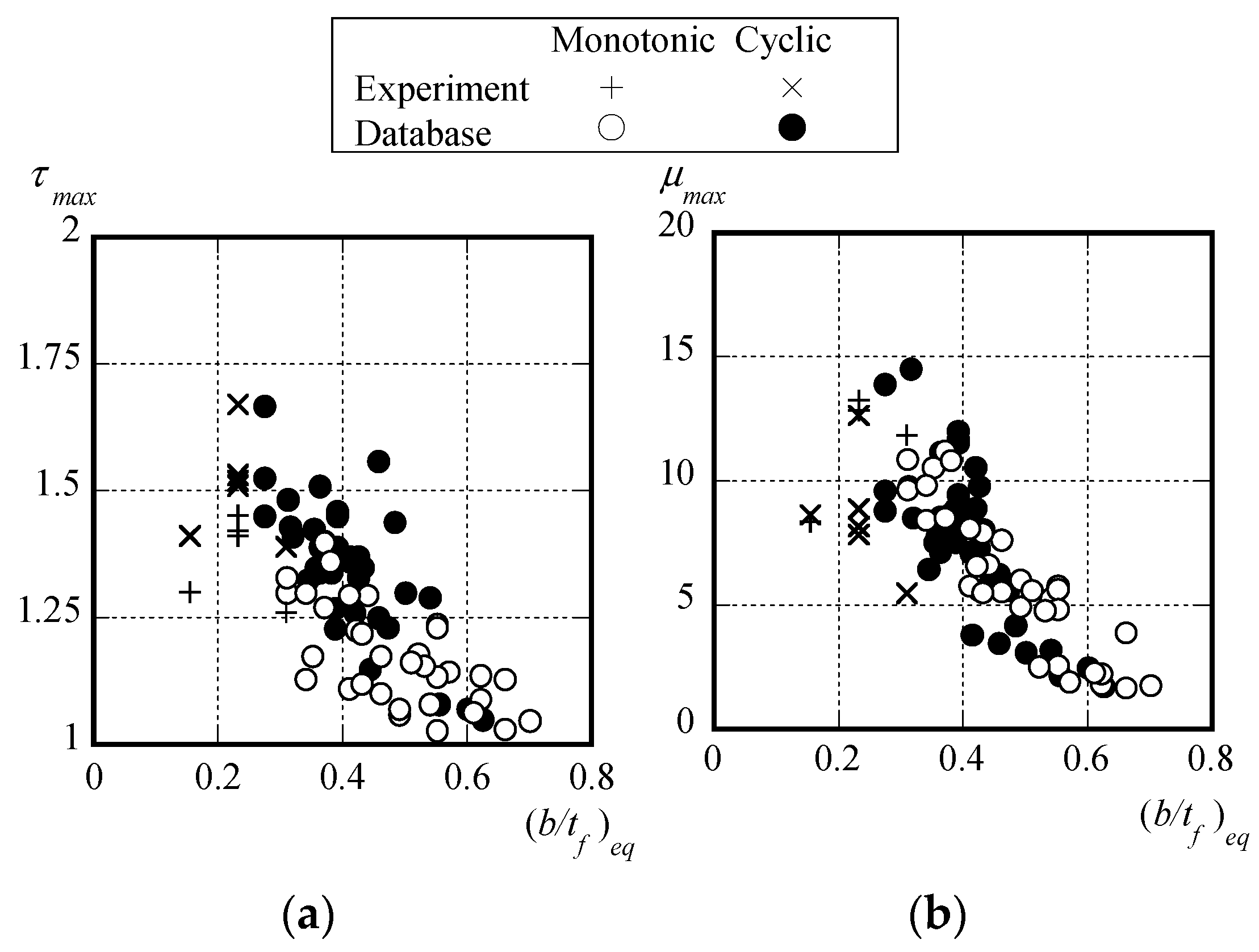
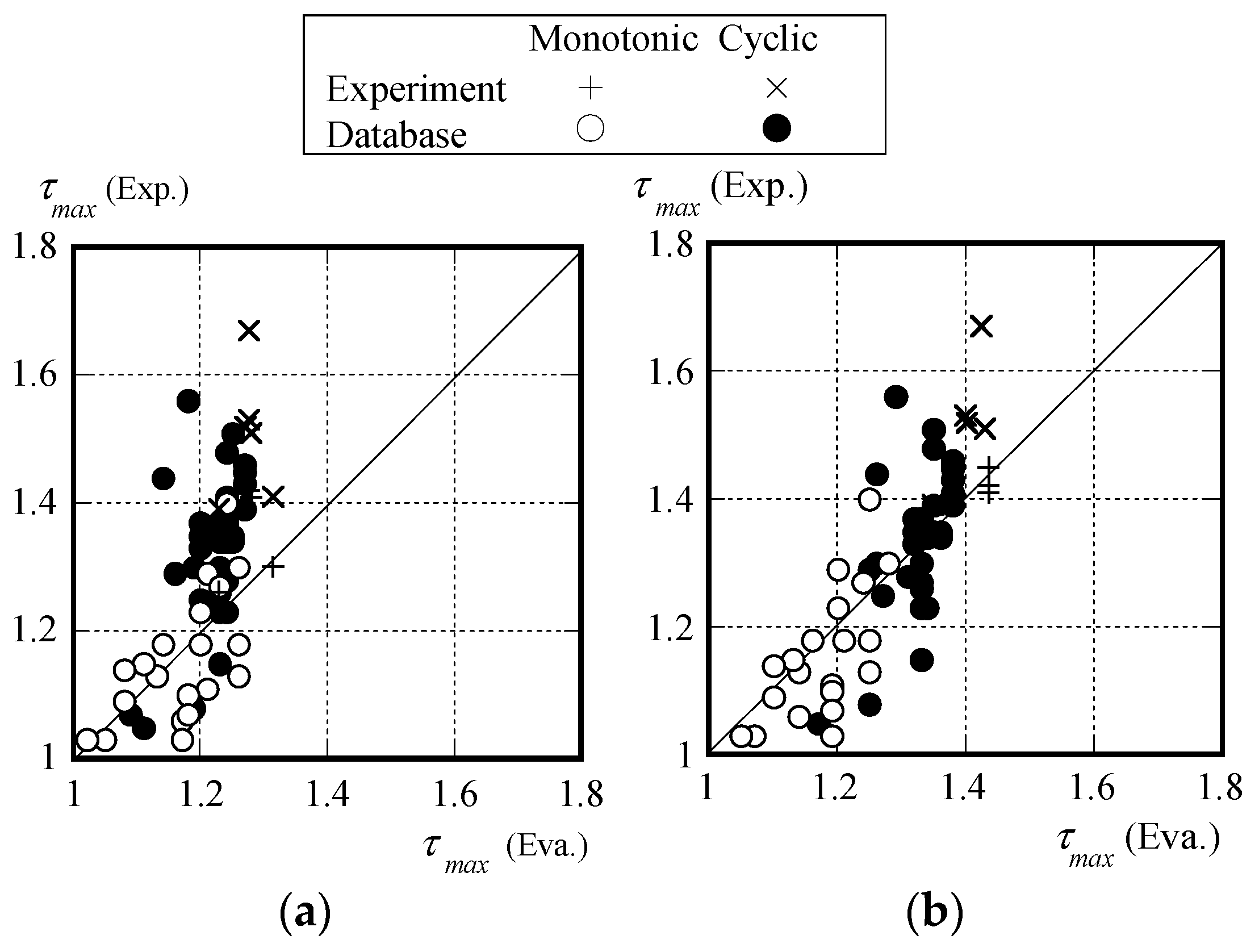
- In the previous experimental equation, particularly in the case of cyclic loading, there are significant errors in the maximum load, rotation capacity, and energy dissipation capacity. On the other hand, the experimental equations proposed in this paper (Equations (7)–(9)) can generally evaluate the ultimate strength ratio, rotation capacity, and energy dissipation capacity regardless of the loading type.
- (4)
- The Bauschinger effect coefficient increases with a more significant number of loading cycles and larger loading amplitudes, and its value can be evaluated using Equation (10). Moreover, hysteretic energy dissipation under cyclic loading can be assessed using Equations (9) and (10).
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Section | L | b/tf | d/tw | L/H | τmax | μmax | ηmax | N | Σμxi | Refs. |
|---|---|---|---|---|---|---|---|---|---|---|
| H-330 × 150 × 4.5 × 9 | 1260 | 8.3 | 69.3 | 3.8 | 1.29 | 3.21 | 2.24 | 11 | 39.07 | [78] |
| H-330 × 150 × 4.5 × 9 | 1266 | 8.3 | 69.3 | 3.8 | 1.05 | 1.76 | 0.68 | 5.5 | 13.34 | [78] |
| H-250 × 150 × 4.5 × 9 | 1496 | 8.3 | 51.6 | 6.0 | 1.25 | 3.5 | 2.33 | 9.5 | 30.49 | [80] |
| H-250 × 150 × 4.5 × 12 | 1492 | 6.3 | 50.2 | 6.0 | 1.28 | 3.83 | 2.89 | 9 | 28.53 | [80] |
| H-250 × 150 × 4.5 × 9 | 1497 | 8.3 | 51.6 | 6.0 | 1.3 | 3.13 | 2.22 | 8.5 | 25.91 | [80] |
| H-250 × 150 × 4.5 × 9 | 1499 | 8.3 | 51.6 | 6.0 | 1.08 | 2.2 | 1.11 | 4.5 | 9.76 | [80] |
| H-200 × 150 × 6 × 9 | 900 | 8.3 | 30.3 | 4.5 | 1.35 | 7.16 | 7.12 | 7 | 49.89 | [81] |
| H-200 × 150 × 6 × 9 | 900 | 8.3 | 30.3 | 4.5 | 1.34 | 11.17 | 11.62 | 11.5 | 113.84 | [81] |
| H-200 × 150 × 6 × 9 | 900 | 8.3 | 30.3 | 4.5 | 1.51 | 8.58 | 9.18 | 5.5 | 38.24 | [81] |
| H-200 × 150 × 6 × 9 | 900 | 8.3 | 30.3 | 4.5 | 1.39 | 8.17 | 8.4 | 5.5 | 35.4 | [81] |
| H-500 × 200 × 9 × 19 | 2400 | 5.3 | 51.3 | 4.8 | 1.23 | 5.6 | 4.23 | 27 | 130.71 | [82] |
| H-450 × 200 × 9 × 12 | 1850 | 8.3 | 47.3 | 4.1 | 1.37 | 5.63 | 4.87 | 7.5 | 40.66 | [83] |
| H-450 × 200 × 9 × 12 | 1850 | 8.3 | 47.3 | 4.1 | 1.35 | 9.82 | 9.78 | 12 | 99.8 | [83] |
| H-450 × 200 × 9 × 12 | 1850 | 8.3 | 47.3 | 4.1 | 1.33 | 7.31 | 6.3 | 10 | 75.72 | [83] |
| H-506 × 201 × 11 × 19 | 1800 | 5.3 | 42.5 | 3.6 | 1.35 | 7.77 | 7.05 | 4 | 29.42 | [84] |
| H-300 × 130 × 6 × 12 | 1200 | 5.4 | 46.0 | 4.0 | 1.45 | 12.03 | 12.35 | 4 | 37.78 | [85] |
| H-300 × 130 × 6 × 12 | 1200 | 5.4 | 46.0 | 4.0 | 1.45 | 11.54 | 12.15 | 4.5 | 47.62 | [85] |
| H-300 × 130 × 6 × 12 | 1200 | 5.4 | 46.0 | 4.0 | 1.39 | 9.5 | 9.69 | 3.5 | 33.05 | [85] |
| H-300 × 130 × 6 × 12 | 1200 | 5.4 | 46.0 | 4.0 | 1.46 | 11.69 | 11.66 | 4 | 39.85 | [85] |
| H-300 × 100 × 9 × 9 | 1200 | 5.6 | 31.3 | 4.0 | 1.41 | 8.52 | 9.24 | 7 | 38.84 | [86] |
| H-300 × 100 × 6 × 6 | 1200 | 8.3 | 48.0 | 4.0 | 1.44 | 4.2 | 3.9 | 4.5 | 14.18 | [86] |
| H-488 × 300 × 11 × 18 | 2150 | 8.3 | 41.1 | 4.4 | 1.56 | 6.26 | 5.41 | 10 | 63.67 | [87] |
| H-600 × 300 × 12 × 22 | 3125 | 6.8 | 46.3 | 5.2 | 1.36 | 7.18 | 6.48 | 5 | 25.28 | [88] |
| H-600 × 300 × 12 × 22 | 3125 | 6.8 | 46.3 | 5.2 | 1.37 | 7.12 | 6.64 | 4 | 22.16 | [88] |
| H-450 × 150 × 9 × 12 | 1425 | 6.3 | 47.3 | 3.2 | 1.35 | 8.06 | 6.08 | 6 | 32.4 | [89] |
| H-250 × 125 × 6 × 9 | 1375 | 6.9 | 38.7 | 5.5 | 1.48 | 9.82 | 10.76 | 6 | 35.5 | [90] |
| H-500 × 200 × 10 × 16 | 2168 | 6.3 | 46.8 | 4.3 | 1.34 | 10.85 | 11.59 | 7.5 | 53.87 | [91] |
| H-500 × 200 × 10 × 16 | 3150 | 6.3 | 46.8 | 6.3 | 1.3 | 10.59 | 10.15 | 5 | 33.56 | [92] |
| H-500 × 200 × 10 × 16 | 3150 | 6.3 | 46.8 | 6.3 | 1.26 | 8.9 | 8.15 | 5 | 31.85 | [92] |
| H-500 × 200 × 10 × 16 | 3150 | 6.3 | 46.8 | 6.3 | 1.15 | 6.24 | 10.57 | 4 | 18.45 | [92] |
| H-500 × 200 × 10 × 16 | 3175 | 6.3 | 46.8 | 6.4 | 1.37 | 8.7 | 8.44 | 4 | 25.51 | [93] |
| H-500 × 200 × 10 × 16 | 3175 | 6.3 | 46.8 | 6.4 | 1.23 | 8.92 | 8.28 | 4.5 | 27.27 | [93] |
| H-500 × 200 × 10 × 16 | 3175 | 6.3 | 46.8 | 6.4 | 1.27 | 8.65 | 8.3 | 4 | 19.91 | [93] |
| H-500 × 200 × 10 × 16 | 3175 | 6.3 | 46.8 | 6.4 | 1.27 | 7.56 | 6.96 | 4 | 20.38 | [93] |
| H-300 × 125 × 4.5 × 9 | 1200 | 6.9 | 62.7 | 4.0 | 1.29 | 6.65 | 6.3 | - | - | [94] |
| H-300 × 125 × 9 × 9 | 1200 | 6.9 | 31.3 | 4.0 | 1.3 | 9.69 | 9.94 | - | - | [94] |
| H-300 × 125 × 6 × 9 | 900 | 6.9 | 47 | 3.0 | 1.4 | 11.21 | 12.45 | - | - | [94] |
| H-300 × 125 × 6 × 9 | 1200 | 6.9 | 47 | 4.0 | 1.27 | 8.55 | 8.33 | - | - | [94] |
| H-180 × 144 × 6 × 9 | 1040 | 8.0 | 27 | 5.8 | 1.18 | 10.56 | 10.31 | - | - | [95] |
| H-180 × 180 × 6 × 9 | 1300 | 10.0 | 27 | 7.2 | 1.11 | 5.81 | 5.11 | - | - | [95] |
| H-180 × 216 × 6 × 9 | 1570 | 12.0 | 27 | 8.7 | 1.06 | 4.96 | 4.07 | - | - | [95] |
| H-180 × 144 × 6 × 9 | 1040 | 8.0 | 27 | 5.8 | 1.13 | 8.46 | 7.98 | - | - | [95] |
| H-300 × 180 × 6 × 9 | 1300 | 10.0 | 47 | 4.3 | 1.1 | 5.59 | 4.69 | - | - | [95] |
| H-420 × 144 × 6 × 9 | 1040 | 8.0 | 67 | 2.5 | 1.07 | 6.03 | 5.23 | - | - | [95] |
| H-420 × 144 × 6 × 9 | 1040 | 8.0 | 67 | 2.5 | 1.13 | 3.93 | 3.15 | - | - | [95] |
| H-300 × 144 × 6 × 9 | 1040 | 8.0 | 47 | 3.5 | 1.03 | 2.6 | 1.77 | - | - | [95] |
| H-270.5 × 108.5 × 4.23 × 5.57 | 1200 | 9.7 | 61.3 | 4.4 | 1.18 | 2.56 | 1.53 | - | - | [96] |
| H-269.6 × 144.3 × 4.23 × 5.57 | 1500 | 13.0 | 61.1 | 5.6 | 1.09 | 1.86 | 0.81 | - | - | [96] |
| H-314.4 × 108.3 × 4.23 × 5.57 | 1450 | 9.7 | 71.7 | 4.6 | 1.15 | 1.93 | 0.96 | - | - | [96] |
| H-315.5 × 143.8 × 4.23 × 5.57 | 1750 | 12.9 | 72.0 | 5.5 | 1.03 | 1.69 | 0.66 | - | - | [96] |
| H-359.7 × 108.8 × 4.23 × 5.57 | 1700 | 9.8 | 82.4 | 4.7 | 1.14 | 2.26 | 1.13 | - | - | [96] |
| H-359.5 × 144.8 × 4.23 × 5.57 | 2050 | 13.0 | 82.4 | 5.7 | 1.03 | 1.78 | 0.68 | - | - | [96] |
| H-250 × 125 × 5.8 × 8.5 | 1250 | 7.4 | 40.2 | 5.0 | 1.23 | 6.62 | 6.2 | - | - | [97] |
| H-450 × 200 × 9 × 14 | 1350 | 7.1 | 46.9 | 3.0 | 1.18 | 7.62 | 7.22 | - | - | [98] |
| b/tf | Flange width–thickness ratio |
| L/H | Shear span-to-depth ratio |
| L | Beam length |
| d/tw | Web width-to-thickness ratio |
| H | Hight of beam |
| B | Width of beam |
| tf | Flange thickness |
| tw | Web thickness |
| δp | Displacement corresponding to full plastic bending moment |
| Mp | Full plastic bending moment |
| δ | Controlled displacement |
| δ0 | Displacement at position of transducer |
| φ | Rotation angle measured by the transducers |
| δmp | Displacements due to bending deformation of beam |
| δsp | Displacements due to shear deformation of beam |
| E | Young’s modulus |
| I | Moment of inertia |
| A | Cross-sectional area |
| G | Shear modulus |
| κ | Shape factor |
| σy | Yield stress |
| σu | Tensile strength |
| Y.R. | Yield ratio (σy /σu) |
| P | Shear force acting on beam |
| Pp | Shear force imposing full plastic bending moment of beam |
| αBηmax | Hysteretic energy dissipation up to ultimate strength |
| αB | Bauschinger effect coefficient |
| μmax | Rotation capacity |
| ηmax | Energy dissipation capacity |
| Generalized flange width-to-thickness ratio | |
| Generalized web width-to-thickness ratio | |
| B/H | Section aspect ratio |
| τmax | Ultimate strength ratio |
| σyf | Yield stress of flange plate |
| σyw | Yield stress of web plate |
| N | Cumulative number of loading cycles until attainment of maximum load |
| μxi | Dimensionless amplitude of loading displacement in i-th cycle |
References
- Bleich, F. Buckling Strength of Metal Structures; McGraw Hill: New York, NY, USA, 1952. [Google Scholar]
- Timoshenko, S.P. Theory of Elastic Stability; McGraw Hill: New York, NY, USA, 1963. [Google Scholar]
- Nethercot, D.A.; Rockey, K.C. A Unified Approach to the Elastic Lateral Buckling of Beams. Struct. Eng. 1971, 7, 96–107. [Google Scholar] [CrossRef]
- Narayanan, R. Beam and Beam Columns-Stability and Strength; Applied Science Publishers: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Salvador, T.G. Lateral Buckling of Eccentrically Loaded I—Columns. Am. Soc. Civ. Eng. 1956, 121, 1163–1179. [Google Scholar] [CrossRef]
- Trahair, N.S. laterally unsupported beams. Eng. Struct. 1996, 18, 759–768. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Moon, J.; Lee, H.E. Lateral–torsional buckling of I-girders with discrete torsional bracings. J. Constr. Steel Res. 2010, 66, 170–177. [Google Scholar] [CrossRef]
- Ji, X.L.D.; Twizell, S.C.; Driver, R.G.; Imanpour, A. Lateral Torsional Buckling Response of Compact I-Shaped Welded Steel Girders. Eng. Struct. 2022, 148, 04022149. [Google Scholar] [CrossRef]
- Mohammadi, E.; Hosseini, S.S.; Rohanimanesh, M.S. Elastic lateral-torsional buckling strength and torsional bracing stiffness requirement for monosymmetric I-beams. Eng. Struct. 2016, 104, 116–125. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Joo, H.S.; Moon, J.; Lee, H.E. Flexural-torsional buckling strength of I-girders with discrete torsional braces under various loading conditions. Eng. Struct. 2022, 36, 337–350. [Google Scholar] [CrossRef]
- Fukunaga, I.; Todaka, T.; Zhang, Z.; Kanao, I. Deformation Capacity of Wide Flange Beam with Lateral Bracings. J. Struct. Constr. Eng. (Trans. AIJ) 2022, 87, 372–380. (In Japanese) [Google Scholar] [CrossRef]
- Bradford, M.A.; Gao, Z. Distortional buckling solutions for continuous composite beams. J. Struct. Eng. 1992, 118, 73–89. [Google Scholar] [CrossRef]
- Kimura, Y.; Yoshino, Y. Required Bracing Capacity on Lateral Buckling Strength for H-Shaped Beams with Bracings. J. Struct. Constr. Eng. (Trans. AIJ) 2011, 76, 2143–2152. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Yoshino, Y.; Ogawa, J. Effect of Lateral-Rotational Restraint and Strength of Continuously Braces on Lateral Buckling Load for H-Shaped Beams. J. Struct. Constr. Eng. (Trans. AIJ) 2013, 78, 193–201. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Yoshino, Y. Effect of Lateral and Rotational Restraint for Bracings on Lateral Buckling Load for H-Shaped Beams under Moment Gradient. J. Struct. Constr. Eng. (Trans. AIJ) 2014, 79, 761–770. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Matsuo, T.; Yoshino, Y. Estimation of Elasto-Plastic Lateral Buckling Stress for H-shaped Beams with Lateral Rotational Braces on subjected to Axial Force and Flexural Moment. J. Struct. Constr. Eng. (Trans. AIJ) 2014, 79, 1299–1308. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Yoshino, Y. Effect of Lateral-Rotational Restraint of Continuous Braces on Lateral Buckling Strength for H-Shaped Beams with Flexural Moment Gradient. J. Struct. Constr. Eng. (Trans. AIJ) 2016, 81, 1309–1319. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Sugita, Y.; Yoshino, Y. Effect of Lateral-Rotational Restraint of Continuous Braces on Lateral Buckling Strength for H-shaped Beams with Compressive Axial Force and Flexural Moment. J. Struct. Constr. Eng. (Trans. AIJ) 2016, 81, 1321–1331. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Sugita, Y. Effect of Lateral-Rotational Restraint of Continuous Braces on Lateral Buckling Strength for H-shaped Beams with Gradient Flexural Moment and Compressive Axial Force. J. Struct. Constr. Eng. (Trans. AIJ) 2016, 82, 1799–1809. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Miya, M.; Liao, W. Effect of Restraint for Continuous Braces on Lateral Buckling Load for H-shaped Beams with Warping Restraint of Beams to Column Joint. J. Struct. Constr. Eng. (Trans. AIJ) 2018, 81, 1353–1363. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Miya, M. Effect of Warping Restraint of Beams to Column Joint on Lateral Buckling Behavior for H-Shaped Beams with Continuous Braces under Gradient Flexural Moment. J. Struct. Constr. Eng. (Trans. AIJ) 2019, 84, 1601–1611. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Sato, Y. Effect of Warping Restraint of Beams to Column Joint on Lateral Buckling Behavior for H-Shaped Beams with Continuous Braces under Gradient Flexural Moment. J. Struct. Constr. Eng. (Trans. AIJ) 2021, 86, 145–155. (In Japanese) [Google Scholar] [CrossRef]
- Yoshino, Y.; Liao, W.; Kimura, Y. Restraint effect on lateral buckling load of continuous braced H-shaped beams based on partial frame loading tests. J. Struct. Constr. Eng. (Trans. AIJ) 2022, 87, 634–645. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Sato, Y.; Suzuki, A. Effect of Fork Restraint of Column on Lateral Buckling Behavior for H-Shaped Beams with Continuous Braces under Flexural Moment Gradient. J. Struct. Constr. Eng. (Trans. AIJ) 2022, 87, 316–327. (In Japanese) [Google Scholar] [CrossRef]
- Yoshino, Y.; Kimura, Y. Rotational Stiffening Performance of Roof Folded Plates in Torsion Tests and the Stiffening Effect of Roof Folded Plates on the Lateral Buckling of H Beams in Steel Structures. Buildings 2024, 14, 1158. [Google Scholar] [CrossRef]
- Rossi, A.; Nicoletti, R.S.; de Souza, A.S.C.; Martins, C.H. Lateral distortional buckling in steel-concrete composite beams: A review. Structures 2020, 27, 1299–1312. [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, Y. Cyclic behavior of component model of composite beam subjected to fully reversed cyclic loading. J. Struct. Eng. 2019, 145, 04019015. [Google Scholar] [CrossRef]
- Suzuki, A.; Abe, K.; Kimura, Y. Restraint performance of stud connection during lateral-torsional buckling under synchronized in-plane displacement and out-of-plane rotation. J. Struct. Eng. 2020, 146, 04020029. [Google Scholar] [CrossRef]
- Suzuki, A.; Abe, K.; Suzuki, K.; Kimura, Y. Cyclic behavior of perfobond-shear connectors subjected to fully reversed cyclic loading. J. Struct. Eng. 2021, 147, 04020355. [Google Scholar] [CrossRef]
- Suzuki, A.; Suzuki, K.; Kimura, Y. Ultimate shear strength of perfobond shear connectors subjected to fully reversed cyclic loading. Eng. Struct. 2021, 248, 113240. [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, K. Mechanical performance of stud connection in steel-concrete composite beam under reversed stress. Eng. Struct. 2021, 249, 113338. [Google Scholar] [CrossRef]
- Suzuki, A.; Hiraga, K.; Kimura, Y. Mechanical performance of puzzle-shaped shear connectors subjected to fully reversed cyclic stress. J. Struct. Eng. 2023, 149, 04023087. [Google Scholar] [CrossRef]
- Suzuki, A.; Hiraga, K.; Kimura, Y. Cyclic behavior of steel-concrete composite dowel by clothoid-shaped shear connectors under fully reversed cyclic stress. J. Adv. Concr. Technol. 2023, 21, 76–91. [Google Scholar] [CrossRef]
- Bedair, O. Stability of web plates in W-shape columns accounting for flange/web interaction. Thin-Walled Struct. 2009, 47, 768–775. [Google Scholar] [CrossRef]
- Roberts, T.M.; Jhita, P.S. Lateral, local and distortional buckling of I-beams. Thin-Walled Struct. 1983, 1, 289–308. [Google Scholar] [CrossRef]
- Bradford, M.A.; Hancock, G.J. Elastic interactions of local and lateral buckling in beams. Thin-Walled Struct. 1984, 2, 1–25. [Google Scholar] [CrossRef]
- Chin, C.K.; Al-Bermani, F.G.A.; Kitipornchai, S. Stability of thin-walled members having arbitrary flange shape and flexible web. Eng. Struct. 1990, 141, 121–132. [Google Scholar] [CrossRef]
- Seif, M.; Schafer, B.W. Local buckling of structural steel shapes. J. Construct. Steel Res. 2010, 66, 1232–1247. [Google Scholar] [CrossRef]
- Han, K.H.; Lee, C.H. Elastic flange local buckling of I-shaped beams considering effect of web restraint. Thin-Walled Struct. 2016, 105, 101–111. [Google Scholar] [CrossRef]
- Gardner, L.; Fieber, A.; Macorini, L. Formulae for calculating elastic local buckling stresses of full structural cross-sections. Structures 2019, 17, 2–20. [Google Scholar] [CrossRef]
- Tankova, T.; da Silva, L.S.; Marques, L.; Tankova, T.; da Silva, L.S.; Marques, L. Buckling resistance of non-uniform steel members based on stress utilization: General formulation. J. Construct. Steel Res. 2019, 149, 239–256. [Google Scholar] [CrossRef]
- Ragheb, W.F. Local buckling of welded steel I-beams considering flange–web interaction. Thin-Walled Struct. 2015, 97, 241–249. [Google Scholar] [CrossRef]
- Gioncu, V. Framed structures. Ductility and seismic response: General Report. J. Constr. Steel Res. 2000, 55, 125–154. [Google Scholar] [CrossRef]
- Gioncu, V.; Mosoarca, M.; Anastasiadis, A. Prediction of available rotation capacity and ductility of wide-flange beams: Part 1: DUCTROT-M computer program. J. Constr. Steel Res. 2011, 69, 8–19. [Google Scholar] [CrossRef]
- Anastasiadis, A.; Mosoarca, M.; Gioncu, V. Prediction of available rotation capacity and ductility of wide-flange beams: Part 2: Applications. J. Constr. Steel Res. 2011, 68, 176–191. [Google Scholar] [CrossRef]
- Shokouhian, M.; Shi, Y. Classification of I-section flexural members based on member ductility. J. Constr. Steel Res. 2014, 95, 198–210. [Google Scholar] [CrossRef]
- Araujo, M.; Macedo, L.; Castro, J. Evaluation of the rotation capacity limits of steel members defined in EC8-3. J. Constr. Steel Res. 2017, 135, 11–29. [Google Scholar] [CrossRef]
- Cardoso, D.; Vieira, J. Comprehensive local buckling equations for FRP I-sections in pure bending or compression. Compos. Struct. 2017, 182, 301–310. [Google Scholar] [CrossRef]
- Ascione, F.; Feo, L.; Lamberti, M.; Minghini, F.; Tullini, N. A closed-form equation for the local buckling moment of pultruded FRP I-beams in major-axis bending. Compos. Part B 2016, 97, 292–299. [Google Scholar] [CrossRef]
- Qiao, P.; Davalos, J.; Wang, J. Local Buckling of Composite FRP Shapes by Discrete Plate Analysis. J. Struct. Engineering. Am. Soc. Civ. Eng. 2001, 127, 245–255. [Google Scholar] [CrossRef]
- Torabian, S.; Schafer, B. Role of local slenderness in the rotation capacity of structural steel members. J. Constr. Steel Res. 2013, 95, 32–43. [Google Scholar] [CrossRef]
- Kato, B.; Akiyama, H.; Obi, Y. Deformation characteristics of H-shaped steel members influenced by local buckling. J. Struct. Constr. Eng. (Trans. AIJ) 1997, 257, 49–57. (In Japanese) [Google Scholar]
- Architectural Institute of Japan (AIJ). Recommendation for Limit State Design of Steel Structures; Maruzen Publishing Co., Ltd.: Tokyo, Japan, 2010. (In Japanese) [Google Scholar]
- American Institute of Steel Construction (AISC). Seismic Provisions for Structural Steel Buildings; AISC: Chicago, IL, USA, 2016. [Google Scholar]
- Architectural Institute of Japan (AIJ). AIJ Recommendations for Plastic Design of Steel Structures; Maruzen Publishing Co., Ltd.: Tokyo, Japan, 2017. (In Japanese) [Google Scholar]
- Lignos, D.G.; Krawinkler, H. Sidesway Collapse of Deteriorating Structural Systems under Seismic Excitations; Report No. TB 172; The John A. Blume Earthquake Engineering Center, Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Lignos, D.G.; Krawinkler, H. A steel database for component deterioration of tubular hollow square steel columns under varying axial load for collapse assessment of steel structures under earthquakes. In Proceedings of the 7th International Conf. on Urban Earthquake Engineering (7CUEE), Tokyo, Japan, 3–5 March 2010. [Google Scholar]
- Lignos, D.G.; Laura Eads Krawinkler, H. Effect of Composite Action on the Dynamic Stability of Special Steel Moment Resisting Frames Designed in Seismic Regions. In Proceedings of the ASCE Structures Congress, Budapest, Hungary, 31 August–2 September 2011. [Google Scholar]
- Lignos, D.G.; Krawinkler, H. Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading. J. Struct. Eng. 2011, 137, 1291–1302. [Google Scholar] [CrossRef]
- Lignos, D.G.; Krawinkler, H.; Whittaker, A. Prediction and validation of sidesway collapse of two scale models of a 4-story steel moment frame. J. Earthq. Eng. Struct. 2011, 40, 807–825. [Google Scholar] [CrossRef]
- Lignos, D.G.; Hikino, T.; Matsuoka, Y.; Nakashima, M. Collapse Assessment of Steel Moment Frames Based on E-Defense Full-Scale Shake Table Collapse Tests. J. Struct. Eng. 2013, 139, 120–132. [Google Scholar] [CrossRef]
- Kanao, I.; Nakashima, M.; Takehara, S. Braced frame model considering buckling and fracture and its responses under near-fault strong motions. J. Struct. Constr. Eng. (Trans. AIJ) 2004, 577, 117–122. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Uang, C.M.; Yu, Q.S.; Gilton, C.S. Effects of loading history on cyclic performance of steel RBS moment connections. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Architectural Institute of Japan (AIJ). Ultimate Strength and Deformation Capacity of Building in Seismic Design (1990); Maruzen Publishing Co., Ltd.: Tokyo, Japan, 1990. (In Japanese) [Google Scholar]
- Architectural Institute of Japan (AIJ). Evaluation Procedure for Performance-Based Design of Buildings-Calculation of Response and Limit Strength, Energy Balance-Based Seismic Resistant Design, Time History Response Analysis; AIJ: Tokyo, Japan, 2005. (In Japanese) [Google Scholar]
- Shimazu, M.; Kimura, Y. Correlation between plastic deformation capacity and energy absorption capacity for H-shaped beams with local buckling. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 2006; pp. 845–846. (In Japanese) [Google Scholar]
- Shimazu, M.; Kimura, Y. Effects of flange width-to-thickness ratio and shear span ratio of plastic deformation capacity and energy absorption capacity for H-shaped beams. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 2007; pp. 627–628. (In Japanese) [Google Scholar]
- Qi, H.; Tada, M.; Tani, N.; Shirai, Y. Monotonic and hysteretic model for H-shaped beams incorporating deterioration behavior owing to the local buckling. Thin-Walled Struct. 2020, 157, 107016. [Google Scholar] [CrossRef]
- Kimura, Y.; Yamanishi, T.; Kasai, K. Cyclic Hysteresis Behavior and Plastic Deformation Capacity for H-shaped Beams on Local Buckling under Compressive and Tensile Forces. J. Struct. Constr. Eng. (Trans. AIJ) 2013, 78, 1307–1316. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Suzuki, A.; Kasai, K. Estimation of plastic deformation capacity for H-shaped beams on local buckling under compressive and tensile forces. J. Struct. Constr. Eng. (Trans. AIJ) 2016, 81, 2133–2142. (In Japanese) [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, Y.; Kasai, K. Plastic deformation capacity of H-shaped beams collapsed with combined buckling under reversed axial forces. J. Struct. Constr. Eng. (Trans. AIJ) 2018, 83, 297–307. (In Japanese) [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, Y.; Kasai, K. Rotation capacity of I-shaped beams under alternating axial forces based on buckling-mode transitions. J. Struct. Eng. 2020, 146, 04020089. (In Japanese) [Google Scholar] [CrossRef]
- Kimura, Y.; Fujak, S.M.; Suzuki, A. Elastic local buckling strength of I-beam cantilevers subjected to bending moment and shear force based on flange-web interaction. Thin-Walled Struct. 2021, 162, 107633. [Google Scholar] [CrossRef]
- Fujak, S.M.; Kimura, Y.; Suzuki, A. Estimation of elastoplastic local buckling capacities and novel classification of I-beams based on beam’s elastic local buckling strength. Structures 2022, 39, 765–781. [Google Scholar] [CrossRef]
- Fujak, S.M.; Suzuki, A.; Kimura, Y. Estimation of ultimate capacities of Moment-Resisting Frame’s subassemblies with Mid-Storey Pin connection based on elastoplastic local buckling. Structures 2023, 48, 410–426. [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, Y. Rotation capacity of I-shaped beam failed by local buckling in buckling-restrained braced frames with rigid beam-column connections. J. Struct. Eng. 2023, 149, 04022243. [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, Y.; Matsuda, Y.; Kasai, K. Rotation capacity of I-shaped beams with concrete slab in buckling-restrained braced frames. J. Struct. Eng. 2024, 150, 04023204. [Google Scholar] [CrossRef]
- Fujikawa, T.; Fujiwara, K. Research on strength and deformation capacity of H-shaped beam under cyclic loading. In Proceedings of Architectural Institute of Japan Kinki Chapter Research Meeting; AIJ: Tokyo, Japan, 1984; pp. 337–340. (In Japanese) [Google Scholar]
- Fujiwara, K.; Kato, S. A study on deformation capacity of H-shaped steel beams with relative large ratio of web depth to thickness under cyclic loading. In Proceedings of Architectural Institute of Japan Kinki Chapter Research Meeting; AIJ: Tokyo, Japan, 1985; pp. 425–428. (In Japanese) [Google Scholar]
- Sakai, J.; Matsui, C.; Kuno, T. Effects of the difference of the value of yield ratio of steel and the collapse-types of frame on the ductility of steel frame. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1990; pp. 1351–1352. (In Japanese) [Google Scholar]
- Fujita, T.; Nakagomi, T.; Mizusaki, Y. The experimental research concern with structural behaviors of welded beam-to-column connections using cold-formed square steel tube column. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1992; pp. 1537–1538. (In Japanese) [Google Scholar]
- Kai, S.; Sera, K.; Abukawa, T.; Yabe, Y.; Terada, G. Structural behavior of H-shaped beam-end connected to RHS-column. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1992; pp. 1541–1542. (In Japanese) [Google Scholar]
- Makishi, T.; Yamamoto, N.; Tsutsui, S.; Fujisawa, K.; Uemori, H.; Ishii, T.; Morita, K. Experimental study on the deformation capacity of welded beam end connection without weld access hole. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1993; pp. 1257–1260. (In Japanese) [Google Scholar]
- Ito, H.; Kimura, M.; Kaneko, H.; Yagi, T.; Ishii, H. Experimental study on beam-to-column welding connection without beam scallops. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1993; pp. 1261–1262. (In Japanese) [Google Scholar]
- Suzuki, T.; Motoyui, S.; Fukazawa, T.; Uchikoshi, T. Study on effect of width-thickness ratio on deformation capacity of beams with scallops. J. Struct. Constr. Eng. (Trans. AIJ) 1996, 486, 107–114. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- KMinami; Fujita, T.; Sasaki, Y. Experimental study on effect of non-scallops on deformation capacities of beam-to-column welded joints. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1996; pp. 631–632. (In Japanese) [Google Scholar]
- Ishimaru, R.; Kagami, S.; Tanaka, A.; Masuda, K. Experimental study on the statical characteristics of the WBFW type beam-to-column connections. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1997; pp. 429–430. (In Japanese) [Google Scholar]
- Sawamoto, Y.; Yoshida, H.; Kihiara, H.; Torii, S.; Tanaka, N. Experimental study on detail of H-shaped beam-to-box column connection. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1998; pp. 375–376. (In Japanese) [Google Scholar]
- Yasuno, T.; Tsujioka, S.; Tada, M. Alternate loading test of haunch-beams made from rolled wide-flange shape. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 2001; pp. 583–586. (In Japanese) [Google Scholar]
- Kamaga, H.; Makino, Y.; Kuroba, K.; Tanaka, M.; Fukudome, Y.; Kobukuro, Y. Testing of beam-to-RHS column connections with-out weld access holes for field welding. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 2001; pp. 919–922. (In Japanese) [Google Scholar]
- Nakano, T.; Masuda, H.; Sasaji, T.; Tanaka, A. Experimental study on behavior of WBFW type beam-to-column connection. J. Struct. Constr. Eng. (Trans. AIJ) 2002, 556, 139–144. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Nakano, T.; Masuda, H.; Tanaka, A. Experimental study on effect of reinforcements at web connected parts of WF beam to SHS column connections. J. Struct. Constr. Eng. (Trans. AIJ) 2003, 566, 145–152. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Ono, T.; Kanebako, Y. The local buckling and inelastic deformation capacity of steel beams under shear bending. J. Struct. Constr. Eng. (Trans. AIJ) 1977, 260, 91–98. (In Japanese) [Google Scholar]
- Kato, T.; Akiyama, H.; Obi, Y. Experimental study of H-shaped beam with relatively large width-thickness ratio on local buckling characteristics. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1976; pp. 1075–1076. (In Japanese) [Google Scholar]
- Yoda, K.; Imai, K.; Kuroba, K.; Ogawa, K.; Kimura, K.; Motoyui, S. Bending capacity of thin-walled welding H-section beams. J. Struct. Constr. Eng. (Trans. AIJ) 1989, 397, 60–72. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, M.; Suzuki, T.; Ogawa, T.; Kimura, K.; Motoyui, S.; Matsuoka, T. Investigation on estimation of inelastic behavior of H-shaped beam with circular hole. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 1993; pp. 1473–1474. (In Japanese) [Google Scholar]
- Ikarashi, K.; Suzuki, T. A study on plastic deformation capacity of H-shaped stiffened beams with web opening. In Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; Japan Society for Finishings Technology: Tokyo, Japan, 2000; pp. 505–506. (In Japanese) [Google Scholar]
- JIS Z 2241; Metallic Materials-Tensile Testing Method of Test at Room Temperature. Japan Industrial Standards (JIS): Tokyo, Japan, 2011.
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- EN 1998-3; Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- Kadono, A.; Sasaki, M.; Okamoto, K.; Akiyama, H.; Matsui, C.; Inoue, K. Experimental study on the effect of yield ratio on the bending strength increasing ratio and the ductility of steel structures’ members. J. Struct. Eng. 1994, 40B, 673–682. (In Japanese) [Google Scholar]
- Suzuki, T.; Ikarashi, K.; Satsukawa, K. Estimate for plastic deformation capacity of steel members with moment gradient reflected material properties. J. Struct. Constr. Eng. (Trans. AIJ) 2000, 537, 129–134. (In Japanese) [Google Scholar] [CrossRef]
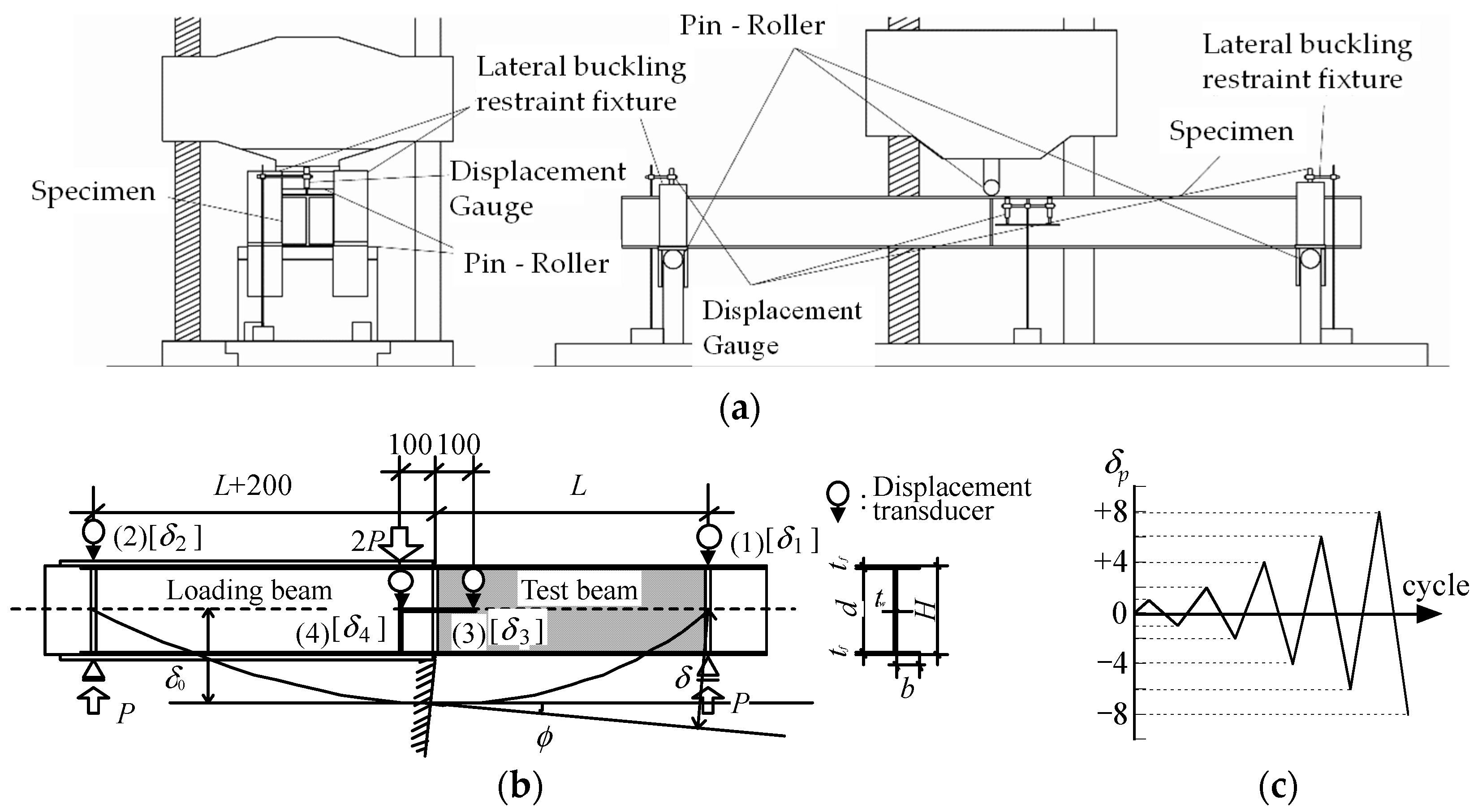


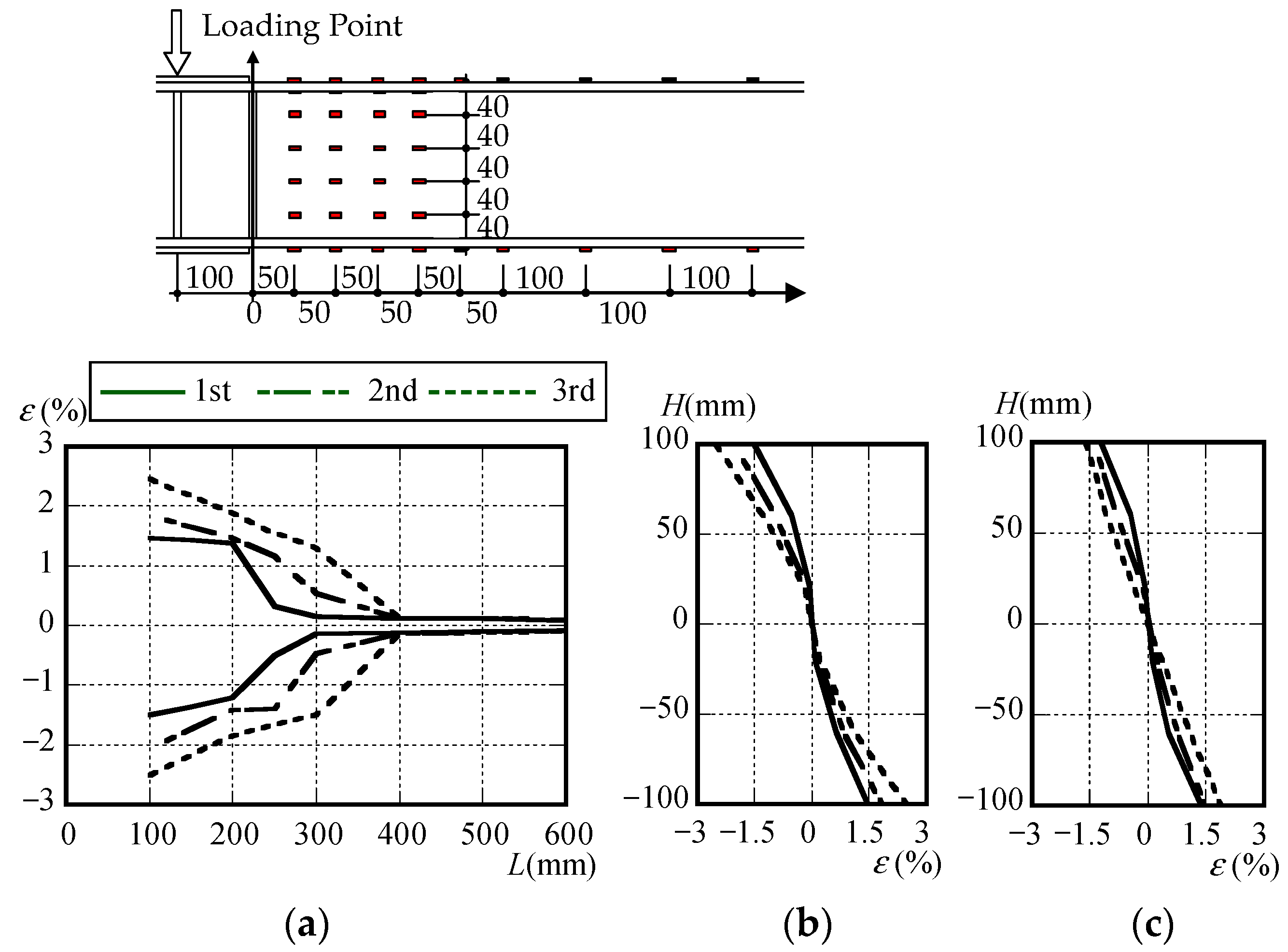

| Designation | L [mm] | b/tf [mm] | d/tw [mm] | L/H [-] | Slenderness Ratio [-] | Protocol | No. of Cycles |
|---|---|---|---|---|---|---|---|
| A-1-1 | 1000 | 6.25 | 22 | 4.95 | 24.55 | Monotonic | - |
| B-1-1 | 4.95 | Cyclic | 1 | ||||
| C-1-1 | 4.98 | Cyclic | 3 | ||||
| A-2-1 | 4.17 | 4.98 | 37.88 | Monotonic | 1 | ||
| B-2-1 | 4.95 | Cyclic | 1 | ||||
| A-3-1 | 8.33 | 4.98 | 18.15 | Monotonic | 1 | ||
| B-3-1 | 4.95 | Cyclic | 1 | ||||
| A-1-2 | 800 | 6.25 | 3.96 | 19.64 | Monotonic | 1 | |
| B-1-2 | Cyclic | 1 | |||||
| A-1-3 | 1200 | 5.97 | 29.46 | Monotonic | 1 | ||
| B-1-3 | Cyclic | 1 |
| Specimen | H [mm] | B [mm] | tf [mm] | tw [mm] |
|---|---|---|---|---|
| A-1-1 | 202 | 150 | 11.9 | 8.20 |
| B-1-1 | 202 | 150 | 12.1 | 8.10 |
| C-1-1 | 201 | 150 | 12.0 | 8.25 |
| A-2-1 | 201 | 101 | 12.0 | 8.25 |
| B-2-1 | 202 | 100 | 12.1 | 8.25 |
| A-3-1 | 201 | 200 | 11.8 | 8.20 |
| B-3-1 | 202 | 201 | 11.8 | 8.20 |
| A-1-2 | 202 | 150 | 12.0 | 8.25 |
| B-1-2 | 202 | 150 | 11.9 | 8.25 |
| A-1-3 | 201 | 150 | 11.9 | 8.35 |
| B-1-3 | 201 | 151 | 12.0 | 8.25 |
| Thickness [mm] | E [N/mm2] | σy [N/mm2] | σu [N/mm2] | Y.R. | Elongation [%] | |
|---|---|---|---|---|---|---|
| Flange | 8 | 1.99 × 106 | 323 | 444 | 0.727 | 21 |
| Web | 12 | 2.00 × 106 | 283 | 428 | 0.661 | 24 |
| Specimen | Failure Modes | Cycle at Failure | μmax | ηmax | αb |
|---|---|---|---|---|---|
| A-1-1 | Local buckling | 13.27 | 15.96 | ||
| B-1-1 | Local buckling | +2δp | 12.65 | 16.16 | 2.06 |
| C-1-1 | Local buckling | +2δp (1st) | 8.17 | 9.45 | 2.48 |
| A-2-1 | Combined buckling (local and lateral buckling) | 8.34 | 7.96 | ||
| B-2-1 | Combined buckling (local and lateral buckling) | −4δp | 8.64 | 13.84 | 1.63 |
| A-3-1 | Local buckling | 11.86 | 13.33 | ||
| B-3-1 | Local buckling and flange failure | +2δp | 5.46 | 10.41 | 1.61 |
| A-1-2 | Local buckling | 20.90 | 26.59 | ||
| B-1-2 | Combined buckling (local and shear buckling) | +6δp | 8.88 | 17.10 | 2.02 |
| A-1-3 | Local buckling | 12.84 | 15.47 | ||
| B-1-3 | Local buckling | +2δp | 7.85 | 14.09 | 1.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kimura, Y. Evaluation of Rotation Capacity and Bauschinger Effect Coefficient of I-Shaped Beams Considering Loading Protocol Influences. Buildings 2024, 14, 1376. https://doi.org/10.3390/buildings14051376
Kimura Y. Evaluation of Rotation Capacity and Bauschinger Effect Coefficient of I-Shaped Beams Considering Loading Protocol Influences. Buildings. 2024; 14(5):1376. https://doi.org/10.3390/buildings14051376
Chicago/Turabian StyleKimura, Yoshihiro. 2024. "Evaluation of Rotation Capacity and Bauschinger Effect Coefficient of I-Shaped Beams Considering Loading Protocol Influences" Buildings 14, no. 5: 1376. https://doi.org/10.3390/buildings14051376
APA StyleKimura, Y. (2024). Evaluation of Rotation Capacity and Bauschinger Effect Coefficient of I-Shaped Beams Considering Loading Protocol Influences. Buildings, 14(5), 1376. https://doi.org/10.3390/buildings14051376






