Full-Scale Field Tests on Concrete Slabs Subjected to Close-In Blast Loads
Abstract
:1. Introduction
2. Field Blast Tests
2.1. Protective Solutions
- Slab S6: A steel sheet (SS) made of S-275 JR steel was located at the center of the span on the side facing the blast charge, with dimensions of 1.50 × 1.46 m and a thickness of 10 mm. The steel sheet was fixed by using an epoxy adhesive.
- Slab S7: The concrete used in this slab was a steel-fiber-reinforced concrete (SFRC) with a fiber content of 120 kg/m3.
- Slab S8: The concrete used in this slab was a polypropylene-fiber-reinforced concrete (PPFRC) with a fiber content of 9 kg/m3.
- Slabs P3 and P5: These slabs were protected with a glass-fiber-reinforced polymer (GFRP) composed of a bi-directional primed glass-fiber-reinforcing sheet with a one-component ready-to-use water and polyurethane-based adhesive. In this case, the GFRP was placed on the side of the slab that was not facing the explosive charge, which was the face where the tensile stresses occurred.
- Slabs P4, P6, and P8: These slabs were protected by using a carbon-fiber-reinforced polymer (CFRP) composed of a high-strength carbon fiber mesh with a thixotropic epoxy adhesive. As in the GFRP, the protected solution was placed on the tensile face of the slabs.
2.2. Test Setup and Monitoring
3. Test Results
3.1. Non-Reinforced Slabs
3.2. Reinforced Slabs
3.2.1. Slab S6: Protected with a Steel Sheet
3.2.2. Slabs S7 and S8: Protected with Fiber-Reinforced Concrete
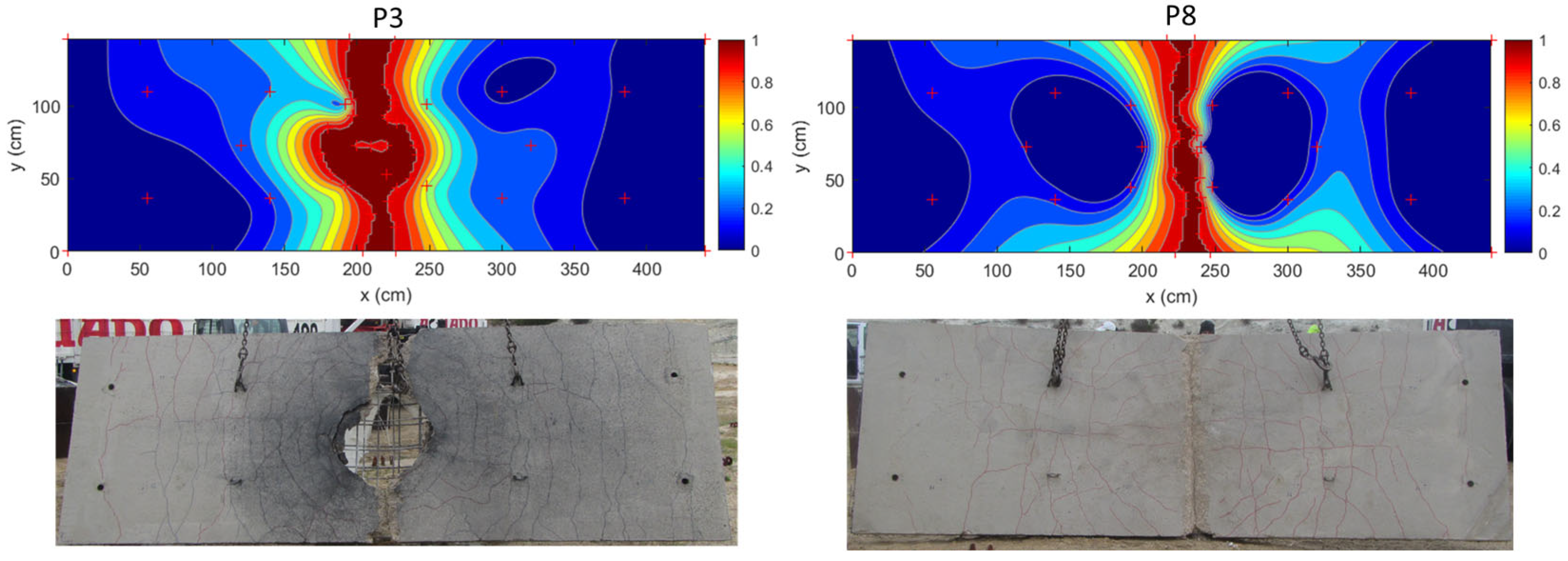
3.2.3. Slabs P3 and P5: Protected with GFRP
3.2.4. Slabs P4, P6, and P8: Protected with CFRP
4. Damage Analysis
5. Results and Discussion
6. Conclusions
- With the explosive charge at 0.5 m from the slab, significant local damage occurred, perforating the slab completely. In these cases, the reinforcements tested did not provide any additional protection, as the slabs were perforated, and they did not contribute to the retention of fragments.
- In the tests with the load at 1 m, the failure mode of the slab was different, with smaller deflections and no complete penetration. The reinforcements that were used significantly contributed to the retention of some fragments that were produced in these tests, and permanent deflections were reduced.
- The difference in deflection found in the slab with carbon fiber mesh reinforcement with respect to the slab without reinforcement was considered to be very positive, and it would be worth further study in future projects to consider this type of reinforcement.
- The addition of steel and polypropylene fibers to the concrete improves its mechanical properties—mainly its tensile strength. This fact, which does not improve in the event of close-in explosions, could be tested at other scaled distances in order to compare the results.
- On the contrary, the use of a steel plate as a protective solution produces a higher level of damage than that with an unreinforced slab.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kosal, M.E. Terrorism Targeting Industrial Chemical Facilities: Strategic Motivations and the Implications for U.S. Security 2017, 30, 41–73. [Google Scholar] [CrossRef]
- Zhu, R.; Li, X.; Hu, X.; Hu, D. Risk Analysis of Chemical Plant Explosion Accidents Based on Bayesian Network. Sustainability 2020, 12, 137. [Google Scholar] [CrossRef] [Green Version]
- Draganić, H.; Gazić, G.; Varevac, D. Experimental Investigation of Design and Retrofit Methods for Blast Load Mitigation—A State-of-the-Art Review. Eng. Struct. 2019, 190, 189–209. [Google Scholar] [CrossRef]
- Goswami, A.; Adhikary, S. Das Retrofitting Materials for Enhanced Blast Performance of Structures: Recent Advancement and Challenges Ahead. Constr. Build. Mater. 2019, 204, 224–243. [Google Scholar] [CrossRef]
- Mao, L.; Barnett, S.; Begg, D.; Schleyer, G.; Wight, G. Numerical Simulation of Ultra High Performance Fibre Reinforced Concrete Panel Subjected to Blast Loading. Int. J. Impact Eng. 2014, 64, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Tabatabaei, Z.S.; Volz, J.S.; Baird, J.; Gliha, B.P.; Keener, D.I. Experimental and Numerical Analyses of Long Carbon Fiber Reinforced Concrete Panels Exposed to Blast Loading. Int. J. Impact Eng. 2013, 57, 70–80. [Google Scholar] [CrossRef]
- Pantelides, C.P.; Garfield, T.T.; Richins, W.D.; Larson, T.K.; Blakeley, J.E. Reinforced Concrete and Fiber Reinforced Concrete Panels Subjected to Blast Detonations and Post-Blast Static Tests. Eng. Struct. 2014, 76, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Foglar, M.; Kovar, M. Conclusions from Experimental Testing of Blast Resistance of FRC and RC Bridge Decks. Int. J. Impact Eng. 2013, 59, 18–28. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.; Yang, H.; Wang, Y.A.N.; Tang, S. Comparison of Fly Ash, PVA Fiber, MGO and Shrinkage-Reducing Admixture on the Frost Resistance of Face Slab Concrete via Pore Structural and Fractal Analysis. Fractals 2021, 29, 2140002. [Google Scholar] [CrossRef]
- Schenker, A.; Anteby, I.; Gal, E.; Kivity, Y.; Nizri, E.; Sadot, O.; Michaelis, R.; Levintant, O.; Ben-Dor, G. Full-Scale Field Tests of Concrete Slabs Subjected to Blast Loads. Int. J. Impact Eng. 2008, 35, 184–198. [Google Scholar] [CrossRef]
- Wu, C.; Huang, L.; Oehlers, D.J. Blast Testing of Aluminum Foam–Protected Reinforced Concrete Slabs. J. Perform. Constr. Facil. 2011, 25, 464–474. [Google Scholar] [CrossRef]
- Merrett, R.P.; Langdon, G.S.; Theobald, M.D. The Blast and Impact Loading of Aluminium Foam. Mater. Des. 2013, 44, 311–319. [Google Scholar] [CrossRef]
- Ghani Razaqpur, A.; Tolba, A.; Contestabile, E. Blast Loading Response of Reinforced Concrete Panels Reinforced with Externally Bonded GFRP Laminates. Compos. B Eng. 2007, 38, 535–546. [Google Scholar] [CrossRef]
- Reifarth, C.; Castedo, R.; Santos, A.P.; Chiquito, M.; López, L.M.; Pérez-Caldentey, A.; Martínez-Almajano, S.; Alañon, A. Numerical and Experimental Study of Externally Reinforced RC Slabs Using FRPs Subjected to Close-in Blast Loads. Int. J. Impact Eng. 2021, 156, 103939. [Google Scholar] [CrossRef]
- Greene, C.E.; Myers, J.J. Flexural and Shear Behavior of Reinforced Concrete Members Strengthened with a Discrete Fiber-Reinforced Polyurea System. J. Compos. Constr. 2013, 17, 108–116. [Google Scholar] [CrossRef]
- Carey, N.L.; Myers, J.J.; Asprone, D.; Menna, C.; Prota, A. Polyurea Coated and Plane Reinforced Concrete Panel Behavior under Blast Loading: Numerical Simulation to Experimental Results. Trends Civ. Eng. Archit. 2018, 1, 87–98. [Google Scholar] [CrossRef]
- Santos, A.P.; Chiquito, M.; Castedo, R.; López, L.M.; Gomes, G.; Mota, C.; Fangueiro, R.; Mingote, J.L. Experimental and Numerical Study of Polyurea Coating Systems for Blast Mitigation of Concrete Masonry Walls. Eng. Struct. 2023, 284, 116006. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, D.; Lu, F.; Wang, S.C.; Tang, F. Experimental Study and Numerical Simulation of the Damage Mode of a Square Reinforced Concrete Slab under Close-in Explosion. Eng. Fail. Anal. 2013, 27, 41–51. [Google Scholar] [CrossRef]
- Zhao, C.F.; Chen, J.Y. Damage Mechanism and Mode of Square Reinforced Concrete Slab Subjected to Blast Loading. Theor. Appl. Fract. Mech. 2013, 63–64, 54–62. [Google Scholar] [CrossRef]
- Thiagarajan, G.; Kadambi, A.V.; Robert, S.; Johnson, C.F. Experimental and Finite Element Analysis of Doubly Reinforced Concrete Slabs Subjected to Blast Loads. Int. J. Impact Eng. 2015, 75, 162–173. [Google Scholar] [CrossRef]
- Tai, Y.S.; Chu, T.L.; Hu, H.T.; Wu, J.Y. Dynamic Response of a Reinforced Concrete Slab Subjected to Air Blast Load. Theor. Appl. Fract. Mech. 2011, 56, 140–147. [Google Scholar] [CrossRef]
- Zhao, C.F.; Chen, J.Y.; Wang, Y.; Lu, S.J. Damage Mechanism and Response of Reinforced Concrete Containment Structure under Internal Blast Loading. Theor. Appl. Fract. Mech. 2012, 61, 12–20. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y.X.; Hazell, P.J. Modelling the Response of Reinforced Concrete Panels under Blast Loading. J. Mater. Des. 2014, 56, 620–628. [Google Scholar] [CrossRef]
- Jayasooriya, R.; Thambiratnam, D.P.; Perera, N.J.; Kosse, V. Blast and Residual Capacity Analysis of Reinforced Concrete Framed Buildings. Eng. Struct. 2011, 33, 3483–3495. [Google Scholar] [CrossRef]
- Castedo, R.; Segarra, P.; Alañon, A.; Lopez, L.M.; Santos, A.P.; Sanchidrian, J.A. Air Blast Resistance of Full-Scale Slabs with Different Compositions: Numerical Modeling and Field Validation. Int. J. Impact Eng. 2015, 86, 145–156. [Google Scholar] [CrossRef]
- Castedo, R.; Santos, A.P.; Alañón, A.; Reifarth, C.; Chiquito, M.; López, L.M.; Martínez-Almajano, S.; Pérez-Caldentey, A. Numerical Study and Experimental Tests on Full-Scale RC Slabs under Close-in Explosions. Eng. Struct. 2021, 231, 111774. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- López, L.M.; Castedo, R.; Chiquito, M.; Segarra, P.; Sanchidrián, J.A.; Santos, A.P.; Navarro, J. Post-Blast Non-Destructive Damage Assessment on Full-Scale Structural Elements. J. Nondestr. Eval. 2019, 38, 30. [Google Scholar] [CrossRef]



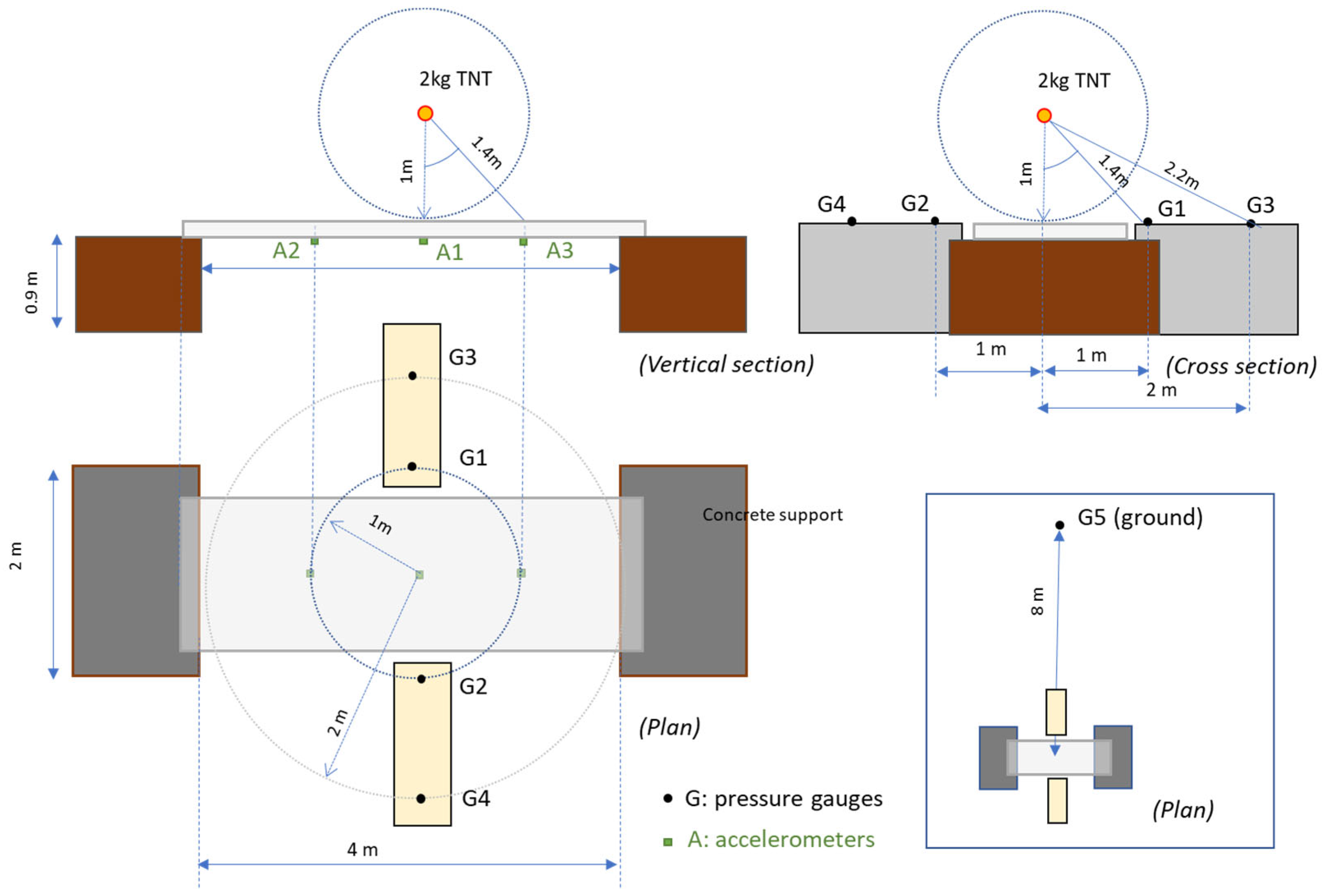











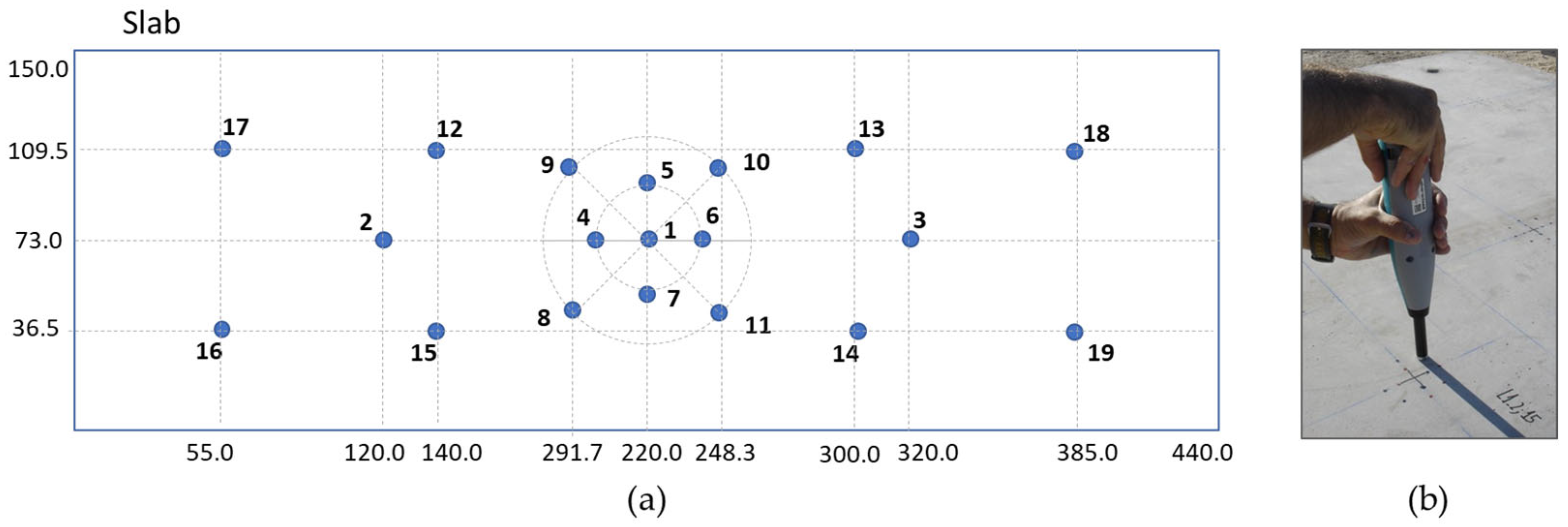
| Test | Reinforcement | Eq. TNT Mass (kg) | Standoff Distance (m) | Scaled Distance (m/kg1/3) |
|---|---|---|---|---|
| S1/S2/S3 | Non-reinforced | 2.00 | 1.0 | 0.79 |
| S4 | Non-reinforced | 15.00 | 1.0 | 0.41 |
| S5 | Non-reinforced | 15.00 | 0.5 | 0.20 |
| S6 | Steel sheet | 15.00 | 0.5 | 0.20 |
| S7 | SFRC | 15.00 | 0.5 | 0.20 |
| S8 | PPFRC | 15.00 | 0.5 | 0.20 |
| P1 | Non-reinforced | 1.74 | 1.0 | 0.83 |
| P2 | Non-reinforced | 13.05 | 0.5 | 0.21 |
| P3 | GFRP | 13.05 | 0.5 | 0.21 |
| P4 | CFRP | 13.05 | 0.5 | 0.21 |
| P5 | GFRP | 13.05 | 1.0 | 0.42 |
| P6 | CFRP | 13.05 | 1.0 | 0.42 |
| P7 | Non-reinforced | 13.05 | 1.0 | 0.42 |
| P8 | CFRP | 13.05 | 1.0 | 0.42 |
| CFRP | GFRP | ||||||
|---|---|---|---|---|---|---|---|
| SS | SFRC | PPFRC | Carbon Fiber | Resin | Glass Fiber | Adhesive | |
| Density (kg/m3) | 7850 | 7810 | 910 | 1830 | 1300 | - | 1100 |
| Length (mm) | - | 50 | 48 | - | - | - | - |
| Diameter (mm) | - | 1 | 0.85 | - | - | - | - |
| Weight (g/m2) | - | - | ≥170 | - | 286 | - | |
| Tensile strength (MPa) | 550 | 1100 | 400 | 5000 | 20 | >1620 | 5.25 |
| Young’s Modulus (GPa) | 200 | - | 6.2 | 252 | 2 | 42 | 0.55 |
| Elongation at failure (%) | - | - | 2 | 1 | 4 | 1.2 | |
| Compressive strength of concrete, fc (MPa) | - | 44.16 | 43.33 | - | - | - | - |
| Tensile strength of concrete (MPa) | - | 8.12 | 5.62 | - | - | - | - |
| Yield strength (MPa) | 275 | - | - | - | - | - | - |
| Tangent modulus (MPa) | 1850 | - | - | - | - | - | - |
| Test | Reinforcement | Eq. TNT Mass (kg) | Standoff Distance (m) | d200 (%) | dA (%) | Deflection (cm) |
|---|---|---|---|---|---|---|
| S1/S1/S3 | Non-reinforced | 2.00 | 1.0 | 0.00 | 0.00 | - |
| S4 | Non-reinforced | 15.00 | 1.0 | 10.00 | 3.00 | - |
| S5 | Non-reinforced | 15.00 | 0.5 | 27.00 | 7.00 | - |
| S6 | Steel sheet | 15.00 | 0.5 | 30.00 | 22.00 | - |
| S7 | SFRC | 15.00 | 0.5 | 27.00 | 5.00 | - |
| S8 | PPFRC | 15.00 | 0.5 | 28.00 | 6.00 | - |
| P1 | Non-reinforced | 1.74 | 1.0 | 0.00 | 0.00 | 0.00 |
| P2 | Non-reinforced | 13.05 | 0.5 | 27.69 | 8.19 | 51.00 |
| P3 | GFRP | 13.05 | 0.5 | 28.93 | 7.63 | 63.00 |
| P4 | CFRP | 13.05 | 0.5 | 28.22 | 7.86 | 57.00 |
| P5 | GFRP | 13.05 | 1.0 | 17.85 | 3.89 | 32.50 |
| P6 | CFRP | 13.05 | 1.0 | 19.33 | 4.55 | 23.20 |
| P7 | Non-reinforced | 13.05 | 1.0 | 18.77 | 5.59 | 34.00 |
| P8 | CFRP | 13.05 | 1.0 | 21.26 | 3.41 | 27.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiquito, M.; López, L.M.; Castedo, R.; Santos, A.P.; Pérez-Caldentey, A. Full-Scale Field Tests on Concrete Slabs Subjected to Close-In Blast Loads. Buildings 2023, 13, 2068. https://doi.org/10.3390/buildings13082068
Chiquito M, López LM, Castedo R, Santos AP, Pérez-Caldentey A. Full-Scale Field Tests on Concrete Slabs Subjected to Close-In Blast Loads. Buildings. 2023; 13(8):2068. https://doi.org/10.3390/buildings13082068
Chicago/Turabian StyleChiquito, María, Lina M. López, Ricardo Castedo, Anastasio P. Santos, and Alejandro Pérez-Caldentey. 2023. "Full-Scale Field Tests on Concrete Slabs Subjected to Close-In Blast Loads" Buildings 13, no. 8: 2068. https://doi.org/10.3390/buildings13082068





