Experimental Study on the Flexural Behaviors of Prestressed Segmental Ultra–High–Performance Concrete Channels and Reinforced Conventional Concrete Deck Composite Girders
Abstract
:1. Introduction
2. Experimental Program
2.1. Specimens Details
2.2. Material Properties
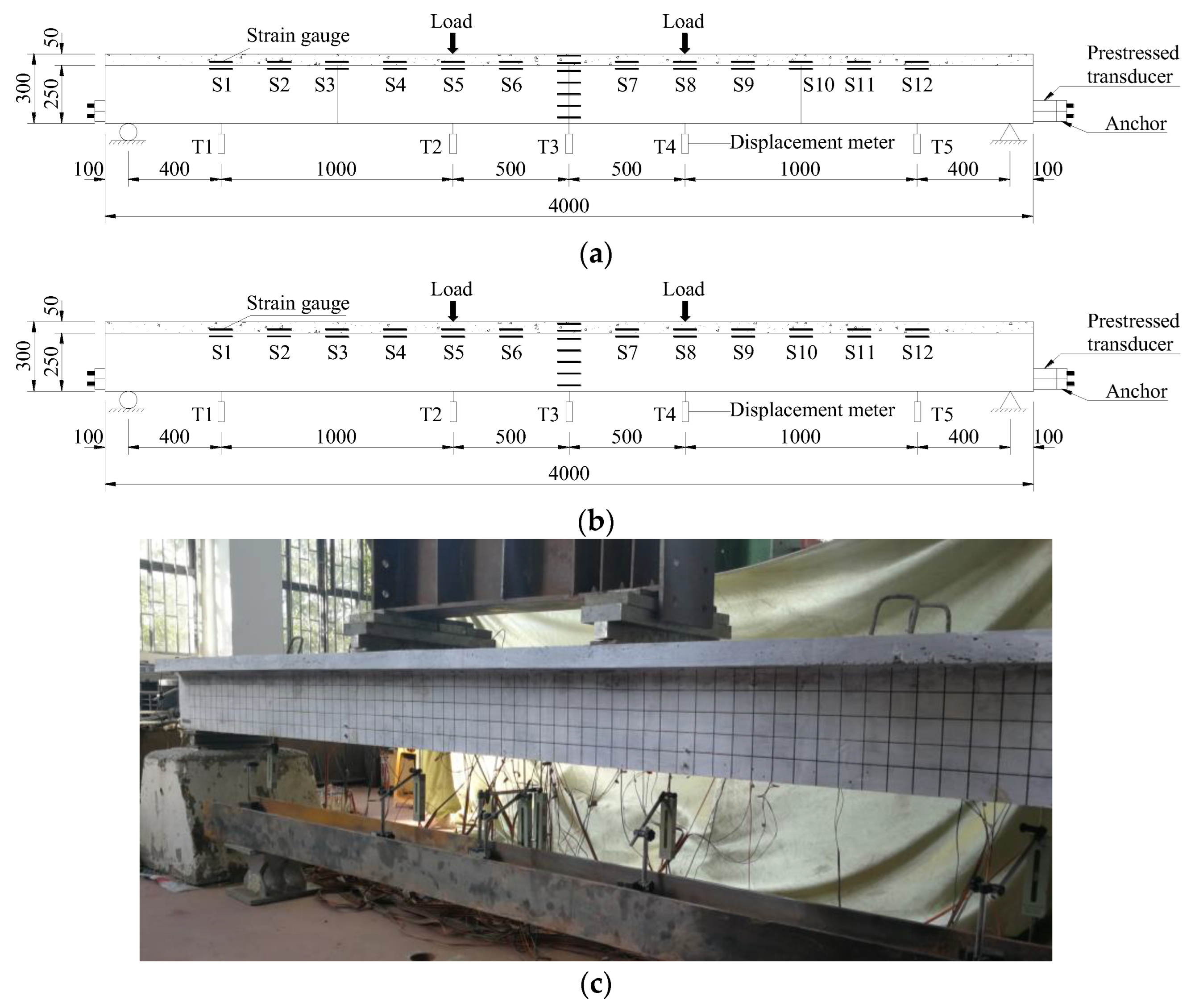
2.3. Test Setup and Arrangement of Measurement Points
3. Experimental Results
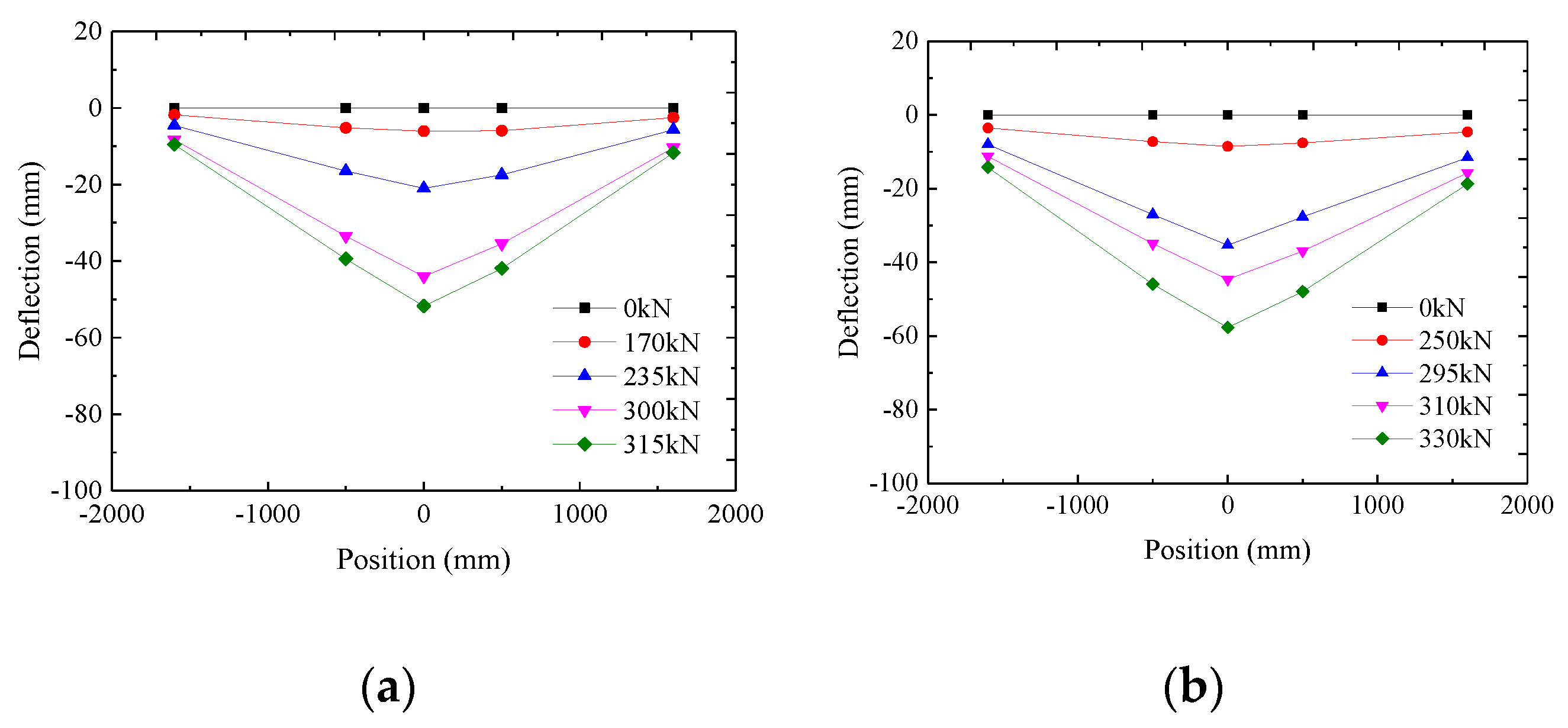
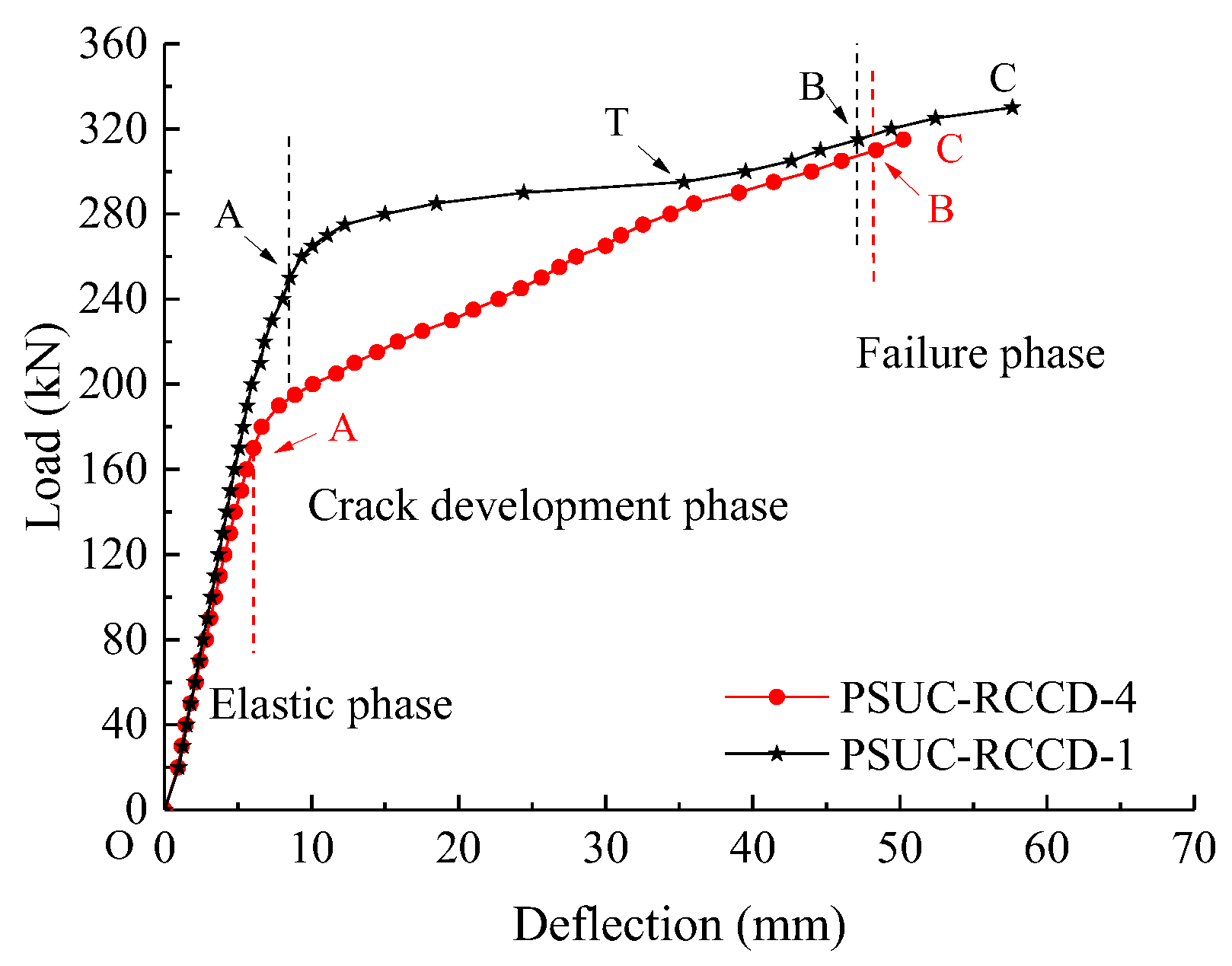
3.1. Load–Deflection Curves
3.2. Crack Patterns
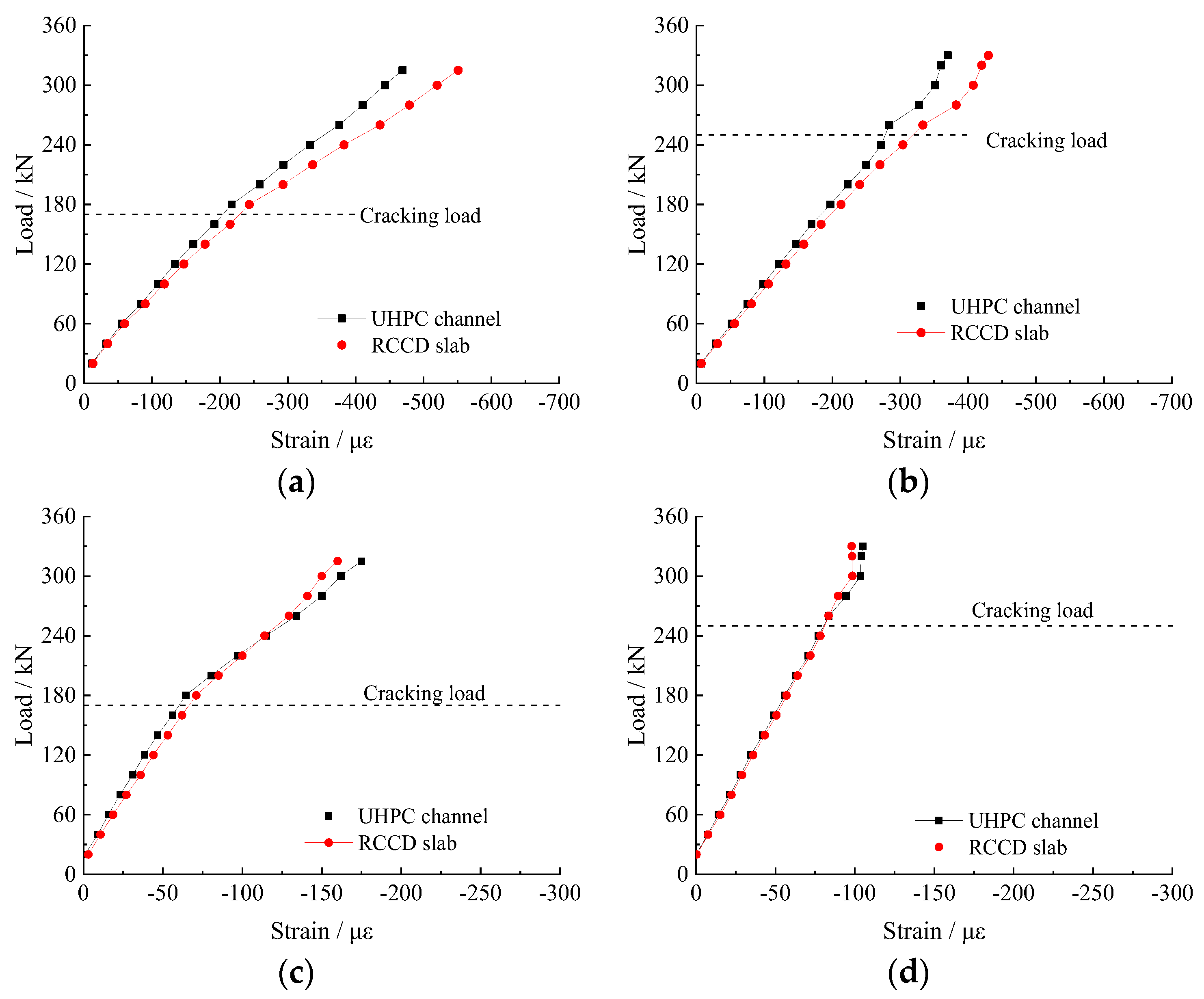
3.3. Load–Concrete Strain Curve
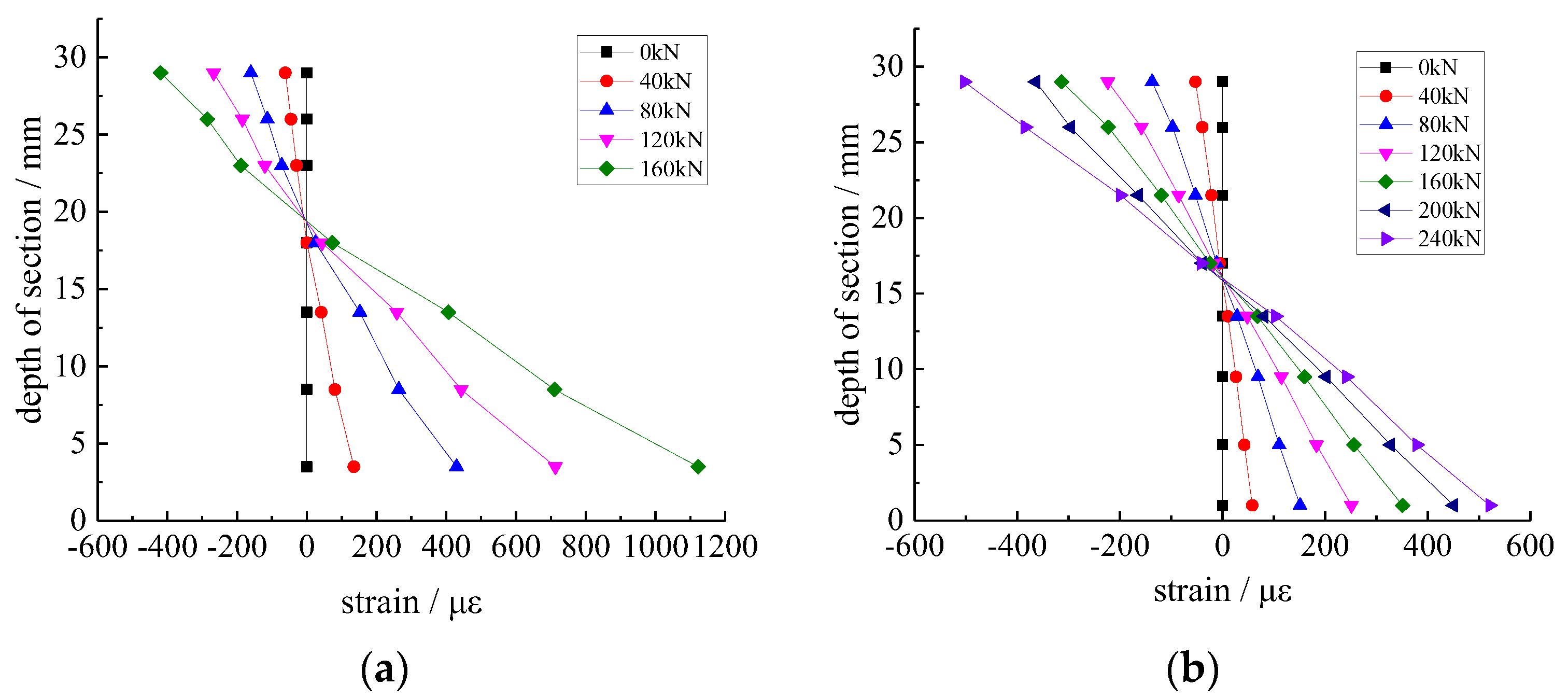
3.3.1. Distribution at Mid-Span
3.3.2. The Interface between the UHPC Channel and the RCCD Slab
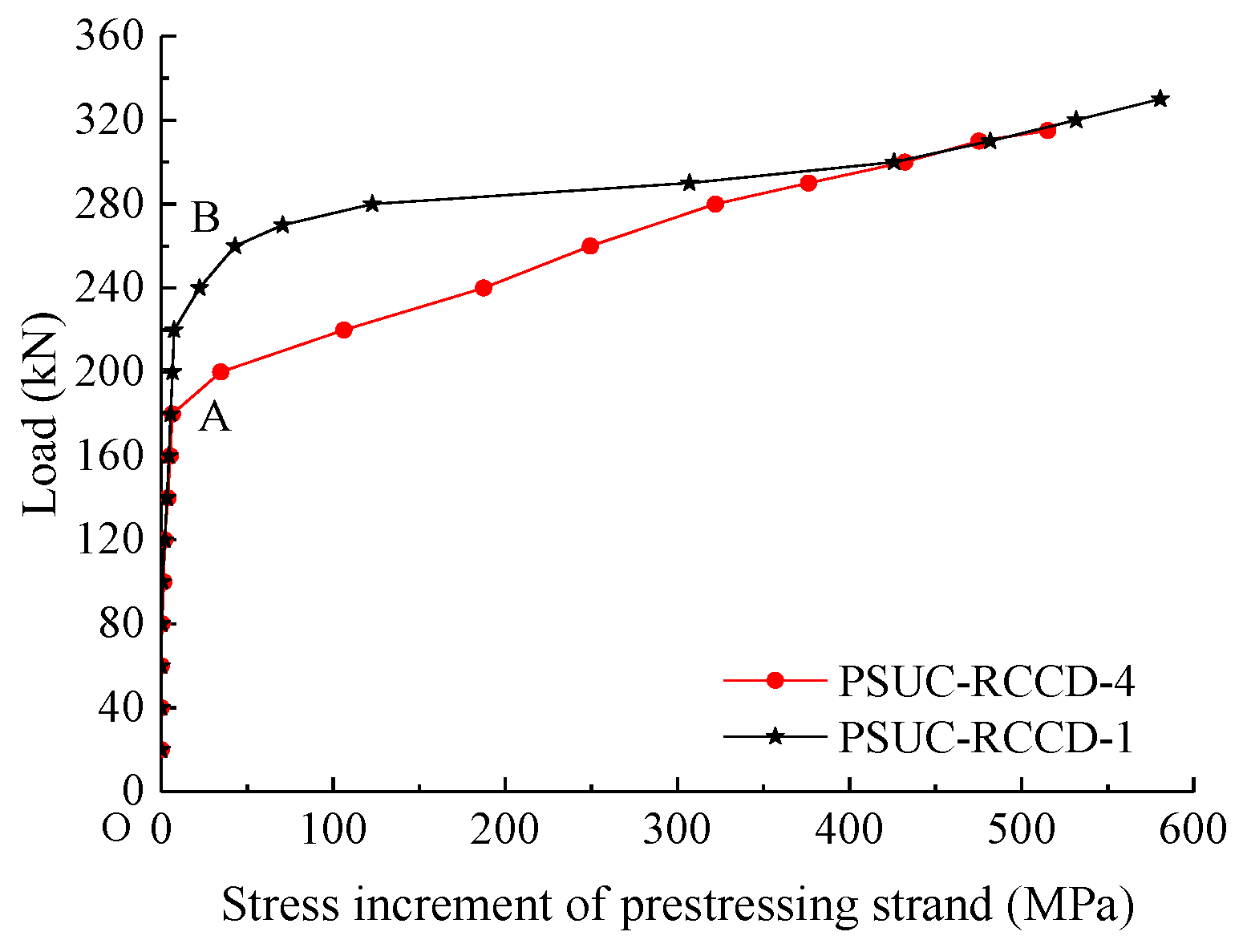
3.4. Curve of Load vs. Stress Increment of the Prestressing Strands
4. Finite Element Method Analysis
4.1. Finite Element Model
4.1.1. Model of Material Properties
4.1.2. Unit Types and Interrelationships
4.1.3. Boundary Conditions, Meshing, and Loading Methods
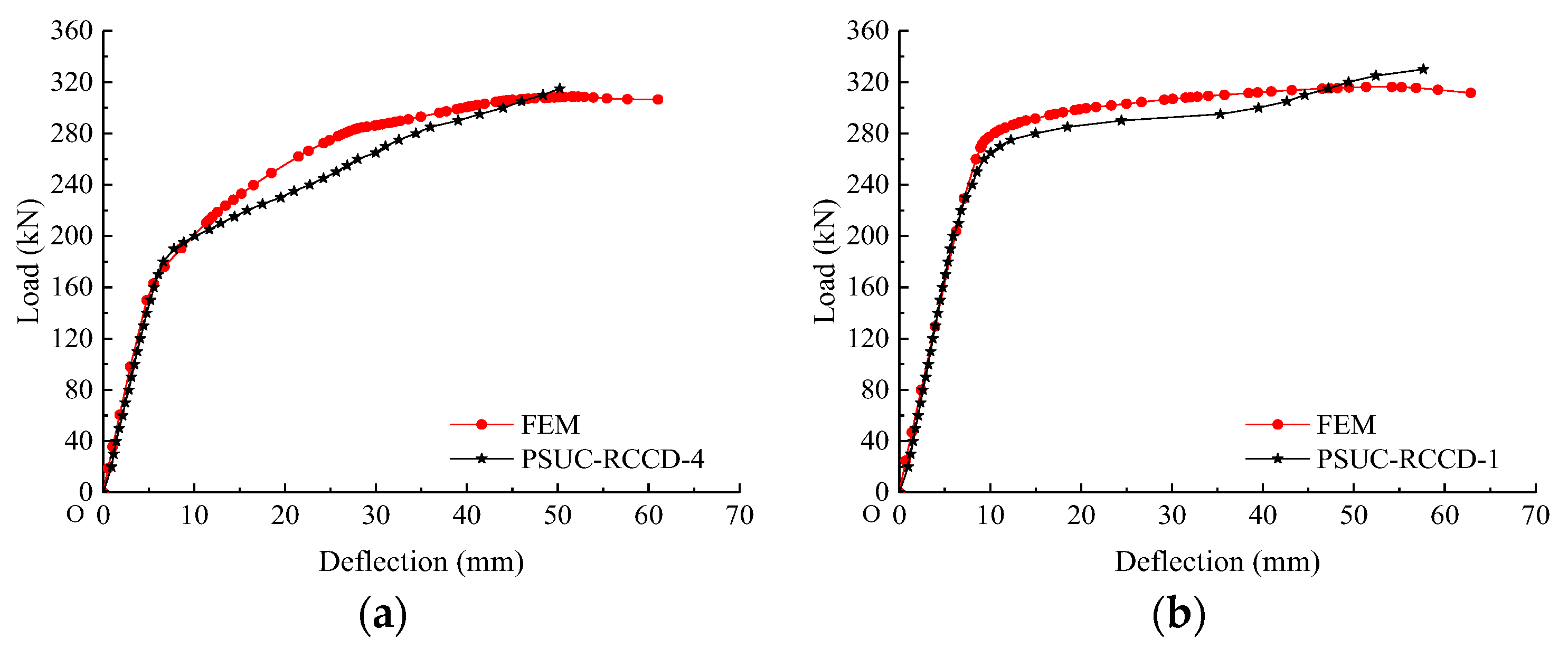
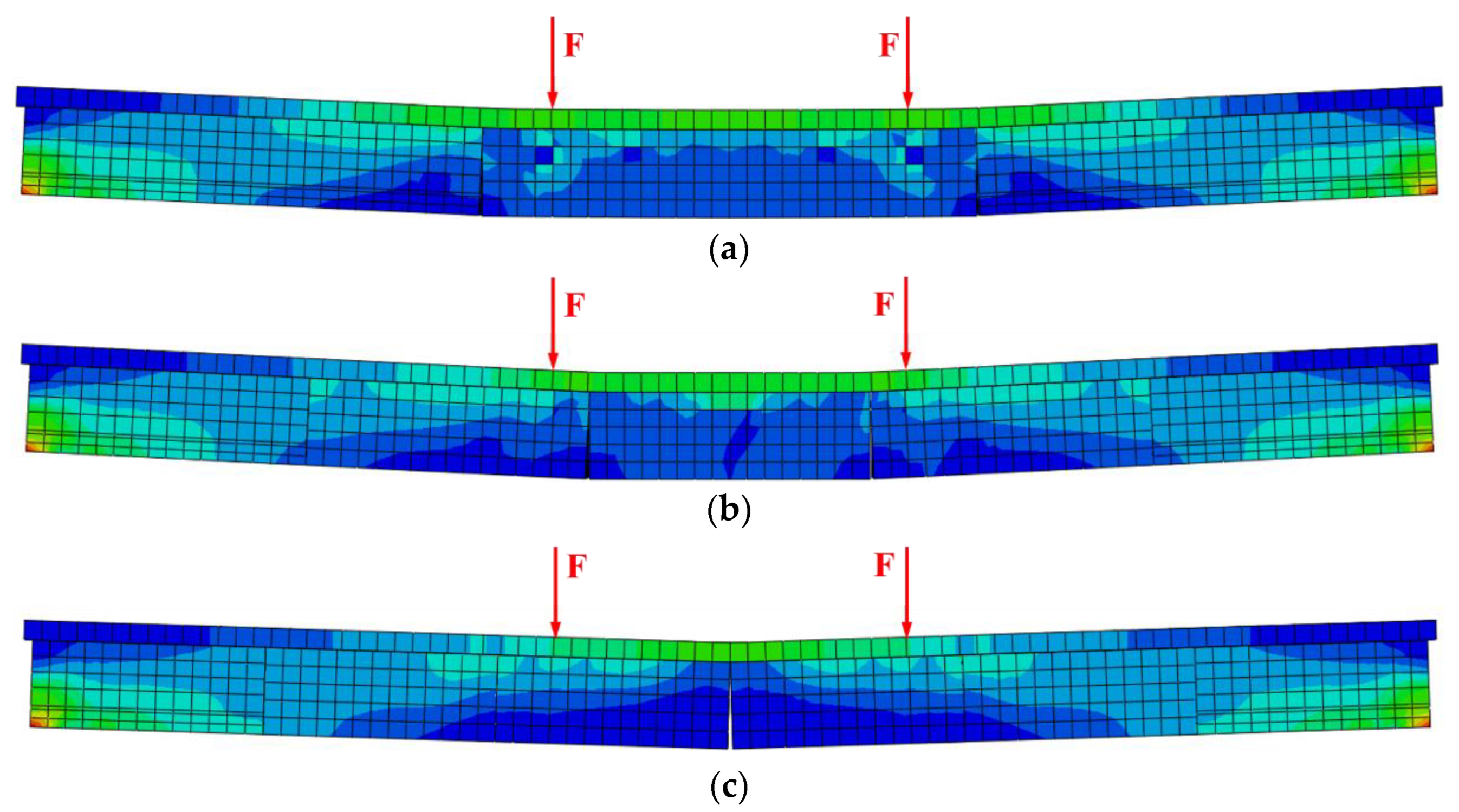
4.1.4. FEM Results
4.2. Parameter Analysis
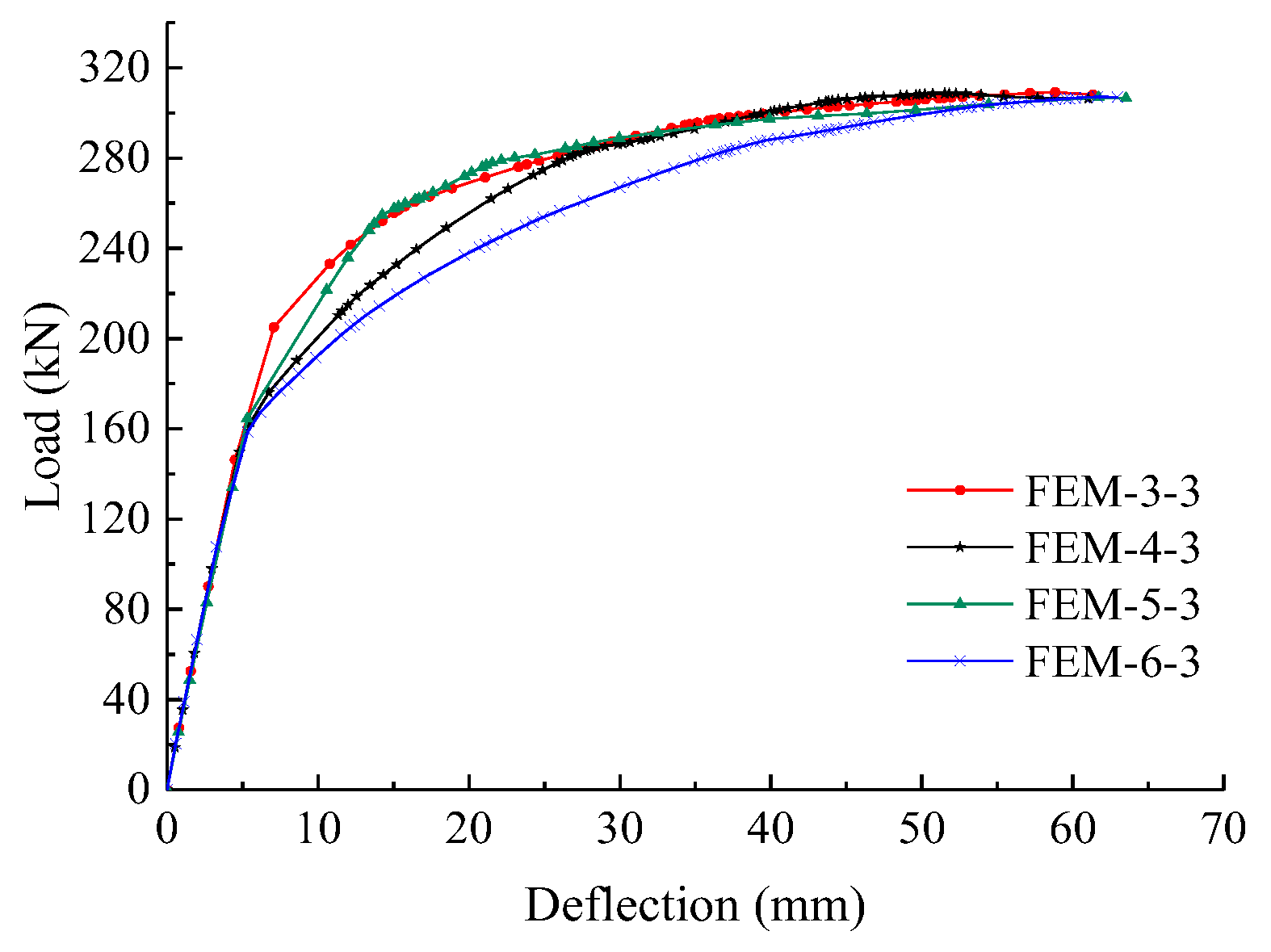
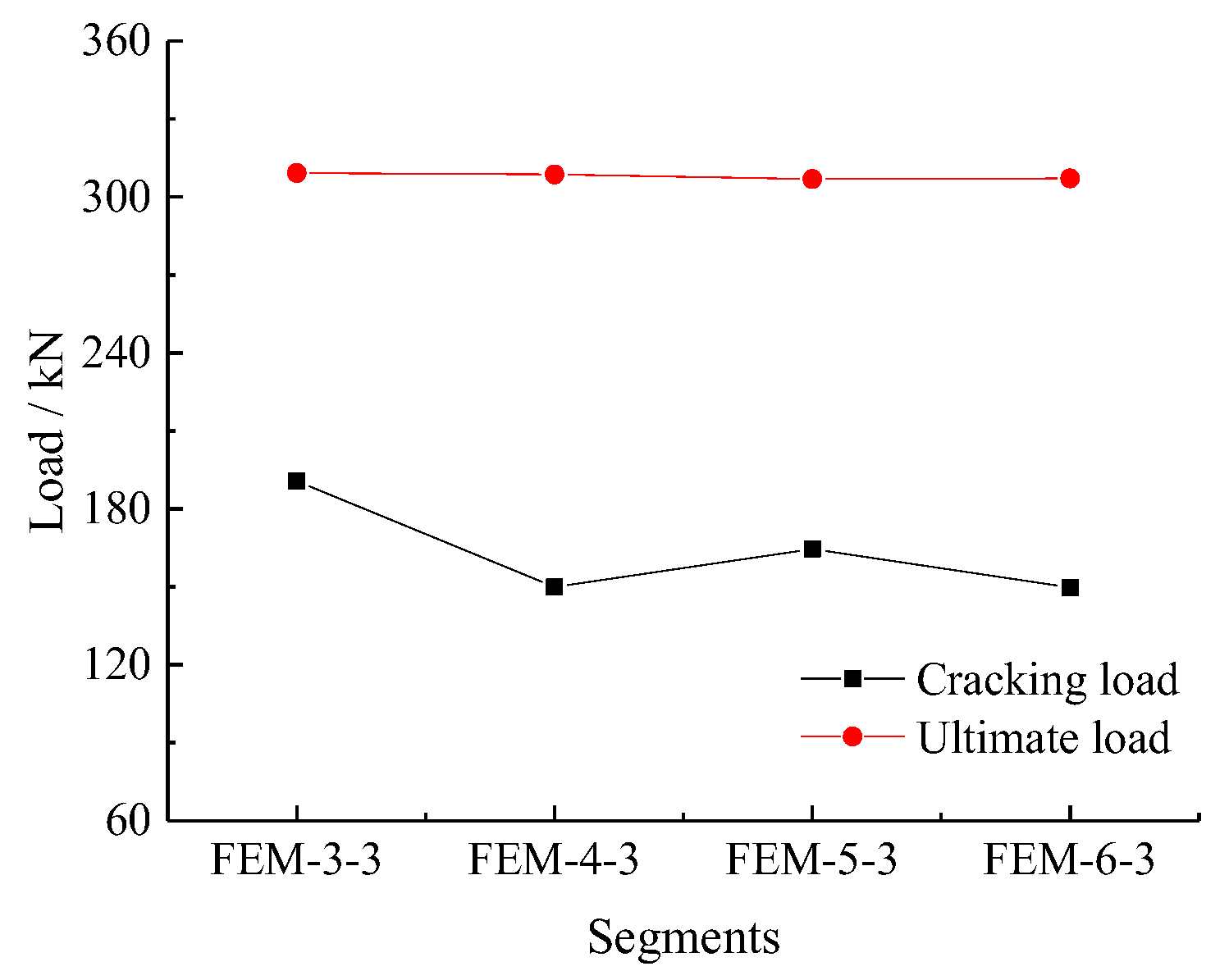
4.2.1. Number of Segments
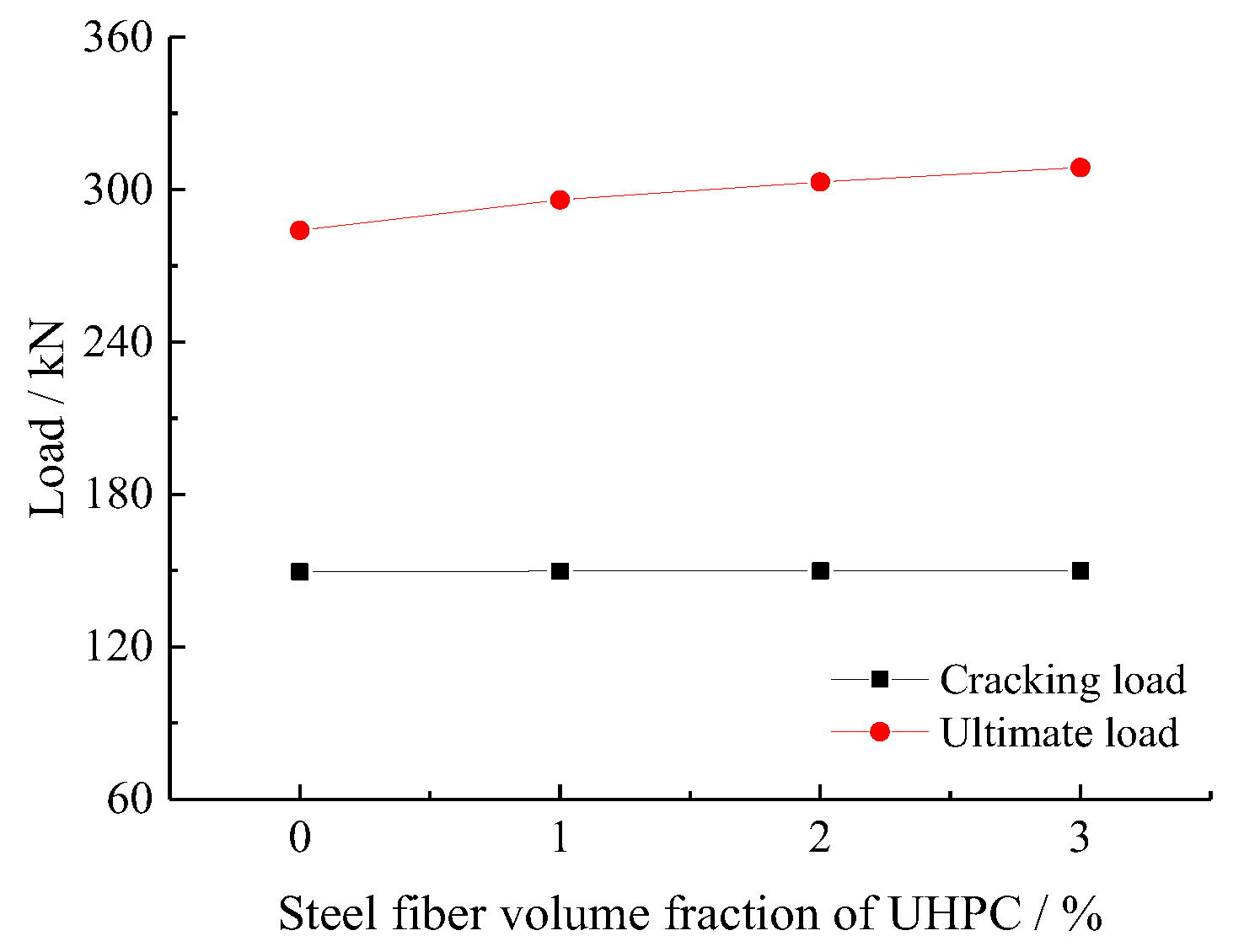
4.2.2. Steel Fiber Volume Fraction of UHPC
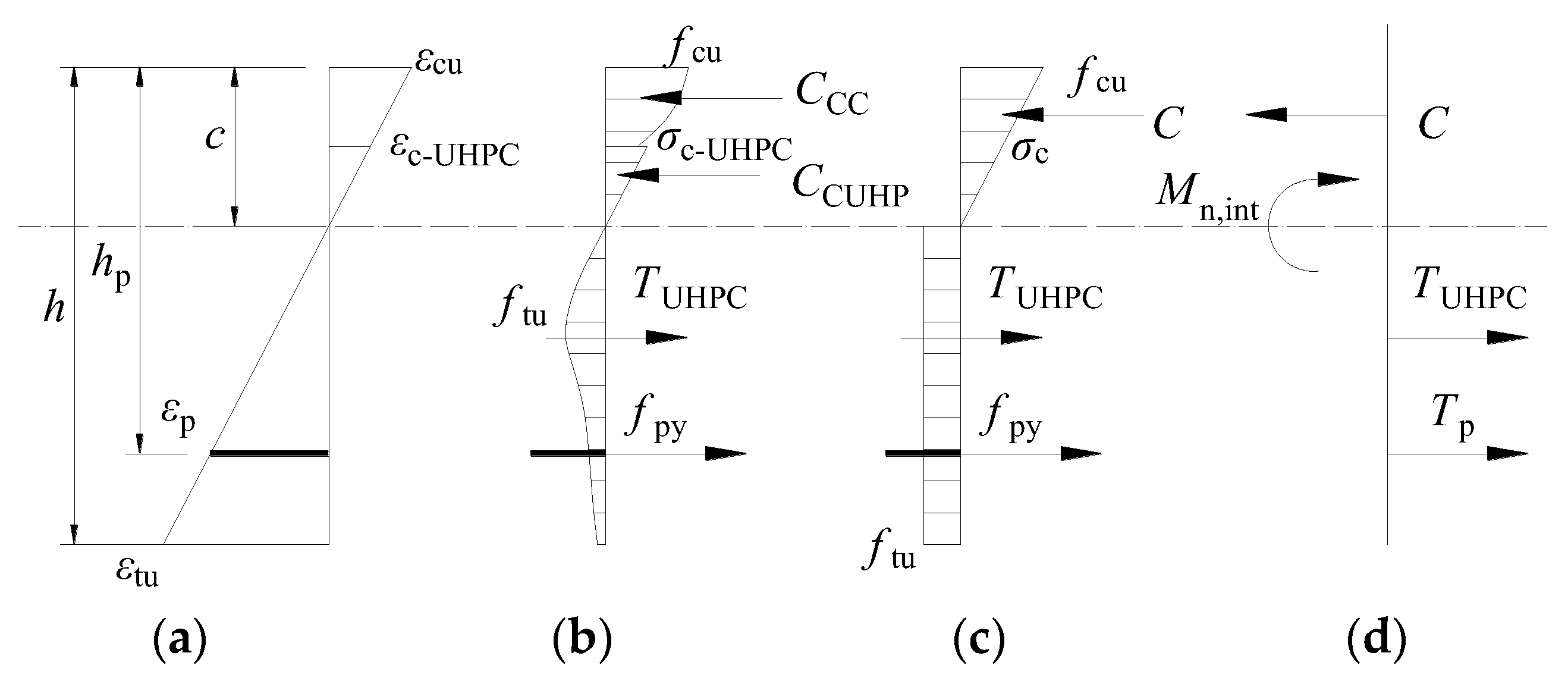
5. Methods of Calculating Flexural Capacity
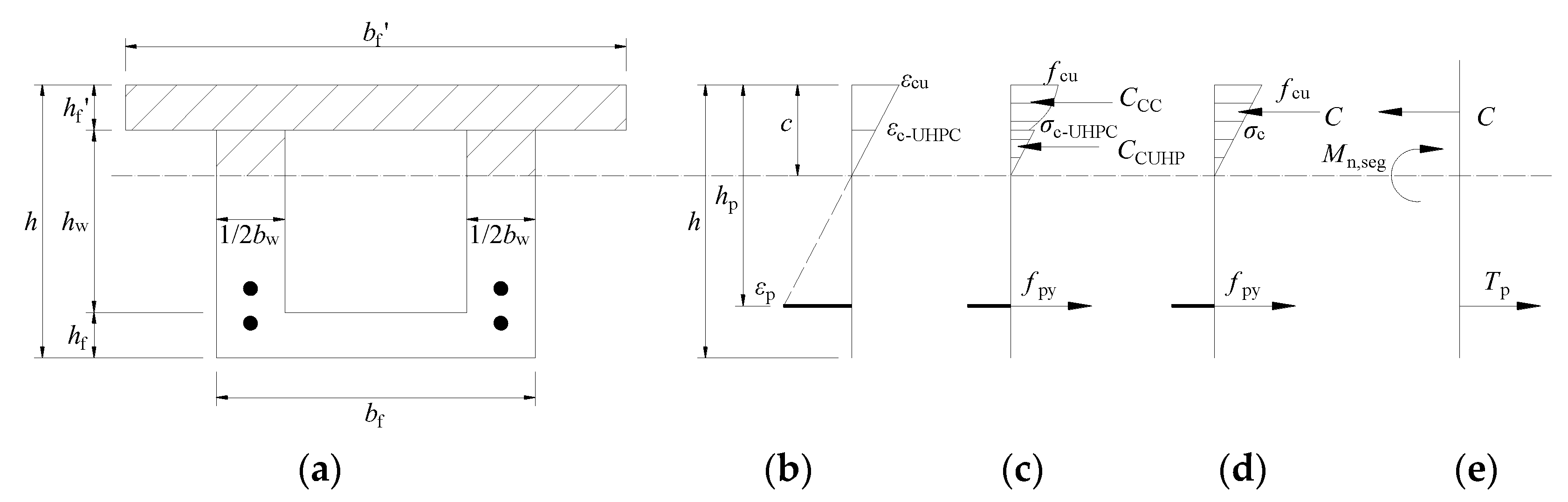
5.1. Semi-Segmental Sections
5.2. Integral Section
5.3. Validation and Discussion of the Methods of Calculating Flexural Capacity
5.3.1. Validation
5.3.2. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, C.J.; Wu, Z.M.; Xiao, J.F.; Wang, D.; Huang, Z.; Fang, Z. A review on ultra high performance concrete: Part I. Raw materials and mixture design. Constr. Build. Mater. 2015, 101, 741–751. [Google Scholar] [CrossRef]
- Wang, D.H.; Shi, C.J.; Wu, Z.M.; Xiao, J.F.; Huang, Z.; Fang, Z. A review on ultra high performance concrete: Part II. Hydration, microstructure and properties. Constr. Build. Mater. 2015, 96, 368–377. [Google Scholar] [CrossRef]
- Zhou, M.; Lu, W.; Song, J.W.; Lee, G.C. Application of ultra-high performance concrete in bridge engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Xue, J.Q.; Briseghella, B.; Huang, F.Y.; Nuti, C.; Tabatabai, H.; Chen, B.C. Review of ultra-high performance concrete and its application in bridge engineering. Constr. Build. Mater. 2020, 260, 119844. [Google Scholar] [CrossRef]
- Graybeal, B.A.; Brühwiler, E.; Kim, B.S.; Toutlemonde, F. International Perspective on UHPC in Bridge Engineering. J. Bridge Eng. 2020, 25, 04020094. [Google Scholar] [CrossRef]
- Mishra, O.; Singh, S.P. An overview of microstructural and material properties of ultra-high-performance concrete. J. Sustain. Cem. 2019, 8, 97–143. [Google Scholar] [CrossRef]
- Ingrid, L.L.; Rein, T.T. The influence of steel fibres on compressive and tensile strength of ultra high performance concrete: A review. Constr. Build. Mater. 2020, 256, 119459. [Google Scholar] [CrossRef]
- Raju, S.; Jeong, G.J.; Prem, P.B. A comprehensive review on effects of mineral admixtures and fibers on engineering properties of ultra-high-performance concrete. J. Build. Eng. 2022, 45, 103314. [Google Scholar] [CrossRef]
- Yang, J.; Chen, B.C.; Su, J.Z.; Xu, G.; Zhang, D.; Zhou, J.L. Effects of fibers on the mechanical properties of UHPC: A review. J. Traffic Transp. Eng. 2022, 9, 363–387. [Google Scholar] [CrossRef]
- Perry, V.H. Ultra-High-Performance-Concrete Advancements and Industrialization—The Need for Standard Testing. Adv. Civ. Eng. Mater. 2015, 4, 20140028. [Google Scholar] [CrossRef]
- Jiang, H.B.; Cao, Q.; Liu, A.R.; Wang, T.L.; Qiu, Y. Flexural behavior of precast concrete segmental beams with hybrid tendons and dry joints. Constr. Build. Mater. 2016, 110, 1–7. [Google Scholar] [CrossRef]
- Liu, T.X.; Wang, Z.; Guo, J.; Wang, J.Q. Shear Strength of Dry Joints in Precast UHPC Segmental Bridges: Experimental and Theoretical Research. J. Bridge Eng. 2018, 24, 04018100.1–04018100.18. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ohtake, A.; Musha, H.; Watanabe, N. Recent innovative application of UFC bridges in Japan. In Proceedings of the FraMCoS-7, 7th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Jeju, Republic of Korea, 23–28 May 2010; pp. 24–27. [Google Scholar]
- Resplendino, J. Ultra-high performance concretes-recent realizations and research programs on UHPFRC bridges in France. In Proceedings of the Second International Symposium on Ultra High Performance Concrete, Kassel, Germany, 5–7 March 2008; pp. 31–43. [Google Scholar]
- Voo, Y.L.; Stephen, J.F. Design and construction of the 100 metre span uhpc batu 6 segmental box girder bridge. In Proceedings of the HiPerMat 2016 4th International Symposium on Ultra-High Performance Concrete and High Performance Materials, Kassel, Germany, 9–11 March 2016; pp. 173–174. [Google Scholar]
- Jeong, M.S.; Park, S.Y.; Han, S.M. Ductile Behavior of Ultra High Performance Fiber Reinforced Concrete Segmental Box Girder. J. Korean Recycl. Constr. Resour. Inst. 2017, 5, 282–289. [Google Scholar]
- Ye, M.; Li, L.F.; Yoo, D.Y.; Li, H.H.; Shao, X.D.; Zhou, C. Mechanistic understanding of precast UHPC segmental beams with external tendons and epoxy joints subject to combined bending and shear. Eng. Struct. 2023, 280, 115698. [Google Scholar] [CrossRef]
- Zeng, J.J.; Chen, S.P.; Feng, P.; Zhuge, Y.; Peng, K.D.; Dai, J.G.; Fan, T.H. FRP bar-reinforced ultra-high-performance concrete plates with a grouting sleeve connection: Development and flexural behavior. Eng. Struct. 2023, 287, 116164. [Google Scholar] [CrossRef]
- Su, J.Z.; Ma, X.L.; Chen, B.C.; Sennah, K. Full-scale Bending Test and Parametric Study on a 30 m Span Prestressed UHPC Box Girder. Adv. Struct. Eng. 2019, 23, 1276–1289. [Google Scholar] [CrossRef]
- Voo, Y.L.; Foster, S.J.; Chen, C.V. Ultrahigh-performance concrete segmental bridge technology: Toward sustainable bridge construction. J. Bridge Eng. 2015, 20, B5014001. [Google Scholar] [CrossRef]
- Voo, Y.L.; Hafezolghorani, M.; Foster, S.J. Application of Ultra- High Performance Fiber Reinforced Concrete Technology for Present and Future. In Proceedings of the 2nd International Conference on UHPC Materials and Structures, Fuzhou, China, 7–10 November 2018; pp. 6–20. [Google Scholar]
- Makhbal, T.O.; Han, S.M.; Kim, D.O. Flexural behavior of ultra high performance fiber reinforced concrete 50m composite box girder. In Proceedings of the 2nd International Conference on UHPC Materials and Structures, Fuzhou, China, 7–10 November 2018; pp. 777–790. [Google Scholar]
- Lee, S.J.; Makhbal, T.O.; Kim, S.T.; Han, S.M. Flexural Behavior of Segmental U-Girder and Composite U-Girder Using Ultra High Performance Concrete. J. Korean Recycl. Constr. Resour. Inst. 2017, 5, 290–297. [Google Scholar] [CrossRef]
- GB/T 31387-2015; Reactive Powder Concrete. Standards Press of China: Beijing, China, 2015. (In Chinese)
- GB/T 50081-2002; Standard for Method of Mechanical Properties on Ordinary Concrete. Standards Press of China: Beijing, China, 2002. (In Chinese)
- Yang, J.; Chen, B.C.; Shen, X.J.; Lin, Y.J. The Optimized Design of Dog-Bones for Tensile Test of Ultra-High Performance Concrete. Eng. Mech. 2018, 35, 37–46+55. [Google Scholar] [CrossRef]
- GB/T 228.1-2010; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2010. (In Chinese)
- GB/T 50152-2012; Standard for Test Method of Concrete Structures. Standards Press of China: Beijing, China, 2012. (In Chinese)
- Guo, Z.H. Strength and Deformation of Concrete—Test Basis and Principal Structure Relationship; Tsinghua University Press: Beijing, China, 1997; pp. 30–52. (In Chinese) [Google Scholar]
- FHWA-HIF-13-032; Design Guide for Precast UHPC Waffle Deck Panel System, Including Connections. U.S.Department of transportation and Federal Highway Administration: Washington, DC, USA, 2013.
- Yang, J.; Chen, B.C.; Nuti, C. Influence of steel fiber on compressive properties of ultra-high performance fiber reinforced concrete. Constr. Build. Mater. 2021, 302, 124104. [Google Scholar] [CrossRef]
- LRFDUS-6; AASHTO LRFD Bridge Design Specifications. American Association of State Highway and Transportation Officials: Washington, DC, USA, 2012.
- DBJ 43/T 325-2017; Technical Specification for Reactive Powder Concrete Structures. China Architecture & Building Press: Beijing, China, 2017. (In Chinese)














| Cement | Silica Fume | Quartz Sand | Quartz Powder | Superplasticizer | Water | ||
|---|---|---|---|---|---|---|---|
| Coarse | Medium | Fine | |||||
| 40–70 | 20–40 | 10–20 | |||||
| 1.000 | 0.300 | 0.140 | 0.410 | 0.526 | 0.094 | 0.025 | 0.204 |
| Cement | Fly Ash | Sand | Coarse Aggregate | Superplasticizer | Water |
|---|---|---|---|---|---|
| 1.000 | 0.151 | 1.426 | 2.234 | 0.019 | 0.319 |
| Material | Cubic Compressive Strength fcu/MPa | Compressive Strength fc/MPa | Tensile Strength ft/MPa | Elastic Modulus Ec/GPa |
|---|---|---|---|---|
| UHPC | 183.7 (3.49) | 164.2 (2.70) | 10.2 (0.64) | 46.2 (2.45) |
| CC | 53.3 (3.90) | 45.8 (3.23) | - | 35.8 (1.88) |
| Material | Diameter d/mm | Yield Strength fy/MPa | Ultimate Strength fu/MPa | Elastic Modulus Es/GPa |
|---|---|---|---|---|
| Prestressing strand | 15.2 | 1490 | 1875 | 198 |
| HRB400 | 6 | 407 | 525 | 203 |
| 8 | 445 | 600 | 203 | |
| 10 | 462 | 635 | 203 |
| Group | Parameters | Girder Notation | Segments (n) | Steel Fiber Volume Fraction of UHPC | Mn,EFM |
|---|---|---|---|---|---|
| Group 1 | Number of segments | FEM-3-3 | 3 | 3 | 216.01 |
| FEM-4-3 | 4 | 216.43 | |||
| FEM-5-3 | 5 | 216.08 | |||
| FEM-6-3 | 6 | 214.84 | |||
| Group 2 | Steel fiber volume fraction of UHPC | FEM-4-0 | 4 | 0 | 197.19 |
| FEM-4-1 | 1 | 204.2 | |||
| FEM-4-2 | 2 | 210.94 | |||
| FEM-4-3 | 3 | 216.43 |
| Girder Notation | (Mn.exp or Mn.FEM)/kN·m | Mn.cal/(Mn.exp or Mn.FEM) |
|---|---|---|
| PSUC–RCCD-1 | 231 | 1.07 |
| PSUC–RCCD-4 | 220.5 | 0.83 |
| FEM-3-3 | 216.01 | 0.85 |
| FEM-4-3 | 216.43 | 0.85 |
| FEM-5-3 | 216.08 | 0.85 |
| FEM-6-3 | 214.84 | 0.86 |
| FEM-4-0 | 197.19 | 0.93 |
| FEM-4-1 | 204.20 | 0.90 |
| FEM-4-2 | 210.94 | 0.87 |
| FEM-4-3 | 216.43 | 0.85 |
| Mean value | 0.87 | |
| Standard deviation | 0.029 |
| Group | Parameters | Girder Notation | Segments (n) | Steel Fiber Volume Fraction of UHPC | Mn,EFM |
|---|---|---|---|---|---|
| Group 3 | Steel fiber volume fraction of UHPC | FEM-1-0 | 1 | 0 | 197.57 |
| FEM-1-1 | 1 | 207.94 | |||
| FEM-1-2 | 2 | 214.79 | |||
| FEM-1-3 | 3 | 221.39 |
| Girder Notation | φ(Mexp.seg/Mexp.int) |
|---|---|
| PSUC–RCCD-4/ PSUC–RCCD-1 | 0.95 |
| FEM-3-3/FEM-1-3 | 0.97 |
| FEM-4-3/FEM-1-3 | 0.97 |
| FEM-5-3 FEM-1-3 | 0.97 |
| FEM-6-3/ FEM-1-3 | 0.96 |
| FEM-4-0/FEM-1-0 | 1.00 |
| FEM-4-1/FEM-1-1 | 0.98 |
| FEM-4-2/FEM-1-2 | 0.98 |
| FEM-4-3/FEM-1-3 | 0.98 |
| Mean value | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhou, J.; Guo, F.; Chen, B.; Nuti, C. Experimental Study on the Flexural Behaviors of Prestressed Segmental Ultra–High–Performance Concrete Channels and Reinforced Conventional Concrete Deck Composite Girders. Buildings 2023, 13, 1841. https://doi.org/10.3390/buildings13071841
Chen Y, Zhou J, Guo F, Chen B, Nuti C. Experimental Study on the Flexural Behaviors of Prestressed Segmental Ultra–High–Performance Concrete Channels and Reinforced Conventional Concrete Deck Composite Girders. Buildings. 2023; 13(7):1841. https://doi.org/10.3390/buildings13071841
Chicago/Turabian StyleChen, Yicong, Jialiang Zhou, Fangzhi Guo, Baochun Chen, and Camillo Nuti. 2023. "Experimental Study on the Flexural Behaviors of Prestressed Segmental Ultra–High–Performance Concrete Channels and Reinforced Conventional Concrete Deck Composite Girders" Buildings 13, no. 7: 1841. https://doi.org/10.3390/buildings13071841






