A Fast and Non-Destructive Prediction Model for Remaining Life of Rigid Pavement with or without Asphalt Overlay
Abstract
:1. Introduction
1.1. Background
1.2. Objective and Scope
2. Concept and Methodology Development
2.1. Inverse Design Concept
2.2. Methodology Development
2.2.1. Remaining Life Prediction Model
2.2.2. Determination of Model Parameters
3. Field Testing
3.1. Pavement Sections
3.2. Data Collection and Process
3.2.1. Traffic Data
3.2.2. Geometrical Data
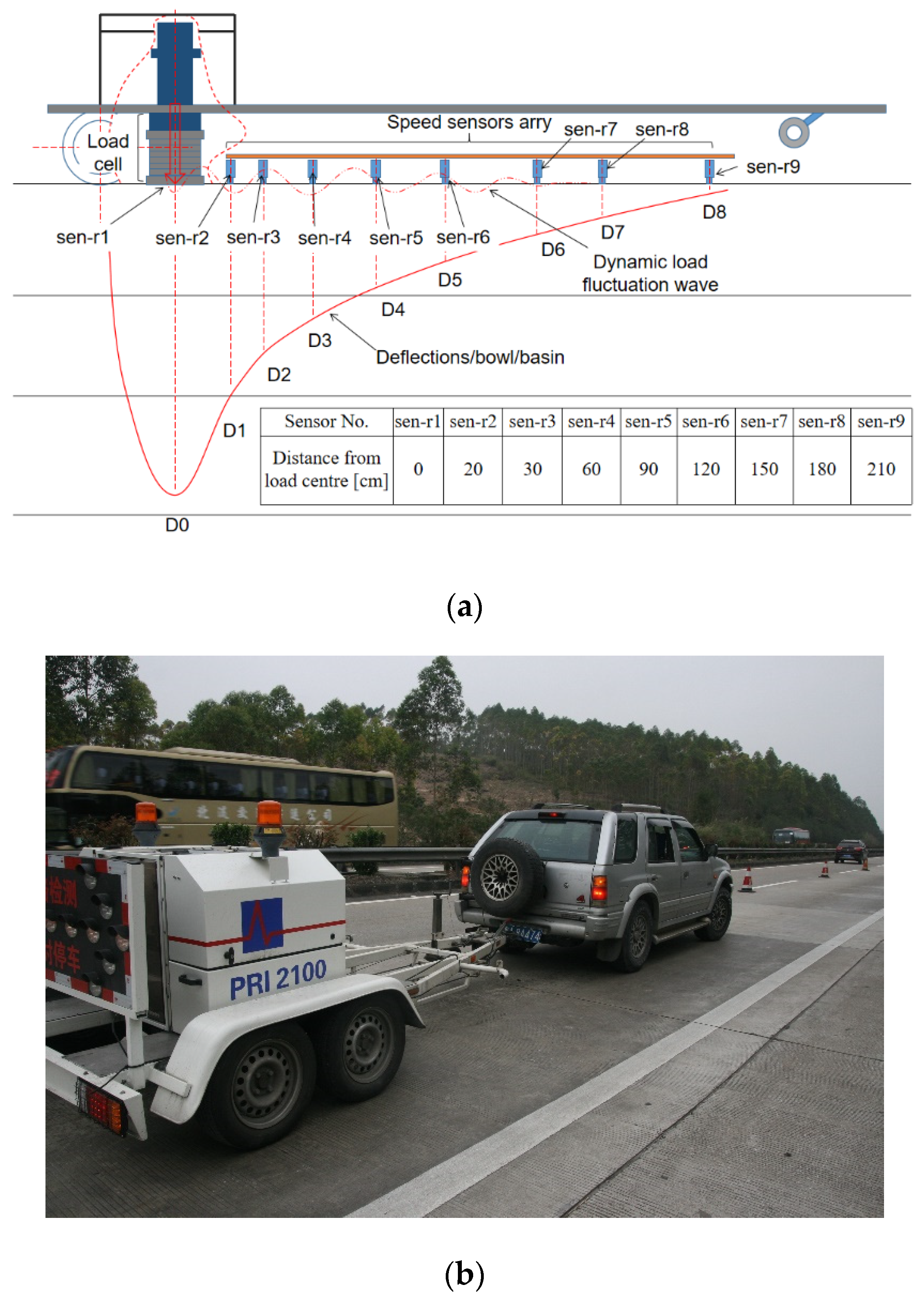
3.2.3. Mechanical Parameters
4. Results and Analysis
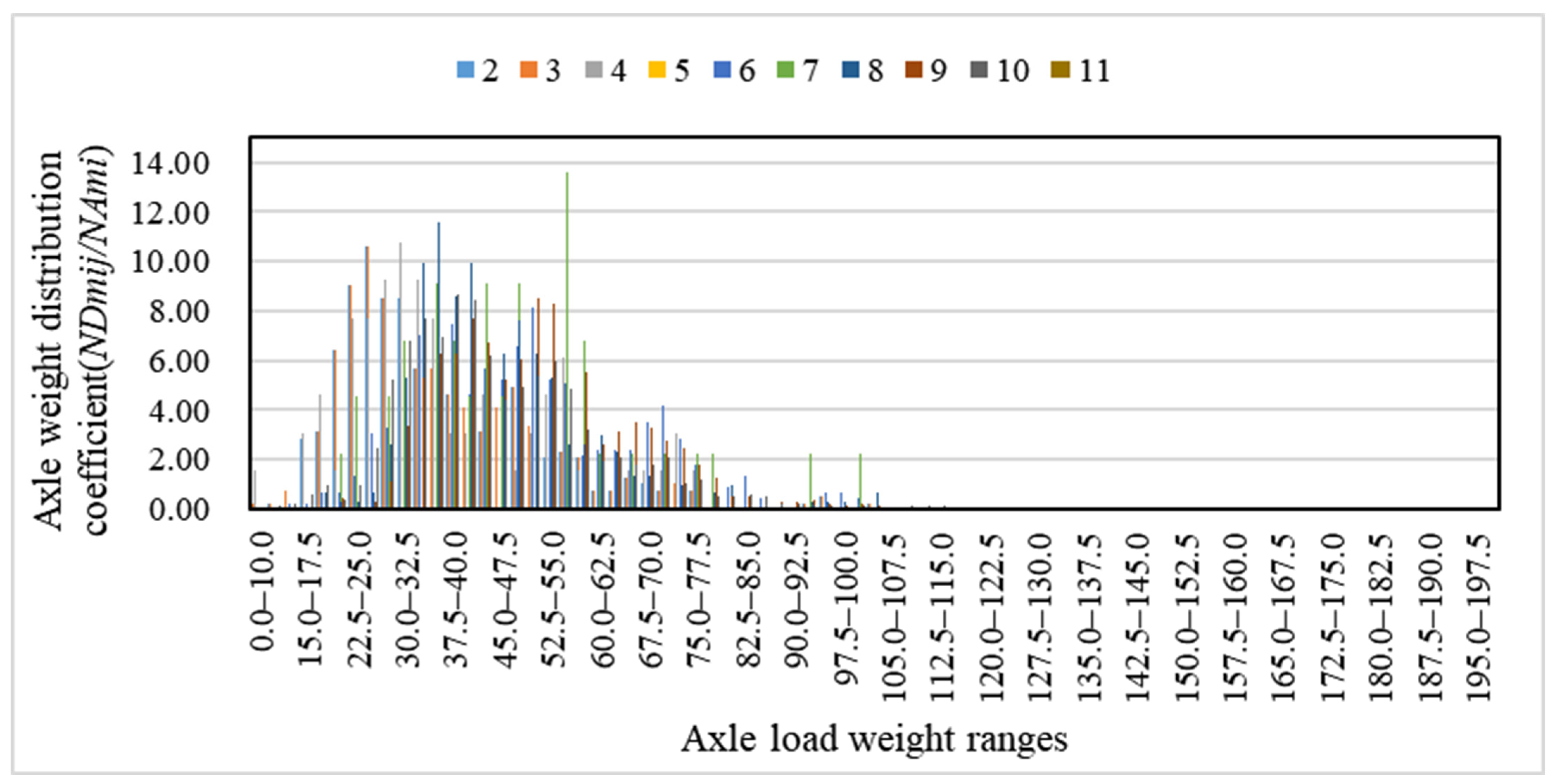
4.1. Traffic Data
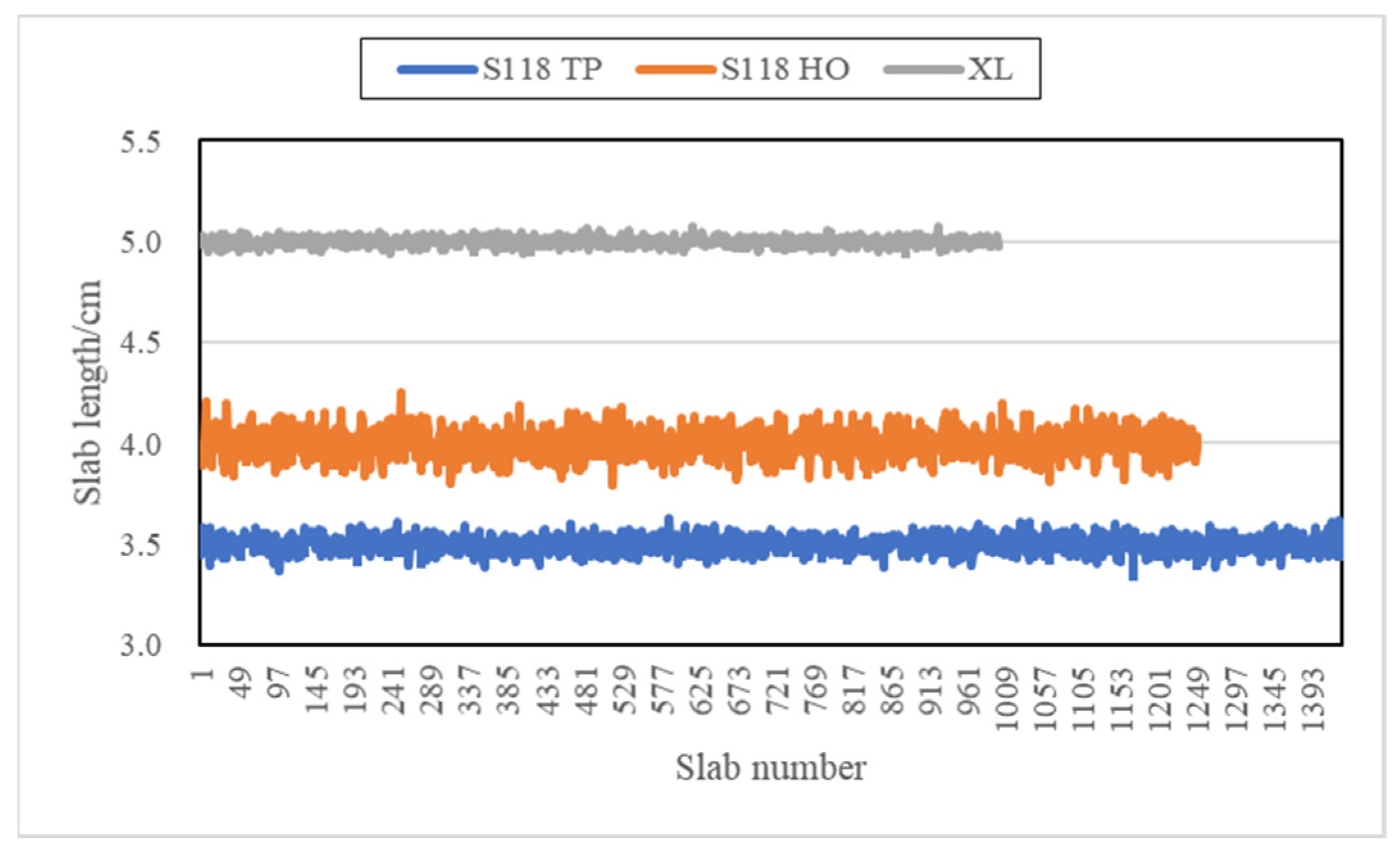
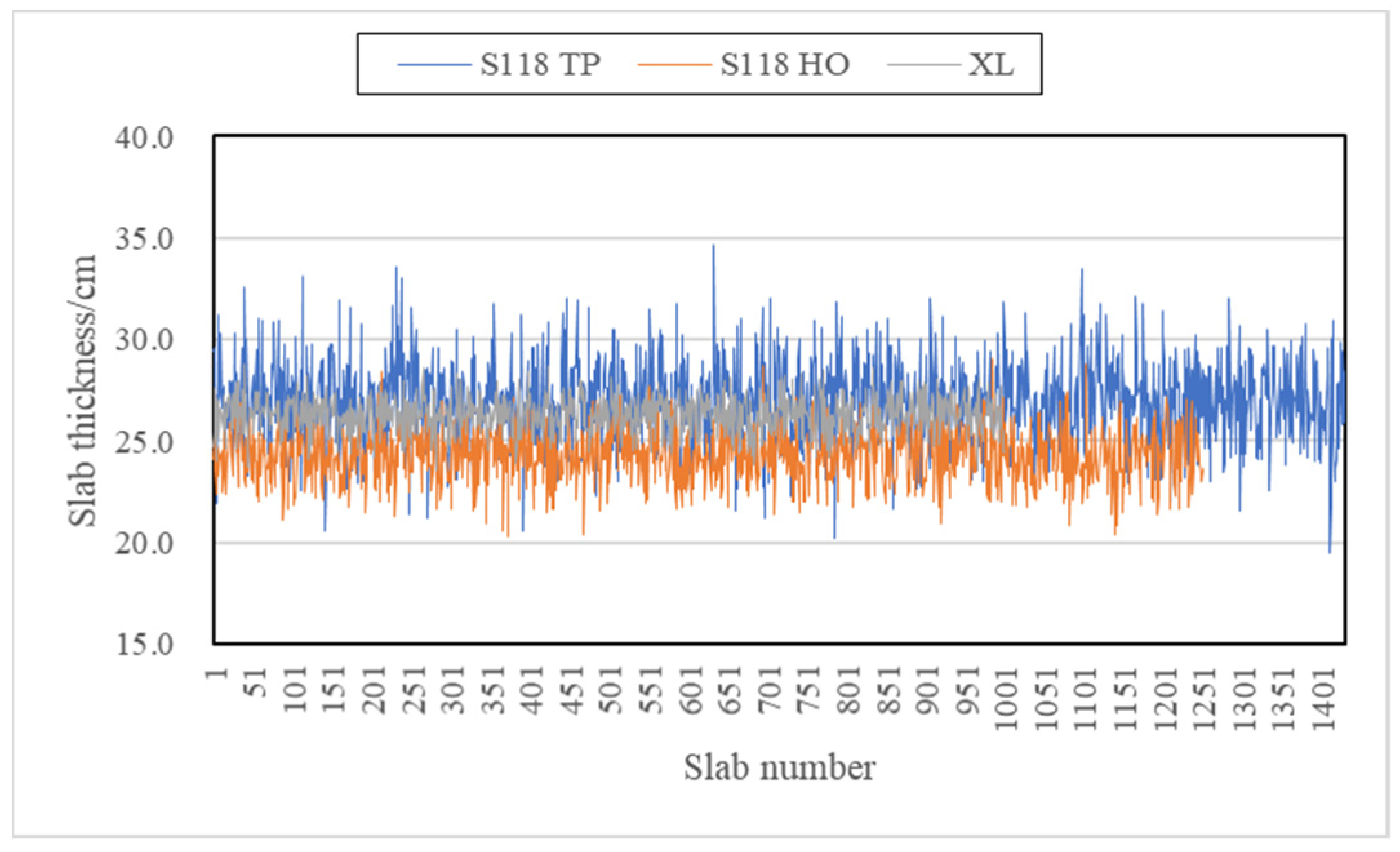
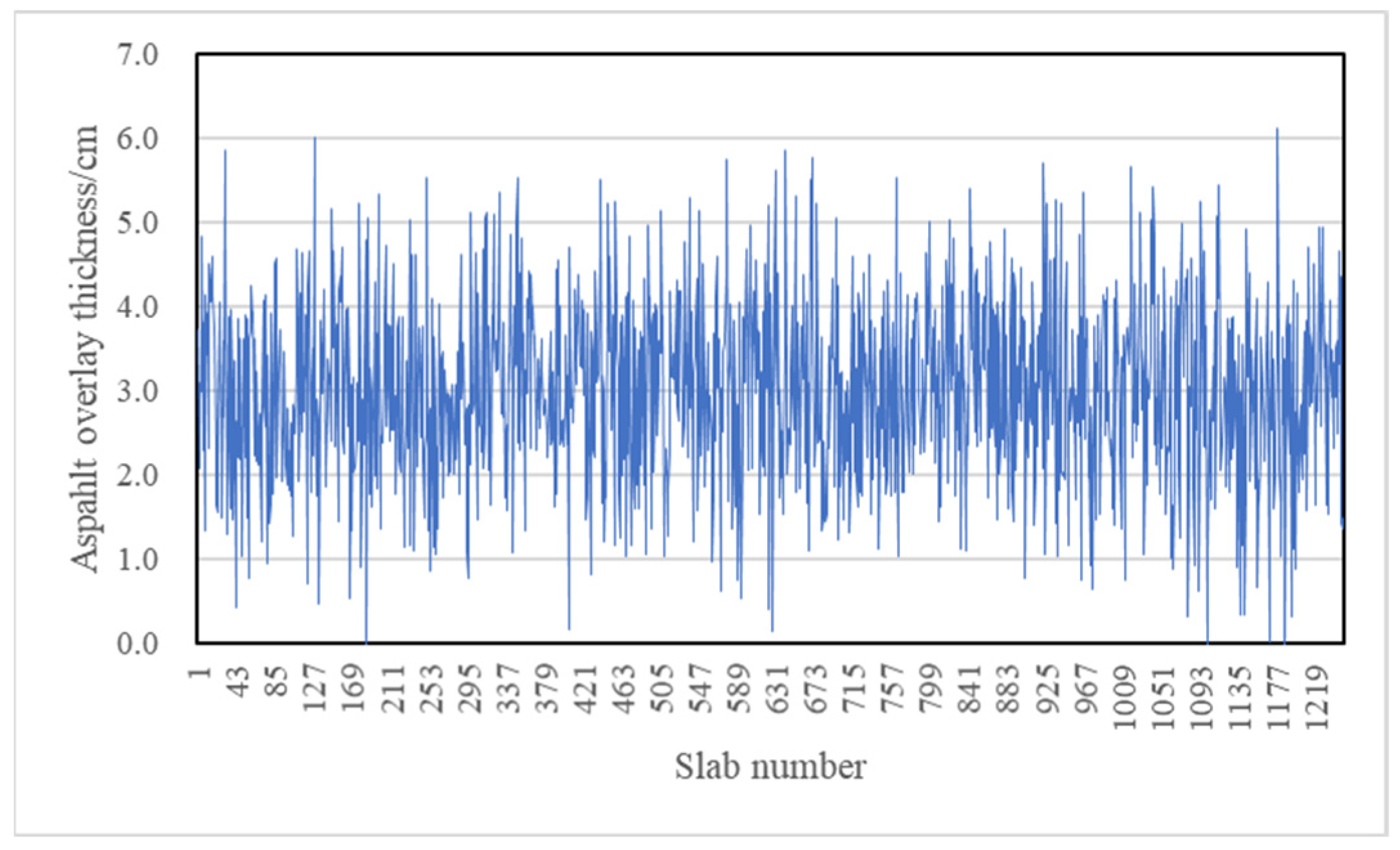
4.2. Geometrical Data
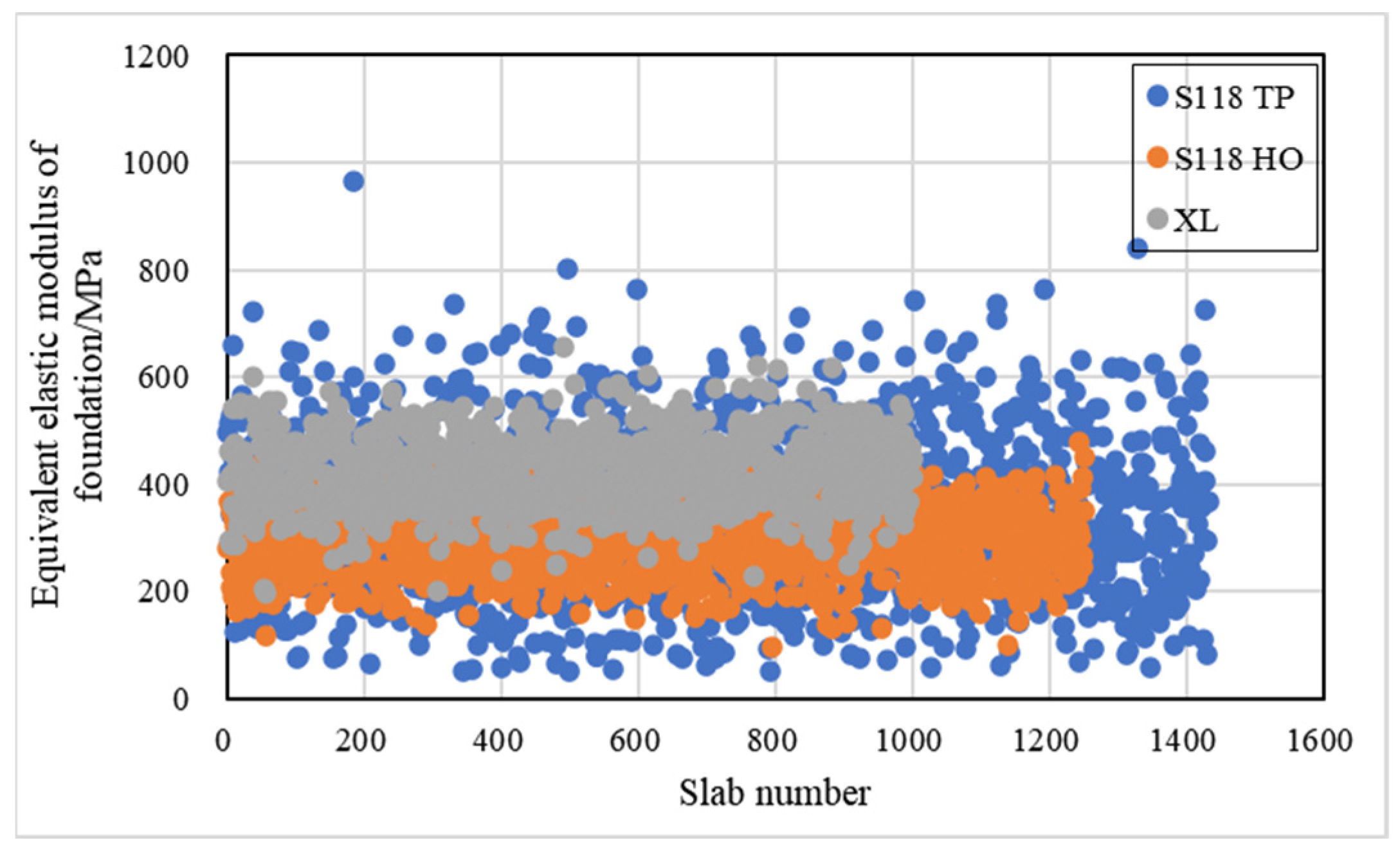
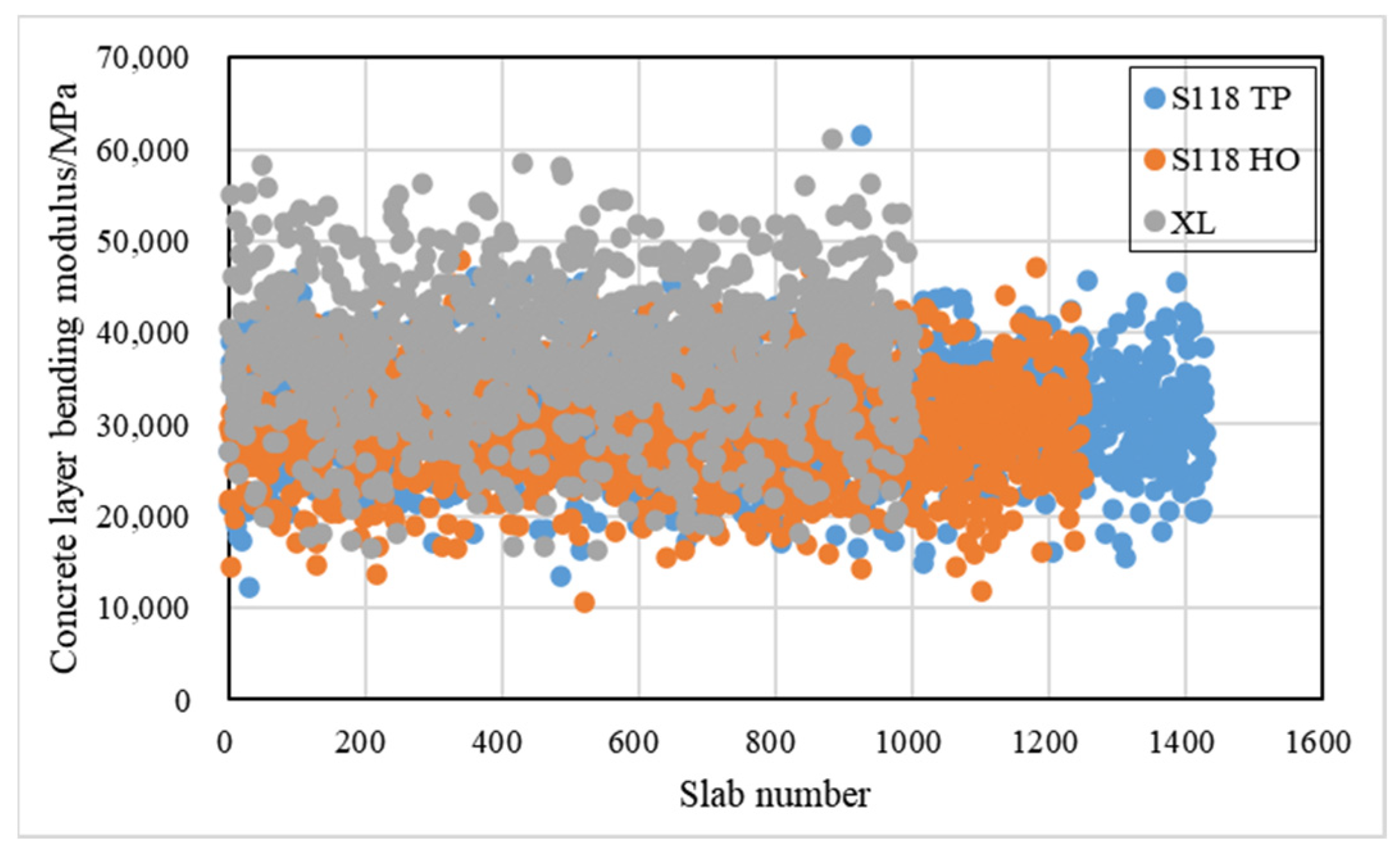
4.3. Mechanical Parameters
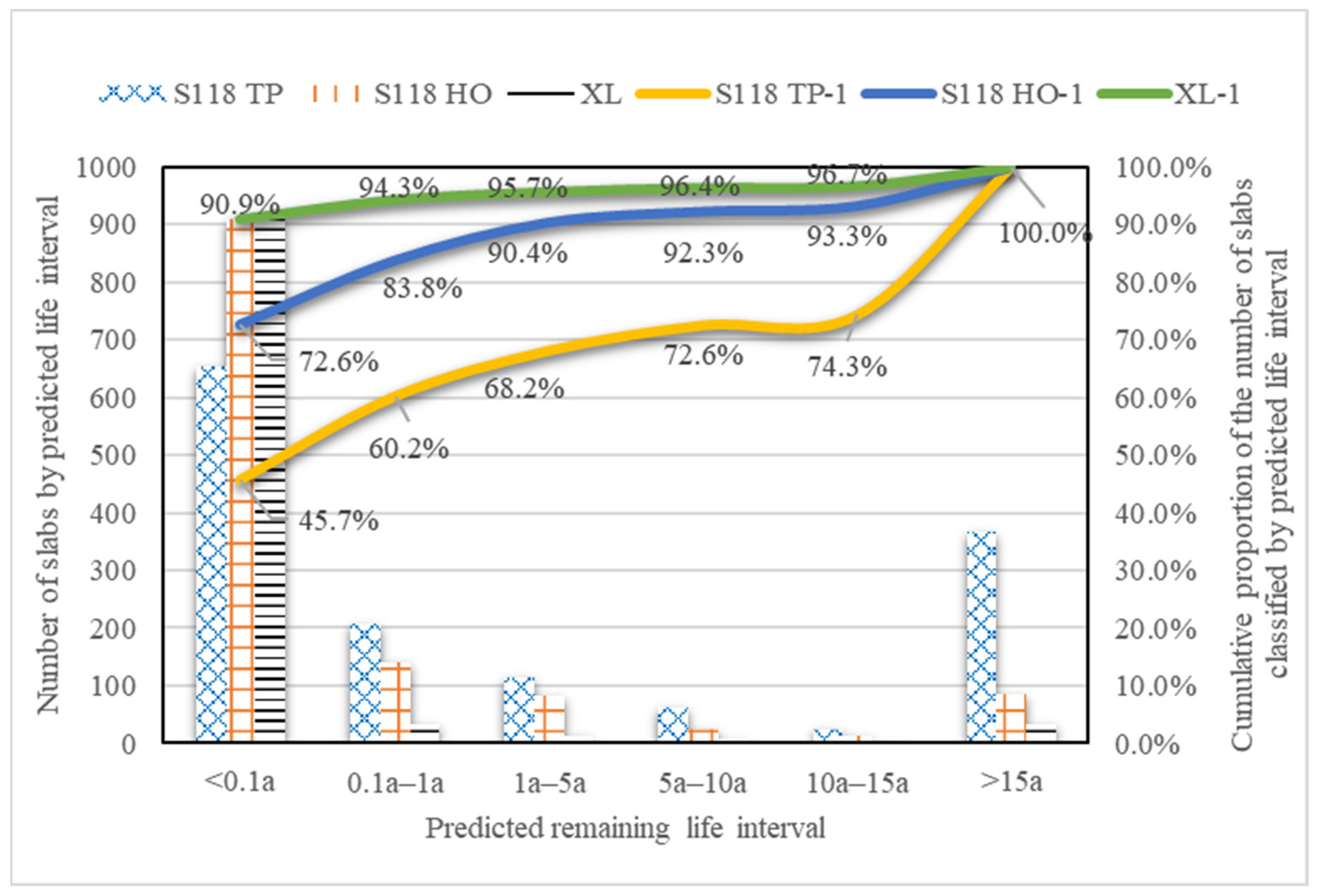
4.4. Feasibility of the Prediction Model
4.5. Application of the Prediction Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DeSantis, J.W.; Sachs, S.G.; Vandenbossche, J.M. Faulting development in concrete pavements and overlays. Int. J. Pavement Eng. 2020, 21, 1445–1460. [Google Scholar] [CrossRef]
- Choi, J.-h. Strategy for reducing carbon dioxide emissions from maintenance and rehabilitation of highway pavement. J. Clean. Prod. 2019, 209, 88–100. [Google Scholar] [CrossRef]
- Chorzepa, M.G.; Johnson, C.; Durham, S.; Kim, S.S. Forensic Investigation of Continuously Reinforced Concrete Pavements in Fair and Poor Condition. J. Perform. Constr. Facil. 2018, 32, 04018031. [Google Scholar] [CrossRef]
- Abdelaty, A.; Jeong, H.D.; Smadi, O. Barriers to Implementing Data-Driven Pavement Treatment Performance Evaluation Process. J. Transp. Eng. Part B Pavements 2018, 144, 04017022. [Google Scholar] [CrossRef]
- Bhattacharya, B.B.; Gotlif, A.; Darter, M.I.; Khazanovich, L. Impact of Joint Spacing on Bonded Concrete Overlay of Existing Asphalt Pavement in the AASHTOWare Pavement ME Design Software. J. Transp. Eng. Part B Pavements 2019, 145, 04019018. [Google Scholar] [CrossRef]
- Qiao, J.Y.; Du, R.; Labi, S.; Fricker, J.D.; Sinha, K.C. Policy implications of standalone timing versus holistic timing of infrastructure interventions: Findings based on pavement surface roughness. Transp. Res. Part A Policy Pract. 2021, 148, 79–99. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, W.; Mei, J.; Yue, G.; Yang, L. Optimization of Structure Parameters of Airfield Jointed Concrete Pavements under Temperature Gradient and Aircraft Loads. Adv. Mater. Sci. Eng. 2019, 2019, 3251590. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Thakkar, C.; Chen, X.; Murrel, S. Life-cycle assessment of airport pavement design alternatives for energy and environmental impacts. J. Clean. Prod. 2016, 133, 163–171. [Google Scholar] [CrossRef]
- Qiao, Y.; Labi, S.; Fricker, J.; Sinha, K.C. Costs and effectiveness of standard treatments applied to flexible and rigid pavements: Case study in Indiana, USA. Infrastruct. Asset Manag. 2019, 6, 15–29. [Google Scholar] [CrossRef]
- Carvalho, A.F.C.; Santos, L.G.d.P. Maintenance of airport pavements: The use of visual inspection and IRI in the definition of degradation trends. Int. J. Pavement Eng. 2017, 20, 425–431. [Google Scholar] [CrossRef]
- Khan, T.U.; Norton, S.T.; Keegan, K.; Gould, J.S.; Jacques, C.D. Use of Multiple Non-Destructive Evaluation Approaches in Connecticut to Establish Accurate Joint Repair and Replacement Estimates for Composite Pavement Rehabilitation. Airfield Highw. Pavements 2017, 2017, 201–208. [Google Scholar]
- Yu, J.; Zhang, X.; Xiong, C. A methodology for evaluating micro-surfacing treatment on asphalt pavement based on grey system models and grey rational degree theory. Constr. Build. Mater. 2017, 150, 214–226. [Google Scholar] [CrossRef]
- Kirillov, A.M.; Zavyalov, M.A. Prediction of Remaining Service Life of Asphalt Pavements. Vestn. MGSU 2018, 3, 356–367. [Google Scholar] [CrossRef] [Green Version]
- Setyawan, A.; Nainggolan, J.; Budiarto, A. Predicting the Remaining Service Life of Road Using Pavement Condition Index. Procedia Eng. 2015, 125, 417–423. [Google Scholar] [CrossRef] [Green Version]
- Goenaga, B.; Fuentes, L.; Mora, O. A Practical Approach to Incorporate Roughness-Induced Dynamic Loads in Pavement Design and Performance Prediction. Arab. J. Sci. Eng. 2018, 44, 4339–4348. [Google Scholar] [CrossRef]
- Zhang, Y.; Vennapusa, P.; White, D.J. Assessment Of Designed And Measured Mechanistic Parameters Of Concrete Pavement Foundation. Balt. J. Road Bridge Eng. 2019, 14, 37–57. [Google Scholar] [CrossRef]
- NSharifi, P.; Chen, S.; You, Z.; van Dam, T.; Gilbertson, C. A review on the best practices in concrete pavement design and materials in wet-freeze climates similar to Michigan. J. Traffic Transp. Eng. 2019, 6, 245–255. [Google Scholar]
- Shi, X.; Mukhopadhyay, A.; Zollinger, D.; Grasley, Z. Economic input-output life cycle assessment of concrete pavement containing recycled concrete aggregate. J. Clean. Prod. 2019, 225, 414–425. [Google Scholar] [CrossRef]
- Kashif, M.; Naseem, A.; Iqbal, N.; de Winne, P.; de Backer, H. Evaluating the Early-Age Crack Induction in Advanced Reinforced Concrete Pavement Using Partial Surface Saw-Cuts. Appl. Sci. 2021, 11, 1659. [Google Scholar] [CrossRef]
- Rasol, M.; Pais, J.C.; Pérez-Gracia, V.; Solla, M.; Fernandes, F.M.; Fontul, S.; Ayala-Cabrera, D.; Schmidt, F.; Assadollahi, H. GPR monitoring for road transport infrastructure: A systematic review and machine learning insights. Constr. Build. Mater. 2022, 324, 126686. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, Z.; Leng, Z.; Wu, C.; Zhang, Z.; Wang, D.; Oeser, M. Effect of mixing sequence on asphalt mixtures containing waste tire rubber and warm mix surfactants. J. Clean. Prod. 2020, 246, 119008. [Google Scholar] [CrossRef]
- Yu, H.; Leng, Z.; Zhou, Z.; Shih, K.; Xiao, F.; Gao, Z. Optimization of preparation procedure of liquid warm mix additive modified asphalt rubber. J. Clean. Prod. 2017, 141, 336–345. [Google Scholar] [CrossRef]
- Yu, H.; Deng, G.; Zhang, Z.; Zhu, M.; Gong, M.; Oeser, M. Workability of rubberized asphalt from a perspective of particle effect. Transp. Res. Part D Transp. Environ. 2021, 91, 102712. [Google Scholar] [CrossRef]
- Yu, J.; Xiong, C.; Zhang, X.; Li, W. More accurate modulus back-calculation by reducing noise information from in situ–measured asphalt pavement deflection basin using regression model. Constr. Build. Mater. 2018, 158, 1026–1034. [Google Scholar] [CrossRef]
- Kheradmandi, N.; Modarres, A. Precision of back-calculation analysis and independent parameters-based models in estimating the pavement layers modulus-Field and experimental study. Constr. Build. Mater. 2018, 171, 598–610. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, H.; Zhang, Q.; Xiong, C. Glass fiber reinforced asphalt membrane for interlayer bonding between asphalt overlay and concrete pavement. Constr. Build. Mater. 2015, 101, 918–925. [Google Scholar] [CrossRef]
- Mohamed, M.; Skinner, A.; Abdel-Rahim, A.; Kassem, E.; Chang, K. Deterioration Characteristics of Waterborne Pavement Markings Subjected to Different Operating Conditions. J. Transp. Eng. Part B Pavements 2019, 145, 04019003. [Google Scholar] [CrossRef]
- Mo, T. JTG D 40-2011 Specifications for Design of Highway Cement Concrete Pavement; People’s Communications Publishing House: Beijing, China, 2011. [Google Scholar]
- White, G. Stochastic strength rating of flexible airport pavements using construction data. Int. J. Pavement Eng. 2018, 21, 1–12. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Specifications for Design of Highway Asphalt Pavement; Ministry of Transport of the People’s Republic of China: Beijing, China, 2017.
- Goodpave. Available online: http://www.goodpave.com/ (accessed on 20 February 2022).
- Daokedaopave. Available online: http://www.daokedaopave.com/ (accessed on 25 February 2022).
- Kang, M.-S.; Kim, N.; Lee, J.J.; An, Y.-K. Deep learning-based automated underground cavity detection using three-dimensional ground penetrating radar. Struct. Health Monit. 2019, 19, 173–185. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Mishra, D. Using FWD deflection basin parameters for network-level assessment of flexible pavements. Int. J. Pavement Eng. 2019, 22, 1–15. [Google Scholar] [CrossRef]
- Xiong, C.; Yu, J.; Zhang, X. Use of NDT systems to investigate pavement reconstruction needs and improve maintenance treatment decision-making. Int. J. Pavement Eng. 2021, 1–15. [Google Scholar] [CrossRef]
- Pantelidis, L. The equivalent modulus of elasticity of layered soil mediums for designing shallow foundations with the Winkler spring hypothesis: A critical review. Eng. Struct. 2019, 201, 109452. [Google Scholar] [CrossRef]



| Classification | Parameters | Expressions | Methods in This Research |
|---|---|---|---|
| Traffic data | two-way annual average daily traffic volume of 2-axle and 6-wheel and above vehicles | Measured by imaging, weighing and other equipment installed on site by the management department | |
| direction factor | |||
| lane coefficient | |||
| type distribution coefficient of m-class vehicles | |||
| total number of i axle types in m-class vehicles | |||
| total number of m-class vehicles | |||
| number of i-type axle in the j-level axle load range in m-class vehicles | |||
| single-axle axle load of i-type axle in j-level axle load range of m-class vehicles | |||
| annual average growth rate of truck traffic during the reference period | Calculated based on historical traffic data | ||
| Geometry | , L | thickness of asphalt overlay and concrete slab, length of slab | Fast detection by radar |
| Mechanical parameter | concrete layer bending modulus | Detected by falling weight deflector and backcalculated modulus | |
| equivalent elastic modulus of foundation underneath the concrete layer |
| Section | S118 TP | S118 HO | XL |
|---|---|---|---|
| Type | Rigid | Rigid with asphalt overlay | Rigid |
| Grade | First class | First class | Highway |
| Length/km | 5 | 5 | 5 |
| Age/a | 26 | 27 | 22 |
| Structure combination | Concrete layer 28 cm + cement stabilized base 24 cm + subgrade | Asphalt overlay 3 cm + concrete layer 25 cm + gravel layer 50 cm + subgrade | Concrete layer 28 cm + limestone stabilized base 20 cm + gravel layer 20 cm + subgrade |
| Parameters | S118 TP | S118 HO | XL |
|---|---|---|---|
| 25,780 | 16,593 | 48,956 | |
| 0.5 | 0.6 | 0.55 | |
| 1 | 1 | 0.7 | |
| 1.5% | 1.2% | 7.0% |
| Type of Vehicle | S118 TP | S118 HO | XL |
|---|---|---|---|
| 2 | 17.80 | 28.90 | 22.00 |
| 3 | 33.00 | 43.80 | 23.30 |
| 4 | 3.40 | 5.50 | 2.70 |
| 5 | 0.00 | 0.00 | 0.00 |
| 6 | 12.50 | 9.40 | 8.30 |
| 7 | 4.40 | 2.00 | 7.50 |
| 8 | 9.10 | 4.60 | 17.10 |
| 9 | 10.60 | 3.40 | 8.50 |
| 10 | 8.50 | 2.30 | 10.60 |
| 11 | 0.70 | 0.10 | 0.00 |
| Type of Vehicle | S118 TP | S118 HO | XL | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Single Axle Single Tire | Single Axle Double Tire | Double Shaft | Triple Shaft | Single Axle Single Tire | Single Axle Double Tire | Double Shaft | Triple Shaft | Single Axle Single Tire | Single Axle Double Tire | Double Shaft | Triple Shaft | |
| 2 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.99 | 0.01 | 0.00 |
| 3 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 |
| 4 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| 5 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 1.00 |
| 6 | 2.00 | 0.38 | 0.62 | 0.00 | 2.00 | 0.43 | 0.57 | 0.00 | 2.00 | 0.50 | 0.50 | 0.00 |
| 7 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| 8 | 1.00 | 0.56 | 0.89 | 0.56 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 0.93 | 0.14 | 0.93 |
| 9 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 |
| 10 | 2.00 | 1.00 | 0.04 | 0.96 | 2.00 | 1.00 | 0.09 | 0.91 | 2.00 | 1.00 | 0.15 | 0.85 |
| 11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Intervals | Physical State | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S118 TP | S118 HO | XL | S118 TP | S118 HO | XL | S118 TP | S118 HO | XL | S118 HO | ||
| Less than 0.1a | 27,430 | 27,465 | 36,813 | 377 | 296 | 424 | 26.0 | 24.1 | 26.3 | 2.9 | Obvious physical defects such as voids, broken slabs, severe reflective cracks in overlay and pumping, etc. |
| 0.1a–1a | 32,006 | 33,873 | 49,915 | 338 | 296 | 414 | 26.9 | 24.7 | 26.5 | 3.3 | Slight physical defects such as voids, broken slabs, severe reflective cracks in overlay and pumping, etc. |
| 1a–5a | 32,992 | 35,688 | 51,498 | 314 | 305 | 407 | 27.3 | 24.9 | 26.6 | 3.5 | Uneven subgrade settlement under the slab, reflective cracks in overlay, etc. |
| 5a–10a | 34,455 | 37,440 | 52,933 | 327 | 305 | 384 | 27.2 | 24.8 | 26.3 | 3.2 | Slight reflective cracks in overlay, etc. |
| 10a–15a | 33,549 | 37,676 | 53,557 | 309 | 309 | 369 | 28.0 | 25.0 | 26.5 | 3.4 | Intact |
| More than 15a | 37,190 | 39,961 | 55,540 | 321 | 295 | 429 | 28.3 | 25.3 | 27.0 | 3.3 | Intact |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, X.; Tan, W.; Xiong, C.; Qiu, Z.; Yu, J.; Wang, D.; Wei, X.; Li, W.; Wang, Z. A Fast and Non-Destructive Prediction Model for Remaining Life of Rigid Pavement with or without Asphalt Overlay. Buildings 2022, 12, 868. https://doi.org/10.3390/buildings12070868
Hong X, Tan W, Xiong C, Qiu Z, Yu J, Wang D, Wei X, Li W, Wang Z. A Fast and Non-Destructive Prediction Model for Remaining Life of Rigid Pavement with or without Asphalt Overlay. Buildings. 2022; 12(7):868. https://doi.org/10.3390/buildings12070868
Chicago/Turabian StyleHong, Xuan, Weilin Tan, Chunlong Xiong, Zhixiong Qiu, Jiangmiao Yu, Duanyi Wang, Xiaopeng Wei, Weixiong Li, and Zhaodong Wang. 2022. "A Fast and Non-Destructive Prediction Model for Remaining Life of Rigid Pavement with or without Asphalt Overlay" Buildings 12, no. 7: 868. https://doi.org/10.3390/buildings12070868






