Applicability of Solid Solution Heat Treatments to Aluminum Foams
Abstract
:1. Introduction
2. Experimental Section
2.1. Preparation of Aluminum Foams
| Diameter/Height (mm/mm) | Foams Density (kg·m−3) | Solid Cylinders | |||
|---|---|---|---|---|---|
| 40/40 | 420 | 660 | 900 | 1200 | Yes |
| 50/50 | 670 | Yes | |||
| 60/60 | 650 | Yes | |||
| 70/70 | 690 | Yes | |||
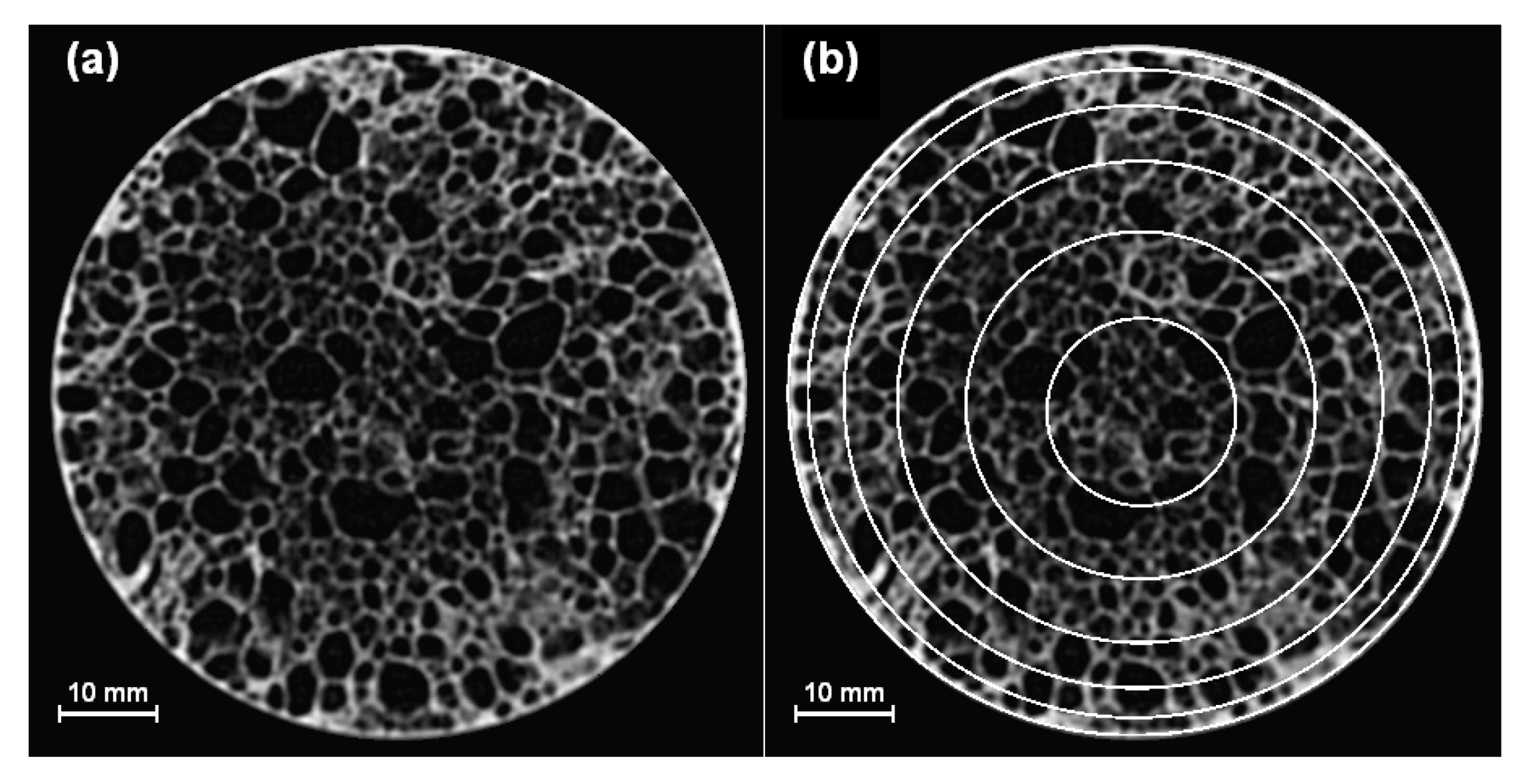
2.2. Mesoscale Density Analysis
 .
.
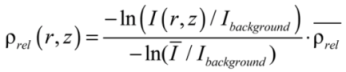
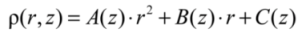
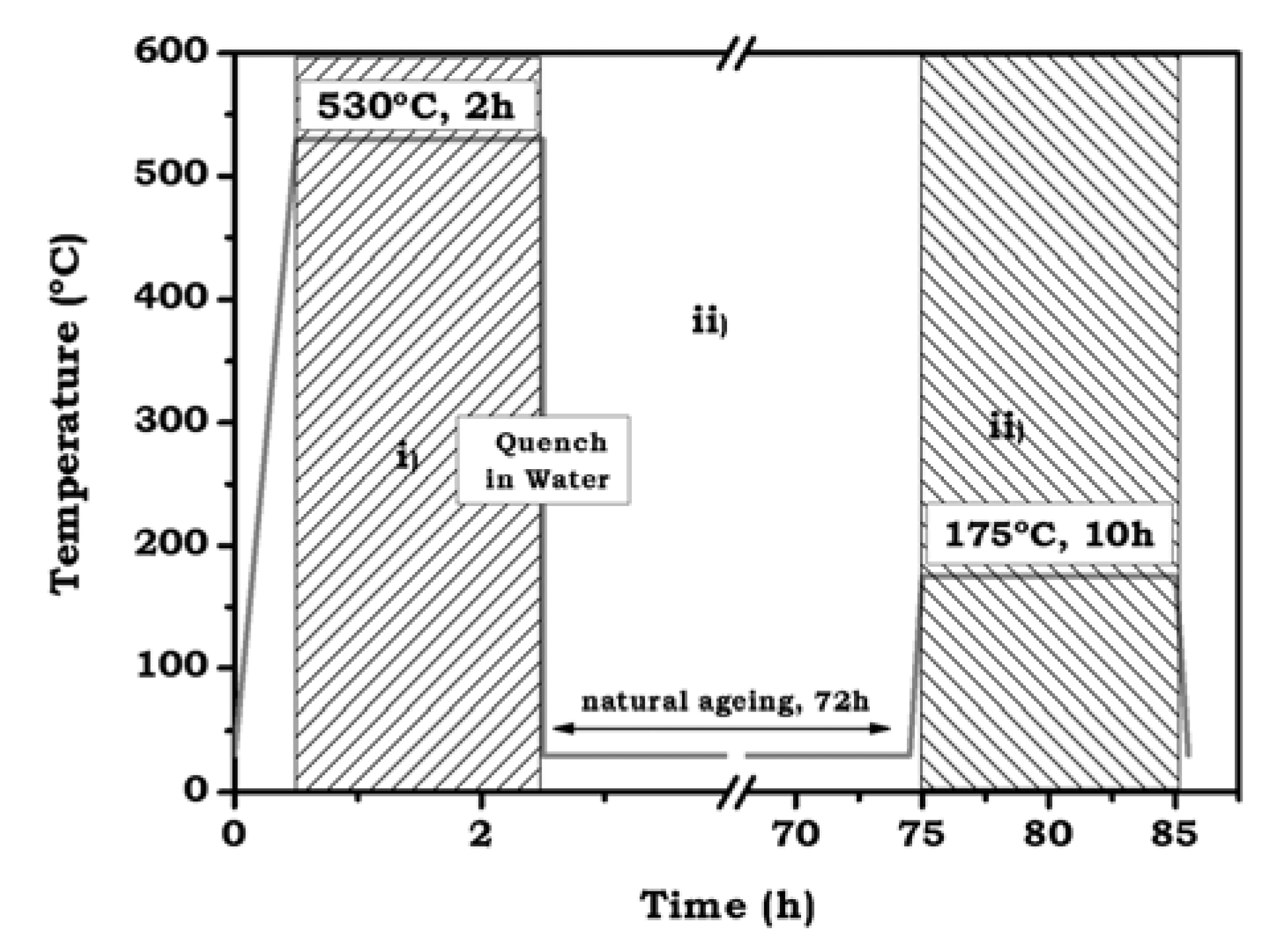
2.3. Heat Treatment and Temperature Measurement
- The specimen is introduced into a pre-heated furnace at 530 °C for 2 h, allowing the solid solution to be formed.
- Sample is extracted from the furnace and rapidly quenched in cold water (~25 °C). Thus, the previous state is stabilized at room temperature, obtaining a supersaturated solid solution. The sample is then kept for 72 h at room temperature in order to promote natural ageing.
- Lastly the sample is introduced into a pre-heated furnace at 175 °C for 10 h (artificial ageing) leading to the formation of precipitates in fine dispersion.
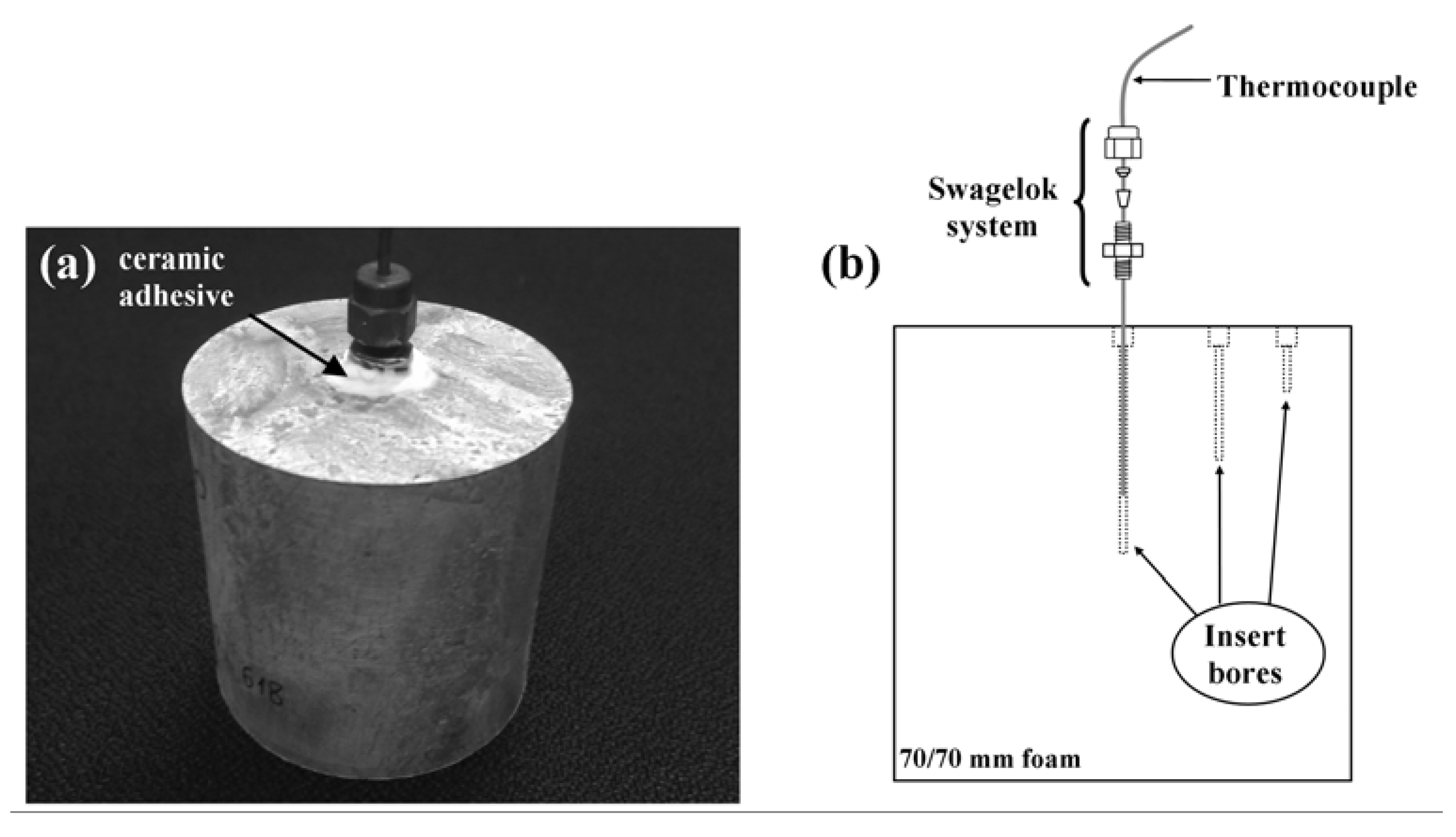
2.4. Heat Transfer Modeling
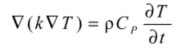
 ) with the external medium, at a certain temperature Text, takes place via a combination of different mechanisms that, in practice, are normally represented by an overall heat transfer coefficient, h, as expressed in Equation 4.Values for this parameter are typically in the range of 10–100 W/m2 K for air and between 500–10000 W/m2 K when using water as external medium [28]. Therefore, vales of the four parameters (k, ρ, CP and h) are need for the modeling calculations.
) with the external medium, at a certain temperature Text, takes place via a combination of different mechanisms that, in practice, are normally represented by an overall heat transfer coefficient, h, as expressed in Equation 4.Values for this parameter are typically in the range of 10–100 W/m2 K for air and between 500–10000 W/m2 K when using water as external medium [28]. Therefore, vales of the four parameters (k, ρ, CP and h) are need for the modeling calculations.
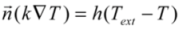
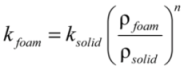
2.5. Microhardness Tests
3. Results and Discussion
3.1. Cellular Structure and Density Distribution
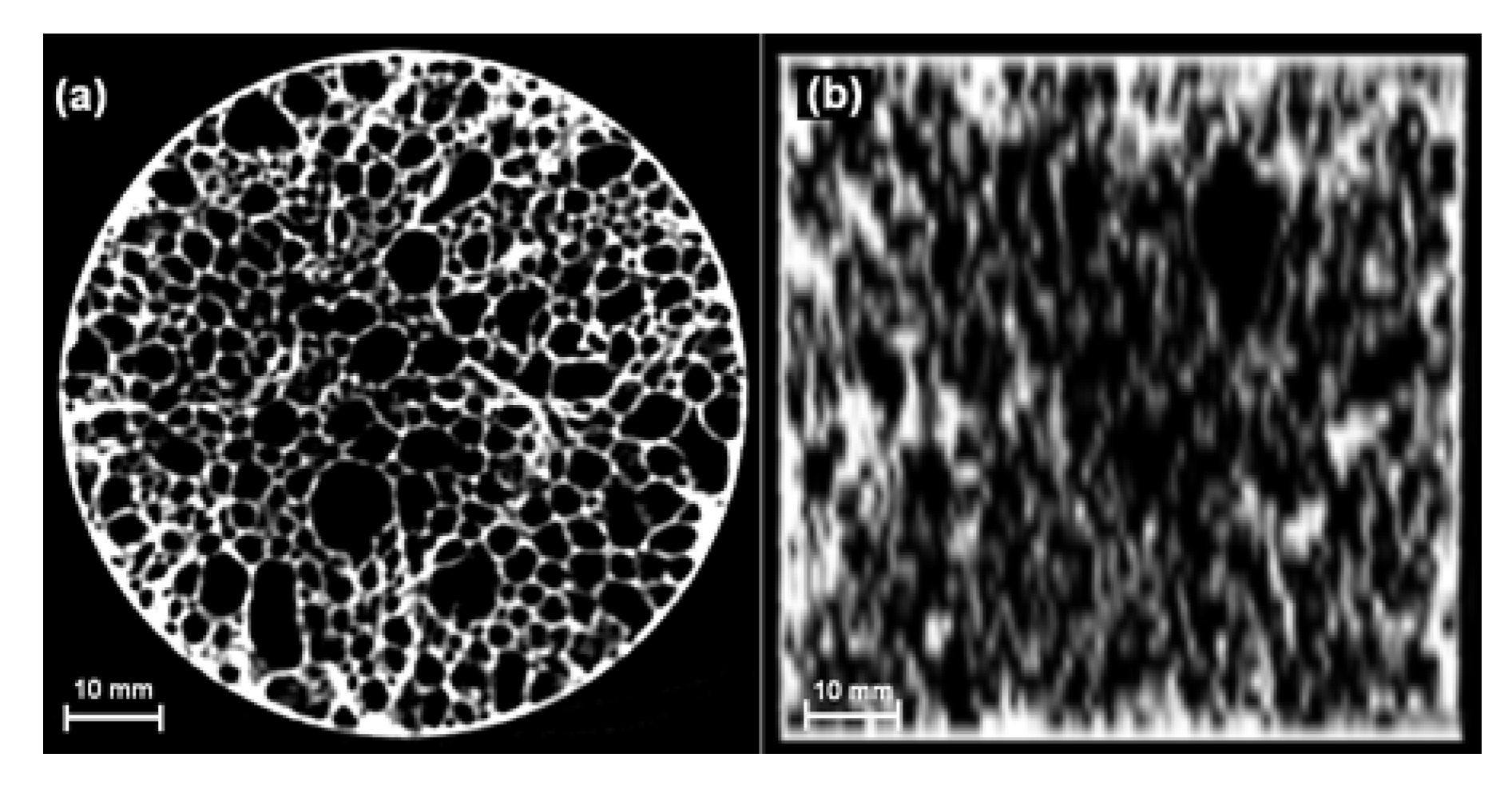

| Diameter/Height (mm/mm) | Experimental density (kg·m−3) | Computed density (kg·m−3) | Percentage difference (%) |
|---|---|---|---|
| 40/40 | 420 | 450 | +7.1 |
| 40/40 | 660 | 690 | +4.5 |
| 40/40 | 900 | 840 | −6.7 |
| 40/40 | 1200 | 1120 | −6.7 |
| 50/50 | 670 | 720 | +7.5 |
| 60/60 | 650 | 700 | +7.7 |
| 70/70 | 690 | 670 | −2.9 |
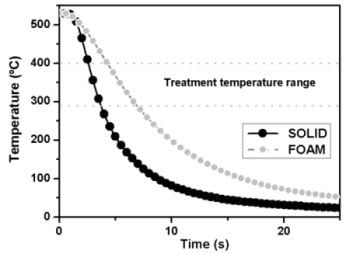
3.2. Temperature Evolution During the Quenching Process
3.2.1. Solid Cylinders
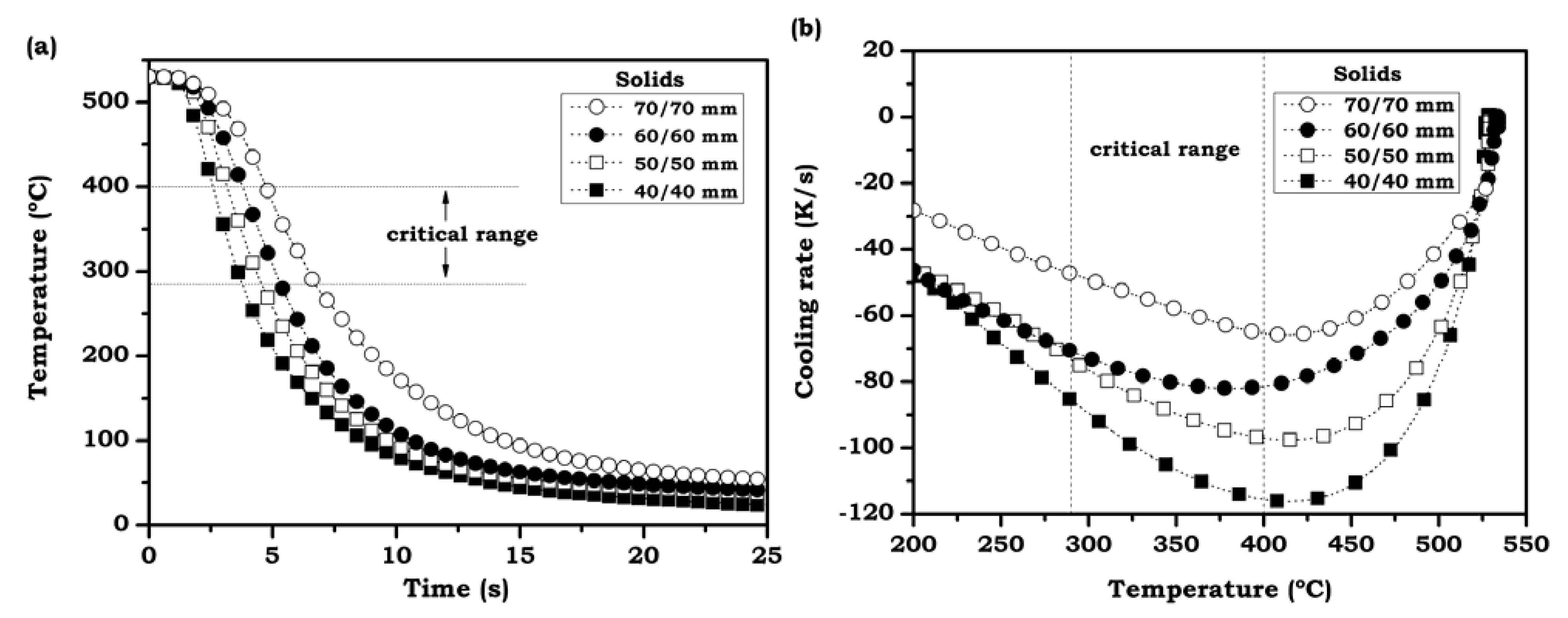
3.2.2. Foamed Cylinders

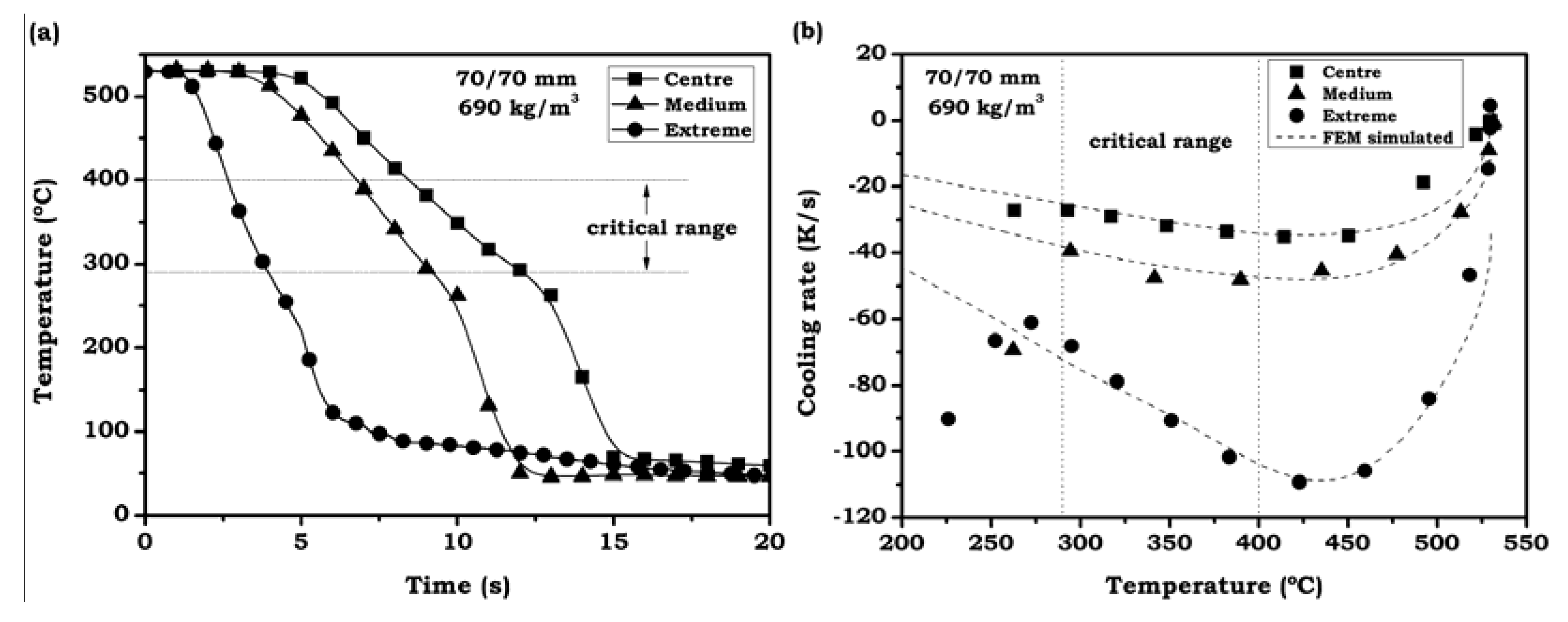
3.2.3. Average Cooling Velocities in the Critical Range

3.2.4. Water Ingression Inside the Foams
3.3. FEM Simulation
3.3.1. Solid Cylinders Verification

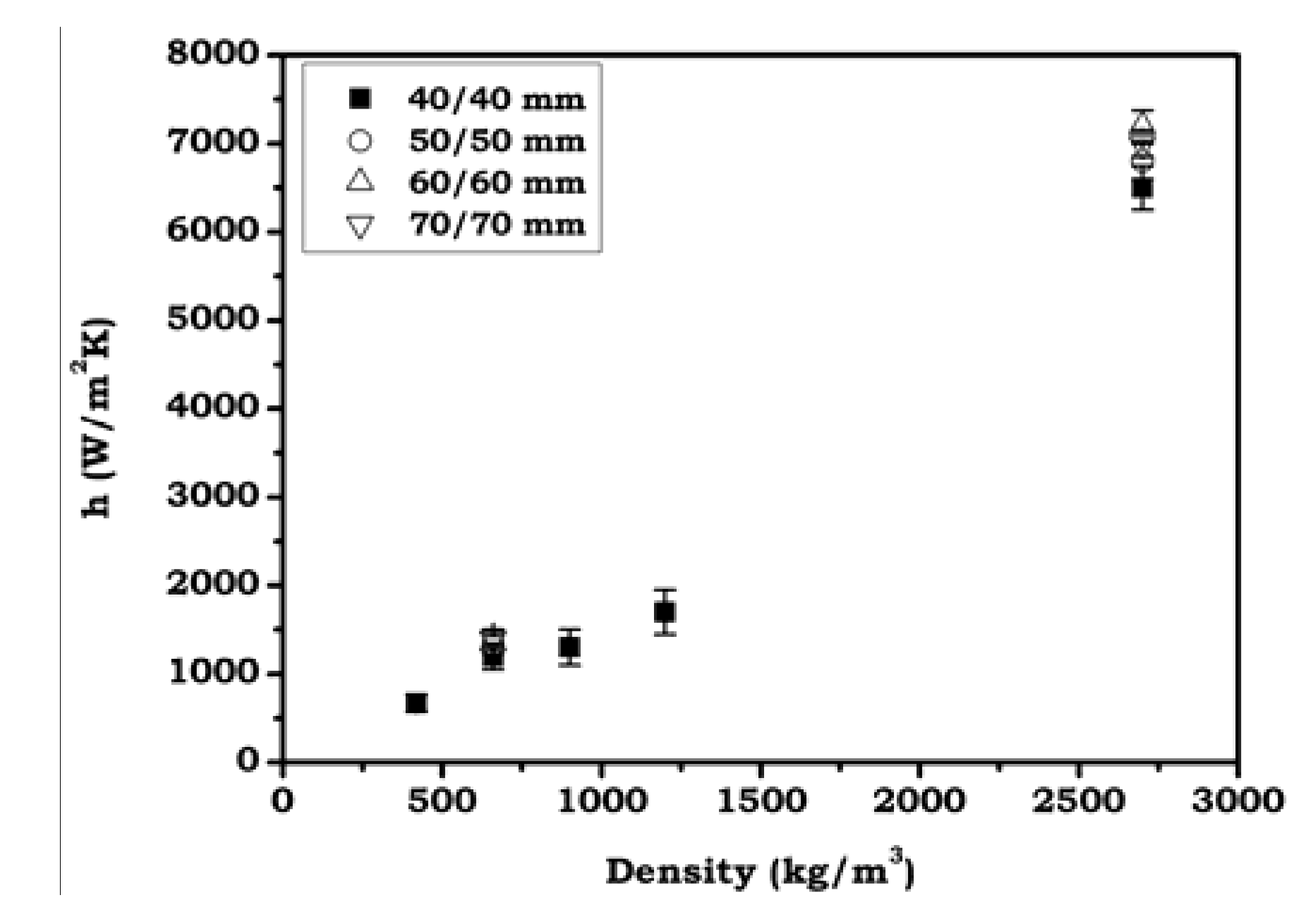
3.3.2. Heat Transfer Coefficients
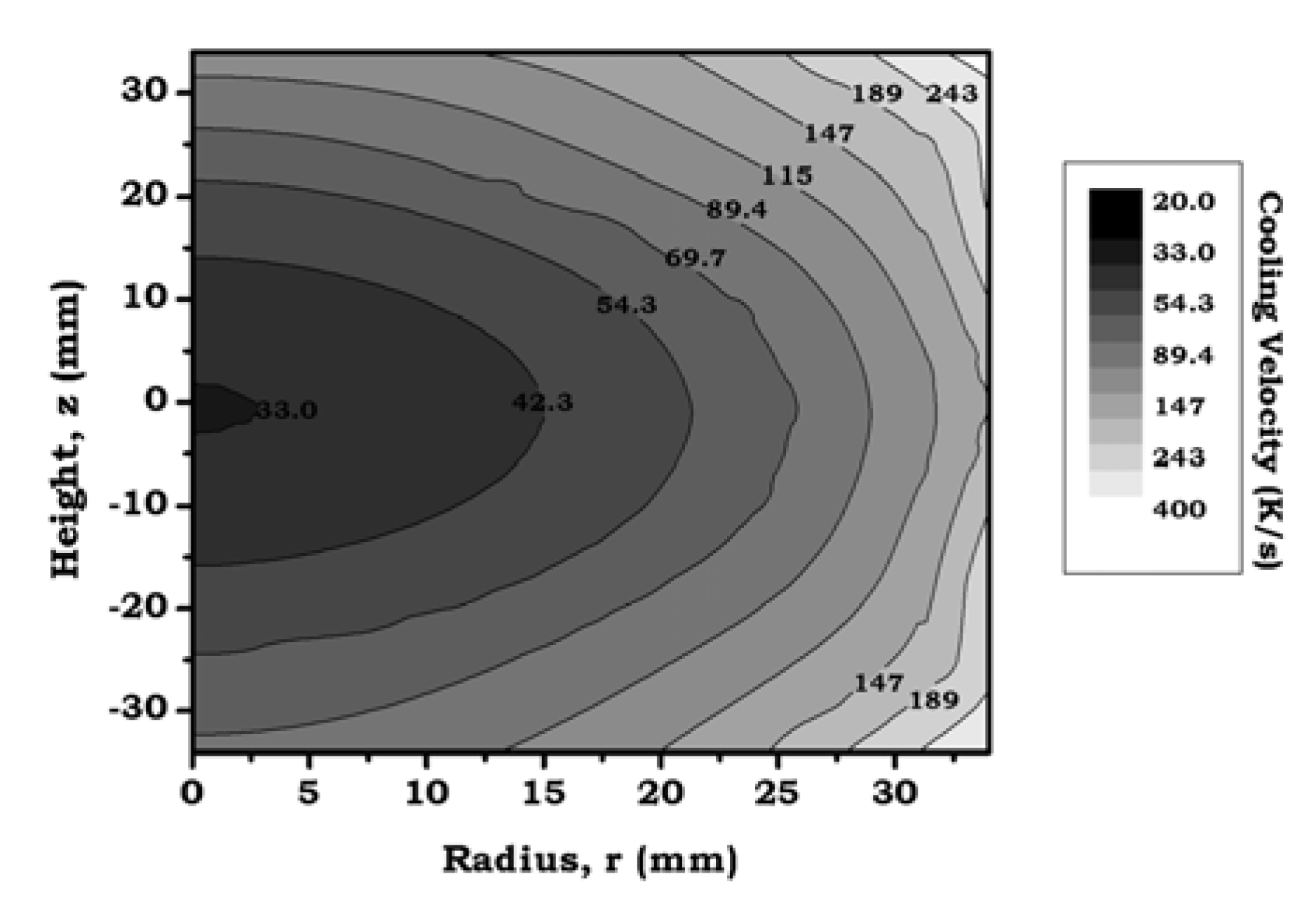
3.3.3. Temperature Distribution and Temporal Evolution
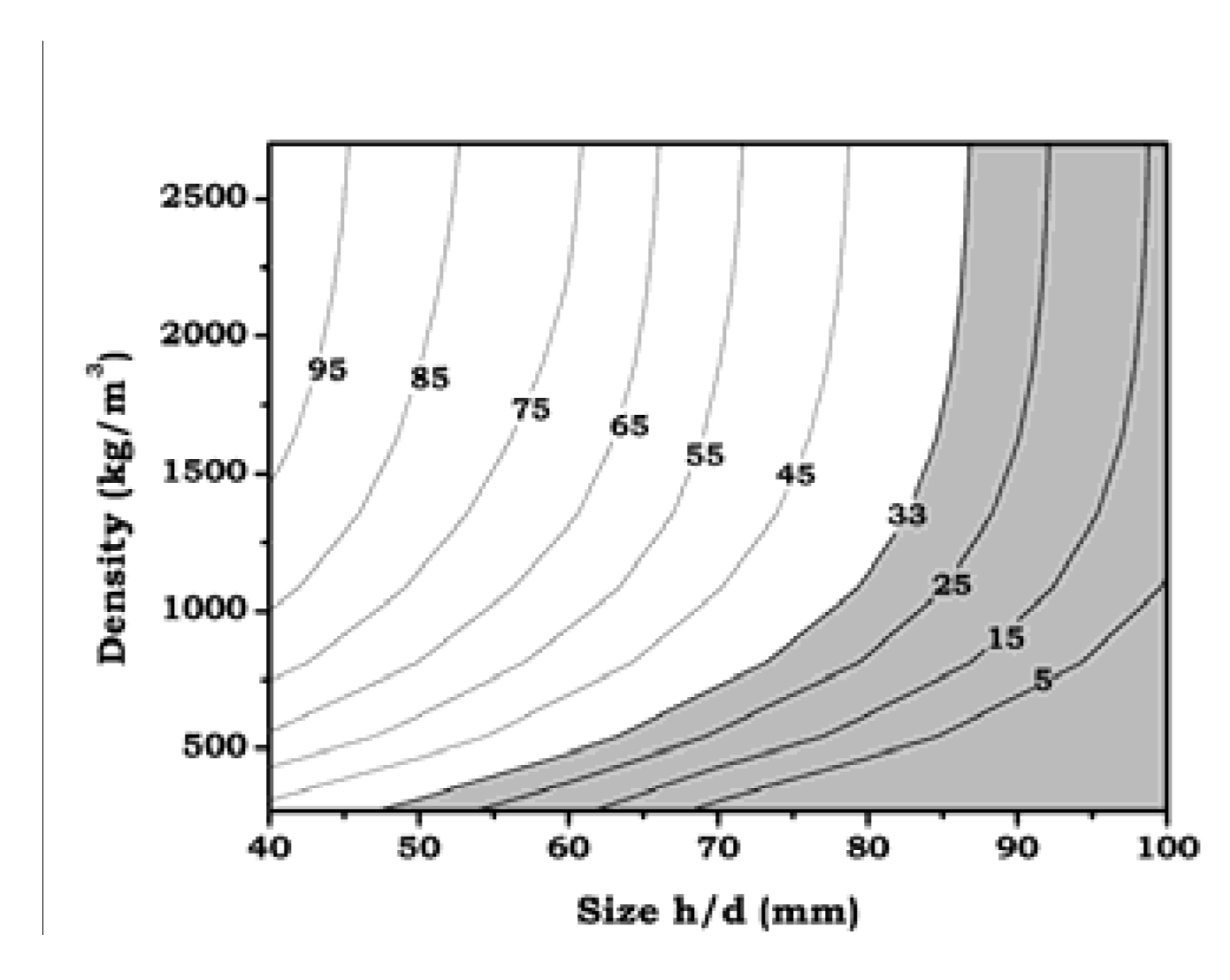
3.3.4. Treatability
3.4. Microhardness Measurements

4. Conclusions
- The developed simulation model has been able to reproduce the experimental temperature evolution inside the foams during the quenching process. To this end, the model must consider the real density distribution -for example by using the SSDD methodology-, otherwise the temperature evolution could only be reproduced for the inner regions.
- The observed water infiltration during the quenching reveals the presence of defects –perforated cell walls– in the cellular structure that can clearly influence the process and should be considered in future modeling. This effect was not directly considered in the present FEM model but was overcome thanks to the IHCP iterative methodology used.
- The lower cooling rates exhibit by Al foams in comparison to solids can be explain in terms of: (i) The increased thermal resistance due to the lower density, the possible inhomogeneities in the inner structure and the small defects like cell wall cracks; (ii) The completely different boundary conditions in the case of foams due to the skin rugosity and internal defects (water infiltration through cracks in cell walls), that change the interface between the sample and the external medium. As a consequence of this, the calculated effective values for h, using the proposed model, have shown to be 3.5 to 6 times lower for aluminum foams (~1500 W/m2·K) in comparison to solid samples (~7000 W/m2·K).
- Both predictions and experimental data confirm the existence of certain limits for a complete treatment of foamed aluminum. In one of the studied cases (70/70 mm foam) it was possible to correlate the simulation predictions with the experimental microhardness profile, confirming the limit of 33 K/s in the critical temperature range for the selected alloy. Based on this, an extended prediction has been proposed for foams of different density and size.
Acknowledgments
References
- Banhart, J. Manufacture, characterization and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Nosko, M.; Simancik, F.; Florek, R. Reproducibility of aluminum foam properties: Effect of precursor distribution on the structural anisotropy and the collapse stress and its dispersion. Mater. Sci. Eng. A 2010, 527, 5900–5908. [Google Scholar] [CrossRef]
- Yu, C.J.; Eifert, H.H.; Banhart, J.; Baumeister, J. Metal foaming by a powder metallurgy method: Production, properties and applications. Mat. Res. Innov. 1998, 2, 181–188. [Google Scholar] [CrossRef]
- Baumgärtner, F.; Duarte, I.; Banhart, J. Industrialization of powder compact foaming process. Adv. Eng. Mater. 2000, 2, 168–174. [Google Scholar] [CrossRef]
- McCullough, K.Y.G.; Fleck, N.A.; Ashby, M.F. Uniaxial stress-strain behaviour of aluminium alloy foams. Acta Mater. 1999, 47, 2323–2330. [Google Scholar] [CrossRef]
- Mukherjee, M.; Garcia-Moreno, F.; Banhart, J. Defect generation during solidification of aluminium foams. Scr. Mater. 2010, 63, 235–238. [Google Scholar] [CrossRef]
- Simone, A.E.; Gibson, L.J. The effects of cell face curvature and corrugations on the stiffness and strength of metallic foams. ActaMater. 1998, 46, 3929–3935. [Google Scholar]
- Olurin, O.B.; Fleck, N.A.; Ashby, M.F. Deformation and fracture of aluminium foams. Mater. Sci. Eng. A 2000, 291, 136–146. [Google Scholar] [CrossRef]
- Seeliger, H.W. Manufacture of aluminum foam sandwich (AFS) components. Adv. Eng. Mater. 2002, 4, 753–758. [Google Scholar] [CrossRef]
- Banhart, J.; Seeliger, H.W. Aluminium foam sandwich panels: Manufacture, metallurgy and applications. Adv. Eng. Mater. 2008, 10, 793–802. [Google Scholar] [CrossRef]
- Simancik, F.; Lucan, L.; Jerz, J. Reinforced Aluminium Foams. In Cellular Metals and Metal Foaming Technology; Banhart, J., Ashby, M.F., Fleck, N.A., Eds.; MIT-Verlag: Bremen, Germany, 2001; pp. 365–368. [Google Scholar]
- Solorzano, E.; Rodriguez-Perez, M.A.; Reglero, J.A.; de Saja, J.A. Mechanical behaviour of internal reinforced aluminium foams. Adv. Eng. Mater. 2007, 9, 955–958. [Google Scholar]
- Helwig, H.M.; Garcia-Moreno, F.; Banhart, J. A study of Mg and Cu additions on the foaming behaviour of Al–Si alloys. J. Mater. Sci. 2011, 46, 5227–5236. [Google Scholar] [CrossRef]
- Lehmhus, D.; Banhart, J.; Rodrigue-Perez, M.A. Adaptation of aluminium foam properties by means of precipitation hardening. Mater. Sci. Tech. 2002, 18, 474–479. [Google Scholar] [CrossRef]
- Lehmhus, D.; Marschner, C.; Banhart, J.; Bomas, H. Influence of heat treatment on compression fatigue of aluminium foams. J. Mater. Sci. 2002, 37, 3447–3451. [Google Scholar] [CrossRef]
- Lehmhus, D.; Banhart, J. Properties of heat-treated aluminium foams. Mater. Sci. Eng. A 2003, 349, 98–110. [Google Scholar]
- Davis, J.R. Alumiumand Aluminum Alloys; ASM International: Materials Park, OH, USA, 1993. [Google Scholar]
- Dorward, R.C.; Bouvier, C. A rationalization of factors affecting strength, ductility and toughness of AA6061-type Al–Mg–Si–(Cu) alloys. Mater. Sci. Eng. A 1998, 254, 33–44. [Google Scholar] [CrossRef]
- Solorzano, E.; Reglero, J.A.; Rodriguez-Perez, M.A.; de Saja, J.A.; Rodriguez-Mendez, M.L. Improvement of the foaming process for 4045 and 6061 aluminium foams by using the Taguchi methodology. J. Mater. Sci. 2007, 42, 7227–7238. [Google Scholar] [CrossRef]
- Kriszt, B.; Martin, U.; Mosler, U.; Maire, E.; Degischer, H.P.; Jottar, A. Characterization of Cellular Metals. In Handbook of Cellular Metals: Production, Processing, Applications; Degischer, H.P., Kriszt, B., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2002; pp. 127–178. [Google Scholar]
- Ohgaki, T.; Toda, H.; Kobayashi, M.; Uesugi, K.; Niinomi, M.; Akahori, T.; Makii, K.; Agura, Y. In situ high-resolution X-ray CT observation of compressive and damage behaviour of aluminium foams by local tomography technique. Philos. Mag. 2006, 86, 4417–4438. [Google Scholar] [CrossRef]
- Solorzano, E.; Rodriguez-Perez, M.A.; Reglero, J.A.; de Saja, J.A. Density gradients in aluminium foams: Characterisation by computed tomography and measurements of the effective thermal conductivity. J. Mater. Sci. 2007, 42, 2557–2564. [Google Scholar]
- Abramoff, M.D.; Magelhaes, P.J.; Ram, S.J. Image processing with image. J. Bioph. Int. 2004, 11, 36–42. [Google Scholar]
- Solorzano, E.; Escudero, J.; Lazaro, J.; Rodriguez-Perez, M.A.; de Saja, J.A. Critical Cooling Velocity Maps for Thermal Hardening Treatments in aluminium Foams. In Porous Metal and Metallic Foams; Lefebvre, L.P., Banhart, J., Dunand, D.C., Eds.; DEStech Publications: Lancaster, PA, USA, 2008; pp. 505–508. [Google Scholar]
- Garcia-Moreno, F.; Fromme, M.; Banhart, J. Real-time X-ray radioscopy on metallic foams using a compact micro-focus source. Adv. Eng. Mater. 2004, 6, 416–420. [Google Scholar] [CrossRef]
- Gergely, V.; Clyne, T.W. Drainage in standing liquid metal foams: Modelling and experimental observations. ActaMater. 2004, 52, 3047–3058. [Google Scholar]
- Lu, T.J.; Chen, C. Thermal transport and fire retardance properties of cellular aluminium alloys. ActaMater. 1999, 47, 1469–1485. [Google Scholar]
- Holman, J.P. Heat Transfer; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Fiedler, T.; Solorzano, E.; Öchsner, A. Numerical and experimental analysis of the thermal conductivity of metallic hollow sphere structures. Mater. Lett. 2008, 62, 1204–1207. [Google Scholar]
- Solorzano, E.; Rodriguez-Perez, M.A.; Lazaro, J.; de Saja, J.A. Influence of solid phase conductivity and cellular structure on the heat transfer mechanisms of cellular materials: Diverse case Studies. Adv. Eng. Mater. 2009, 11, 818–824. [Google Scholar]
- Lazaro, J.; Escudero, J.; Solorzano, E.; Rodriguez-Perez, M.A.; de Saja, J.A. Heat transport in closed cell aluminium foams: Application notes. Adv. Eng. Mater. 2009, 11, 825–831. [Google Scholar] [CrossRef]
- Hugo, J.M.; Topin, F. Metal Foams Design for Heat Exchangers: Structure and Effectives Transport. In Heat and Mass Transfer in Porous Media; Delgado, J.M.P.Q., Ed.; Springer: Berlin, Germany, 2012; pp. 219–244. [Google Scholar]
- Solorzano, E.; Reglero, J.A.; Rodriguez-Perez, M.A.; Lehmhus, D.; Wichmann, M.; de Saja, J.A. An experimental study on the termal conductivity of aluminium foams by using the transient plane source method. Int. J. Heat Mass Tran. 2008, 51, 6259–6267. [Google Scholar] [CrossRef]
- Solorzano, E.; Rodriguez-Perez, M.A.; de Saja, J.A. Thermal conductivity of cellular metals measured by the transient plane source method. Adv. Eng. Mater. 2008, 10, 596–602. [Google Scholar]
- Cverna, F. Thermal Properties of Metals; ASM International: Materials Park, OH, USA, 2002; pp. 221–482. [Google Scholar]
- Chen, H.T.; Wu, X.Y. Investigation of heat transfer coefficients in two-dimensional inverse heat conduction problems using the hybrid inverse scheme. Int. J. Num. Method Eng. 2008, 73, 107–122. [Google Scholar] [CrossRef]
- Grysa, K. Iverse Heat Conduction Problems. In Heat Conduction: Basic Research; Vikhrenko, V.S., Ed.; InTech: Rikeja, Croatia, 2011; pp. 3–36. [Google Scholar]
- ASTM E384-11e1 Standard Test Method for Knoop and Vickers Hardness of Materials. Available online: http://www.astm.org/Standards/E384.htm (accessed on 13 December 2012).
- Hufnagel, W. Manual del Aluminio; Reverté: Barcelona, Spain, 1992; p. 520. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lázaro, J.; Solórzano, E.; Escudero, J.; De Saja, J.A.; Rodríguez-Pérez, M. Applicability of Solid Solution Heat Treatments to Aluminum Foams. Metals 2012, 2, 508-528. https://doi.org/10.3390/met2040508
Lázaro J, Solórzano E, Escudero J, De Saja JA, Rodríguez-Pérez M. Applicability of Solid Solution Heat Treatments to Aluminum Foams. Metals. 2012; 2(4):508-528. https://doi.org/10.3390/met2040508
Chicago/Turabian StyleLázaro, Jaime, Eusebio Solórzano, Javier Escudero, Jose Antonio De Saja, and Miguel Rodríguez-Pérez. 2012. "Applicability of Solid Solution Heat Treatments to Aluminum Foams" Metals 2, no. 4: 508-528. https://doi.org/10.3390/met2040508