Comparative Study of Elastoplastic Constitutive Models for Deformation of Metallic Glasses
Abstract
:1. Introduction
2. Constitutive Theories
2.1. Free Volume Model
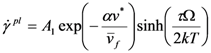
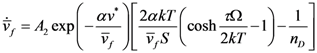
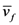 the free volume averaged by atom numbers, Ω the atomic volume, k the Boltzmann constant and T the temperature.
the free volume averaged by atom numbers, Ω the atomic volume, k the Boltzmann constant and T the temperature. 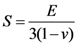 is the effective elastic modulus given by Eshelby’s solution for elastic inclusion [24]. nD is a constant related to diffusion with a value ranging between 3–10.
is the effective elastic modulus given by Eshelby’s solution for elastic inclusion [24]. nD is a constant related to diffusion with a value ranging between 3–10.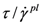 is reduced. Consequently, the material will be softened more at locations with high concentration of free volumes, which is the main reason perceived for strain localization. Note that this observation is based on the assumption that the material is viscoelastic and the deformation is more like a viscous flow than an elastic or a plastic deformation. In addition, in this model, only the shear stress τ is taken into account as the driving force of both the strain and free volume. In addition, with these two scalar functions, however, we are not able to deal with the second order stress tensor in multiaxial stress state. To simplify the problem, as shown below, idealized material models are introduced and different yield criterions are employed to give an effective stress.
is reduced. Consequently, the material will be softened more at locations with high concentration of free volumes, which is the main reason perceived for strain localization. Note that this observation is based on the assumption that the material is viscoelastic and the deformation is more like a viscous flow than an elastic or a plastic deformation. In addition, in this model, only the shear stress τ is taken into account as the driving force of both the strain and free volume. In addition, with these two scalar functions, however, we are not able to deal with the second order stress tensor in multiaxial stress state. To simplify the problem, as shown below, idealized material models are introduced and different yield criterions are employed to give an effective stress.2.2. Elastoplastic Model with von Mises Yield Criterion
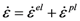
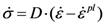
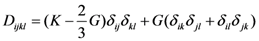 is the elastic material matrix with K the bulk modulus and G the shear modulus in an isotropic solid.
is the elastic material matrix with K the bulk modulus and G the shear modulus in an isotropic solid.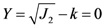
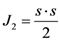 with s = σ − pI is the deviatoric stress tensor,
with s = σ − pI is the deviatoric stress tensor, 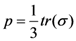 is the hydrostatic stress, and I is the identity tensor. Note here that the hydrostatic stress p has a positive sign in tension and negative in compression, unlike that used in the engineering convention. The associated flow rule is then defined by
is the hydrostatic stress, and I is the identity tensor. Note here that the hydrostatic stress p has a positive sign in tension and negative in compression, unlike that used in the engineering convention. The associated flow rule is then defined by
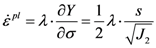
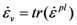 will vanish. The effective stress is defined from yield function 5 therefore as
will vanish. The effective stress is defined from yield function 5 therefore as
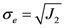
2.3. The von Mises Model Modified by Hydrostatic Stress Effect
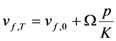
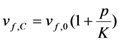
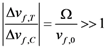 . The large difference is also confirmed recently by Guo and Li [26] in an atomistic modeling of the equation of state of a model of NiZr metallic glasses. As a modification to the von Mises model discussed in section 2.2, the free volume change will also contribute partly to the volumetric strain increment, which is assumed to follow Hooke’s law,
. The large difference is also confirmed recently by Guo and Li [26] in an atomistic modeling of the equation of state of a model of NiZr metallic glasses. As a modification to the von Mises model discussed in section 2.2, the free volume change will also contribute partly to the volumetric strain increment, which is assumed to follow Hooke’s law,
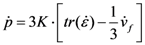
2.4. Coulomb-Mohr Model
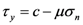
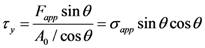
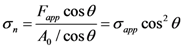
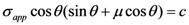
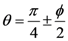
2.5. Drucker-Prager Model
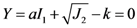
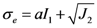
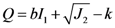
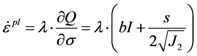
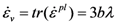 , which is not zero, provided that b ≠ 0. This property means that in the Drucker-Prager model, the dependence on hydrostatic stress will introduce an accompanying volume change during deformation, or vice versa [30]. This effect is physically consistent with the dilatational feature of the free volume theory, as well as the experimental results. Moreover, also from the data of molecular dynamics (MD) simulation, volume dilatation is believed to be the reason for shear softening [12].
, which is not zero, provided that b ≠ 0. This property means that in the Drucker-Prager model, the dependence on hydrostatic stress will introduce an accompanying volume change during deformation, or vice versa [30]. This effect is physically consistent with the dilatational feature of the free volume theory, as well as the experimental results. Moreover, also from the data of molecular dynamics (MD) simulation, volume dilatation is believed to be the reason for shear softening [12].2.6. Constitutive Equations
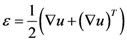
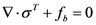
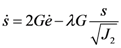
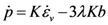
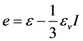 is the deviatoric part of the strain tensor with εv = tr(ε) the volumetric part of the strain.
is the deviatoric part of the strain tensor with εv = tr(ε) the volumetric part of the strain. 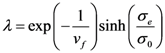
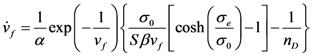
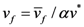 , σ0 = 2kT/Ω, and β = v* / Ω. Note that the constitutive equations derived here are for the Drucker-Prager model. By simply setting the parameters a = b = 0, the DP equations will reduce to the case of the von Mises criterion.
, σ0 = 2kT/Ω, and β = v* / Ω. Note that the constitutive equations derived here are for the Drucker-Prager model. By simply setting the parameters a = b = 0, the DP equations will reduce to the case of the von Mises criterion.3. Simulation Procedures
3.1. Three Elastoplastic Models
- (a) The von Mises model (J2 model): For the Equations 20–25, set a = b = 0, the model becomes the von Mises type.
- (b) The von Mises model plus hydrostatic stress effect (J2P model): In addition to model (a), Equations 8–10 will be also included. The procedure is that before solving Equations 20–25, we calculate the initial free volume modified by hydrostatic stress from Equations 8 and 9, then run the time integration to obtain the solutions at that time step, and finally apply Equation 10 to update the hydrostatic stress in addition.
- (c) The Drucker-Prager model (DP model): a, b ≠ 0, the hydrostatic component of stress is included in Equations 20–25.
3.2. Material Constants and Parameters
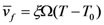 , where ξ is the thermal expansion coefficient with the value of 4.0 × 10−5 K−1 for this Zr-based BMG. Thus, after normalization,
, where ξ is the thermal expansion coefficient with the value of 4.0 × 10−5 K−1 for this Zr-based BMG. Thus, after normalization, 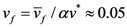 . β = v* / Ω = 0.8, the geometrical factor α = 0.105. σ0 = 2kT/Ω is used to normalize the stress with the order of 1 GPa. nD is taken to be 3.
. β = v* / Ω = 0.8, the geometrical factor α = 0.105. σ0 = 2kT/Ω is used to normalize the stress with the order of 1 GPa. nD is taken to be 3.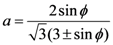
3.3. Samples and Loading
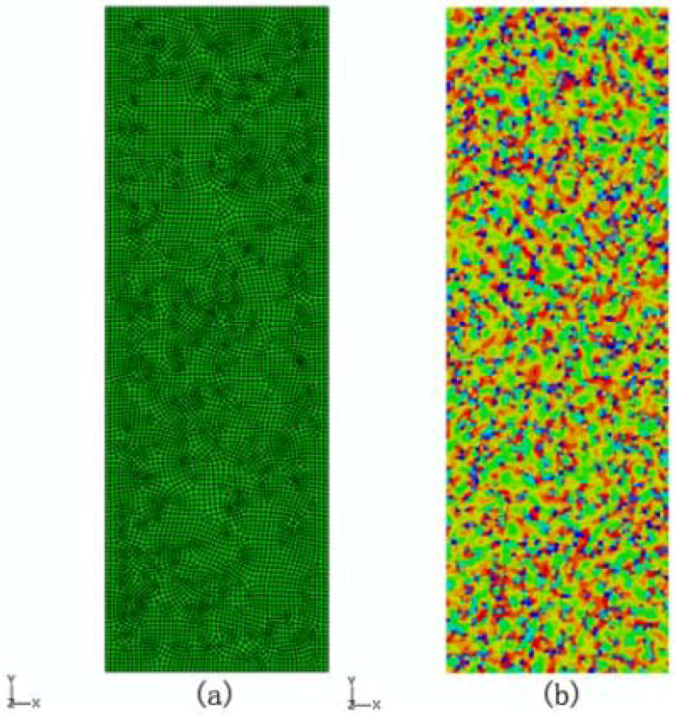
4. Results and Discussions
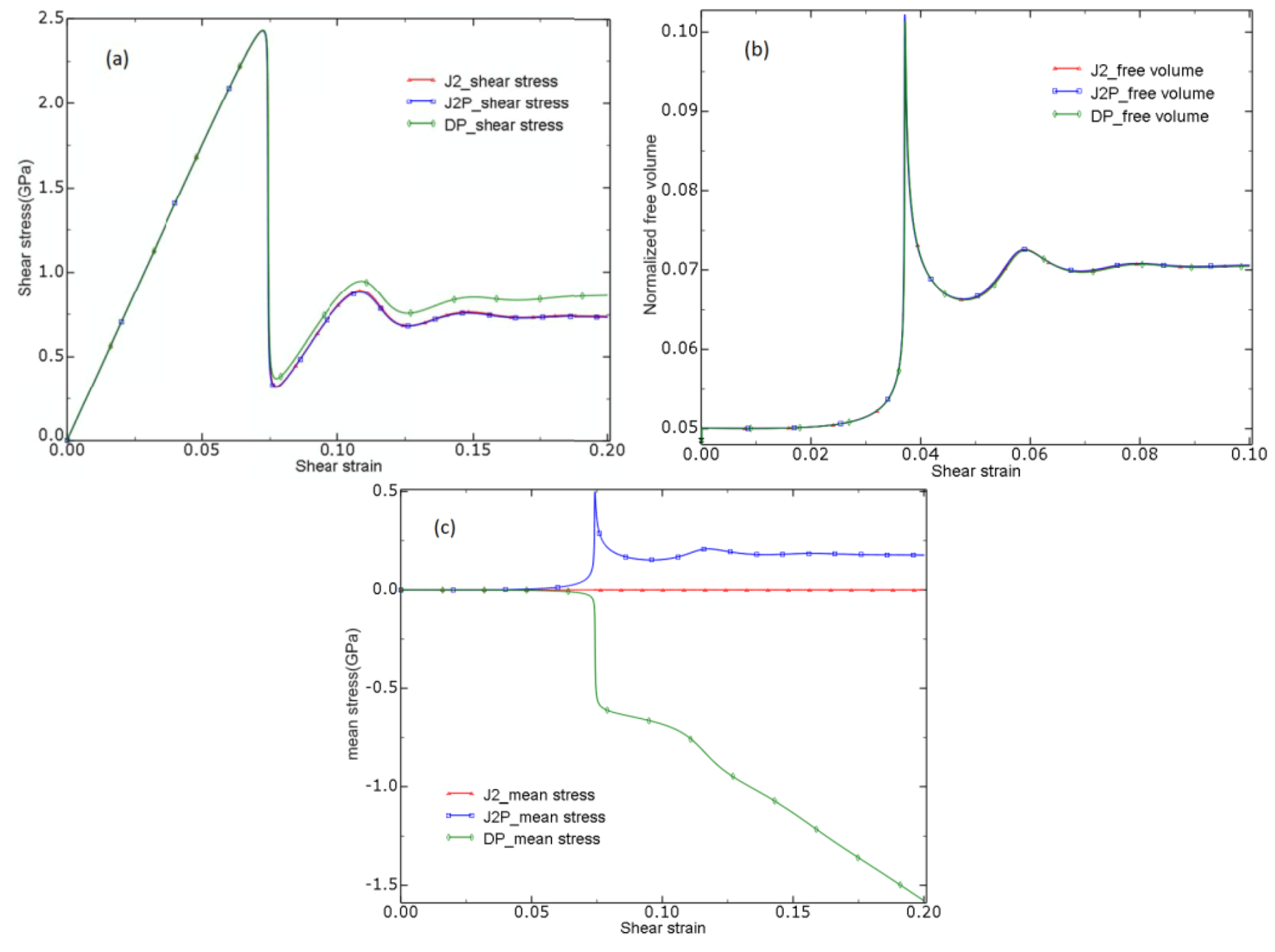
4.1.Shear-Induced Dilatation
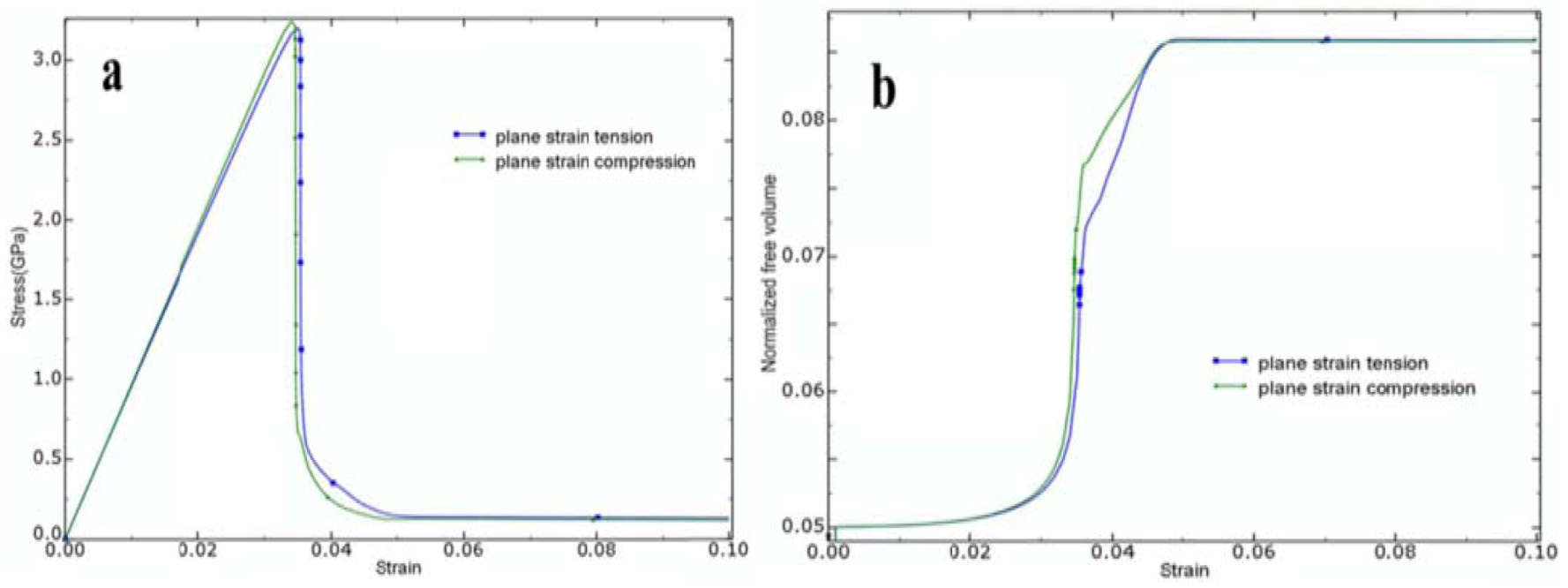
4.2. Shear Band Formation under Plane Strain Tension and Compression
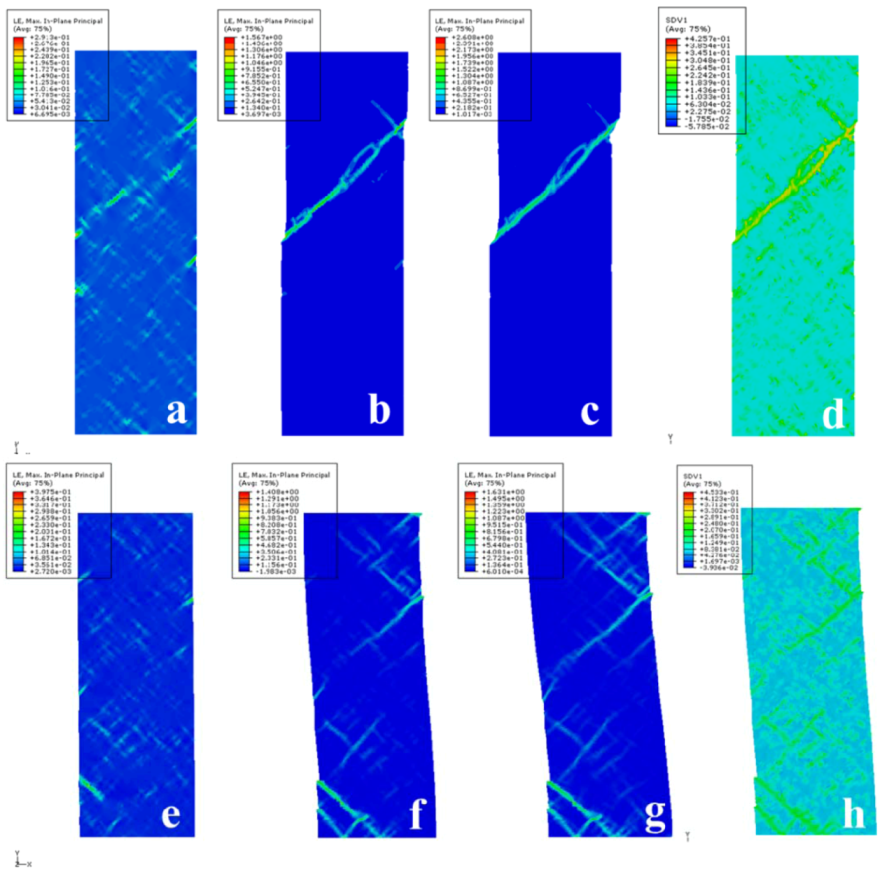
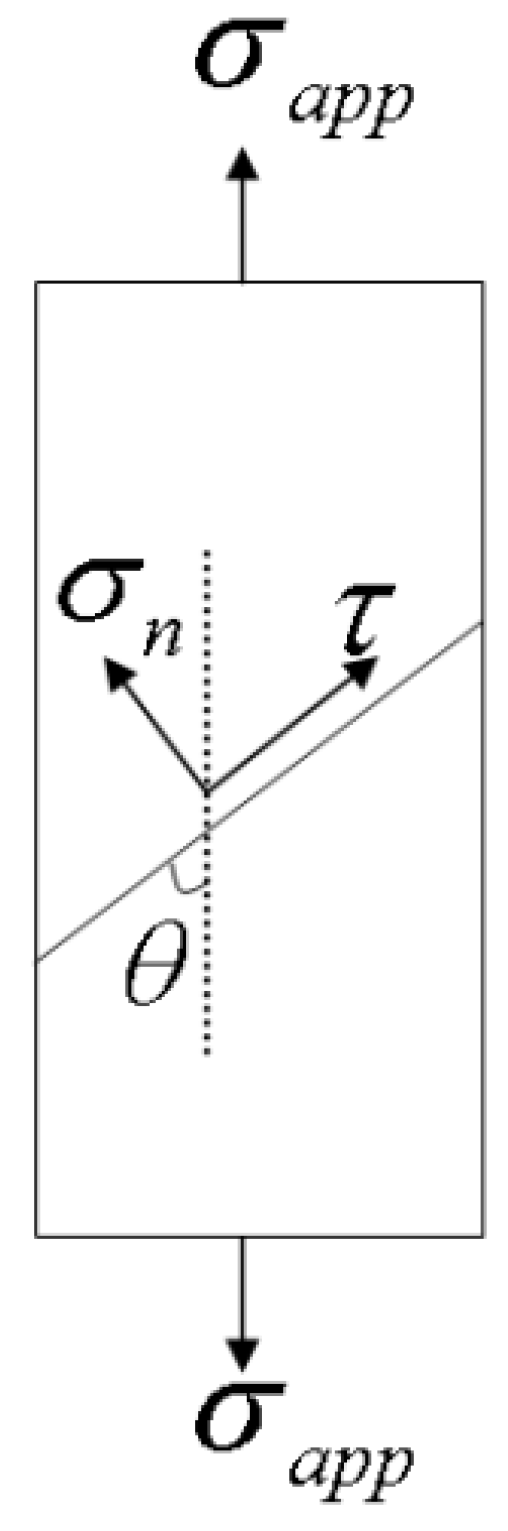
4.3. Shear Band Inclination Angles and Strength Differential Effect
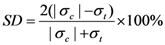
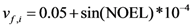
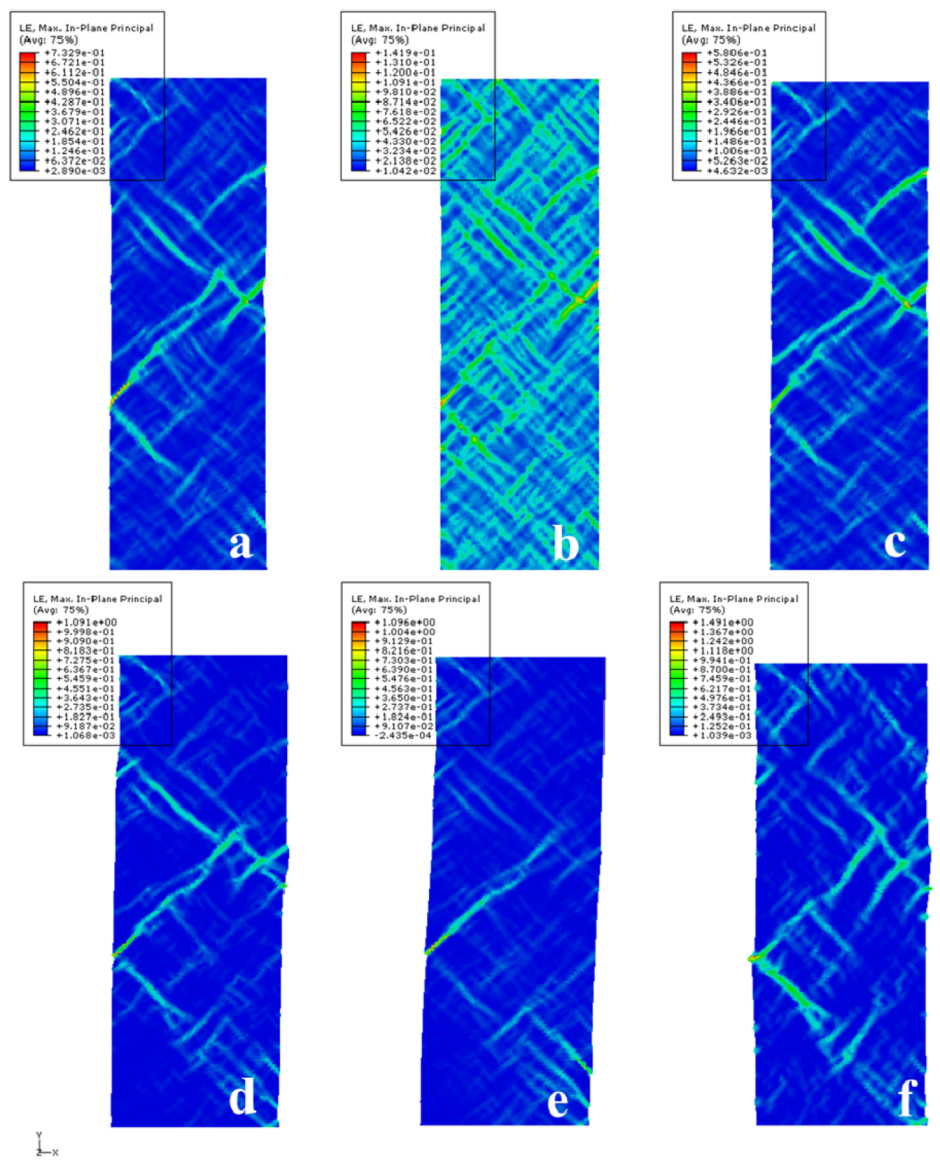
5. Conclusions
- Shear banding as the inhomogeneous deformation mode of metallic glass was first simulated by the J2 model for both plane strain tension and compression. The results show the detailed dynamic process of formation of shear bands. Starting from the randomly distributed initial free volume configuration, severe strain localization in the form of shear bands was observed when the material yields, which is accompanied with abrupt increases of free volume.
- Shear band angles and SD effect are two commonly observed phenomena. The shear band angles were first compared among the three models. The DP model gives a larger than 45° shear band angle in tension and a smaller than 45° in compression, all in agreement with experimental findings, while J2 and J2P models predicted the same 45° in both tension and compression. The results show that the shear band inclination angle change is related to the hydrostatic stress during the localized deformation of metallic glasses.
- While the J2 does not predict SD effect at all, the J2P and DP models do. The SD effect described by DP model was also found to show increasing dependence of coefficient a. The most reasonable SD (24%) corresponds to the coefficient a of the value 0.17, which agrees well with the experimental result.
Acknowledgment
Conflict of Interest
References
- Webb, T.W.; Zhu, X.H.; Aifantis, E.C. A simple method for calculating shear band angles for pressure sensitive plastic materials. Mech. Res. Commun. 1997, 24, 69–74. [Google Scholar] [CrossRef]
- Peker, A.; Johnson, W.L. A highly processable metallic glass—Zr41.2Ti13.8Cu12.5Ni10.0Be22.5. Appl. Phys. Lett. 1993, 63, 2342–2344. [Google Scholar] [CrossRef]
- Ashby, M.F.; Greer, A.L. Metallic glasses as structural materials. Scr. Mater. 2006, 54, 321–326. [Google Scholar] [CrossRef]
- Loffler, J.F. Bulk metallic glasses. Intermetallics 2003, 11, 529–540. [Google Scholar] [CrossRef]
- Conner, R.D.; Rosakis, A.J.; Johnson, W.L.; Owen, D.M. Fracture toughness determination for a beryllium-bearing bulk metallic glass. Scr. Mater. 1997, 37, 1373–1378. [Google Scholar] [CrossRef]
- Demetriou, M.D.; Launey, M.E.; Garrett, G.; Schramm, J.P.; Hofmann, D.C.; Johnson, W.L.; Ritchie, R.O. A damage-tolerant glass. Nat. Mater. 2011, 10, 123. [Google Scholar]
- Schuh, C.A.; Nieh, T.G. A nanoindentation study of serrated flow in bulk metallic glasses. Acta Mater. 2003, 51, 87–99. [Google Scholar] [CrossRef]
- Spaepen, F. Microscopic mechanism for steady-state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar]
- Argon, A.S. Plastic-deformation in metallic glasses. Acta Metall. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Hufnagel, T.C. Preface to the viewpoint set on mechanical behavior of metallic glasses. Scr. Mater. 2006, 54, 317–319. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, plasticity, and diffusion as examples of absolute reaction rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Li, Q.K.; Li, M. Atomistic simulations of correlations between volumetric change and shear softening in amorphous metals. Phys. Rev. B 2007, 75, 094101. [Google Scholar] [CrossRef]
- Li, Q.K.; Li, M. Molecular dynamics simulation of intrinsic and extrinsic mechanical properties of metallic glasses. Intermetallics 2006, 14, 1005. [Google Scholar] [CrossRef]
- Li, Q.K.; Li, M. Atomic scale characterization of shear bands in an amorphous metal. Appl. Phys. Lett. 2006, 88, 241903. [Google Scholar]
- Guo, Y.Z.; Li, M. Equation of state and topological transitions in amorphous solids under hydrostatic compression. J. Appl. Phys. 2010, 108, 113510. [Google Scholar]
- Li, Q.K.; Li, M. Effects of surface imperfections on deformation and failure of amorphous metals. Appl. Phys. Lett. 2006, 87, 031910. [Google Scholar]
- Steif, P.S. Ductile versus brittle behavior of amorphous metals. J. Mech. Phys. Solids 1983, 31, 359–388. [Google Scholar] [CrossRef]
- Huang, R.; Suo, Z.; Prevose, J.H.; Nix, W.D. Inhomogeneous deformation in metallic glasses. J. Mech. Phys. Solids 2002, 50, 1011–1027. [Google Scholar]
- Gao, Y.F. An implicit finite element method for simulating inhomogeneous deformation and shear bands of amorphous alloys based on the free-volume model. Modell. Simul. Mater. Sci. Eng. 2006, 14, 1329–1345. [Google Scholar] [CrossRef]
- Donovan, P.E. A yield criterion for Pd40Ni40P20 metallic-glass. Acta Metall. 1989, 37, 445–456. [Google Scholar] [CrossRef]
- Bruck, H.A.; Christman, T.; Rosakis, A.J.; Johnson, W.L. Quasi-static constitutive behavior of Zr41.25Ti13.75Ni10Cu12.5Be22.5 bulk amorphous-alloys. Scr. Metall. Mater. 1994, 30, 429–434. [Google Scholar]
- Lewandowski, J.J.; Lowhaphandu, P. Effects of hydrostatic pressure on the flow and fracture of a bulk amorphous metal. Philos. Mag. 2002, 82, 3427–3441. [Google Scholar] [CrossRef]
- Anand, L.; Su, C. A theory for amorphous viscoplastic materials undergoing finite deformations, with application to metallic glasses. J. Mech. Phys. Solids 2005, 53, 1362–1396. [Google Scholar]
- Eshelby, J.D. The continuum theory of lattice defects. Solid State Phys. 1956, 3, 79–144. [Google Scholar] [CrossRef]
- Flores, K.M.; Dauskardt, R.H. Mean stress effects on flow localization and failure in a bulk metallic glass. Acta Mater. 2001, 49, 2527–2537. [Google Scholar] [CrossRef]
- Guo, Y.Z.; Li, M. Atomistic simulation of a NiZr model metallic glass under hydrostatic pressure. Appl. Phys. Lett. 2009, 94, 051901. [Google Scholar] [CrossRef]
- Anand, L.; Gu, C. Granular materials: Constitutive equations and strain localization. J. Mech. Phys. Solids 2000, 48, 1701–1733. [Google Scholar] [CrossRef]
- Bowden, P.B.; Jukes, J.A. The plastic-flow of isotropic polymers. J. Mater. Sci. 1972, 7, 52–63. [Google Scholar]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar]
- Chen, W.F. Plasticity in Reinforced Concrete; J. Ross Publishing: New York, NY, USA, 1982. [Google Scholar]
- Zhao, M.; Li, M. Interpreting the change in shear band inclination angle in metallic glasses. Appl. Phys. Lett. 2008, 93, 241906. [Google Scholar] [CrossRef]
- Steif, P.S.; Spaepen, F.; Hutchinson, J.W. Strain localization in amorphous metals. Acta Metall. 1982, 30, 447–455. [Google Scholar]
- Abaqus online manual. Available online: http://www.3ds.com/products/simulia/support/documentation/ (accessed on 3 December 2012).
- Loret, B.; Prevost, J.H. Accurate numerical-solutions for drucker-prager elastic-plastic models. Comput. Method. Appl. Mech. Eng. 1986, 54, 259–277. [Google Scholar] [CrossRef]
- Hjiai, M.; Fortin, J.; de Saxce, G. A complete stress update algorithm for the non-associated Drucker-Prager model including treatment of the apex. Int. J. Eng. Sci. 2003, 41, 1109–1143. [Google Scholar] [CrossRef]
- Zhao, M.; Li, M. A constitutive theory and modeling on deviation of shear band inclination angles in bulk metallic glasses. J. Mater. Res. 2009, 24, 2688–2696. [Google Scholar] [CrossRef]
- Pampillo, C.A. Flow and fracture of amorphous alloys. J. Mater. Sci. 1975, 10, 1194. [Google Scholar] [CrossRef]
- Wright, W.J; Hufnagel, T.C.; Nix, W.D. Free volume coalescence and void formation in shear bands in metallic glass. J. Appl. Phys. 2003, 93, 1432. [Google Scholar] [CrossRef]
- Zhao, M.; Li, M. Local heating in shear banding of metallic glasses. Scr. Mater. 2011, 65, 493. [Google Scholar] [CrossRef]
- Lund, A.C.; Schuh, C.A. The Mohr-Coulomb criterion from unit shear processes in metallic glass. Intermetallics 2004, 12, 1159–1165. [Google Scholar] [CrossRef]
- Zhang, Z.F.; He, G.; Eckert, J.; Schultz, L. Fracture mechanisms in bulk metallic glassy materials. Phys. Rev. Lett. 2003, 91, 045505. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, M.; Li, M. Comparative Study of Elastoplastic Constitutive Models for Deformation of Metallic Glasses. Metals 2012, 2, 488-507. https://doi.org/10.3390/met2040488
Zhao M, Li M. Comparative Study of Elastoplastic Constitutive Models for Deformation of Metallic Glasses. Metals. 2012; 2(4):488-507. https://doi.org/10.3390/met2040488
Chicago/Turabian StyleZhao, Ming, and Mo Li. 2012. "Comparative Study of Elastoplastic Constitutive Models for Deformation of Metallic Glasses" Metals 2, no. 4: 488-507. https://doi.org/10.3390/met2040488





